Framework Torch: konfigurace neuronových sítí a použití různých typů aktivačních funkcí

30. 11. 2017

Doba čtení: 24 minut

Líbí se vám článek?
Podpořte redakci

Na úvodní článek o způsobu tvorby, tréninku, verifikace a použití neuronových sítí ve frameworku Torch dnes navážeme. Ukážeme si totiž různé možnosti konfigurací neuronových sítí a co se stane při přetrénování sítě.

Obsah

1. Framework Torch: konfigurace neuronových sítí a použití různých typů aktivačních funkcí

2. Umělá neuronová síť popsaná minule – výpočet součtu dvou reálných čísel

3. Přidání podpory pro zobrazení odhadu sítě v porovnání s očekávaným výsledkem

4. Zobrazení odhadu neuronové sítě součtu dvou čísel

5. Zlepšení odhadu sítě: vliv zvýšení počtu neuronů v prostřední (skryté) vrstvě i rozsahu trénovacích dat

6. Nastavení příliš velké míry učení neuronové sítě

7. Ukázka nastavení míry učení na hodnotu 0,15

8. Ukázka nastavení míry učení na hodnotu 0,25

9. Grafické zobrazení odhadu sítě počítající zobecněný xor

10. Dvě skryté vrstvy neuronů

11. Jak se projeví přidání další skryté vrstvy do neuronové sítě?

12. Přetrénování neuronové sítě

13. Aktivační funkce dostupné ve frameworku Torch

14. Zobrazení průběhu vybraných aktivačních funkcí

15. Aktivační funkce, které nejsou diferencovatelné

16. Diferencovatelné aktivační funkce

17. Rozdíly mezi funkcemi Tanh, Sigmoid a SoftSign

18. Repositář s demonstračními příklady

19. Odkazy na Internetu

1. Framework Torch: konfigurace neuronových sítí a použití různých typů aktivačních funkcí

V předchozí části seriálu o frameworku Torch jsme se seznámili s postupem, který se používá při tvorbě umělých neuronových sítí s pravidelnou strukturou tvořenou jednotlivými vrstvami, u nichž učení probíhá s využitím backpropagation algoritmu (algoritmu zpětného šíření, k němu se ještě vrátíme). Ukázali jsme si jednoduché sítě se třemi vrstvami neuronů, v nichž se používaly aktivační funkce Tanh i ReLU. Dnes se touto problematikou budeme zabývat více do hloubky; pokusíme se vykreslit výsledky (odhady) získané naší neuronovou sítí, přidáme další vrstvy neuronů, vyzkoušíme použít odlišné aktivační funkce a taktéž se pokusíme z již naučené sítě vyčíst váhy přiřazené ke vstupům jednotlivých neuronů (připomeňme si, že právě tyto váhy představují stav neuronů, tj. funkce, na kterou byly neurony natrénovány – naučeny).

Obrázek 1: Idealizovaný model neuronu s biasem, který jsme si popsali minule.

Poznámka: stále budeme používat neuronové sítě tvořené pravidelnými vrstvami neuronů. Další typy sítí a neuronů budou popsány v části věnované rozpoznávání obrázků.

2. Umělá neuronová síť popsaná minule – výpočet součtu dvou reálných čísel

V dalších kapitolách budeme postupně upravovat umělou neuronovou síť, s jejíž konstrukcí jsme se seznámili v závěru předchozího článku. Při porovnání s reálně používanými sítěmi se jedná vlastně o minisíť s dvojicí neuronů na vstupní vrstvě, dvojicí neuronů v prostřední (skryté, neviditelné) vrstvě a jediným neuronem na výstupní vrstvě:

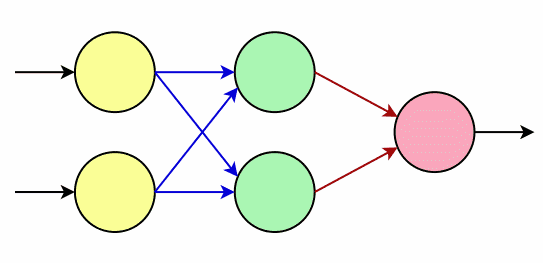
Obrázek 2: Neuronová síť s dvojicí neuronů na vstupní vrstvě, dvojicí neuronů na prostřední (skryté, neviditelné) vrstvě a jedním neuronem na vrstvě výstupní. Červené šipky naznačují spoje (synapse) s nelineárními funkcemi, první řada modrých šipek pouze přenáší vstupní (váhovaný) signál.

Postupně budeme upravovat parametry této sítě a sledovat, jak dobře či špatně se bude síť učit a odhadovat výsledky. Většina parametrů je uvedena hned na začátku zdrojového kódu; větší zásahy provedeme jen při přidávání dalších vrstev neuronů apod.:

require("nn")
 
TRAINING_DATA_SIZE = 500
 
INPUT_NEURONS = 2
HIDDEN_NEURONS = 2
OUTPUT_NEURONS = 1
 
MAX_ITERATION = 200
LEARNING_RATE = 0.01
 
 
function prepare_training_data(training_data_size)
    local training_data = {}
    function training_data:size() return training_data_size end
    for i = 1,training_data_size do
        local input = torch.randn(2)
        local output = torch.Tensor(1)
        output[1] = input[1] + input[2]
        training_data[i] = {input, output}
    end
    return training_data
end
 
 
function construct_neural_network(input_neurons, hidden_neurons, output_neurons)
    local network = nn.Sequential()
 
    network:add(nn.Linear(input_neurons, hidden_neurons))
    --network:add(nn.ReLU())
    network:add(nn.Tanh())
    network:add(nn.Linear(hidden_neurons, output_neurons))

    return network
end
 
 
function train_neural_network(network, training_data, learning_rate, max_iteration)
    local criterion = nn.MSECriterion()
    local trainer = nn.StochasticGradient(network, criterion)
    trainer.learningRate = learning_rate
    trainer.maxIteration = max_iteration
    trainer:train(training_data)
end
 
 
function validate_neural_network(network, validation_data)
    for i,d in ipairs(validation_data) do
        local d1, d2 = d[1], d[2]
        local input = torch.Tensor({d1, d2})
        local prediction = network:forward(input)[1]
        local correct = d1 + d2
        local err = math.abs(100.0 * (prediction-correct)/correct)
        local msg = string.format("%2d  %+6.3f  %+6.3f  %+6.3f  %+6.3f  %4.0f%%", i, d1, d2, correct, prediction, err)
        print(msg)
    end
end
 
 
network = construct_neural_network(INPUT_NEURONS, HIDDEN_NEURONS, OUTPUT_NEURONS)
training_data = prepare_training_data(TRAINING_DATA_SIZE)
train_neural_network(network, training_data, LEARNING_RATE, MAX_ITERATION)
print(network)
 
 
x=torch.Tensor({0.5, -0.5})
prediction = network:forward(x)
print(prediction)
 
validation_data = {
    { 1.0,  1,0},
    { 0.5,  0.5},
    { 0.2,  0.2},
    -------------
    {-1.0,  1.1},
    {-0.5,  0.6},
    {-0.2,  0.3},
    -------------
    { 1.0, -1.1},
    { 0.5, -0.6},
    { 0.2, -0.3},
    -------------
    {-1.0, -1,0},
    {-0.5, -0.5},
    {-0.2, -0.2},
}
 
validate_neural_network(network, validation_data)

3. Přidání podpory pro zobrazení odhadu sítě v porovnání s očekávaným výsledkem

Předchozí příklad nyní nepatrně rozšíříme takovým způsobem, aby se chyby v odhadu sítě zobrazily ve formě grafu. Takto líp uvidíme, ve kterých místech síť dokáže dobře odhadnout výsledky a kde již ne. Již předem přitom víme, že odhad by měl být nejlepší v okolí nulového součtu, protože síť trénujeme náhodnými hodnotami s normálním rozložením (okolo nuly). První funkce přidaná do příkladu vykreslí graf pro dva tenzory s hodnotami průběhů dvou funkcí:

function plot_graph(filename, x, y1, y2)
    gnuplot.pngfigure(filename)
    gnuplot.title("Adder NN")
    gnuplot.xlabel("x")
    gnuplot.ylabel("x+y")
    gnuplot.movelegend("left", "top")
 
    gnuplot.plot({"correct", x, y1},
                 {"predict", x, y2})

    gnuplot.plotflush()
    gnuplot.close()
end

Druhá funkce slouží pro přípravu tenzorů s výsledky, přičemž první tenzor bude obsahovat přesné výsledky a druhý výsledky odhadnuté neuronovou sítí. Vzhledem k tomu, že použijeme 2D graf, bude jedním ze vstupů pro tvorbu grafu konstanta použitá ve funkci prvního operandu součtu:

function prepare_graph(filename, from, to, items, d1)
    local x = torch.linspace(from, to, items)
    local size = x:size(1)
 
    local y1 = torch.Tensor(size)
    local y2 = torch.Tensor(size)
 
    for i = 1, size do
        local d2 = x[i]
        -- presny vysledek
        y1[i] = d1 + d2
 
        -- vstup do neuronove site
        local input = torch.Tensor({d1, d2})
        -- vysledek odhadnuty neuronovou siti
        local prediction = network:forward(input)[1]
        y2[i] = prediction
    end
    plot_graph(filename, x, y1, y2)
end

Poznámka: můžete si samozřejmě vykreslit i graf dvou nezávislých proměnných, ale ten mi připadá poměrně nepřesný – špatně se na něm odečítají jednotlivé hodnoty a porovnávají oba průběhy:

4. Zobrazení odhadu neuronové sítě součtu dvou čísel

Po natrénování neuronové sítě vykreslíme průběh očekávaných i odhadnutých výsledků pro různé rozsahy vstupních hodnot. Připomeňme si, že první tři parametry udávají rozsah hodnot druhého vstupního operandu součtu kdežto parametr poslední je přímá hodnota prvního vstupního operandu:

prepare_graph("adder_a1.png", -2, 2, 21, 0.5)
prepare_graph("adder_a2.png", -10, 10, 21, 0.5)
prepare_graph("adder_a3.png", -2, 2, 21, 2.0)
prepare_graph("adder_a4.png", -2, 2, 21, 5.0)

První průběh vypadá naprosto dokonale – výsledky součtu (puntíky) jsou umístěny prakticky přesně na sobě:

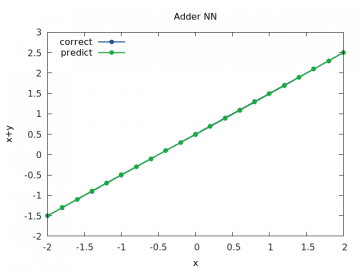
Obrázek 3: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=1/2.

U druhého průběhu je patrné, že se síť nenaučila správně pracovat s hodnotami vzdálenějšími od nuly, což je ale naše chyba, protože jsme použili nedokonalá trénovací data (to se v praxi stává velmi často!):

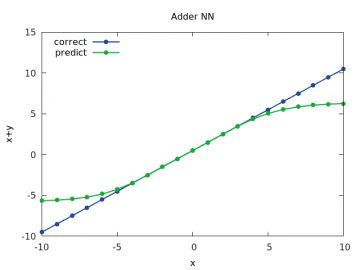
Obrázek 4: Výpočet a odhad součtu x+y pro y v rozsahu < –10, 10> a x=1/2.

Třetí průběh s prvním operandem součtu nastaveným na hodnotu 2.0 opět naznačuje, že síť neumí dobře pracovat s hodnotami vzdálenějšími od nuly. Je to patrné z pravého horního rohu (i když prozatím jen minimálně):

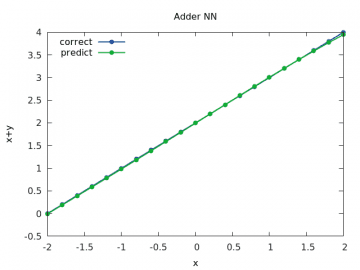
Obrázek 5: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=2.0.

Ještě větší vzdálení jednoho z operandů od nuly ukáže chybu odhadu sítě ve větším měřítku:

Obrázek 6: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=5.0.

5. Zlepšení odhadu sítě: vliv zvýšení počtu neuronů v prostřední (skryté) vrstvě i rozsahu trénovacích dat

Odhad sítě můžeme zlepšit několika způsoby, například zvětšením počtu neuronů v prostřední vrstvě, více cykly učení i zvětšením rozsahu trénovacích dat. První úprava spočívá ve změně dvou konstant (změny jsou zvýrazněny tučně):

TRAINING_DATA_SIZE = 500
 
INPUT_NEURONS = 2
HIDDEN_NEURONS = 200
OUTPUT_NEURONS = 1
 
MAX_ITERATION = 500
LEARNING_RATE = 0.01

Druhá – zcela nezávislá – úprava spočívá v tom, že trénovací náhodně generovaná data jednoduše vynásobíme vhodnou konstantou (změna je opět zvýrazněna tučně):

function prepare_training_data(training_data_size)
    local training_data = {}
    function training_data:size() return training_data_size end
    for i = 1,training_data_size do
        local input = 2*torch.randn(2)
        local output = torch.Tensor(1)
        output[1] = input[1] + input[2]
        training_data[i] = {input, output}
    end
    return training_data
end

Podívejme se na výsledky

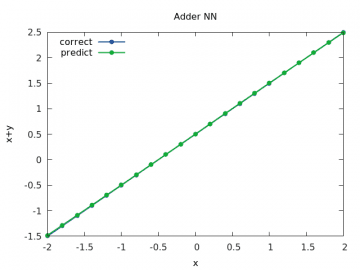
Obrázek 7: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=1/2.

Obrázek 8: Výpočet a odhad součtu x+y pro y v rozsahu < –10, 10> a x=1/2.

Obrázek 9: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=2.0.

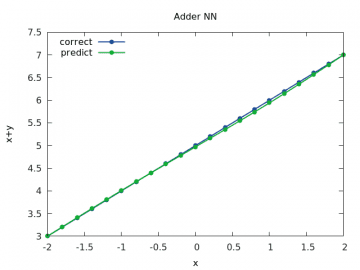
Obrázek 10: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=5.0.

6. Nastavení příliš velké míry učení neuronové sítě

Vraťme se nyní k parametrům původní neuronové sítě se dvěma neurony v prostřední vrstvě. Teoreticky je možné se přiblížit k natrénované síti nejenom zvýšením počtu iterací, ale také zvýšením míry učení neuronové sítě. Ovšem změna této konstanty je velmi ošemetná, protože může vést k tomu, že celý systém (a sít při učení není nic jiného než složitý dynamický systém) nebude stabilizovaný, ale naopak dosti „rozkolísaný“.

7. Ukázka nastavení míry učení na hodnotu 0,15

Zkusme si nejdříve provést nastavení této konstanty na hodnotu 0,15:

TRAINING_DATA_SIZE = 500
 
INPUT_NEURONS = 2
HIDDEN_NEURONS = 2
OUTPUT_NEURONS = 1
 
MAX_ITERATION = 200
LEARNING_RATE = 0.15

Problémy jsou patrné již při učení (tréninku) sítě, kdy chyba neklesá, ale spíše osciluje:

# StochasticGradient: training
# current error = 0.55244895994336
# current error = 0.3334583279015
# current error = 0.81414780242313
# current error = 0.40710655586281
# current error = 0.43634506822938
# current error = 0.3447418376122
...
...
...
# current error = 0.39266952933391
# current error = 0.34122992196533
# current error = 0.40248194421392
# current error = 0.42076971146368
# current error = 0.32053764526033
# current error = 0.73534488513395

Více naznačí grafy s výsledky odhadu sítě:

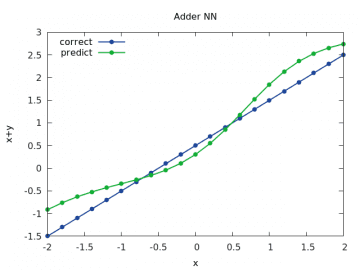
Obrázek 11: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=1/2.

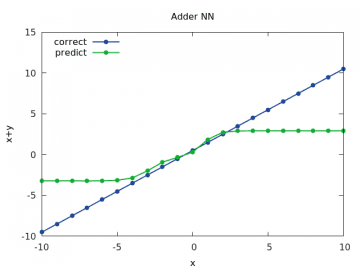
Obrázek 12: Výpočet a odhad součtu x+y pro y v rozsahu < –10, 10> a x=1/2.

Obrázek 13: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=2.0.

8. Ukázka nastavení míry učení na hodnotu 0,25

V případě, že míru učení nastavíme v naší malé a tudíž i potenciálně nestabilní neuronové síti, na ještě vyšší hodnotu, stanou se výsledky zcela nepoužitelné:

TRAINING_DATA_SIZE = 500
 
INPUT_NEURONS = 2
HIDDEN_NEURONS = 2
OUTPUT_NEURONS = 1
 
MAX_ITERATION = 200
LEARNING_RATE = 0.25

Problémy jsou opět patrné již v průběhu tréninku:

# StochasticGradient: training
# current error = 2.0282085038056
# current error = 2.1131774159933
# current error = 1.8229747604834
# current error = 1.8642793520045
# current error = 1.3175683358286
# current error = 1.7643987097681
# current error = 1.69223744766
# current error = 2.0611422784959
# current error = 1.7310729650179
# current error = 1.8672282085826
# current error = 1.9981641715903
# current error = 1.9526019628646
# current error = 1.6777214313218
# current error = 1.4955751676312

A zcela vyniknou na vygenerovaných grafech:

Obrázek 14: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=1/2.

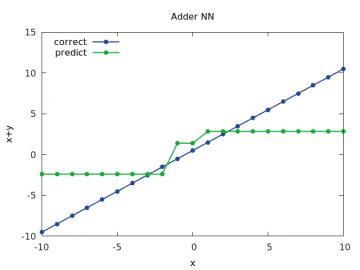
Obrázek 15: Výpočet a odhad součtu x+y pro y v rozsahu < –10, 10> a x=1/2.

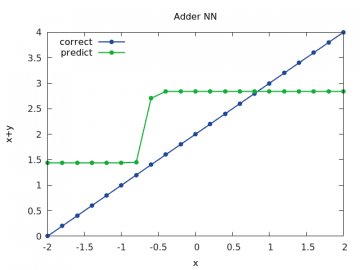
Obrázek 16: Výpočet a odhad součtu x+y pro y v rozsahu < –2, 2> a x=2.0.

9. Grafické zobrazení odhadu sítě počítající zobecněný xor

Upravit můžeme i zcela první příklad, v němž byla vytvořena neuronová sít počítající zobecněnou funkci xor na základě znaménka vstupujících operandů. U této sítě nejdříve nastavíme parametry naschvál tak, aby výsledky nebyly dokonalé:

TRAINING_DATA_SIZE = 1000
 
INPUT_NEURONS = 2
HIDDEN_NEURONS = 5
OUTPUT_NEURONS = 1
 
MAX_ITERATION = 200
LEARNING_RATE = 0.01

Podívejme se opět na grafické znázornění výsledků. Vždy se očekává skok v nule (z -1 na 1 či naopak, podle znaménka vstupních operandů). Ovšem první výsledky u sítě s pěti neurony v prostřední vrstvě ukazují, že průběh vůbec není takto jednoznačný:

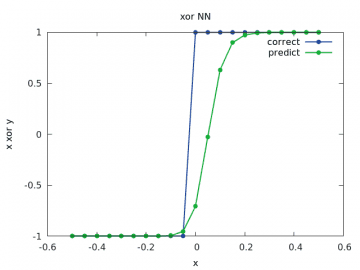
Obrázek 17: Výpočet a odhad zobecněné funkce xor pro y v rozsahu < –1/2, 1/2> a x=-1/2.

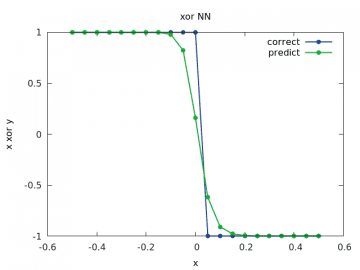
Obrázek 18: Výpočet a odhad zobecněné funkce xor pro y v rozsahu < –1/2, 1/2> a x=1/2.

Předchozí průběhy se v rámci možností překrývaly s očekávanými výsledky, ovšem pro větší rozsah hodnoty vstupního operandu už tomu tak není, což je vlastně logické, neboť na tyto hodnoty nebyla síť natrénována:

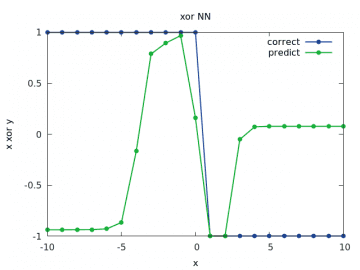
Obrázek 19: Výpočet a odhad zobecněné funkce xor pro y v rozsahu < –10, 10> a x=1/2.

10. Dvě skryté vrstvy neuronů

Neuronovou síť opět vylepšíme, ovšem jinak, než jsme to doposud dělali. Namísto pouhého zvetšení počtu neuronů v jediné skryté vrstvě přidáme do sítě další skrytou vrstvu. Výsledek bude vypadat nějak takto (počty neuronů budou ve skutečnosti vyšší, ale to se mi již nechtělo kreslit :-):

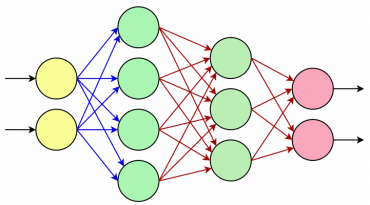
Obrázek 20: Neuronová síť s dvojicí neuronů na vstupní vrstvě, čtyřmi neurony na první skryté vrstvě, třemi neurony na druhé skryté vrstvě a dvěma neuronu na vrstvě výstupní. Červené šipky naznačují spoje (synapse) s nelineárními funkcemi, první řada modrých šipek pouze přenáší vstupní (váhovaný) signál. Povšimněte si, jak se pouhým přidáním několika neuronů skokově zvýšila složitost celé sítě.

Úprava parametrů sítě bude vypadat následovně:

TRAINING_DATA_SIZE = 1000
 
INPUT_NEURONS = 2
HIDDEN_NEURONS_LAYER_1 = 9
HIDDEN_NEURONS_LAYER_2 = 10
OUTPUT_NEURONS = 1
 
MAX_ITERATION = 500
LEARNING_RATE = 0.01

Nutná je samozřejmě i úprava kódu:

function construct_neural_network(input_neurons, hidden_neurons_layer1, hidden_neurons_layer2, output_neurons)
    local network = nn.Sequential()
 
    network:add(nn.Linear(input_neurons, hidden_neurons_layer1))
    network:add(nn.Tanh())
    network:add(nn.Linear(hidden_neurons_layer1, hidden_neurons_layer2))
    network:add(nn.Tanh())
    network:add(nn.Linear(hidden_neurons_layer2, output_neurons))
    network:add(nn.Tanh())
 
    return network
end

Takto je struktura sítě vypsána po její konstrukci:

nn.Sequential {
  [input -> (1) -> (2) -> (3) -> (4) -> (5) -> (6) -> output]
  (1): nn.Linear(2 -> 9)
  (2): nn.Tanh
  (3): nn.Linear(9 -> 10)
  (4): nn.Tanh
  (5): nn.Linear(10 -> 1)
  (6): nn.Tanh
}

11. Jak se projeví přidání další skryté vrstvy do neuronové sítě?

Samozřejmě si opět můžeme ukázat, jak dobře nově zkonstruovaná a natrénovaná neuronová síť s dvojicí skrytých vrstev neuronů odhaduje výsledky:

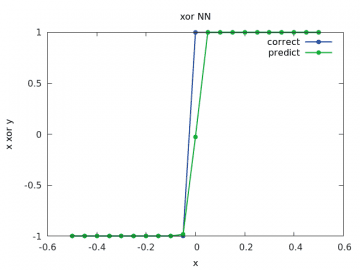
Obrázek 21: Výpočet a odhad zobecněné funkce xor pro y v rozsahu < –1/2, 1/2> a x=-1/2.

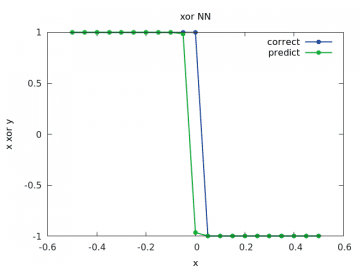
Obrázek 22: Výpočet a odhad zobecněné funkce xor pro y v rozsahu < –1/2, 1/2> a x=1/2.

Obrázek 23: Výpočet a odhad zobecněné funkce xor pro y v rozsahu < –10, 10> a x=1/2.

Vidíme, že výsledky jsou již mnohem lepší, než tomu bylo u sítě z deváté kapitoly.

12. Přetrénování neuronové sítě

Neustálé zvětšování trénovací množiny nemusí vést k lepšímu natrénování sítě. Může tomu být – a často i bývá – přesně naopak, protože síť může ztrácet obecné rysy a začne se „specializovat“ pouze přesně na tu oblast, pro kterou byla připravena trénovací data. Ukážeme si to na extrémním případu (a to z toho důvodu, že se přetrénování projeví spíše u složitějších sítí). V našem příkladu budeme mít pouze deset trénovacích vzorků, ovšem síť s nimi natrénujeme desetkrát za sebou. To je podobné případu, kdy budeme mít síť rozpoznávající (například) dopravní značky a budeme ji trénovat jen na fotkách získaných za slunečného letního dne:

TRAINING_DATA_SIZE = 10
 
INPUT_NEURONS = 2
HIDDEN_NEURONS_LAYER_1 = 9
HIDDEN_NEURONS_LAYER_2 = 10
OUTPUT_NEURONS = 1
 
MAX_ITERATION = 500
LEARNING_RATE = 0.01

Funkce pro natrénování sítě se změní takto:

function train_neural_network(network, training_data, learning_rate, max_iteration)
    local criterion = nn.MSECriterion()
    local trainer = nn.StochasticGradient(network, criterion)
    trainer.learningRate = learning_rate
    trainer.maxIteration = max_iteration
    for i=1,10 do
        trainer:train(training_data)
    end
end

Trénink dopadl zdánlivě velmi úspěšně, protože se síť pěkně naučila trénovací data rozpoznávat s relativně malou chybou:

# StochasticGradient: you have reached the maximum number of iterations
# training error = 0.0001331571570523

Ovšem praktické výsledky jsou již o dost horší.

Zde je odhad zcela špatný:

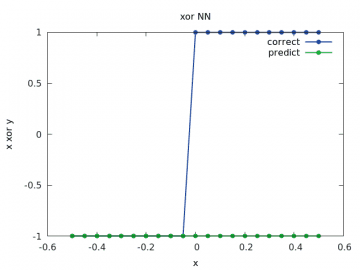
Obrázek 24: Výpočet a odhad zobecněné funkce xor pro y v rozsahu < –1/2, 1/2> a x=-1/2.

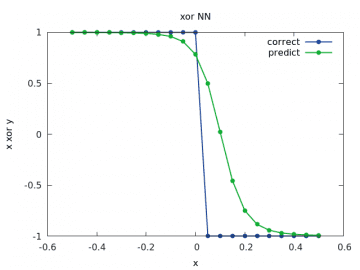
Obrázek 25: Výpočet a odhad zobecněné funkce xor pro y v rozsahu < –1/2, 1/2> a x=1/2.

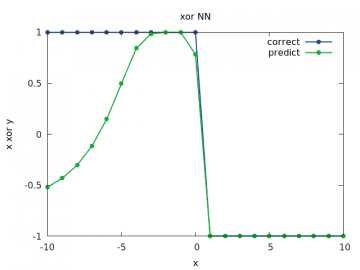
Obrázek 26: Výpočet a odhad zobecněné funkce xor pro y v rozsahu < –10, 10> a x=1/2.

13. Aktivační funkce dostupné ve frameworku Torch

Prozatím jsme v našich testovacích neuronových sítích používali pouze dva typy aktivačních funkcí. Jednalo se o hyperbolický tangens pojmenovaný Tanh, který se v této oblasti používá již velmi dlouho. Dále jsme do sítě vkládali funkce ReLU (REctified Linear Unit), mezi jejíž četné výhody patří velmi rychlý výpočet, což se pozitivně projeví v rozsáhlých neuronových sítích (rozpoznávání obrazu atd.). Ovšem k dispozici máme i mnoho dalších aktivačních funkcí, které budou popsány v navazujících kapitolách. Zde si popíšeme, jak se vlastně do aktivačních funkcí předávají vstupní hodnoty a jak se získávají výsledky. I přesto, že se používá označení „funkce“, nejedná se ve skutečnosti o běžné funkce v takovém smyslu, jak je chápeme v kontextu programovacího jazyka Lua (či jakéhokoli jiného běžného programovacího jazyka).

Spustíme interpret frameworku Torch:

$ th
 
  ______             __   |  Torch7
 /_  __/__  ________/ /   |  Scientific computing for Lua.
  / / / _ \/ __/ __/ _ \  |  Type ? for help
 /_/  \___/_/  \__/_//_/  |  https://github.com/torch
                          |  http://torch.ch

Explicitně naimportujeme modul nn, protože implicitně je načten pouze modul tortch:

th> import("nn")

Vytvoříme tenzor obsahující vstupní hodnoty do zkoumané aktivační funkce. Číslo 11 zde udává počet vygenerovaných hodnot (používám schválně liché číslo, aby byla zahrnuta i nula):

th> x = torch.linspace(-5, 5, 11)

Získáme instanci zkoumané funkce a předáme jí tenzor se vstupními hodnotami. Povšimněte si, že se funkce vlastně chová stejně, jako další části neuronové sítě i jako samotná síť, protože se pro „propasování“ informací přes funkci taktéž používá metoda forward:

th> func = nn.Tanh()
 
th> y = func:forward(x)

Právě v tomto bodě se aktivační funkce liší od běžných funkcí a musíme na ně nahlížet spíše jako na objekty či na uzávěry (closures). To má své výhody, například zde existuje možnost předávat funkcím při jejich konstrukci konfigurační parametry apod.

Nyní si pouze vypíšeme hodnoty vrácené funkcí. Opět se jedná o tenzor, tentokrát o stejné velikosti (počtu komponent), jako měl tenzor vstupní:

th> y
-0.9999
-0.9993
-0.9951
-0.9640
-0.7616
 0.0000
 0.7616
 0.9640
 0.9951
 0.9993
 0.9999
[torch.DoubleTensor of size 11]

14. Zobrazení průběhu vybraných aktivačních funkcí

Průběh jakékoli vybrané aktivační funkce si samozřejmě můžeme zobrazit, a to kombinací možností nabízených moduly nn a gnuplot. Následující příklad nejdříve vypočte sto hodnot aktivační funkce Tanh pro vstupní hodnoty v rozsahu < –5, 5> a následně tuto funkci vykreslí do grafu. Nastavení os, barvy a stylu vykreslení křivky atd. prozatím pro větší stručnost ponecháme na implicitních hodnotách. Povšimněte si, že s využitím tenzorů jakožto základního datového typu používaného jak aktivační funkcí, tak i při kreslení grafů, jsme se obešli bez použití programových smyček:

 
require("gnuplot")
require("nn")
 
x = torch.linspace(-5, 5)
func = nn.Tanh()
y = func:forward(x)
 
gnuplot.pngfigure("tanh.png")
gnuplot.title("tanh x")
gnuplot.plot(x, y)
gnuplot.grid(true)
gnuplot.plotflush()
gnuplot.close()

Po spuštění tohoto příkladu by se měl do rastrového obrázku tanh.png vykreslit následující graf:

Obrázek 27: Průběh funkce Tanh vykreslený předchozím demonstračním příkladem.

15. Aktivační funkce, které nejsou diferencovatelné

V této kapitole si ve stručnosti popíšeme ty aktivační funkce, které nejsou diferencovatelné v celém svém rozsahu platnosti. Tyto funkce většinou obsahují buď jedno „koleno“ nebo dokonce jeden či dva skoky, což v praxi znamená, že se výstupní hodnota z neuronu může prudce změnit, a to i pro malé rozdíly na vstupu. V některých případech může být tato vlastnost neuronů užitečná, ovšem o to víc je chování sítě závislé na jejím správném natrénování. Mezi tyto funkce patří především:

Jméno funkce	Hodnoty	Základní vlastnosti
ReLU	f(x)=0 pro x≤0, f(x)=x pro x>0	má jedno koleno při vstupu 0, velmi často používaná v praxi
ReLU6	f(x)=0 pro x≤0, f(x)=x pro 0<x<6, f(x)=6 pro x≥6	má dvě kolena při vstupech 0 a 6, opět velmi často používaná v praxi
HardTanh	f(x)=-1 pro x< –1, f(x)=1 pro x>1, jinak f(x)=x	funkce s lineárním průběhem pro –1≤x≤1, má dvě kolena

ELU	f(x) = max(0, x) + min(0, α * (e^x – 1))	pro některé hodnoty α je diferencovatelná

SoftShrink	f(x)=x-λ pro x>λ, f(x)=x+λ pro x< -λ, jinak f(x)=0	funkce s lineárním průběhem pro x>λ a x< -λ, dvě kolena na hodnotách -λ a λ
HardShrink	f(x)=x pro x< -λ a x>λ, jinak f(x)=0	funkce s lineárním průběhem a dvěma skoky na hodnotách -λ a λ
PReLU	podobné funkci ReLU, ale má volitelný sklon pro záporné hodnoty x
RReLU	podobné předchozí funkce, ale pro záporné hodnoty x je vstup náhodně posunut (jen v režimu tréninku)
AddConstant	f(x)=x+k	používá se například při ladění, k je skalární a neměnná hodnota
MulConstant	f(x)=x*k	používá se například při ladění, k je skalární a neměnná hodnota

Poznámka: diferencovatelnost je poměrně důležitá vlastnost, která se mj. projeví i při tréninku umělé neuronové sítě.

Obrázek 28: Průběh funkcí ReLU, ReLU6, HardTanh, SoftShrink i HardShrink.

Obrázek 29: Průběh funkcí ReLU, ReLU6, HardTanh, SoftShrink i HardShrink, zvětšení na okolí počátku souřadného systému.

16. Diferencovatelné aktivační funkce

Další funkce, které jsou frameworkem Torch nabízeny, jsou již diferencovatelné. Nejčastěji se používají první dvě funkce, tedy Sigmoid a Tanh:

Jméno funkce	Způsob výpočtu
Sigmoid	f(x) = 1 / (1 + e^-x) = e^x / (e^x+1)
Tanh	f(x) = (e^x – e^-x) / (e^x + e^-x)

SoftMax	provede normalizaci vstupního tenzoru, provede výpočet f_i(x) = e^{x_i – max_i(x_i)} / sum_j exp^{x_j – max_i(x_i)}
SoftMin	dtto, ale vypočte f_i(x) = e^{-x_i – max_i(-x_i)} / sum_j e^{-x_j – max_i(-x_i)}
SoftPlus	f_i(x) = 1/beta * log(1 + e^{beta * x_i})
SoftSign	f_i(x) = x_i / (1+\|x_i\|)

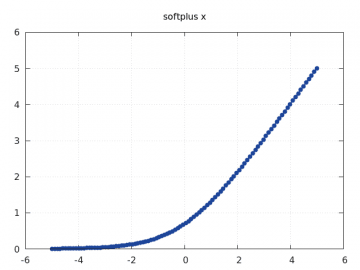
Obrázek 30: Průběh funkce SoftPlus.

17. Rozdíly mezi funkcemi Tanh, Sigmoid a SoftSign

Funkce Tanh, Sigmoid a SoftSign sice mají podobný tvar křivky, ovšem jejich skutečný průběh je ve skutečnosti odlišný. O tom se můžeme velmi snadno přesvědčit, když si všechny funkce necháme vykreslit do jednoho grafu a budeme měnit rozsah hodnot na x-ové ose. O vykreslení všech tří zmíněných funkcí se postará následující příklad:

require("gnuplot")
require("nn")
 
function create_graph(from, to, filename)
    x = torch.linspace(from, to)
 
    func1 = nn.SoftSign()
    y1 = func1:forward(x)
 
    func2 = nn.Tanh()
    y2 = func2:forward(x)
 
    func3 = nn.Sigmoid()
    y3 = func3:forward(x)
 
    gnuplot.pngfigure(filename)
    gnuplot.title("mix of various functions")
    gnuplot.xlabel("x")
    gnuplot.ylabel("SoftSign, Tanh, Sigmoid")
    gnuplot.movelegend("left", "top")
 
    gnuplot.plot({"SoftSign", x, y1, "-"},
                 {"Tanh",     x, y2, "-"},
                 {"Sigmoid",  x, y3, "-"})
 
    gnuplot.grid(true)
    gnuplot.plotflush()
    gnuplot.close()
end
 
create_graph(-5, 5, "mix_-5_to_5.png")
create_graph(-10, 10, "mix_-10_to_10.png")
create_graph(-20, 20, "mix_-20_to_20.png")

Obrázek 31: Průběh funkcí Tanh, Sigmoid a SoftSign pro rozsah vstupních hodnot < –5, 5>.

Vidíme, že se kromě tvaru průběhů funkce liší i obor hodnot.

Obrázek 32: Průběh funkcí Tanh, Sigmoid a SoftSign pro rozsah vstupních hodnot < –10, 10>.

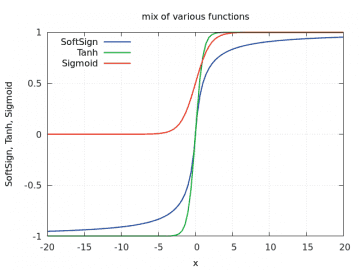
Obrázek 33: Průběh funkcí Tanh, Sigmoid a SoftSign pro rozsah vstupních hodnot < –20, 20>.

18. Repositář s demonstračními příklady

Všechny demonstrační příklady, které jsme si popsali v předchozích kapitolách i v předchozí části tohoto seriálu, najdete v GIT repositáři dostupném na adrese https://github.com/tisnik/torch-examples.git. Následují odkazy na zdrojové kódy jednotlivých příkladů:

Příklad	Adresa
01_xor_problem.lua	https://github.com/tisnik/torch-examples/blob/master/nn/01_xor_problem.lua
02_better_parameters.lua	https://github.com/tisnik/torch-examples/blob/master/nn/02_better_parameters.lua
03_not_enough_neurons.lua	https://github.com/tisnik/torch-examples/blob/master/nn/03_not_enough_neurons.lua
04_adder.lua	https://github.com/tisnik/torch-examples/blob/master/nn/04_adder.lua
05_adder_with_graphs.lua	https://github.com/tisnik/torch-examples/blob/master/nn/05_adder_with_graphs.lua
06_too_many_neurons.lua	https://github.com/tisnik/torch-examples/blob/master/nn/06_too_many_neurons.lua
07_high_learning_rate.lua	https://github.com/tisnik/torch-examples/blob/master/nn/07_high_learning_rate.lua
08_xor_with_graphs.lua	https://github.com/tisnik/torch-examples/blob/master/nn/08_xor_with_graphs.lua
09_more_layers.lua	https://github.com/tisnik/torch-examples/blob/master/nn/09_more_layers.lua
10_overtraining.lua	https://github.com/tisnik/torch-examples/blob/master/nn/10_overtraining.lua

transfer_functions/01_tanh.lua	https://github.com/tisnik/torch-examples/blob/master/nn/transfer_functions/01_tanh.lua
transfer_functions/02_relu.lua	https://github.com/tisnik/torch-examples/blob/master/nn/transfer_functions/02_relu.lua
transfer_functions/03_relu6.lua	https://github.com/tisnik/torch-examples/blob/master/nn/transfer_functions/03_relu6.lua

19. Odkazy na Internetu

Rectifier (neural networks)
https://en.wikipedia.org/wiki/Rectifier_%28neural_networks%29
Stránka projektu Torch
http://torch.ch/
Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md
Torch: modul image
https://github.com/torch/image/blob/master/README.md
Torch na GitHubu (několik repositářů)
https://github.com/torch
Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29
Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md
Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet
Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md
Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear
Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok
Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network
Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/
Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/
Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5
Učení s učitelem (Wikipedia)
https://cs.wikipedia.org/wiki/U%C4%8Den%C3%AD_s_u%C4%8Ditelem
Plotting with Torch7
http://www.lighting-torch.com/2015/08/24/plotting-with-torch7/
Plotting Package Manual with Gnuplot
https://github.com/torch/gnuplot/blob/master/README.md
An Introduction to Tensors
https://math.stackexchange.com/questions/10282/an-introduction-to-tensors
Gaussian filter
https://en.wikipedia.org/wiki/Gaussian_filter
Gaussian function
https://en.wikipedia.org/wiki/Gaussian_function
Laplacian/Laplacian of Gaussian
http://homepages.inf.ed.ac.uk/rbf/HIPR2/log.htm
Odstranění šumu
https://cs.wikipedia.org/wiki/Odstran%C4%9Bn%C3%AD_%C5%A1umu
Binary image
https://en.wikipedia.org/wiki/Binary_image
Erosion (morphology)
https://en.wikipedia.org/wiki/Erosion_%28morphology%29
Dilation (morphology)
https://en.wikipedia.org/wiki/Dilation_%28morphology%29
Mathematical morphology
https://en.wikipedia.org/wiki/Mathematical_morphology
Cvičení 10 – Morfologické operace
http://midas.uamt.feec.vutbr.cz/ZVS/Exercise10/content_cz.php
Differences between a matrix and a tensor
https://math.stackexchange.com/questions/412423/differences-between-a-matrix-and-a-tensor
Qualitatively, what is the difference between a matrix and a tensor?
https://math.stackexchange.com/questions/1444412/qualitatively-what-is-the-difference-between-a-matrix-and-a-tensor?
BLAS (Basic Linear Algebra Subprograms)
http://www.netlib.org/blas/
Basic Linear Algebra Subprograms (Wikipedia)
https://en.wikipedia.org/wiki/Basic_Linear_Algebra_Subprograms
Comparison of deep learning software
https://en.wikipedia.org/wiki/Comparison_of_deep_learning_software
TensorFlow
https://www.tensorflow.org/
Caffe2 (A New Lightweight, Modular, and Scalable Deep Learning Framework)
https://caffe2.ai/
PyTorch
http://pytorch.org/
Seriál o programovacím jazyku Lua
http://www.root.cz/serialy/programovaci-jazyk-lua/
LuaJIT – Just in Time překladač pro programovací jazyk Lua
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (2)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-2/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (3)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-3/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (4)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-4/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (5 – tabulky a pole)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-5-tabulky-a-pole/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (6 – překlad programových smyček do mezijazyka LuaJITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-6-preklad-programovych-smycek-do-mezijazyka-luajitu/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (7 – dokončení popisu mezijazyka LuaJITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-7-dokonceni-popisu-mezijazyka-luajitu/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (8 – základní vlastnosti trasovacího JITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-8-zakladni-vlastnosti-trasovaciho-jitu/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (9 – další vlastnosti trasovacího JITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-9-dalsi-vlastnosti-trasovaciho-jitu/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (10 – JIT překlad do nativního kódu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-10-jit-preklad-do-nativniho-kodu/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (11 – JIT překlad do nativního kódu procesorů s architekturami x86 a ARM)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-11-jit-preklad-do-nativniho-kodu-procesoru-s-architekturami-x86-a-arm/
LuaJIT – Just in Time překladač pro programovací jazyk Lua (12 – překlad operací s reálnými čísly)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-12-preklad-operaci-s-realnymi-cisly/
Lua Profiler (GitHub)
https://github.com/luaforge/luaprofiler
Lua Profiler (LuaForge)
http://luaforge.net/projects/luaprofiler/
ctrace
http://webserver2.tecgraf.puc-rio.br/~lhf/ftp/lua/
The Lua VM, on the Web
https://kripken.github.io/lua.vm.js/lua.vm.js.html
Lua.vm.js REPL
https://kripken.github.io/lua.vm.js/repl.html
lua2js
https://www.npmjs.com/package/lua2js
lua2js na GitHubu
https://github.com/basicer/lua2js-dist
Lua (programming language)
http://en.wikipedia.org/wiki/Lua_(programming_language)
LuaJIT 2.0 SSA IRhttp://wiki.luajit.org/SSA-IR-2.0
The LuaJIT Project
http://luajit.org/index.html
LuaJIT FAQ
http://luajit.org/faq.html
LuaJIT Performance Comparison
http://luajit.org/performance.html
LuaJIT 2.0 intellectual property disclosure and research opportunities
http://article.gmane.org/gmane.comp.lang.lua.general/58908
LuaJIT Wiki
http://wiki.luajit.org/Home
LuaJIT 2.0 Bytecode Instructions
http://wiki.luajit.org/Bytecode-2.0
Programming in Lua (first edition)
http://www.lua.org/pil/contents.html
Lua 5.2 sources
http://www.lua.org/source/5.2/
REPL
https://en.wikipedia.org/wiki/Read%E2%80%93eval%E2%80%93print_loop
The LLVM Compiler Infrastructure
http://llvm.org/ProjectsWithLLVM/
clang: a C language family frontend for LLVM
http://clang.llvm.org/
LLVM Backend („Fastcomp“)
http://kripken.github.io/emscripten-site/docs/building_from_source/LLVM-Backend.html#llvm-backend
Lambda the Ultimate: Coroutines in Lua,
http://lambda-the-ultimate.org/node/438
Coroutines Tutorial,
http://lua-users.org/wiki/CoroutinesTutorial
Lua Coroutines Versus Python Generators,
http://lua-users.org/wiki/LuaCoroutinesVersusPythonGenerators

Seriál: Torch: framework pro strojové učení

Framework Torch: základy práce s neuronovými sítěmi
Framework Torch: konfigurace neuronových sítí a použití různých typů aktivačních funkcí
Framework Torch: problematika rozpoznávání a klasifikace obrázků

Přečtěte si všechny díly seriálu Torch: framework pro strojové učení nebo sledujte jeho RSS

Vstoupit do diskuse (10 názorů)

Pavel Tišnovský

Vystudoval VUT FIT a v současné době pracuje na projektech vytvářených v jazycích Python a Go.

Díky. Mimochodem Torch je dostupný i jako image pro Docker, podívám se, na čem to založili (asi Alpine Linux). Klidně se zúčastním nějakého testování Torch+Gentoo, kdyby bylo potřeba.

Pavel Tišnovský

Zlatý podporovatel

Sdílet

Obsah

1. Framework Torch: konfigurace neuronových sítí a použití různých typů aktivačních funkcí

2. Umělá neuronová síť popsaná minule – výpočet součtu dvou reálných čísel

3. Přidání podpory pro zobrazení odhadu sítě v porovnání s očekávaným výsledkem

4. Zobrazení odhadu neuronové sítě součtu dvou čísel

5. Zlepšení odhadu sítě: vliv zvýšení počtu neuronů v prostřední (skryté) vrstvě i rozsahu trénovacích dat

6. Nastavení příliš velké míry učení neuronové sítě

7. Ukázka nastavení míry učení na hodnotu 0,15

8. Ukázka nastavení míry učení na hodnotu 0,25

9. Grafické zobrazení odhadu sítě počítající zobecněný xor

10. Dvě skryté vrstvy neuronů

11. Jak se projeví přidání další skryté vrstvy do neuronové sítě?

12. Přetrénování neuronové sítě

13. Aktivační funkce dostupné ve frameworku Torch

14. Zobrazení průběhu vybraných aktivačních funkcí

15. Aktivační funkce, které nejsou diferencovatelné

16. Diferencovatelné aktivační funkce

17. Rozdíly mezi funkcemi Tanh, Sigmoid a SoftSign

18. Repositář s demonstračními příklady

19. Odkazy na Internetu

Framework Torch: základy práce s neuronovými sítěmi