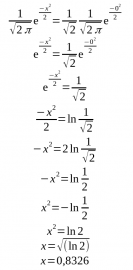Dalekohled sice zvětšuje, ale nemá takovou ostrost. Kolikanásobně tedy skutečně vzroste rozlišení? Změříme rozmazání, které je přítomno ve fotografiích.
Dalekohled aplikuje na obraz konvoluci – rozmazání. Každý pixel se nahradí malým obrázkem, jak by vypadal Diracův impuls (bod, astronomická hvězda), kdybychom se na něj podívali dalekohledem. Tyto malé obrázky jsou centrovány v původních pozicích pixelů a překrývají se; sečtou se. Konvoluce je pouze frekvenční filtrování obrazu, něco jako když v hudbě změníme basy a výšky.
Další konvoluce se provede fotoaparátem smartphonu a další se provede filtry odstranění Bayerovy masky v dcraw. Jednotlivé konvoluční obrázky mohou mít různý tvar (tzv. bokeh), ale podle centrální limitní věty, pokud je jakýchkoliv „rozumných“ rozmazání více, jejich výsledek konverguje ke Gaussovskému neboli normálnímu rozdělení (to samé rozmazání jako v GIMPu Gaussian Blur, v G'MIC -blur). Tohoto předpokladu využijeme.
Mohli bychom vyfotit bod a zkoumat, jak široký je kopeček rozmazání. Nevíme ale, zda byl bod původně dostatečně ostrý. Dokonale ostrý bod je nekonečně malý, a tak neviditelný. Vyfotíme proto ostrou hranu mezi uniformní světlou a tmavou plochou, která je integrálem bodu. Dokonale ostrá hrana se realizuje snadno, např. kde končí budova a začíná nebe. Protože integrál je také pouze frekvenční filtr, je jedno, zda se dá na začátek nebo na konec. Integrál gaussovského rozdělení je moje oblíbená funkce, distribuční funkce normálního rozdělení.
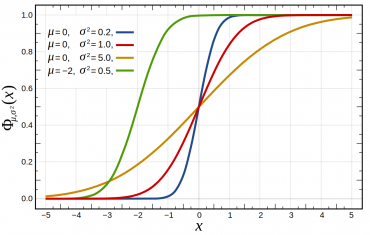
Distribuční funkce normálních rozdělení. Znázorňuje profil neostré hrany s různou silou neostrosti σ a různou pozicí hrany μ. Nahoře je bílá, dole černá. Na ose x je pixelový offset.
Představme si, že do zobrazovací soustavy vstoupí nekonečně ostrý obrázek, soustava pustí GIMP, dá Gaussian Blur, a nakliká nějaké číslo jako rozmazání (σ – sigma – směrodatná odchylka) a výsledek vypustí na výstup. My chceme teď vědět, jakou směrodatnou odchylku tam ta soustava naklikala. Mezi +/- 1 směrodatnou odchylkou je 68,2% měření, čili pomyslný pruh šedých hodnot kolem 50% šedé o šířce 68,2% rozsahu mezi bílou a černou bude mít pixelovou šířku 2 směrodatné odchylky. Tedy mezi 50%-68,2%/2=15,9% a 50%+68,2%/2=84,1%. Úvaha se provádí v lineárním (počtu fotonů) prostoru a je třeba zohlednit, že hrana nemusí být mezi úplně bílou a černou.
- Zvolíme obrázek s nepřeexponovanou hranou blízko středu, kde jsme si jisti, že jsme dokonale zaostřili
- Převedeme do lineárního 32-bitového floatu
- Převedeme do šedé pomocí Colors > Desaturate > Desaturate > Luminance
- Vyřízneme větší okolí hrany
- Zoomujeme kubicky na 1000%
- Vytáhneme pravítko a rotací korigujeme hranu přesně svisle nebo vodorovně
- Gaussovsky hranu rozmažeme pouze podle její délky v délce přiměřené situaci (např. 30), v kolmém směru 0.
- Vyřízneme region 1 pixel tenký tak, aby neprocházel žádnými rušivými strukturami (okny).
- Tenký řez naškálujeme na širší, abychom vůbec něco viděli.
- Adjust Color Levels přepneme na „Adjust levels in linear light“. Budou vidět 2 kopečky – odpovídají tmavé a světlé ploše – nastavíme černou a bílou úroveň na jejich vrcholy.
- Color pickerem CIE xyY bez sample average hledáme úrovně Y 0.159 a 0.841. Zapamatujeme si pixelové pozice.
- Pozice odečteme a vydělíme 10 (zoomovali jsme 10×) a ještě 2 (směrodatná odchylka na obě strany). To je směrodatná odchylka Gaussova rozdělení, které nám obrázek rozmazalo.

Vlevo: roztažený jednopixelový řez hrany na okraji budovy. Uprostřed: úrovně nastaveny, aby byla hrana mezi bílou a černou. Vpravo: odečítání pixelové pozice, na které je Y rovno pokud možno 0,841.
| Situace | Směrodatná odchylka σ rozmazání [pixely] |
|---|---|
| Budova 5 km skrz dalekohled | 1,525 |
| Budova 5 km telefonem kamerou „2ד | 0,97 |
| Budova cca. 100 m telefonem kamerou „2ד | 1,28 |
| Umělá hrana vytvořená v GIMPu | 0,55 |
Vidíme tedy, že dalekohled zhorší rozmazání obrazu z 0,97 pixelu na 1,525 pixelu. Tedy asi faktorem 1,57. Čili skutečné rozlišení optické soustavy pomocí dalekohledu 7× zvětšujícího je 4,5-násobné (7/1,57=4,5).
Souvislost mezi rozmazáním a frekvenční šířkou pásma
Představte si, že by výrobce sluchátek neudával, že sluchátka hrají do 20 kHz, ale udával by místo toho, že rozmazávají zvuk normálním rozdělením se směrodatnou odchylkou 12 μs. Co by to znamenalo? Jakou šířku pásma by sluchátka měla?
Stejně tak nás může zajímat, jaká je frekvenční odezva naší zobrazovací soustavy, když vím, že s dalekohledem mi to fotí s rozmazáním se směrodatnou odchylkou 1,525 pixelů. Nejvyšší frekvence, která v obrazu může být, je 0,5 cyklů na pixel – střídají se světlé a tmavé pixely, která odpovídá úhlové rychlosti 0,5×2π radiánů na pixel neboli π rad/pixel. To je 100% šířky pásma obrazu složeného z pixelů.
Mluvíme-li o frekvencích, čeho to jsou frekvence? Jsou to frekvence sinusovek, na které budeme naši funkci (Gaussovský kopeček) rozkládat. Původně se to dělalo jakýmsi plynovým sporákem s rotujícím zrcadlem, pak mechanickým analogovým počítačem – harmonickým analyzátorem – od toho pána, co rozbil fyziku a způsobil teorii relativity, poté jakýmsi soustruhem a nakonec přišly přístroje založené na analogových obvodech a konečně se to dělá matematicky v počítači.
Fourierova transformace je abstraktní matematická verze tohoto stroje, do kterého se vloží křivka závislosti hodnoty na čase (pro zvuk) nebo pixelové souřadnice (pro obraz) a vypadne graf, jak je který kmitočet silně zastoupen.
Pro nás je teď podstatný trik, že Gaussova funkce je vlastní funkcí Fourierovy transformace – je to taková písnička, která je současně i svým vlastním spektrem (až na vertikální škálování):
"The Fourier transform of a normal density f with mean μ and standard deviation σ is
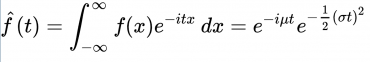
x je pozice v pixelech. t je úhlová rychlost ve spektrálním prostoru, v radiánech na pixel. σ je směrodatná odchylka. f(x) je vstupní funkce do Fourierovy transformace, v tomto případě je f(x) hustota pravděpodobnosti normálního rozdělení pro pozici μ a směrodatnou odchylku σ, tedy f(x)=σ-1(2π)-1/2e-0,5((x-μ)/σ)2
[…] the standard normal distribution φ is an eigenfunction of the Fourier transform." – Wikipedia: Normal Distribution. Fourierova transformace má dvě verze, a citát nedefinuje, která je myšlena, nemá dle mého názoru tedy žádnou matematickou informativní hodnotu pro čtenáře, který není specialistou na Fourierovu transformaci. Toto je mimochodem podle mě častý problém Wikipedie, že je nečitelná pro nespecialisty.
Budeme muset reverse engineerovat matematický strojový kód. Vidíme, že v exponentu e je výraz -itx, čili se jedná o verzi Fourierovy transformace s úhlovými rychlostmi, nikoliv frekvencemi. Kdyby to byla verze s frekvencemi, bude tam –2πitx. Citát tedy znamená, že pokud spektrum kreslíme, že na škále grafu jsou úhlové rychlosti, tak rozmazání normálním rozdělením se směrodatnou odchylkou 1 bude odpovídat spektrální odezvě, jejíž graf je (až na vertikální zoom) také normální rozdělení se směrodatnou odchylkou 1.
| Význam | Výraz |
|---|---|
| Na které pixelové pozici má kopeček vrchol | μ |
| Směrodatná odchylka: jak je kopeček široký. Lineární zoomování kopečku ve vodorovném směru. | σ |
| Standardní normální rozdělení: nezadáváme nic. μ má defaultní hodnotu 0 a σ má defaultní hodnotu 1. | f(x)=(2π)-0,5e-0,5×2 |
| Obecné normální rozdělení centrované, že vrchol kopečku je pro x=0. Zadáváme pouze směrodatnou odchylku σ. μ má defaultní hodnotu 0. | f(x)=σ-1(2π)-0,5e-0,5(x/σ)2 |
| Obecné normální rozdělení. Zadáváme jak směrodatnou odchylku σ (horizontální zoom), tak horizontální pozici vrcholu (μ). | f(x)=σ-1(2π)-0,5e-0,5((x-μ)/σ)2 |
Podle principu neurčitosti pokud fotoaparát rozmazává 2 krát širším kopečkem Gaussova rozdělení, s 2× větší směrodatnou odchylkou, pak frekvenční odezva bude 2× slabší, šířka pásma bude 2× nižší, spektrální obrázek frekvenční odezvy bude 2× užší (přímá úměra). Vidíme to v exponentu na konci výše uvedené velké rovnice, pro naši centrovanou situaci, kde μ=0 první exponenciála odpadá a druhá má v exponentu výraz σt, čili t (úhlová rychlost), se škáluje, substituuje parametrem σ, a to tak, že vyššímu σ odpovídá užší kopeček. Normálně se vstupní proměnná x písmenkem σ dělí, čímž se kopeček rozšiřuje. Tady se vstupní proměnná t písmenkem σ násobí, takže se zužuje.
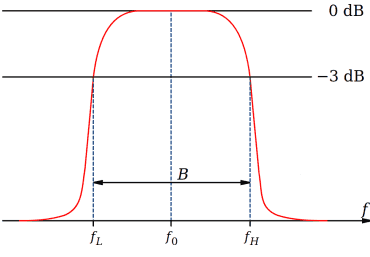
Šířka pásma se běžně udává do bodu, kde klesne o 3 dB neboli amplituda na 2-1/2=0,7071. Čili potřebujeme vědět, jaká část směrodatné odchylky odpovídá tomu, že bod na hustotě pravděpodobnostního rozdělení má výšku pouze 70,71% vrcholu kopečku.
Zařešíme si:
Provizorní závěr: pokud je obraz rozmazán gaussovským rozmazáním se směrodatnou odchylkou 1 pixel, jeho frekvenční odezva vypadá jako gaussovský kopeček se směrodatnou odchylkou 1 rad/pixel, a má šířku pásma sqrt(ln(2))=0,8326 rad/pixel. To jsme počítali pro směrodatnou odchylku σ=1. Teď si to naškálujeme σ a přepočteme radiány na cykly pomocí π:
Jestliže moje soustava má směrodatnou odchylku rozmazání σ=1,525, pak šířka pásma je 0,17 cyklů na pixel a odpovídá 35% plného rozlišení obrazu. Čili kdybychom zanedbali ztrátu rozlišení zmenšovacím algoritmem a to, že šířka pásma nepopisuje krabicové pásmo, které je rovné a náhle utne, mohli bychom obrázek v GIMPu zmenšit na 35% a o nic bychom nepřišli.
Víme teď také, že sluchátka co rozmazávají zvuk gaussovským kopečkem o směrodatné odchylce 12 μs hrají do 22 kHz.
| Směrodatná odchylka rozmazání [pixely] | Šířka pásma [cykly/pixel] | Šířka pásma [pixely/cyklus] | Šířka pásma jako šířka čáry [pixely] | Šířka pásma [% maximálního rozlišení obrazu] | Ukázka | Poznámka |
|---|---|---|---|---|---|---|
| 0 | ∞ | 0 | 0 | ∞ | ukázka | Nekonečně ostrá hrana v realitě, bez pixelizace |
| 0,53 | 0,5 | 2 | 1 | 100% | ukázka | Šířka pásma odpovídající střídajícím se tmavým a světlým pixelům. Zhruba rozmazání naší měřící metody (ve skutečnosti rozmazání kubického zvětšování v GIMPu). Zhruba rozmazání difrakcí na čočce kamery „2ד iPhone X. |
| 1 | 0,265 | 3,77 | 1,89 | 53% | ukázka | Zhruba rozmazání samotné kamery „2ד iPhonu X |
| 1,525 | 0,174 | 5.74 | 2.87 | 35% | ukázka | Toto rozmazání jsem naměřil u budovy na mnohakilometrovou vzdálenost u dalekohledu Bausch & Lomb 7×50 a iPhone X kamery „2ד |
| 2 | 0,133 | 7,54 | 3,77 | 27% | ukázka | |
| 3 | 0,088 | 11,32 | 5,66 | 18% | ukázka |
Vidíme, že šířka pásma fotoaparátu telefonu bez dalekohledu je jen asi 50% maximální možné, protože má rozmazání se směrodatnou odchylkou kolem 1 pixelu. Vysvětluji si to součtem různých jevů:
- difrakcí na apertuře čočky. Kamera „2ד má aperturu 2,5 mm neboli 4500 vlnových délek, na které světlo utrpí difrakci, jejímž efektem je neostrý bod, tzv. Airyho disk. Píší, že se dobře aproximuje Gaussovým profilem, a pokud chceme vypočítat směrodatnou odchylku, do jejich vzorečku místo 1,22 dosadíme 0,42. Vemu vlnovou délku největší citlivosti oka 555 nm a vyjde mi směrodatná odchylka rozmazání 93 μrad. Ze staršího článku víme, že tato kamera „2ד má rozlišení 165 μrad. Čili směrodatná odchylka vlivem difrakce způsobuje rozmazání 0,56 pixelu.
- Senzor by správně měl mít optický rozmazávací filtr (AAF, AA, OLPF, blur filter).
- Hrana se někdy trefí napůl cesty mezi 2 pixely, a tak se zbytečně rozmaže
- Možná je obtížné vytvořit čočku s odpovídající ostrostí pro rozlišení 4032×3024
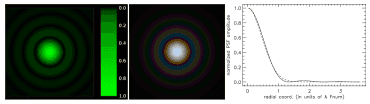
Vypočtený Airyho disk pro jednu vlnovou délku (vlevo) a součet různě velkých Airyho disků pro různé vlnové délky (uprostřed). Vpravo vidíme, jak se Airyho disk pro jednu vlnovou délku (plná čára) dá krásně aproximovat Gaussovou křivkou (přerušovaná). Vodorovná osa: rozdíl vzdáleností bodu CMOS senzoru od pravého a levého okraje čočky vyjádřený ve vlnových délkách. Svislá osa: jas.
(Autorem fotografií je Karel Kulhavý, není-li uvedeno jinak.)