Stochastické fraktály

Obsah

1. Úvodní informace o nepravidelných (náhodných, stochastických) fraktálech
   1.1 Simulace Brownova pohybu (Brownian Motion)
   1.2 Metoda přesouvání prostředního bodu (Midpoint Displacement Method)
   1.3 Spektrální syntéza (Spectral Synthesis)
2. Simulace difúze
3. Princip práce metody aplikace Brownova pohybu
4. Trajektorie Brownova pohybu
5. Skalární Brownův pohyb
6. Zlomkovitý Brownův pohyb
7. Literatura a odkazy na internetu
8. Obsah dalšího pokračování tohoto seriálu

1. Úvodní informace o nepravidelných (náhodných, stochastických) fraktálech

Rozsáhlou a v tomto seriálu až do dneška zcela opomíjenou skupinou fraktálů jsou nepravidelné neboli náhodné či také stochastické fraktály. Zatímco všechny předchozí skupiny (resp. typy) fraktálních útvarů byly v určitém smyslu měřítkově symetrické, tj. soběpodobné, nepravidelné fraktály vnáší při svém generování do algoritmu náhodu, tj. jsou „pouze“ soběpříbuzné, nikoli soběpodobné). Při praktické implementaci algoritmů na počítačích se však místo pravé náhody musíme spolehnout na pseudonáhodné generátory čísel – PRNG. Tento typ fraktálů také umožňuje zdaleka nejlepší popis přírodních objektů.

Zatímco při generování stromu klasickým L-systémem nebo IFS koláží dostaneme jako výsledek perfektně symetrický strom, je skutečnost už na první pohled zcela jiná. Strom rostoucí v přírodě má nepravidelné délky a tloušťky větví, úhel růstu větví také není vždy stejný, strom rostoucí v lese má jiný tvar než tentýž druh stromu rostoucí osamoceně apod. Z těchto důvodů je velmi vhodné zavést do generování fraktálů náhodu. Způsob, jakým se náhodnost bude podílet na procesu generování fraktálů, bude vždy určovat tvar fraktálu a současně i jeho Hausdorffovu dimenzi. Pro generování náhodných čísel se používá například gaussovský generátor nebo generátor bílého šumu, některé postupy však vyžadují odlišný PRNG.

Náhodné fraktály můžeme vytvářet více způsoby. První způsob spočívá v simulaci Brownova pohybu buď v ploše nebo v prostoru. Druhý způsob spočívá v použití metody přesouvání středního bodu a třetí způsob využívá spektrální syntézu. Pojďme si nyní v krátkosti jednotlivé metody tvorby stochastických fraktálů popsat:

1.1 Simulace Brownova pohybu (Brownian Motion)

Během simulace Brownova pohybu (známého z molekulární fyziky a postupně zkoumaného mnoha světoznámými vědci) se vytváří fraktální objekt, jehož Hausdorffova dimenze je úměrná absolutní velikosti změny při jednom iteračním kroku. Tato metoda se používá například při generování modelů tekoucích řek. Není příliš vhodná pro trojrozměrné objekty, a to ze stejného důvodu, jaký vedl k problémům u trojrozměrných systémů iterovaných funkcí IFS – vytvořený model se skládá z jednotlivých bodů a dnešní grafické akcelerátory mají s těmito entitami značné problémy, protože jsou optimalizovány na vykreslování trojúhelníků a dalších plošných entit. Existují však i specializované postupy a dokonce hardwarové prostředky zaměřené na vykreslování jednotlivých bodů či orientovaných plošek (surfelů) v prostoru.

Obrázek 1: Ukázka stochastického fraktálu napodobujícího travinu či keřík, který vznikl aplikací algoritmu difúze (simulací Brownova pohybu)

1.2 Metoda přesouvání prostředního bodu (Midpoint Displacement Method)

Mezi typické metody generování stochastických fraktálů patří metoda přesouvání prostředního bodu, aplikovatelná jak na ploše, tak i v trojrozměrném prostoru. Tato metoda se velmi často používá v počítačové grafice k vygenerování a následné vizualizaci přírodní krajiny, povrchů vesmírných těles apod. Volbou maximální odchylky při posunu prostředního bodu je možné lze měnit celkový ráz krajiny od pouště přes pahorkatinu až po vysokohorskou krajinu. Maximální odchylka a průběh jejího klesání také určuje Hausdorffovu dimenzi vytvořeného modelu.

Obrázek 2: Postupné vytváření a zjemňování modelu krajiny pomocí metody přesouvání prostředního bodu

1.3 Spektrální syntéza (Spectral Synthesis)

Další často používanou metodou je spektrální syntéza, která vychází z principu výpočtu Fourierovy řady. Metoda spočívá v tom, že náhodně vygenerujeme Fourierovy obrazy, které mají spektrální hustotu úměrnou zadané Hausdorffově dimenzi. Potom provedeme inverzní Fourierovu transformaci s těmito koeficienty. Výsledkem je fraktální objekt. Pomocí této metody lze generovat – podobně jako metodou předchozí – krajiny, hory či povrchy planet. Výhodou je, že lze přímo zadat požadovanou Hausdorffovu dimenzi výsledného objektu.

Obrázek 3: Model krajiny vytvořený pomocí stochastických fraktálů

2. Simulace difúze

Po krátkém seznámení se základními typy stochastických fraktálů se budeme věnovat velmi zajímavé a přitom téměř nepoužívané metodě, pomocí které je možné vytvářet tvarově složité přírodní útvary, například modely stromů, keřů nebo trávy. Prostorové útvary, jež jsou vygenerované touto metodou, se vyznačují částečnou (statistickou) soběpodobností (tj. soběpříbuz­ností), velkou tvarovou složitostí a fraktální strukturou (jak jsem se již zmínil v několika předchozích částech tohoto seriálu, patří soběpodobnost mezi význačné vlastnosti fraktálních objektů). Pro zvýšení modelovacích schopností popisované metody difúze a rychlosti vytváření modelu zde také bude popsána zcela nová metoda návrhu omezujících podmínek, které je zapotřebí při generování prostorových útvarů dodržet. Pomocí omezujících podmínek lze měnit charakteristiku vytvářených těles ve větší části prostoru, zatímco změnou parametrů algoritmu difúze se mění jak celkový vzhled modelu, tak i lokální hustota a charakter vytvářených tvarů.

Výsledkem aplikace dále popsaných metod, postupů a algoritmů jsou plošné či prostorové modely přírodních útvarů, které jsou pro účely zobrazení složeny z orientovaných elementárních prvků plochy (surfelů) či neorientovaných bodů, jež se nachází v prostoru E³ (částice) nebo na ploše E² (body, speciálně po diskretizaci do pravidelné bitmapy pixely). Z geometrického hlediska jsou tyto modely tvořeny stochastickými fraktály, jejichž fraktální dimenze se může pohybovat v rozmezí od nuly do tří. Na dalším obrázku je zobrazen plošný (rastrový) model traviny, který vznikl aplikací dále popsaného algoritmu difúze. Mezi nejzávažnější důvody, kvůli kterým není tato metoda při tvorbě modelů přírodních těles více používaná, patří především dvě skutečnosti:

1. Prvním důvodem je fakt, že proces vytváření trojrozměrného modelu je sice algoritmicky jednoduchý, ale extrémně časově náročný, zejména v případě tvorby prostorového modelu. Velkou časovou složitost je však možné částečně zmenšit vhodným omezením prostoru pro nově vytvářené body. Bližší informace o omezujících podmínkách, které pro urychlení vytváření modelu navrhuji, budou podány v dalších odstavcích a pokračováních, stejně jako další možné modifikace algoritmu difúze.
2. Druhý důvod spočívá ve vlastní formě vzniklého modelu. Jedná se totiž o množinu jednotlivých bodů či elementárních plošek bez vzájemných explicitních vazeb, které je značně obtížné až nemožné efektivně převést do polygonální hraniční reprezentace – převod je samozřejmě možný, ale výsledkem je velké množství malých trojúhelníčků, které se musí vykreslovat. Zde se ukazuje velká výhoda použití bodových primitiv (orientovaných surfelů a neorientovaných částic), neboť body vytvářené algoritmem difúze můžeme za tyto stavební prvky scény jednoduše zaměnit a žádné složité převody neprovádět.

Obrázek 4: Další model keře vytvořený metodou simulace difúze

3. Princip práce metody aplikace Brownova pohybu

Princip práce této metody pro vytváření fraktálních objektů vychází ze simulace difúze, což je (velmi zjednodušeně řečeno) přírodní jev, při kterém jsou pevné, kapalné či plynné částečky jedné hmoty postupně roznášeny v jiné kapalné či plynné hmotě. Pohyb těchto částeček, který se nazývá Brownovým pohybem (Brownian Motion), vzniká vlivem náhodných nárazů molekul jedné hmoty a hmoty druhé – viz další ilustrační obrázek. Poprvé byl Brownův pohyb popsán jako pohyb mikroskopických částeček pylu ve vodě. Zdůvodnění fyzikální podstaty tohoto pohybu však bylo podáno až Einsteinem v roce 1905.

Základem pro studium různých rozšíření a zobecnění Brownova pohybu je takzvaný Weinerův skalární Brownův pohyb. Jedná se o gaussovskou náhodnou funkci B(t) ze skaláru t do skaláru B, pro kterou musí platit následující rovnost:

E(B(t)-B(0))² = t^2H

Kde pro Weinerův skalární Brownův pohyb navíc platí omezení, že H=1/2:

E(B(t)-B(0))² = t^2×1/2 = t

Vzhledem k tomu, že Weinerův skalární Brownův pohyb představuje pouze dále neredukovatelný základ teorie Brownova pohybu, je možné provést několik zobecnění, z nichž ty nejvýznamnější jsou popsány v následujícím seznamu:

1. První zobecnění Weinerova skalárního Brownova pohybu do obecnějšího tvaru spočívá v náhradě původního skaláru B n-dimenzionálním vektorem či bodem (v souvislosti s Brownovým pohybem není zapotřebí rozlišovat mezi bodem a vektorem) B, jehož všechny souřadnice představují samostatné, na sobě nezávislé Brownovy pohyby.
2. Druhé zobecnění, které je však vytvořeno nezávisle na zobecnění prvním, protože B je v tomto případě opět skalár, spočívá v náhradě původně konstantní hodnoty H=1/2 za hodnotu jinou. Nová hodnota však vždy musí ležet v rozsahu od 0 do 1. Toto zobecnění vede k popisu takzvaného zlomkovitého Brownova pohybu fBm, jehož základní vlastnosti budou popsány v následujících odstavcích.
3. Třetí zobecnění Weinerova skalárního Brownova pohybu spočívá v náhradě skaláru t bodem P. V dalším textu budu beze ztráty obecnosti předpokládat, že se jedná o bod z E² nebo E³, Brownův pohyb je však možné specifikovat v libovolném prostoru, nad kterým je definována metrika (tj. pojem vzdálenosti dvou bodů).

Z hlediska využití Brownova pohybu při simulaci difúze je důležité, že lze všechna tři výše popsaná zobecnění vzájemně kombinovat a vytvořit tak například Brownův pohyb, ve kterém je B vektorem v E² nebo E³ a konstanta H může nabývat libovolné hodnoty od 0 do 1. Možné jsou i další kombinace výše zmíněných zobecnění Brownova pohybu.

V dalším textu se budu zabývat především Brownovým pohybem B_H(t), který může být popsán následovně: pro každou dvojici časových okamžiků t_i a t_i+Δt>t_i se definuje vektor přemístění bodu (v reálném světě se bezrozměrný hmotný bod stává částečkou hmoty s nenulovým objemem) jakožto vektor v_i jdoucí od bodu P(t_i) do bodu P(t_i+Δt):

v_i=P(t_i+Δt) – P(t_i)

Tento vektor musí splňovat následující tři podmínky:

1. Směr i délka vektoru v_i není závislá ani na počáteční poloze bodu P(t_i) ani na polohách bodu P(t) v okamžicích předcházejících času t_i. Zjednodušeně řečeno lze říci, že systém nemá „paměť“ svých předchozích vztahů.
2. Vektor v_i je izotropní, tj. jeho velikost je nezávislá na směru a orientaci.
3. Délka vektoru v_i je taková, že průmět vektoru (resp. množiny vektorů) na jakoukoli souřadnou osu splňuje gaussovské rozdělení.

Obrázek 5: Středový fraktál vytvořený pomocí simulace difúze

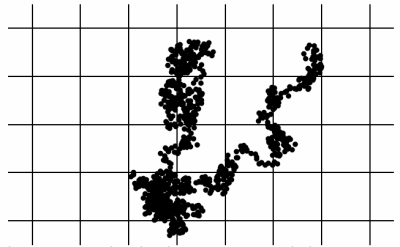
4. Trajektorie Brownova pohybu

Trajektorii Brownova pohybu, resp. pohybu jednotlivých částeček hmoty, jejichž polohu v rovině E² či prostoru E³ je možné změřit, můžeme schematicky znázornit lomenou čarou (polyčarou – polyline), která vznikne spojením vrcholů představujících polohu částeček – hmotných bodů – P(t_i), jež jsou změřené v konstantních časových intervalech. Počet bodů P(t) a tím i tvar a přesnost lomené čáry však závisí na zvolené časové posloupnosti T={t₀, t_0+Δt, … t_0+n×Δt}, zejména na počátečním čase t₀ a časovém intervalu Δt.

Pokud by byly časové intervaly Δt mezi měřením poloh částeček příliš velké, vznikla by lomená čára s malým počtem bodů, která by pouze hrubě odpovídala skutečné trajektorii částečky. Pokud by naopak byly zvoleny menší časové intervaly, zvětšil by se počet bodů tvořících vrcholy lomené čáry a tím by se obraz trajektorie Brownova pohybu zjemnil a současně i zpřesnil. Zmenšování časových intervalů lze teoreticky provádět až k limitnímu případu:

t_i-t_i+Δt → 0

V takovém případě se lomená čára, jež znázorňuje trajektorii Brownova pohybu, rozpadne na křivku reprezentovanou nekonečným počtem bodů a délka trajektorie je v tomto (ryze teoretickém) případě nekonečná, což implikuje fraktální podstatu trajektorie Brownova pohybu. Prakticky se však částečky hmoty pohybují po trajektorii, jejíž délka je konečná, tj. existuje určité měřítko pohledu, při kterém by bylo možné nalézt části trajektorie reprezentované úsečkou či spojitou křivkou (ve skutečnosti se však spíše bude jednat o skoky).

Obrázek 6: Brownův pohyb jedné částice

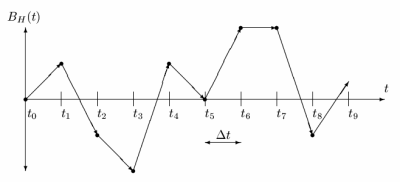
5. Skalární Brownův pohyb

Mezi nejjednodušší Brownův pohyb patří skalární Brownův pohyb, u kterého jsou výsledkem funkce B_H(t) jednorozměrné body – skaláry. Tento Brownův pohyb je možné zobrazit pomocí grafu, na jehož horizontální osu jsou vynášeny časové okamžiky t_i a na vertikální osu polohy jednorozměrných bodů v těchto okamžicích B_H(t_i). Ukázka skalárního Brownova pohybu je zobrazena na následujícím obrázku. Skalární Brownův pohyb lze zobecnit do n-rozměrů tak, že každá souřadnice bodů trajektorie bude generovaná vlastní funkcí Brownova pohybu, která je nezávislá na funkcích ostatních.

Obrázek 7: Skalární Brownův pohyb

6. Zlomkovitý Brownův pohyb

Zlomkovitý Brownův pohyb fB_H(t) vzniká modifikací skalárního Brownova pohybu jeho zjemněním, čímž se ve všech měřítkách zmenšuje jeho nepravidelnost. Intenzita tohoto zjemnění, a tudíž i perzistence úrovní, závisí na jediném parametru H_Є(0,1). Hodnota H=1/2 je dohodou stanovena tak, že představuje nemodifikovaný Brownův pohyb, u kterého žádné zjemnění (či naopak zesílení) nepravidelnosti neexistuje – viz též předchozí rovnice. Perzistence úrovní vzrůstá s tím, jak hodnota H roste od 1/2 do 1, pro H jdoucí k nule perzistence úrovní naopak klesá. Dále platí důležité tvrzení, že fraktální dimenze zlomkovitého Brownova pohybu D odpovídá hodnotě 1/H. Pro nemodifikovaný skalární Brownův pohyb s H=1/2 tedy platí následující vztah:

D=1/H=1/(1/2)=2

Jelikož H je vždy menší než 1, musí nutně platit D>1, vždy se tedy jedná o spojitou křivku, nikoli o izolované body. Pro 0<H<1/2 se trajektorie Brownova pohybu „zamotává“ (jednotlivé body se překrývají) a její fraktální dimenze je větší než 2, tedy větší než topologická dimenze plochy E²!

Obrázek 8: Stopa pohybu částice provádějící zlomkovitý Brownův pohyb

7. Literatura a odkazy na internetu

1. Barnsley Michael, Devaney R. L., Mandelbrot Benoit B., Peitgenn Heinz-Otto, Saupe Dietmar, Voss Richard: <i>The Science of Fractal Images</i>,
   Springer-Verlag, New York, 1988
2. Mandelbrot Benoit B.: <i>The Fractal Geometry of Nature</i>,
   W. H. Freeman, New York; San Francisco, 1982, ISBN 0–7167–1186–9
3. Wegner Timothy, Peterson Mark: <i>Fractal Creations, First Edition</i>,
   The Waite Group Press, 1991
4. Wegner Timothy, Tyler Bert: <i>Fractal Creations, Second Edition</i>,
   The Waite Group Press, 1993
5. Wegner Timothy, Tyler Bert, Peterson Mark, Branderhorst Pierer: <i>Fractals for Windows</i>,
   The Waite Group Press, 1992
6. Žára J., Beneš B., Felkel P.: <i>Moderní počítačová grafika</i>,
   Computer Press, Praha, 1998, ISBN 80–7226–049–9
7. Žára J., Limpouch A., Beneš B., Werner T.: <i>Počítačová grafika &#8211; principy a algoritmy</i>,
   Grada, 1992

Obrázek 9: „Plasma“ vytvořená metodou přesouvání prostředního bodu

8. Obsah dalšího pokračování tohoto seriálu

V následujícím pokračování tohoto seriálu si popíšeme metodu pro simulaci difúze, která je založená na heuristice. Také si popíšeme některé způsoby urychlení celé simulace a její následné využití pro vytváření plošných i trojrozměrných modelů travin a keřů. Všechny popisované postupy budou samozřejmě implementované v demonstračních příkladech.