Obsah
1. Balíček scikit-learn: modely provádějící regresní analýzu
2. Regresní analýza a lineární regrese
3. Datová sada California housing
4. Přístup k atributům jednotlivých domů, zjištění jmen atributů i cen domů
5. Korelační diagram pro dvojici vybraných proměnných
6. Korelační diagram pro všechny kombinace dvojic proměnných
7. Dvourozměrné hodnoty reprezentované jako dvojice atributů
9. Model LinearRegression nad uměle vytvořenými daty
10. Predikce modelu provádějícího lineární regresi
11. Chování modelu pro zcela náhodná data
12. Výpočet chyby – základní metriky modelu lineární regrese
13. Praktický příklad: výpočet chyby a skóre modelu pro čtyři odlišné datové sady
14. Predikce modelu pro datovou sadu California housing
15. Lineární regrese nad daty s nelineární závislostí
17. Polynomická regrese nad daty s nelinearitou
18. Vyšší stupeň polynomu = lepší model?
19. Repositář s demonstračními příklady
1. Balíček scikit-learn: modely provádějící regresní analýzu
V předchozím článku o knihovně scikit-learn jsme si ukázali některé základní koncepty, které se aplikují při práci s modely provádějícími takzvanou klasifikaci. Jedná se o takové modely, které pro nějaká (neznámá) vstupní data odhadnou, resp. přesněji řečeno vypočítají hodnotu, která patří do nějaké spočetné (a typicky relativně malé) množiny. Příkladem může být model, který rozpoznává číslice na obrázku. Výsledkem je potom celočíselná hodnota v rozsahu „0“ až „9“.
A samozřejmě i naše jednoduché modely určené pro rozpoznávání druhů kosatců odpovídaly celočíselnými hodnotami „0“ až „2“, které jsou přiřazeny druhům „Iris setoza“, „Iris versicolor“ a „Iris virginica“. Nebo se například může jednat o model, kterému se předá e-mail a výsledkem bude hodnota „spam“ nebo „není to spam“. Podobných modelů a příkladů klasifikace lze najít velké množství.
2. Regresní analýza a lineární regrese
Existuje však ještě jeden typ problémů, které lze řešit s využitím (natrénovaných) modelů. U těchto problémů očekáváme, že model odpoví nějakou číselnou hodnotou, která ovšem typicky sice spadá do nějakého intervalu, ale hodnoty netvoří nějakou malou množinu a typicky se ani nejedná o hodnoty celočíselné. Příkladem mohou být modely předpovídající nějakou událost v rozsahu 0–100%, modely naznačující, kolik akcií koupit nebo prodat (kladná či záporná hodnota), model který na základě různých zadaných údajů odhadne cenu nemovitosti atd. – takových problémů a jejich řešení pomocí modelů opět existuje celá řada.
Modely s tímto typem odpovědí se nazývají modely provádějící regresní analýzu. Nejjednodušší je přitom využití lineární regrese, která je velmi užitečná, protože parametrům regresní přímky je typicky možné přiřadit reálný význam – a tak pochopit, co se vlastně model naučil a jaké fakty si odvodil (to u složitějších modelů bývá problematické).
3. Datová sada California housing
V dnešním článku využijeme datovou sadu, která je součástí knihovny scikit-learn. Tato datová sada se jmenuje California housings a obsahuje parametry domů (resp. celých bloků) a jejich cenu. Cena může být prakticky libovolná, takže tuto datovou sadu skutečně budeme zpracovávat pomocí modelů provádějících regresní analýzu.
Načtení datové sady California housings je prakticky stejně snadné, jako načtení sady Iris. Je zde ovšem jedna změna – při prvním spuštění příkladu se stáhne soubor cal_housing_py3.pkz, který se uloží v domovském adresáři do podadresáře scikit_learn_data. Tento soubor je následně používán:
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# jakeho typu je vlastne datova sada?
print(type(housings))
print("-" * 100)
# dostupne atributy a metody
print(dir(housings))
Načtená datová sada je opět typu Bunch a obsahuje nám známé atributy:
<class 'sklearn.utils._bunch.Bunch'> ---------------------------------------------------------------------------------------------------- ['DESCR', 'data', 'feature_names', 'frame', 'target', 'target_names']
Pro zajímavost si zobrazme i metainformace o načtené datové sadě:
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
print(dir(housings))
print("-" * 100)
# podrobny popis datove sady
print(housings["DESCR"])
Výsledek:
['DESCR', 'data', 'feature_names', 'frame', 'target', 'target_names']
----------------------------------------------------------------------------------------------------
.. _california_housing_dataset:
California Housing dataset
--------------------------
**Data Set Characteristics:**
:Number of Instances: 20640
:Number of Attributes: 8 numeric, predictive attributes and the target
:Attribute Information:
- MedInc median income in block group
- HouseAge median house age in block group
- AveRooms average number of rooms per household
- AveBedrms average number of bedrooms per household
- Population block group population
- AveOccup average number of household members
- Latitude block group latitude
- Longitude block group longitude
:Missing Attribute Values: None
This dataset was obtained from the StatLib repository.
https://www.dcc.fc.up.pt/~ltorgo/Regression/cal_housing.html
The target variable is the median house value for California districts,
expressed in hundreds of thousands of dollars ($100,000).
This dataset was derived from the 1990 U.S. census, using one row per census
block group. A block group is the smallest geographical unit for which the U.S.
Census Bureau publishes sample data (a block group typically has a population
of 600 to 3,000 people).
A household is a group of people residing within a home. Since the average
number of rooms and bedrooms in this dataset are provided per household, these
columns may take surprisingly large values for block groups with few households
and many empty houses, such as vacation resorts.
It can be downloaded/loaded using the
:func:`sklearn.datasets.fetch_california_housing` function.
.. topic:: References
- Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,
Statistics and Probability Letters, 33 (1997) 291-297
4. Přístup k atributům jednotlivých domů, zjištění jmen atributů i cen domů
Samotné informace o domech/blocích jsou dostupné v atributu nazvaném data, popř. pod klíčem „data“, pokud budeme k datové sadě přistupovat tak, jakoby se jednalo o slovník. Všechny atributy jsou uloženy formou n-dimenzionálního pole knihovny NumPy, což je datová struktura, se kterou jsme se již na Rootu několikrát setkali. V tomto konkrétním případě bude pole dvourozměrné, takže si ho můžeme představit jako matici se 20640 řádky (počet záznamů) a osmi sloupci:
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
print("Feature data:")
print(data)
print("-" * 100)
# typ a "tvar" n-dimenzionalniho pole
print("Data type:")
print(type(data))
print()
print("Data shape:")
print(data.shape)
Takto by měly vypadat výsledky (samotné pole je zobrazeno ve zkrácené podobě):
Feature data:
[[ 8.3252 41. 6.98412698 ... 2.55555556
37.88 -122.23 ]
[ 8.3014 21. 6.23813708 ... 2.10984183
37.86 -122.22 ]
[ 7.2574 52. 8.28813559 ... 2.80225989
37.85 -122.24 ]
...
[ 1.7 17. 5.20554273 ... 2.3256351
39.43 -121.22 ]
[ 1.8672 18. 5.32951289 ... 2.12320917
39.43 -121.32 ]
[ 2.3886 16. 5.25471698 ... 2.61698113
39.37 -121.24 ]]
----------------------------------------------------------------------------------------------------
Data type:
<class 'numpy.ndarray'>
Data shape:
(20640, 8)
Jednotlivé atributy (taktéž proměnné), což jsou v našem konkrétním případě atributy domů/bloků, jsou pojmenovány, přičemž tato jména nalezneme v atributu objektu typu Bunch, který se jmenuje feature_names, popř. pod stejně pojmenovaným klíčem. Jedná se o pole obsahující osmici řetězců obsahujících jak měřenou veličinu, tak i její jednotku. V atributu target_names je nyní jediná položka: cena domu. A jednotlivé ceny jsou uloženy v atributu targets. Jedná se o vektor (tedy vlastně o jednorozměrné pole) s 20640 prvky:
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# jmena atributu
print("Feature names:")
print(housings["feature_names"])
print("-" * 100)
# vazba mezi numerickou hodnotou a lidskym vyjadrenim hodnoty
# atributu
print("Target names:")
print(housings["target_names"])
print("-" * 100)
# druhy rostlin z datove sady v numericke podobe
print("Targets:")
print(housings["target"])
Opět se podívejme na zobrazené výsledky:
Feature names: ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude'] ---------------------------------------------------------------------------------------------------- Target names: ['MedHouseVal'] ---------------------------------------------------------------------------------------------------- Targets: [4.526 3.585 3.521 ... 0.923 0.847 0.894]
5. Korelační diagram pro dvojici vybraných proměnných
Podobně jako u sady Iris i nyní můžeme při zkoumání dat začít klasickým korelačním diagramem a zjistit, jaký je vztah (například) mezi dvěma proměnnými (vyberme MedInc a AveRooms, tedy medián příjmů a průměrný počet místností pro domácnost – zajímavá volba pro korelaci). To je pro knihovnu Matplotlib snadný úkol. Užitečné je ovšem vědět, jak z pole (matice) s rozměry květů získat příslušné sloupce. Navíc jednotlivé body korelačního diagramu obarvíme podle zjištěné ceny (tuto informaci máme k dispozici a používá se pro trénink modelů, jak již víme):
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# vykresleni korelacniho diagramu pro dvojici vybranych atributu
# prvni sloupec: x-ove souradnice
# druhy sloupec: y-ove souradnice
plt.scatter(data[:, 0], data[:, 2], c=housings.target, s=2)
plt.title("Classes")
# popisky os
plt.xlabel(housings.feature_names[0])
plt.ylabel(housings.feature_names[2])
# ulozeni diagramu do souboru
plt.savefig("76.png")
# zobrazeni diagramu
plt.show()
Výsledek by mohl vypadat následovně:
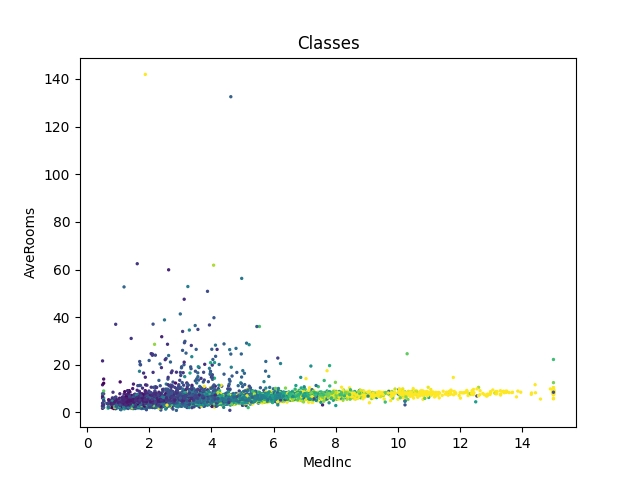
Obrázek 1: Korelace (existuje?) mezi mediánem příjmů (MedInc) a průměrným počtem místností (AveRooms) v domácnosti. Barevně jsou odlišeny ceny jednotek, které (zdá se) více odpovídají mediánu příjmů. Ovšem to za nás již zjistí model.
Podobně si můžeme zobrazit závislost mezi celkovým počtem místností v bloku a počtem ložnic. Zde již očekáváme skutečnou korelaci:
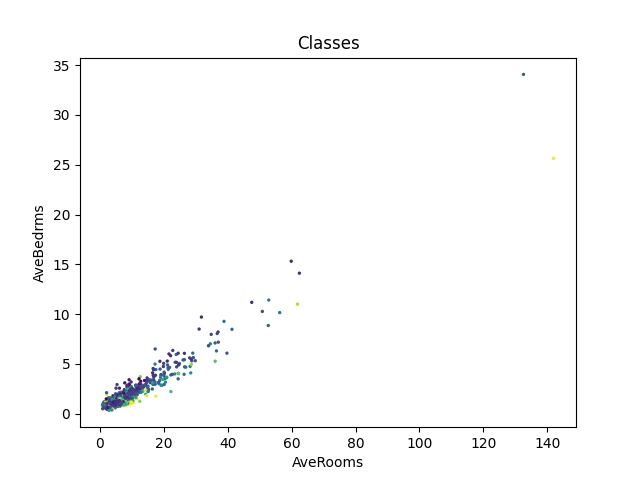
Obrázek 2: Korelace mezi celkovým počtem místností v bloku a počtem ložnic (AveRooms, AveBdrms).
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
FIRST_DIM = 2
SECOND_DIM = 3
# vykresleni korelacniho diagramu pro dvojici vybranych atributu
# prvni sloupec: x-ove souradnice
# druhy sloupec: y-ove souradnice
plt.scatter(data[:, FIRST_DIM], data[:, SECOND_DIM], c=housings.target, s=2)
plt.title("Classes")
# popisky os
plt.xlabel(housings.feature_names[FIRST_DIM])
plt.ylabel(housings.feature_names[SECOND_DIM])
# ulozeni diagramu do souboru
plt.savefig("76_B.png")
# zobrazeni diagramu
plt.show()
6. Korelační diagram pro všechny kombinace dvojic proměnných
V datové sadě, kterou zpracováváme, je pro každý blok domů uloženo celkem osm atributů, ovšem v korelačním diagramu dokážeme přiměřeným způsobem zobrazit vztahy mezi dvěma atributy, maximálně mezi třemi atributy (když zobrazíme 3D diagram, který ovšem ztrácí přehlednost). Abychom zjistili, mezi jakou kombinací atributů existuje nějaký vztah (pokud existuje), budeme muset skutečně zobrazit všechny možné kombinace, což je ukázáno v dalším skriptu:
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# vykresleni mrizky korelacnich diagramu
fig, axes = plt.subplots(nrows=8, ncols=8)
# rozmery vysledneho obrazku
fig.set_figheight(15)
fig.set_figwidth(15)
# vyplneni mrizky
for row in range(8):
for column in range(8):
ax = axes[row][column]
if row == column:
# na diagonale jsou prazdna mista
fig.delaxes(ax)
continue
# pridat korelacni diagram do mrizky
# sloupec row: x-ove souradnice
# sloupec column: y-ove souradnice
scatter = ax.scatter(data[:, row], data[:, column], c=housings.target, s=1)
# popisky os
ax.set(xlabel=housings.feature_names[row], ylabel=housings.feature_names[column])
# zbavit se prazdneho mista okolo bunek mrizky
plt.tight_layout()
# ulozeni diagramu do souboru
plt.savefig("77.png")
# zobrazeni diagramu
plt.show()
Výsledek může vypadat následovně:
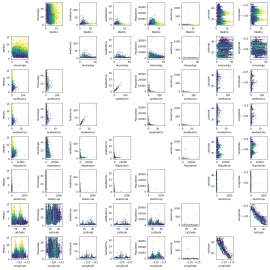
Obrázek 3: Všechny kombinace korelací dvou atributů (proměnných).
7. Dvourozměrné hodnoty reprezentované jako dvojice atributů
Mnohdy se setkáme s tím, že vícerozměrné hodnoty jsou v datové sadě reprezentované jako dvojice, trojice atd. atributů, protože scikit-learn každý záznam chápe jako jednorozměrné pole (vektor). To je ostatně i případ datové sady California housings, protože sedmý a osmý atribut obsahují souřadnice bloku (zeměpisnou výšku a délku). Ostatně nejlépe bude význam těchto dvou atributů patrný ve chvíli, kdy si je vykreslíme do korelačního diagramu. To je snadné:
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
FIRST_DIM = 6
SECOND_DIM = 7
# vykresleni korelacniho diagramu pro dvojici vybranych atributu
# prvni sloupec: x-ove souradnice
# druhy sloupec: y-ove souradnice
plt.scatter(data[:, FIRST_DIM], data[:, SECOND_DIM], s=2)
plt.title("Classes")
# popisky os
plt.xlabel(housings.feature_names[FIRST_DIM])
plt.ylabel(housings.feature_names[SECOND_DIM])
# ulozeni diagramu do souboru
plt.savefig("78.png")
# zobrazeni diagramu
plt.show()
Výsledek by přitom měl vypadat následovně:
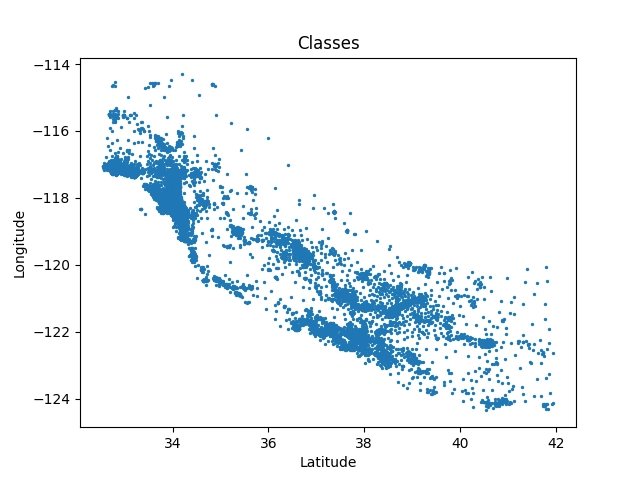
Obrázek 4: Vynesením souřadnic bloků jsme vlastně do určité míry získali mapu zastavění sledované oblasti.
8. Regresní analýza
Prozatím jsme datovou sadu California housings zkoumali pouze základními vizualizačními prostředky; nyní ovšem konečně přichází na řadu použití modelů. V dnešním článku se zaměříme především na model založený na klasické regresní analýze, konkrétně s využitím lineární regrese. Jedná se o interně velmi jednoduchý model, což je velká výhoda i nevýhoda současně. Výhodou je, že po naučení (natrénování) si můžeme zobrazit koeficienty modelu a mnohdy z nich pochopit, co se model vlastně naučil a jaké jsou skutečné vztahy mezi atributy (proměnnými) a výslednou hodnotou. To je mnohdy velmi důležité. Nevýhodou je to, že zdaleka ne všechny závislosti v reálném světě mají lineární charakter (tedy například že pravděpodobnost nakažení nějakou přenosnou nemocí závisí lineárně na času stráveného s nemocným a taktéž lineárně na jeho věku a řekněme váze). Při nelineárních závislostech je vhodnější použít komplikovanější modely, k nimž se ostatně ještě později vrátíme.
9. Model LinearRegression nad uměle vytvořenými daty
Ukažme si nyní použití modelu nazvaného LinearRegression pro proložení nějakých (pseudo)naměřených dat přímkou, tedy polynomem stupně jedna. Jedná se o klasickou lineární regresi používanou v mnoha technických oborech. Povšimněte si, že hodnoty na x-ové ose pravidelně rostou, zatímco na y-ové ose hodnoty sice taktéž obecně rostou, ale navíc jsou náhodně modifikovány:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
VALUES = 50
x = np.linspace(0, 10, VALUES)
y = np.linspace(-1, 1, VALUES) + 0.5*np.random.rand(VALUES)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(x.reshape(-1, 1), y)
# predikce modelu
y_pred = lr.predict(x.reshape(-1, 1))
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# vykreslení výsledku
plt.scatter(x, y, color="black", s=2)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title("Linear regression")
# osy
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig("79.png")
# zobrazeni diagramu
plt.show()
Skript po svém spuštění nejdříve vypíše koeficient regresního modelu, což je vlastně směrnice úsečky, kterou jsou data proložena. Dále se vypíše hodnota odpovídající y-ovému posunu:
Coefficients: [0.1991314] Intercept: -0.7428300973657997
A samozřejmě se vykreslí jak body, pro které se lineární regrese počítala a úsečka vypočtená modelem:
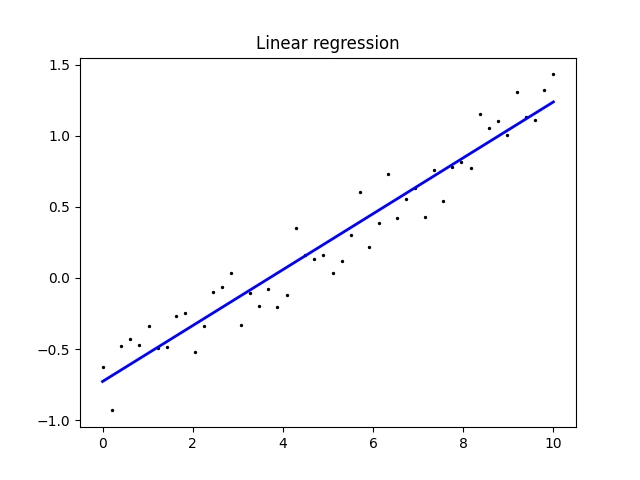
Obrázek 5: Proložení bodů úsečkou (lineární regrese) tak, aby čtverec chyb byl co nejmenší.
Pokusme se nyní z dat odstranit náhodnost, což znamená, že všechny body budou ležet na stejné přímce:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
VALUES = 50
x = np.linspace(0, 10, VALUES)
y = np.linspace(-1, 1, VALUES)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(x.reshape(-1, 1), y)
# predikce modelu
y_pred = lr.predict(x.reshape(-1, 1))
1# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# vykreslení výsledku
plt.scatter(x, y, color="black", s=2)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title("Linear regression")
# osy
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig("79.png")
# zobrazeni diagramu
plt.show()
Nyní bude směrnice vypočtené úsečky rovna přesně 0,2 (vypočteno jako 2/10) a její posun –1 ve směru y-ové osy:
Coefficients: [0.2] Intercept: -1.0
Takovou úsečku lze nakreslit snadno:
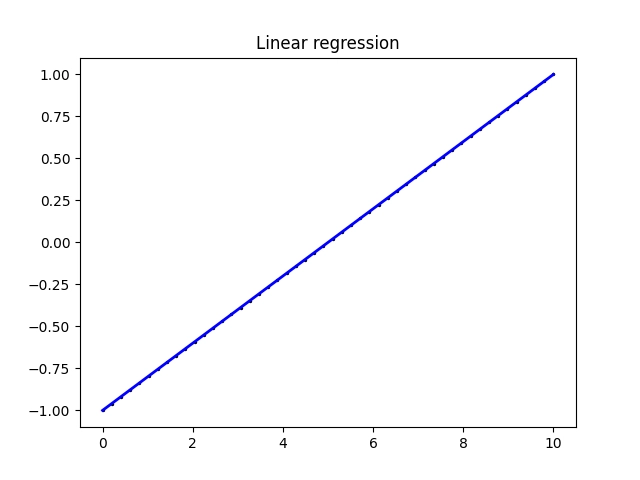
Obrázek 6: Nyní úsečka přesně prochází všemi body.
10. Predikce modelu provádějícího lineární regresi
Ve skutečnosti není model LinearRegression používán pouze pro proložení dat úsečkou, ale můžeme s ním provádět i predikce. Je to ve skutečnosti velmi snadné a vlastně se nejedná o žádnou novinku, ale naopak o postup, který již dobře známe – data rozdělíme na tréninkovou část a testovací část. Následně model natrénujeme pouze s využitím tréninkových dat a necháme model předpovědět hodnoty pro testovací data, což v našem umělém příkladu budou pouze x-ové souřadnice. Model pro každou takovou x-ovou souřadnici vypočítá souřadnici y-ovou, a to tak, aby ležela na vypočtené úsečce (model si totiž pamatuje jen směrnici a posun této úsečky):
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
VALUES = 100
x = np.linspace(0, 10, VALUES)
y = np.linspace(-1, 1, VALUES) + 0.5*np.random.rand(VALUES)
# rozdělení dat na trénovací a testovací část
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.6)
print("Array sizes:")
print(f"x_train: {len(x_train)}")
print(f"y_train: {len(y_train)}")
print(f"x_test: {len(x_test)}")
print(f"y_test: {len(y_test)}")
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(x_train.reshape(-1, 1), y_train)
# predikce modelu
y_pred = lr.predict(x_test.reshape(-1, 1))
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# vykreslení výsledku
plt.scatter(x_test, y_test, color="black", s=2)
plt.plot(x_test, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title("Linear regression")
# osy
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig("80.png")
# zobrazeni diagramu
plt.show()
Skript běžným způsobem spustíme:
Array sizes: x_train: 40 y_train: 40 x_test: 60 y_test: 60 Coefficients: [0.20740958] Intercept: -0.7674754384139917
Ve výsledném obrázku se zobrazí testovací body (nikoli body trénovací) i předpověď modelu, tj. vlastně body ležící na úsečce (tyto body skutečně úsečkou spojíme):
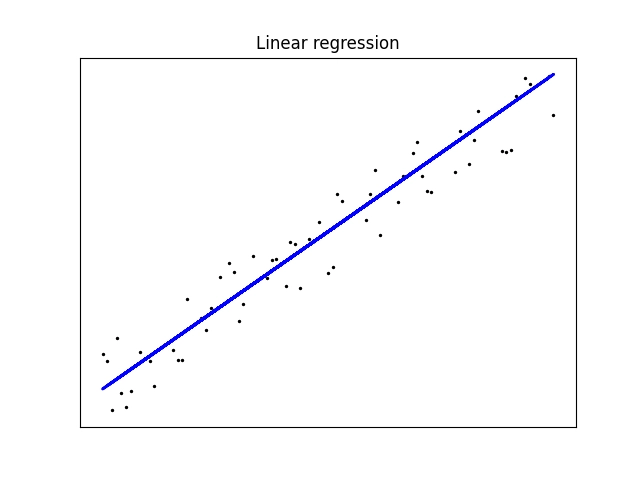
Obrázek 7: Testovací data (body) a odhadnutí výsledků modelem.
Model ovšem musíme vhodně natrénovat. Pokud mu předáme jen malé množství dat pro trénink, může se stál, že vypočtená úsečka „ulétne“:
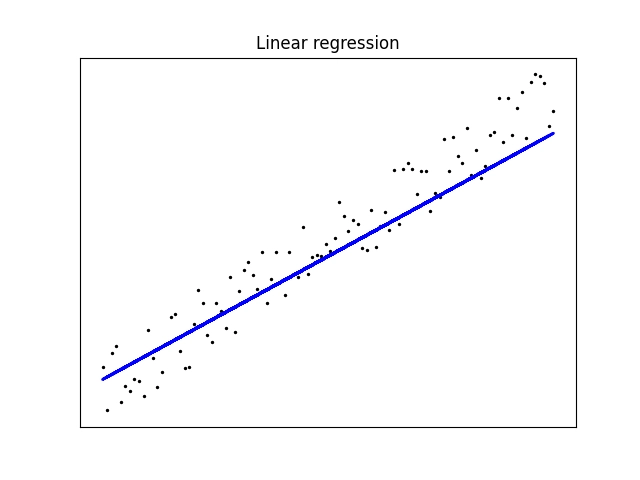
Obrázek 8: Nyní bylo pro trénink použito jen velmi malé množství dat (bodů).
Nyní jsme modelu předali jen minimum dat pro trénink:
VALUES = 100
x = np.linspace(0, 10, VALUES)
y = np.linspace(-1, 1, VALUES) + 0.5*np.random.rand(VALUES)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.97)
print("Array sizes:")
print(f"x_train: {len(x_train)}")
print(f"y_train: {len(y_train)}")
print(f"x_test: {len(x_test)}")
print(f"y_test: {len(y_test)}")
...
...
...
To je ostatně patrné již po spuštění skriptu:
Array sizes: x_train: 3 y_train: 3 x_test: 97 y_test: 97 Coefficients: [0.18461929] Intercept: -0.6401611268416783
11. Chování modelu pro zcela náhodná data
Model založený na lineární regresi je interně, jak již ostatně víme, velmi jednoduchý a nedokáže korektně zpracovat například náhodná data. V takovém případě bude výpočet směrnice a posunu úsečky, ale výsledná predikce i chyba budou příliš velké a v praxi prakticky nepoužitelné. Ostatně si to můžeme opět velmi snadno ověřit. Povšimněte si, jakým způsobem jsou vypočteny y-ové souřadnice bodů použitých pro trénink i testování:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
VALUES = 100
x = np.linspace(0, 10, VALUES)
y = -1 + 2*np.random.rand(VALUES)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.6)
print("Array sizes:")
print(f"x_train: {len(x_train)}")
print(f"y_train: {len(y_train)}")
print(f"x_test: {len(x_test)}")
print(f"y_test: {len(y_test)}")
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(x_train.reshape(-1, 1), y_train)
# predikce modelu
y_pred = lr.predict(x_test.reshape(-1, 1))
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
# vykreslení výsledku
plt.scatter(x_test, y_test, color="black", s=2)
plt.plot(x_test, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title("Linear regression")
# osy
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig("81.png")
# zobrazeni diagramu
plt.show()
Vypočtená směrnice a posun úsečky po spuštění a tréninku modelu:
Array sizes: x_train: 40 y_train: 40 x_test: 60 y_test: 60 Coefficients: [0.04072739] Intercept: -0.2650716913256721
A takto bude vypadat výsledný diagram s testovacími daty a s odpovědí modelu (modré body pospojované úsečkami):
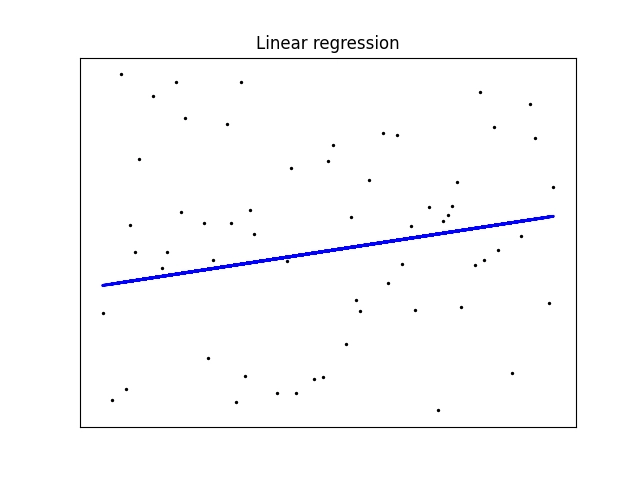
Obrázek 9: Model založený na lineární regresi a náhodná data.
12. Výpočet chyby – základní metriky modelu lineární regrese
V navazujícím textu se budeme věnovat „ladění“ modelů. V tomto případě je vhodné zjistit, jak dobrý odhad vlastně model lineární regrese má. To je poměrně snadné určit, protože nám k tomu knihovna scikit-learn nabízí prostředky. Jedná se především o výpočet střední kvadratické chyby (mean squared error neboli MSE). Pro každý bod odhadnutý modelem se vypočítá čtverec jeho vzdálenosti od skutečné pozice bodu; z takto získaných výsledků se vypočte střední hodnota. Pro různě nakonfigurovaný model se stejnými testovacími daty potom můžeme tyto hodnoty porovnat, přičemž čím menší hodnotu získáme, tím lépe model odpovídal (pro různá data to není možné, protože výsledkem je hodnota s rozměrem).
Můžeme taktéž použít výpočet R2 score, který nám poskytne relativní skóre (ohodnocení modelu). Nejlepší modely, které odpovídají vždy přesně, mají skóre rovno 1, horší modely budou mít skóre nižší, klidně i záporné.
Postup je snadný. Nejdříve model natrénujeme tak, jak to již známe:
# trénink modelu lr.fit(x_train.reshape(-1, 1), y_train)
Dále necháme model odhadnout výsledky pro trénovací data:
# predikce modelu y_pred = lr.predict(x_test.reshape(-1, 1))
Naimportujeme dvě výše zmíněné funkce pro hodnocení modelu:
from sklearn.metrics import mean_squared_error, r2_score
A na základě odhadnutých dat a očekávaných hodnot můžeme model ohodnotit (a později porovnat):
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred))
13. Praktický příklad: výpočet chyby a skóre modelu pro čtyři odlišné datové sady
Ukažme si na praktickém příkladu, jak vlastně probíhá výpočet chyby a skóre modelu lineární regrese. Použijeme přitom čtyři zcela odlišné datové sady:
- Body ležící na přímce, ovšem s přidanou náhodností (šumem)
- Body ležící přímo na přímce
- Náhodně rozmístěné body
- Body získané z datové sady California housings (souřadnice bloků)
Zdrojový kód příkladu vypadá následovně:
import numpy as np
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
def errors_and_score_for_linear_regression(x_train, x_test, y_train, y_test):
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(x_train.reshape(-1, 1), y_train)
# predikce modelu
y_pred = lr.predict(x_test.reshape(-1, 1))
# výpis vypočtených koeficientů modelu
print(" Coefficients: ", lr.coef_)
print(" Intercept: ", lr.intercept_)
# chyba predikce
print(" Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# 1 = nejlepší predikce modelu
print(" Coefficient of determination: %.2f" % r2_score(y_test, y_pred))
print()
# ------------------------------------------------------------------------
# zcela nenáhodná data
VALUES = 100
x = np.linspace(0, 10, VALUES)
y = np.linspace(-1, 1, VALUES)
# rozdělení na trénovací a testovací data
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.6)
print("Non-random data that are on one line:")
errors_and_score_for_linear_regression(x_train, x_test, y_train, y_test)
# ------------------------------------------------------------------------
# data obsahující náhodné odchylky
VALUES = 100
x = np.linspace(0, 10, VALUES)
y = np.linspace(-1, 1, VALUES) + 0.5*np.random.rand(VALUES)
# rozdělení na trénovací a testovací data
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.6)
print("Data with added randomness that are on one line:")
errors_and_score_for_linear_regression(x_train, x_test, y_train, y_test)
# ------------------------------------------------------------------------
# zcela náhodná data
VALUES = 100
x = np.linspace(0, 10, VALUES)
y = -1 + 2*np.random.rand(VALUES)
# rozdělení na trénovací a testovací data
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.6)
print("Totally random data:")
errors_and_score_for_linear_regression(x_train, x_test, y_train, y_test)
# ------------------------------------------------------------------------
# California housings
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
FIRST_DIM = 6
SECOND_DIM = 7
# rozdělení na trénovací a testovací data
x_train, x_test, y_train, y_test = train_test_split(data[:, FIRST_DIM], data[:, SECOND_DIM], test_size=0.6)
print("California housings data: longitude/lattitude:")
errors_and_score_for_linear_regression(x_train, x_test, y_train, y_test)
Výsledky odpovídají očekávání, což se týká výsledného skóre:
Non-random data that are on one line:
Coefficients: [0.2]
Intercept: -0.9999999999999999
Mean squared error: 0.00
Coefficient of determination: 1.00
Data with added randomness that are on one line:
Coefficients: [0.19224885]
Intercept: -0.7319112328028108
Mean squared error: 0.02
Coefficient of determination: 0.94
Totally random data:
Coefficients: [0.05727984]
Intercept: -0.32444669595342196
Mean squared error: 0.46
Coefficient of determination: -0.13
California housings data: longitude/lattitude:
Coefficients: [-0.87110537]
Intercept: -88.54126270759419
Mean squared error: 0.59
Coefficient of determination: 0.85
14. Predikce modelu pro datovou sadu California housing
Prozatím jsme lineární regresní analýzu používali nad umělými daty. Pokusme se tedy nyní model natrénovat takovým způsobem, aby dokázal na základě předaného počtu místností v bloku odhadnout, kolik z těchto místností je ložnicemi. Dopředu ovšem nevíme, zda se jedná o lineární závislost či nikoli. Napovědět nám pomůže jak graf s vykreslenými odhady modelu pro testovací data, tak i výpočet chyby a skóre modelu:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
FIRST_DIM = 2
SECOND_DIM = 3
# rozdělení na trénovací a testovací data
x_train, x_test, y_train, y_test = train_test_split(data[:, FIRST_DIM], data[:, SECOND_DIM], test_size=0.6)
print("Array sizes:")
print(f"x_train: {len(x_train)}")
print(f"y_train: {len(y_train)}")
print(f"x_test: {len(x_test)}")
print(f"y_test: {len(y_test)}")
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(x_train.reshape(-1, 1), y_train)
# predikce modelu
y_pred = lr.predict(x_test.reshape(-1, 1))
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
# chyba predikce
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# 1 = nejlepší predikce modelu
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred))
# vykreslení výsledku
plt.scatter(x_test, y_test, color="black", s=1)
plt.plot(x_test, y_pred, color="blue", linewidth=3)
# osy
plt.xlabel(housings.feature_names[FIRST_DIM])
plt.ylabel(housings.feature_names[SECOND_DIM])
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig("82.png")
# zobrazeni diagramu
plt.show()
Výsledek bude vypadat následovně:
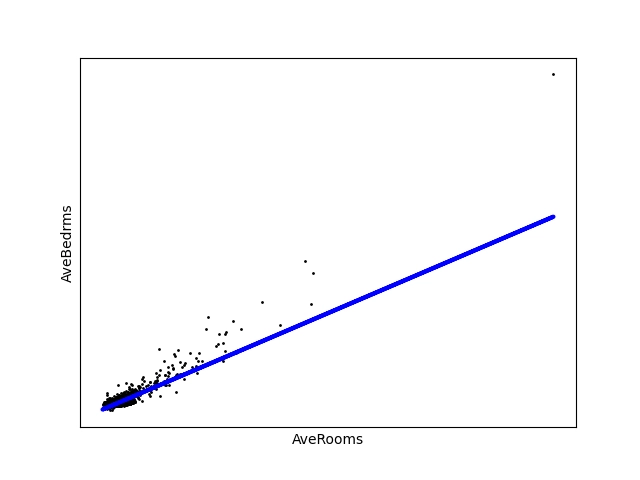
Obrázek 10: Odhad počtu ložnic na celkovém počtu místností v bloku.
15. Lineární regrese nad daty s nelineární závislostí
Lineární regrese je sice pro mnoho účelů skvělý nástroj, ovšem (logicky) nebude příliš funkční nad daty, které nemají interní lineární závislost. To jsme částečně mohli vidět u náhodných dat, ovšem pojďme si vyzkoušet, co se stane, když modelu předložíme data, v nichž se navíc nachází i „skok“ (což je nejlépe patrné z výsledného grafu):
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score
VALUES = 100
x = np.linspace(0, 10, VALUES)
y1 = 0.5*np.random.rand(VALUES//2)
y2 = 1 + 0.5*np.random.rand(VALUES//2)
# nelinearita - skok
y = np.concatenate((y1, y2))
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(x.reshape(-1, 1), y)
# predikce modelu
y_pred = lr.predict(x.reshape(-1, 1))
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# chyba predikce
print("Mean squared error: %.2f" % mean_squared_error(y, y_pred))
# 1 = nejlepší predikce modelu
print("Coefficient of determination: %.2f" % r2_score(y, y_pred))
# vykreslení výsledku
plt.scatter(x, y, color="black", s=2)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title("Linear regression")
# osy
plt.xticks()
plt.yticks()
# ulozeni diagramu do souboru
plt.savefig("88.png")
# zobrazeni diagramu
plt.show()
Výsledky naznačují, že predikce modelu není zcela úspěšná:
[0.14891026] Intercept: 0.018213198056308944 Mean squared error: 0.08 Coefficient of determination: 0.71
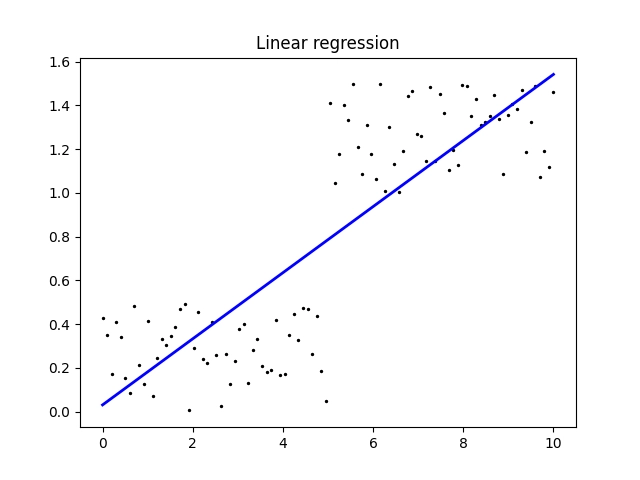
Obrázek 11: Model lineární regrese se snaží proložit úsečkou data, v nichž je skok.
16. Polynomická regrese
V mnoha případech je namísto modelu s interní lineární závislostí mezi vstupem a výstupem použít polynom vyššího stupně. I to nám knihovna scikit-learn umožňuje, i když možná poněkud matoucím způsobem (ovšem jen zdánlivě matoucím):
pr = linear_model.LinearRegression() poly = PolynomialFeatures(degree=degree) poly_features = poly.fit_transform(x.reshape(-1, 1)) # trénink modelu pr.fit(poly_features, y) # predikce modelu y_pred = pr.predict(poly_features)
Jedná se vlastně o obecný případ lineární regrese, kdy se jedná o lineární kombinaci funkcí, v tomto případě funkcí typu xn pro nějaké omezené n. Hodnotu n se přitom snažíme volit co nejmenší, aby bylo možné z nalezených koeficientů odvodit, co se vlastně model naučil. Na druhou stranu musí být n dostatečně vysoké na to, aby model dokázal odhadovat výsledky.
Koeficienty modelu s kvadratickým polynomem mohou vypadat následovně:
Coefficients: [0. 0.11345465 0.00357484] Intercept: 0.06366079775076627
Povšimněte si, že první koeficient je nulový. Jedná se o posun (konstantu), která je obsažena v intercept. Model však můžeme inicializovat s parametrem fit_intercept=False a poté bude posun přesunut do prvního koeficientu a atribut intercept bude nulový (což je v tomto případě lepší řešení):
Coefficients: [0.02078658 0.1302669 0.0017247 ] Intercept: 0.0
17. Polynomická regrese nad daty s nelinearitou
Pokusme se nyní použít polynomickou regresi s polynomy řádu 1 až 11, přičemž vždy vykreslíme odhad modelu jakožto lomenou úsečku, která vlastně aproximuje polynom, jehož koeficienty se model naučil při tréninku:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error, r2_score
VALUES = 100
x = np.linspace(0, 10, VALUES)
y1 = 0.5*np.random.rand(VALUES//2)
y2 = 1 + 0.5*np.random.rand(VALUES//2)
y = np.concatenate((y1, y2))
for degree in range(1, 12):
# konstrukce modelu
pr = linear_model.LinearRegression()
poly = PolynomialFeatures(degree=degree)
poly_features = poly.fit_transform(x.reshape(-1, 1))
# trénink modelu
pr.fit(poly_features, y)
# predikce modelu
y_pred = pr.predict(poly_features)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", pr.coef_)
print("Intercept: \n", pr.intercept_)
# chyba predikce
print("Mean squared error: %.2f" % mean_squared_error(y, y_pred))
# 1 = nejlepší predikce modelu
print("Coefficient of determination: %.2f" % r2_score(y, y_pred))
# vykreslení výsledku
plt.scatter(x, y, color="black", s=1)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title(f"Degree={degree}")
# osy
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig(f"83_{degree}.png")
# zobrazeni diagramu
plt.show()
Povšimněte si, že v tomto případě je vhodnější použít polynom lichého stupně, což vlastně velmi dobře odpovídá vstupním datům:
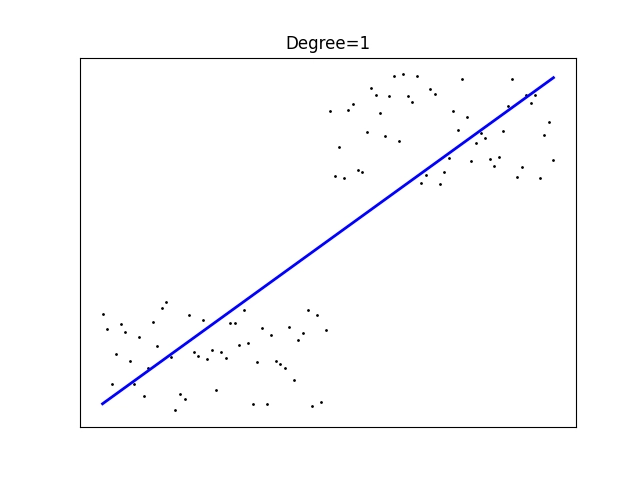
Obrázek 12: Polynomická regrese polynomem stupně 1.
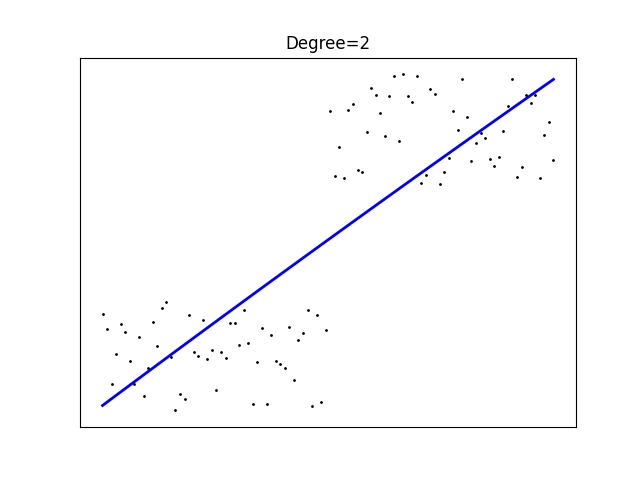
Obrázek 13: Polynomická regrese polynomem stupně 2.
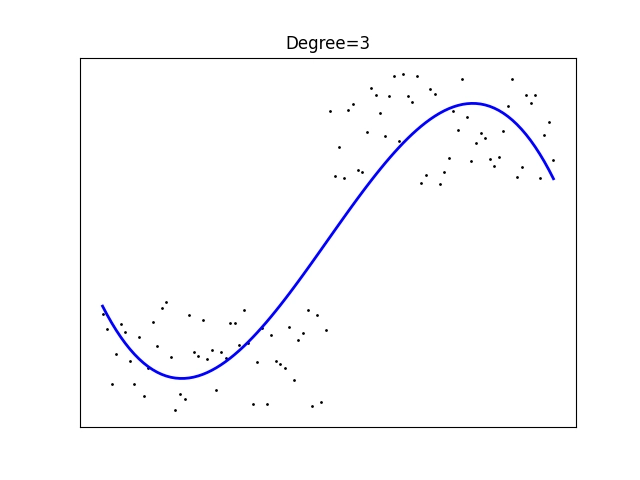
Obrázek 14: Polynomická regrese polynomem stupně 3.
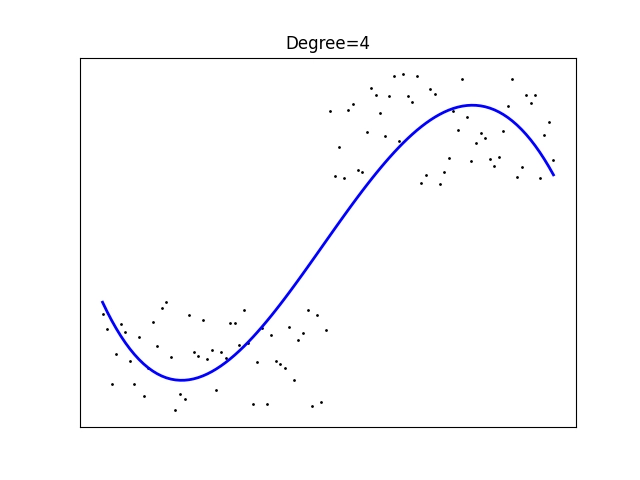
Obrázek 15: Polynomická regrese polynomem stupně 4.
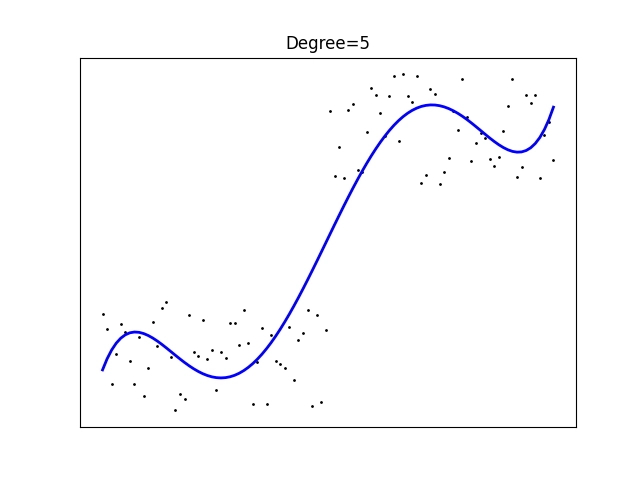
Obrázek 16: Polynomická regrese polynomem stupně 5.
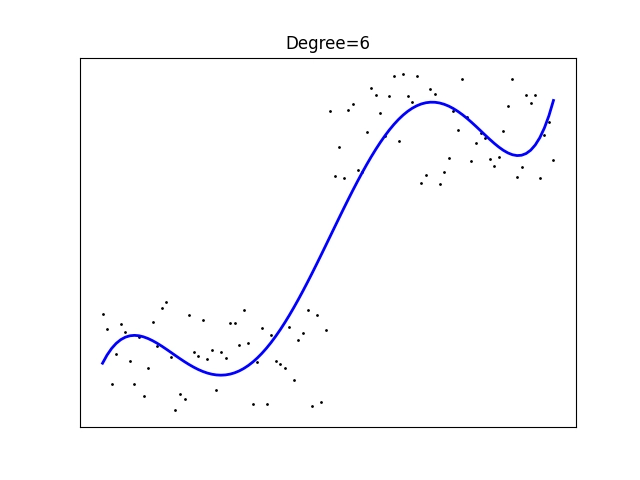
Obrázek 17: Polynomická regrese polynomem stupně 6.
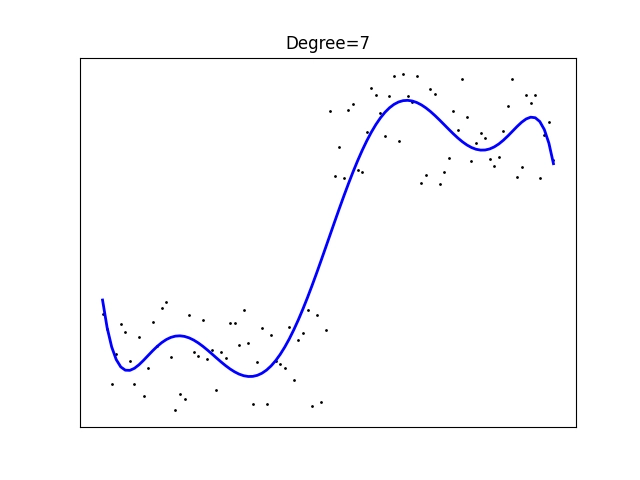
Obrázek 18: Polynomická regrese polynomem stupně 7.
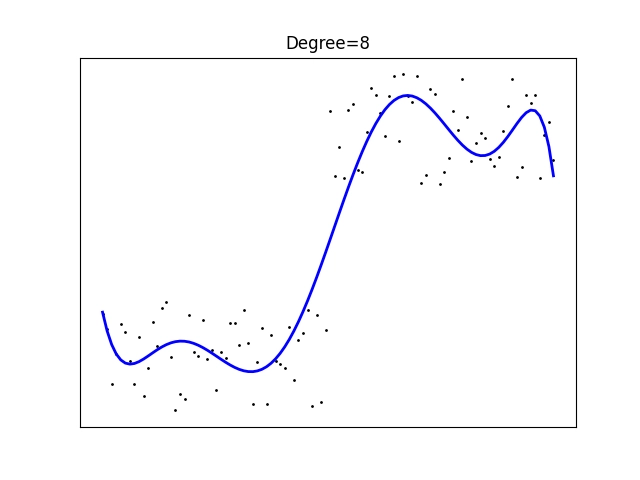
Obrázek 19: Polynomická regrese polynomem stupně 8.
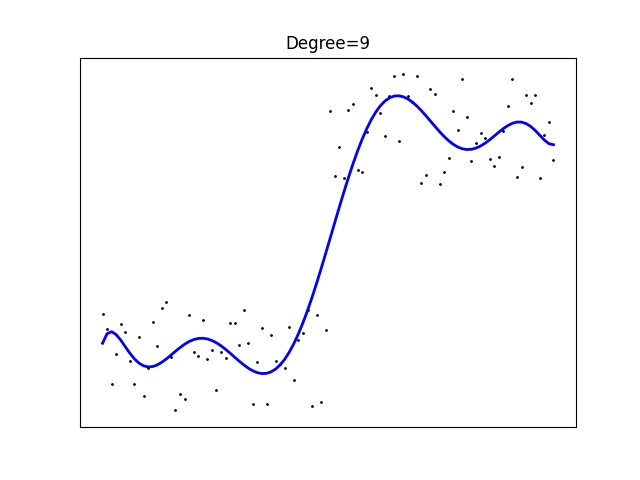
Obrázek 20: Polynomická regrese polynomem stupně 9.
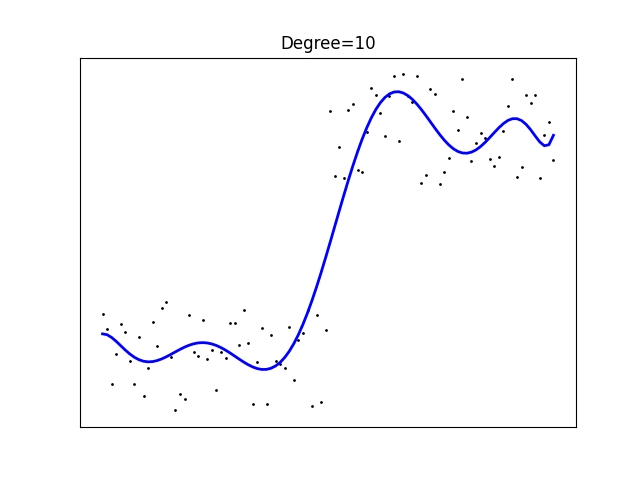
Obrázek 21: Polynomická regrese polynomem stupně 10.
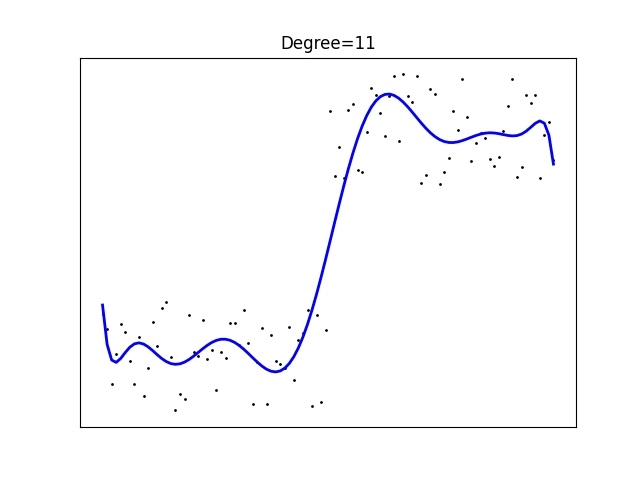
Obrázek 22: Polynomická regrese polynomem stupně 11.
18. Vyšší stupeň polynomu = lepší model?
Obecně ovšem neplatí, že čím vyšší stupeň polynomu zvolíme, tím lépe. Model se totiž může přeučit a „zakmitávat“. S tímto problémem se podrobněji seznámíme příště, ovšem již nyní si můžeme ukázat závislosti mezi stupněm polynomu a chybou i skóre:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error, r2_score
VALUES = 100
x = np.linspace(0, 10, VALUES)
y1 = 0.5*np.random.rand(VALUES//2)
y2 = 1 + 0.5*np.random.rand(VALUES//2)
y = np.concatenate((y1, y2))
degrees = []
mses = []
r2_scores = []
for degree in range(1, 50):
# konstrukce modelu
pr = linear_model.LinearRegression(fit_intercept=False)
poly = PolynomialFeatures(degree=degree)
poly_features = poly.fit_transform(x.reshape(-1, 1))
# trénink modelu
pr.fit(poly_features, y)
# predikce modelu
y_pred = pr.predict(poly_features)
degrees.append(degree)
mse = mean_squared_error(y, y_pred)
r2 = r2_score(y, y_pred)
mses.append(mse)
r2_scores.append(r2)
print(degree, mse, r2)
plt.plot(degrees, mses, degrees, r2_scores)
# titulek grafu
plt.title("Mode prediction")
plt.legend(["MSE", "R2 score"])
# osy
plt.xticks()
plt.yticks()
# ulozeni diagramu do souboru
plt.savefig("89.png")
# zobrazeni diagramu
plt.show()
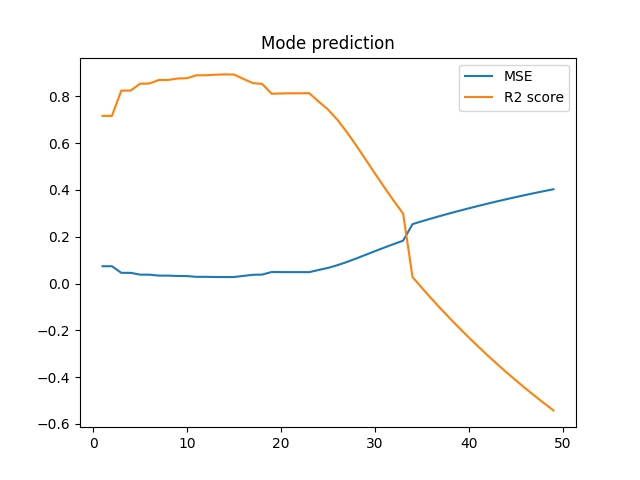
Obrázek 23: Chyba a skóre modelů pro různé stupně polynomu.
Numerické výsledky:
1 0.08854350477181652 0.6727776670574832 2 0.08847105481617644 0.6730454138963645 3 0.06352553393094755 0.7652343504148237 4 0.06352363502305206 0.7652413680393599 5 0.05139097616802354 0.8100789531967275 6 0.051360414474032764 0.8101918973232574 7 0.04282549807457683 0.8417336265883979 8 0.04272801081159937 0.842093901570802 9 0.037628039473641815 0.860941410752273 10 0.03762741402964682 0.8609437221498588 11 0.03654030854048818 0.8649612409417097 12 0.03649603934320596 0.8651248426655122 13 0.033551344371300515 0.8760072892209562 14 0.034587421482685336 0.8721783514533651 15 0.0349144348488055 0.8709698373241697 16 0.03883429903924582 0.8564835448680573 17 0.0439054993310688 0.8377423622755509 18 0.04718657143483762 0.8256167967570557 19 0.06068608267845382 0.775727857143657 20 0.06067219921030257 0.7757791650385669 21 0.060546395766387956 0.7762440856051972 22 0.06054664801379553 0.7762431533969523 23 0.060416619348441204 0.7767236887375885 24 0.06766439714886716 0.7499387227864862 25 0.07517323686503591 0.722188973598805 26 0.08558129686149148 0.6837248346173771 27 0.09850570476460575 0.6359612531230979 28 0.11332248094826584 0.5812042149642964 29 0.1295420132490688 0.5212631361422777 30 0.1465486596302491 0.4584131900200912 31 0.1638999092609902 0.3942897244054083 32 0.1812521964418129 0.33016242440943333 33 0.19844435668492633 0.26662689125461947 34 0.284832041072001 -0.052628368580522444 35 0.29895181099387746 -0.10480954286716115 36 0.31230328573680555 -0.15415139718909043 37 0.32493332104343997 -0.20082709213513872 38 0.33689126278510223 -0.24501899084054113 39 0.34822667356365017 -0.2869102573922446 40 0.3589877377267896 -0.32667896238626026 41 0.36920578835842205 -0.3644409007060072 42 0.3789544071733879 -0.40046800173189534 43 0.38827003463206067 -0.43489493522301825 44 0.3971522552977659 -0.4677201658871135 45 0.4056720613291159 -0.499206053112615 46 0.4138479677051003 -0.5294210210559303 47 0.4217077493464011 -0.558467715014038 48 0.42928089265327807 -0.5864551052463374 49 0.43657927470983254 -0.6134270848331644
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
V repositáři nalezneme taktéž projektový soubor a Jupyter Notebook s vysvětlením, jak lze modely využít pro rozpoznávání obsahu rastrových obrázků:
| # | Příklad | Stručný popis | Adresa příkladu |
|---|---|---|---|
| 1 | pyproject.toml | projektový soubor (pro PDM) se všemi závislostmi | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pyproject.toml |
| 2 | pdm.lock | lock soubor s konkrétními verzemi všech přímých i tranzitivních závislostí | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pdm.lock |
| 3 | Rozpoznání_obrazu_scikit-learn.ipynb | Jupyter notebook s celým postupem | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/Rozpoznání_obrazu_scikit-learn.ipynb |
| 4 | particle_life.py | emergence: příklad vzniku struktury | https://github.com/tisnik/most-popular-python-libs/blob/master/particles/particle_life.py |
20. Odkazy na Internetu
- Shluková analýza (clustering) a knihovna Scikit-learn
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn/ - Shluková analýza (clustering) a knihovna Scikit-learn (2)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-2/ - Shluková analýza (clustering) a knihovna Scikit-learn (z plochy do 3D prostoru)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-z-plochy-do-3d-prostoru/ - Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
https://www.root.cz/clanky/rozpoznavani-obrazku-knihovnou-scikit-learn-prvni-kroky/ - scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Spectral clustering
https://en.wikipedia.org/wiki/Spectral_clustering - Emergence
https://cs.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - 3D rendering
https://en.wikipedia.org/wiki/3D_rendering - 3D computer graphics
https://en.wikipedia.org/wiki/3D_computer_graphics - Primary 3D view planes
https://matplotlib.org/stable/gallery/mplot3d/view_planes_3d.html - Getting started in scikit-learn with the famous iris dataset
https://www.youtube.com/watch?v=hd1W4CyPX58 - Training a machine learning model with scikit-learn
https://www.youtube.com/watch?v=RlQuVL6-qe8 - Iris (plant)
https://en.wikipedia.org/wiki/Iris_(plant) - Kosatec
https://cs.wikipedia.org/wiki/Kosatec - Iris setosa
https://en.wikipedia.org/wiki/Iris_setosa - Iris versicolor
https://en.wikipedia.org/wiki/Iris_versicolor - Iris virginica
https://en.wikipedia.org/wiki/Iris_virginica - Druh
https://cs.wikipedia.org/wiki/Druh - Iris subg. Limniris
https://en.wikipedia.org/wiki/Iris_subg._Limniris - Iris Dataset Classification with Python: A Tutorial
https://www.pycodemates.com/2022/05/iris-dataset-classification-with-python.html - Iris flower data set
https://en.wikipedia.org/wiki/Iris_flower_data_set - List of datasets for machine-learning research
https://en.wikipedia.org/wiki/List_of_datasets_for_machine-learning_research - Analýza hlavních komponent
https://cs.wikipedia.org/wiki/Anal%C3%BDza_hlavn%C3%ADch_komponent - Principal component analysis
https://en.wikipedia.org/wiki/Principal_component_analysis - Scikit-learn Crash Course – Machine Learning Library for Python
https://www.youtube.com/watch?v=0B5eIE_1vpU - calm-notebooks
https://github.com/koaning/calm-notebooks - Should you teach Python or R for data science?
https://www.dataschool.io/python-or-r-for-data-science/ - nbviewer: A simple way to share Jupyter Notebooks
https://nbviewer.org/ - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/ - Matplotlib vs. seaborn vs. Plotly vs. MATLAB vs. ggplot2 vs. pandas
https://ritza.co/articles/matplotlib-vs-seaborn-vs-plotly-vs-MATLAB-vs-ggplot2-vs-pandas/ - Matplotlib, Seaborn or Plotnine?
https://www.reddit.com/r/datascience/comments/jvrqxt/matplotlib_seaborn_or_plotnine/ - @Rabeez: Rabeez/plotting_comparison.ipynb
https://gist.github.com/Rabeez/ffc0b59d4a41e20fa8d944c44a96adbc - Matplotlib, Seaborn, Plotly and Plotnine Comparison
https://python.plainenglish.io/matplotlib-seaborn-plotly-and-plotnine-comparison-baf2db5a9c40 - Data Visualization 101: How to Choose a Python Plotting Library
https://towardsdatascience.com/data-visualization-101-how-to-choose-a-python-plotting-library-853460a08a8a - Data science in Python: pandas, seaborn, scikit-learn
https://www.youtube.com/watch?v=3ZWuPVWq7p4 - 7.2. Real world datasets
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - 7.2.7. California Housing dataset
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - Comprehensive Guide to Classification Models in Scikit-Learn
https://www.geeksforgeeks.org/comprehensive-guide-to-classification-models-in-scikit-learn/ - Tidy Data Visualization: ggplot2 vs seaborn
https://blog.tidy-intelligence.com/posts/ggplot2-vs-seaborn/ - seaborn: statistical data visualization
https://seaborn.pydata.org/