Obsah
1. FAISS: knihovna pro rychlé a efektivní vyhledávání podobných vektorů
3. Je FAISS vektorovou databází?
4. Řešený problém: nalezení nejbližších k bodů k zadaným souřadnicím
6. Instalace balíčků faiss-cpu a numpy do virtuálního prostředí
7. Definice souřadnic bodů v rovině
8. Konstrukce matice se souřadnicemi bodů
9. Konstrukce indexu pro vyhledávání na základě vzdálenosti
10. Nalezení nejbližších bodů k zadaným souřadnicím
11. Výpis souřadnic bodů nejbližších k zadaným souřadnicím
12. Vizualizace nejbližších nalezených bodů
13. Výběry vektorů na základě jejich podobnosti: volba metriky
14. Výběr podobných vektorů pomocí skalárního součinu: nekorektní verze
15. Normalizace vektorů v indexu
16. Rychlost vyhledání nejbližších bodů
19. Repositář s demonstračními příklady
1. FAISS: knihovna pro rychlé a efektivní vyhledávání podobných vektorů
V současnosti můžeme sledovat poměrně výrazné a stále častější nasazování vektorových databází. Jedná se (většinou) o specializované databáze, které umožňují ukládat vektory numerických hodnot a především efektivně vyhledávat vektory podle jejich podobnosti (například se zadaným vzorem), přičemž podobností může být v tomto kontextu myšlena například vzdálenost koncových bodů vektorů v Eukleidovském prostoru, kosinus úhlu mezi vektory, výsledek skalárního součinu (pro normalizované vektory) atd.
Tyto operace se používají v mnoha oblastech, například při rozpoznávání a zpracování přirozeného jazyka (NLP – Natural Language Processing), při rozpoznávání obrázků, rozpoznávání hlasů, detekci anomálií, ale i (a to zejména) v souvislosti s velkými jazykovými modely (k tomuto tématu se ještě vrátíme v samostatném článku).
Na stránkách Roota jsme se již v článku pgvector: vektorová databáze postavená na Postgresu seznámili s vektorovou databází pgvector, která je postavena nad Postgresem. Dnes si popíšeme základní vlastnosti knihovny nazvané FAISS, což je jméno, které vzniklo ze sousloví Facebook AI Similarity Search (ovšem tato knihovna se používá i v mnoha projektech, které nemají s Facebookem nebo Metou cokoli společného). FAISS je šířena pod MIT licencí, což umožňuje její relativně snadné zařazení do dalších projektů.
2. Svět vektorových databází
S rozvojem systémů určených pro zpracování přirozeného jazyka i generativních AI (zejména velkých jazykových modelů) došlo i k velkému rozmachu vektorových databází. Dnes jich existuje minimálně několik desítek (pokud počítáme ty nejznámější a/nebo veřejně dostupné), ovšem spíše jich bude několik set.
V tabulce pod tímto odstavcem jsou vypsány ty nejznámější vektorové databáze, které pochopitelně mají rozdílné vlastnosti a každá z nich se hodí pro jiné způsoby nasazení:
| Aerospike |
| AllegroGraph |
| Apache Cassandra |
| Azure Cosmos DB |
| Chroma |
| ClickHouse |
| Couchbase |
| CrateDB |
| DataStax |
| Elasticsearch |
| HAKES |
| HDF5 Query Indexing |
| JaguarDB |
| LanceDB |
| Lantern |
| LlamaIndex |
| MariaDB |
| Marqo |
| Meilisearch |
| Milvus |
| MongoDB Atlas |
| Neo4j |
| ObjectBox |
| OpenSearch |
| Oracle Database |
| Pinecone |
| Pixeltable (Incremental Embedding) |
| Postgres with pgvector |
| Qdrant |
| Redis Stack |
| Snowflake |
| SurrealDB |
| Typesense |
| Vespa |
| Weaviate |
3. Je FAISS vektorovou databází?
V některých článcích se můžeme dočíst, že FAISS je vektorovou databází. Ovšem to ve skutečnosti není pravda, protože FAISS „pouze“ poskytuje algoritmy určené pro efektivní vyhledávání podobných vektorů a pro jejich shlukování (clustering). Neřeší ovšem problém uložení vektorů v nějakém strukturovaném formátu. Naopak, některé skutečné vektorové databáze, mezi které patří například Milvus nebo OpenSearch, využívají FAISS pro vyhledávání, ovšem způsob uložení a načítání vektorů řeší ve své vlastní režii.
4. Řešený problém: nalezení nejbližších k bodů k zadaným souřadnicím
V navazujícím kapitolách se s využitím knihovny FAISS pokusíme vyřešit následující problém: v 2D prostoru máme patnáct bodů a budeme chtít najít k bodů, které jsou neblíže k zadaným souřadnicím. Pokud bude k=1, tak budeme chtít nalézt nejbližší bod atd. Body jsou přitom v rovině rozmístěny následujícím způsobem a u vybraných bodů jsou zapsány i jejich souřadnice:
│ y
│
│
│
│ [5,5]
o o │ o o o
│ o o o
o │ o o o
[-4,3] │ [3,3] [5,3]
│
─────────────────────────────────────[0,0]──────────────────────────────────────
│ x
│ o
│
│ o o
│ [5,-5]
│
│
│
│
5. Příprava projektu
V prvním kroku si připravíme projekt v Pythonu a následně do něj nainstalujeme všechny potřebné knihovny. Pro vytvoření projektu použijeme nástroj PDM – viz též PDM: moderní správce balíčků a virtuálních prostředí Pythonu. Projekt bude vytvořen v novém (původně prázdném) adresáři:
$ mkdir faiss-demo $ cd faiss-demo
Následně si necháme vytvořit projektový soubor nazvaný pyproject.toml. Na všechny odpovědi kladené nástrojem PDM můžeme s klidem odpovědět jen klávesou Enter:
$ pdm init
Creating a pyproject.toml for PDM...
Please enter the Python interpreter to use
0. cpython@3.12 (/usr/bin/python)
1. cpython@3.13 (/usr/bin/python3.13)
2. cpython@3.12 (/usr/bin/python3.12)
3. cpython@3.11 (/usr/bin/python3.11)
Please select (0):
Virtualenv is created successfully at /tmp/ramdisk/faiss-demo/.venv
Project name (faiss-demo): Project version (0.1.0): Do you want to build this project for distribution(such as wheel)?
If yes, it will be installed by default when running `pdm install`. [y/n] (n):
License(SPDX name) (MIT):
Author name (Pavel Tisnovsky):
Author email (tisnik@nikdo.nikde.com):
Python requires('*' to allow any) (==3.12.*):
Project is initialized successfully
Výsledný projektový soubor pyproject.toml by měl vypadat následovně (samozřejmě kromě jména, mailu a zvolené verze Pythonu):
[project]
name = "faiss-demo"
version = "0.1.0"
description = "Default template for PDM package"
authors = [
{name = "Pavel Tisnovsky", email = "tisnik@nikdo.nikde.com"},
]
dependencies = []
requires-python = "==3.12.*"
readme = "README.md"
license = {text = "MIT"}
[tool.pdm]
distribution = false
6. Instalace balíčků faiss-cpu a numpy do virtuálního prostředí
Ve druhém kroku do virtuálního prostředí vytvořeného pro nový projekt přidáme dva balíčky – faiss-cpu a numpy. Druhý z balíčků byl přidán z toho důvodu, abychom mohli tvořit vektory, s nimiž bude faiss pracovat:
$ pdm add faiss-cpu numpy Adding packages to default dependencies: faiss-cpu, numpy 0:00:03 🔒 Lock successful. Changes are written to pyproject.toml. Synchronizing working set with resolved packages: 3 to add, 0 to update, 0 to remove ✔ Install packaging 25.0 successful ✔ Install numpy 2.3.1 successful ✔ Install faiss-cpu 1.11.0 successful 0:00:05 🎉 All complete! 3/3
Projektový soubor nyní vypadá následovně:
[project]
name = "faiss-demo"
version = "0.1.0"
description = "Default template for PDM package"
authors = [
{name = "Pavel Tisnovsky", email = "ptisnovs@redhat.com"},
]
dependencies = ["faiss-cpu>=1.11.0", "numpy>=2.3.1"]
requires-python = "==3.12.*"
readme = "README.md"
license = {text = "MIT"}
[tool.pdm]
distribution = false
Ověříme si, zda je modul faiss skutečně dostupný:
$ pdm run WARNING: No command is given, default to the Python REPL. Python 3.12.10 (main, Apr 22 2025, 00:00:00) [GCC 14.2.1 20240912 (Red Hat 14.2.1-3)] on linux Type "help", "copyright", "credits" or "license" for more information. >>> import faiss >>> help(faiss)
Měla by se zobrazit nápověda:
Help on package faiss:
NAME
faiss
DESCRIPTION
# Copyright (c) Facebook, Inc. and its affiliates.
#
# This source code is licensed under the MIT license found in the
# LICENSE file in the root directory of this source tree.
PACKAGE CONTENTS
_swigfaiss
_swigfaiss_avx2
_swigfaiss_avx512
array_conversions
class_wrappers
contrib (package)
extra_wrappers
gpu_wrappers
loader
setup
swigfaiss
swigfaiss_avx2
swigfaiss_avx512
CLASSES
7. Definice souřadnic bodů v rovině
Souřadnice bodů umístěných v rovině (viz čtvrtou kapitolu s jejich vizualizací) je možné uložit do běžných Pythonovských seznamů nebo do n-tic. Bodů je celkem patnáct a souřadnice v rovině mají jen dvě dimenze, takže reprezentace souřadnice je v tomto případě snadná:
# x-ove souradnice bodu v rovine x = [-5, -4, -3, 3, 4, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5] # y-ove souradnice bodu v rovine y = [ 5, 3, 5, -5, -3, -5, 3, 4, 5, 3, 4, 5, 3, 4, 5]
Z těchto dvou oddělených seznamů je možné vytvořit seznam souřadnic (dvojic) velmi snadno:
# x-ove souradnice bodu v rovine x = [-5, -4, -3, 3, 4, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5] # y-ove souradnice bodu v rovine y = [ 5, 3, 5, -5, -3, -5, 3, 4, 5, 3, 4, 5, 3, 4, 5] print(x) print(y) # seznam souradnic print(list(zip(x, y)))
Výsledky:
[-5, -4, -3, 3, 4, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5] [5, 3, 5, -5, -3, -5, 3, 4, 5, 3, 4, 5, 3, 4, 5] [(-5, 5), (-4, 3), (-3, 5), (3, -5), (4, -3), (5, -5), (3, 3), (3, 4), (3, 5), (4, 3), (4, 4), (4, 5), (5, 3), (5, 4), (5, 5)]
8. Konstrukce matice se souřadnicemi bodů
Knihovna FAISS ovšem na svém vstupu neočekává standardní Pythonovské seznamy, ale (typicky) matice ve formátu podporovaném knihovnou Numpy (interně se jedná o obecnou strukturu reprezentující n-rozměrná pole). V takovém případě je matice homogenní, tj. všechny její prvky jsou stejného typu. Navíc musíme zaručit, že tento typ bude buď float32 nebo float16 popř. bfloat16. Ukažme si tedy, jakým způsobem lze vytvořit dvourozměrné pole souřadnic, ve kterém budou všechny prvky typu float32:
import numpy as np
# x-ove souradnice bodu v rovine
x = [-5, -4, -3, 3, 4, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5]
# y-ove souradnice bodu v rovine
y = [ 5, 3, 5, -5, -3, -5, 3, 4, 5, 3, 4, 5, 3, 4, 5]
# konstrukce 2D matice, v niz kazdy radek obsahuje souradnice jednoho bodu v
# rovine
points = np.column_stack((x,y)).astype("float32")
print(points)
Výsledek nyní bude vypadat následovně:
[[-5. 5.] [-4. 3.] [-3. 5.] [ 3. -5.] [ 4. -3.] [ 5. -5.] [ 3. 3.] [ 3. 4.] [ 3. 5.] [ 4. 3.] [ 4. 4.] [ 4. 5.] [ 5. 3.] [ 5. 4.] [ 5. 5.]]
9. Konstrukce indexu pro vyhledávání na základě vzdálenosti
Nyní již máme k dispozici vstupní vektory (v našem případě sadu patnácti dvouprvkových vektorů) připraveny ve formátu, který je kompatibilní s knihovnou FAISS. Tyto vektory nyní využijeme pro konstrukci takzvaného indexu. To je datová struktura umožňující rychlé vyhledávání nejbližších vektorů na základě zvolené metriky určující vzdálenosti (pojem vzdálenosti je zde ovšem zobecněn a nemusí znamenat pouze Eukleidovskou vzdálenost).
V dalším demonstračním příkladu se zkonstruuje index typu L2, což značí Eukleidovskou vzdálenost L2:
import faiss
import numpy as np
# x-ove souradnice bodu v rovine
x = [-5, -4, -3, 3, 4, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5]
# y-ove souradnice bodu v rovine
y = [ 5, 3, 5, -5, -3, -5, 3, 4, 5, 3, 4, 5, 3, 4, 5]
# konstrukce 2D matice, v niz kazdy radek obsahuje souradnice jednoho bodu v
# rovine
points = np.column_stack((x,y)).astype("float32")
print(points)
# konstrukce indexu pro vyhledavani na zaklade vzdalenosti
index = faiss.IndexFlatL2(2)
index.add(points)
print()
print("Dimension(s): ", index.d)
print("Total values in index:", index.ntotal)
print("Is index trained: ", index.is_trained)
Po konstrukci indexu si necháme vypsat jeho základní charakteristiky – počet dimenzí, počet záznamů v indexu a taktéž příznak, zda je index natrénován (viz navazující článek):
[[-5. 5.] [-4. 3.] [-3. 5.] [ 3. -5.] [ 4. -3.] [ 5. -5.] [ 3. 3.] [ 3. 4.] [ 3. 5.] [ 4. 3.] [ 4. 4.] [ 4. 5.] [ 5. 3.] [ 5. 4.] [ 5. 5.]] Dimension(s): 2 Total values in index: 15 Is index trained: True
10. Nalezení nejbližších bodů k zadaným souřadnicím
Nyní se konečně dostáváme k ústřednímu tématu dnešního článku, tedy k realizaci skriptu, který má nalézt nejbližších k bodů (nebo, chcete-li, vektorů) k zadaným souřadnicím v rovině. Začněme těmito souřadnicemi. I ty je nutné realizovat formou matice, v našem případě matice s jediným řádkem se souřadnicemi [3, 3]. A opět platí, že typ prvků této matice musí být buď float32 nebo float16 popř. bfloat16. Použijeme typ float32, tedy stejný typ, jaký mají prvky vstupní matice vektorů:
query_vector = np.array([[3, 3]]).astype("float32")
print(query_vector)
Následně si necháme vyhledat k nejbližších bodů (vektorů) k těmto souřadnicím. V praxi může k nabývat hodnoty od 1 (nejbližší bod) až po počet vstupních vektorů:
k = len(x) distances, indices = index.search(query_vector, k)
Body/vektory budou v tomto případě vráceny v pořadí od nejbližšího k nejvzdálenějšímu (viz první hodnoty distances):
# tisk vysledku
print("Nearest neighbors:")
print("neighbour distance index")
print("--------------------------")
for i in range(k):
print(f"{i+1:3} {distances[0][i]:5} {indices[0][i]:2}")
Výsledky budou vypadat následovně:
Nearest neighbors: neighbour distance index -------------------------- 1 0.0 6 2 1.0 7 3 1.0 9 4 2.0 10 5 4.0 8 6 4.0 12 7 5.0 11 8 5.0 13 9 8.0 14 10 37.0 4 11 40.0 2 12 49.0 1 13 64.0 3 14 68.0 0 15 68.0 5
A takto vypadá celý skript, který výše popsaný výpočet provádí:
import faiss
import numpy as np
# x-ove souradnice bodu v rovine
x = [-5, -4, -3, 3, 4, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5]
# y-ove souradnice bodu v rovine
y = [ 5, 3, 5, -5, -3, -5, 3, 4, 5, 3, 4, 5, 3, 4, 5]
# konstrukce 2D matice, v niz kazdy radek obsahuje souradnice jednoho bodu v
# rovine
points = np.column_stack((x,y)).astype("float32")
print(points)
# konstrukce indexu pro vyhledavani na zaklade vzdalenosti
index = faiss.IndexFlatL2(2)
index.add(points)
print()
print("Dimension(s): ", index.d)
print("Total values in index:", index.ntotal)
print("Is index trained: ", index.is_trained)
# vektor, ke kteremu budeme pocitat vzdalenost
query_vector = np.array([[3, 3]]).astype("float32")
print(query_vector)
# pocet nejblizsich bodu
k = len(x)
distances, indices = index.search(query_vector, k)
# tisk vysledku
print("Nearest neighbors:")
print("neighbour distance index")
print("--------------------------")
for i in range(k):
print(f"{i+1:3} {distances[0][i]:5} {indices[0][i]:2}")
11. Výpis souřadnic bodů nejbližších k zadaným souřadnicím
V předchozím skriptu se vypisovaly pouze indexy nejbližších bodů/vektorů. Ovšem my máme k dispozici i původní souřadnice těchto bodů, takže si můžeme vypsat přímo tyto souřadnice:
Nearest neighbors: neighbour distance coordinates ---------------------------------- 1 0.0 [3. 3.] 2 1.0 [3. 4.] 3 1.0 [4. 3.] 4 2.0 [4. 4.] 5 4.0 [3. 5.] 6 4.0 [5. 3.] 7 5.0 [4. 5.] 8 5.0 [5. 4.] 9 8.0 [5. 5.] 10 37.0 [ 4. -3.] 11 40.0 [-3. 5.] 12 49.0 [-4. 3.] 13 64.0 [ 3. -5.] 14 68.0 [-5. 5.] 15 68.0 [ 5. -5.]
Celý upravený skript nyní vypadá následovně:
import faiss
import numpy as np
# x-ove souradnice bodu v rovine
x = [-5, -4, -3, 3, 4, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5]
# y-ove souradnice bodu v rovine
y = [ 5, 3, 5, -5, -3, -5, 3, 4, 5, 3, 4, 5, 3, 4, 5]
# konstrukce 2D matice, v niz kazdy radek obsahuje souradnice jednoho bodu v
# rovine
points = np.column_stack((x,y)).astype("float32")
print(points)
# konstrukce indexu pro vyhledavani na zaklade vzdalenosti
index = faiss.IndexFlatL2(2)
index.add(points)
print()
print("Dimension(s): ", index.d)
print("Total values in index:", index.ntotal)
print("Is index trained: ", index.is_trained)
# vektor, ke kteremu budeme pocitat vzdalenost
query_vector = np.array([[3, 3]]).astype("float32")
print(query_vector)
# pocet nejblizsich bodu
k = len(x)
distances, indices = index.search(query_vector, k)
# tisk vysledku
print("Nearest neighbors:")
print("neighbour distance coordinates ")
print("----------------------------------")
for i in range(k):
print(f"{i+1:3} {distances[0][i]:5} {points[indices[0][i]]}")
12. Vizualizace nejbližších nalezených bodů
Upravme si nyní předchozí skript do takové podoby, aby vracel jen tři body nejbližší k souřadnicím [-4, 4]. Úprava je v tomto případě snadná. Modifikovaná místa jsou podtržena:
# vektor, ke kteremu budeme pocitat vzdalenost
query_vector = np.array([[-4, 4]]).astype("float32")
print(query_vector)
# pocet nejblizsich bodu
k = 3
distances, indices = index.search(query_vector, k)
Výsledkem výše uvedeného dotazu je trojice vektorů, které jsou nejpodobnější vektoru [-4, 4]:
[[-4. 4.]] Nearest neighbors: neighbour distance coordinates ---------------------------------- 1 1.0 [-4. 3.] 2 2.0 [-5. 5.] 3 2.0 [-3. 5.]
Což si pochopitelně můžeme vizualizovat v rovině. Hvězdičkou je naznačen bod/vektor z podmínky (pro který hledáme nejbližší sousedy), kolečkem vektory vrácené jako výsledek dotazu a tečkou ostatní vektory, které neodpovídají dotazu (nejsou vráceny):
│ y
│
│
│
│
o o │ . . .
* │ . . .
o │ . . .
│
│
─────────────────────────────────────[0,0]──────────────────────────────────────
│ x
│
│ .
│
│ . .
│
│
│
│
13. Výběry vektorů na základě jejich podobnosti: volba metriky
Prozatím jsme pro výpočty podobnosti (resp. vzdálenosti) vektorů používali klasickou Eukleidovskou metriku, tedy skutečnou vzdálenost bodů v prostoru (v tomto případě vzdálenost koncových bodů vektorů v 2D rovině). Tato metrika se taktéž označuje L2 nebo přesněji L2, ovšem knihovna FAISS podporuje i odlišnou metriku založenou na výpočtu skalárního součinu (dot product). Vychází se přitom z faktu, že pokud mají dva vektory jednotkovou délku, bude jejich skalární součin největší v případě, že jsou vektory totožné, nulový ve chvíli, kdy jsou vektory na sebe kolmé a záporný tehdy, pokud je jeden vektor oproti druhému otočen o 180°. Jedná se o velmi často používanou metriku pro hledání podobných vektorů, ovšem v praxi nesmíme zapomenout na její základní vlastnosti:
- Všechny vektory musí být normalizovány na jednotkovou délku (kromě nulového vektoru)
- Jedná se o metriku, nikoli o vzdálenost. Naopak – čím podobnější jsou vektory, tím větší bude výsledek (opak vzdálenosti).
- Pozor je nutné dát na nulové vektory, které není možné normalizovat (speciální případ)
14. Výběr podobných vektorů pomocí skalárního součinu: nekorektní verze
Vyzkoušejme si nyní nahradit hledání podobných vektorů na základě vzdálenosti za hledání s využitím skalárního součinu. Ve skriptu prozatím provedeme jedinou změnu, a to konkrétně záměnu funkce pro konstrukci indexů. Namísto:
index = faiss.IndexFlatL2(2)
zavoláme:
index = faiss.IndexFlatIP(2)
Výsledky budou vypadat takto:
Nearest neighbors: neighbour distance coordinates ---------------------------------- 1 30.0 [5. 5.] 2 27.0 [5. 4.] 3 27.0 [4. 5.] 4 24.0 [5. 3.] 5 24.0 [4. 4.] 6 24.0 [3. 5.] 7 21.0 [4. 3.] 8 21.0 [3. 4.] 9 18.0 [3. 3.] 10 6.0 [-3. 5.] 11 3.0 [ 4. -3.] 12 0.0 [ 5. -5.] 13 0.0 [-5. 5.] 14 -3.0 [-4. 3.] 15 -6.0 [ 3. -5.]
Například první výpočet vypadá následovně: 3×5+3×5=15+15=30. A poslední výpočet 3×3+3×(-5)=9–15=-6. Tedy čím podobnější jsou vektory, tím větší bude hodnota, zatímco u L2 metriky tomu bylo naopak!
Celý skript byl upraven do této podoby:
import faiss
import numpy as np
# x-ove souradnice bodu v rovine
x = [-5, -4, -3, 3, 4, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5]
# y-ove souradnice bodu v rovine
y = [ 5, 3, 5, -5, -3, -5, 3, 4, 5, 3, 4, 5, 3, 4, 5]
# konstrukce 2D matice, v niz kazdy radek obsahuje souradnice jednoho bodu v
# rovine
points = np.column_stack((x,y)).astype("float32")
print(points)
# konstrukce indexu pro vyhledavani na zaklade skalarniho soucinu
index = faiss.IndexFlatIP(2)
index.add(points)
print()
print("Dimension(s): ", index.d)
print("Total values in index:", index.ntotal)
print("Is index trained: ", index.is_trained)
# vektor, ke kteremu budeme pocitat vzdalenost
query_vector = np.array([[3, 3]]).astype("float32")
print(query_vector)
# pocet nejblizsich bodu
k = len(x)
distances, indices = index.search(query_vector, k)
# tisk vysledku
print("Nearest neighbors:")
print("neighbour distance coordinates ")
print("----------------------------------")
for i in range(k):
print(f"{i+1:3} {distances[0][i]:5} {points[indices[0][i]]}")
15. Normalizace vektorů v indexu
Výpočet metriky založené na skalárním součinu předpokládá, že vektory jsou již dopředu normalizovány, tj. že jejich délka je buď rovna jedné nebo nule. V praxi je tedy nutné již při konstrukci indexů použít normalizované vektory. To se provede relativně snadno (a zejména – pouze jedenkrát při inicializaci):
# normalizace for i in range(len(points)): vector = points[i] normalized = np.linalg.norm(vector) vector /= normalized points[i] = vector
Index se zkonstruuje s využitím normalizovaných vektorů:
# konstrukce indexu pro vyhledavani na zaklade vzdalenosti index = faiss.IndexFlatIP(2) index.add(points)
I vektor, pro který hledáme nejshodnější „sousedy“ je nutné normalizovat a teprve poté provést vyhledávání:
# vektor, ke kteremu budeme pocitat vzdalenost
query_vector = np.array([[3, 3]]).astype("float32")
normalized = np.linalg.norm(query_vector)
query_vector /= normalized
print(query_vector)
# pocet nejblizsich bodu
k = len(x)
distances, indices = index.search(query_vector, k)
Výsledky vyhledávání budou (podle očekávání) odlišné:
Nearest neighbors: neighbour distance coordinates ---------------------------------- 1 +1.0000 [0.7071068 0.7071068] 2 +1.0000 [0.70710677 0.70710677] 3 +1.0000 [0.70710677 0.70710677] 4 +0.9939 [0.78086877 0.62469506] 5 +0.9939 [0.62469506 0.78086877] 6 +0.9899 [0.8 0.6] 7 +0.9899 [0.6 0.8] 8 +0.9701 [0.857493 0.5144958] 9 +0.9701 [0.5144958 0.857493 ] 10 +0.2425 [-0.5144958 0.857493 ] 11 +0.1414 [ 0.8 -0.6] 12 +0.0000 [-0.70710677 0.70710677] 13 -0.0000 [ 0.70710677 -0.70710677] 14 -0.1414 [-0.8 0.6] 15 -0.2425 [ 0.5144958 -0.857493 ]
Opět si ukažme úplný zdrojový kód takto upraveného skriptu:
import faiss
import numpy as np
# x-ove souradnice bodu v rovine
x = [-5, -4, -3, 3, 4, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5]
# y-ove souradnice bodu v rovine
y = [ 5, 3, 5, -5, -3, -5, 3, 4, 5, 3, 4, 5, 3, 4, 5]
# konstrukce 2D matice, v niz kazdy radek obsahuje souradnice jednoho bodu v
# rovine
points = np.column_stack((x,y)).astype("float32")
print(points)
# normalizace
for i in range(len(points)):
vector = points[i]
normalized = np.linalg.norm(vector)
vector /= normalized
points[i] = vector
print()
print("Normalized:")
print(points)
# konstrukce indexu pro vyhledavani na zaklade vzdalenosti
index = faiss.IndexFlatIP(2)
index.add(points)
print()
print("Dimension(s): ", index.d)
print("Total values in index:", index.ntotal)
print("Is index trained: ", index.is_trained)
# vektor, ke kteremu budeme pocitat vzdalenost
query_vector = np.array([[3, 3]]).astype("float32")
normalized = np.linalg.norm(query_vector)
query_vector /= normalized
print(query_vector)
# pocet nejblizsich bodu
k = len(x)
distances, indices = index.search(query_vector, k)
# tisk vysledku
print("Nearest neighbors:")
print("neighbour distance coordinates ")
print("----------------------------------")
for i in range(k):
print(f"{i+1:3} {distances[0][i]:+7.4f} {points[indices[0][i]]}")
16. Rychlost vyhledání nejbližších bodů
Při vyhledávání na základě podobnosti vektorů v rozsáhlých databázích je důležité, aby byl algoritmus vyhledávání dostatečně rychlý. V knihovně FAISS je z tohoto důvodu implementováno hned několik algoritmů používaných v různých situacích. Dnes se budeme primárně zabývat výchozím algoritmem, u kterého se pokusíme odhadnout (a příště i popsat) jeho časovou složitost. Vytvoříme proto benchmark, který bude pracovat s různě velkými indexy a bude postupně měřit dobu vyhledávání (a pro zajímavost i další časy trvání). Celý benchmark je prozatím poměrně naivní, ovšem pro prvotní odhad složitost může postačovat:
from time import time
import faiss
import numpy as np
import matplotlib.pyplot as plt
def similarity_search(n, k):
DIMENSIONS=128
t1 = time()
# nahodne vektory
data = np.random.rand(n, 128).astype('float32')
t2 = time()
# konstrukce indexu pro vyhledavani na zaklade vzdalenosti
index = faiss.IndexFlatL2(DIMENSIONS)
index.add(data)
t3 = time()
# vektor, ke kteremu budeme pocitat vzdalenost
query_vector = np.random.rand(1, DIMENSIONS).astype("float32")
# pocet nejblizsich bodu
distances, indices = index.search(query_vector, k)
t4 = time()
assert len(distances) == k
assert len(indices) == k
return n, t2-t1, t3-t2, t4-t3
ns = []
ts_rand = []
ts_index = []
ts_search = []
for n in np.linspace(1000000, 10000000, 10):
print(n)
n, t_rand, t_index, t_search = similarity_search(int(n), 1)
ns.append(n)
ts_rand.append(t_rand)
ts_index.append(t_index)
ts_search.append(t_search)
plt.plot(ns, ts_rand, "r-", label="numpy.random.rand")
plt.plot(ns, ts_index, "b-", label="index creation")
plt.plot(ns, ts_search, "m-", label="similarity search")
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
plt.savefig("faiss_benchmark_2.png")
# zobrazení grafu
plt.show()
17. Výsledky benchmarku
Numerické výsledky benchmarku vypadají následovně:
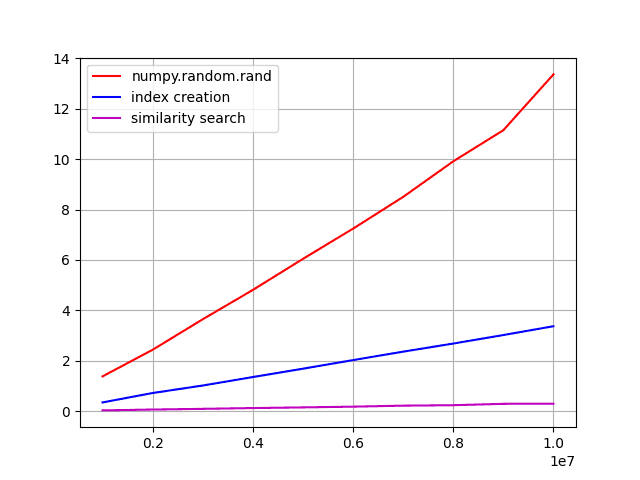
n Konstrukce matice Konstrukce indexu Vlastní vyhledávání --------------------------------------------------------------------- 1000000 1.313993215560913 0.3532786369323731 0.03192019462585449 2000000 2.543938875198364 0.7037720680236816 0.06934928894042969 3000000 3.741727113723755 1.0349786281585693 0.09357905387878418 4000000 4.819754600524902 1.3467643260955810 0.11976456642150879 5000000 6.031541824340820 1.6814656257629395 0.14942240715026855 6000000 7.295117855072022 2.1264710426330566 0.17904376983642578 7000000 8.616289138793945 2.3469836711883545 0.23292398452758790 8000000 11.428938865661621 2.7663018703460693 0.24178504943847656 9000000 21.055070638656616 3.2713224887847900 0.27842283248901367 10000000 27.235011577606200 3.4759612083435060 0.29420256614685060
Lepší však bude si výsledky prohlédnou v grafické podobně. Nejprve všechny časy:
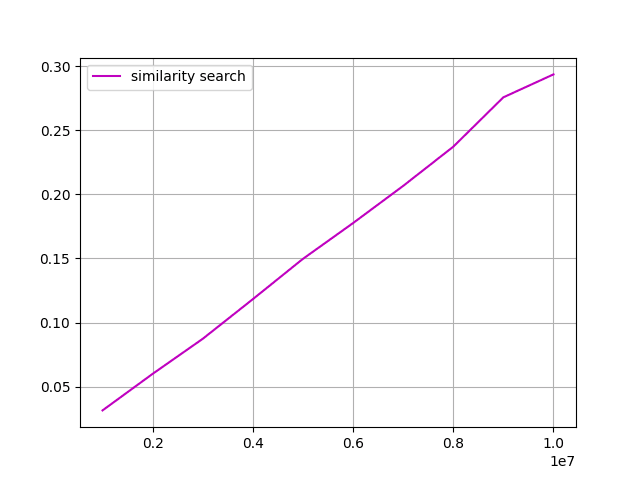
Ovšem nejvíce nás zajímají časy vyhledávání, takže si zobrazme pouze tyto naměřené výsledky:
18. Obsah navazujícího článku
Knihovna FAISS není vývojáři oblíbena ani tak kvůli tomu, jaké operace umí realizovat (ostatně jednoduchý similarity search lze naprogramovat v řádu minut), ale jak rychle je dokáže provádět. K dispozici je totiž hned několik algoritmů výpočtů, které se vybírají na základě velikosti vstupní množiny vektorů, počtu dimenzí vektorů, taktéž na základě toho, jestli jsou vektory uloženy v operační paměti nebo přesahují její rozsah atd. Navíc je možné výsledky (tedy nejbližší vektory nalezené na základě zadané metriky) v případě potřeby pouze „odhadovat“, tj. nemusí se nalézt skutečně ty nejbližší vektory, ale vektory dostatečně blízké. To sice nemusí znít příliš prakticky, ale ve skutečnosti se tyto algoritmy v praxi poměrně často používají zejména při realizacích RAG databází. O těchto optimalizacích si řekneme podrobnější informace v navazujícím článku.
19. Repositář s demonstračními příklady
Demonstrační příklady vytvořené v Pythonu a popsané v dnešním článku najdete v repositáři https://github.com/tisnik/most-popular-python-libs/. Následují odkazy na jednotlivé příklady:
20. Odkazy na Internetu
- FAISS (Facebook AI Similarity Search)
https://en.wikipedia.org/wiki/FAISS - FAISS documentation
https://faiss.ai/ - Introduction to Facebook AI Similarity Search (Faiss)
https://www.pinecone.io/learn/series/faiss/faiss-tutorial/ - Faiss: Efficient Similarity Search and Clustering of Dense Vectors
https://medium.com/@pankaj_pandey/faiss-efficient-similarity-search-and-clustering-of-dense-vectors-dace1df1e235 - Top 8 Vector Databases in 2025: Features, Use Cases, and Comparisons
https://synapsefabric.com/top-8-vector-databases-in-2025-features-use-cases-and-comparisons/ - Is FAISS a Vector Database? Complete Guide
https://mljourney.com/is-faiss-a-vector-database-complete-guide/ - Vector database
https://en.wikipedia.org/wiki/Vector_database - Similarity search
https://en.wikipedia.org/wiki/Similarity_search - Nearest neighbor search
https://en.wikipedia.org/wiki/Nearest_neighbor_search#Approximation_methods - Decoding Similarity Search with FAISS: A Practical Approach
https://www.luminis.eu/blog/decoding-similarity-search-with-faiss-a-practical-approach/ - MetricType and distances
https://github.com/facebookresearch/faiss/wiki/MetricType-and-distances - RAG – Retrieval-augmented generation
https://en.wikipedia.org/wiki/Retrieval-augmented_generation - pgvector na GitHubu
https://github.com/pgvector/pgvector - Why we replaced Pinecone with PGVector
https://www.confident-ai.com/blog/why-we-replaced-pinecone-with-pgvector - PostgreSQL as VectorDB – Beginner Tutorial
https://www.youtube.com/watch?v=Ff3tJ4pJEa4 - What is a Vector Database? (neobsahuje odpověď na otázku v titulku :-)
https://www.youtube.com/watch?v=t9IDoenf-lo - PGVector: Turn PostgreSQL Into A Vector Database
https://www.youtube.com/watch?v=j1QcPSLj7u0 - Milvus
https://milvus.io/ - Vector Databases simply explained! (Embeddings & Indexes)
https://www.youtube.com/watch?v=dN0lsF2cvm4 - Vector databases are so hot right now. WTF are they?
https://www.youtube.com/watch?v=klTvEwg3oJ4 - Step-by-Step Guide to Installing “pgvector” and Loading Data in PostgreSQL
https://medium.com/@besttechreads/step-by-step-guide-to-installing-pgvector-and-loading-data-in-postgresql-f2cffb5dec43 - Best 17 Vector Databases for 2025
https://lakefs.io/blog/12-vector-databases-2023/ - Top 15 Vector Databases that You Must Try in 2025
https://www.geeksforgeeks.org/top-vector-databases/ - Picking a vector database: a comparison and guide for 2023
https://benchmark.vectorview.ai/vectordbs.html - Top 9 Vector Databases as of Feburary 2025
https://www.shakudo.io/blog/top-9-vector-databases - What is a vector database?
https://www.ibm.com/think/topics/vector-database - SQL injection
https://en.wikipedia.org/wiki/SQL_injection - Cosine similarity
https://en.wikipedia.org/wiki/Cosine_similarity - Euclidean distance
https://en.wikipedia.org/wiki/Euclidean_distance - Dot product
https://en.wikipedia.org/wiki/Dot_product - Hammingova vzdálenost
https://cs.wikipedia.org/wiki/Hammingova_vzd%C3%A1lenost - Jaccard index
https://en.wikipedia.org/wiki/Jaccard_index - Manhattanská metrika
https://cs.wikipedia.org/wiki/Manhattansk%C3%A1_metrika - pgvector: vektorová databáze postavená na Postgresu
https://www.root.cz/clanky/pgvector-vektorova-databaze-postavena-na-postgresu/