GLib: Binární stromy (2)

Procházení stromem GTree

void g_tree_traverse(GTree *tree,
                     GTraverseFunc traverse_func,
                     GTraverseType traverse_type,
                     gpointer data);

gint(*GTraverseFunc)(gpointer key, gpointer value,
                     gpointer data);

Funkce g_tree_traverse() je velice podobná funkcím, které známe z dřívějška a které nesly společný název „ foreach“.

g_tree_traverse() 

Funkci typu GTraverseFunc se předávají klíče key a data value každého prvku společně s pointerem data, což jsou uživatelská data předaná funkci g_tree_traverse() jako čtvrtý parametr. Jestliže funkce typu GTraverseFunc ( traverse_func) vrátí TRUE, procházení stromem končí (jestliže vrátí FALSE bude se pokračovat na dalším prvku stromu, pokud ještě nějaký zbývá).

Třetím argumentem funkce g_tree_traverse() je typ procházení stromem. Výčtový typ GTraverseType vyjmenovává všechny možnosti:

typedef enum {
  G_IN_ORDER,
  G_PRE_ORDER,
  G_POST_ORDER,
  G_LEVEL_ORDER
} GTraverseType;

Jednotlivé volby určují pořadí, v jakém se budou uzly procházet a znamenají toto:

• G_PRE_ORDER  – g_tree_traverse() navštíví nejprve uzel a potom jeho následovníky v pořadí levý, pravý.
• G_IN_ORDER  – nejprve se navštíví levý následovník, pak samotný uzel a nakonec pravý následovník. Tuto volbu použijte, chcete-li získat prvky v seřazeném pořadí. Skutečně totiž platí, že když se prvky čtou takto, je to vlastně seřazeně podle kritéria daného funkcí key_compare_func, která je argumentem g_tree_new().
• G_POST_ORDER  – navštíví nejprve levého a pravého následovníka a pak teprve samotný uzel.
• G_LEVEL_ORDER  – tato volba není pro vyvážené binární stromy implementována. Její využití je jen při práci s mnohonásobnými stromy. (Viz později.)

Předcházející vysvětlení voleb GTraverseType bylo poněkud strohé a ne každému může být okamžitě jasné, jak vše doopravdy funguje. Podívejme se tedy na procházení stromem názorně na příkladu. Předpokládejme, že máme vybudovaný strom o šesti prvcích (čísla 1 až 6) a je uspořádaný tak, jako na obrázku 1.

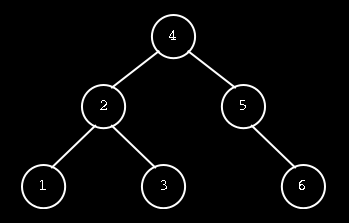
Obrázek 1 – Vzorový strom o šesti prvcích

Pro procházení stromem použijme třeba metodu G_POST_ORDER. Uzly stromu z obrázku 1 se navštíví v tomto pořadí: 1, 3, 2, 6, 5, 4. Jak je to možné?

Procházení stromem probíhá rekurzivně. Na každý uzel se zavolá jistá funkce, která se pokusí rekurzivně zavolat sama sebe i na následovníky uzlu. Nemá-li už uzel žádné následovníky, nebo došlo-li už k návratu rekurzivních volání na následovníky, jednoduše se právě zpracovávaný uzel „navštíví“. („Navštívit uzel“ v tomto textu znamená, že se na něj zavolá uživatelská funkce  GTraverseFunc.)

Formálně bychom funkci realizující procházení stromem metodou G_POST_ORDER mohli zapsat třeba takto:

funkce_pro_post_order(aktualni_uzel)
{
  if (aktualni_uzel == NULL) exit;

  /* vola sama sebe na nasledovniky uzlu */
  funkce_pro_post_order(levy_nasledovnik(aktualni_uzel));
  funkce_pro_post_order(pravy_nasledovnik(aktualni_uzel));

  /* "navstiveni" uzlu */
  traverse_func(aktualni_uzel);
}

Mechanizmus pak proběhne třeba takto:

Začne se v kořenu, tedy v uzlu 4.  G_POST_ORDER velí navštívit nejprve levého a pravého následovníka a teprve pak samotný uzel. Přejde se tedy na uzel 2. I pro něj platí, že se mají navštívit nejprve následovníci: pozornost se tedy přesune na uzel 1. Ten již žádné následovníky nemá, proto se „navštíví“. Přesuneme se zpět k jeho rodiči, k uzlu 2. Levý následovník „dvojky“ (uzel 1) již navštíven byl, zbývá proto pravý následovník (uzel 3). „Trojka“ už žádné následovníky nemá, proto se navštíví. Opět se přesuneme k uzlu 2. Všichni jeho následovníci už byli navštívení, proto se navštíví i samotná „dvojka“. Poté se přesuneme k rodiči uzlu 2, k uzlu 4. Levý následovník „čtyřky“ (2) už navštíven byl, ale pravý (5) ne, proto se na něj přesuneme. „Pětka“ levého následovníka nemá a tak se pokračuje pravým – uzlem číslo 6. Jelikož „šestka“ je listem a tudíž už nelze nikam pokračovat, jednoduše se navštíví. Následuje přesun zpět na rodičovskou „pětku“, která už má všechny následovníky navštívené a tedy splňuje kritérium G_POST_ORDER k tomu, aby mohla být navštívena. Naposledy se přesuneme k rodiči uzlu 5, k uzlu 4. Také ten již má všechny následovníky navštívené, proto se navštíví i on sám a cyklus je u konce. Uff.

Analogicky fungují i ostatní metody. Následující tabulka shrnuje pořadí prvků, jaká byste dostali použitím různých metod procházení naším stromem:

Nevěříte-li, zkuste si následující příklad.

Příklad:

#include <glib.h> /* Makro, abych se neupsal k smrti */ #define my_insert(t, k) \   g_tree_insert((t), GINT_TO_POINTER(k), GINT_TO_POINTER(k))

/* porovnavaci funkce */
gint my_compare(gconstpointer a, gconstpointer b)
{
  if (GPOINTER_TO_INT(a) == GPOINTER_TO_INT(b)) {
    return(0);
  } else if (GPOINTER_TO_INT(a) < GPOINTER_TO_INT(b)) {
    return(-1);
  } else {
    return(1);
  }
}

/* co se ma provest na kazdem uzlu */
my_traverse(gpointer key, gpointer value, gpointer data)
{
  printf("%d\n", GPOINTER_TO_INT(key));
  return (FALSE);
}

gint main(void)
{
  GTree *tree;

  /* vytvoreni stromu */
  tree = g_tree_new(my_compare);
  my_insert(tree, 4);
  my_insert(tree, 2);
  my_insert(tree, 5);
  my_insert(tree, 1);
  my_insert(tree, 3);
  my_insert(tree, 6);

  /* ruzne druhy prochazeni stromem */
  puts("PRE:");
  g_tree_traverse(tree, my_traverse, G_PRE_ORDER, NULL);
  puts("\nIN:");
  g_tree_traverse(tree, my_traverse, G_IN_ORDER, NULL);
  puts("\nPOST:");
  g_tree_traverse(tree, my_traverse, G_POST_ORDER, NULL);

  /* dealokace stromu */
  g_tree_destroy(tree);
}

Poznámka:

Jak již bylo řečeno minule, při přidávání prvků do stromu se provádí jeho tzv. vyvažování. Důsledkem toho je fakt, že se umístění prvků ve stromu může dramaticky měnit. Prvky se všelijak přeskupují, aby se dosáhlo toho, že výška stromu bude co nejmenší.

Další funkce

gint g_tree_nnodes(GTree *tree); 

…vrátí počet uzlů ve vyváženém binárním stromu tree.

gint g_tree_height(GTree *tree); 

…vrátí výšku stromu tree. Každý si asi intuitivně dokáže představit, co se tou výškou míní. Tak například strom na obrázku 1 má výšku 3. Kdyby strom tree byl prázdný, bude mít výšku 0. Kdyby obsahoval jen kořen, vrátí g_tree_height() hodnotu 1. Kdyby tento kořen měl nějaké následovníky, bude výška stromu 2 a podobně.

Jinými slovy, výška stromu je velikost nejdelší cesty od kořene k listům.

void g_tree_remove(GTree *tree, gpointer key); 

…ze stromu tree odstraní podle hodnoty klíče key dvojici klíč–data. Pokud jste klíč nebo data alokovali dynamicky, musíte se sami postarat o to, abyste je také dealokovali.

Jako poslední funkci zmíním rutinu g_tree_search(), která je trochu neobvyklá.

gpointer g_tree_search(GTree *tree,
                       GSearchFunc search_func,
                       gpointer data);
gint(*GSearchFunc)(gpointer key, gpointer data);

Jejím úkolem je vyhledat ve stromu tree danou položku. Vyhledávání se realizuje pomocí funkce search_func, která slouží k rozhodování o tom, byla-li položka nalezena nebo nikoliv.

Tato funkce není tak užitečná, jak by se mohlo zdát. Umožňuje sice použití jiné (nové, další) funkce pro realizaci porovnávání, ale ta musí stejně vracet přesně shodné výsledky jako funkce key_compare_func, která se předává funkci g_tree_new() při vytváření nového stromu.

Funkce typu GSearchFunc je tedy spouštěna na každý uzel a jako parametr jí je předán klíč key prvku stromu a uživatelská data (pozor, tento parametr nejsou data uložená ve stromu pod klíčem key, ale tentýž pointer, který se předá funkci g_tree_search() jako parametr data). Funkce musí vrátit 0, jestliže požadovaný klíč byl nalezen, záporné číslo, jestliže požadovaný klíč je menší než key (jestliže pořadově patří před klíč key) a kladnou hodnotu, jestliže požadovaný klíč patří pořadově za klíč  key.

Funkce g_tree_search() vrátí pointer na uložená data odpovídající požadovanému klíči nebo NULL, nebyl-li takový klíč nalezen.

Prosím všimněte si, že hledaný klíč se nikde nezapisuje jako parametr. Je tedy na programátorovi, jak funkce typu GSearchFunc zjistí, co má vlastně hledat. Jednou možností je právě využití onoho uživatelského datového parametru data, který se předává každému volání funkce search_func.

Příklad:

Nakonec ještě jednoduchý příklad na klasickou práci se stromy: přidávání a získávání uložených hodnot.

#include <glib.h>

gint my_compare(gconstpointer a, gconstpointer b)
{
  return (strcmp((gchar *) a, (gchar *) b));
}

gint main(void)
{
  GTree *tree;

  /* inicializace stromu */
  tree = g_tree_new(my_compare);
  g_tree_insert(tree, "Karel", GINT_TO_POINTER(100));
  g_tree_insert(tree, "Petr", GINT_TO_POINTER(200));
  g_tree_insert(tree, "Josef", GINT_TO_POINTER(150));
  g_tree_insert(tree, "Adam", GINT_TO_POINTER(620));
  g_tree_insert(tree, "Pavel", GINT_TO_POINTER(490));

  /* ziskani hodnot */
  printf("Josef ma %d Kc\n", g_tree_lookup(tree, "Josef"));

  /* dealokace */
  g_tree_destroy(tree);
}

Závěr

GLib nedefinuje funkce pro práci s binárními stromy na úrovni uzlů. Operace ručního procházení stromem, zakládání a rušení větví jsou zde bezpředmětné. Dá se říct, že binární stromy slouží výhradně jako mechanizmus rychlého vyhledávání dat.

Chcete-li přesto pracovat se stromy na nižší úrovni a mít pod kontrolou jeho větve a uzly, přečtěte si další díl článku o knihovně GLib: příště se budeme bavit o stromech s mnohonásobnými větvemi, pomocí nichž můžete budovat jakkoliv složité stromy, procházet po jejich větvích a podobně.