Obsah
1. Diskrétní kosinová transformace (DCT)
2. Jednorozměrná diskrétní kosinová transformace (1D DCT)
3. První demonstrační příklad – bázové funkce 1D DCT
4. Dvourozměrná diskrétní kosinová transformace (2D DCT)
5. Druhý demonstrační příklad – bázové funkce 2D DCT
6. DCT a standard JPEG
7. Odkazy na další informační zdroje
8. Obsah dalšího pokračování tohoto seriálu
1. Diskrétní kosinová transformace (DCT)
Diskrétní kosinová transformace (DCT – Discrete Cosine Transform) patří do skupiny metod provádějících takzvané transformační kódování nad diskrétním (vzorkovaným) jednorozměrným či vícerozměrným signálem. Do stejné skupiny patří i optimální KLT (Karhunen-Loéve Transform – Karhunen-Loéveho transformace) či známá FFT (Fast Fourier Transform – rychlá diskrétní Fourierova transformace). Základem prakticky všech v praxi používaných transformačních kódování je v případě zpracování obrazu, který můžeme pro tyto účely považovat za dvourozměrný vzorkovaný signál, nalezení korelace mezi sousedními, popř. i vzdálenějšími pixely – jedná se o takzvanou mezipixelovou redundanci. Při práci s videem se kromě mezipixelové redundance uplatní i redundance mezisnímková.
Většinou se při transformacích provádí převod (či mapování, resp. zobrazení) zpracovávaného signálu z časové (prostorové) oblasti do oblasti frekvenční, protože existuje předpoklad, že například obrazy reálných předmětů neobsahují mnoho energie ve vyšších frekvencích a je tedy vhodné shromáždit co největší množství relevantních dat do malého množství koeficientů. Kódování by mělo ve svém důsledku vést k celkovému snížení počtu bitů nesoucích vizuální informaci (psychovizuální redundance). V dalším textu se již soustředíme na popis diskrétní kosinové transformace, ostatní typy transformací (KLT, FFT, vlnková) se totiž ve standardu JPEG neuplatní (vlnková transformace je základem prozatím nepříliš úspěšného formátu JPEG 2000).
Existuje více typů diskrétních kosinových transformací, které jsou v literatuře označovány římskými číslicemi jako DCT I až DCT IV. My si v dalším textu představíme „pouze“ DCT II. Ta je zdaleka nejpoužívanější a tvoří základ pro většinu praktických úloh, které DCT nějakým způsobem využívají. Dvourozměrná diskrétní kosinová transformace typu II je v současnosti použita například v mnoha souborových formátech i formátech určených pro přenos videa. Například se jedná o standardy JPEG, MPEG 1, MPEG 2, MPEG 4, JVT (H.263), H.261 atd. Sice existují i jiné transformace vhodné pro některé úlohy, například velmi populární vlnková transformace (Wavelet Transform), KLT atd., ty však z několika důvodů (implementačních, obchodních i patentových) prozatím DCT v praxi nepřekonaly.
Mezi vlastnosti DCT patří:
- Energie 1D, 2D či nD signálu je po provedení diskrétní kosinové transformace většinou soustředěna v několika málo koeficientech. Toho se využívá při následném kvantování vypočtených koeficientů.
- Výsledek DCT transformace je blízký optimální KLT transformaci, především z důvodu minimalizace zbytkové korelace. DCT je však implementačně mnohem jednodušší než KLT.
- Existují rychlé implementace přímé i inverzní DCT. Při optimalizacích se většinou využívá symetrie výpočtů a separabilita (2D DCT pomocí série 1D DCT).
- Při implementaci je možné použít jak aritmetiku v plovoucí řádové čárce (FP), tak i aritmetiku prováděnou v pevné řádové čárce (FX).
- Rekurzivní struktura – vhodné při implementaci vícerozměrných DCT.
- DCT má i některé nectnosti, především blokovou strukturu, která může být viditelná například při nastavení velkých komprimačních faktorů (malého koeficientu Q) při komprimaci pomocí JPEGu. Totéž platí i při zápisu videa do některého z formátů MPEG.
2. Jednorozměrná diskrétní kosinová transformace (1D DCT)
Jednorozměrná diskrétní kosinová transformace typu II (zkráceně ji budeme označovat jako 1D DCT) slouží ke zpracování jednorozměrného diskrétního (tj. vzorkovaného) signálu, získaného například ze zvukové stopy CDčka. Nemusí se však jednat pouze o celočíselné vzorky, pomocí DCT lze zpracovat i reálný či dokonce komplexní signál. Každou hodnotu tohoto signálu označme symbolem s(n), kde n je pozice (index) vzorku v signálu. Po aplikaci jednorozměrné diskrétní kosinové transformace získáme sadu transformovaných koeficientů, které budeme značit t(k). Vztah pro výpočet 1D DCT má následující tvar:
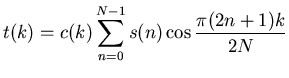
kde N značí řád/velikost DCT (v praktických aplikacích typicky 8 či 16) a hodnota indexu k leží v rozsahu 0..N-1. Konstanta c(k) je rovna (1/N)1/2 v případě, že k=0, v ostatních případech platí c(k)=(2/N)1/2:
Pomocí jednorozměrné diskrétní kosinové transformace tedy můžeme zpracovat vždy maximálně N vzorků, v případě jejich většího počtu se vzorec periodicky opakuje pro dalších N vzorků vstupního signálu. Teoreticky je možné za N zvolit délku celého vstupního signálu, v praxi se však tato činnost neprovádí, protože přináší některé implementační problémy (pomalá operace, velká spotřeba paměti, nevýhodnost z hlediska ztrátové komprimace atd.).
3. První demonstrační příklad – bázové funkce 1D DCT
V dnešním prvním demonstračním příkladu si ozřejmíme význam takzvaných bázových funkcí diskrétní kosinové transformace. V předchozí kapitole jsme si uvedli vzorec pro výpočet jednorozměrné diskrétní kosinové transformace. V tomto vzorci představuje podvýraz:

vyjádření bázové kosinové funkce. Pro zadaný řád transformace N mají bázové funkce typický průběh, který je pomocí dnešního prvního demonstračního příkladu vykreslen do rastrového obrázku. Ve zdrojovém kódu příkladu se na jeho začátku nachází definice symbolické konstanty N, kterou je možné před překladem změnit. Smysluplné hodnoty této konstanty jsou 8, 16 či 32, přičemž musíme mít na paměti, že čím větší je dosazená hodnota, tím větší vertikální rozlišení bude mít výsledný obrázek. Platí totiž vztah: vertikální rozlišení=100×N.
Horizontální rozlišení vytvářeného obrázku zůstává zachováno; to znamená, že při větší hodnotě N jsou vzorky bázových kosinových funkcí zobrazeny s vyšší hustotou. Po překladu a spuštění příkladu se vytvoří rastrový obrázek ve formátu TGA (Targa), ve které je zakreslen průběh bázových funkcí pro dané N. Na následující trojici obrázků jsou ukázány bázové kosinové funkce pro konstantu N nastavenou na hodnoty 8, 16 a 32.
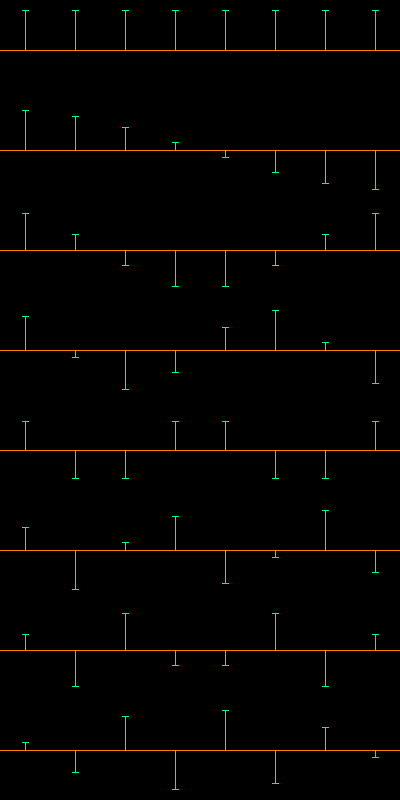
Bázové kosinové funkce 1D DCT pro N=8

Bázové kosinové funkce 1D DCT pro N=16

Bázové kosinové funkce 1D DCT pro N=32
Na třech předchozích obrázcích s průběhy bázových kosinových funkcí stojí za povšimnutí, že první průběh je vždy konstantní. Z toho vyplývá jeho označení jako DC složka (Direct Current – stejnosměrná složka). Druhý průběh představuje poloviční periodu funkce cos, třetí průběh již celou periodu atd. – dochází prakticky ke zvyšování frekvence. Zdrojový kód prvního demonstračního příkladu je dostupný jak ve formě plaintextu, tak i ve formátu HTML se zvýrazněnou syntaxí. Samotný výpočet bázových funkcí je spolu s jejich vykreslením soustředěn v následující části kódu:
//-----------------------------------------------------------------------------
// Vykreslení bázových funkcí jednorozměrné diskrétní kosinové transformace
//-----------------------------------------------------------------------------
void draw1d_dct(const pixmap *pix, int n)
{
#define PI 3.1415927
// počitadlo indexu bázových funkcí
int u;
// pozicování průběhu bázových funkcí
// ve výsledném obrázku
int xoffset=25*8/N, yoffset=50;
int xdelta=50*8/N, ydelta=100;
float amplitude=40.0;
// vykreslit všech "n" bázových funkcí
for (u=0; u<n; u++) {
int x;
// pozice horizontální osy pro danou
// bázovou funkci s indexem "u"
int y0=yoffset+ydelta*u;
float y;
// vykreslení horizontální osy
hline(pix,
0, // x1
pix->width-1, // x2
y0, // y
255, // červená barvová složka
128, // zelená barvová složka
0); // modrá barvová složka
// výpočet všech bodů bázové funkce s indexem "u"
for (x=0; x<n; x++) {
float alfa=PI*(2.0*x+1.0)*u/(2.0*n);
// hodnota bázové funkce pro dané "x"
y=amplitude*cos(alfa);
// kontrolní výpis hodnot
printf("%d %d -> %f\n", u, x, alfa);
// vykreslení vertikální hodnoty do grafu
vline(pix,
xoffset+xdelta*x, // x1
y0, // x2
y0-y, // y
0, // červená barvová složka
255, // zelená barvová složka
128); // modrá barvová složka
// zvýraznění koncového bodu (vypočtené hodnoty)
// pomocí horizontální čárky dlouhé sedm pixelů
hline(pix,
xoffset+xdelta*x-3, // x1
xoffset+xdelta*x+3, // x2
y0-y, // y
0, // červená barvová složka
255, // zelená barvová složka
128); // modrá barvová složka
}
}
}
// finito
4. Dvourozměrná diskrétní kosinová transformace (2D DCT)
Dvourozměrná diskrétní kosinová transformace typu II (zkráceně 2D DCT) vzniká zobecněním jednorozměrné DCT. Vstupem do 2D DCT je vzorkovaný signál (prakticky uložený jako rastrový obrázek či matice), který označme symbolem s(m,n). Výstupem DCT je taktéž rastrový obrázek (matice) hodnot t(i,j). Řád či velikost dvourozměrné DCT je obecně typu M×N, v praxi se však většinou dosazuje M=N, což vede k rychlejším a především jednodušším výpočtům bez většího vlivu na průběh dalšího zpracování. Vzorec pro výpočet 2D DCT v tomto případě dostává tvar:
Konstanty c(i,j) vznikají vzájemným vynásobením jejich „jednorozměrných“ protějšků c(k).
5. Druhý demonstrační příklad – bázové funkce 2D DCT
V dnešním druhém demonstračním příkladu si ukážeme jeden ze způsobů zobrazení bázových funkcí dvourozměrné diskrétní kosinové transformace. Na rozdíl od příkladu prvního si nebudeme zobrazovat přímo průběh diskrétních signálů, ale každou hodnotu bázové funkce vyjádříme stupněm šedi na vykreslovaném rastrovém obrázku. Bázové funkce 2D DCT můžeme jednoduše získat ze vzorce uvedeného v předchozí kapitole:

Zdrojový kód druhého demonstračního příkladu si můžete stáhnout (podobně jako příklad předchozí) jak ve formě plaintextu, tak i ve formátu HTML se zvýrazněnou syntaxí. Samotný výpočet bázových funkcí je spolu s jejich vykreslením soustředěn v následující části kódu:
//-----------------------------------------------------------------------------
// Vykreslení bázových funkcí dvourozměrné diskrétní kosinové transformace
// do rastrového obrázku ve formě čtverců v různých stupních šedi
//-----------------------------------------------------------------------------
void draw2d_dct(const pixmap *pix, int n)
{
#define PI 3.1415927
int u, v;
// změna koeficientu "v" ve vertikálním směru
for (v=0; v<n; v++) {
// změna koeficientu "u" v horizontálním směru
for (u=0; u<n; u++) {
// výpočet počátečních souřadnic čtverce
// ve vykreslovaném obrázku (tento čtverec
// bude rozdělen na n*n částí, každá část
// odpovídá jedné hodnotě 2D DCT)
int x0=u*100;
int y0=v*100;
int x, y;
// výpočet hodnot dvourozměrné diskrétní
// kosinové transformace
// pro dané koeficienty "u" a "v"
for (y=0; y<n; y++) {
for (x=0; x<n; x++) {
float alfa=PI*(2.0*x+1.0)*u/(2.0*n);
float beta=PI*(2.0*y+1.0)*v/(2.0*n);
// výpočet hodnoty 2D DCT spolu
// s přepočtem na stupně šedi
// v rozsahu 0..255
float value=127.5+127.5*cos(alfa)*cos(beta);
// vykreslení jedné hodnoty dvourozměrné
// diskrétní kosinové transformace do obrázku
box(pix,
x0+64*x/n, // x1 (n-tina strany čtverce)
y0+64*y/n, // y1 (-//-)
x0+64*(x+1)/n, // x2
y0+64*(y+1)/n, // y2
value, // červená barvová složka
value, // zelená barvová složka
value); // modrá barvová složka
}
}
}
}
}
// finito Na následujících třech obrázcích jsou vizualizovány bázové kosinové funkce 2D DCT velikosti 8×8, 16×16 a 32×32. Všimněte si především charakteristické podoby DC složky (konstantní plocha N×N hodnot) a viditelného zvyšování frekvencí průběhů funkcí.
Bázové kosinové funkce 2D DCT pro N=8
Bázové kosinové funkce 2D DCT pro N=16
Bázové kosinové funkce 2D DCT pro N=32
6. DCT a standard JPEG
Již v první části článku o grafickém formátu JPEG jsme si řekli, že ústředním krokem při zpracování obrazových dat v průběhu jejich ztrátové komprimace pomocí JPEGu je dvourozměrná diskrétní kosinová transformace. Tato transformace, která je mimo JPEGu použita například i u video formátu MPEG a H.261, je prováděna odděleně pro jednotlivé barvové složky barvového modelu YCbCr, tj. až po transformaci obrázků do tohoto barvového modelu a případném podvzorkování barvonosných složek Cb a Cr – viz následující schématický obrázek s vyznačením popisovaného funkčního bloku spolu s návazností na předcházející a následující bloky (jedná se o blok provádějící podvzorkování barvonosných složek a blok kvantování DCT koeficientů).
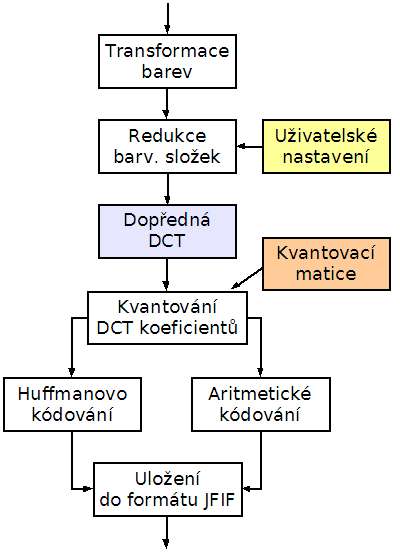
Funkční blok provádějící diskrétní kosinovou transformaci při kódování dle JPEGu
Před aplikací diskrétní kosinové transformace je pro každou barvovou složku samostatně provedeno rozdělení celého obrázku na pravidelné bloky o velikosti 8×8 hodnot. Při rozdělování obrázku na bloky se nemusí obrázek celý načítat do paměti, postačuje pouze osm aktuálních obrazových řádků. To je výhodné zejména při implementaci JPEGu na specializovaných čipech používaných například v kamerách nebo digitálních fotoaparátech. Pokud není šířka či výška obrázku dělitelná osmi (resp. šestnácti při podvzorkování barvonosných složek), je nutné zbývající hodnoty doplnit, nejlépe tak, aby se do co největší míry snížil podíl energie ve vyšších frekvencích – to obecně vede k lepšímu komprimačnímu poměru. Způsob doplňování chybějících hodnot je ponechán na aplikaci, většinou však postačí „zrcadlení“ známých pixelů do pixelů ležících za hranicemi obrázku.
Výsledkem aplikace 2D DCT na vstupní blok 8×8 barvových složek je vždy matice 8×8 hodnot. Tato matice je zpracována v bloku provádějícím kvantování uložených složek pomocí takzvané kvantovací matice. Tomuto postupu se však budeme podrobněji věnovat v navazující části tohoto seriálu.
7. Odkazy na další informační zdroje
- Syed Ali Khayam: The Discrete Cosine Transform (DCT): Theory and Application
Michigan State University, March 2003 - Popis DCT na Wikipedii (anglicky):
http://en.wikipedia.org/wiki/Discrete_cosine_transform - Některé urychlovací metody výpočtu DCT:
http://f-cpu.seul.org/whygee/dct_fc0/dct_fc0.html - Fast DCT (Discrete Cosine Transform) algorithms:
http://www.faqs.org/faqs/compression-faq/part1/section-19.html - Image Compression Using the Discrete Cosine Transform:
http://vision.arc.nasa.gov/publications/mathjournal94.pdf - JPEG – Frequently Asked Questions:
http://www.faqs.org/faqs/jpeg-faq/
8. Obsah dalšího pokračování tohoto seriálu
V následující části tohoto seriálu si ukážeme, jakým způsobem se zpracovávají číselné hodnoty získané pomocí dnes popisované dvourozměrné diskrétní kosinové transformace v dalších funkčních blocích specifikovaných ve standardu JPEG. Bude se jednat o funkční blok, ve kterém se provádí kvantizace DCT koeficientů a jejich následná linearizace do proudu bytů (DC složky se linearizují přímo, AC složky pomocí procházení maticí 8×8 hodnot metodou „cik-cak“), který je dále zpracováván buď Huffmanovým či aritmetickým entropickým kódováním.































