Superelipsoidy a kvadriky v POV-Rayi

25. 3. 2008

Doba čtení: 17 minut

Líbí se vám článek?
Podpořte redakci

V páté části seriálu o raytraceru POV-Ray si popíšeme dva typy objektů s poněkud záhadnými názvy. Bude se jednat o takzvané superelipsoidy a kvadriky. Jedná se o objekty, jejichž povrch je popsán pomocí implicitní rovnice, takže jejich vykreslování je s využitím raytracingu rychlé a přitom přesné.

Obsah

1. Superelipsoidy a kvadriky v POV-Rayi
2. Implicitní funkce pro superelipsoidy
3. První demonstrační příklad – vykreslení jednoho superelipsoidu
4. Druhý demonstrační příklad – superelipsoidy odvozené od krychle
5. Třetí demonstrační příklad – superelipsoidy odvozené od válce a hvězdice
6. Implicitní funkce pro kvadriky
7. Čtvrtý demonstrační příklad – různé tvary kvadrik
8. Literatura
9. Obsah následující části tohoto seriálu

1. Superelipsoidy a kvadriky v POV-Rayi

Mnoho aplikací typu CAD, ale i značná část dalších modelovacích programů umožňuje vytváření trojrozměrných těles pomocí trojúhelníkových sítí a parametrických ploch, typicky ploch Bézierových či NURBS. Už v předchozích částech tohoto seriálu jsme si řekli, že POV-Ray je v tomto pohledu poněkud odlišný, protože je v něm možné složitá tělesa skládat z těles základních s využitím konstruktivní geometrie těles (CSG). Ovšem tvarová variabilita prozatím popsaných základních těles, tj. koule, válce, kužele, krychle a toroidu, má své hranice a některé složitější tvary by se s jejich pomocí modelovaly obtížně. Z tohoto důvodu obsahuje POV-Ray mnohem větší sadu těles, kterou je možné vhodnou aplikací CSG operací dále rozšiřovat. Pro tvorbu trojrozměrných modelů, ve kterých se požadují zaoblené hrany (což jsou ve skutečnosti prakticky všechny běžné předměty), jsou určeny takzvané superelipsoidy a také kvadriky. Právě tyto dva druhy těles si popíšeme v dalších kapitolách.

Několik superelipsoidů vykreslených za pomoci POV-Raye

Společnou vlastností superelipsoidů a kvadrik je poměrně jednoduchý popis jejich povrchu. Tvar superelipsoidu je popsán (definován) pomocí pouhých dvou reálných čísel a tvar kvadrik deseti reálnými čísly. To není mnoho, zvláště když si uvědomíme, že například Bézierovu bikubickou plochu je nutné popsat celkem šestnácti řídicími body, přičemž každý bod má tři souřadnice – celkem se tedy jedná o 48 reálných čísel. Vzhledem k tomu, že superelipsoidy i kvadriky jsou popsány implicitními funkcemi, lze jednoduše (pomocí numerických metod) vypočítat souřadnice průsečíku paprsku s tělesem i normálový vektor v místě tohoto průsečíku, což urychluje a zpřesňuje vykreslování. Zatímco superelipsoidy tvoří vždy konečná a uzavřená tělesa topologicky totožná s koulí (u nichž je jasně definována vnitřní a vnější část), mají kvadriky různou topologii, od koule, přes nekonečné (neuzavřené) válce až po paraboloidy a parabolické hyperboloidy. Seznam těch nejzajímavějších kvadrik sepsal Paul Bourke ve svém článku Quadrics.

Sada kvadrik vykreslená POV-Rayem

2. Implicitní funkce pro superelipsoidy

Před vlastním popisem trojrozměrných superelipsoidů se nejdříve podívejme na jejich dvourozměrnou variantu – takzvanou superelipsu. Superelipsa vznikla zobecněním běžné elipsy. Parametricky lze elipsu se středem ležícím v počátku souřadné soustavy a s poloměry obou poloos r_x a r_y popsat dvojicí rovnic s jedním nezávislým parametrem φ, který nabývá hodnot z rozsahu 0..2π:

x(φ) = r_xcos(φ)
y(φ) = r_ysin(φ)

U parametrických rovnic superelipsy je navíc funkce sinus a kosinus umocněna zadanou konstantou n>1, pomocí níž lze dále tvar superelipsy modifikovat:

x(φ) = r_xcosⁿ(φ)
y(φ) = r_ysinⁿ(φ)

Elipsu lze kromě parametrického tvaru popsat také jedinou implicitní funkcí, která vyjadřuje podmínku platnou pro všechny body ležící na elipse:

f(x,y) = (x/r_x)²+(y/r_y)²-1 = 0

Totéž lze samozřejmě provést i u superelipsy:

f(x,y) = (x/r_x)^2/n+(y/r_y)^2/n-1 = 0

Zajímavé je, jak se pomocí konstanty n dá měnit tvar výsledné superelipsy:

Hodnota n	Výsledný tvar	Tvar pro r_x=r_y
0	obdélník	čtverec
<1	zaoblený obdélník	zaoblený čtverec
1	elipsa	kružnice
2	diamant	diamant
>2	hvězda	hvězda
>>2	limitně tvar kříže

Postupná změna tvaru superelipsy s rostoucí hodnotou n

Nyní přejděme od plošných útvarů k útvarům trojrozměrným. Základem tvorby mnoha těles popsaných parametricky je takzvaný sphere product. Jedná se o způsob kombinace dvou plošných křivek (popsaných vždy dvojicí funkcí) tak, aby vzniklo trojrozměrné těleso. Například kouli je možné vyjádřit kombinací kružnice a polokružnice, rotační elipsoid kombinací elipsy a polokružnice atd. Obecný postup použití sphere productu pro dvě plošné křivky h(β) a m(α) popsaných vždy dvojicí funkcí (první funkce slouží k výpočtu x-ové souřadnice, druhá funkce k výpočtu souřadnice y-ové):

h(β) = [h_x(β), h_y(β)]
m(α) = [m_x(α), m_y(α)]

spočívá ve vytvoření kombinace obou křivek tak, aby vznikl parametrický zápis trojrozměrného tělesa:

s(α, β) = [m_x(α) h_x(β), m_x(α) h_y(β), m_y(α)]

Podobným způsobem jako superelipsu je možné vytvořit prostorový superelipsoid. Souřadnice bodů ležících na povrchu elipsoidu, jehož tvar je odvozen od koule, pouze se mění poloměry jeho tří poloos, je možné vyjádřit trojicí funkcí:

x(α,β) = r_xcos(α)cos(β)
y(α,β) = r_ycos(α)sin(β)
z(α,β) = r_zsin(α)

Do rovnic popisujících superelipsoid jsou přidány mocniny n a e jednotlivých goniometrických funkcí:

x(α,β) = r_xcosⁿ(α)cos^e(β)
y(α,β) = r_ycosⁿ(α)sin^e(β)
z(α,β) = r_zsinⁿ(α)

Pro jednoduchost nebudeme uvažovat rozdílné poloměry všech tří poloos r_x, r_y, r_z, protože v POV-Rayi lze na těleso aplikovat lineární transformace, včetně změny měřítka, které je pro jednotlivé směry souřadných os rozdílné. Tím se nám parametrický popis superelipsoidu poněkud zjednoduší:

x(α,β) = cosⁿ(α)cos^e(β)
y(α,β) = cosⁿ(α)sin^e(β)
z(α,β) = sinⁿ(α)

Po převodu výše uvedené trojice funkcí do implicitního tvaru dostaneme kýženou jedinou rovnici, která je platná pro všechny body ležící na povrchu superelipsoidu:

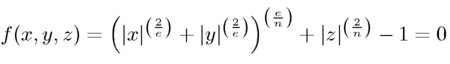
Všimněte si, že se v této rovnici (implicitní funkci) vyskytují pouze dvě konstanty, které můžeme měnit – jsou to právě ony mocniny n a e. Tyto mocniny mají na tvar trojrozměrného superelipsoidu stejný vliv, jako mocnina n u dvourozměrné superelipsy, přičemž je však nutné vzít v úvahu to, že každý z parametrů ovlivňuje tvar superelipsoidu buď v „severojižním směru“ (parametr n jako North) či ve směru „východozápadním“ (parametr e jako East). Parametry jsou na sobě nezávislé, není tedy problém vytvořit například tvar, který má v jednom směru (po řezu rovinou) tvar kružnice a ve druhém směru (po řezu kolmou rovinou) například tvar hvězdy. Variabilita všech možných tvarů je tedy poměrně široká, zvláště, když si uvědomíme, že se používají pouze dva parametry:

Mocnina je nulová: superelipsoid má v daném řezu tvar čtverce
Mocnina je rovna jedné: superelipsoid má v daném řezu tvar kružnice
Mocnina je rovna dvěma: superelipsoid má v daném řezu tvar čtverce, ovšem otočeného o 45°
Mocnina je větší než 2: superelipsoid má v daném řezu tvar hvězdice

3. První demonstrační příklad – vykreslení jednoho superelipsoidu

Z předchozí kapitoly již víme, že tvar superelipsoidu je popsán pouze pomocí dvou reálných mocnin (parametrů) n a e, protože jak velikost superelipsoidu, tak jeho případné zploštění je možné zajistit vhodnou lineární transformací, tj. aplikací operací translate, rotate a scale. Z tohoto důvodu je samotný zápis superelipsoidu v POV-Rayi velmi jednoduchý – v bloku nazvaném superelipsoid je uveden vektor dvou číselných hodnot odpovídajících mocninám e a n. Poté mohou následovat další podbloky běžné pro všechna další tělesa, například pro definici textury, materiálu povrchu či lineární transformace. Vytvoření superelipsoidu je ukázáno v prvním demonstračním příkladu, jehož zdrojový kód je následující:

// ------------------------------------------------------------
// Jednoduchá scéna se superelipsoidem a rovinou.
//
// rendering lze spustit příkazem:
//     povray +W800 +H600 +B100 +FN +D +Isuper1.pov +Osuper1.png
// (pro náhled postačí zadat povray super1.pov)
// ------------------------------------------------------------

#include "colors.inc"
#include "woods.inc"

global_settings {
    assumed_gamma 2.2
}

camera {
   location <0, 0, -2.5>                 // umístění kamery
   right    4/3 * x                      // vektor směřující doprava
   up       y                            // a nahoru
   look_at  <0, 0, 0>                    // bod, na který se kamera zaměřila
}

light_source {                           // první světelný zdroj
    <2, 10, -10>                         // pozice světelného zdroje
    color red 0.7 green 0.7 blue 0.7     // barva světelného zdroje
}

light_source {                           // druhý světelný zdroj
    <0, 0, -10000>                       // pozice světelného zdroje
    color red 0.7 green 0.7 blue 0.7     // barva světelného zdroje
    shadowless                           // zákaz tvorby stínů
}

plane {                                  // rovina tvořící pozadí scény
    <0, 0, 1>, 2                         // posun a orientace roviny
    hollow on
    texture {
        T_Wood14                         // procedurální textura
    }
    finish {                             // optické vlastnosti materiálu povrchu
        ambient 0.1
        diffuse 0.4
    }
}

superellipsoid {                         // superelipsoid
    <1.0, 2.5>                           // hodnoty exponentů "e" a "n"
    rotate <45, 65, 0>                   // natočení tělesa
    texture{
        pigment {
            color rgb <0.5, 1.0, 0.5>    // barva povrchu
        }
        finish {                         // optické vlastnosti materiálu povrchu
            ambient  0.2
            diffuse  0.4
            specular 0.6
            phong    0.9
            phong_size 3
            reflection 0.15
        }
    }
}

// ------------------------------------------------------------
// finito
// ------------------------------------------------------------

První demonstrační příklad po vykreslení v POV-Rayi

4. Druhý demonstrační příklad – superelipsoidy odvozené od krychle

Ve druhé kapitole jsme si řekli a také ukázali na animovaném obrázku, že pokud je hodnota některé z mocnin e či n rovna nule, má řez superelipsoidem rovinou odpovídající danému směru, tvar čtverce. V případě, že je hodnota mocniny rovna dvěma, má řez také tvar čtverce, tentokrát ovšem otočeného o 45° a patřičně zmenšeného (superelipsoid totiž vždy protíná všechny tři souřadné osy ve stejném bodě, nezávisle na hodnotách mocnin). Ve druhém demonstračním příkladu je ukázáno, jak se mění tvar superelipsoidu v případě, že jedna z jeho mocnin je rovna nule (červené objekty) či dvěma (modré objekty), zatímco druhá mocnina je průběžně měněna od hodnoty 0,1 do 4,0. Limitnímu případu, kdy e=0 a současně n=0 jsem se raději vyhnul, protože způsobuje vizuální chyby při vykreslování. Z jakého důvodu jsou tyto superelipsoidy „odvozené od krychle“? Stačí se podívat na ty objekty, u nichž je druhá mocnina menší než 1 – je vykreslena krychle se zaoblenými hranami.

// ------------------------------------------------------------
// Několik superelipsoidů odvozených od základního tvaru krychle.
//
// rendering lze spustit příkazem:
//     povray +W800 +H600 +B100 +FN +D +Isuper2.pov +Osuper2.png
// (pro náhled postačí zadat povray super2.pov)
// ------------------------------------------------------------

global_settings {
    assumed_gamma 2.2
}

camera {
   orthographic                          // vypnutí perspektivního zkreslení
   location <0, 0, -10>                  // umístění kamery
   right    4/3 * x * 20                 // vektor směřující doprava
   up       y * 20                       // a nahoru
   look_at  <0, 0, 0>                    // bod, na který se kamera zaměřila
}

light_source {                           // první světelný zdroj
    <50, 50, -100>                       // pozice světelného zdroje
    color red 0.7 green 0.7 blue 0.7     // barva světelného zdroje
}

light_source {                           // druhý světelný zdroj
    <0, 0, -10000>                       // pozice světelného zdroje
    color red 0.7 green 0.7 blue 0.7     // barva světelného zdroje
    shadowless                           // zákaz tvorby stínů
}

plane {                                  // rovina tvořící pozadí scény
    <0, 0, 1>, 3                         // posun a orientace roviny
    hollow on
    pigment {                            // procedurální textura
        agate
        agate_turb 0.3
    }
    finish {                             // optické vlastnosti materiálu povrchu
        ambient 0.1
        diffuse 0.4
    }
}

// pozice jednotlivých objektů ve scéně
#declare Row1 =  +8;
#declare Row2 =  +3;
#declare Row3 =   0;
#declare Row4 =  -3;
#declare Row5 =  -8;
#declare Col1 = -10;
#declare Col2 =  -5;
#declare Col3 =   0;
#declare Col4 =  +5;
#declare Col5 = +10;

// textura prvních deseti objektů
#declare Tex1 =
texture {
    pigment {
        color red 1 green 0 blue 0
    }
    finish {
        ambient 0.2 diffuse 0.4 phong 0.5 phong_size 5
    }
}

// textura druhých deseti objektů
#declare Tex2 =
texture {
    pigment {
        color red 0 green 0 blue 1
    }
    finish {
        ambient 0.2 diffuse 0.4 phong 0.5 phong_size 5
    }
}

// následují jednotlivé superelipsoidy
// s rozdílnými hodnotami parametrů e a n

superellipsoid { <0.0, 0.1> scale 1.5 rotate <-15, 30, 0> translate <Col1, Row1, 0> texture { Tex1 } }
superellipsoid { <0.0, 0.2> scale 1.5 rotate <-15, 30, 0> translate <Col2, Row1, 0> texture { Tex1 } }
superellipsoid { <0.0, 0.3> scale 1.5 rotate <-15, 30, 0> translate <Col3, Row1, 0> texture { Tex1 } }
superellipsoid { <0.0, 0.8> scale 1.5 rotate <-15, 30, 0> translate <Col4, Row1, 0> texture { Tex1 } }
superellipsoid { <0.0, 1.0> scale 1.5 rotate <-15, 30, 0> translate <Col5, Row1, 0> texture { Tex1 } }

superellipsoid { <0.0, 1.5> scale 1.5 rotate <-15, 30, 0> translate <Col1, Row2, 0> texture { Tex1 } }
superellipsoid { <0.0, 2.0> scale 1.5 rotate <-15, 30, 0> translate <Col2, Row2, 0> texture { Tex1 } }
superellipsoid { <0.0, 2.5> scale 1.5 rotate <-15, 30, 0> translate <Col3, Row2, 0> texture { Tex1 } }
superellipsoid { <0.0, 3.0> scale 1.5 rotate <-15, 30, 0> translate <Col4, Row2, 0> texture { Tex1 } }
superellipsoid { <0.0, 4.0> scale 1.5 rotate <-15, 30, 0> translate <Col5, Row2, 0> texture { Tex1 } }

superellipsoid { <2.0, 0.1> scale 1.5 rotate <-15, 30, 0> translate <Col1, Row4, 0> texture { Tex2 } }
superellipsoid { <2.0, 0.2> scale 1.5 rotate <-15, 30, 0> translate <Col2, Row4, 0> texture { Tex2 } }
superellipsoid { <2.0, 0.3> scale 1.5 rotate <-15, 30, 0> translate <Col3, Row4, 0> texture { Tex2 } }
superellipsoid { <2.0, 0.8> scale 1.5 rotate <-15, 30, 0> translate <Col4, Row4, 0> texture { Tex2 } }
superellipsoid { <2.0, 1.0> scale 1.5 rotate <-15, 30, 0> translate <Col5, Row4, 0> texture { Tex2 } }

superellipsoid { <2.0, 1.5> scale 1.5 rotate <-15, 30, 0> translate <Col1, Row5, 0> texture { Tex2 } }
superellipsoid { <2.0, 2.0> scale 1.5 rotate <-15, 30, 0> translate <Col2, Row5, 0> texture { Tex2 } }
superellipsoid { <2.0, 2.5> scale 1.5 rotate <-15, 30, 0> translate <Col3, Row5, 0> texture { Tex2 } }
superellipsoid { <2.0, 3.0> scale 1.5 rotate <-15, 30, 0> translate <Col4, Row5, 0> texture { Tex2 } }
superellipsoid { <2.0, 4.0> scale 1.5 rotate <-15, 30, 0> translate <Col5, Row5, 0> texture { Tex2 } }

// ------------------------------------------------------------
// finito
// ------------------------------------------------------------

Druhý demonstrační příklad po vykreslení v POV-Rayi

5. Třetí demonstrační příklad – superelipsoidy odvozené od válce a hvězdice

Ve třetím demonstračním příkladu jsou taktéž vykresleny superelipsoidy, u nichž se mění pouze jedna mocnina, ovšem základem je v tomto případě buď válec (červené objekty) či hvězda (modré objekty). První mocniny mají v tomto případě hodnotu 1 (válec) a 3 (hvězda). Zdrojový kód třetího příkladu má tvar:

// ------------------------------------------------------------
// Několik superelipsoidů odvozených od základního tvaru válce
// a hvězdy.
//
// rendering lze spustit příkazem:
//     povray +W800 +H600 +B100 +FN +D +Isuper3.pov +Osuper3.png
// (pro náhled postačí zadat povray super3.pov)
// ------------------------------------------------------------

global_settings {
    assumed_gamma 2.2
}

camera {
   orthographic                          // vypnutí perspektivního zkreslení
   location <0, 0, -10>                  // umístění kamery
   right    4/3 * x * 20                 // vektor směřující doprava
   up       y * 20                       // a nahoru
   look_at  <0, 0, 0>                    // bod, na který se kamera zaměřila
}

light_source {                           // první světelný zdroj
    <50, 50, -100>                       // pozice světelného zdroje
    color red 0.7 green 0.7 blue 0.7     // barva světelného zdroje
}

light_source {                           // druhý světelný zdroj
    <0, 0, -10000>                       // pozice světelného zdroje
    color red 0.7 green 0.7 blue 0.7     // barva světelného zdroje
    shadowless                           // zákaz tvorby stínů
}

plane {                                  // rovina tvořící pozadí scény
    <0, 0, 1>, 3                         // posun a orientace roviny
    hollow on
    pigment {                            // procedurální textura
        agate
        agate_turb 0.3
    }
    finish {                             // optické vlastnosti materiálu povrchu
        ambient 0.1
        diffuse 0.4
    }
}

// pozice jednotlivých objektů ve scéně
#declare Row1 =  +8;
#declare Row2 =  +3;
#declare Row3 =   0;
#declare Row4 =  -3;
#declare Row5 =  -8;
#declare Col1 = -10;
#declare Col2 =  -5;
#declare Col3 =   0;
#declare Col4 =  +5;
#declare Col5 = +10;

// textura prvních deseti objektů
#declare Tex1 =
texture {
    pigment {
        color red 1 green 0 blue 0
    }
    finish {
        ambient 0.2 diffuse 0.4 phong 0.5 phong_size 5
    }
}

// textura druhých deseti objektů
#declare Tex2 =
texture {
    pigment {
        color red 0 green 0 blue 1
    }
    finish {
        ambient 0.2 diffuse 0.4 phong 0.5 phong_size 5
    }
}

// následují jednotlivé superelipsoidy
// s rozdílnými hodnotami parametrů e a n

superellipsoid { <1.0, 0.1> scale 1.5 rotate <-15, 30, 0> translate <Col1, Row1, 0> texture { Tex1 } }
superellipsoid { <1.0, 0.2> scale 1.5 rotate <-15, 30, 0> translate <Col2, Row1, 0> texture { Tex1 } }
superellipsoid { <1.0, 0.3> scale 1.5 rotate <-15, 30, 0> translate <Col3, Row1, 0> texture { Tex1 } }
superellipsoid { <1.0, 0.8> scale 1.5 rotate <-15, 30, 0> translate <Col4, Row1, 0> texture { Tex1 } }
superellipsoid { <1.0, 1.0> scale 1.5 rotate <-15, 30, 0> translate <Col5, Row1, 0> texture { Tex1 } }

superellipsoid { <1.0, 1.5> scale 1.5 rotate <-15, 30, 0> translate <Col1, Row2, 0> texture { Tex1 } }
superellipsoid { <1.0, 2.0> scale 1.5 rotate <-15, 30, 0> translate <Col2, Row2, 0> texture { Tex1 } }
superellipsoid { <1.0, 2.5> scale 1.5 rotate <-15, 30, 0> translate <Col3, Row2, 0> texture { Tex1 } }
superellipsoid { <1.0, 3.0> scale 1.5 rotate <-15, 30, 0> translate <Col4, Row2, 0> texture { Tex1 } }
superellipsoid { <1.0, 4.0> scale 1.5 rotate <-15, 30, 0> translate <Col5, Row2, 0> texture { Tex1 } }

superellipsoid { <3.0, 0.1> scale 1.5 rotate <-15, 30, 0> translate <Col1, Row4, 0> texture { Tex2 } }
superellipsoid { <3.0, 0.2> scale 1.5 rotate <-15, 30, 0> translate <Col2, Row4, 0> texture { Tex2 } }
superellipsoid { <3.0, 0.3> scale 1.5 rotate <-15, 30, 0> translate <Col3, Row4, 0> texture { Tex2 } }
superellipsoid { <3.0, 0.8> scale 1.5 rotate <-15, 30, 0> translate <Col4, Row4, 0> texture { Tex2 } }
superellipsoid { <3.0, 1.0> scale 1.5 rotate <-15, 30, 0> translate <Col5, Row4, 0> texture { Tex2 } }

superellipsoid { <3.0, 1.5> scale 1.5 rotate <-15, 30, 0> translate <Col1, Row5, 0> texture { Tex2 } }
superellipsoid { <3.0, 2.0> scale 1.5 rotate <-15, 30, 0> translate <Col2, Row5, 0> texture { Tex2 } }
superellipsoid { <3.0, 2.5> scale 1.5 rotate <-15, 30, 0> translate <Col3, Row5, 0> texture { Tex2 } }
superellipsoid { <3.0, 3.0> scale 1.5 rotate <-15, 30, 0> translate <Col4, Row5, 0> texture { Tex2 } }
superellipsoid { <3.0, 4.0> scale 1.5 rotate <-15, 30, 0> translate <Col5, Row5, 0> texture { Tex2 } }

// ------------------------------------------------------------
// finito
// ------------------------------------------------------------

Třetí demonstrační příklad po vykreslení v POV-Rayi

6. Implicitní funkce pro kvadriky

Druhým typem těles, které si v dnešní části seriálu o POV-Rayi popíšeme, jsou takzvané kvadriky. Jedná se o tělesa, jejichž povrch je popsán implicitní funkcí, tj. rovnicí platnou pro všechny body ležící na povrchu tohoto tělesa. Konkrétně se jedná o rovnici:

A x² + B y² + C z² + D xy + E xz + F yz + G x + H y + I z + J = 0

jde A až J jsou uživatelem zadávané koeficienty. Tyto koeficienty je možné rozdělit do čtyř skupin. V první skupině se nachází koeficienty ovlivňující druhé mocniny souřadnic x², y² a z², ve druhé skupině koeficienty použité u jednotlivých kombinací souřadnic xy, xz a yz, ve třetí skupině násobicí koeficienty uvedené přímo u souřadnic x, y a z a konečně čtvrtou skupinu představuje samostatný koeficient J, který ovlivňuje velikost tělesa. Rozdělení koeficientů do skupin respektuje i způsob zápisu kvadriky do vytvářené scény, protože jsou použity tři třísložkové vektory a poslední numerický koeficient J je zapsán samostatně:

quadric {
        <A,B,C>, <D,E,F>, <G,H,I>, J
    }

S pomocí kvadrik lze vytvářet jak běžná základní tělesa, jako je koule (A=B=C=1, D=E=F=G=H=I=0) či elipsoid, tak i například nekonečné válce (bez základen), nekonečné kužele, paraboloidy, parabolické hyperboloidy aj. Některé kvadriky mají konečný objem i povrch, další však nejsou uzavřené a tím pádem je jejich povrch nekonečný. Z tohoto důvodu je většinou nutné kvadriky ve scéně nějakým způsobem omezit, typicky modifikátorem clipped_by, který bude popsán v dalších částech tohoto seriálu.

7. Čtvrtý demonstrační příklad – různé tvary kvadrik

Ve čtvrtém a současně i posledním demonstračním příkladu je ukázáno několik kvadrik. Jedná se o tři nekonečné válce, jejichž osy jsou rovnoběžné vždy s jednou souřadnou osou, tři nekonečné kužely, tři paraboloidy, dva hyperboloidy a konečně jeden elipsoid. Čtvrtý demonstrační příklad, ve kterém jsou použity definice kvadrik získané ze standardního vkládaného souboru dodávaného spolu s POV-Rayem, má tvar:

// ------------------------------------------------------------
// Demonstrační scéna s několika kvadriky.
//
// rendering lze spustit příkazem:
//     povray +W800 +H600 +B100 +FN +D +Isuper1.pov +Oquadric.png
// (pro náhled postačí zadat povray quadric.pov)
// ------------------------------------------------------------

#version 3.1;                            // specifikace verze POV-Raye

global_settings {
    assumed_gamma 2.2
}

#include "colors.inc"
#include "woods.inc"

// makra použitá pro rozmístění kvadrik v prostoru
#declare Radius =2.5;
#declare RowSpace=1.1;
#declare ColSpace=1.1;
#declare Dist=-3;
#declare Row3= 2;
#declare Row2=Row3+Radius*RowSpace*2;
#declare Row1=Row2+Radius*RowSpace*2;
#declare Col1= -Radius*ColSpace*3;
#declare Col2= Col1+Radius*ColSpace*2;
#declare Col3= Col2+Radius*ColSpace*2;
#declare Col4= Col3+Radius*ColSpace*2;
#declare Col5= Col4+Radius*ColSpace*2;

camera {
    location  <0, 0, -60>
    direction <0, 0,  10>
    look_at   <0, 0,   0>
    translate <0, Row2, -110>            // umístění kamery v prostoru
}

light_source {
    <1000, 1000, -2000>
    color White
}

plane {                                  // rovina tvořící pozadí scény
    <0, 0, 1>, 1.01                      // posun a orientace roviny
    hollow on
    pigment {                            // procedurální textura
        agate
        agate_turb 0.3
    }
    finish {                             // optické vlastnosti materiálu povrchu
        ambient 0.1
        diffuse 0.4
    }
}

#declare Solid=
texture {                                // vlastnosti materiálu
    pigment {                            // použitého pro kvadriky
        Green
    }
    finish {
        phong 1
    }
}

#declare UnitBox = box {                 // omezující těleso pro nekonečné kvadriky
    <-1, -1, -1>, <1, 1, 1>
}

// deklarace jednotlivých typů kvadrik

// osově orientované nekonečné válce
#declare Cylinder_X = quadric {
    <0, 1, 1>, <0, 0, 0>, <0, 0, 0>, -1
}

#declare Cylinder_Y = quadric {
    <1, 0, 1>, <0, 0, 0>, <0, 0, 0>, -1
}

#declare Cylinder_Z = quadric {
    <1, 1, 0>, <0, 0, 0>, <0, 0, 0>, -1
}

// osově orientované nekonečné kužely
#declare QCone_X = quadric {
    <-1, 1, 1>, < 0, 0, 0>, < 0, 0, 0>, 0
}

#declare QCone_Y = quadric {
    <1, -1, 1>, <0, 0, 0>, <0, 0, 0>, 0
}

#declare QCone_Z = quadric {
    <1, 1, -1>, <0, 0, 0>, <0, 0, 0>, 0
}

// osově orientované paraboloidy
/* y^2 + z^2 - x = 0 */
#declare Paraboloid_X = quadric {
    < 0, 1, 1>, < 0, 0, 0>, <-1, 0, 0>, 0
}

/* x^2 + z^2 - y = 0 */
#declare Paraboloid_Y = quadric {
    <1,  0,  1>, <0,  0,  0>, <0, -1,  0>, 0
}

/* x^2 + y^2 - z = 0 */
#declare Paraboloid_Z = quadric {
    <1,  1,  0>, <0,  0,  0>, <0,  0, -1>, 0
}

// dva různé hyperboloidy
/* y - x^2 + z^2 = 0 */
#declare Hyperboloid = quadric {
    <-1,  0,  1>, < 0,  0,  0>, < 0,  1,  0>, 0
}

#declare Hyperboloid_Y = quadric {
    <1, -1,  1>, <0,  0,  0>, <0,  0,  0>, -1
}

// elipsoid (jednoduchou úpravou lze vytvořit kouli)
#declare QEllipsoid = quadric {
    <1,  1,  1>, <1,  0,  1>, <0,  0,  0>, -2
}

// umístění jednotlivých objektů tvořených kvadrikami v prostoru
// spolu se specifikací textury a obalového tělesa
quadric {Cylinder_X    texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col1, Row1, Dist>}
quadric {Cylinder_Y    texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col1, Row2, Dist>}
quadric {Cylinder_Z    texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col1, Row3, Dist>}

quadric {QCone_X       texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col2, Row1, Dist>}
quadric {QCone_Y       texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col2, Row2, Dist>}
quadric {QCone_Z       texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col2, Row3, Dist>}

quadric {Paraboloid_X  texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col3, Row1, Dist>}
quadric {Paraboloid_Y  texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col3, Row2, Dist>}
quadric {Paraboloid_Z  texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col3, Row3, Dist>}

quadric {QEllipsoid    texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col4, Row1, Dist>}
quadric {Hyperboloid   texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col4, Row2, Dist>}
quadric {Hyperboloid_Y texture {Solid} clipped_by { object{UnitBox scale 2}} translate <Col4, Row3, Dist>}

// ------------------------------------------------------------
// finito
// ------------------------------------------------------------

Čtvrtý demonstrační příklad po vykreslení v POV-Rayi

8. Literatura

Barr, A.H.: Superquadrics and Angle Preserving Transformations,
IEEE Computer Graphics and Applications, January 1981
Bourke Paul: Quadrics,
July 1996
Bourke Paul: Superellipse and Superellipsoid,
January 1990
Faux, I.D. a Pratt, M.J.: Computational Geometry for Design and Manufacture,
Ellis Horwood Ltd., Wiley & Sons, 1979
Wallace A.: Differential Topology,
Benjamin/Cummings Co., Reading, Massachussetts, USA, 1968

9. Obsah následující části tohoto seriálu

V navazující části seriálu o raytraceru POV-Ray se seznámíme s pravděpodobně nejzajímavějšími typy těles, se kterými je možné v tomto renderovacím programu pracovat. Jedná se o takzvané implicitní plochy známé také pod názvem blobs či metaballs. Předností těchto objektů je velmi snadné a především rychlé modelování složitých přírodních tvarů s možností jejich animace.

Seriál: Vykreslujeme 3D scény s POV-Ray

Použití konstruktivní geometrie těles v praxi
Superelipsoidy a kvadriky v POV-Rayi
Implicitní plochy (metaballs) v POV-Rayi

Přečtěte si všechny díly seriálu Vykreslujeme 3D scény s POV-Ray nebo sledujte jeho RSS

Vstoupit do diskuse

Líbí

Nelíbí

Pavel Tišnovský

Vystudoval VUT FIT a v současné době pracuje na projektech vytvářených v jazycích Python a Go.

Sdílet