Tvorba procedur, příkaz repeat a želví grafika

Obsah

1. Tvorba procedur, příkaz repeat a želví grafika
2. Nové procedury a rozdělení řešeného problému na podproblémy
3. Demonstrační příklady: kresba základních geometrických obrazců
4. Opakování části programu pomocí příkazu repeat
5. Demonstrační příklady: základní geometrické obrazce podruhé
6. Předávání parametrů při volání procedur
7. Demonstrační příklady: zobecnění kresby n-úhelníků
8. Vykreslování kružnic a obrazců složených z kružnic
9. Obsah následující části tohoto seriálu

1. Tvorba procedur, příkaz repeat a želví grafika

Procedury a funkce patří mezi základní stavební prvky prakticky každého vyššího programovacího jazyka. Jejich vytváření je samozřejmě podporováno i v Logu, dokonce je možné říci, že tvorba nových procedur je jedním ze základních kamenů Loga, protože pomocí nich dítě (či jakýkoli jiný uživatel) Logo „učí“ nové dovednosti, což je jeden z principů konstruktivního myšlení. V následujících kapitolách si vysvětlíme tvorbu nových procedur bez parametrů i procedur s parametry. Kromě toho si ve čtvrté a páté kapitole vysvětlíme práci příkazu repeat, pomocí nějž je možné tvořit iterační smyčky. Ty lze využít například při vykreslování složitějších grafických obrazců, což si ukážeme na několika demonstračních příkladech.

2. Nové procedury a rozdělení řešeného problému na podproblémy

Mezi jednu ze základních vlastností prakticky jakéhokoli vyššího programovacího jazyka (snad s výjimkou těch nejjednodušších interpreterů Basicu) patří možnost rozšiřování schopnosti tohoto jazyka pomocí tvorby nových procedur a funkcí, popřípadě i maker. Příkladem může být nějaký programovací jazyk (třeba Pascal), který sice obsahuje goniometrické funkce sin a cos, ale funkce tan v něm již není implementována. Toto zdánlivé omezení je možné jednoduše odstranit vytvořením nové funkce tan, která bude interně používat již zavedené funkce sin a cos. Matematické schopnosti daného jazyka se přidáním nové funkce rozšířily. Druhou oblastí, kde možnost tvorby nových funkcí a procedur našla svoje uplatnění, je rozdělení problému, který má program algoritmicky řešit, na snáze řešitelné podproblémy. Jedná se o klasickou metodu „rozděl a panuj“, která stála i u vzniku objektově orientovaného programování (OOP).

Tvorba nových procedur a funkcí je samozřejmě dostupná i v Logu. K tomuto účelu jsou v jazyku rezervovány příkazy to a end (přesněji řečeno, příkaz to je ve skutečnosti takzvaná „speciální forma“, my však v této chvíli pojmy „příkaz“ a „speciální forma“ nemusíme striktně rozlišovat). Zadáním příkazu to do příkazového řádku Loga či do jeho textového editoru je zahájen proces „učení“, tj. uživatel Logu říká, jakým způsobem se má nově vytvářený příkaz ve skutečnosti (přesněji řečeno až po svém zavolání) provádět. Po tomto příkazu musí následovat jméno nově vytvářené procedury a za jménem může být uveden seznam parametrů. U jednodušších procedur se však žádné parametry předávat nemusí. Po takto zapsané hlavičce procedury následuje její tělo, což není nic jiného, než libovolné množství příkazů, včetně volání dalších procedur (dokonce i procedury právě vytvářené). Tělo procedury je ukončeno příkazem end. Formálně vypadá zápis procedury bez parametrů následovně:

to jméno_procedury
    libovolné příkazy
    ...
    ...
end 

Formální zápis procedury s parametry vypadá takto:

to jméno_procedury parametr_1 parametr_2 ... parametr_n
    libovolné příkazy
    ...
    ...
end 

Při zápisu nové procedury přímo na příkazový řádek interpreteru Loga indikuje první (needitovatelný) znak na řádku, v jakém stavu se Logo nachází. Pokud je na začátku řádku zobrazen znak ?, očekává se zadávání příkazů, které se ihned provedou (například otočí želvu o 10°). V případě, že se Logo „učí“ novou proceduru, změní se první znak na >, aby se indikoval režim, ve kterém se příkazy přímo neprovádí. Po zadání příkazu end, kterým se definice procedury ukončuje, se Logo automaticky přepne zpět do režimu zadávání a okamžitého provádění příkazů. Ve třetí kapitole si ukážeme tvorbu procedur bez parametrů a v kapitole šesté procedury s parametry. Na tento popis navážeme v dalších částech tohoto seriálu, ve kterých bude vysvětlen princip rekurze.

3. Demonstrační příklady: kresba základních geometrických obrazců

V předchozí části tohoto seriálu jsme si ukázali několik sekvencí příkazů Loga, které je možné použít pro kresbu základních geometrických obrazců, například čtverce, rovnoramenného trojúhelníku, pravidelného šestiúhelníku apod. Zkusme nyní tyto sekvence „zapouzdřit“ do vhodně pojmenovaných procedur, aby je bylo možné snadněji používat, například při opakovaném kreslení těchto obrazců. Jeden z minule uvedených příkladů se týkal vykreslení čtverce o délce hrany 100 kroků. Zdrojový kód tohoto jednoduchého příkladu používal pouze tři základní příkazy Loga (clearscreen – smazání grafické plochy, forward – posun želvy dopředu o zadaný počet kroků a right – otočení želvy doprava o zadaný úhel) a skládal se z osmi kroků:

clearscreen
forward 100
right 90
forward 100
right 90
forward 100
right 90
forward 100 

První příkaz použitý ve výše uvedeném příkladu, tj. příkaz clearscreen, se netýká vlastního vykreslení čtverce, proto ho do námi vytvářené procedury nebudeme vkládat. Naopak je vhodné na konec procedury vložit ještě jeden dodatečný příkaz right 90, který želvu natočí do orientace, ve které se začal čtverec vykreslovat. V dalších demonstračních příkladech uvidíme, že návrat želvy zpět do původní pozice může být využit při vykreslování složitějších obrazců. Nová procedura, kterou pojmenujeme ctverec, získala následující tvar:

to ctverec1
    forward 100
    right 90
    forward 100
    right 90
    forward 100
    right 90
    forward 100
    right 90
end 

K této proceduře ještě přidáme proceduru nazvanou test_ctverec1, která čtverec skutečně vykreslí. Vzhledem k tomu, že jsem jako prostředí pro testování zvolil implementaci Loga nazvanou TurtleTracks, obsahuje testovací procedura i příkaz draw, pomocí kterého se zobrazí okno s grafickou plochou, po které se želva pohybuje. V jiných implementacích Loga není zapotřebí tento příkaz uvádět, protože se grafická plocha zobrazí ihned po zavolání prvního příkazu, který pracuje se želvou (přesněji řečeno, tyto implementace ani příkaz draw neobsahují, proto jeho volání může skončit chybovým hlášením a ukončením běhu procedury):

to test_ctverec1
    draw
    clearscreen
    ctverec1
end 

Obrázek 1: Čtverec nakreslený po spuštění procedury test_ctverec1

Připomeňme si ještě, jakým způsobem obě uvedené procedury do prostředí Loga vložíme. Při psaní všech programů v Logu můžeme postupovat v zásadě třemi způsoby: celý text postupně přepsat do příkazové řádky interpreteru Loga, zavolat interní či externí editor a program napsat v něm, nebo načíst již vytvořený zdrojový text programu ze souboru. V prostředí TurtleTracks je nejjednodušší vyvolat interní textový editor pomocí klávesové zkratky [Ctrl+N], zdrojový text do editoru překopírovat přes schránku a poté stlačit klávesu [Ctrl+E], pomocí které se zapsané příkazy začnou interpretovat.

Obrázek 2: Vyvolání okna s editorem v aplikaci TurtleTracks

Pro otestování procedury ctverec1 je nutné v příkazovém řádku Loga zadat příkaz test_ctverec1.

Obrázek 3: Spuštění kódu zapsaného v interním editoru aplikace TurtleTracks

Před vyvoláním zkratky [Ctrl+E] by měl editor mít zhruba následující obsah:

Obrázek 4: Obsah interního editoru se zapsaným demonstračním příkladem

Podobným způsobem je možné vytvořit i další procedury, které vykreslí pravidelný trojúhelník, pravidelný pětiúhelník a pravidelný šestiúhelník. Tyto procedury mají následující tvar:

to trojuhelnik1
    forward 100
    right 120
    forward 100
    right 120
    forward 100
    right 120
end

to test_trojuhelnik1
    clearscreen
    trojuhelnik1
end 

Obrázek 5: Trojúhelník vykreslený procedurou test_trojuhelnik1

to petiuhelnik1
    forward 100
    right 72
    forward 100
    right 72
    forward 100
    right 72
    forward 100
    right 72
    forward 100
    right 72
end

to test_petiuhelnik1
    clearscreen
    petiuhelnik1
end

to sestiuhelnik1
    forward 100
    right 60
    forward 100
    right 60
    forward 100
    right 60
    forward 100
    right 60
    forward 100
    right 60
    forward 100
    right 60
end

to test_sestiuhelnik1
    clearscreen
    sestiuhelnik1
end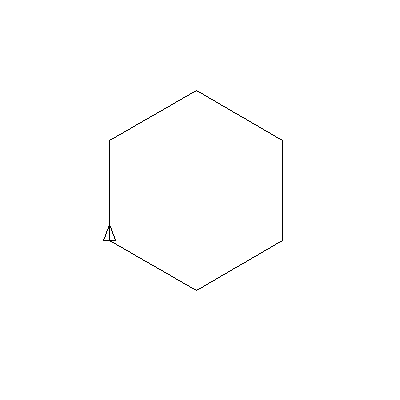 

Obrázek 6: Šestiúhelník vykreslený procedurou test_sestiuhel­nik1

4. Opakování části programu pomocí příkazu repeat

Při bližším pohledu na demonstrační příklady vypsané v předchozí kapitole jste si pravděpodobně všimli, že se v nich opakují stále stejné posloupnosti příkazů. Například při vykreslování šestiúhelníku se musí želva šestkrát posunout o sto kroků a současně šestkrát natočit o 60°, aby byly správně vykresleny všechny jeho strany. Jistě by bylo vhodnější a také méně pracné i méně náchylné k chybám, aby se tyto příkazy nemusely tolikrát zapisovat do zdrojového kódu programu, ale aby je bylo možné zapsat formou nějaké programové (iterační) smyčky. Tvůrci jazyka Logo samozřejmě na tuto možnost mysleli, a tak do jazyka zařadili příkaz nazvaný příhodně repeat. V dalších odstavcích si ukážeme, jakým způsobem je možné tento příkaz použít.

Za příkazem repeat je nutné uvést dva parametry. Prvním parametrem je počet opakování a druhým parametrem buď jeden příkaz, nebo (a to mnohem častěji) seznam příkazů, které se mají opakovaně provést. V Logu se seznamy zapisují do hranatých závorek, přičemž je nutné mezi prvky seznamu vložit alespoň jednu mezeru nebo prázdný řádek. Pro vysvětlení chování příkazu repeat je nejvhodnější vše vyzkoušet na jednoduchém demonstračním příkladu. V předchozí kapitole byl uveden tvar procedury petiuhelnik1. Budeme chtít zjistit, jaký obrazec se vytvoří v případě, že tuto proceduru budeme volat 36×, přičemž se pokaždé želva natočí o 10°doleva (celkem tedy dojde k otočce o 36×10°=360°, tedy o celý kruh). Odpověď nám dá následující program:

to petiuhelnik1
    forward 100
    right 72
    forward 100
    right 72
    forward 100
    right 72
    forward 100
    right 72
    forward 100
    right 72
end

draw
clearscreen
repeat 36 [
    petiuhelnik1
    left 10
] 

Výsledkem běhu předešlého programu je tento obrazec:

Obrázek 7: Výsledek 36 opakování procedury petiuhelnik1

5. Demonstrační příklady: základní geometrické obrazce podruhé

Pomocí příkazu repeat je možné zjednodušit procedury pro vykreslování základních geometrických tvarů. Místo opakovaného zápisu příkazů pro posun želvy a její natočení se tyto příkazy v programu budou vyskytovat pouze jednou, ale musí být vloženy do seznamu příkazu repeat. Počet opakování smyčky je jednoduše zjistitelný: každá smyčka bude opakována tolikrát, kolik stran má mít výsledný geometrický tvar. Také si všimněte toho, že se želva při kresbě těchto tvarů otočí přesně o 360°, tj. zastaví se na stejné pozici a ve stejné orientaci jako na začátku kreslení. V případě čtverce jde o čtyři natočení po 90°, v případě pětiúhelníku o pět otočení po 72° atd. Zjednodušené verze procedur pro vykreslení základních geometrických tvarů dostanou následující (jak uvidíme dále, tak stále ještě prozatímní) podobu:

to trojuhelnik2
    repeat 3 [
        forward 100
        right 120
    ]
end

to ctverec2
    repeat 4 [
        forward 100
        right 90
    ]
end

to petiuhelnik2
    repeat 5 [
        forward 100
        right 72
    ]
end

to sestiuhelnik2
    repeat 6 [
        forward 100
        right 60
    ]
end 

Obrázek 8: Vykreslení všech čtyř tvarů bez smazání grafické plochy

6. Předávání parametrů při volání procedur

Naše procedury pro vykreslování základních geometrických tvarů se sice použitím iteračního příkazu repeat do značné míry zjednodušily, stále se však nejedná o obecnou podobu, kterou by tyto procedury mohly a v ideálním případě také měly mít. Při požadavku na vykreslení například sedmiúhelníku či desetiúhelníku by bylo zapotřebí vytvořit pro každý tvar novou proceduru, tu vhodně pojmenovat a ručně spočítat úhel, o který se želva musí v každém opakování iterační smyčky natočit. Také pro vykreslení obrazce o jiné velikosti, tj. s jinou délkou stran, by bylo zapotřebí vytvořit nové procedury, což je pracné a náchylné k chybám. Chvályhodnou snahou většiny programátorů je však napsat jednotlivé části kódu co nejobecněji (pokud tomu nebrání jiné požadavky, například časové efektivity). V tomto případě by se jednalo o vytvoření jediné procedury, která by byla schopna vykreslit jakýkoli pravidelný n-úhelník s libovolnou délkou strany (a tím i libovolnou celkovou velikostí).

Metoda, jak takovou obecnou proceduru napsat, spočívá v předávání parametrů. Ve druhé kapitole jsme si řekli, že formální zápis procedury s parametry má tento tvar:

to jméno_procedury parametr_1 parametr_2 ... parametr_n
    libovolné příkazy
    ...
    ...
end 

Za povšimnutí stojí, že se mezi jednotlivé parametry nevkládají čárky ani jiné znaky kromě mezery či libovolného většího počtu mezer. Parametry také nejsou uzavřeny v závorkách. Z tohoto zápisu je patrné, že syntaxe Loga je jednodušší, než u jeho předchůdce (tj. jazyka LISP) i mnoha dalších programovacích jazyků. Hodnoty předávaných parametrů jsou ve volané proceduře přístupny pomocí zápisu :jméno_parametru. Nad onou dvojtečkou, kterou uživatelé Loga nazývají „dots“, prozatím pouze zakroutíme hlavou, později si ukážeme, z jakého důvodu je nutné dvojtečku uvádět. V dnešní části si ukážeme volání procedur s numerickými parametry, v následujících částech tohoto seriálu se zaměříme i na předávání proměnných, seznamů a řetězců.

7. Demonstrační příklady: zobecnění kresby n-úhelníků

Jako ukázku předávání parametrů procedurám vytvoříme proceduru pro vykreslení obecného n-úhelníku o délce strany rovné padesáti krokům želvy. Tato procedura při svém volání vyžaduje, aby jí byl předán počet stran n-úhelníku, který se má vykreslit. Poté je v programové smyčce n× vykreslena jedna strana n-úhelníku a želva se pootočí o úhel rovný 360/n (úhel otočení je jednoduché zjistit, protože po dokončení kresby musí želva opsat celý kruh a vrátit se do původní pozice). Na dále uvedeném příkladu stojí za povšimnutí především způsob zápisu parametru s dvojtečkou („dots“) před svým jménem a také to, že pokud se v matematickém výrazu nepoužije mezera, nemusí se tento výraz zapisovat do závorek (v případě zápisu mezery by Logo část výrazu za mezerou chápalo jako další parametr).

to n_uhelnik :pocet_stran
    repeat :pocet_stran [
        forward 50
        right 360/:pocet_stran
    ]
end

draw
setpos [-150 -50]
clean
n_uhelnik 8
n_uhelnik 10
n_uhelnik 12 

V případě, že by bylo zapotřebí vykreslit n-úhelník jiné velikosti, tj. s odlišnou délkou stran, je možné v deklaraci procedury přidat další parametr, jehož hodnota se bude předávat příkazu forward.

Obrázek 9: Vykreslování pomocí obecného n-úhelníku

8. Vykreslování kružnic a obrazců složených z kružnic

V předchozích částech tohoto seriálu jsme se seznámili se základními příkazy želví grafiky. Doposud jsme si však neřekli, jakým způsobem je možné vykreslovat kružnice a obrazce složené převážně z kružnic. Mnoho implementací Loga vůbec neobsahuje příkaz pro vykreslení kružnice, ovšem se znalostí vykreslování obecných n-úhelníků si můžeme potřebný příkaz vytvořit sami. Kružnici je možné vykreslovat mnoha způsoby (známý je například Bresenhamův algoritmus), které však mohou být implementačně poměrně složité.

Pokud ale na grafickou plochu vykreslíme n-úhelník s dostatečně velkým počtem stran, výsledkem bude obrazec prakticky totožný s kružnicí – stačí si uvědomit, že grafická plocha se skládá z diskrétních obrazových bodů (pixelů), které zdola omezují přesnost všech kreseb. Vše si ukážeme na jednoduchém příkladu, ve kterém je vytvořena nové procedura kruznice, která je použita pro vykreslení čtyř kružnic s rozdílnou velikostí:

to kruznice :krok
    repeat 360 [
        forward :krok
        left 1
    ]
end

draw
kruznice 0.4
kruznice 0.8
kruznice 1.2
kruznice 1.6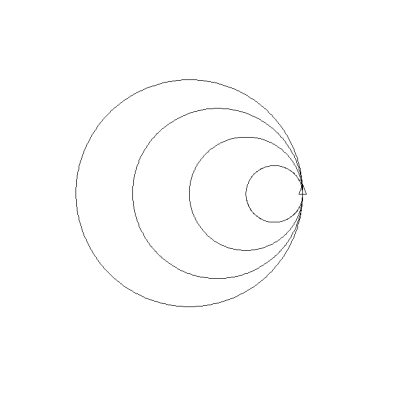 

Obrázek 10: Několik kružnic vykreslených pomocí předchozího příkladu

Můžeme vytvořit i složitější příklad, ve kterém je kružnice vykreslena několikrát, pokaždé s jiným počátečním natočením želvy. Vznikne tak jednoduchý květ. Všimněte si podobnosti podobnosti těla procedury kruznice s tělem procedury kvet:

to kruznice :krok
    repeat 360 [
        forward :krok
        left 1
    ]
end

to kvet :pocet
    repeat :pocet [
        kruznice 1
        left 360/:pocet
    ]
end

draw
kvet 10 

Obrázek 11: Květ vykreslený s využitím procedur kruznice a kvet

9. Obsah následující části tohoto seriálu

V následující části seriálu o programovacím jazyku Logo se seznámíme s velmi důležitou programátorskou technikou – rekurzí. Pomocí rekurze se v Logu řeší mnoho problémů, pro které jsou v jiných jazycích určeny iterační smyčky; my si však ukážeme, jakým způsobem je možné tyto smyčky do Loga implementovat.