Obsah
1. Zobrazení objemových dat v POV-Rayi
2. Objemová reprezentace
3. Vyčíslení objemu obsazeného tělesem
4. Typická použití objemových dat zapsaných pomocí voxelů
5. Přednosti a zápory popisu geometrie tělesa pomocí voxelů, technická a programová podpora
6. Způsoby vizualizace objemových dat
7. Algoritmy zobrazující povrchy
8. Objemové algoritmy
9. Obsah dalšího pokračování seriálu
1. Zobrazení objemových dat v POV-Rayi
Raytracer POV-Ray dokáže ve vykreslovaných scénách použít i objekty reprezentované objemovými elementy (voxely), které tvoří pravidelnou rastrovou mřížku. Každý voxel je přitom zapsaný osmibitovou, šestnáctibitovou či dokonce třicetidvoubitovou hodnotou, kterou je možné považovat za „hustotu“ hmoty v daném objemu prostoru (ovšem tuto hodnotu voxelu lze mapovat i na barvu pomocí nám již známých barvových map). Tímto – z hlediska klasických modelovacích programů – poněkud nekonvenčním způsobem, kterým disponuje relativně malé množství aplikací, je možné v jedné scéně zkombinovat různé typy prostorových dat, které jsou uloženy s využitím hraniční reprezentace (tvar tělesa je popsán svým povrchem), objemové reprezentace (těleso je popsáno svým objemem, tj. výčtem těch částí prostoru, které tvoří hmotu – vnitřek – tělesa) i reprezentace procedurální (těleso není přímo zadáno geometrickými daty, jako v předchozích dvou reprezentacích, ale algoritmem, který umožní vypočítat povrch tělesa či objem tělesa, konkrétně se jedná například o objekty typu julia_fractal). POV-Ray byl kvůli své schopnosti zobrazovat objemové mřížky využit v několika vědeckých projektech, kde sloužil jako front-end pro vizualizaci naměřených i vypočtených trojrozměrných dat.
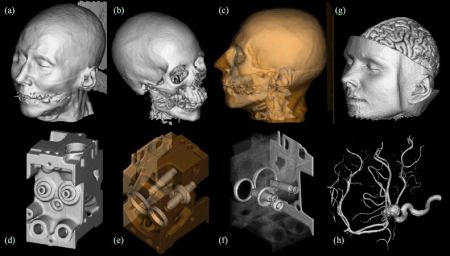
Obrázek 1: Tato objemová data, konkrétně CT mozku, byla vizualizována pomocí raytraceru POV-Ray
2. Objemová reprezentace
Většina současných modelovacích programů pracuje s prostorovými tělesy, jejichž geometrické vlastnosti jsou popsány jejich povrchem, přesněji řečeno hranicí mezi vnějším a vnitřním prostorem – proto se tomuto způsobu popisu těles říká hraniční reprezentace (boundary representation). Tento způsob popisu těles má několik předností, především relativně malé nároky na paměť (alespoň v porovnání s alternativou popsanou v následujících odstavcích) a také masivní a především dostatečně levnou podporu ze strany grafických akcelerátorů, které dovedou v reálném čase vystínovat a zobrazit i velmi složitou prostorovou scénu. Hraniční reprezentace však není jediná možná – podobně jako v ploše lze předměty popsat buď jejich geometrií (vektorová grafika) či je naopak rozdělit na elementární obrazové elementy (rastrová grafika), lze i v prostoru těleso buď popsat jeho povrchem nebo objemem rozděleným na objemové elementy. Popis těles objemem je metodou kvalitativně (a mnohdy i kvantitativně) odlišnou od hraniční reprezentace. Při použití této metody například neexistují, na rozdíl od dnes častěji používané hraniční reprezentace, problémy při rozhodování, zda daný bod v prostoru leží uvnitř či vně tělesa.

Obrázek 2: Některé často používané způsoby popisu hranice (povrchu) těles
U popisu těles objemem navíc prakticky odpadají potíže při vyhodnocování průchodu světla průhlednými objekty ve scéně. Při analytickém popisu (což je jedna z variant objemového popisu těles, kterou jsme si již v tomto seriálu podrobně vysvětlili) se také snadno zjišťuje normálový vektor k povrchu tělesa v každém bodě povrchu, která je v mnoha algoritmech potřebná pro výpočet osvětlení, viditelnosti či pro různé simulace. Objemová reprezentace založená na objemových elementech (voxelech), kterou se dnes budeme zabývat, je využívána především v souvislosti s metodami pro získávání trojrozměrných dat o tělesech, především CT (Computer Tomography) a MR (magnetická rezonance). Zařízení CT a MR produkují trojrozměrná data ve formě rovinných řezů tělesem, které lze přímočarým způsobem převést na objemové elementy. Problémem však zůstává vytváření a následná editace složitějších těles a scén. Jedním z možných řešení tohoto problému je použití CSG modelu (viz předchozí části tohoto seriálu ) popř. použití implicitních ploch, které jsme si též popsali.
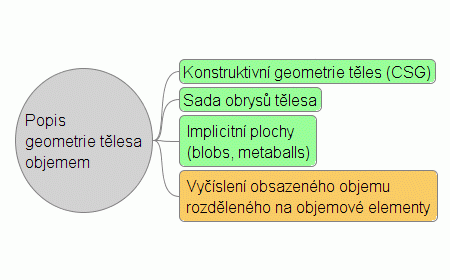
Obrázek 3: Vybrané způsoby popisu geometrie tělesa jeho objemem. Posledním uvedeným způsobem se zabýváme v dnešní části seriálu o POV-Rayi
Poznámky:
Počítačová tomografie (Computer Tomography – CT) byla poprvé představena Hounsfieldem v sedmdesátých letech minulého století. CT pro získání objemových dat používá rentgenové paprsky, snímače rentgenových paprsků a počítač pro vytvoření obrazu příčného řezu tělem pacienta. Oproti standardní radiografii dosahuje rozlišení CT hodnot okolo 1/3 mm, což je sice poměrně hrubá jednotka, pro mnoho diagnostických účelů je však dostačující. Rozměry voxelové mřížky získané pomocí CT mohou nabývat hodnot až 512×512×200 voxelů s bitovou hloubkou typicky 12 bitů na voxel (při zobrazování se mnohdy provádí decimace na osm bitů).
Magnetická rezonance (Magnetic Resonance – MR) byla poprvé experimentálně ověřena v roce 1946 americkými vědci F. Blochem a E. Purcellem. V roce 1971 (P. Lauterbur) bylo využito změn gradientu magnetického pole k získání dvourozměrného tomografického obrazu rezonujících jader. V roce 1974 (P. Mansfield) byl publikován první medicínský obraz získaný pomocí MR.
3. Vyčíslení objemu obsazeného tělesem
Tento způsob reprezentace těles vznikl jednoduchým a přímočarým rozšířením dvourozměrných rastrových obrazů (bitmap resp. pixmap) do třech rozměrů. Část trojrozměrného prostoru je rozdělena na velké množství pravidelných elementárních objemových jednotek, které se nazývají voxely. Termín voxel vznikl zkrácením anglického termínu Volume Element. Svou, na první pohled nelogickou, zkratkou – písmeno „X“ ve slovním základu – ukazuje na svou podobnost s pixelem, což je zkratka termínu Picture Element. Při použití voxelů jako základních nosičů „objemové“ informace se původně spojitý trojrozměrný prostor diskretizuje na jednotlivé mikroobjemy, podobně jako je tomu v případě bitmap a pixmap u dvourozměrných obrazů, kde je původně spojitá plocha rozdělena na dále nedělitelné plošky (pixely). Voxely mívají většinou tvar osově orientované krychle nebo kvádru. V základní podobě, kdy potřebujeme pouze vyjádřit, zda daná část v prostoru náleží či nenáleží do tělesa, mohou voxely nabývat pouze dvou stavů – obsazeno, neobsazeno. Pro každý voxel tedy v tomto případě stačí zaznamenat pouze jeden bit jehož hodnota signalizuje obsazenost či neobsazenost voxelu tělesem.
Voxelům však můžeme přiřazovat i další informace, ať už spojité nebo diskrétní. Například při zpracování medicínských dat získaných výše zmíněnými metodami CT a MR je každý voxel reprezentovaný osmibitovou až dvanáctibitovou hodnotou, která udává buď hustotu rentgenových paprsků přečtenou z čidel snímače (metody CT) nebo hustotu resp. počet protonových jader (metoda magnetické rezonance) v nasnímaném objemu. Část prostoru, ve kterém se nachází těleso či celá scéna, je popsaná množinou voxelů, které jsou pravidelně rozmístěny v osově orientované krychli či kvádru. Na těleso (resp. na část prostoru, ve kterém se těleso nachází) můžeme nahlížet dvěma způsoby:
- Jedná se o trojrozměrnou ortogonální mřížku, jejíž hodnoty v uzlech určují průměrné hodnoty (například průhlednost, či hustotu) ve svém okolí.
- Jde o množinu pravidelně uspořádaných mikroobjemů ve tvaru malých krychliček či hranolků.
Pouze ve druhém případě je korektní hovořit o voxelech (elementárních objemech), protože v prvním případě vlastně ukládáme průměrné hodnoty v bezrozměrných bodech. Oba tyto pohledy se však v praxi vzájemně prolínají, protože uzly mřížky jsou umístěny v geometrických středech mikroobjemů. Hodnoty uzlů mřížky a hodnoty mikroobjemů si tak vzájemně odpovídají. Principiální rozdíl mezi hodnotami uloženými v uzlech trojrozměrné mřížky a pravidelně uspořádanými mikroobjemy je ukázán na následujícím obrázku. Na tomto obrázku jsou pro jednoduchost zobrazeny pouze plošné projekce, ve skutečnosti se samozřejmě pracuje s trojrozměrnou mřížkou.

Obrázek 4: Rozdíl mezi ortogonální mřížkou s hodnotami uloženými v uzlech a pravidelně uspořádanými mikroobjemy ve tvaru krychliček či hranolů – voxelech
4. Typická použití objemových dat zapsaných pomocí voxelů
Časté a v dnešní době i typické je použití objemových dat popsaných pomocí voxelů v medicínských aplikacích, zejména pro reprezentaci dat získaných z prostorových snímků a diagnostických zařízení (již několikrát zmíněné metody CT a MR). Nasazení v medicíně však klade velké nároky na přesnost dat. Z toho také vyplývá, že se používají poměrně velká rozlišení (pracuje se na samé hranici, která je technologiemi CT a MR dosažitelná) a vysoké bitové hloubky voxelů (od 8 do 12 bitů na voxel). Se vzrůstajícím výkonem počítačů a jejich paměťové kapacity je možné stále více diagnostických postupů v medicíně i jiných odvětvích automatizovat a voxelová data zpracovávat strojově. Skutečnost je však taková, že nejdůležitější aplikací zůstává „pouhé“ zobrazování a ukládání voxelových dat. Jasným požadavkem při zobrazování je maximální názornost a snadnost ovládání zobrazovacích nástrojů. Ukazuje se také, že jedním z nejvýznamnějších prvků ergonomického zobrazení je možnost animace (především natáčení a zvětšování zajímavých oblastí) a zobrazení objemových dat v reálném čase.

Obrázek 5: Řez břišní dutinou pacienta získaný pomocí metody CT (snímek není obarven, úroveň šedi reprezentuje míru „průhlednosti“ dané tkáně v oblasti rentgenového záření. Zcela bílá je tak především páteř (uprostřed dole) a žebra (bílé plošky na okrajích)
5. Přednosti a zápory popisu geometrie tělesa pomocí voxelů, technická a programová podpora
Mezi největší přednosti této formy objemové reprezentace patří přímá návaznost na různé zdroje potencionálních prostorových dat (často se například používají již dříve zmíněné metody MR a CT) a značná jednoduchost a s ní související rychlost algoritmů pro základní operace s tělesy (sjednocení, průnik, rozdíl). Mezi nevýhody patří vznik mnoha geometrických chyb (například vlivem aliasu) při provádění některých transformací, zejména otáčení a změně měřítka. Původ a význam těchto chyb je analogický plošným bitmapám; ty také není možné beze ztráty kvality natáčet či měnit jejich velikost. Dále je pro ukládání objemových dat zapotřebí velkého množství paměti, což na některých systémech může limitovat velikost použité mřížky a tím i přesnost modelu tělesa. Velikost potřebné paměti lze sice snížit vhodnou metodou ukládání dat do hierarchických struktur (například oktalové stromy – octree – nebo hierarchické mřížky), ale při práci s reálnými daty, ve kterých může být přítomen šum nebo jsou data již ze své podstaty hodně proměnná, ztrácí tyto metody účinnost.
Poněkud diskutabilní je technická podpora pro vykreslování objemových dat. Existují sice přídavné karty, které urychlují vykreslování (jako příklad lze uvést akcelerační kartu Volume Pro), ale tyto karty se prozatím nedočkaly širšího uplatnění, proto jejich cena zůstává poměrně vysoká a i programové vybavení zaostává, zejména v porovnání s vybavením akceleračních karet určených pro zobrazování polygonů. V této oblasti však lze, jak jsme si již řekli v úvodních odstavcích, očekávat větší pokrok, protože stále vzrůstá počet systémů pro získávání a zpracování objemových dat a tak bude stále větší poptávka po vhodné technologii vhodné na zobrazování těchto dat.

Obrázek 6: Grafický akcelerátor Volume Pro určený pro vizualizaci objemových dat
Při používání akceleračních karet pro zobrazování voxelových dat je nutné řešit problematiku potřeby velkého množství dat nutných pro zobrazení scény. U grafických akcelerátorů pro zobrazování polygonů se tento problém částečně řeší uložením textur nebo i geometrických dat scény do lokální paměti grafického akcelerátoru. Velikost této paměti se pohybuje v desítkách megabytů. U grafického akcelerátoru určeného pro zobrazování voxelových dat samozřejmě můžeme použít tutéž techniku (uložení dat do lokální paměti akcelerátoru), tato paměť však musí pro běžně používaná data mít kapacitu řádově vyšší, jednoduchým výpočtem lze snadno zjistit, že pro dnes běžné voxelové mřížky o velikosti 5123 voxelů a pro bitovou hloubku 8 bitů na voxel je zapotřebí použít paměť s kapacitou minimálně 128MB.
V oblasti programové podpory pro práci s objemovými daty existuje především programové rozhraní (API) s názvem SGI Volumizer od firmy SGI. Nejedná se přímo o knihovnu pro práci s voxelovými daty, protože jde pouze o nástroj definující funkce pro zobrazení voxelových dat s využitím grafických akcelerátorů. Programové rozhraní je vytvořeno přes knihovnu OpenGL. Existují i specializované knihovny pro vykreslování voxelových dat (volume rendering). Jednou z těchto knihoven je VolPack Volume Rendering Library, která byla vyvíjena jako součást výzkumného projektu zobrazování objemových dat. Tato knihovna je postavena na nové skupině rychlých algoritmů zobrazování objemů. Autorem knihovny VolPack je Philippe Lacroute. Knihovna nevyžaduje ani nepoužívá žádný specializovaný hardware a je přenositelná na většinu platforem, přičemž dosahuje velmi rychlých časů zobrazování. Na pracovní stanici SGI Indigo, což je z dnešního pohledu již zastaralý počítač, trvá zobrazení struktury o velikosti 2563 voxelů přibližně jednu sekundu.
Kromě specializovaných knihoven existují i komplexní nástroje pro práci s voxelovými daty. Nejznámější nástroje jsou vyvíjeny společností Volume Graphics pod názvem VGL. VGL je rozšiřitelné a vysoce flexibilní 3D programovací prostředí pro tvorbu různých aplikací založených na zobrazování objemů. Může se jednat jak o specializované medicínské aplikace, tak i o zobrazování zvláštních efektů ve filmovém průmyslu. Výhodou VGL je značná rychlost zobrazení i na standardních platformách PC, nevýhodou je nepřístupnost zdrojových kódů a komerční ochrana formátů a rozhraní.
6. Způsoby vizualizace objemových dat
Velikost objemových dat, která běžně vznikají v průběhu různých měření nebo jsou získána jako výsledek simulací, se běžně pohybuje v řádech desítek megabytů, v mezních případech až gigabytů. Tak velké množství informací musí být zpracováváno pomocí efektivních algoritmů a výkonných výpočetních systémů. Již dnes jsou k dispozici, jak jsme si řekli v předchozích kapitolách, podpůrné programové a technické prostředky (specializované grafické akcelerátory) pro vizualizaci středně velkých balíků objemových dat. Vývoj vizualizačních nástrojů poměrně rychle pokračuje, a to jak v oblasti technických prostředků, tak i algoritmů pro efektivní práci s objemovými daty. Algoritmy pro vizualizaci vícerozměrných informací lze podle typu zpracovávaných dat rozdělit do dvou skupin, které budou podrobněji popsány v dalším textu:
- V první skupině se nachází algoritmy, které zobrazují skalární plošné, prostorové či vícerozměrné mřížky nebo skalární data v jiném (i nepravidelném) uspořádání. Z pohledu vizualizace přitom většinou považujeme skalární prostorové mřížky za klasická objemová data používaná v počítačové grafice.
- Do druhé skupiny jsou zařazeny algoritmy, které zobrazují vektorová nebo tenzorová pole. Vzhledem k vysoké informační hodnotě a vnitřní provázanosti těchto dat je nutné tyto informace zobrazovat s použitím speciálních algoritmů.
Obrázek 7: Různé metody zobrazení objemových dat
Algoritmy, které zobrazují skalární prostorové mřížky (volume rendering of 3D scalar data algorithms), se obecně dělí do dvou skupin – na algoritmy zobrazující povrchy a na přímé objemové algoritmy.
7. Algoritmy zobrazující povrchy
Algoritmy zobrazující povrchy surface-fitting algorithms většinou musí nejdříve ze vstupních dat (tj. prostorového pole/mřížky skalárních hodnot – voxelů) vytvořit pomocnou geometrickou strukturu, pomocí které je vyjádřen povrch. Tyto algoritmy tedy pracují se vstupními daty nepřímo, protože nejprve vytvoří povrch, který je reprezentován jednoduššími geometrickými primitivy, nejčastěji trojúhelníky, které tvoří nepravidelnou síť trojúhelníků (TIN – Triangular Irregular Network). Tyto trojúhelníky se posléze zobrazují s využitím standardních grafických knihoven (například OpenGL, Direct 3D) s případnou technickou podporou (tj. urychlení zobrazování) ve formě grafických akcelerátorů. Pro vykreslení převedených dat ve vysoké kvalitě lze samozřejmě použít i POV-Ray, samotný převod na trojúhelníky se však musí provést v jiné aplikaci. Při zobrazování tímto způsobem lze využít prakticky všechny zobrazovací postupy používané v 3D počítačové grafice, například texturování, osvětlení, antialiasing, poloprůhlednost povrchu atd.
Pro převod dat z formy skalární prostorové mřížky do povrchové (hraniční) reprezentace se nejčastěji používají klasické algoritmy určené k převodu dat z objemové reprezentace. Mezi tyto algoritmy patří například algoritmus Marching Cubes popř. algoritmus Marching Tetrahedra.

Obrázek 8: Vyhlazený povrch modelu kosti
Další možností, jak zobrazit povrch zkoumaného pole, je použití upraveného algoritmu pro zpětné sledování paprsku (raytracing) nebo vrhání paprsku (raycasting). Vyjádření bodů na povrchu se při použití těchto metod provádí přímo při vykreslování, kdy je zapotřebí vypočítat souřadnice průniku paprsku s povrchem. Pro aplikace, kde je zapotřebí explicitně znát body na povrchu, však ztrácí použití těchto metod svoji největší výhodu. Algoritmy pro vyjádření a následné zobrazení povrchů musí v první řadě vypočítat souřadnice povrchu ze zadaných dat prostorové mřížky. Povrch je v nejjednodušším případě chápán jako ekvipotenciální plocha, tj. plocha spojující body se stejnými vlastnosti. Uživatel tedy buď interaktivně nebo výpočtem zvolí některou veličinu uloženou v prostorové mřížce a její konkrétní hodnotu, pro kterou se následně ekvipotenciální plocha vypočítá a zobrazí. Vzhledem k tomu, že tato technika není přímo v POV-Rayi podporována, nebudeme se jí dále zabývat.

Obrázek 9: Vyhlazený povrch skutečného předmětu, jehož tvar byl nasnímán 3D skenerem
8. Objemové algoritmy
Objemové algoritmy (Direct volume rendering algorithms) zobrazují skalární data přímo, neprovádí tedy prvotní převod do povrchové reprezentace. Tyto algoritmy umožňují zobrazovat i poloprůhledné objemy čehož lze využít například při vizualizaci kapalin nebo struktur obsažených uvnitř jiných struktur. Nevýhodou těchto algoritmů je prozatím malá technická (hardwarová) podpora, protože současné grafické akcelerátory jsou určeny převážně pro vykreslování těles složených z plošných polygonů. Programové a technické prostředky pro vykreslování objemových dat samozřejmě existují, jak již bylo řečeno v předchozích odstavcích, jejich rozšířenost a možnosti však prozatím zaostávají za možnostmi uplatnění polygonových modelů. V této oblasti se však očekává další rozsáhlý vývoj. Další nevýhodou je nemožnost provádět natáčení zkoumaných dat na obrazovce o libovolný úhel bez nutnosti přepočtu celého obrázku. Pro interaktivní zobrazení jsou tedy vhodnější algoritmy zobrazující povrchy, kde lze po prvotním převodu objemových dat na data povrchová výsledným objektem libovolně natáčet nebo provádět změnu měřítka.

Obrázek 10: Výsledek simulace proudění po vizualizaci výsledných objemových dat
9. Obsah dalšího pokračování seriálu
V následující části seriálu o raytraceru POV-Ray si na praktických příkladech ukážeme, jakým způsobem je možné zpracovat objemová data a zařadit je do vykreslované scény. Také si popíšeme formát souboru používaný pro uchování objemových dat i to, jak lze tyto soubory jednoduše vytvářet pomocí vlastních programů.