Obsah
1. Zhodnocení jednotlivých metod výpočtu pravděpodobností transformací
2. Metody vybarvení IFS koláže
3. Algoritmy pro výpočet IFS koláží
4. Algoritmus náhodné procházky (RWA)
5. První demonstrační příklad – aplikace algoritmu náhodné procházky
6. Deterministický algoritmus (DIA)
7. Druhý demonstrační příklad – aplikace deterministického algoritmu
8. Obsah dalšího pokračování tohoto seriálu
1. Zhodnocení jednotlivých metod výpočtu pravděpodobností transformací
V předcházející části tohoto seriálu jsem popsal některé známé a používané i nové možnosti výpočtu pravděpodobností jednotlivých transformací systému iterovaných funkcí. Na tomto místě stojí za připomenutí, že zatímco transformační matice (resp. jednotlivé transformace) jsou přesně zadané a přímo odpovídají informacím, které (většinou interaktivním způsobem) specifikoval uživatel, výpočet pravděpodobností jednotlivých transformací už tak jednoznačný není. K tomuto tvrzení mám několik důvodů:
- První nejednoznačnost vyplývá z vlastního výpočtu pravděpodobnosti. V tomto případě je nejpřesnější ta metoda, která porovná plochu či obsah bázového objektu s transformovaným objektem. Tato metoda musí počítat pravděpodobnosti transformací přímo ze zadaných dat bázového objektu (souřadnice vrcholů) a ne pouze z transformačních matic.
- Druhá nejednoznačnost nastane, není-li bázový objekt zcela přesně pokryt transformovanými objekty. V tom případě nebude po základním výpočtu součet všech pravděpodobností roven jedné. Ve vypočtených pravděpodobnostech je samozřejmě zapotřebí provést takovou úpravu, aby byl součet roven jedné, jinak by nebylo možné provést korektní generování IFS koláže. Problémem však stále zůstává úprava jednotlivých pravděpodobností tak, aby byl jejich součet jednotkový. Je možné zbývající část do jednotky rozdělit rovnoměrně mezi všechny pravděpodobnosti nebo se může zohlednit hodnota jednotlivých pravděpodobností (rozdělení dle váhy). Žádná z těchto úprav není přesná, neboť u špatně provedeného pokrytí bázového objektu neexistuje jednoznačný vztah mezi transformací a její pravděpodobností. Tento vztah platí pouze v případě přesného pokrytí, tj. v případě, že transformované objekty úplně pokryjí bázový objekt, přičemž se tyto objekty navzájem nepřekrývají.
Všechny tyto skutečnosti se musí zohlednit při porovnávání pravděpodobností, které vznikly výpočtem podle různých metod.
2. Metody vybarvení IFS koláže
Při vytváření IFS koláže, tj. rastrového obrázku s atraktorem systému iterovaných funkcí, můžeme jednotlivé pixely, jejichž souřadnice jsou zjištěny pomocí dále popisovaných algoritmů, obarvit více různými způsoby. V dnešní části, konkrétně v páté a sedmé kapitole, budou uvedeny demonstrační příklady, ve kterých jsou použity čtyři různé metody obarvování pixelů. Následuje stručný popis těchto metod:
- Prakticky nejpoužívanější metodou je obarvení vygenerovaných pixelů konstantní barvou. Tato metoda je velmi jednoduchá a výsledné obrázky jsou poměrně pěkné, ovšem pouze za předpokladu, že je použito velké rozlišení výsledného rastrového obrázku, například při tisku na laserových tiskárnách. Na displejích s malým rozlišením je jednobarevný obrázek poměrně nezajímavý (ztrácí se zde informace o hustotě souřadnic pixelů).
- Druhá metoda spočívá ve vyobrazení plošného histogramu, tj. rastrového obrázku, ve kterém je každému pixelu přiřazena taková barva, jež odpovídá počtu „zápisů“ na dané souřadnice. Čím větší je hustota vygenerovaných souřadnic v nějaké oblasti, tím světlejší (popř. při inverzním zobrazení tmavší) budou pixely z této oblasti.
- Třetí metoda je také často používaná. Její princip spočívá v tom, že se barva vygenerovaného pixelu zvolí podle toho, která transformace z množiny transformací IFS systému byla pro výpočet souřadnic použita. Mohlo by se zdát, že barvy přiřazené jednotlivým transformacím budou po obrázku rozmístěny náhodně (podle jejich náhodného výběru), opak je však pravdou: každé transformaci v obrázku přísluší jedna poměrně výrazně odlišená oblast.
- Čtvrtá metoda vznikla sloučením metody druhé a třetí, tj. zobrazuje se plošný histogram, tentokrát jsou však barvy pixelů filtrovány podle toho, která transformace posloužila k výpočtu souřadnic daného pixelu.
V dále uvedených demonstračních příkladech se metoda pro vybarvení IFS koláže volí stiskem jedné z kláves [F1] až [F4].
Obrázek 1: Porovnání všech čtyř metod vybarvení IFS koláže
3. Algoritmy pro výpočet IFS koláží
Poté, co jsou zadané všechny transformace systému iterovaných funkcí φi a vypočítané pravděpodobnosti jednotlivých transformací πi, je možné vygenerovat výslednou IFS koláž, tj. buď rastrový obraz nebo prostorový objekt složený z částic nebo surfelů. Pro generování IFS koláže se používají takzvané generativní metody. Tyto metody jsou většinou velmi jednoduché pro implementaci. Generativních metod pro vytváření IFS koláží existuje velké množství. V tomto seriálu budou popsány čtyři metody, které lze dále modifikovat a rozvíjet:
- Algoritmus náhodné procházky (RWA – Random Walk Algorithm) – je popsán ve čtvrté kapitole
- Deterministický algoritmus (DIA – Deterministic Iteration Algorithm) – je popsán v šesté kapitole
- Upravený algoritmus pro náhodnou procházku (M-RWA) – bude popsán příště
- Algoritmus pro generování minima pixelů (MPA – Minimal Plotting Algorithm) – bude popsán příště
Takové množství metod zde uvádím především z toho důvodu, že výsledná IFS koláž tvořena nekonečně členitým tvarem – fraktálem. Je tedy z matematického hlediska tvořena nekonečným množstvím bodů. Z toho vyplývá, že pro vygenerování a následné zobrazení celého fraktálního objektu by bylo zapotřebí provést nekonečné množství iterací, které by byly spočítány v nekonečném čase.
Protože je pro praktickou aplikaci vykreslování nutné, aby byl čas počítání (resp. generování) IFS fraktálu konečný, je zapotřebí zavést určitá zjednodušení. Z toho důvodu se negeneruje nekonečné množství bodů, ale většinou pevně zadaný počet bodů (řádově se jedná o desítky až stovky tisíc iterací, podle požadované kvality vykreslení a rozlišení obrázku). Výsledkem je tedy pouze přibližný tvar fraktálu generovaného pomocí systému iterovaných funkcí.
Výstupní rastrové grafické zařízení, na jakém se bude výsledný IFS fraktál vykreslovat, má určitou rozlišovací schopnost. To znamená, že prostor, do kterého se má fraktál mapovat, není spojitý, ale diskrétní a současně prostorově omezený. Tato skutečnost je použita u některých generativních metod, které zohledňují konečnou rozlišovací schopnost výstupních zařízení. Takové metody tedy pracují s konečnou velikostí pixelů či surfelů a snaží se negenerovat ty body fraktálu, které již jsou nakresleny (do jednoho pixelu lze mapovat nekonečné množství bodů z určitého spojitého intervalu). Příkladem tohoto přístupu je dále prezentovaný algoritmus generování minima pixelů – MPA.
Zbývá tedy vhodně vybrat takové body, které co nejlépe reprezentují daný IFS fraktál, přičemž je zapotřebí vzít v úvahu dva protichůdné faktory. Jedním z nich je, aby byl čas pro generování fraktálu co nejkratší (musí se tedy minimalizovat počet generovaných bodů). Druhým faktorem je co nejlepší reprezentace výsledného IFS fraktálu (tedy generovat co největší počet relevantních bodů).
Pro provedení jedné transformace (tj. vygenerování jednoho bodu či pixelu) je zapotřebí u systému iterovaných funkcí vytvořených v ploše provést čtyři násobení a šest sečítání; u IFS systému v prostoru se jedná již o devět násobení a dvanáct sečítání. To není mnoho, ale musíme si uvědomit, že pro vykreslení jednoho obrázku se musí provést přibližně sto tisíc těchto transformací. Takové množství operací může na dnešních počítačích trvat jednotky i desítky sekund. Není tedy možné takovým způsobem generovat například videosekvence, kde je potřeba zobrazit minimálně deset snímků za sekundu (jak již víme z dřívějšího popisu, lze IFS použít pro obecně ztrátovou komprimaci grafických údajů). Pro tyto aplikace jsou vytvořeny speciální metody generování IFS fraktálů.
Obrázek 2: Slavná kapradina Michaela Barnsleye v monochromatickém provedení
Obrázek 3: Kapradina Michaela Barnsleye v odstínech černá-zelená-bílá
4. Algoritmus náhodné procházky (RWA)
Algoritmus náhodné procházky (RWA – Random Walk Algorithm), který jsme si ve stručnosti popsali už v předchozích částech tohoto seriálu, patří mezi nejjednodušší algoritmy pro generování fraktálních objektů pomocí systémů iterovaných funkcí. Jeho předností je jednoduchost a malá paměťová náročnost. Mezi jeho nevýhody patří nutnost generování velkého množství bodů pro reprezentaci fraktálu. Některé části fraktálu se generují vícekrát, zatímco některé pouze jednou a při malém počtu iterací může dokonce docházet k tomu, že se některé části fraktálu nevykreslí.
Generování IFS fraktálu se nastartuje tak, že se zvolí náhodný bod P0 v rovině E2 či prostoru E3. Poloha počátečního bodu nemá na výslednou koláž žádný větší vliv, nemusí tedy nutně ležet uvnitř atraktoru systému iterovaných funkcí. Poté je náhodně vybrána nějaká transformace φi z množiny Φ. Při výběru transformace je nutné přihlédnout k tomu, aby počet použití dané transformace odpovídal její pravděpodobnosti πi, jinak se bude výsledná koláž generovat neúměrně dlouho. Poté co byla některá transformace vybrána, je možné ji aplikovat na daný bod. Souřadnice tohoto bodu se změní (bod se podrobní transformaci). Na tento nový bod je posléze iterativně aplikována další náhodně vybraná transformace. Iterace probíhají tak dlouho, dokud není dosaženo zadaného maximálního počtu iterací.
Jelikož první bod P0 nemusí nutně ležet v atraktoru IFS, je nutné několik prvních iterací počátečního bodu nezobrazovat. Z teorie IFS systémů, kterou jsem uvedl v předchozích částech tohoto seriálu, vyplývá, že se systém automaticky dostane po několika iteracích do svého atraktoru, v němž již setrvá. Kvalitu výsledného fraktálního objektu lze ovlivnit zadáním maximálního počtu iterací, které se mají provést. Malý počet iterací způsobuje, že je obrázek složený z malého počtu bodů a tím pádem je hůře viditelný. Příliš velký počet iterací naopak způsobuje dlouhou dobu generování výsledné IFS koláže s tím, že některé pixely jsou překresleny vícekrát (viz výsledky plošného histogramu).
Obrázek 4: Fraktální spirála vytvořená algoritmem RWA
V neformálním programovacím jazyce je možné algoritmus náhodné procházky pro generování IFS koláže popsat následovně:
- Vstupy programu:
- Uspořádaná dvojice (Φ, Π)=({φ1, φ2, … φn},{π1, π2, … πn}), kterou je definovaný celý systém iterovaných funkcí.
- Maximální počet iterací itermax (celé kladné číslo).
- Počet startovních iterací iterstart, přičemž platí podmínka iterstart < itermax.
- Výstup programu:
- Rastrový obrazec či prostorový objekt složený z množiny navzájem izolovaných bodů (pixelů či surfelů), který reprezentuje atraktor systému IFS.
- Inicializační sekvence:
- Automaticky zvol počáteční polohu bodu P0, který bude v dalších iteračních krocích transformován. Poloha bodu P0 nemá na tvar výsledného fraktálního obrazce velký význam, proto lze většinou pro jednoduchost algoritmu dosadit P0=[0, 0] pro obrazec v rovině E2, resp. P0=[0, 0, 0] pro prostorový útvar v E3.
- Nastav čítač počtu iterací iter:=0.
- Hlavní smyčka:
- Pro iter probíhající od 0 do itermax-1 opakuj smyčku:
- Vygeneruj náhodné číslo π v rozsahu (1, n), kde n je počet transformací φ.
- Podle hodnoty π najdi příslušnou transformaci φi.
- Aplikuj transformaci φi na bod Piter a vypočti nový bod Piter+1.
- Bod Piter+1 bude novým výchozím bodem pro další iteraci.
- Pokud platí podmínka iter>iterstart
- Pak vykresli pixel na pozici bodu Piter, nebo na této pozici vygeneruj bod či surfel v prostoru.
- Konec hlavní smyčky
- Konec programu
Obrázek 5: Fraktální drak vytvořený algoritmem RWA
5. První demonstrační příklad – aplikace algoritmu náhodné procházky
Výše uvedený algoritmus pro vykreslení IFS koláže je možné implementovat jako funkci v programovacím jazyku C například následujícím způsobem:
//-----------------------------------------------------------------------------
// Překreslení systému iterovaných funkcí IFS pomocí algoritmu RWA
//-----------------------------------------------------------------------------
void recalcIFSusingRWA(pixmap *pix, // pixmapa pro vykreslování
int maxiter, // maximální počet iterací
double scale, // měřítko obrazce
double xpos, // posun obrazce
double ypos,
int type, // vybraný IFS systém
int rf, int gf, int bf, // příznaky barvových složek
int dr, int dg, int db, // přírustky barvových složek
DrawType drawType) // způsob vykreslení
{
int iter=0; // počitadlo iterací
int threshold=50; // hranice počtu iterací pro vykreslování
float x, y, hlp; // poloha iterovaného bodu
float pp; // pravděpodobnost pro výběr transformace
float sum;
int k; // číslo vybrané transformace
float (*t)[][7]; // ukazatel na vybranou množinu transformací
unsigned char red=rf ? dr : 0; // reálné přírustky barvových složek
unsigned char green=gf ? dg : 0;
unsigned char blue=bf ? db : 0;
unsigned char pal[8][3]={
{0xff, 0x00, 0x00},
{0x00, 0xff, 0x00},
{0x00, 0x00, 0xff},
{0xff, 0xff, 0x00},
{0x00, 0xff, 0xff},
{0xff, 0x00, 0xff},
{0xff, 0xff, 0xff},
{0x80, 0x80, 0x80},
};
switch (type) { // výběr IFS systému
case 0: t=&IFS_triangle; break;
case 1: t=&IFS_tree; break;
case 2: t=&IFS_spiral; break;
case 3: t=&IFS_spiral2; break;
case 4: t=&IFS_dragon; break;
case 5: t=&IFS_swirl; break;
case 6: t=&IFS_crystal; break;
case 7: t=&IFS_Z; break;
case 8: t=&IFS_ferny; break;
case 9: t=&IFS_fern; break;
default:t=&IFS_spiral; break;
}
x=0;
y=0; // nastavení počáteční polohy bodu
srand(0);
xpos+=pix->width/2; // posun do středu okna
ypos+=pix->height/2;
while (iter++<maxiter*100) { // iterační smyčka
pp=((float)rand())/RAND_MAX; // p leží v rozsahu 0.0-1.0
k=0; // proměnná cyklu vyhledání transformace
sum=0;
while (sum<=pp) { // podle náhodného čísla
sum=sum+(*t)[k][6]; // vybrat transformaci
k++;
} // k určuje index transformace
k--; // úprava ze smyčky while
hlp=(*t)[k][0]*x+(*t)[k][1]*y+(*t)[k][4];// provedení
y =(*t)[k][2]*x+(*t)[k][3]*y+(*t)[k][5];// transformace
x =hlp;
if (iter>threshold) // je-li dosaženo hranice iterací
switch (drawType) { // výběr vykreslovacího režimu
case IterPutPixel:
putpixel(pix, x*scale+xpos, y*scale+ypos, rf ? 0xff:0x00, gf ? 0xff:0x00, bf ? 0xff:0x00);
break;
case IterAddPixel:
addpixel(pix, x*scale+xpos, y*scale+ypos, red, green, blue);
break;
case TransfPutPixel:
putpixel(pix, x*scale+xpos, y*scale+ypos, pal[k&7][0], pal[k&7][1], pal[k&7][2]);
break;
case TransfAddPixel:
addpixel(pix, x*scale+xpos, y*scale+ypos, (!!pal[k&7][0])*dr, (!!pal[k&7][1])*dg, (!!pal[k&7][2])*db);
break;
default:
break;
}
}
} Funkce recalcIFSusingRWA() je použita v dnešním prvním demonstračním příkladu. Po překladu a spuštění tohoto demonstračního příkladu se zobrazí IFS systém ve tvaru soběpodobného draka. Typ fraktálu i způsob jeho zobrazení je možné měnit pomocí mnoha kláves, jejichž seznam je uveden v tabulce:
| Klávesa | Význam |
|---|---|
| F1 | výběr vykreslovací metody s konstantní barvou (IterPutPixel) |
| F2 | výběr vykreslovací metody s plošným histogramem (IterAddPixel) |
| F3 | výběr vykreslovací metody s barvou závisející na transformaci (TransfPutPixel) |
| F4 | výběr vykreslovací metody kombinující plošný histogram s barvou transformace (TransfAddPixel) |
| F5 | snížení změny červené barvové složky při tvorbě plošného histogramu |
| F6 | zvýšení změny červené barvové složky při tvorbě plošného histogramu |
| F7 | snížení změny zelené barvové složky při tvorbě plošného histogramu |
| F8 | zvýšení změny zelené barvové složky při tvorbě plošného histogramu |
| F9 | snížení změny modré barvové složky při tvorbě plošného histogramu |
| F10 | zvýšení změny modré barvové složky při tvorbě plošného histogramu |
| S | uložení rastrového obrázku s fraktálem do externího souboru |
| Q | ukončení demonstračního příkladu |
| Esc | ukončení demonstračního příkladu |
| , | snížení maximálního počtu iterací o 1000 |
| . | zvýšení maximálního počtu iterací o 1000 |
| < | snížení maximálního počtu iterací o 10000 |
| > | zvýšení maximálního počtu iterací o 10000 |
| R | povolení/zákaz použití červené barvové složky při vykreslování |
| G | povolení/zákaz použití zelené barvové složky při vykreslování |
| B | povolení/zákaz použití modré barvové složky při vykreslování |
| ← | posun obrazce s fraktálem o pět pixelů doleva |
| → | posun obrazce s fraktálem o pět pixelů doprava |
| ↑ | posun obrazce s fraktálem o pět pixelů nahoru |
| ↓ | posun obrazce s fraktálem o pět pixelů dolů |
| Page ↑ | změna měřítka obrazce o 10% (zvětšení) |
| Page ↓ | změna měřítka obrazce o 10% (zmenšení) |
| 0 | výběr IFS systému: Sierpinského trojúhelník |
| 1 | výběr IFS systému: binární strom |
| 2 | výběr IFS systému: soběpodobné spirály |
| 3 | výběr IFS systému: další typ soběpodobné spirály |
| 4 | výběr IFS systému: fraktální drak |
| 5 | výběr IFS systému: spirální květ |
| 6 | výběr IFS systému: krystalická struktura |
| 7 | výběr IFS systému: kaligrafické písmeno Z |
| 8 | výběr IFS systému: kapradina |
| 9 | výběr IFS systému: originální kapradina Michaela Barnsleye |
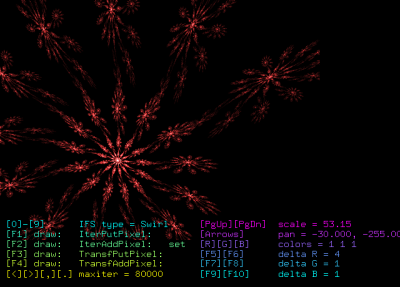
Obrázek 6: Screenshot prvního demonstračního příkladu
6. Deterministický algoritmus (DIA)
Deterministický algoritmus pro generování IFS koláže (DIA – Deterministic Iteration Algorithm) pracuje na poněkud odlišném principu než algoritmus pro náhodnou procházku (RWA), který jsme si popsali v předchozích kapitolách.
Zatímco se v algoritmu pro náhodnou procházku v každé iteraci vypočte vždy pouze jeden bod, v deterministickém algoritmu se v každé iteraci provede vyčíslení celé množiny bodů. Také se již nemusí počítat s pravděpodobnostmi jednotlivých transformací, poněvadž se na množinu bodů aplikují vždy všechny transformace z daného systému iterovaných funkcí.
Z tohoto faktu vyplývá i název popisovaného algoritmu. Zatímco se v předchozím algoritmu používala náhodná čísla a celý průběh generování fraktálního objektu byl stochastický, zde popisovaný algoritmus používá pro výpočet všechny transformace v jedné iteraci současně. To mimo jiné znamená, že se nemusí žádným způsobem vybírat určitá transformace.
Generování fraktálního objektu pomocí systému iterovaných funkcí se nastartuje tak, že se náhodně zvolí několik bodů ležících v rovině či prostoru. Poloha těchto bodů nemá (stejně jako v předchozím algoritmu) vliv na tvar výsledného fraktálu. Na tuto množinu jsou v každé iteraci aplikovány všechny transformace, které tvoří IFS systém. Všechny body, které vzniknou při těchto transformacích, tvoří množinu pro další iteraci.
Při malém počtu iterací (1000) vznikne velmi pravidelný obrázek, který se značně odlišuje od obrázku vzniklého aplikací algoritmu náhodné procházky, což je patrné na zobrazených screenshotech.
Obrázek 7: Porovnání algoritmů RWA a DIA: IFS vytvořený pomocí RWA
Obrázek 8: Porovnání algoritmů RWA a DIA: IFS vytvořený pomocí DIA
Zápis algoritmu DIA použitého pro generování fraktálních objektů z IFS systémů lze v neformálním programovacím jazyce napsat následovně:
- Vstupy programu:
- Množina Φ={φ1, φ2, … φn}, kterou je definovaný celý systém iterovaných funkcí.
- Maximální počet iterací itermax (celé kladné číslo).
- Počet startovních iterací iterstart, přičemž platí podmínka iterstart < itermax.
- Počet transformací v IFS systému Nφ.
- Výstup programu:
- Rastrový obrazec či prostorový objekt složený z množiny navzájem izolovaných bodů (pixelů či surfelů), který reprezentuje atraktor systému IFS.
- Inicializační sekvence:
- Vyber počáteční množinu bodů X0={X01, X02, … X0n}.
- Hlavní smyčka:
- Pro iter probíhající od 1 do itermax opakuj smyčku:
- Pro k probíhající od 1 do Nφ opakuj smyčku:
- Pro každý bod X ležící v Xiter-1 proveď: Xiter=Xiter U φk(X)
- Konec vnitřní smyčky
- Pokud platí podmínka iter>iterstart
- Pak vykresli všechny body uložené v množině Xiter.
- Konec vnější smyčky
- Konec programu
V průběhu inicializační sekvence se provádí náhodný výběr počátečních bodů z plochy E2 nebo E3. Bod může být vybrán pouze jeden, protože po první aplikaci transformací se tato množina zvětší o počet transformací. Ideální je výběr pevných bodů transformací tvořících IFS systém, není to však podmínkou; z toho důvodu můžeme použít:
X0={X01}; X01=[0,0]
Vnější smyčka se provede tolikrát, kolik je zadaných iterací. Zde bez dalších důkazů poznamenejme, že počet iterací v tomto algoritmu může být menší než počet iterací v algoritmu předchozím. Zatímco v předchozím algoritmu se s každou iterací vygeneroval pouze jeden bod, v tomto algoritmu se bodů vygeneruje více a jejich počet dokonce exponenciálně stoupá s rostoucím počtem iterací. Vnitřní smyčka se provede pro každou transformaci, které tvoří celý systém iterovaných funkcí. Tato smyčka je, na rozdíl od předchozího algoritmu náhodné procházky, deterministická, proto je také celý algoritmus DIA deterministický. V těle vnitřní smyčky se na každý bod z množiny aplikují všechny transformace. Nově vyčíslené body se vloží do nové množiny, zatímco starou množinu je možné zrušit.
Pro implementaci algoritmu DIA lze také použít jeho rekurzivní verzi, jejíž zápis je v programovacím jazyce jednodušší a běh algoritmu je mnohdy rychlejší (zde ovšem již záleží na konkrétní implementaci). Rekurzivní verze vypadá následovně:
- Vstupy rekurzivní funkce:
- Množina Φ={φ1, φ2, … φn}, kterou je definovaný celý systém iterovaných funkcí.
- Maximální počet iterací itermax (celé kladné číslo).
- Počet startovních iterací iterstart, přičemž platí podmínka iterstart < itermax.
- Číslo aktuální iterace iter, přičemž platí podmínka iter <= itermax.
- Počet transformací v IFS systému Nφ.
- Souřadnice bodu Xiter-1 v ploše či prostoru.
- Výstup rekurzivní funkce:
- Jeden pixel v ploše či bod (surfel) v prostoru, který leží v atraktoru systému IFS.
- Zpracování počátečních podmínek:
- Pokud platí podmínka iter=itermax
- Pak ukonči funkci.
- Pokud platí podmínka iter>iterstart
- Pak vykresli bod Xiter-1.
- Hlavní smyčka:
- Pro k probíhající od 1 do Nφ opakuj smyčku:
- Pro bod Xiter-1 rekurzivně zavolej tutéž funkci s parametry:
Φ, itermax, iterstart, iter+1, Nφ a φk(Xiter-1). - Konec smyčky
- Konec rekurzivní funkce
Algoritmus DIA generuje výsledný fraktál zcela odlišným způsobem než předchozí algoritmus, což je patrné zejména při záměrném zpomalení výpočtů spolu se zobrazením mezivýsledků. Také není zapotřebí generovat náhodná čísla a vybírat na jejich základě vhodnou transformaci φi. Velkou nevýhodou je však vyšší spotřeba paměti. Pro každou iteraci se generuje nová množina bodů. Tato množina se s každou následnou iterací exponenciálně zvětšuje. Jestliže je systém iterovaných funkcí tvořen dvojicí transformací a generování se zpočátku provádí s jedním startovním bodem, budou se v množině X1 nacházet po první iteraci body dva, po druhé iteraci body čtyři atd. Pro větší počet transformací je samozřejmě tento růst ještě prudší. Tato negativní vlastnost algoritmu DIA se musí obejít buď tím, že je nastaven relativně malý počet iterací itermax, nebo se musí omezit velikost množiny Xi.
Obrázek 9: IFS vytvořený pomocí algoritmu DIA
7. Druhý demonstrační příklad – aplikace deterministického algoritmu
Algoritmus DIA je možné implementovat v programovacím jazyku C například následujícím způsobem. Všimněte si, že kvůli snížení nároků na paměťovou kapacitu zásobníku jsou v co nejvyšší míře použity globální proměnné a v parametrech funkce se předávají jen ty nejnutnější informace:
//-----------------------------------------------------------------------------
// Překreslení systému iterovaných funkcí IFS pomocí rekurzivního algoritmu DIA
//-----------------------------------------------------------------------------
void recalcIFSusingDIA(float x, float y, int depth)
{
float xn, yn; // poloha iterovaného bodu
int k; // číslo transformace
if (depth) {
for (k=0; k<transf; k++) { // pro všechny transformace v IFS
xn=(*t)[k][0]*x+(*t)[k][1]*y+(*t)[k][4];// provedení
yn=(*t)[k][2]*x+(*t)[k][3]*y+(*t)[k][5];// transformace
iter++;
if (iter>threshold) // je-li dosaženo hranice iterací
switch (drawType) { // výběr vykreslovacího režimu
case IterPutPixel:
putpixel(pixIFS, x*scale+xpos, y*scale+ypos, rf ? 0xff:0x00, gf ? 0xff:0x00, bf ? 0xff:0x00);
break;
case IterAddPixel:
addpixel(pixIFS, x*scale+xpos, y*scale+ypos, red, green, blue);
break;
case TransfPutPixel:
putpixel(pixIFS, x*scale+xpos, y*scale+ypos, pal[k&7][0], pal[k&7][1], pal[k&7][2]);
break;
case TransfAddPixel:
addpixel(pixIFS, x*scale+xpos, y*scale+ypos, (!!pal[k&7][0])*deltar, (!!pal[k&7][1])*deltag, (!!pal[k&7][2])*deltab);
break;
default:
break;
}
recalcIFSusingDIA(xn, yn, depth-1); // rekurze - výpočet dalších "transf" pixelů
}
}
} Výše uvedená funkce recalcIFSusingDIA() je použita v dnešním druhém demonstračním příkladu. Ovládání tohoto demonstračního příkladu je shodné s příkladem prvním, proto ho zde již nebudu uvádět; jediná odlišnost spočívá v tom, že se nezadává maximální počet iterací, ale hloubka rekurze. Ta je následně upravena podle počtu transformací v systému iterovaných funkcí.
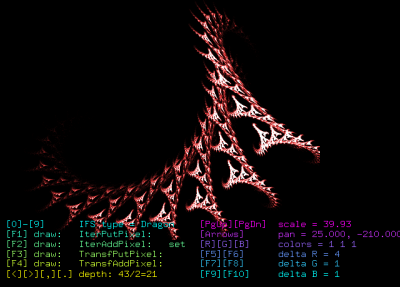
Obrázek 10: Screenshot druhého demonstračního příkladu
8. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování tohoto seriálu budou popsány další dva algoritmy pro vytváření IFS koláží. Bude se jednat o modifikovaný algoritmus náhodné procházky (M-RWA) a dále o pravděpodobně doposud nejrychlejší a nejpropracovanější algoritmus pro vykreslování IFS – algoritmus generování minima pixelů (MPA).