Obsah
1. Modifikovaný algoritmus náhodné procházky (M-RWA)
2. První demonstrační příklad – aplikace algoritmu M-RWA bez použití pravděpodobností transformací
3. Druhý demonstrační příklad – aplikace algoritmu M-RWA s využitím pravděpodobností transformací
4. Algoritmus generování minima pixelů (MPA)
5. Vzájemné porovnání algoritmů pro generování IFS fraktálů
6. Obsah dalšího pokračování tohoto seriálu
1. Modifikovaný algoritmus náhodné procházky (M-RWA)
V předchozí části tohoto seriálu jsme si popsali nejznámější a současně i nejpoužívanější algoritmus pro generování obrázků systémů iterovaných funkcí. Jednalo se o algoritmus náhodné procházky (RWA – Random Walk Algorithm). Dále jsme si popsali deterministický algoritmus (DIA – Deterministic Iteration Algorithm). V dnešní části budou popsány další dvě metody určené pro generování IFS koláží: modifikovaný algoritmus náhodné procházky (M-RWA – Modified Random Walk Algorithm) a algoritmus generování minima pixelů (MPA – Minimal Plotting Algorithm).
Začneme popisem modifikovaného algoritmu náhodné procházky. Tato metoda v sobě spojuje některé výhody algoritmu pro náhodnou procházku RWA a deterministického algoritmu DIA. Algoritmus pracuje tak, že v každé iteraci se iterovaný bod podrobí všem transformacím, ale pouze několik nových bodů (minimálně jeden) z nich se použije pro další iteraci. Předností tohoto algoritmu je podobná paměťová náročnost, jakou má algoritmus pro náhodnou procházku a poměrně rychlé generování výsledného fraktálu. Tuto metodu lze také s výhodou použít v případě, že je zapotřebí generovat pouze výřez z celého fraktálního objektu. Výběr transformací pro další iteraci lze provést například stejným způsobem, jako u algoritmu náhodné procházky, nebo na základě vhodně zvolené hashovací funkce, jejímž vstupem mohou být souřadnice vygenerovaného bodu.
- Vstupy programu:
- Uspořádaná dvojice (Φ, Π)=({φ1, φ2, … φn},{π1, π2, … πn}), kterou je definovaný celý systém iterovaných funkcí.
- Maximální počet iterací itermax (celé kladné číslo).
- Počet startovních iterací iterstart, přičemž platí iterstart < itermax.
- Počet transformací v IFS systému Nφ.
- Výstup programu:
- Rastrový obrazec či prostorový objekt složený z množiny navzájem izolovaných bodů (pixelů či surfelů), který reprezentuje atraktor systému IFS.
- Inicializační sekvence:
- Automaticky zvol počáteční polohu bodu P0, který bude v dalších iteračních krocích transformován. Poloha bodu P0 nemá na tvar výsledného fraktálního obrazce velký vliv, proto lze většinou pro jednoduchost algoritmu dosadit P0=[0, 0] pro obrazec v rovině E2, resp. P0=[0, 0, 0] pro prostorový útvar v E3.
- Nastav čítač počtu iterací iter:=0.
- Hlavní smyčka:
- Pro iter probíhající od 0 do itermax-1 opakuj smyčku:
- Pro k probíhající od 1 do Nφ opakuj smyčku:
- Aplikuj transformaci φk na bod Piter a vypočti souřadnici nového bodu Piter+1.
- Pokud platí podmínka iter>iterstart:
- Pak vykresli pixel na pozici bodu Piter, nebo na této pozici vygeneruj bod.
- Jeden nebo více bodů Piter+1 se stane novým výchozím bodem pro další iteraci.
- Konec vnitřní smyčky
- Konec vnější smyčky
- Konec programu
Modifikovaný algoritmus náhodné procházky je v mnohém podobný klasickému algoritmu pro náhodnou procházku. Jediná změna spočívá v tom, že se v každé iteraci provedou všechny transformace, takže se výsledný fraktál generuje o poznání rychleji, než tomu bylo u RWA algoritmu. Při výběru transformace pro další iteraci je vhodné zohlednit velikost kontrakce všech transformací.
Z toho, že se pro další iteraci vybere pouze několik transformací (které mohou být vybírány náhodně – stochastickým procesem) vyplývá, že tento algoritmus není deterministický. Determinismu však lze v případě potřeby dosáhnout (animace, morfing atd.) vhodným výběrem transformací pomocí hešovacích funkcí.
Na prvním a druhém ilustračním obrázku je patrný rozdíl mezi IFS fraktálem vygenerovaným pomocí M-RWA bez využití pravděpodobností transformací a s využitím pravděpodobností jednotlivých transformací.
Obrázek 1: IFS fraktál vytvořený metodou M-RWA bez využití pravděpodobností transformací
Obrázek 2: IFS fraktál vytvořený metodou M-RWA s využitím pravděpodobností transformací
2. První demonstrační příklad – aplikace algoritmu M-RWA bez použití pravděpodobností transformací
V dnešním prvním demonstračním příkladu je použita funkce recalcIFSusingMRWA1(), ve které je v každé iteraci spočten a vykreslen takový počet bodů, jaký odpovídá celkovému počtu transformací v systému iterovaných funkcí. Pro výběr jednoho bodu vstupujícího do další iterace je použit generátor náhodných čísel, který náhodně a uniformně vybere jednu z transformací IFS systému a bod posléze této transformaci podrobí:
//-----------------------------------------------------------------------------
// Překreslení systému iterovaných funkcí IFS pomocí algoritmu M-RWA.
// Bod x(n) je vybírán na základě náhodného čísla.
//-----------------------------------------------------------------------------
void recalcIFSusingMRWA1(pixmap *pix, // pixmapa pro vykreslování
int maxiter, // maximální počet iterací
double scale, // měřítko obrazce
double xpos, // posun obrazce
double ypos,
int type, // vybraný IFS systém
int rf, int gf, int bf, // příznaky barvových složek
int dr, int dg, int db, // přírustky barvových složek
DrawType drawType) // způsob vykreslení
{
int iter=0; // počítadlo iterací
int threshold=50; // hranice počtu iterací pro vykreslování
float x, y, hlp; // poloha iterovaného bodu
float pp; // pravděpodobnost pro výběr transformace
float sum;
int k; // číslo vybrané transformace
int maxTransf; // maximální počet transformací
float (*t)[][7]; // ukazatel na vybranou množinu transformací
unsigned char red=rf ? dr : 0; // reálné přírustky barvových složek
unsigned char green=gf ? dg : 0;
unsigned char blue=bf ? db : 0;
unsigned char pal[8][3]={
{0xff, 0x00, 0x00},
{0x00, 0xff, 0x00},
{0x00, 0x00, 0xff},
{0xff, 0xff, 0x00},
{0x00, 0xff, 0xff},
{0xff, 0x00, 0xff},
{0xff, 0xff, 0xff},
{0x80, 0x80, 0x80},
};
switch (type) { // výběr IFS systému
case 0: t=&IFS_triangle; break;
case 1: t=&IFS_tree; break;
case 2: t=&IFS_spiral; break;
case 3: t=&IFS_spiral2; break;
case 4: t=&IFS_dragon; break;
case 5: t=&IFS_swirl; break;
case 6: t=&IFS_crystal; break;
case 7: t=&IFS_Z; break;
case 8: t=&IFS_ferny; break;
case 9: t=&IFS_fern; break;
default:t=&IFS_spiral; break;
}
x=0;
y=0; // nastavení počáteční polohy bodu
srand(0);
xpos+=pix->width/2; // posun do středu okna
ypos+=pix->height/2;
// pomocná smyčka, ve které se zjistí počet transformací
for (sum=0.0, maxTransf=0; sum<1.0; sum+=(*t)[maxTransf][6], maxTransf++) ;
while (iter++<maxiter*100) { // iterační smyčka
// smyčka, ve které se provedou všechny transformace
for (k=0; k<maxTransf; k++) {
float xn=(*t)[k][0]*x+(*t)[k][1]*y+(*t)[k][4];
float yn=(*t)[k][2]*x+(*t)[k][3]*y+(*t)[k][5];
if (iter>threshold) { // je-li dosaženo hranice iterací
switch (drawType) { // výběr vykreslovacího režimu
case IterPutPixel:
putpixel(pix, xn*scale+xpos, yn*scale+ypos, rf ? 0xff:0x00, gf ? 0xff:0x00, bf ? 0xff:0x00);
break;
case IterAddPixel:
addpixel(pix, xn*scale+xpos, yn*scale+ypos, red, green, blue);
break;
case TransfPutPixel:
putpixel(pix, xn*scale+xpos, yn*scale+ypos, pal[k&7][0], pal[k&7][1], pal[k&7][2]);
break;
case TransfAddPixel:
addpixel(pix, xn*scale+xpos, yn*scale+ypos, (!!pal[k&7][0])*dr, (!!pal[k&7][1])*dg, (!!pal[k&7][2])*db);
break;
default:
break;
}
}
}
k=rand()%maxTransf; // výběr bodu x(n) na základě náhodného čísla
hlp=(*t)[k][0]*x+(*t)[k][1]*y+(*t)[k][4]; // provedení
y =(*t)[k][2]*x+(*t)[k][3]*y+(*t)[k][5]; // transformace
x =hlp;
}
} Ovládání prvního demonstračního příkladu pomocí klávesnice je sepsáno v následující tabulce:
| Klávesa | Význam |
|---|---|
| F1 | výběr vykreslovací metody s konstantní barvou (IterPutPixel) |
| F2 | výběr vykreslovací metody s plošným histogramem (IterAddPixel) |
| F3 | výběr vykreslovací metody s barvou závisející na transformaci (TransfPutPixel) |
| F4 | výběr vykreslovací metody kombinující plošný histogram s barvou transformace (TransfAddPixel) |
| F5 | snížení změny červené barvové složky při tvorbě plošného histogramu |
| F6 | zvýšení změny červené barvové složky při tvorbě plošného histogramu |
| F7 | snížení změny zelené barvové složky při tvorbě plošného histogramu |
| F8 | zvýšení změny zelené barvové složky při tvorbě plošného histogramu |
| F9 | snížení změny modré barvové složky při tvorbě plošného histogramu |
| F10 | zvýšení změny modré barvové složky při tvorbě plošného histogramu |
| S | uložení rastrového obrázku s fraktálem do externího souboru |
| Q | ukončení demonstračního příkladu |
| Esc | ukončení demonstračního příkladu |
| , | snížení maximálního počtu iterací o hodnotu 1000 |
| . | zvýšení maximálního počtu iterací o hodnotu 1000 |
| < | snížení maximálního počtu iterací o hodnotu 10000 |
| > | zvýšení maximálního počtu iterací o hodnotu 10000 |
| R | povolení/zákaz použití červené barvové složky při vykreslování |
| G | povolení/zákaz použití zelené barvové složky při vykreslování |
| B | povolení/zákaz použití modré barvové složky při vykreslování |
| ← | posun obrazce s fraktálem o pět pixelů doleva |
| → | posun obrazce s fraktálem o pět pixelů doprava |
| ↑ | posun obrazce s fraktálem o pět pixelů nahoru |
| ↓ | posun obrazce s fraktálem o pět pixelů dolů |
| Page ↑ | změna měřítka obrazce o 10% (zvětšení) |
| Page ↓ | změna měřítka obrazce o 10% (zmenšení) |
| 0 | výběr IFS systému: Sierpinského trojúhelník |
| 1 | výběr IFS systému: binární strom |
| 2 | výběr IFS systému: soběpodobné spirály |
| 3 | výběr IFS systému: další typ soběpodobné spirály |
| 4 | výběr IFS systému: fraktální drak |
| 5 | výběr IFS systému: spirální květ |
| 6 | výběr IFS systému: krystalická struktura |
| 7 | výběr IFS systému: kaligrafické písmeno Z |
| 8 | výběr IFS systému: kapradina |
| 9 | výběr IFS systému: originální kapradina Michaela Barnsleye |
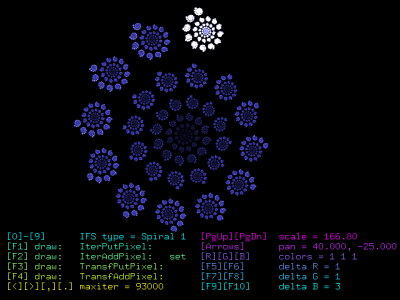
Obrázek 3: Screenshot prvního demonstračního příkladu
3. Druhý demonstrační příklad – aplikace algoritmu M-RWA s využitím pravděpodobností transformací
Druhý demonstrační příklad se do značné míry podobá příkladu prvnímu. Jediný rozdíl spočívá v tom, že se v každé iteraci pro provedení všech transformací (a vykreslení příslušných bodů) zvolí bod x pro další transformaci na základě pravděpodobnosti jednotlivých transformací IFS systému – je tedy použit stejný postup jako u klasického algoritmu náhodné procházky. Funkce recalcIFSusingMRWA2() má v tomto případě tvar:
//-----------------------------------------------------------------------------
// Překreslení systému iterovaných funkcí IFS pomocí algoritmu M-RWA.
// Bod x(n) je vybírán na základě pravděpodobnosti jednotlivých transformací.
//-----------------------------------------------------------------------------
void recalcIFSusingMRWA2(pixmap *pix, // pixmapa pro vykreslování
int maxiter, // maximální počet iterací
double scale, // měřítko obrazce
double xpos, // posun obrazce
double ypos,
int type, // vybraný IFS systém
int rf, int gf, int bf, // příznaky barvových složek
int dr, int dg, int db, // přírustky barvových složek
DrawType drawType) // způsob vykreslení
{
int iter=0; // počítadlo iterací
int threshold=50; // hranice počtu iterací pro vykreslování
float x, y, hlp; // poloha iterovaného bodu
float pp; // pravděpodobnost pro výběr transformace
float sum;
int k; // číslo vybrané transformace
int maxTransf; // maximální počet transformací
float (*t)[][7]; // ukazatel na vybranou množinu transformací
unsigned char red=rf ? dr : 0; // reálné přírustky barvových složek
unsigned char green=gf ? dg : 0;
unsigned char blue=bf ? db : 0;
unsigned char pal[8][3]={
{0xff, 0x00, 0x00},
{0x00, 0xff, 0x00},
{0x00, 0x00, 0xff},
{0xff, 0xff, 0x00},
{0x00, 0xff, 0xff},
{0xff, 0x00, 0xff},
{0xff, 0xff, 0xff},
{0x80, 0x80, 0x80},
};
switch (type) { // výběr IFS systému
case 0: t=&IFS_triangle; break;
case 1: t=&IFS_tree; break;
case 2: t=&IFS_spiral; break;
case 3: t=&IFS_spiral2; break;
case 4: t=&IFS_dragon; break;
case 5: t=&IFS_swirl; break;
case 6: t=&IFS_crystal; break;
case 7: t=&IFS_Z; break;
case 8: t=&IFS_ferny; break;
case 9: t=&IFS_fern; break;
default:t=&IFS_spiral; break;
}
x=0;
y=0; // nastavení počáteční polohy bodu
srand(0);
xpos+=pix->width/2; // posun do středu okna
ypos+=pix->height/2;
// pomocná smyčka, ve které se zjistí počet transformací
for (sum=0.0, maxTransf=0; sum<1.0; sum+=(*t)[maxTransf][6], maxTransf++) ;
while (iter++<maxiter*100) { // iterační smyčka
// smyčka, ve které se provedou všechny transformace
for (k=0; k<maxTransf; k++) {
float xn=(*t)[k][0]*x+(*t)[k][1]*y+(*t)[k][4];
float yn=(*t)[k][2]*x+(*t)[k][3]*y+(*t)[k][5];
if (iter>threshold) { // je-li dosaženo hranice iterací
switch (drawType) { // výběr vykreslovacího režimu
case IterPutPixel:
putpixel(pix, xn*scale+xpos, yn*scale+ypos, rf ? 0xff:0x00, gf ? 0xff:0x00, bf ? 0xff:0x00);
break;
case IterAddPixel:
addpixel(pix, xn*scale+xpos, yn*scale+ypos, red, green, blue);
break;
case TransfPutPixel:
putpixel(pix, xn*scale+xpos, yn*scale+ypos, pal[k&7][0], pal[k&7][1], pal[k&7][2]);
break;
case TransfAddPixel:
addpixel(pix, xn*scale+xpos, yn*scale+ypos, (!!pal[k&7][0])*dr, (!!pal[k&7][1])*dg, (!!pal[k&7][2])*db);
break;
default:
break;
}
}
}
// nalezení jedné transformace pro další iteraci
// na základě pravděpodobnosti jednotlivých transformací
pp=((float)rand())/RAND_MAX; // p leží v rozsahu 0.0-1.0
k=0; // proměnná cyklu vyhledání transformace
sum=0;
while (sum<=pp) { // podle náhodného čísla
sum=sum+(*t)[k][6]; // vybrat transformaci
k++;
} // k určuje index transformace
k--; // úprava ze smyčky while
hlp=(*t)[k][0]*x+(*t)[k][1]*y+(*t)[k][4]; // provedení
y =(*t)[k][2]*x+(*t)[k][3]*y+(*t)[k][5]; // transformace
x =hlp; // a výpočet bodu pro další iteraci
}
} Obrázek 4: Screenshot druhého demonstračního příkladu
4. Algoritmus generování minima pixelů (MPA)
Zásadní problém všech předchozích metod určených pro generování fraktálního objektu pomocí systému iterovaných funkcí spočívá ve faktu, že se tyto algoritmy snaží konstruovat (generovat a následně zobrazit) výsledný fraktál přesně, zatímco ve skutečnosti je zapotřebí zobrazit jen určitou reprezentativní část fraktálu. Přesné zobrazení fraktálu je ve skutečnosti nereálné, protože by bylo zapotřebí provést nekonečné množství iterací, což není v konečném čase uskutečnitelné.
Vizuálně reprezentativní část fraktálu je konečná, to znamená, že je vytvořena pouze konečným počtem pixelů v ploše či bodů (částic, surfelů) v prostoru. To mimo jiné znamená, že tato část fraktálu může být vždy zobrazena v konečném čase. Zde popisovaný algoritmus pro generování minima pixelů/surfelů (MPA – Minimal Plotting Algorithm) je určen pro vytvoření reprezentativní části fraktálního objektu. Efektivita tohoto algoritmu spočívá ve faktu, že pracuje přímo s diskrétními pixely v E2 (či voxely v E3) a ne s bezrozměrnými body ve spojitém prostoru.
Obrázek 5: Obrázek IFS systému vytvořený v programu IFS Builder 3d
Bezrozměrný geometrický bod je nekonečně malý a může mít libovolné souřadnice. To znamená, že mezi dvěma body leží nekonečné množství dalších bodů, které mají odlišné souřadnice. Naproti tomu pixel či voxel má určitou konstantní velikost a leží v diskrétním prostoru. Mezi dvěma pixely leží pouze konečné množství pixelů. Stejné podmínky platí pro voxely ležící v diskrétním prostoru (voxel space).
Tento rozdíl mezi matematicky chápaným bodem a diskrétním pixelem je použit ve více algoritmech počítačové grafiky, například v algoritmu pro odstranění aliasu nebo při raytracingu. Použijeme ho i ve zde popisovaném algoritmu. Pro vizuální reprezentaci fraktálního objektu generovaného pomocí systému iterovaných funkcí je použitý buď diskrétní rastrový obraz (bitmapa či pixmapa), nebo pravidelná ekvidistantní prostorová mřížka, která představuje třírozměrnou variantu diskrétního obrazu.
V dalším textu budu pro jednoduchost popisovat plošnou variantu algoritmu, popisovaný postup je však možné použít i v prostoru. Jako pomocný datový typ bude sloužit fronta (queue), ve které budou uloženy adresy jednotlivých pixelů. V algoritmu MPA je ukládání adres pixelů do fronty méně paměťově náročné, než ukládání do zásobníku (stack), které bylo skrytě použito v rekurzivní verzi deterministického algoritmu DIA. Fronta také bude při běhu algoritmu průběžně vyprazdňována, kdežto zásobník byl nejprve (spolu s generováním bodů) naplňován a teprve poté proběhlo jeho vyprázdnění.
Algoritmus MPA se také liší od všech předešlých algoritmů v tom, že se počáteční polohy bodů nevybírají náhodně. Pro každou transformaci φi v IFS systému je nejprve vypočten pevný bod x0i, který je použit jako jeden z počátečních bodů. Adresy pevných bodů jsou uloženy do fronty, ze které jsou adresy postupně vybírány a poté jsou se souřadnicemi pixelů prováděny jednotlivé transformace. Na základě korespondence nově vypočtených adres pixelů s pixely již vykreslenými se může pixel buď vykreslit (a jeho adresa uložit do fronty), nebo být zahozen.
Další vlastností, která odlišuje algoritmus MPA od algoritmů RWA a DIA je, že se nemusí provádět počítání proběhlých iterací. Ukončení běhu algoritmu je signalizováno vyprázdněním fronty adres pixelů. Ta na počátku obsahuje pouze adresy pixelů odpovídajících pevným bodům jednotlivých transformací. Při průběhu jedné smyčky se může do fronty vložit až Nφ nových adres, maximální počet je však omezen celkovým počtem pixelů v rastrovém obrazu. Pro provedení algoritmu také není zapotřebí provádět výpočet pravděpodobností jednotlivých transformací, protože běh algoritmu je deterministický.
Obrázek 6: Obrázek IFS systému vytvořený v programu IFS Builder 3d
V symbolickém programovacím jazyce může být algoritmu MPA popsán následovně:
- Vstupy programu:
- Množina transformací Φ={φ1, φ2, … φn}, pomocí které je definovaný systém iterovaných funkcí. Množina pravděpodobností jednotlivých transformací není pro běh algoritmu MPA zapotřebí.
- Počet transformací v IFS systému Nφ.
- Výstup programu:
- Rastrový obrazec či prostorový objekt složený z množiny navzájem izolovaných bodů (pixelů či surfelů), který reprezentuje atraktor systému IFS.
- Inicializační sekvence:
- Najdi pevné body x0i pro všechny transformace φi.
- Vykresli pixely, které korespondují s těmito body.
- Proveď inicializaci fronty s pomocí adres vykreslených pixelů.
- Hlavní smyčka:
- Opakuj smyčku:
- Vyjmi adresu pixelu ze začátku fronty a převeď ji na souřadnice bodu P.
- Pro k probíhající od 1 do Nφ opakuj smyčku:
- Aplikuj transformaci φk na bod P a vypočti souřadnici bodu Pk.
- Zaokrouhli souřadnice bodu Pk tak, aby korespondoval s jedním pixelem.
- Pokud bod na dané souřadnici ještě nebyl vykreslen:
- Pak vykresli bod Pk a vlož adresu tohoto bodu na konec fronty.
- Konec vnitřní smyčky
- Opakuj vnější smyčku dokud fronta není prázdná.
- Konec programu
Obrázek 7: Obrázek IFS systému vytvořený v programu IFS Builder 3d
Velkou předností výše popsaného algoritmu MPA je, že se každý pixel na obrazovce vykreslí pouze jedenkrát. Pro jednou počítaný bod se také nebudou provádět žádné další transformace. Z výše uvedeného vyplývá, že algoritmus musí vždy skončit v konečném čase, neboť i v nejhorším případě se provede vygenerování pouze všech pixelů na obrazovce. Má-li tedy obrazovka rozlišení například 800 × 600 pixelů, provede se maximálně 800 × 600=480000 iterací.
Proto je tento algoritmus nejefektivnější, to znamená, že generuje výsledný fraktální obrazec s minimálním počtem bodů. Také paměťové nároky nejsou velké. Vedle bitmapy či pixmapy pro uložení rastrového obrazu je zapotřebí alokovat pouze frontu s adresami pixelů. Jedno místo ve frontě bude mít pro běžná rozlišení obrazovky velikost 4 byte, což není mnoho.
První nevýhodou tohoto algoritmu je nutnost hledat pro každý vypočítaný pixel jeho protějšek ve frontě, nebo v rastrovém obrazu. To zapříčiní zkomplikování výpočtů a tím i prodloužení celkové doby generování celého fraktálního obrazce.
Druhou nevýhodou je, že tento algoritmus je určen pouze pro generování obrazu celého fraktálu. Je-li zapotřebí vygenerovat pouze výřez z fraktálu, stává se tento algoritmus neefektivní, protože bude nutně počítat i body ležící mimo obrazovku. Tuto nevýhodu má i deterministický algoritmus DIA, u nějž také není možné efektivně generovat výřez z fraktálu.
Obrázek 8: Obrázek IFS systému vytvořený v programu IFS Builder 3d
5. Vzájemné porovnání algoritmů pro generování IFS fraktálů
Algoritmy pro generování fraktálních objektů pomocí systémů iterovaných funkcí je možné porovnávat podle více hledisek. V prvé řadě se musí uvažovat čas potřebný pro vygenerování IFS koláže, v řadě druhé se jedná o spotřebu paměti při běhu programu.
Z hlediska paměťových nároků je nejméně náročný (a současně implementačně nejjednodušší) algoritmus pro náhodnou procházku RWA, nebo jeho modifikovaná verze. Tyto algoritmy pracují přímo z výslednou bitmapou či prostorem s vygenerovanými body a jediná další potřebná paměťová struktura je poloha iterovaného bodu. Paměťově nejnáročnější je deterministický algoritmus DIA, zejména kvůli nutnosti vytváření množiny vygenerovaných bodů. Seřazení algoritmů pro generování IFS koláží podle paměťové složitosti je uvedeno v následující tabulce.
| Pořadí | Název algoritmu | Zkratka |
|---|---|---|
| 1 | Algoritmus pro náhodnou procházku | RWA |
| 2 | Modifikovaný algoritmus pro náhodnou procházku | M-RWA |
| 3 | Algoritmus pro generování minima pixelů | MPA |
| 4 | Deterministický algoritmus | DIA |
Z hlediska rychlosti generování fraktálních objektů je v mnoha případech nejvýkonnější algoritmus pro vykreslení minima pixelů MPA – viz též následující tabulka. Tento algoritmus má také tu přednost, že zaručeně vždy skončí v konečném čase. Proto je vhodný i pro kódování videa v případech, kdy je zadána nízká propustnost datového kanálu. Při nízkých bitových rychlostech se s tímto algoritmem dosahuje poměrně kvalitního videa, které stačí například pro provozování videotelefonů. Tato problematika však již přesahuje rámec těchto článků, proto ji zde nebudu dále rozvádět.
| Pořadí | Název algoritmu | Zkratka |
|---|---|---|
| 1 | Algoritmus pro generování minima pixelů | MPA |
| 2 | Deterministický algoritmus | DIA |
| 3 | Modifikovaný algoritmus pro náhodnou procházku | M-RWA |
| 4 | Algoritmus pro náhodnou procházku | RWA |
Jak vyplývá z předchozích dvou tabulek, není výběr nejvhodnější metody jednoznačný, neboť závisí na aplikaci, ve které se budou IFS koláže používat.
Obrázek 9: Obrázek IFS systému vytvořený v programu IFS Builder 3d
6. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování tohoto seriálu si popíšeme linearizované systémy iterovaných funkcí, které vznikají omezením afinních transformací; na druhou stranu je však pro jejich tvorbu možné použít interaktivní postupy a generovat tak velmi zajímavé obrázky, které se na první pohled odlišují od klasických IFS koláží.
Obrázek 10: Obrázek linearizovaného systému iterovaných funkcí