Obsah
1. Animace plasmy
2. První demonstrační příklad – animace plasmy
3. Jednorozměrná spektrální syntéza
4. Druhý demonstrační příklad – 1D spektrální syntéza
5. Dvourozměrná spektrální syntéza
6. Třetí demonstrační příklad – 2D spektrální syntéza
7. Obsah dalšího pokračování tohoto seriálu
1. Animace plasmy
V mnoha počítačových demech se často můžeme setkat s různými formami animované plasmy. Animace v tomto případě není představována ničím jiným než průběžnou změnou jednoho parametru či několika parametrů při procedurálním generování plasmy; volba logicky padá na takové parametry, které nevyžadují nový výpočet plasmy v každém kroku animace, to by totiž bylo časově velmi náročné, zejména na pomalejších počítačích (animovanou plasmu totiž můžeme vidět i na osmibitových počítačích – Atari, Commodore C64 apod.). V jednodušších případech (dema vzniklá v rozmezí cca 1990–1995) se dokonce setkáváme pouze s tím, že jsou přes sebe posouvány dva obrázky plasmy, přičemž dochází k součtu „barev“ jejich pixelů, nebo k operaci XOR mezi jednotlivými pixely.

Obrázek 1: Screenshot z dema „DrunkChessboard“ běžícího na Atari 800XL
Uvozovky v předchozí větě jsou zcela na místě, protože se většinou jedná o obrázky s barvovou paletou, takže jednotlivé pixely obsahují místo skutečné informace o barvě pouze index do barvové palety. Při požadavku na složitější efekty je možné měnit například koeficienty jednotlivých harmonických složek při spektrální syntéze plasmy (viz kapitolu 5), vždy si však musíme uvědomit, že v demech je nejdůležitější výsledný audiovizuální efekt, takže přesnost výpočtů či jejich naprostou matematickou korektnost není zapotřebí dodržet.

Obrázek 2: Další screenshot z dema „DrunkChessboard“ běžícího na Atari 800XL
2. První demonstrační příklad – animace plasmy
Dnešní první demonstrační příklad ukazuje, jakým způsobem přibližně vznikaly animované plasmy v některých počítačových demech datovaných okolo let 1990–1995. Animace tohoto typu je založena na vzájemném překrytí dvou stejných či naopak různých obrázků plasmy. Před vlastní animací je zapotřebí provést výpočet dvou obrázků plasmy. Tyto obrázky jsou při animacích přes sebe navzájem posunovány a indexy pixelů, jež leží přesně nad sebou, jsou sečítány s tím, že při přetečení hodnoty indexu přes 255 se začíná opět od nulové hodnoty (tomu musí odpovídat i použitá barvová paleta). Tuto operaci je možné provádět různým způsobem, nejjednodušeji tak, že se sčítají dvě bytové hodnoty s ignorováním přenosu. Další způsob spočívá ve využití instrukcí MMX, pomocí kterých lze spočítat hodnoty několika pixelů současně (typicky osmi pixelů) a to i s využitím sčítání se saturací, tj. bez přetečení.
Při praktické implementaci se nemusí sčítání pixelů provádět ručně, ale je možné využít blendingu podporovaného grafickou knihovnou OpenGL (v některých případech však může být programový výpočet výhodnější, například při požadavku na speciální efekty). V tomto demonstračním příkladu jsou nejprve vypočteny dva obrázky plasmy a ty jsou v pravidelných časových intervalech překresleny přes sebe s nastavenou směšovací funkcí. To ve svém důsledku vede k efektu postupného míchání obou obrázků.
Obrázek 3: Screenshot prvního demonstračního příkladu
Zdrojový kód prvního demonstračního příkladu je dostupný jak ve formě zdrojového textu, tak i jako HTML stránka s obarvenou syntaxí. Pomocí kláves [0] až [8] je možné ovlivnit funkci, která se používá při míchání obou obrázků plasmy (první čtyři klávesy nastavují zdrojový faktor, druhé čtyři klávesy faktor cílový). Klávesa [S] slouží k zastavení a znovuspuštění animace a konečně klávesa [Q] či [Esc] celý demonstrační příklad ukončí.
Funkce, která je cyklicky volána pro vytváření animace, má následující tvar:
//-----------------------------------------------------------------------------
// Tato callback funkce je zavolána při každém překreslení okna. Okno je
// pravidelně překreslováno z uživatelského časovače.
//-----------------------------------------------------------------------------
void onDisplay(void)
{
#define RADIUS 100.0 // poloměr kružnice, po kterých se obrázky pohybují
int x1, y1, x2, y2;
glClear(GL_COLOR_BUFFER_BIT); // vymazání všech bitových rovin barvového bufferu
glDrawBuffer(GL_BACK); // pixmapa se bude kreslit do zadního barvového bufferu
x1=RADIUS+RADIUS*cos(t/10.0); // pozice první pixmapy
y1=RADIUS+RADIUS*sin(t/7.0);
x2=RADIUS+RADIUS*sin(t/11.0); // pozice druhé pixmapy
y2=RADIUS+RADIUS*cos(t/13.0);
glEnable(GL_SCISSOR_TEST); // ořezání vykreslování
glScissor(RADIUS*2, RADIUS*2, PIXMAP_WIDTH, PIXMAP_HEIGHT);
glRasterPos2i(x1, y1); // nastavení souřadnic levého spodního rohu první pixmapy
drawPixmap(pix1); // vykreslení první pixmapy
glEnable(GL_BLEND);
glBlendFunc(blendSrc[src], blendDst[dst]); // povolení a nastavení míchací funkce
glRasterPos2i(x2, y2); // nastavení souřadnic levého spodního rohu druhé pixmapy
drawPixmap(pix2); // vykreslení druhé pixmapy
glDisable(GL_BLEND); // zákaz použití míchací funkce
glDisable(GL_SCISSOR_TEST); // zákaz ořezávání
drawInfo(x1, y1, x2, y2); // průběžný výpis informací o animaci a jejích parametrech
glFlush(); // provedení a vykreslení všech změn
glutSwapBuffers();
}
3. Jednorozměrná spektrální syntéza
V předchozích částech tohoto seriálu jsme si ukázali, jakým způsobem je možné vytvářet stochastickou jednorozměrnou (z hlediska topologické dimenze) křivku s fraktální charakteristikou pomocí metody náhodného přesouvání prostředního bodu (Midpoint Displacement Method). Dnes si ukážeme metodu zcela odlišnou, která spočívá v provádění spektrální syntézy (Spectral Synthesis), což je postup založený na známé a v mnoha oborech často používané Fourierově transformaci, přesněji řečeno na inverzní (zpětné) Fourierově transformaci.
Obrázek 4: Spektrální syntéza, jejímž výsledkem je stochastická jednorozměrná křivka s fraktální dimenzí rovnou 1,5.
Celá myšlenka spektrální syntézy je postavena na důležitém faktu, že pro požadovanou fraktální dimenzi stochastického fraktálu (v našem případě jednorozměrné křivky) je možné nalézt spektrální hustotu jejich Fourierova obrazu. Jestliže známe spektrální hustotu, můžeme k ní nalézt koeficienty Ak a Bk a provést s nimi inverzní (zpětnou) diskrétní Fourierovu transformaci:
X(t)=∑(Akcos(kt)+Bksin(kt))
Jakým způsobem však můžeme na základě požadované fraktální dimenze získat koeficienty Ak a Bk? Pro funkci x(t) definovanou na intervalu (0,T) je možné nalézt její Fourierův obraz X(u) pomocí výpočetní metody, kterou znají prakticky všichni elektronici. Spektrální hustotu S(f) Fourierova obrazu X(u) lze vypočítat pomocí limity:
S(f)=lim 1/T |X(u)|2 (pro T jdoucí k nekonečnu)
Spektrální hustota je opět pojem známý z elektroniky; jedná se o veličinu používanou při zpracování signálů a návrhu různých filtrů. Pro zlomkovitý Brownův pohyb je možné dokázat, že spektrální hustota je úměrná hodnotě 1/fβ:
S(f)~1/fβ
Ve výše uvedeném vztahu je koeficient β, který může nabývat hodnot od jedné do tří, svázán s minule popisovaným Hurstovým koeficientem rovností:
β=2H+1
Vzhledem k tomu, že z minula již víme, že fraktální dimenzi je možné na základě Hurstova exponentu vypočítat dle vzorce:
D=2-H
dojdeme po dosazení a úpravě zlomku ke vztahu:
D=(5-β)/2
To znamená, že pro požadovanou fraktální dimenzi D je možné vypočítat koeficient β a s jeho pomocí pak spektrální hustotu, která musí odpovídat hodnotě 1/fβ. Už jsme si ukázali vztah pro inverzí Fourierovu transformaci:
X(t)=∑(Akcos(kt)+Bksin(kt))
Fourierovy obrazy požadované spektrální hustoty je možné získat generováním náhodných koeficientů Ak a Bk tak, aby vyhovovaly vztahu:
E(Ak2+Bk2)~1/(kβ)
Konkrétní postup pro výpočet koeficientů Ak a Bk je uveden v následující kapitole.
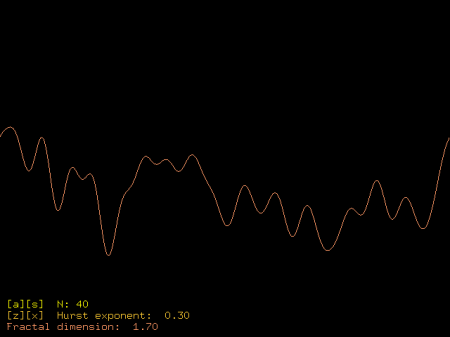
Obrázek 5: Stochastická jednorozměrná křivka s fraktální dimenzí rovnou 1,7.
4. Druhý demonstrační příklad – 1D spektrální syntéza
Dnešní druhý demonstrační příklad je určený pro vykreslení jednorozměrné stochastické křivky s fraktální charakteristikou a fraktální dimenzí, která se pohybuje v rozsahu 1,0..2,0. Po překladu a spuštění tohoto demonstračního příkladu se otevře jediné okno programu a do něj se vykreslí křivka. Program posléze čeká na modifikaci parametrů ovlivňujících tvar křivky. Pomocí kláves [A] a [S] je možné měnit počet koeficientů zpětné Fourierovy transformace v rozsahu 2..50, klávesy [Z] a [X] slouží k určení Hurstova koeficientu a tím i fraktální dimenze vytvořené křivky (ta může nabývat hodnot z rozsahu 1,0..2,0). Všechny parametry se vypisují ve spodní části okna. Aplikaci je možné ukončit stiskem klávesy [Q] nebo [Esc]. Zdrojový kód druhého demonstračního příkladu je dostupný jak ve formě zdrojového textu, tak i jako HTML stránka s obarvenou syntaxí.
Obrázek 6: Screenshot druhého demonstračního příkladu
Mezi nejdůležitější funkce, které jsou ve druhém demonstračním příkladu využity, patří funkce sloužící k vygenerování náhodného čísla v rozsahu 0..1 s přibližným Gaussovým rozložením, která má tvar:
//---------------------------------------------------------
// Vygenerování náhodného čísla v rozsahu 0..1
// s přibližným Gaussovým rozložením
//---------------------------------------------------------
float randomGauss(void)
{
#define N 10
float sum=0.0;
int i;
for (i=0; i<N; i++)
sum+=(float)rand()/(float)RAND_MAX;
return sum/N;
} Dále je zde použita funkce pro vygenerování náhodného čísla v rozsahu 0..1 s rovnoměrným rozložením. Tato funkce pro svoji činnost využívá standardní céčkovskou knihovní funkci rand():
//---------------------------------------------------------
// Vygenerování náhodného čísla v rozsahu 0..1
// s rovnoměrným rozložením
//---------------------------------------------------------
float randomN(void)
{
return (float)rand()/(float)RAND_MAX;
} Vlastní implementaci spektrální syntézy zajišťuje v dnešním druhém demonstračním příkladu funkce spectralSynthesis1D(), ve které jsou nejdříve vypočteny koeficienty Ak a Bk a tyto koeficienty jsou posléze použity při inverzí Fourierově transformaci:
//---------------------------------------------------------
// Spektrální syntéza v 1D
//---------------------------------------------------------
void spectralSynthesis1D(void)
{
#define PI 3.1415927
float A[n/2]; // koeficienty Ak
float B[n/2]; // koeficienty Bk
float beta=2.0*h+1; // proměnná svázaná s Hurstovým koeficientem
int i, j, k; // počitadla smyček
srand(123456); // zajištění, aby se vždy generovala
// stejná posloupnost náhodných čísel
glBegin(GL_LINE_STRIP);
// výpočet koeficientů Ak a Bk
for (i=0; i<n/2; i++) {
float rad=pow((i+1), -beta/2.0)*randomGauss();
float phase=2.0*PI*randomN();
A[i]=rad*cos(phase);
B[i]=rad*sin(phase);
// kontrolní výpis koeficientů
printf("%d\t%f\t%f\n", i, A[i], B[i]);
}
// vykreslení funkce přes celé okno aplikace
for (j=0; j<width; j++) {
float x=j;
float y=0;
for (k=0; k<n/2; k++) {
// horizontální vyrovnání funkce na střed okna
float t=(j-n/2)*2.0*PI/width;
// koeficient pro k-tou harmonickou
y+=A[k]*cos(k*t)+B[k]*sin(k*t);
}
// vertikální vyrovnání funkce
// na střed okna a změna amplitudy
glVertex2f(x, height/2.0+(height/4.0)*y);
}
glEnd();
}
5. Dvourozměrná spektrální syntéza
Spektrální syntéza je mimořádně vhodná pro použití v počítačové grafice, a to zejména z toho důvodu, že je ji možné rozšiřovat do více dimenzí (rozměrů). Prozatím jsme si ukazovali jednorozměrný příklad, jehož výsledkem byla křivka. Rozšíření do dvou dimenzí je jednoduché – výsledkem bude obrázek plasmy a/nebo trojrozměrné výškové pole, které může představovat například model krajiny. Při použití tří dimenzí dostaneme jako výsledek trojrozměrnou mřížku, ve které jednotlivé objemové elementy (voxely) mohou představovat například hustotu prostoru v místě jejich výskytu. Tuto hustotu je posléze možné použít při generování reálně vypadajících modelů trojrozměrných oblak – to je velký rozdíl oproti oblakům vytvořených jako dvourozměrné textury, jejichž „dvojrozměrnost“ je při některých projekcích patrná.

Obrázek 7: Plasma vytvořená pomocí třetího demonstračního příkladu pro N=4 a H=0,5
V případě dvourozměrné spektrální syntézy je fraktální dimenze výsledného obrázku rovna:
D=3-H
Přičemž hodnota Hurstova exponentu se pohybuje v rozsahu 0,0..1,0. Z toho vyplývá, že fraktální dimenze výsledné plasmy se pohybuje v rozsahu 2,0..3,0.
Oproti jednorozměrnému případu nastává rozdíl v tom, že je zapotřebí vypočítat koeficienty Akl a Bkl, které tvoří dvourozměrné pole. Pomocí těchto koeficientů je následně s využitím inverzní diskrétní Fourierovy transformace vypočten požadovaný obrázek plasmy:
X(x,y)=∑∑(Aklcos(kx+ly)+Bklsin(kx+ly))
Konkrétní implementace výpočtů bude uvedena v následující kapitole.

Obrázek 8: Plasma vytvořená pomocí třetího demonstračního příkladu pro N=8 a H=0,5
6. Třetí demonstrační příklad – 2D spektrální syntéza
V dnešním třetím a současně i posledním demonstračním příkladu je ukázána praktická implementace spektrální syntézy v rovině E2. Výsledkem výpočtů je dvourozměrný obrázek plasmy zobrazený na ilustračních obrázcích 7 – 10. Po překladu a spuštění třetího demonstračního příkladu se otevře jediné okno aplikace, do kterého je vykreslen obrázek plasmy o rozlišení 256×256 pixelů ve stupních šedi. Pomocí kláves [A] a [S] je možné měnit počet koeficientů zpětné Fourierovy transformace v rozsahu 2..50, klávesy [Z] a [X] slouží k určení Hurstova koeficientu a tím i (nepřímo) fraktální dimenze vytvořené křivky v požadovaném rozsahu 2,0..3,0. Aplikaci je možné ukončit stiskem klávesy [Q] nebo [Esc]. Zdrojový kód druhého demonstračního příkladu je dostupný jak ve formě zdrojového textu, tak i jako HTML stránka s obarvenou syntaxí.

Obrázek 9: Screenshot třetího demonstračního příkladu
Vlastní výpočet plasmy probíhá ve funkci spectralSynthesis2D(), která má tvar:
//-----------------------------------------------------------------------------
// Spektrální syntéza v 2D
//-----------------------------------------------------------------------------
void spectralSynthesis2D(void)
{
#define PI 3.1415927
float bitmap[PIXMAP_HEIGHT][PIXMAP_WIDTH];
float min=1e10, max=-1e10; // proměnné použité pro přepočet intenzit pixelů
float fmin=1e10, fmax=-1e10; // proměnné použité pro přepočet intenzit pixelů
float A[n/2][n/2]; // koeficienty A_kl
float B[n/2][n/2]; // koeficienty B_kl
float beta=2.0*h+1; // proměnná svázaná s Hurstovým koeficientem
// pomocí vztahu beta=2H+1
int i, j, k, l; // počitadla smyček
for (j=0; j<PIXMAP_HEIGHT; j++) // vymazání pracovní bitmapy
for (i=0; i<PIXMAP_WIDTH; i++)
bitmap[j][i]=0.0;
srand(123456); // zajištění, aby se vždy generovala
// stejná posloupnost náhodných čísel
for (j=0; j<n/2; j++) { // výpočet koeficientů A_kl a B_kl
for (i=0; i<n/2; i++) {
float rad_i=pow((i+1), -beta/2.0)*randomGauss();
float rad_j=pow((j+1), -beta/2.0)*randomGauss();
float phase_i=2.0*PI*randomN();
float phase_j=2.0*PI*randomN();
A[j][i]=rad_i*cos(phase_i)*rad_j*cos(phase_j);
B[j][i]=rad_i*sin(phase_i)*rad_j*sin(phase_j);
}
}
for (j=0; j<PIXMAP_HEIGHT; j++) { // generování plasmy pro všechny
for (i=0; i<PIXMAP_WIDTH; i++) { // pixely pracovní bitmapy
float z=0;
for (k=0; k<n/2; k++) { // inverzní Fourierova transformace
for (l=0; l<n/2; l++) {
float u=(i-n/2)*2.0*PI/PIXMAP_WIDTH; // transformace na
float v=(j-n/2)*2.0*PI/PIXMAP_HEIGHT; // střed obrázku
z+=A[k][l]*cos(k*u+l*v)+B[k][l]*sin(k*u+l*v); // jeden člen IDFT
}
}
bitmap[j][i]=z; // zápis výsledku do bitmapy
}
}
// získání statistiky o vytvořeném rastrovém obrázku
for (j=0; j<PIXMAP_HEIGHT; j++)
for (i=0; i<PIXMAP_WIDTH; i++) {
if (max<bitmap[j][i]) max=bitmap[j][i];
if (min>bitmap[j][i]) min=bitmap[j][i];
}
// výpis zjištěných informací o rastrovém obrázku
printf("min=%f\nmax=%f\n", min, max);
// změna kontrastu a kopie bitmapy
for (j=0; j<PIXMAP_HEIGHT; j++)
for (i=0; i<PIXMAP_WIDTH; i++) {
float f=bitmap[j][i];
f-=min;
f*=255.0/(max-min);
if (fmin>f) fmin=f;
if (fmax<f) fmax=f;
putpixel(pix, i, j, (int)f, (int)f, (int)f);
}
// výpis koeficientů použitých při změně kontrastu
printf("fmin=%f\nfmax=%f\n", fmin, fmax);
} 
Obrázek 10: Další plasma vzniklá pomocí třetího demonstračního příkladu pro N=36 a H=0,5
7. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování tohoto seriálu si konečně ukážeme, jakým způsobem se prakticky vytváří trojrozměrné modely krajiny pomocí obrázků plasmy, a to jak plasmy generované metodou náhodného přesouvání prostředního bodu, tak i plasmy vytvořené spektrální syntézou.