Obsah
1. FAISS: knihovna pro rychlé a efektivní vyhledávání podobných vektorů (2. část)
2. Vizualizace koncových bodů vektorů v rovině
3. Vykreslení nejpodobnějších vektorů získaných na základě L2 metriky
4. Úplný zdrojový kód druhého demonstračního příkladu
6. Úplný zdrojový kód třetího demonstračního příkladu
7. Vliv normalizace vektorů při vyhledávání na základě skalárního součinu
8. Úplný zdrojový kód čtvrtého demonstračního příkladu
9. Vykreslení nejpodobnějších vektorů před jejich normalizací
10. Úplný zdrojový kód pátého demonstračního příkladu
11. Vykreslení vektorů formou orientovaných šipek
12. Úplný zdrojový kód pátého demonstračního příkladu
13. Vykreslení vektorů po jejich normalizaci formou orientovaných šipek
14. Úplný zdrojový kód šestého demonstračního příkladu
15. Vyhledání a vykreslení nejvíce NEpodobných vektorů
16. Úplný zdrojový kód sedmého demonstračního příkladu
17. Datové typy prvků vektorů: float32, float16 a bfloat16
18. Benchmark: porovnání rychlosti vyhledávání vektorů s prvky typu float16 a float32
19. Repositář s demonstračními příklady
1. FAISS: knihovna pro rychlé a efektivní vyhledávání podobných vektorů (2. část)
Na úvodní článek o knihovně FAISS dnes navážeme. Zabývat se přitom budeme sice na první pohled relativně snadnou otázkou, která však má několik odpovědí – které vektory považujeme za podobné a které nikoli. Odpověď pochopitelně do značné míry závisí na tom, jakou metriku při porovnávání vektorů použijeme. Z mnoha teoreticky použitelných metrik se nejčastěji využívá metrika L2 a taktéž metrika založená na výpočtu skalárního součinu normalizovaných vektorů. Dnes si na několika demonstračních příkladech vysvětlíme, jakým způsobem se tyto metriky od sebe odlišují, proč musí být vektory normalizovány (při použití skalárního součinu) i to, jakým způsobem je možné nalézt vektory, které se od zadaného vektoru nejvíce odlišují.
2. Vizualizace koncových bodů vektorů v rovině
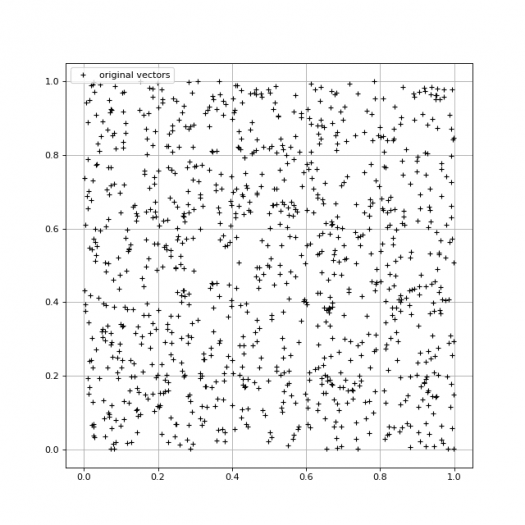
Ve všech demonstračních příkladech, s nimiž se postupně seznámíme v dnešním článku, budeme nějakým způsobem vizualizovat dvoudimenzionální vektory v rovině. K dispozici máme dvě základní metody. Buď vykreslíme pouze koncové body vektorů a nebo vektory vykreslíme formou orientovaných šipek. Podívejme se nejdříve na první z těchto způsobů, protože je jednodušší a navíc nám umožní vykreslení i několika tisíc vektorů. K vizualizaci pro jednoduchost použijeme knihovnu Matplotlib s jejímiž (některými) možnostmi jsme se seznámili v článku Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib.
Nejprve si necháme vygenerovat N vektorů s DIMENSIONS dimenzemi (přičemž DIMENSIONS=2):
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
Výsledkem bude dvourozměrná matice se dvěma sloupci a N řádky. První sloupec obsahuje x-ové souřadnice, sloupec druhý pak souřadnice y-ové. Takové body lze s využitím Matplotlibu vykreslit snadno:
# vykreslení všech náhodně vygenerovaných bodů plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5)
Do grafu přidáme legendu (popisek, razítko), mřížku a graf si necháme vykreslit a popř. i uložit do souboru:
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-9.png")
# zobrazení grafu
plt.show()
Výsledek může vypadat následovně:
Úplný zdrojový kód skriptu:
# Knihovna FAISS
#
# - vizualizace koncových bodů vektorů v rovině
import numpy as np
import matplotlib.pyplot as plt
DIMENSIONS=2
N=1000
K=100
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
# velikost grafu
plt.figure(figsize=(8, 8), dpi=80)
# vykreslení všech náhodně vygenerovaných bodů
plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5)
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-9.png")
# zobrazení grafu
plt.show()
3. Vykreslení nejpodobnějších vektorů získaných na základě L2 metriky
V dalším kroku v grafu zvýrazníme ty vektory, které jsou nejpodobnější zadanému vstupnímu vektoru. Podobnost bude rozpoznávána na základě standardní L2 metriky, což znamená, že se vlastně získá sekvence vektorů, jejichž koncové body jsou nejblíže zadanému vektoru. Opět budeme pracovat v rovině, tj. konstanta DIMENSIONS bude nastavena na hodnotu 2.
V prvním kroku vytvoříme množinu N dvoudimenzionálních vektorů a zkonstruujeme z nich index založený na již zmíněné metrice L2:
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
# konstrukce indexu pro vyhledávání na základě vzdáleností
index = faiss.IndexFlatL2(DIMENSIONS)
index.add(vectors)
Dále v této množině nalezneme K vektorů, jejichž koncové body jsou nejblíže koncovému bodu vektoru query_vector:
# najít K nejbližších vektorů distances, indices = index.search(query_vector, K)
Vykreslení grafu bude nyní probíhat ve třech krocích:
- Vykreslení původní množiny náhodných vektorů
- Vykreslení nejpodobnějších vektorů odlišnou barvou (původní vektory resp. jejich koncové body se překreslí)
- Vykreslení zvýrazněného koncového bodu vektoru query_vector
Vykreslení bude probíhat následovně:
# vykreslení všech náhodně vygenerovaných bodů plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5) # vykreslení nejbližších bodů xs = vectors[:,0][indices][0] ys = vectors[:,1][indices][0] plt.plot(xs, ys, "+r", label="nearest vectors", markersize=5) # vykreslení koncového bodu vektoru, ke kterému hledáme K nejbližších vektorů x = query_vector[0][0] y = query_vector[0][1] plt.plot(x, y, "ob", label="query vector", markersize=10)
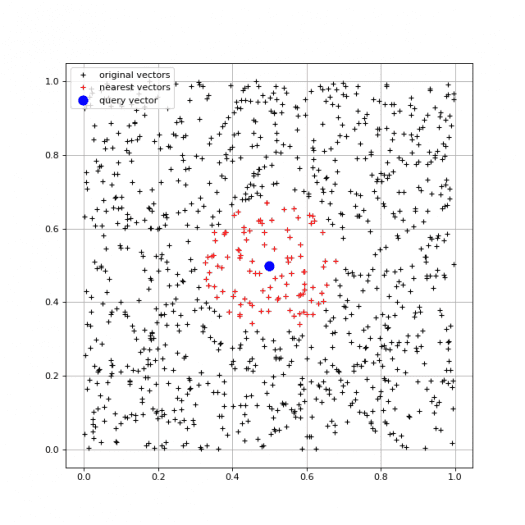
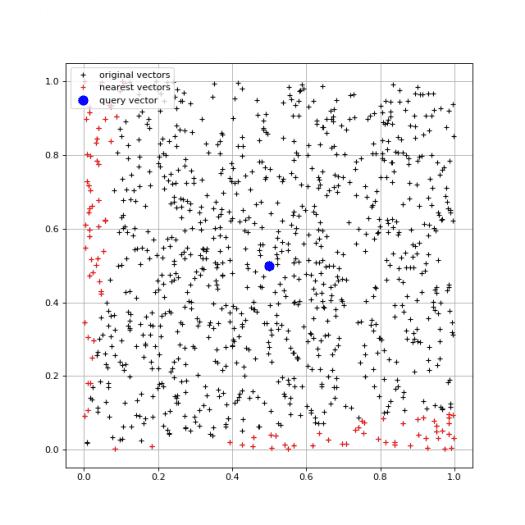
A takto by mohl vypadat výsledek:
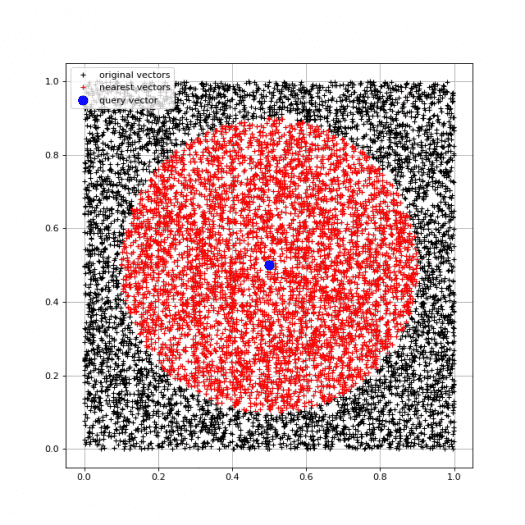
Obrázek 3: Na tomto grafu je zobrazeno 10000 koncových bodů vektorů, přičemž 5000 z nich je zvýrazněno, protože jsou nejpodobnější vektoru s koncovým bodem [0.5, 0.5]
4. Úplný zdrojový kód druhého demonstračního příkladu
Úplný zdrojový kód demonstračního příkladu, který po svém spuštění vykreslí koncové body tisícovky vektorů s vyznačením jednoho sta vektorů, které se nejvíce podobají vektoru [0.5, 0.5], vypadá následovně. Celkový počet vektorů je možné ovlivnit hodnotou konstanty N, počet nejpodobnějších vektorů pak konstantou K:
# Knihovna FAISS
#
# - vykreslení nejpodobnějších vektorů získaných na základě L2 metriky
# - vektory nejsou normalizovány
import faiss
import numpy as np
import matplotlib.pyplot as plt
DIMENSIONS=2
N=1000
K=100
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
# konstrukce indexu pro vyhledávání na základě vzdáleností
index = faiss.IndexFlatL2(DIMENSIONS)
index.add(vectors)
# vektor, ke kterému budeme počítat vzdálenost
query_vector = np.array([[0.5, 0.5]]).astype("float32")
# najít K nejbližších vektorů
distances, indices = index.search(query_vector, K)
# --- graf ---
# velikost grafu
plt.figure(figsize=(8, 8), dpi=80)
# vykreslení všech náhodně vygenerovaných bodů
plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5)
# vykreslení nejbližších bodů
xs = vectors[:,0][indices][0]
ys = vectors[:,1][indices][0]
plt.plot(xs, ys, "+r", label="nearest vectors", markersize=5)
# vykreslení koncového bodu vektoru, ke kterému hledáme K nejbližších vektorů
x = query_vector[0][0]
y = query_vector[0][1]
plt.plot(x, y, "ob", label="query vector", markersize=10)
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-A.png")
# zobrazení grafu
plt.show()
5. Nalezení nejpodobnějších vektorů získaných na základě skalárního součinu: varianta s nenormovanými vektory
Pokusme se nyní vyhledat nejpodobnější vektory nikoli na základě metriky L2, ale podle hodnoty skalárního součinu vektoru query_vector s vektory z původní množiny. Pro tento účel upravíme zdrojový kód provádějící konstrukci indexu do následující podoby:
# konstrukce indexu pro vyhledávání na základě skalárního součinu index = faiss.IndexFlatIP(DIMENSIONS) index.add(vectors)
Zbytek demonstračního příkladu, tj. vykreslení koncových bodů náhodných vektorů, nejpodobnějších vektorů a taktéž koncového bodu vektoru query_vector, zůstane naprosto stejný:
# vykreslení všech náhodně vygenerovaných bodů plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5) # vykreslení nejbližších bodů xs = vectors[:,0][indices][0] ys = vectors[:,1][indices][0] plt.plot(xs, ys, "+r", label="nearest vectors", markersize=5) # vykreslení koncového bodu vektoru, ke kterému hledáme K nejbližších vektorů x = query_vector[0][0] y = query_vector[0][1] plt.plot(x, y, "ob", label="query vector", markersize=10)
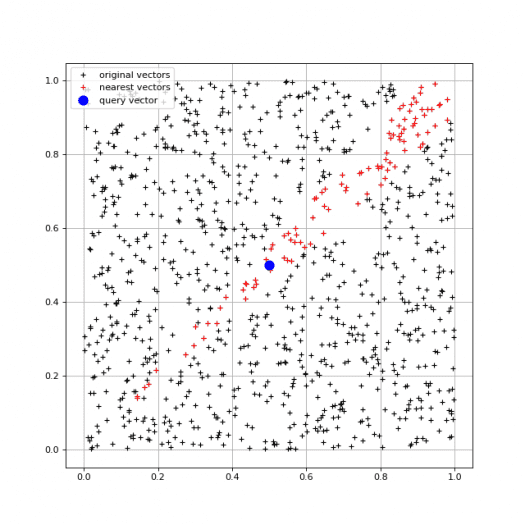
Výsledky ovšem v tomto případě budou zcela odlišné, protože nejpodobnější vektory nyní ani zdaleka nebudou vektory „nejbližšími“. To je zcela jasně patrné z grafu, který je skriptem vykreslen:
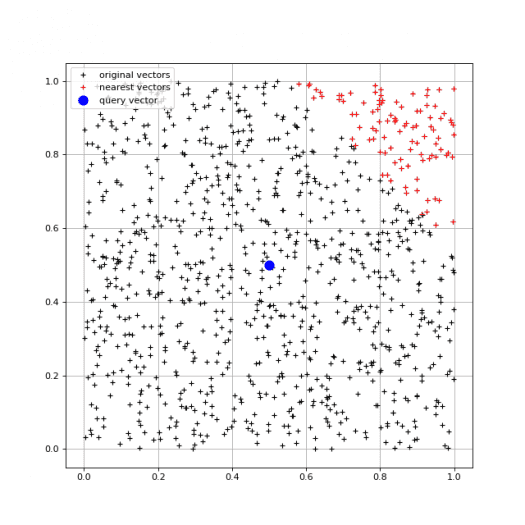
Obrázek 4: Nalezení nejpodobnějších vektorů získaných na základě skalárního součinu: varianta s nenormovanými vektory
6. Úplný zdrojový kód třetího demonstračního příkladu
Úplný zdrojový kód dnešního třetího demonstračního příkladu, který po svém spuštění nejpodobnější vektory na základě skalárního součinu, vypadá takto:
# Knihovna FAISS
#
# - vykreslení nejpodobnějších vektorů získaných na základě skalárního součinu
# - vektory nejsou normalizovány
import faiss
import numpy as np
import matplotlib.pyplot as plt
DIMENSIONS=2
N=1000
K=100
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
# konstrukce indexu pro vyhledávání na základě skalárního součinu
index = faiss.IndexFlatIP(DIMENSIONS)
index.add(vectors)
# vektor, ke kterému budeme počítat vzdálenost
query_vector = np.array([[0.5, 0.5]]).astype("float32")
# najít K nejbližších vektorů
distances, indices = index.search(query_vector, K)
# --- graf ---
# velikost grafu
plt.figure(figsize=(8, 8), dpi=80)
# vykreslení všech náhodně vygenerovaných bodů
plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5)
# vykreslení nejbližších bodů
xs = vectors[:,0][indices][0]
ys = vectors[:,1][indices][0]
plt.plot(xs, ys, "+r", label="nearest vectors", markersize=5)
# vykreslení koncového bodu vektoru, ke kterému hledáme K nejbližších vektorů
x = query_vector[0][0]
y = query_vector[0][1]
plt.plot(x, y, "ob", label="query vector", markersize=10)
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-B.png")
# zobrazení grafu
plt.show()
7. Vliv normalizace vektorů při vyhledávání na základě skalárního součinu
Již minule jsme si řekli, že aby vyhledávání podobných vektorů na základě skalárního součinu dávalo korektní výsledky, musí být vektory normalizovány. Přitom je nutné normalizovat jak vektory vkládané do indexu, tak i query_vector, tj. vektor, k němuž hledáme jemu nejpodobnější vektory z indexu.
Normalizaci je možné v praxi realizovat různými způsoby (některé nabízí přímo knihovna Numpy atd.), ovšem můžeme ji provést i „ručně“, tj. například následujícím kódem, který postupně nahradí všechny nenormalizované vektory jejich normalizovanými variantami:
# normalizace vektorů for i in range(len(vectors)): vector = vectors[i] normalized = np.linalg.norm(vector) vector /= normalized vectors[i] = vector
Stejným způsobem můžeme provést normalizaci vektoru query_vector:
# vektor, ke kterému budeme počítat vzdálenost query_vector = np.array([[0.5, 0.5]]) normalized = np.linalg.norm(query_vector) query_vector /= normalized
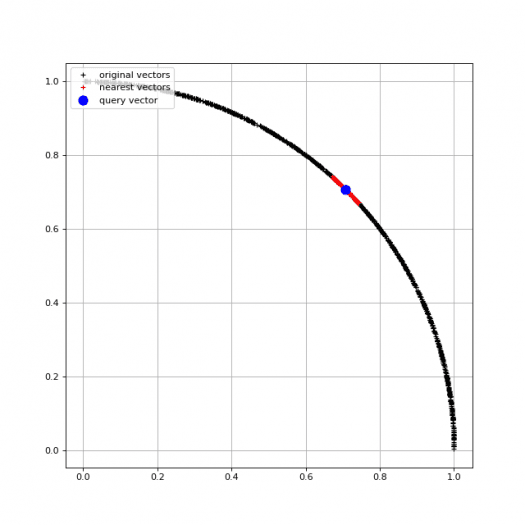
Nyní by mělo být z výsledného grafu patrné, že se skutečně našly nejpodobnější vektory, což v případě vektorů normalizovaných (jejich koncové body leží na jednotkové kružnici) znamená vektory s podobnými směrnicemi. Všechny tyto podobné vektory (červené značky) tedy nalezneme nalevo a napravo od query_vectoru (modrá tečka):
8. Úplný zdrojový kód čtvrtého demonstračního příkladu
Úplný zdrojový kód dnešního čtvrtého demonstračního příkladu, který po svém spuštění vyhledá a vykreslí nejpodobnější normalizované vektory na základě skalárního součinu, vypadá následovně:
# Knihovna FAISS
#
# - vykreslení nejpodobnějších vektorů získaných na základě skalárního součinu
# - vektory jsou normalizovány
import faiss
import numpy as np
import matplotlib.pyplot as plt
DIMENSIONS=2
N=1000
K=100
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
# normalizace vektorů
for i in range(len(vectors)):
vector = vectors[i]
normalized = np.linalg.norm(vector)
vector /= normalized
vectors[i] = vector
# konstrukce indexu pro vyhledávání na základě skalárního součinu
index = faiss.IndexFlatIP(DIMENSIONS)
index.add(vectors)
# vektor, ke kterému budeme počítat vzdálenost
query_vector = np.array([[0.5, 0.5]])
normalized = np.linalg.norm(query_vector)
query_vector /= normalized
# najít K nejbližších vektorů
distances, indices = index.search(query_vector, K)
# --- graf ---
# velikost grafu
plt.figure(figsize=(8, 8), dpi=80)
# vykreslení všech náhodně vygenerovaných bodů
plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5)
# vykreslení nejbližších bodů
xs = vectors[:,0][indices][0]
ys = vectors[:,1][indices][0]
plt.plot(xs, ys, "+r", label="nearest vectors", markersize=5)
# vykreslení koncového bodu vektoru, ke kterému hledáme K nejbližších vektorů
x = query_vector[0][0]
y = query_vector[0][1]
plt.plot(x, y, "ob", label="query vector", markersize=10)
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-C.png")
# zobrazení grafu
plt.show()
9. Vykreslení nejpodobnějších vektorů před jejich normalizací
Nyní si předchozí demonstrační příklad nepatrně upravíme. Budeme sice stále hledat nejpodobnější vektory s využitím skalárního součinu (aplikovaného na normalizované vektory – což je jediný korektní způsob), ovšem vykreslovat budeme vektory původní, tj. ještě před jejich normalizací. To si vyžádá určité zásahy do zdrojového kódu.
Normalizace vektorů z matice vectors do nové matice pojmenované normalized (kopie původní matice je ovšem poměrně nešťastný trik):
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
normalized = np.matrix.copy(vectors)
# normalizace vektorů
for i in range(len(vectors)):
vector = vectors[i]
norm = np.linalg.norm(vector)
normalized[i] = vector / norm
Index bude zkonstruován na základě normalizovaných vektorů:
# konstrukce indexu pro vyhledávání na základě skalárního součinu index = faiss.IndexFlatIP(DIMENSIONS) index.add(normalized)
I query_vector bude mít svoji normalizovanou podobu uloženou do proměnné normalized_query_vector:
# vektor, ke kterému budeme počítat vzdálenost query_vector = np.array([[0.5, 0.5]]) norm = np.linalg.norm(query_vector) normalized_query_vector = query_vector / norm
Vykreslovat ovšem budeme původní varianty vektorů – viz podtržené části kódu:
# vykreslení všech náhodně vygenerovaných bodů plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5) # vykreslení nejbližších bodů xs = vectors[:,0][indices][0] ys = vectors[:,1][indices][0] plt.plot(xs, ys, "+r", label="nearest vectors", markersize=5) # vykreslení koncového bodu vektoru, ke kterému hledáme K nejbližších vektorů x = query_vector[0][0] y = query_vector[0][1] plt.plot(x, y, "ob", label="query vector", markersize=10)
Z vizualizovaných výsledků je patrné, že nejpodobnější jsou takové vektory, které mají směrnici blízkou vektoru query_vector, ovšem zcela se ignoruje vzdálenost koncových bodů (ta nemá na výsledky vyhledání žádný vliv):
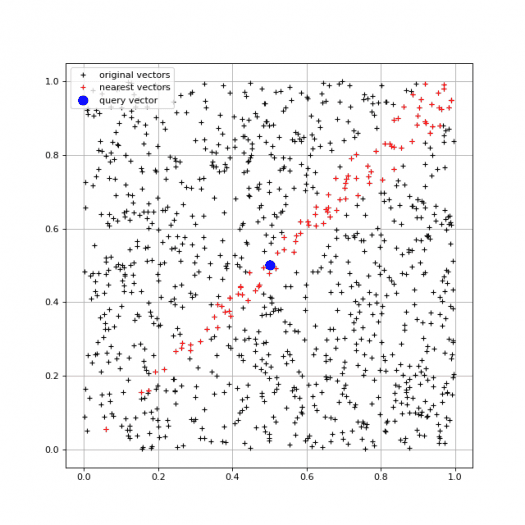
Obrázek 6: Nejpodobnější vektory nalezené s využitím skalárního součinu jejich normalizovaných variant.
10. Úplný zdrojový kód pátého demonstračního příkladu
Úplný zdrojový kód dnešního pátého demonstračního příkladu, který po svém spuštění vykreslí nejpodobnější nejpodobnější vektory v jejich původní (nenormalizované) podobě na základě skalárního součinu, vypadá následovně:
# Knihovna FAISS
#
# - vykreslení nejpodobnějších vektorů získaných na základě skalárního součinu
# - vektory jsou normalizovány
# - vykresleny jsou ovšem původní vektory
import faiss
import numpy as np
import matplotlib.pyplot as plt
DIMENSIONS=2
N=1000
K=100
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
normalized = np.matrix.copy(vectors)
# normalizace vektorů
for i in range(len(vectors)):
vector = vectors[i]
norm = np.linalg.norm(vector)
normalized[i] = vector / norm
# konstrukce indexu pro vyhledávání na základě skalárního součinu
index = faiss.IndexFlatIP(DIMENSIONS)
index.add(normalized)
# vektor, ke kterému budeme počítat vzdálenost
query_vector = np.array([[0.5, 0.5]])
norm = np.linalg.norm(query_vector)
normalized_query_vector = query_vector / norm
# najít K nejbližších vektorů
distances, indices = index.search(normalized_query_vector, K)
# --- graf ---
# velikost grafu
plt.figure(figsize=(8, 8), dpi=80)
# vykreslení všech náhodně vygenerovaných bodů
plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5)
# vykreslení nejbližších bodů
xs = vectors[:,0][indices][0]
ys = vectors[:,1][indices][0]
plt.plot(xs, ys, "+r", label="nearest vectors", markersize=5)
# vykreslení koncového bodu vektoru, ke kterému hledáme K nejbližších vektorů
x = query_vector[0][0]
y = query_vector[0][1]
plt.plot(x, y, "ob", label="query vector", markersize=10)
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-D.png")
# zobrazení grafu
plt.show()
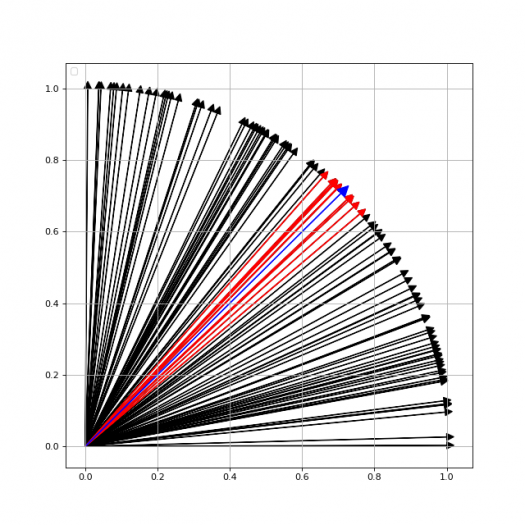
11. Vykreslení vektorů formou orientovaných šipek
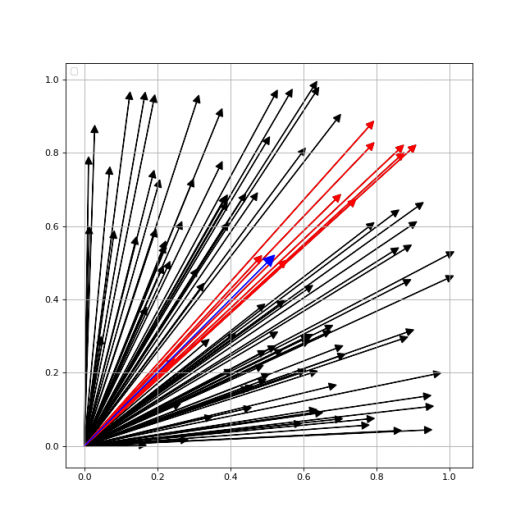
Prozatím jsme vektory vykreslovali formou bodů, přesněji řečeno souřadnic jejich koncových bodů. Ovšem zejména při zkoumání výsledné skupiny vektorů získaných s využitím skalárního součinu může být výhodnější všechny vektory vykreslit formou orientovaných šipek. Ty mohou (ale nemusí) vycházet z počátku souřadného systému. Jak toho dosáhnout v knihovně Matplotlib? Jedna z možností spočívá v tom, že se každý vektor vykreslí do grafu funkcí matplotlib.pyplot.arror. To znamená úpravy našeho skriptu:
# vykreslení všech náhodně vygenerovaných vektorů
for i in range(vectors.shape[0]):
plt.arrow(0, 0, vectors[i, 0], vectors[i, 1], head_width=0.02, head_length=0.02, color="black")
# vykreslení nejpodobnějších vektorů
xs = vectors[:,0][indices][0]
ys = vectors[:,1][indices][0]
for i in range(xs.shape[0]):
plt.arrow(0, 0, xs[i], ys[i], head_width=0.02, head_length=0.02, color="red")
# vykreslení vektoru, ke kterému hledáme K nejbližších vektorů
x = query_vector[0][0]
y = query_vector[0][1]
plt.arrow(0,0, x, y, head_width=0.03, head_length=0.03, color="blue")
Celé vykreslení grafu je pomalejší, ovšem netvoříme interaktivní aplikace, takže nepatrné zdržení nemusí být v tomto případě kritické.
Výsledný graf může vypadat následovně:
12. Úplný zdrojový kód pátého demonstračního příkladu
Úplný zdrojový kód dnešního pátého demonstračního příkladu, který po svém spuštění vykreslí všechny vektory (vstupní i nalezené) formou orientovaných šipek, vypadá následovně:
# Knihovna FAISS
#
import faiss
import numpy as np
import matplotlib.pyplot as plt
DIMENSIONS=2
N=100
K=10
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
normalized = np.matrix.copy(vectors)
# normalizace vektorů
for i in range(len(vectors)):
vector = vectors[i]
norm = np.linalg.norm(vector)
normalized[i] = vector / norm
# konstrukce indexu pro vyhledávání na základě skalárního součinu
index = faiss.IndexFlatIP(DIMENSIONS)
index.add(normalized)
# vektor, ke kterému budeme počítat vzdálenost
query_vector = np.array([[0.5, 0.5]])
norm = np.linalg.norm(query_vector)
normalized_query_vector = query_vector / norm
# najít K nejbližších vektorů
distances, indices = index.search(normalized_query_vector, K)
# --- graf ---
# velikost grafu
plt.figure(figsize=(8, 8), dpi=80)
# vykreslení všech náhodně vygenerovaných vektorů
for i in range(vectors.shape[0]):
plt.arrow(0, 0, vectors[i, 0], vectors[i, 1], head_width=0.02, head_length=0.02, color="black")
# vykreslení nejpodobnějších vektorů
xs = vectors[:,0][indices][0]
ys = vectors[:,1][indices][0]
for i in range(xs.shape[0]):
plt.arrow(0, 0, xs[i], ys[i], head_width=0.02, head_length=0.02, color="red")
# vykreslení vektoru, ke kterému hledáme K nejbližších vektorů
x = query_vector[0][0]
y = query_vector[0][1]
plt.arrow(0,0, x, y, head_width=0.03, head_length=0.03, color="blue")
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-E.png")
# zobrazení grafu
plt.show()
13. Vykreslení vektorů po jejich normalizaci formou orientovaných šipek
Triviálním způsobem lze navíc upravit způsob vykreslení grafu tak, že se sice vektory budou stále vykreslovat formou orientovaných šipek, ovšem nyní pro vykreslení použijeme normalizované formy vektorů, nikoli jejich původní podoby. To znamená, že následující část skriptu nepatrně upravíme:
# vykreslení všech náhodně vygenerovaných vektorů
for i in range(vectors.shape[0]):
plt.arrow(0, 0, vectors[i, 0], vectors[i, 1], head_width=0.02, head_length=0.02, color="black")
# vykreslení nejpodobnějších vektorů
xs = vectors[:,0][indices][0]
ys = vectors[:,1][indices][0]
for i in range(xs.shape[0]):
plt.arrow(0, 0, xs[i], ys[i], head_width=0.02, head_length=0.02, color="red")
# vykreslení vektoru, ke kterému hledáme K nejbližších vektorů
x = query_vector[0][0]
y = query_vector[0][1]
plt.arrow(0,0, x, y, head_width=0.03, head_length=0.03, color="blue")
Provedeme náhradu podtržených částí kódu na:
# vykreslení všech náhodně vygenerovaných vektorů v jejich normalizované podobě
for i in range(normalized.shape[0]):
plt.arrow(0, 0, normalized[i, 0], normalized[i, 1], head_width=0.02, head_length=0.02, color="black")
# vykreslení nejpodobnějších vektorů v jejich normalizované podobě
xs = normalized[:,0][indices][0]
ys = normalized[:,1][indices][0]
for i in range(xs.shape[0]):
plt.arrow(0, 0, xs[i], ys[i], head_width=0.02, head_length=0.02, color="red")
# vykreslení vektoru (v normalizované podobě), ke kterému hledáme K nejbližších vektorů
x = normalized_query_vector[0][0]
y = normalized_query_vector[0][1]
plt.arrow(0,0, x, y, head_width=0.03, head_length=0.03, color="blue")
Opět se podívejme na to, jak vypadá výsledný graf získaný tímto způsobem upraveným skriptem:
14. Úplný zdrojový kód šestého demonstračního příkladu
Úplný zdrojový kód dnešního šestého demonstračního příkladu, který po svém spuštění vykreslí všechny vektory (vstupní i nalezené – ovšem po jejich normalizaci) formou orientovaných šipek, vypadá následovně:
# Knihovna FAISS
#
import faiss
import numpy as np
import matplotlib.pyplot as plt
DIMENSIONS=2
N=100
K=10
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
normalized = np.matrix.copy(vectors)
# normalizace vektorů
for i in range(len(vectors)):
vector = vectors[i]
norm = np.linalg.norm(vector)
normalized[i] = vector / norm
# konstrukce indexu pro vyhledávání na základě skalárního součinu
index = faiss.IndexFlatIP(DIMENSIONS)
index.add(normalized)
# vektor, ke kterému budeme počítat vzdálenost
query_vector = np.array([[0.5, 0.5]])
norm = np.linalg.norm(query_vector)
normalized_query_vector = query_vector / norm
# najít K nejbližších vektorů
distances, indices = index.search(normalized_query_vector, K)
# --- graf ---
# velikost grafu
plt.figure(figsize=(8, 8), dpi=80)
# vykreslení všech náhodně vygenerovaných vektorů
for i in range(vectors.shape[0]):
plt.arrow(0, 0, normalized[i, 0], normalized[i, 1], head_width=0.02, head_length=0.02, color="black")
# vykreslení nejpodobnějších vektorů
xs = normalized[:,0][indices][0]
ys = normalized[:,1][indices][0]
for i in range(xs.shape[0]):
plt.arrow(0, 0, xs[i], ys[i], head_width=0.02, head_length=0.02, color="red")
# vykreslení vektoru, ke kterému hledáme K nejbližších vektorů
x = normalized_query_vector[0][0]
y = normalized_query_vector[0][1]
plt.arrow(0,0, x, y, head_width=0.03, head_length=0.03, color="blue")
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-F.png")
# zobrazení grafu
plt.show()
15. Vyhledání a vykreslení nejvíce NEpodobných vektorů
S vyhledáváním nejpodobnějších vektorů na základě skalárního součinu souvisí i ještě jedna zajímavá a potenciálně užitečná funkcionalita – schopnost vyhledat ty vektory, které jsou nejméně podobné původnímu vektoru. Celý postup je vlastně až triviálně jednoduchý – sice budeme stále vyhledávat nejpodobnější vektory, ovšem nikoli k původnímu vektoru query_vector, ale k jeho otočené podobě -query_vector (resp. přesněji řečeno k jeho normalizované otočené podobě). To je vlastně jediná potřebná změna (viz podtržená část zdrojového kódu):
# vektor, ke kterému budeme počítat vzdálenost query_vector = np.array([[0.5, 0.5]]) norm = np.linalg.norm(query_vector) normalized_query_vector = query_vector / norm # najít K nejbližších vektorů distances, indices = index.search(-normalized_query_vector, K)
Výsledek by měl vypadat zhruba následovně – zvýrazněny jsou ty vektory, jejichž směrnice je nejvíce odkloněna:
16. Úplný zdrojový kód sedmého demonstračního příkladu
Úplný zdrojový kód dnešního sedmého demonstračního příkladu, který po svém spuštění získá a zvýrazní nejvíce nepodobné vektory, vypadá takto:
# Knihovna FAISS
#
import faiss
import numpy as np
import matplotlib.pyplot as plt
DIMENSIONS=2
N=1000
K=100
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float32")
normalized = np.matrix.copy(vectors)
# normalizace vektorů
for i in range(len(vectors)):
vector = vectors[i]
norm = np.linalg.norm(vector)
normalized[i] = vector / norm
# konstrukce indexu pro vyhledávání na základě skalárního součinu
index = faiss.IndexFlatIP(DIMENSIONS)
index.add(normalized)
# vektor, ke kterému budeme počítat vzdálenost
query_vector = np.array([[0.5, 0.5]])
norm = np.linalg.norm(query_vector)
normalized_query_vector = query_vector / norm
# najít K nejbližších vektorů
distances, indices = index.search(-normalized_query_vector, K)
# --- graf ---
# velikost grafu
plt.figure(figsize=(8, 8), dpi=80)
# vykreslení všech náhodně vygenerovaných bodů
plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5)
# vykreslení nejbližších bodů
xs = vectors[:,0][indices][0]
ys = vectors[:,1][indices][0]
plt.plot(xs, ys, "+r", label="nearest vectors", markersize=5)
# vykreslení koncového bodu vektoru, ke kterému hledáme K nejbližších vektorů
x = query_vector[0][0]
y = query_vector[0][1]
plt.plot(x, y, "ob", label="query vector", markersize=10)
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-G.png")
# zobrazení grafu
plt.show()
17. Datové typy prvků vektorů: float32, float16 a bfloat16
V úvodním článku o knihovně FAISS jsme si řekli, že prvky vektorů, které knihovna FAISS dokáže zpracovat, musí být typu float32, float16 nebo bfloat16. Všechny tři datové typy mají své využití – float32 poskytuje nejpřesnější výsledky (pokud jsou vyžadovány), float16 dokáže zmenšit paměťové nároky modelů na polovinu a bfloat16 lze navíc realizovat i na GPU (a mnohé modely jsou z tohoto důvodu založeny na vektorech s prvky tohoto typu).
Typ float32 je v současnosti naprosto standardní (dopovídá float v céčku) a je plně podporován moderními mikroprocesory v rozšířeních instrukčních sad SSE i AVX. Typ float16 je podporován jen minimálně v rozšíření F16C (CVT16) v SSE5 (vlastně se jen jedná o čtyři konverzní instrukce) a taktéž v F16 (AVX-512) – zde již jsou podporovány všechny základní operace. A formát bfloat16 je podporován v rozšíření BF16 (taktéž AVX-512). Zde můžeme vidět zvláštní rozdíl mezi float16 a bfloat16, protože rozšíření BF16 je minimalistické, ovšem podporuje i skalární součin (aneb konzistence na prvním místě).
Vzhledem k tomu, že knihovna Numpy podporuje práci s hodnotami typu float16, můžeme si otestovat, jak vlastně probíhá konstrukce indexu i vyhledání nejpodobnějších vektorů v případě, že prvky vektorů jsou právě tohoto typu (a jsou tedy méně přesné a s menším rozsahem):
# Knihovna FAISS
#
# - vykreslení nejpodobnějších vektorů získaných na základě jejich vzdálenosti
# - vykresleny jsou původní vektory
# - složky všech vektorů jsou typu float16
import faiss
import numpy as np
import matplotlib.pyplot as plt
DIMENSIONS=2
N=1000
K=100
# náhodné vektory v rovině [0,0] - [1,1]
vectors = np.random.rand(N, DIMENSIONS).astype("float16")
normalized = np.matrix.copy(vectors)
# normalizace vektorů
for i in range(len(vectors)):
vector = vectors[i]
norm = np.linalg.norm(vector)
normalized[i] = vector / norm
# konstrukce indexu pro vyhledávání na základě skalárního součinu
index = faiss.IndexFlatL2(DIMENSIONS)
index.add(normalized)
# vektor, ke kterému budeme počítat vzdálenost
query_vector = np.array([[0.5, 0.5]]).astype("float16")
norm = np.linalg.norm(query_vector)
normalized_query_vector = query_vector / norm
# najít K nejbližších vektorů
distances, indices = index.search(normalized_query_vector, K)
# --- graf ---
# velikost grafu
plt.figure(figsize=(8, 8), dpi=80)
# vykreslení všech náhodně vygenerovaných bodů
plt.plot(vectors[:,0], vectors[:,1], "+k", label="original vectors", markersize=5)
# vykreslení nejbližších bodů
xs = vectors[:,0][indices][0]
ys = vectors[:,1][indices][0]
plt.plot(xs, ys, "+r", label="nearest vectors", markersize=5)
# vykreslení koncového bodu vektoru, ke kterému hledáme K nejbližších vektorů
x = query_vector[0][0]
y = query_vector[0][1]
plt.plot(x, y, "ob", label="query vector", markersize=10)
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
# vykreslení grafu do souboru
plt.savefig("faiss-H.png")
# zobrazení grafu
plt.show()
I přes menší přesnost výpočtů by výsledky měly být prakticky totožné s demonstračním příkladem, ve kterém byly vektory reprezentovány s využitím prvků typu float32:
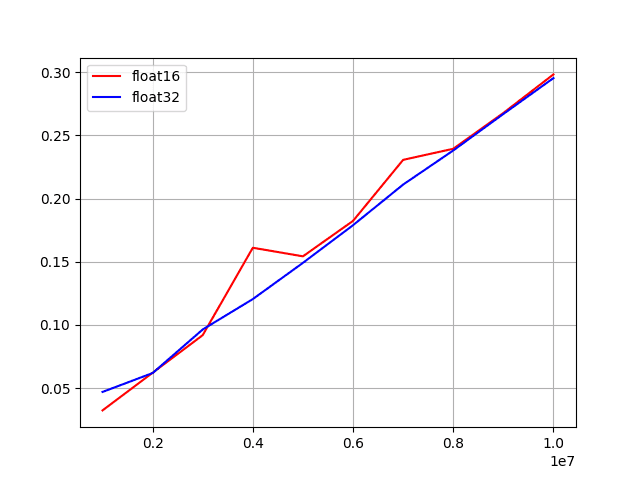
18. Benchmark: porovnání rychlosti vyhledávání vektorů s prvky typu float16 a float32
Nyní bude zajímavé zjistit, jak rychlé či naopak pomalé je vyhledávání podobných vektorů v případě, že namísto prvků typu float32 použijeme prvky typu float16 (a tedy přibližně jen polovinu operační paměti). Testování je provedeno na počítači s rozšířením instrukční sady AVX, ovšem již ne AVX-512 (ovšem F16C podporováno je). Pro tento účel upravíme benchmark z původního článku do této podoby:
# Knihovna FAISS
#
# - benchmark rychlosti nalezení nejpodobnějších vektorů
# - vizualizace výsledků formou grafu
# - porovnání float16 a float32# - porovnání float16 a float32# - porovnání float16 a float32
from time import time
import faiss
import numpy as np
import matplotlib.pyplot as plt
def similarity_search(n, k, float_type):
# pocet dimenzi
DIMENSIONS=128
# nahodne vektory
data = np.random.rand(n, 128).astype(float_type)
# konstrukce indexu pro vyhledavani na zaklade vzdalenosti
index = faiss.IndexFlatL2(DIMENSIONS)
index.add(data)
t1 = time()
# vektor, ke kteremu budeme pocitat vzdalenost
query_vector = np.random.rand(1, DIMENSIONS).astype(float_type)
# pocet nejblizsich bodu
distances, indices = index.search(query_vector, k)
t2 = time()
return n, t2-t1
def benchmark(from_n, to_n, steps, float_type):
ns = []
ts_search = []
for n in np.linspace(from_n, to_n, steps):
print(n)
n, t_search = similarity_search(int(n), 1, float_type)
ns.append(n)
ts_search.append(t_search)
return ns, ts_search
#for n in np.linspace(1000000, 10000000, 10):
from_n = 1000000
to_n = 10000000
steps = 10
ns, float16_times = benchmark(from_n, to_n, steps, "float16")
_, float32_times = benchmark(from_n, to_n, steps, "float32")
plt.plot(ns, float16_times, "r-", label="float16")
plt.plot(ns, float32_times, "b-", label="float32")
# přidání legendy
plt.legend(loc="upper left")
# povolení zobrazení mřížky
plt.grid(True)
plt.savefig(f"faiss_benchmark_3.png")
# zobrazení grafu
plt.show()
Z výsledků je patrné, že při použití CPU (FAISS existuje i pro GPU) nejsou časové rozdíly prakticky patrné:
19. Repositář s demonstračními příklady
Demonstrační příklady vytvořené v Pythonu a popsané v předchozím i v dnešním článku najdete v repositáři https://github.com/tisnik/most-popular-python-libs/. Následují odkazy na jednotlivé příklady:
| # | Příklad | Stručný popis | Adresa |
|---|---|---|---|
| 1 | faiss-1.py | seznamy souřadnic bodů v rovině | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-1.py |
| 2 | faiss-2.py | konstrukce matice se souřadnicemi bodů | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-2.py |
| 3 | faiss-3.py | konstrukce indexu pro vyhledávání na základě vzdálenosti | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-3.py |
| 4 | faiss-4.py | nalezení nejbližších bodů k zadaným souřadnicím – výpis indexů nalezených bodů | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-4.py |
| 5 | faiss-5.py | nalezení nejbližších bodů k zadaným souřadnicím – výpis souřadnic nalezených bodů | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-5.py |
| 6 | faiss-6.py | vyhledávání bodů na základě skalárního součinu bez normalizace vektorů | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-6.py |
| 7 | faiss-7.py | vyhledávání bodů na základě skalárního součinu s normalizací vektorů | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-7.py |
| 8 | faiss-8.py | jednoduchý benchmark rychlosti vyhledávání knihovnou FAISS | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-8.py |
| 9 | faiss-9.py | vizualizace koncových bodů vektorů v rovině | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-9.py |
| 10 | faiss-A.py | vykreslení nejpodobnějších vektorů získaných na základě L2 metriky | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-A.py |
| 11 | faiss-B.py | nalezení nejpodobnějších vektorů získaných na základě skalárního součinu: varianta s nenormovanými vektory | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-B.py |
| 12 | faiss-C.py | nalezení nejpodobnějších vektorů získaných na základě skalárního součinu: varianta s normovanými vektory | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-C.py |
| 13 | faiss-D.py | vykreslení nejpodobnějších vektorů před jejich normalizací | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-D.py |
| 14 | faiss-E.py | vykreslení vektorů formou orientovaných šipek | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-E.py |
| 15 | faiss-F.py | vykreslení vektorů po jejich normalizaci formou orientovaných šipek | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-F.py |
| 16 | faiss-G.py | vyhledání a vykreslení nejvíce NEpodobných vektorů | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-G.py |
| 17 | faiss-H.py | vyhledání podobných vektorů se složkami typu float16 | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-H.py |
| 18 | faiss-I.py | jednoduchý benchmark rychlosti vyhledávání knihovnou FAISS: rozdíly mezi float16 a float32 | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/faiss-I.py |
| 19 | pyproject.toml | soubor s projektem a definicí závislostí | https://github.com/tisnik/most-popular-python-libs/blob/master/faiss/pyproject.toml |
20. Odkazy na Internetu
- FAISS (Facebook AI Similarity Search)
https://en.wikipedia.org/wiki/FAISS - FAISS documentation
https://faiss.ai/ - Introduction to Facebook AI Similarity Search (Faiss)
https://www.pinecone.io/learn/series/faiss/faiss-tutorial/ - Faiss: Efficient Similarity Search and Clustering of Dense Vectors
https://medium.com/@pankaj_pandey/faiss-efficient-similarity-search-and-clustering-of-dense-vectors-dace1df1e235 - Cosine Distance vs Dot Product vs Euclidean in vector similarity search
https://medium.com/data-science-collective/cosine-distance-vs-dot-product-vs-euclidean-in-vector-similarity-search-227a6db32edb - F16C
https://en.wikipedia.org/wiki/F16C - FP16 (AVX-512)
https://en.wikipedia.org/wiki/AVX-512#FP16 - Top 8 Vector Databases in 2025: Features, Use Cases, and Comparisons
https://synapsefabric.com/top-8-vector-databases-in-2025-features-use-cases-and-comparisons/ - Is FAISS a Vector Database? Complete Guide
https://mljourney.com/is-faiss-a-vector-database-complete-guide/ - Vector database
https://en.wikipedia.org/wiki/Vector_database - Similarity search
https://en.wikipedia.org/wiki/Similarity_search - Nearest neighbor search
https://en.wikipedia.org/wiki/Nearest_neighbor_search#Approximation_methods - Decoding Similarity Search with FAISS: A Practical Approach
https://www.luminis.eu/blog/decoding-similarity-search-with-faiss-a-practical-approach/ - MetricType and distances
https://github.com/facebookresearch/faiss/wiki/MetricType-and-distances - RAG – Retrieval-augmented generation
https://en.wikipedia.org/wiki/Retrieval-augmented_generation - pgvector na GitHubu
https://github.com/pgvector/pgvector - Why we replaced Pinecone with PGVector
https://www.confident-ai.com/blog/why-we-replaced-pinecone-with-pgvector - PostgreSQL as VectorDB – Beginner Tutorial
https://www.youtube.com/watch?v=Ff3tJ4pJEa4 - What is a Vector Database? (neobsahuje odpověď na otázku v titulku :-)
https://www.youtube.com/watch?v=t9IDoenf-lo - PGVector: Turn PostgreSQL Into A Vector Database
https://www.youtube.com/watch?v=j1QcPSLj7u0 - Milvus
https://milvus.io/ - Vector Databases simply explained! (Embeddings & Indexes)
https://www.youtube.com/watch?v=dN0lsF2cvm4 - Vector databases are so hot right now. WTF are they?
https://www.youtube.com/watch?v=klTvEwg3oJ4 - Step-by-Step Guide to Installing “pgvector” and Loading Data in PostgreSQL
https://medium.com/@besttechreads/step-by-step-guide-to-installing-pgvector-and-loading-data-in-postgresql-f2cffb5dec43 - Best 17 Vector Databases for 2025
https://lakefs.io/blog/12-vector-databases-2023/ - Top 15 Vector Databases that You Must Try in 2025
https://www.geeksforgeeks.org/top-vector-databases/ - Picking a vector database: a comparison and guide for 2023
https://benchmark.vectorview.ai/vectordbs.html - Top 9 Vector Databases as of Feburary 2025
https://www.shakudo.io/blog/top-9-vector-databases - What is a vector database?
https://www.ibm.com/think/topics/vector-database - SQL injection
https://en.wikipedia.org/wiki/SQL_injection - Cosine similarity
https://en.wikipedia.org/wiki/Cosine_similarity - Euclidean distance
https://en.wikipedia.org/wiki/Euclidean_distance - Dot product
https://en.wikipedia.org/wiki/Dot_product - Hammingova vzdálenost
https://cs.wikipedia.org/wiki/Hammingova_vzd%C3%A1lenost - Jaccard index
https://en.wikipedia.org/wiki/Jaccard_index - Manhattanská metrika
https://cs.wikipedia.org/wiki/Manhattansk%C3%A1_metrika - pgvector: vektorová databáze postavená na Postgresu
https://www.root.cz/clanky/pgvector-vektorova-databaze-postavena-na-postgresu/ - Matplotlib Home Page
http://matplotlib.org/ - matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Dot Product
https://mathworld.wolfram.com/DotProduct.html