Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib

Obsah

1. Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib

2. Vykreslení průběhů dvou funkcí do jediného grafu

3. Změna stylu vykreslování a přidání legendy

4. Vyplnění plochy pod funkcí

5. Kombinace různých stylů vykreslování grafů

6. Zobrazení mřížky a nastavení rozsahů na obou osách

7. Přidání popisků do grafů

8. Základní polární graf

9. Vykreslení průběhů většího množství funkcí v polárním grafu

10. Vyplnění plochy pod funkcí v polárním grafu

11. Graf používající „schodky“

12. Jednoduchý sloupcový graf

13. Sloupcový graf se dvěma skupinami sloupců

14. Zobrazení histogramu

15. Koláčový graf

16. Změna stylu vykreslování koláčových grafů

17. Sloupcový graf se zobrazením odchylek (či chyb)

18. Pokročilejší nastavení způsobu vykreslení odchylek

19. Repositář s demonstračními příklady (diáři)

20. Odkazy na Internetu

1. Tvorba grafů v Jupyter Notebooku

Na úvodní článek o nástroji Jupyter Notebook dnes navážeme. Ukážeme si totiž, jakým způsobem je možné v tomto velmi užitečném nástroji vytvářet různé typy grafů zobrazujících jak průběhy funkcí (výuka), tak i grafy založené na načtených datech. A právě kombinace Jupyter Notebooku (interaktivita, možnost opravit či upravit již zapsané příkazy v buňkách, vytváření slajdů) společně s možností zobrazení grafů přímo ve vytvářeném diáři je velmi silnou zbraní tohoto nástroje. Pro samotné vytvoření grafů se používá několik knihoven, ovšem primární knihovnou (zejména pokud jsou diáře založeny na programovacím jazyku Python) je stále knihovna nazvaná Matplotlib, která se velmi dobře doplňuje s knihovnou Numpy, jež podporuje mj. i efektivní operace s vektory a maticemi (grafy je možné i animovat, to však vyžaduje poněkud více úsilí a jedná se o téma mimo rozsah dnešního článku).

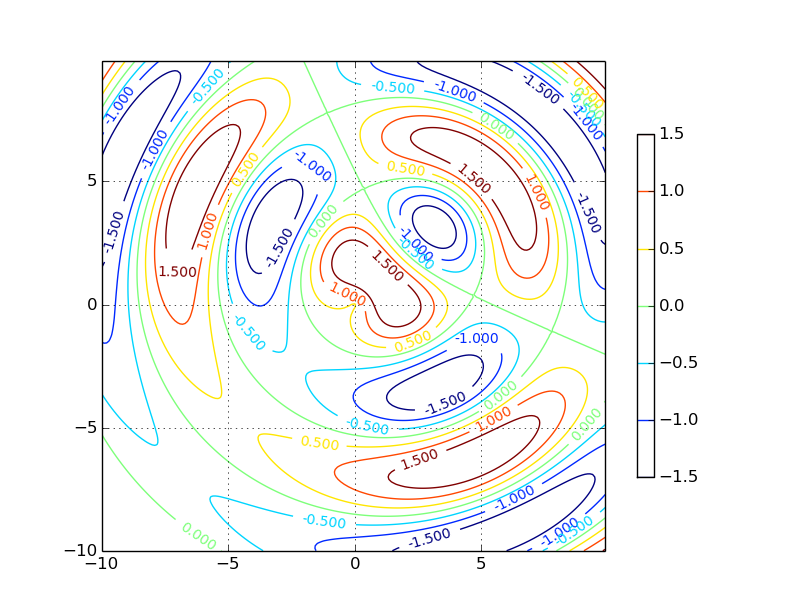
Obrázek 1: Jeden typ grafu podporovaný knihovnou Matplotlib – Funkce typu z=f(x,y) zobrazená formou vrstevnic.

Právě vzájemnou kombinací obou výše zmíněných knihoven, tedy Numpy+Matplotlib lze relativně snadno dosáhnout velmi pěkných výsledků plně porovnatelných s výsledky vytvořenými komerčními balíky. V dnešním článku se seznámíme pouze se základy práce s knihovnou Matplotlib. Nejprve si ukážeme tvorbu klasických grafů funkcí jedné proměnné, následně do grafu přidáme průběh další funkce, popisky os, legendu, popisky vlastních průběhů atd. V závěru si pak ukážeme další typy grafů, zejména polární grafy, koláčové grafy, histogramy apod.

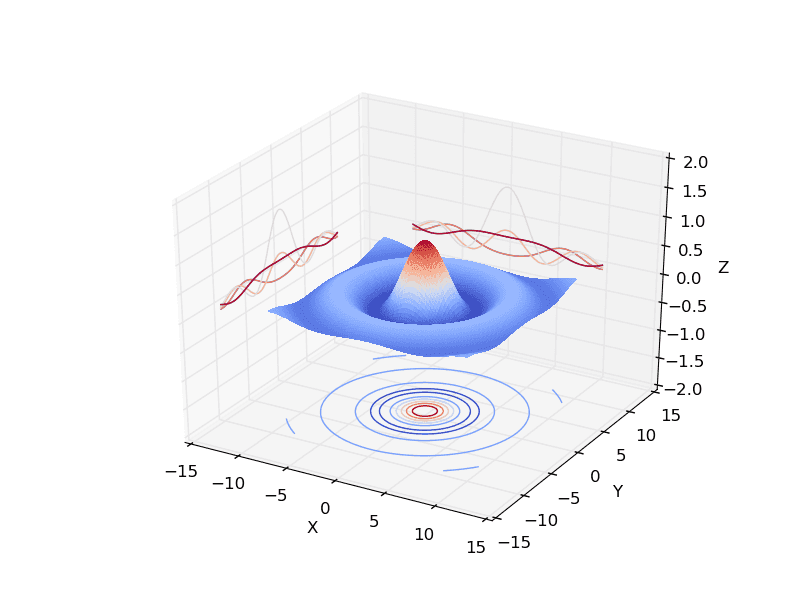
Obrázek 2: Podporována je i relativně široká skupina 3D grafů, což je téma navazujícího článku.

V navazující části si pak ukážeme tvorbu grafů s konturami, 3D grafů funkcí se dvěma nezávislými proměnnými, 3D grafů funkcí typu x,y=f(t), x,y,z=f(t) apod. Přesvědčíme se, že možnosti knihovny Matplotlib jsou skutečně široké a přitom je její použití poměrně jednoduché a snadno pochopitelné (pokud samozřejmě vynecháme některé pokročilejší operace, popř. snahy o vyladění vzhledu grafu – to je již mnohdy komplikovanější činnost).

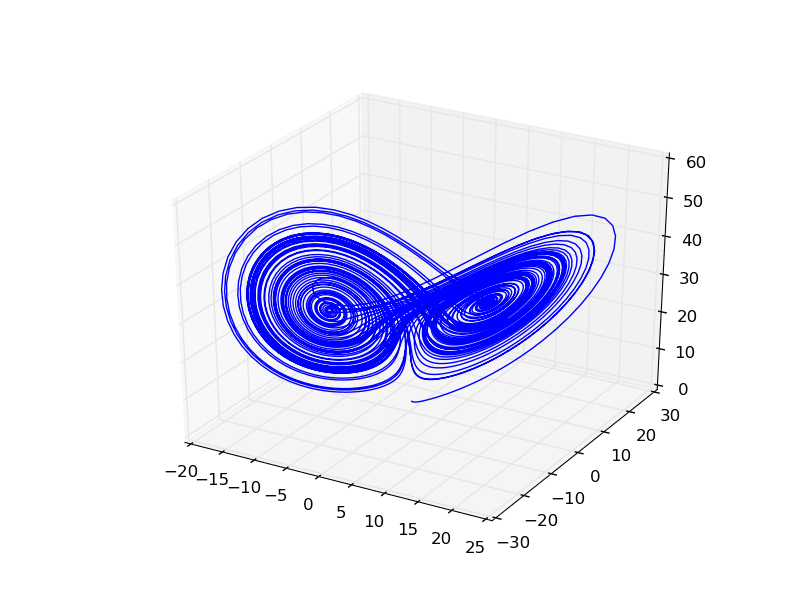
Obrázek 3: Slavný Lorenzův atraktor vykreslený knihovnou Matplotlib.

Na úvod a jako malou rozcvičku si ukážeme velmi jednoduchý diář (naprogramovaný v Pythonu 3), který po svém spuštění vykreslí graf s průběhem funkce sinus. V diáři nalezneme pouze několik programových řádků (ty lze rozdělit do buněk podle přání programátora). Nejprve je nutné naimportovat hlavní modul knihovny Numpy nazvaný numpy a následně i submodul plt z knihovny Matplotlib. Většina aplikací, ale i demonstračních diářů, s nimiž se setkáte, používá pro importované moduly zkratky np a plt, čehož se z důvodu zachování konzistence budeme držet i my. Následně je s využitím funkce numpy.linspace() vytvořeno pole sta prvků s hodnotami od 0 do 2π. Na toto pole je aplikována funkce numpy.sin(), jejímž výsledkem je nové stoprvkové pole (hodnoty prvků leží v rozsahu od –1 do 1). Funkcí matplotlib.pyplot.plot() je vykreslen průběh funkce, ovšem graf ještě není zobrazen, takže do něj můžeme přidat popis obou os a graf následně zobrazit příkazem matplotlib.pyplot.show().

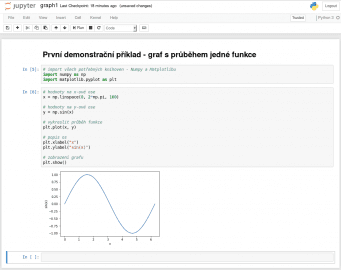
Obrázek 4: Diář s kódem pro vykreslení grafu.

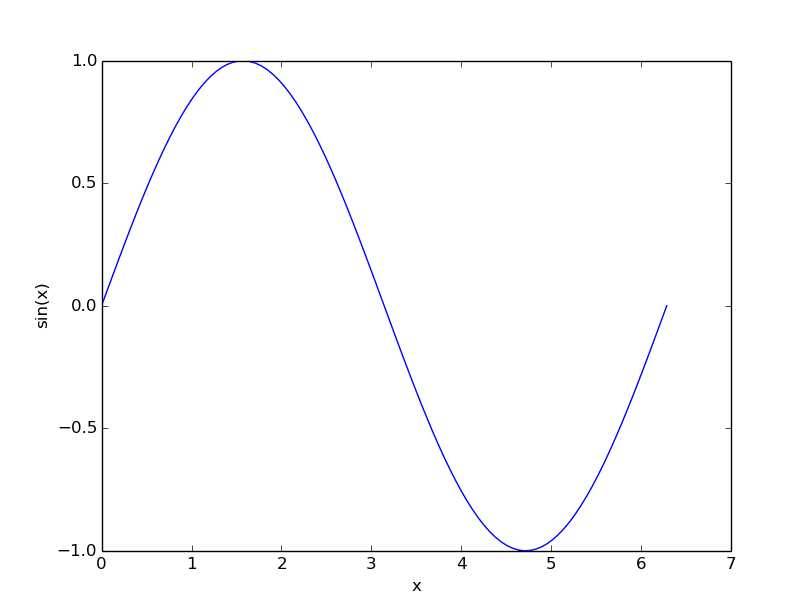
Obrázek 5: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# První demonstrační příklad:
# - vykreslení průběhu funkce sin
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
 
# hodnoty na y-ové ose
y = np.sin(x)
 
# vykreslit průběh funkce
plt.plot(x, y)
 
# popis os
plt.xlabel("x")
plt.ylabel("sin(x)")
 
# zobrazení grafu
plt.show()

2. Vykreslení průběhů dvou funkcí do jediného grafu

Velmi často se můžeme setkat i s požadavkem vložení průběhů několika funkcí do jediného grafu. V tomto ohledu knihovna Matplotlib svým uživatelům nabízí větší množství řešení. Je například možné do jednoho obrázku či dokumentu vložit více grafů s totožnou x-ovou osou (a většinou odlišným měřítkem na y-ových osách), popř. lze skutečně sloučit větší množství průběhů v jediném grafu. Ukažme si nejdříve druhou zmiňovanou možnost, tj. vytvoření grafu se dvěma funkcemi, ovšem s totožnými x-ovými a y-ovými osami (to není vždy ideální řešení). I u takto vytvořeného grafu můžeme použít již zmíněnou funkci matplotlib.pyplot.plot(), které se ovšem předají čtyři pole: hodnoty na ose x, hodnoty první funkce, opět hodnoty na ose x (pro nás stejné pole) a hodnoty druhé funkce. Žádné další operace nejsou zapotřebí, což je ostatně patrné i při pohledu na zdrojový kód dalšího jednoduchého diáře:

Obrázek 5: Diář s kódem pro vykreslení grafu.

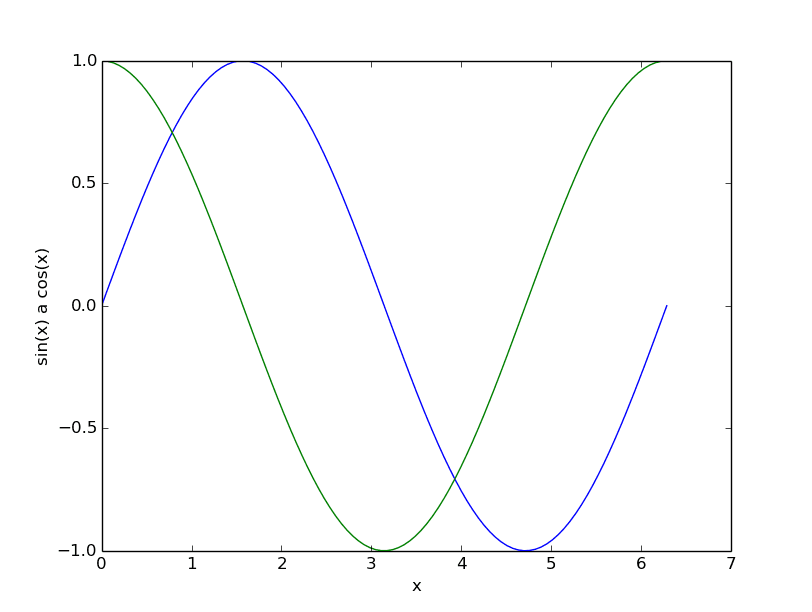
Obrázek 6: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Druhý demonstrační příklad:
# - vykreslení průběhů funkcí sin a cos
#   do jediného grafu
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
 
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
 
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x)
 
# vykreslit průběh obou funkcí
plt.plot(x, y1, x, y2)
 
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a cos(x)")
 
# zobrazení grafu
plt.show()

3. Změna stylu vykreslování a přidání legendy

Při pohledu na graf vykreslený na předchozím diáři je patrné, že knihovna Matplotlib automaticky zvolila pro průběh každé funkce odlišnou barvu, ovšem styl vykreslení (šířka čáry atd.) zůstal stejný. Pokud budeme potřebovat ovlivnit styl vykreslování průběhů funkcí, lze to samozřejmě zařídit a to poměrně jednoduše. Funkci matplotlib.pyplot.plot() je totiž možné předat nepovinný (a nepojmenovaný) parametr typu řetězec, v němž je „zakódována“ jak barva (první písmeno anglického názvu barvy), tak i styl vykreslování (– je plná čára, – čárkovaná čára, . tečkovaná čára apod.). Dalším nepovinným parametrem, tentokrát již pojmenovaným, je parametr „label“, pomocí něhož je možné libovolný průběh funkce označit jménem. Toto jméno se následně použije například v legendě přidané do grafu funkcí matplotlib.pyplot.legend(). Nepovinným pojmenovaným parametrem loc se popíše, do kterého místa grafu se má legenda vložit:

Obrázek 7: Diář s kódem pro vykreslení grafu.

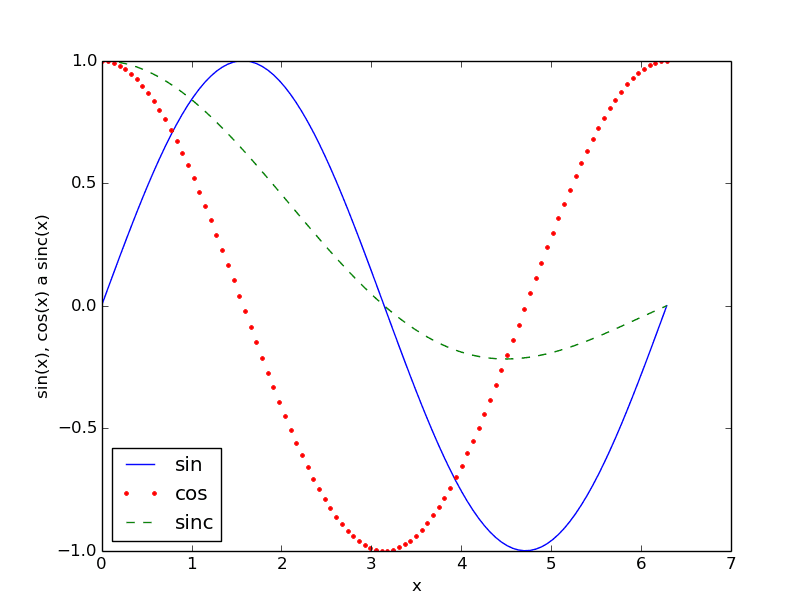
Obrázek 8: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Třetí demonstrační příklad:
# - vykreslení průběhů funkcí sin a cos a sinc
#   do jediného grafu
# - změna stylu vykreslování průběhů funkcí
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.linspace(0.01, 2*np.pi, 100)
 
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
 
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x)
 
# hodnoty na y-ové ose: třetí funkce
y3 = np.sin(x)/x
 
# vykreslit průběh všech tří funkcí
# se změnou stylu vykreslování
plt.plot(x, y1, "b-", label="sin")
plt.plot(x, y2, "r.", label="cos")
plt.plot(x, y3, "g--", label="sinc")
 
# přidání legendy
plt.legend(loc="lower left")
 
# popis os
plt.xlabel("x")
plt.ylabel("sin(x), cos(x) a sinc(x)")
 
# zobrazení grafu
plt.show()

4. Vyplnění plochy pod funkcí

V případě, že se namísto funkce matplotlib.pyplot.plot() použije pro vykreslení grafu funkce pojmenovaná matplotlib.pyplot.fill(), změní se poměrně zásadním způsobem styl vykreslení. Namísto (lomené) čáry se totiž plocha pod funkcí vyplní konstantní barvou. Tu je možné zadat slovně, například „red“, „yellow“ atd. Ovšem ve chvíli, kdy se funkce překrývají, by dříve vykreslený průběh nebyl viditelný, protože by jedna barevná plocha překreslila plochu druhou. Abychom tomuto problému předešli, stačí knihovně matplotlib předepsat průhlednost barvy v rozsahu 0.0 až 1.0. Konkrétně to znamená, že při požadavku na vykreslení dvou funkcí a použití barev s průhledností 30% můžeme zadat příkaz plt.fill(x, y1, „red“, x, y2, „yellow“, alpha=0.3). Podívejme se na úplné znění zdrojového kódu dalšího diáře, v němž je tento příkaz použit:

Obrázek 9: Diář s kódem pro vykreslení grafu.

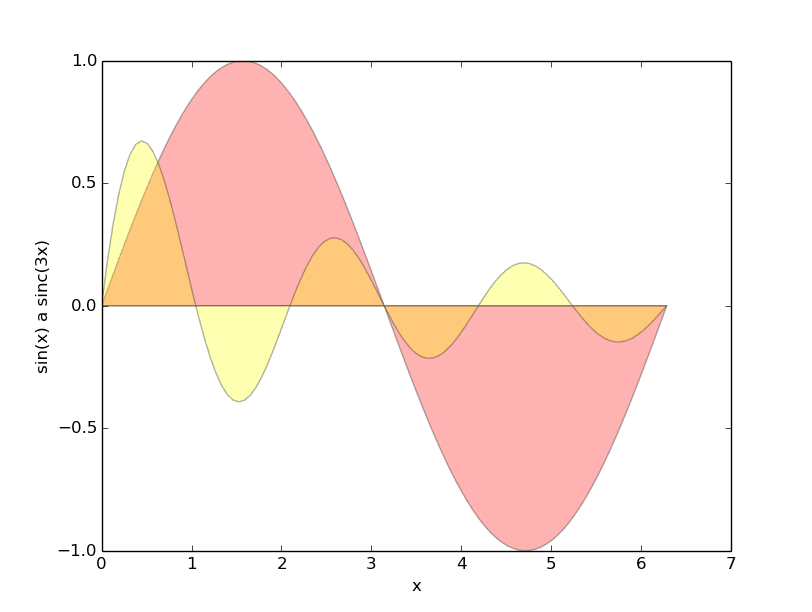
Obrázek 10: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Čtvrtý demonstrační příklad:
# - vykreslení průběhů funkcí sin a sinc
#   do jediného grafu
#   s vyplněním plochy pod průběhu
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
 
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
 
# hodnoty na y-ové ose: druhá funkce
y2 = np.sin(3*x)/(x+1)
 
# vykreslit průběh obou funkcí
# se změnou stylu vykreslování
plt.fill(x, y1, "red", x, y2, "yellow", alpha=0.3)
 
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a sinc(3x)")
 
# zobrazení grafu
plt.show()

5. Kombinace různých stylů vykreslování grafů

V knihovně Matplotlib je v případě potřeby možné jednotlivé příkazy pro vykreslení funkcí vzájemně kombinovat. V dalším demonstračním diáři je vykreslena funkce sinus, dále pak známá funkce sinc (s posunutou osou) a následně dva průběhy funkcí, které vlastně tvoří obálku sinc. Funkce sinus i sinc jsou vykresleny takovým (vhodně naaranžovaným) způsobem, že je plocha pod průběhem funkce vyplněna, zatímco obálky jsou pouze naznačeny čárkovanými čarami. Legenda se navíc přesunula do pravého horního rohu, kde je pro ni mnohem více místa, což je více patrné na zvětšeném grafu:

Obrázek 11: Diář s kódem pro vykreslení grafu.

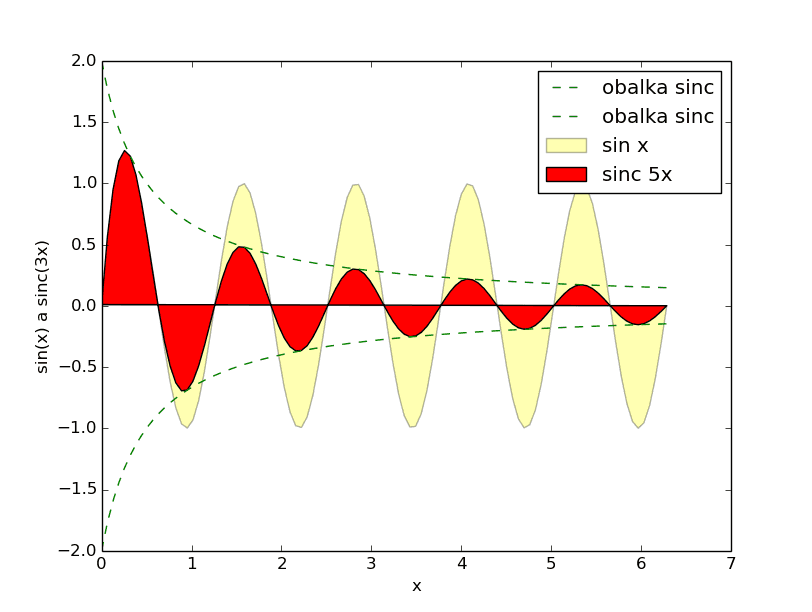
Obrázek 12: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Pátý demonstrační příklad:
# - vykreslení průběhů čtyř různých funkcí
#   do jediného grafu
#   s vyplněním plochy pod průběhu
# - kombinace různých stylů vykreslení
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.linspace(0.001, 2*np.pi, 100)
 
# hodnoty na y-ové ose: první funkce
y1 = np.sin(5*x)
 
# hodnoty na y-ové ose: druhá funkce
y2 = np.sin(5*x)/(x+1/2)
 
# hodnoty na y-ové ose: třetí čtvrtá funkce
y3 = 1/(x+1/2)
y4 = -y3
 
# vykreslit průběh obou funkcí
# se změnou stylu vykreslování
plt.fill(x, y1, "yellow", alpha=0.3, label="sin x")
plt.fill(x, y2, "r.", alpha=1.0, label="sinc 5x")
plt.plot(x, y3, "g--", label="obalka sinc")
plt.plot(x, y4, "g--", label="obalka sinc")
 
# přidání legendy
plt.legend(loc="upper right")
 
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a sinc(3x)")
 
# zobrazení grafu
plt.show()

6. Zobrazení mřížky a nastavení rozsahů na obou osách

Doposud nakreslené grafy ve skutečnosti nevypadaly příliš profesionálně, a to mj. i proto, že bylo poměrně obtížné rozeznat počátek souřadnic (souřadného systému) atd. Poměrně snadno je možné tento nedostatek napravit, a to konkrétně přidáním mřížky příkazem matplotlib.pyplot.grid(True). Navíc ještě můžeme zvětšit oblast grafu s využitím matplotlib.pyplot.axis([-1, 8, –1.5, 1.5]), kde čtveřice čísel značí postupně x_min, x_max, y_min a y_max (přesněji řečeno se nezvětší samotný obrázek s grafem, ale dojde ke změně jeho měřítka). Vlastní průběh funkce tedy přestane zasahovat do samotných hranic grafu, takže nový výsledek vypadá mnohem lépe:

Obrázek 13: Diář s kódem pro vykreslení grafu.

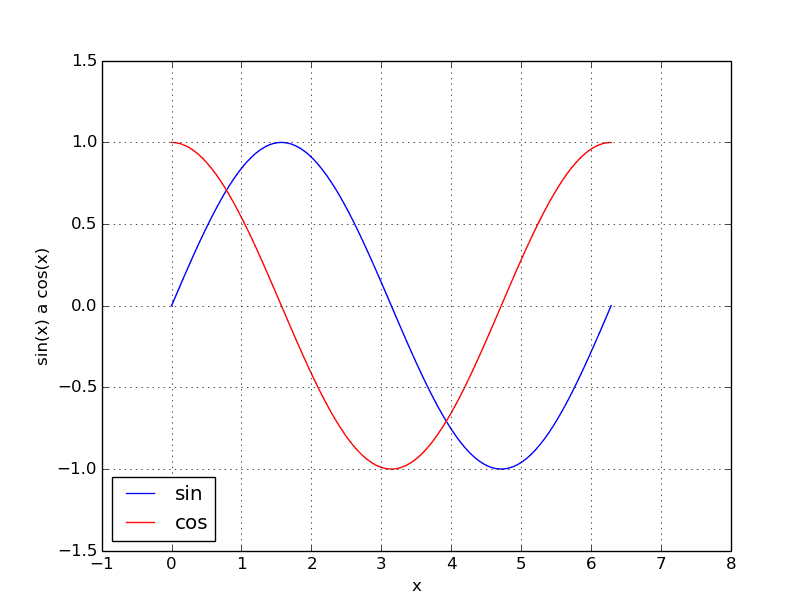
Obrázek 14: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Šestý demonstrační příklad:
# - vykreslení průběhů funkcí sin a cos
# - nastavení mřížky
# - nastavení rozsahů na obou osách
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
 
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
 
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x)
 
# vykreslit průběh obou funkcí
# se změnou stylu vykreslování
plt.plot(x, y1, "b-", label="sin")
plt.plot(x, y2, "r-", label="cos")
 
# přidání legendy
plt.legend(loc="lower left")
 
# nastavení rozsahů na obou osách
plt.axis([-1, 8, -1.5, 1.5])
 
# povolení zobrazení mřížky
plt.grid(True)
 
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a cos(x)")
 
# zobrazení grafu
plt.show()

7. Přidání popisků do grafů

Nyní se již dostáváme k poněkud složitějšímu úkolu. Předpokládejme, že je do grafu se dvěma funkcemi zapotřebí přidat popisky se šipkami ukazujícími na určité místo na křivce. Výsledek by měl vypadat nějak takto:

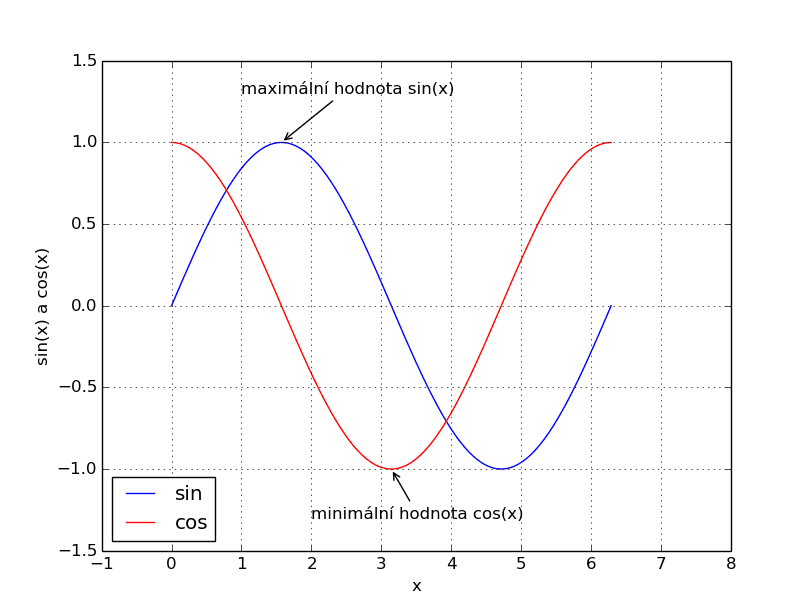
Obrázek 15: Graf s přidanými popiskami.

Průběhy obou funkcí si necháme vykreslit nám již známým způsobem, zde tedy k žádné podstatné změně nedojde. Ovšem pro přidání popisků již musíme použít novou funkci, konkrétně funkci pojmenovanou matplotlib.pyplot.annotate(). Této funkci se předá jeden nepojmenovaný parametr s popiskem, tj. například „maximální hodnota sin(x)“. Dále budou následovat pojmenované parametry, konkrétně parametr se jménem xy a přesnou souřadnicí vrcholu šipky (tj. místa, kam šipka míří), dále pak parametr se jménem xytext, jehož hodnotou je souřadnice umístění textu (n-tice) a posledním parametrem je parametr s názvem arrowprops (properties), přes nějž nastavíme styl vykreslené šipky.

Do grafu ve skutečnosti vložíme dva popisky, což je ostatně patrné z výpisu zdrojového kódu tohoto diáře:

Obrázek 16: Diář s kódem pro vykreslení grafu.

Úplný skript:

# Jupyter Notebook
#
# Sedmý demonstrační příklad:
# - vykreslení průběhů funkcí sin a cos
# - nastavení mřížky
# - nastavení rozsahů na obou osách
# - přidání popisku přímo do grafu
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
 
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
 
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x)
 
# vykreslit průběh obou funkcí
# se změnou stylu vykreslování
plt.plot(x, y1, "b-", label="sin")
plt.plot(x, y2, "r-", label="cos")
 
# přidání legendy
plt.legend(loc="lower left")
 
# nastavení rozsahů na obou osách
plt.axis([-1, 8, -1.5, 1.5])
 
# povolení zobrazení mřížky
plt.grid(True)
 
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a cos(x)")
 
# vložit první popisek do grafu
plt.annotate("maximální hodnota sin(x)",
             xy=(np.pi/2, 1.0),
             xytext=(1, 1.3),
             arrowprops=dict(arrowstyle="->"))
 
# vložit druhý popisek do grafu
plt.annotate("minimální hodnota cos(x)",
             xy=(np.pi, -1.0),
             xytext=(2, -1.3),
             arrowprops=dict(arrowstyle="->"))
 
# zobrazení grafu
plt.show()

8. Základní polární graf

Pokud je zapotřebí vykreslit polární graf, je možné postupovat následujícím způsobem. Nejprve se plocha obrázku či dokumentu určená pro vykreslení grafu rozdělí do pomyslné mřížky o velikosti 1×1 buňka. Do této mřížky se funkcí matplotlib.pyplot.subplot() vloží „podgraf“, u něhož se pojmenovaným parametrem projection specifikuje použitá projekce. Magická konstanta 111 při volání této funkce značí, že se skutečně má vytvořit mřížka 1×1 buňka a podgraf se má vložit do této buňky (ta má index 1). Další vykreslování již vlastně známe, ovšem s tím nepatrným rozdílem, že se nevolá funkce matplotlib.pyplot.plot(), ale metoda objektu získaného výše zmíněnou funkcí matplotlib.pyplot.subplot(). Dále si povšimněte toho, že namísto polí pojmenovaných x a y používáme pole hodnot se jmény theta a radius, což se pro tento typ grafu hodí mnohem více:

Obrázek 17: Diář s kódem pro vykreslení grafu.

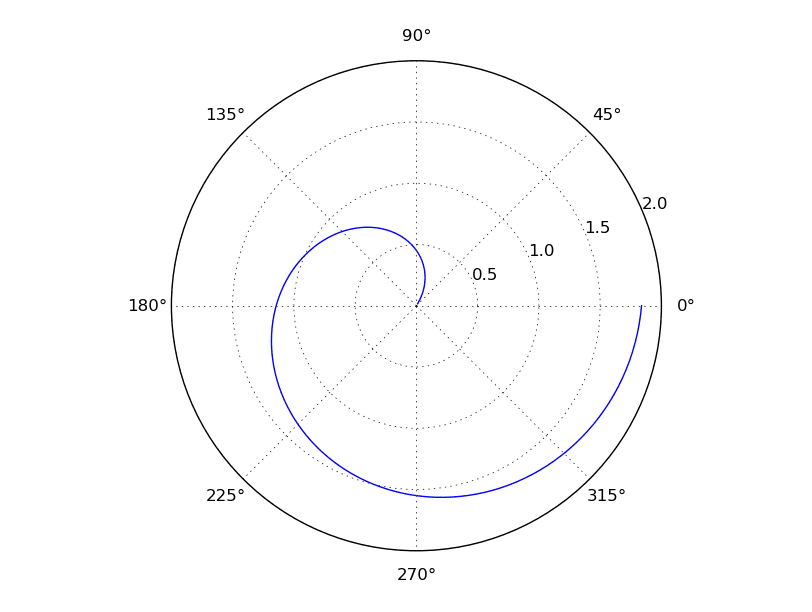
Obrázek 18: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Osmý demonstrační příklad:
# - základní polární graf
 
import numpy as np
import matplotlib.pyplot as plt
 
# úhel v polárním grafu
theta = np.linspace(0.01, 2*np.pi, 150)
 
# vzdálenost od středu
radius = np.log(theta)
 
ax = plt.subplot(111, projection="polar")
 
# vykreslit průběh funkce
# v polárním grafu
ax.plot(theta, radius)
 
# zobrazení grafu
plt.show()

9. Vykreslení průběhů většího množství funkcí v polárním grafu

Podobně, jako tomu bylo u normálního grafu se dvěma na sebe kolmými osami, i v polárním grafu je možné současně zobrazit větší množství průběhů funkcí; postačuje pouze volat několikrát metodu plot objektu získaného voláním funkce matplotlib.pyplot.subplot(). Taktéž je možné specifikovat styl zobrazení průběhu jednotlivých funkcí, pojmenovat daný průběh (resp. přesněji řečeno mu přiřadit jméno) apod. V dnešním předposledním demonstračním příkladu jsou v polárním grafu zobrazeny průběhy tří funkcí – dvě funkce vytvoří spirálu (první je lineární, druhá pak logaritmická), třetí funkce má v polárním grafu tvar srdce. Podívejme se na zdrojový kód tohoto diáře:

Obrázek 19: Diář s kódem pro vykreslení grafu.

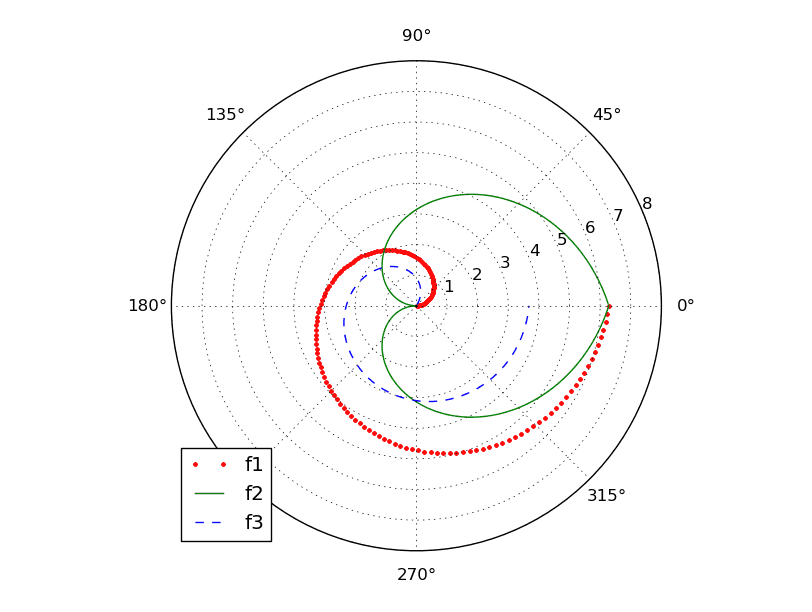
Obrázek 20: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Devátý demonstrační příklad:
# - vykreslení průběhů několika funkcí
# - do polárního grafu
 
import numpy as np
import matplotlib.pyplot as plt
 
# úhel v polárním grafu
theta = np.linspace(0.01, 2*np.pi, 150)
 
# první funkce: vzdálenost od středu
radius1 = theta
 
# druhá funkce: vzdálenost od středu
radius2 = 2*np.abs(theta-np.pi)
 
# třetí funkce: vzdálenost od středu
radius3 = 2*np.log(theta)
 
ax = plt.subplot(111, projection="polar")
 
# vykreslit průběh první funkce
# v polárním grafu
ax.plot(theta, radius1, "r.", label="f1")
 
# vykreslit průběh druhé funkce
# v polárním grafu
ax.plot(theta, radius2, "g", label="f2")
 
# vykreslit průběh třetí funkce
# v polárním grafu
ax.plot(theta, radius3, "b--", label="f3")
 
# přidání legendy
plt.legend(loc="lower left")
 
# zobrazení grafu
plt.show()

10. Vyplnění plochy pod funkcí v polárním grafu

I funkce, jejichž průběh má být vykreslen v polárním grafu, mohou být pod svou křivkou vyplněny, postačuje pouze namísto metody nazvané plot() zavolat metodu pojmenovanou fill(). Většinou je navíc nutné u vyplněného průběhu funkce specifikovat kromě barvy i průhlednost vykreslované plochy (v našem případě bude nastavena na 30%). V dalším diáři jsou vykresleny dvě funkce, jedna s použitím metody plot(), druhá pak pomocí fill(). Navíc si povšimněte další zajímavé vlastnosti – pole theta obsahující úhly je naplněno prvky s hodnotami od 0 až do 4π. Co to znamená v praxi? – z pohledu na obrázek s grafem je patrné, že jsou zobrazeny dvě celé otočky spirály, protože 4π rad odpovídá 720°:

Obrázek 21: Diář s kódem pro vykreslení grafu.

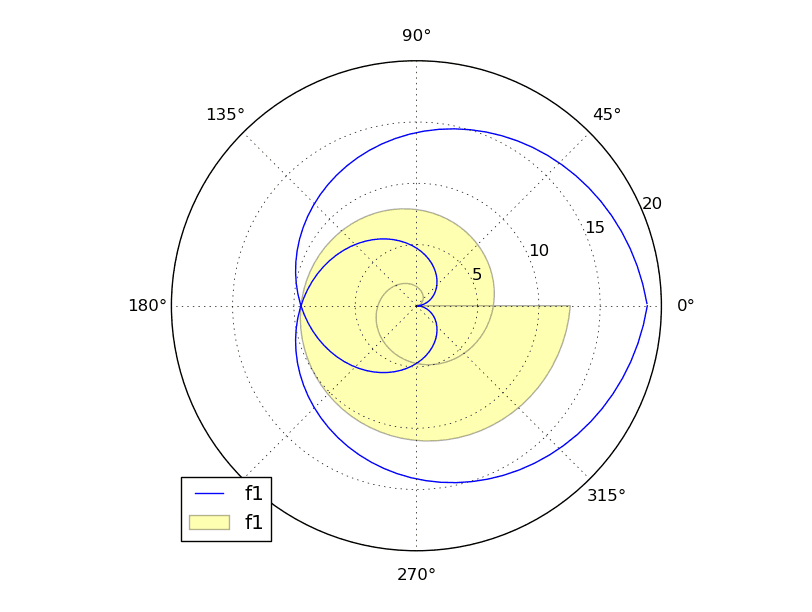
Obrázek 22: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Desátý demonstrační příklad:
# - vykreslení průběhů několika funkcí
# - do polárního grafu
 
import numpy as np
import matplotlib.pyplot as plt
 
# úhel v polárním grafu
theta = np.linspace(0.01, 4*np.pi, 150)
 
# první funkce: vzdálenost od středu
radius1 = theta
 
# druhá funkce: vzdálenost od středu
radius2 = 3*np.abs(theta-2*np.pi)
 
ax = plt.subplot(111, projection="polar")
 
# vykreslit průběh první funkce
# v polárním grafu
ax.plot(theta, radius2, "b", label="f1")
 
# vykreslit průběh druhé funkce
# v polárním grafu
ax.fill(theta, radius1, "yellow", alpha=0.3, label="f1")
 
# přidání legendy
plt.legend(loc="lower left")
 
# zobrazení grafu
plt.show()

11. Graf používající „schodky“

V některých případech nám nemusí výše popsaný způsob vykreslení průběhů funkcí vyhovovat. Knihovna Matplotlib nám samozřejmě vychází vstříc, protože nabízí i další styly vykreslování, přičemž poměrně zajímavý a užitečný styl je založen na vykreslení „schodů“. Jedná se vlastně o přechodový typ grafu, v němž se sice stále vykresluje (spojitá) křivka, ovšem její tvar se již začíná podobat sloupcovému grafu (to je někdy poměrně důležité, protože můžeme naznačit například vzorkování apod.). Použití „schodků“ je vlastně velmi jednoduché, protože do příkazu pro vykreslení průběhu jedné funkce postačuje doplnit pojmenovaný parametr drawstyle a přiřadit mu hodnotu default:

Podívejme se na jednoduchý demonstrační příklad, v němž se v jednom grafu kombinují oba dva způsoby vykreslování – obálky funkce sinc jsou vykresleny lomenou čarou zatímco samotná funkce sinc je vykreslena s využitím „schodů“. Parametr drawstyle lze samozřejmě vynechat ve chvíli, kdy je mu přiřazena hodnota „default“:

Obrázek 23: Diář s kódem pro vykreslení grafu.

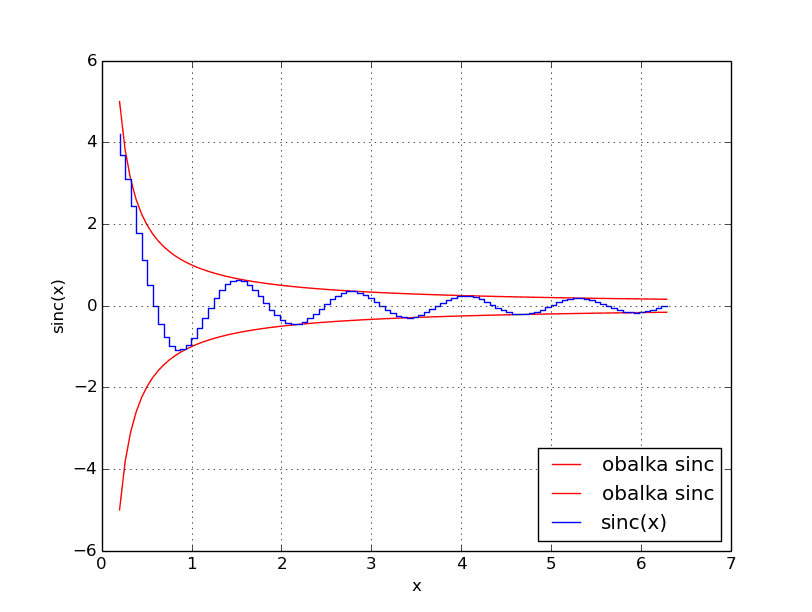
Obrázek 24: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Dvanáctý demonstrační příklad:
# - vykreslení průběhu funkce sinc
# - při vykreslování se použijí "schodky"
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.linspace(0.2, 2*np.pi, 100)
 
# hodnoty na y-ové ose
y = np.sin(5*x)/x
y2 = 1/x
y3 = -y2
 
# vykreslit průběh funkce
plt.plot(x, y2, color='red',  label='obalka sinc', drawstyle='default')
plt.plot(x, y3, color='red',  label='obalka sinc', drawstyle='default')
plt.plot(x, y,  color='blue', label='sinc(x)',     drawstyle='steps')
 
# povolení zobrazení mřížky
plt.grid(True)
 
# popis os
plt.xlabel("x")
plt.ylabel("sinc(x)")
 
# přidání legendy
plt.legend(loc="lower right")
 
# zobrazení grafu
plt.show()

12. Jednoduchý sloupcový graf

Nyní se již dostáváme k dalšímu populárnímu a velmi často používanému typu grafu. Jedná se o sloupcový graf, přičemž sloupce (odpovídající naměřeným nebo vypočteným hodnotám) mohou být buď vodorovné nebo – a to častěji – svislé. Pro tvorbu sloupcového grafu se používají funkce matplotlib.pyplot.bar() (sloupce jsou svislé), popř. matplotlib.pyplot.barh() (sloupce jsou vodorovné). První dva parametry těchto funkcí jsou povinné – v obou případech se jedná o pole, přičemž první pole obsahuje x-ové souřadnice sloupců (většinou se tedy jedná o pole vytvořené příkazem numpy.arange(počet_prvků)) a pole druhé obsahuje výšky sloupců. Třetí parametr je nepovinný, ovšem poměrně důležitý, protože obsahuje relativní šířku sloupců. Tu můžeme zadat buď skalární hodnotou (což je obvyklé řešení) nebo taktéž pomocí pole. To znamená, že je možné vykreslit graf se sloupci, které mají rozdílnou šířku.

Pro demonstrační příklad na vykreslení sloupcového grafu jsem vybral reálná data. Konkrétně se jedná o (v době vydaní článku již historické) ceny ropy uvedené v dolarech za barel (předevčírem by graf musel zobrazit záporné hodnoty). Při vykreslování byly funkci matplotlib.pyplot.bar() předány tři nepovinné parametry určující barvu výplně sloupců, barvu okrajů sloupců a popisek datové řady:

Obrázek 25: Diář s kódem pro vykreslení grafu.

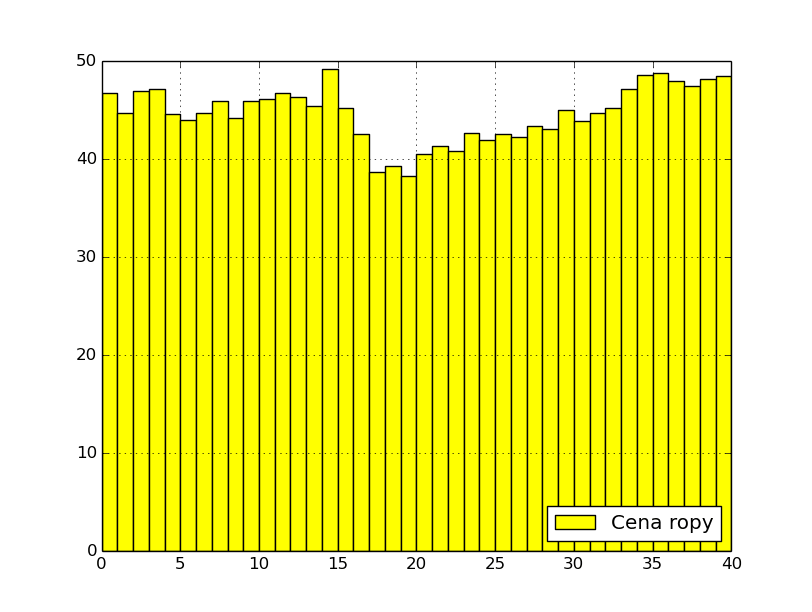
Obrázek 26: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Třináctý demonstrační příklad:
# - jednoduchý sloupcový graf
 
import numpy as np
import matplotlib.pyplot as plt
 
# historické ceny ropy
cena_ropy = [
    46.68, 44.68, 46.90, 47.15, 44.59, 44.00, 44.63, 45.92, 44.15, 45.94,
    46.05, 46.75, 46.25, 45.41, 49.20, 45.22, 42.56, 38.60, 39.31, 38.24,
    40.45, 41.32, 40.80, 42.62, 41.87, 42.50, 42.23, 43.30, 43.08, 44.96,
    43.87, 44.66, 45.15, 47.12, 48.52, 48.79, 47.98, 47.39, 48.14, 48.45]
 
# počet prvků
N = len(cena_ropy)
 
# indexy prvků
indexes = np.arange(N)
 
# šířka sloupců
width = 1.00
 
# sloupcový graf
plt.bar(indexes, cena_ropy, width, color='yellow', edgecolor='black',
        label='Cena ropy')
 
# povolení zobrazení mřížky
plt.grid(True)
 
# přidání legendy
plt.legend(loc="lower right")
nbsp;
# zobrazení grafu
plt.show()

13. Sloupcový graf se dvěma skupinami sloupců

Popišme si, co se stane ve chvíli, kdy se pokusíme do jediného grafu vykreslit dvě datové řady. Předpokládejme, že hodnoty první datové řady jsou uloženy v poli vals1, hodnoty řady druhé pak v poli pojmenovaném vals2. Indexy, tj. vlastně x-ové souřadnice sloupců, jsou shodné. Takto navržený graf nám v mnoha případech pochopitelně nebude vyhovovat. Řešení je však jednoduché – postačuje posunout sloupce pro druhou (třetí, čtvrtou …) řadu doprava. To se provede jednoduše přičtením skalární hodnoty k poli indexes. Proč toto řešení bude funkční? V knihovně Numpy byl pro operace s poli (vektory, maticemi) přetížen operátor +, který zadanou skalární hodnotu přičte ke všem prvkům.

Obrázek 27: Diář s kódem pro vykreslení grafu.

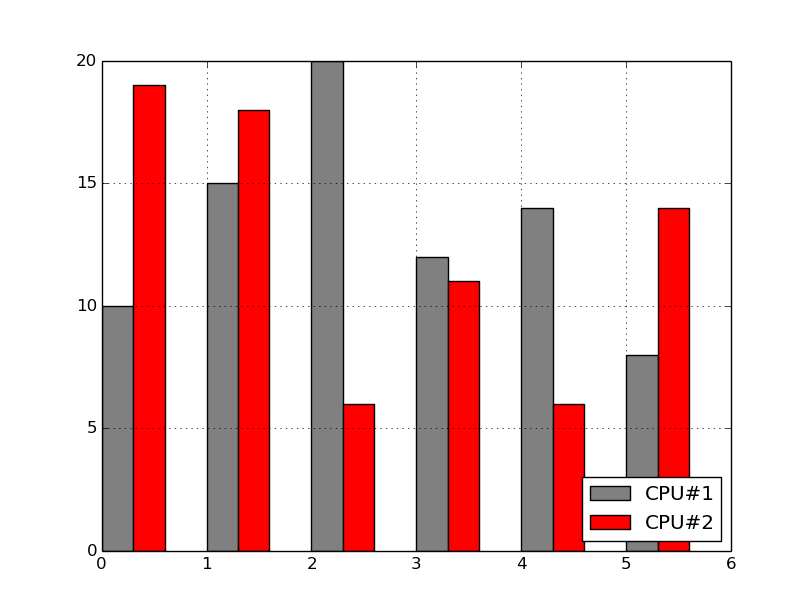
Obrázek 28: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Čtrnáctý demonstrační příklad:
# - sloupcový graf se dvěma skupinami sloupců
 
import numpy as np
import matplotlib.pyplot as plt
 
# první pole hodnot
vals1 = [10, 15, 20, 12, 14, 8]
 
# druhé pole hodnot
vals2 = [19, 18,  6, 11,  6, 14]
 
# počet prvků
N = len(vals1)
 
# indexy prvků
indexes = np.arange(N)
 
# šířka sloupců
width = 0.30
 
# sloupcový graf se dvěma skupinami sloupců
plt.bar(indexes, vals1, width, color='gray', edgecolor='black', label='CPU#1')
# posunuté sloupce
plt.bar(indexes+width, vals2, width, color='red', edgecolor='black',
        label='CPU#2')
 
# povolení zobrazení mřížky
plt.grid(True)
 
# přidání legendy
plt.legend(loc="lower right")
 
# zobrazení grafu
plt.show()

14. Zobrazení histogramu

Dalším typem grafu, který je možné při použití knihovny Matplotlib použít, je histogram. Ten se vykresluje funkcí pojmenovanou logicky matplotlib.pyplot.hist(). Povinným parametrem jsou podle očekávání data, která se mají do histogramu vykreslit, ovšem funkce matplotlib.pyplot.hist() podporuje i další nepovinné parametry, zejména parametr normed řídicí normalizaci histogramu. Dalším mnohdy důležitým nepovinným parametrem je bins, jehož hodnotou se řídí šířka intervalů (tříd), tj. nepřímo počet sloupců v histogramu. Podívejme se na několik ukázek, z nichž bude použití nepovinného parametru bins patrné:

Obrázek 29: Diář s kódem pro vykreslení grafu.

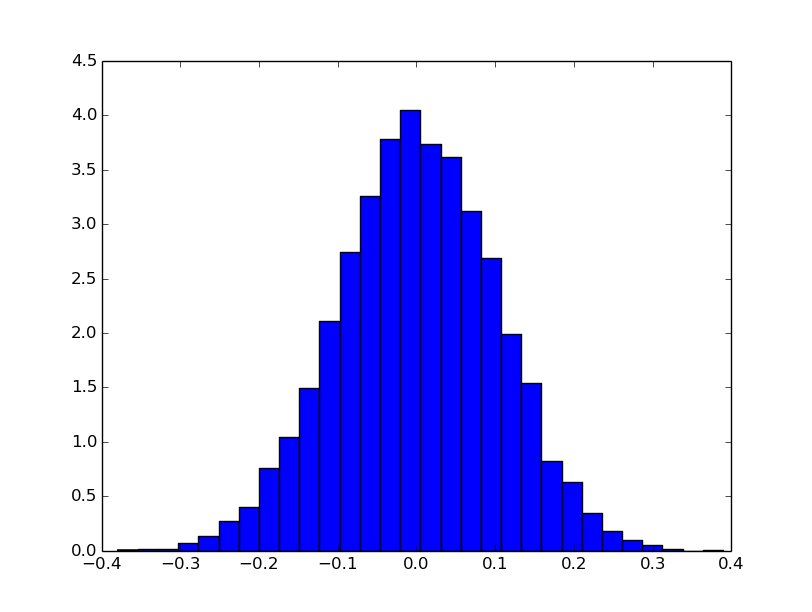
Obrázek 30: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Patnáctý demonstrační příklad:
# - jednoduchý histogram
 
import numpy as np
import matplotlib.pyplot as plt
 
# náhodné hodnoty
y = np.random.normal(0, 0.1, 10000)
 
plt.hist(y, bins=30, range=None, density=True)
 
# zobrazení grafu
plt.show()

15. Koláčový graf

Dalším typem grafu, s nímž se v dnešním článku seznámíme, jsou takzvané koláčové grafy, které již každý čtenář zcela jistě viděl. Tyto typy grafů se používají v případě, že nás nezajímají absolutní hodnoty, ale hodnoty relativní, konkrétně vzájemné poměry. Nejprve se podívejme, jak může koláčový graf vykreslený knihovnou Matplotlib vypadat. V grafu je zobrazeno zastoupení skriptovacích jazyků, přičemž nás nyní nezajímá, v kolika projektech se jednotlivé jazyky použily, ale jaké jsou poměry tohoto zastoupení:

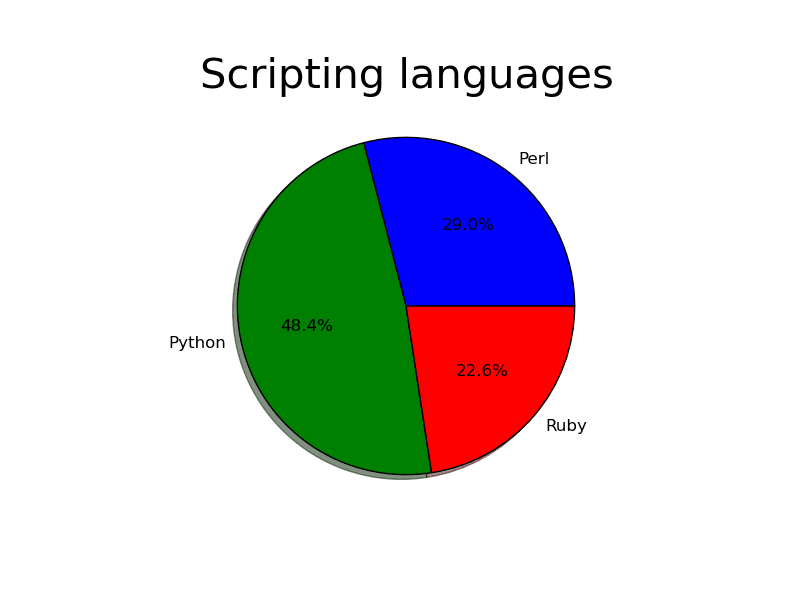
Obrázek 31: Výsledný graf.

Při vykreslení koláčového grafu můžeme použít přímo funkci matplotlib.pyplot.pie(), popř. lze použít podobný postup, jakým jsme o několik kapitol výše vykreslili polární graf. Důležitý je především fakt, že koláčovému grafu můžeme předat pole s libovolnými hodnotami, nemusí se tedy jednat ani o procentuální poměry (se součtem 100%) ani o relativní hodnoty (se součtem 1.00). Knihovna Matplotlib si z předaných hodnot poměry vypočte automaticky. Dále si povšimněte použití nepovinného pojmenovaného parametru labels (s popisem jednotlivých výřezů) a parametru shadow, kterým se povoluje či zakazuje zobrazení 3D stínu:

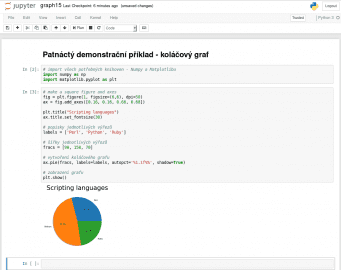
Obrázek 32: Diář s kódem pro vykreslení grafu.

Úplný skript:

# Jupyter Notebook
#
# Šestnáctý demonstrační příklad:
# - koláčový graf
 
from matplotlib import pyplot as plt
from matplotlib import font_manager as fm
 
# make a square figure and axes
fig = plt.figure(1, figsize=(6, 6), dpi=50)
ax = fig.add_axes([0.16, 0.16, 0.68, 0.68])
 
plt.title("Scripting languages")
ax.title.set_fontsize(30)
 
# popisky jednotlivých výřezů
labels = ['Perl', 'Python', 'Ruby']
 
# šířky jednotlivých výřezů
fracs = [90, 150, 70]
 
# vytvoření koláčového grafu
ax.pie(fracs, labels=labels, autopct='%1.1f%%', shadow=True)
 
# zobrazení grafu
plt.show()

16. Změna stylu vykreslování koláčových grafů

Koláčové grafy je samozřejmě možné upravovat. V této kapitole si ukážeme, jak se v grafu změní barvy jednotlivých výřezů a jak se jeden (nebo v případě potřeby i větší množství) výřezů „vysune“ od středové osy. Výsledkem bude následující obrázek:

Změnu velikosti nadpisu zařizuje metoda set_fontsize(), změnu stylu písma pak kombinace set_size() společně s nastavením vlastností (properties) písma. Pravděpodobně nejdůležitější je však nepovinný parametr explode funkce matplotlib.pyplot.pie(), kterému se předá pole s relativními hodnotami určujícími míru vysunutí jednotlivých řezů:

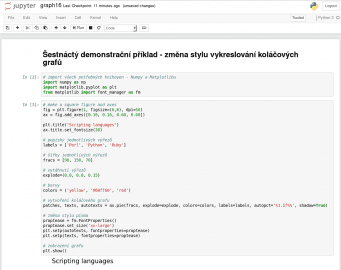
Obrázek 33: Diář s kódem pro vykreslení grafu.

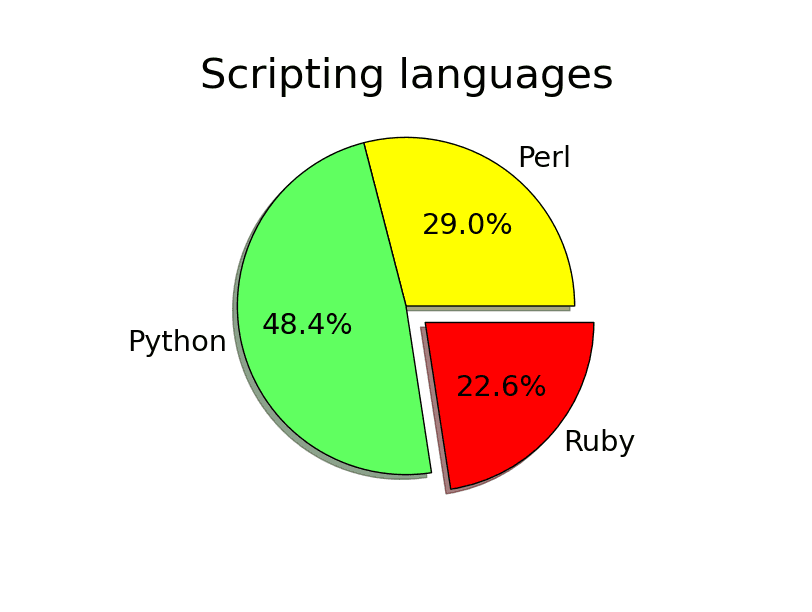
Obrázek 34: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Sedmnáctý demonstrační příklad:
# - změna stylu koláčových grafů
 
from matplotlib import pyplot as plt
from matplotlib import font_manager as fm
 
 
# make a square figure and axes
fig = plt.figure(1, figsize=(6, 6), dpi=50)
ax = fig.add_axes([0.16, 0.16, 0.68, 0.68])
 
plt.title("Scripting languages")
ax.title.set_fontsize(30)
 
# popisky jednotlivých výřezů
labels = ['Perl', 'Python', 'Ruby']
 
# šířky jednotlivých výřezů
fracs = [90, 150, 70]
 
# vytáhnutí výřezů
explode = (0.0, 0.0, 0.15)
 
# barvy
colors = ('yellow', '#60ff60', 'red')
 
# vytvoření koláčového grafu
patches, texts, autotexts = ax.pie(fracs, explode=explode, colors=colors,
                                   labels=labels, autopct='%1.1f%%',
                                   shadow=True)
 
# změna stylu písma
proptease = fm.FontProperties()
proptease.set_size('xx-large')
plt.setp(autotexts, fontproperties=proptease)
plt.setp(texts, fontproperties=proptease)
 
# zobrazení grafu
plt.show()

17. Sloupcový graf se zobrazením odchylek (či chyb)

Vraťme se ještě na chvíli ke sloupcovým grafům. V některých případech je nutné ke sloupcům přidat i povolené odchylky či chyby. I to je samozřejmě možné, a to díky existenci nepovinného pojmenovaného parametru yerr, kterému se předá buď skalární hodnota nebo pole o stejné délce, jakou má samotné vstupní pole hodnot. Podívejme se na způsob úpravy sloupcového grafu se dvěma datovými řadami o zobrazení odchylek. Tyto odchylky jsou uloženy v polích delta1 a delta2:

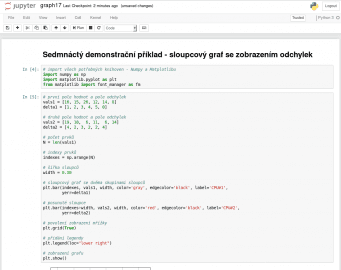
Obrázek 35: Diář s kódem pro vykreslení grafu.

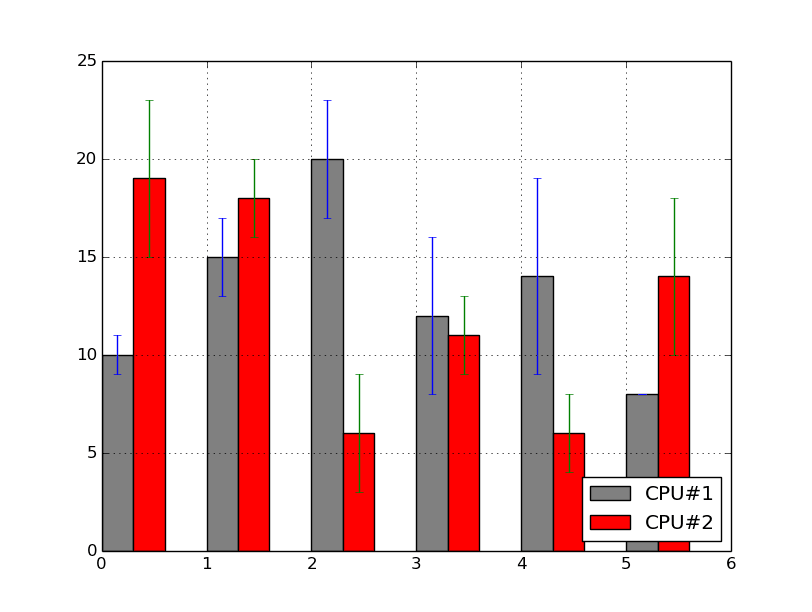
Obrázek 36: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Osmnáctý demonstrační příklad:
# - sloupcový graf se dvěma skupinami sloupců
#   a se zobrazením odchylek
 
import numpy as np
import matplotlib.pyplot as plt
 
# první pole hodnot a pole odchylek
vals1 = [10, 15, 20, 12, 14, 8]
delta1 = [1, 2, 3, 4, 5, 0]
 
# druhé pole hodnot a pole odchylek
vals2 = [19, 18,  6, 11,  6, 14]
delta2 = [4, 2, 3, 2, 2, 4]
 
# počet prvků
N = len(vals1)
 
# indexy prvků
indexes = np.arange(N)
 
# šířka sloupců
width = 0.30
 
# sloupcový graf se dvěma skupinami sloupců
plt.bar(indexes, vals1, width, color='gray', edgecolor='black', label='CPU#1',
        yerr=delta1)
 
# posunuté sloupce
plt.bar(indexes+width, vals2, width, color='red', edgecolor='black',
        label='CPU#2', yerr=delta2)
 
# povolení zobrazení mřížky
plt.grid(True)
 
# přidání legendy
plt.legend(loc="lower right")
 
# zobrazení grafu
plt.show()

18. Pokročilejší nastavení způsobu vykreslení odchylek

Pokud budeme potřebovat změnit styl vykreslení odchylek/chyb, záhy zjistíme, že funkce matplotlib.pyplot.pie() nemá žádné povinné ani nepovinné parametry, které by bylo pro tento účel možné přímo použít! Ve skutečnosti se totiž všechny podobné parametry ukládají do slovníku (dictionary) předaného v pojmenovaném parametru error_kw. Podívejme se tedy, jak se změní barva a šířka úsečky vykreslených odchylek (přímo při vytváření slovníku ho i inicializujeme):

Obrázek 37: Diář s kódem pro vykreslení grafu.

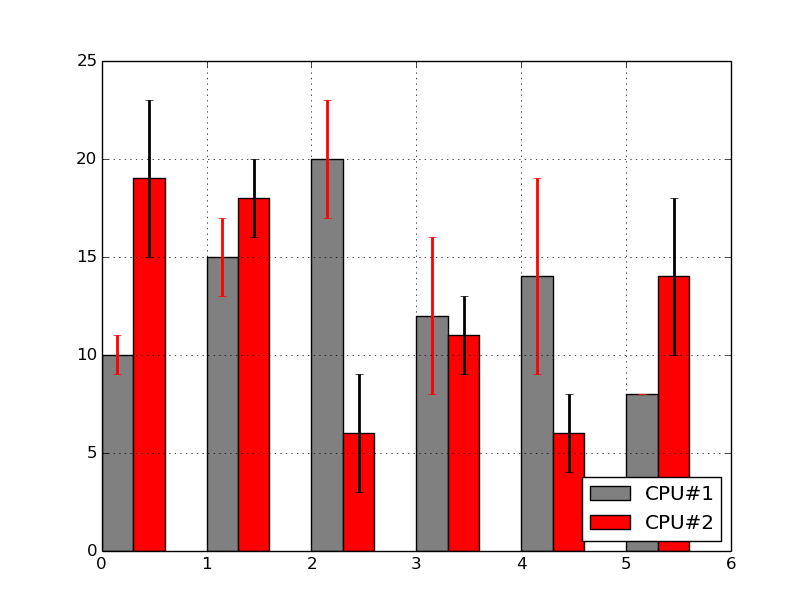
Obrázek 38: Výsledný graf.

Úplný skript:

# Jupyter Notebook
#
# Devatenáctý demonstrační příklad:
# - sloupcový graf se dvěma skupinami sloupců
#   a se zobrazením odchylek
 
import numpy as np
import matplotlib.pyplot as plt
 
# první pole hodnot a pole odchylek
vals1 = [10, 15, 20, 12, 14, 8]
delta1 = [1, 2, 3, 4, 5, 0]
 
# druhé pole hodnot a pole odchylek
vals2 = [19, 18,  6, 11,  6, 14]
delta2 = [4, 2, 3, 2, 2, 4]
 
# počet prvků
N = len(vals1)
 
# indexy prvků
indexes = np.arange(N)
 
# šířka sloupců
width = 0.30
 
# sloupcový graf se dvěma skupinami sloupců
plt.bar(indexes, vals1, width, color='gray', edgecolor='black', label='CPU#1',
        yerr=delta1, error_kw=dict(elinewidth=2, ecolor='red'))
 
# posunuté sloupce
plt.bar(indexes+width, vals2, width, color='red', edgecolor='black',
        label='CPU#2',
        yerr=delta2, error_kw=dict(elinewidth=2, ecolor='black'))
 
# povolení zobrazení mřížky
plt.grid(True)
 
# přidání legendy
plt.legend(loc="lower right")
 
# zobrazení grafu
plt.show()

19. Repositář s demonstračními příklady (diáři)

Všechny demonstrační příklady (resp. přesněji řečeno diáře), s nimiž jsme se seznámili v předchozích kapitolách, byly uloženy do Git repositáře umístěného na GitHubu (https://github.com/tisnik/jupyter-notebook-examples/). Poslední verze souborů s diáři naleznete pod odkazy uvedenými v tabulce pod tímto odstavcem. Diář by se měl otevřít přímo v rámci stránky GitHubu:

20. Odkazy na Internetu

1. Notebook interface
   https://en.wikipedia.org/wi­ki/Notebook_interface
2. Jypyter: open source, interactive data science and scientific computing across over 40 programming languages
   https://jupyter.org/
3. Matplotlib Home Page
   http://matplotlib.org/
4. Matplotlib (Wikipedia)
   https://en.wikipedia.org/wi­ki/Matplotlib
5. Popis barvových map modulu matplotlib.cm
   https://gist.github.com/en­dolith/2719900#id7
6. Ukázky (palety) barvových map modulu matplotlib.cm
   http://matplotlib.org/exam­ples/color/colormaps_refe­rence.html
7. Galerie grafů vytvořených v Matplotlibu
   https://matplotlib.org/3.2.1/gallery/
8. showcase example code: xkcd.py
   https://matplotlib.org/xkcd/e­xamples/showcase/xkcd.html
9. Customising contour plots in matplotlib
   https://philbull.wordpres­s.com/2012/12/27/customising-contour-plots-in-matplotlib/
10. Graphics with Matplotlib
    http://kestrel.nmt.edu/~ra­ymond/software/python_notes/pa­per004.html
11. The IPython Notebook
    http://ipython.org/notebook.html
12. nbviewer: a simple way to share Jupyter Notebooks
    https://nbviewer.jupyter.org/
13. Back to the Future: Lisp as a Base for a Statistical Computing System
    https://www.stat.auckland­.ac.nz/~ihaka/downloads/Com­pstat-2008.pdf
14. gg4clj: a simple wrapper for using R's ggplot2 in Clojure and Gorilla REPL
    https://github.com/JonyEpsilon/gg4clj
15. Analemma: a Clojure-based SVG DSL and charting library
    http://liebke.github.io/analemma/
16. Clojupyter: a Jupyter kernel for Clojure
    https://github.com/roryk/clojupyter
17. Incanter is a Clojure-based, R-like platform for statistical computing and graphics.
    http://incanter.org/
18. Evolution of incanter (Gource Visualization)
    https://www.youtube.com/wat­ch?v=TVfL5nPELr4
19. Questions tagged [incanter] (na Stack Overflow)
    https://stackoverflow.com/qu­estions/tagged/incanter?sor­t=active
20. Data Sorcery with Clojure
    https://data-sorcery.org/contents/
21. What is REPL?
    https://pythonprogramminglan­guage.com/repl/
22. What is a REPL?
    https://codewith.mu/en/tu­torials/1.0/repl
23. Programming at the REPL: Introduction
    https://clojure.org/guides/re­pl/introduction
24. What is REPL? (Quora)
    https://www.quora.com/What-is-REPL
25. Gorilla REPL: interaktivní prostředí pro programovací jazyk Clojure
    https://www.root.cz/clanky/gorilla-repl-interaktivni-prostredi-pro-programovaci-jazyk-clojure/
26. R Markdown: The Definitive Guide
    https://bookdown.org/yihui/rmarkdown/
27. Single-page application
    https://en.wikipedia.org/wiki/Single-page_application
28. Video streaming in the Jupyter Notebook
    https://towardsdatascience.com/video-streaming-in-the-jupyter-notebook-635bc5809e85
29. How IPython and Jupyter Notebook work
    https://jupyter.readthedoc­s.io/en/latest/architectu­re/how_jupyter_ipython_wor­k.html
30. Jupyter kernels
    https://github.com/jupyter/ju­pyter/wiki/Jupyter-kernels
31. Keras: The Python Deep Learning library
    https://keras.io/
32. TensorFlow
    https://www.tensorflow.org/
33. PyTorch
    https://pytorch.org/
34. Seriál Torch: framework pro strojové učení
    https://www.root.cz/serialy/torch-framework-pro-strojove-uceni/
35. Scikit-learn
    https://scikit-learn.org/stable/
36. Java Interop (Clojure)
    https://clojure.org/referen­ce/java_interop
37. Obrazy s balíčky Jupyter Notebooku pro Docker
    https://hub.docker.com/u/jupyter/#!
38. Správce balíčků Conda (dokumentace)
    https://docs.conda.io/en/latest/
39. Lorenzův atraktor
    https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-vi/#k02
40. Lorenzův atraktor
    https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03
41. Graphics with Matplotlib
    http://kestrel.nmt.edu/~ra­ymond/software/python_notes/pa­per004.html