Obsah
1. Fraktály kolem nás
2. Fyzikální jevy, při nichž lze pozorovat fraktály
3. Difúze
4. Stav magnetického materiálu při Courierově teplotě
5. Blesky
6. Využití fraktálů v technice, biologii a medicíně
6.1 Fraktální antény
6.2 Rozmístění součástek na plošném spoji
6.3 Biologie a medicína
6.4 Architektura
7. Fraktály a zpracování obrazu
7.1 Fraktální komprimace obrazů
7.2 Rozpoznávání obrazů
8. Odkazy na další informační zdroje
9. Obsah dalšího pokračování tohoto seriálu
1. Fraktály kolem nás
Dvě velmi významné knihy, které se zabývají fraktální geometrií, soběpodobností a vztahem mezi řádem a chaosem, se jmenují Fractal Geometry of Nature (autorem je známý Benoit B. Mandelbrot) a Fractals Everywhere (autorem je neméněznámý Michael Barnsley). Názvy těchto knižních titulů v žádném případě nepřehánějí – mnoho přírodních objektů vykazuje fraktální vlastnosti, například soběpodobnost či soběpříbuznost. A nejenom to: na fraktály můžeme narazit ve fyzice, chemii, biologii a mnoha dalších vědních disciplínách, které nemají se studiem geometrických objektů zdánlivě nic společného. Některé jevy, ve kterých lze nalézt fraktály, si ukážeme v následujících kapitolách.

V přírodě je možné na objekty s fraktální strukturou narazit doslova na každém kroku. Každý strom či keř je v určitých měřítkách soběpříbuzný, fraktální strukturu můžeme nalézt i u nižších rostlin, oblak, povrchu kamenů atd. Dnes již klasickým případem jsou pobřeží ostrovů a břehy říčních toků, které je možné modelovat pomocí stochastických fraktálů. Také povrch planet, zejména pohoří, mají zřetelnou fraktální strukturu, na což ostatně poukázal i Benoit Mandelbrot ve výše zmíněné publikaci.
2. Fyzikální jevy, při nichž lze pozorovat fraktály
S fraktálními objekty a fyzikálními jevy vykazujícími fraktální charakteristiky (soběpodobnost, soběpříbuznost, nezávislost na změně měřítka) se můžeme setkat kupodivu velmi často. V dalších dvou kapitolách si popíšeme pravděpodobně nejznámější fyzikální jevy, které mají společnou jednu vlastnost – jejich modelování je možné s úspěchem provádět právě pomocí fraktálů. Jedná se o známou difúzi, resp. prostorový či plošný obrazec, který můžeme pozorovat při difúzi jedné kapaliny do kapaliny druhé (místo kapaliny se však obecně může jednat i o plyn či pevné částice), a dále o stav materiálu při teplotě blízké Courierovu bodu, tj. v okamžiku, kdy se materiál se zvyšující se teplotou stává nemagnetickým (či naopak magnetickým, pokud se teplota snižuje).

3. Difúze
Difúze je (velmi zjednodušeně řečeno) přírodní jev, při kterém jsou pevné, kapalné či plynné částečky jedné hmoty postupně roznášeny v jiné pevné, kapalné či plynné hmotě. Pohyb těchto částeček, který se nazývá Brownovým pohybem (Brownian Motion), vzniká vlivem náhodných nárazů molekul jedné hmoty a hmoty druhé – viz další ilustrační obrázek. Poprvé byl Brownův pohyb popsán již v předminulém století jako pohyb mikroskopických částeček pylu ve vodě. Zdůvodnění fyzikální podstaty tohoto pohybu však bylo podáno až Einsteinem v roce 1905. Základem pro studium různých rozšíření a zobecnění Brownova pohybu je takzvaný Weinerův skalární Brownův pohyb – ten lze, jakožto nejjednodušší formu Brownova pohybu, snadno analyzovat. Na difúzi se můžeme dívat jako na stochastický fraktální objekt, na kterém je mnohdy už na první pohled patrná soběpříbuznost. Současně se jedná o typický příklad takzvaného větévkatého fraktálu.

4. Stav magnetického materiálu při Courierově teplotě
Další vědní oblastí (na pomezí fyziky a chemie), ve které byly objeveny a využity fraktály, je zkoumání změny stavu některých materiálů. Podrobně byla studována například změna stavu magnetického materiálu na materiál nemagnetický (a naopak). Materiál je uspořádán z elementarních magnetů, které v závislosti na teplotě určují, zda je dané těleso jako celek magnetické či nikoliv. Při nízkých teplotách je materiál jako celek magnetický, ale při mikroskopickém pohledu existují jisté lokální fluktuace, kde nejsou elementární magnety uspořádané. Naopak, za dostatečně vysoké teploty je materiál jako celek nemagnetický, ale existují malé domény, ve kterých jsou elementární magnety uspořádány.

Vlastnost magnetismu je tedy závislá na měřítku pohledu na materiál. Při kritické teplotě (takzvaná Curierova teplota) materiál přechází z magnetického stavu do stavu nemagnetického a naopak. Jestliže je materiál zahříván na tuto teplotu, vypadají jeho magnetické domény stejně (či podobně) ve všech měřítkách (zvětšeních) a přitom mají fraktální strukturu. Při této teplotě také nemůžeme jednoznačně určit, zda je materiál magnetický či nikoli. Objev fraktální podstaty magnetických domén při kritické teplotě některé vědce překvapil, protože panovala domněnka, že přechod z magnetického materiálu na materiál nemagnetický je v podstatě skokovou záležitostí – „rozpad“ orientace magnetů v nějaké části by se podle těchto domněnek měl velkou rychlostí šířit všemi směry.

Tato fraktální struktura domén s určitou charakteristikou existuje například i při změně skupenství látky, jako je tání ledu či vypařování vody. Zakladní stavy hmoty jsou z makroskopického hlediska tři (pevné, kapalné, plynné), můžeme přidat i plazmu a fyzikové by našli i další (například degenerovanou hmotu). Z mikroskopického hlediska je ovšem těchto stavů mnohem více. Fraktální strukturu hmoty potom můžeme pozorovat při přechodu hmoty z jednoho stavu do stavu druhého. Mnohdy můžeme kromě fraktální struktury při těchto přechodech pozorovat i turbulenci, což je jeden z nejčastějších projevů chaosu.
5. Blesky
I tvary blesků, ať už přírodních či uměle vytvořených, je možné považovat za jednu z forem větévkatých fraktálů, podobně jako plošné či trojrozměrné obrázky difúze. Blesk totiž není tvořen pouze jednosměrným uspořádaným proudem elektronů (klasická klikatá čára). Na začátku a konci blesku nastává rozdělení celého proudu do několika menších větví, které se dále dělí podle vodivosti země a také podle jejího tvaru (ostré předměty narušují homogenitu pole, proto blesky také více „přitahují“).
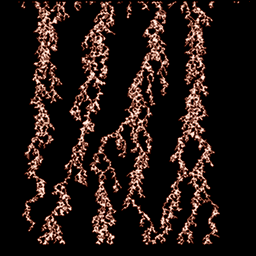
Blesk jako celek je z těchto důvodů nápadně podobný ostatním větévkatým fraktálům a samozřejmě vykazuje i běžnou fraktální charakteristiku – soběpříbuznost (jde totiž o stochastický fraktál). Na šestém a sedmém obrázku je zobrazen pokus o jednoduchou simulaci tvaru blesku pomocí upraveného algoritmu difúze. Existují však i sofistikovanější modely, které používají například energetici.

6. Využití fraktálů v technice, biologii a medicíně
Poměrně úspěšné je využití fraktálů v technických disciplínách, biologii a medicíně. V následujících čtyřech podkapitolách si uvedeme některé známější aplikace fraktálů. Kromě výše zmíněných oborů se s fraktály můžeme setkat i v teoretických disciplínách, zejména matematice (komplexní funkce, pravděpodobnost a náhodné jevy apod.) a geometrii. Fraktály a dynamické systémy se také používají při studiu chaosu – ostatně na fraktály se můžeme dívat jako na objekty ležící na hranici mezi řádem a (deterministickým či stochastickým) chaosem.

6.1 Fraktální antény
Velmi zajímavou aplikací fraktálů v technické praxi jsou takzvané fraktální antény. Jedná se o speciálně zkonstruované antény, jejichž tvar je odvozen od nějakého L-systému (například křivky Helge von Kocha) – jejich vlnová délka je tedy různá. Tyto antény se vyznačují širokým pásmovým rozsahem a přitom jsou malé a kompaktní, což je předurčuje k využití například v mobilní technice nebo v armádě. Na Internetu je dostupný zajímavý článek o těchto anténách: Fractals' new era in military antenna design od Nathana Cohena. Pro vážné zájemce: americké patenty týkající se fraktálních antén mají čísla: 6476766, 6452553, 6445352, 6140975, 6127977 a 6104349

6.2 Rozmístění součástek na plošném spoji
Už Benoit B. Mandelbrot ve své první knize o fraktálech uvedl jednu z možností aplikace fraktální geometrie. Jedná se o způsob umisťování součástek s velkou integrací na plošných spojích. Jedním z velkých problémů je návrh vodivých cest mezi jednotlivými součástkami (například mezi mikroprocesorem a pamětí). Mandelbrot navrhl metodu, při které se součástky s největším počtem vývodů rozmístí po spoji v pravidelné mřížce, poté se v menší mřížce provede rozmístění součástek s menší integrací (resp. s nižším počtem vývodů, což bývá totéž) a tímto způsobem, tj. rozmisťováním součástek s menší integrací do mřížky s menším rozměrem, se celý plošný spoj naplní. V mnoha případech tak může dojít ke snížení celkové délky vodivých spojů a/nebo k jejich menší složitosti.

6.3 Biologie a medicína
Posledních několik let můžeme vidět snahu využít fraktály a fraktální geometrii i v biologii, biochemii a medicíně. Například při zkoumání některých vlastností krve se měří Hausdorffova dimenze jejích částeček. Někteří odborníci také zkoumají, zda má nějakou souvislost Hausdorffova dimenze povrchu mozku a inteligence člověka, jeho paměťové schopnosti či rychlost reakcí (povrch mozku je tvořen mozkovými závity, které svým počtem, členitostí a hustotou pravděpodobně ukazují na různé schopnosti mozku, například paměť či inteligenci).

6.4 Architektura
Možná nevědomky byla fraktální geometrie použita při návrhu podoby několika obrovských měst. Místo živelné výstavby měst se v tomto případě architekti řídili záměrem, aby bylo možné města dále rozšiřovat bez některých negativních dopadů na jejich centra či naopak periferní oblasti (typicky se jedná o dopravní problémy). Výsledkem těchto snah byl návrh hierarchicky členěných ulic. Celý půdorys města byl rozdělen na velké čtverce o straně několika kilometrů. Na hranách těchto čtverců vedly největší komunikace s největší dopravní kapacitou (například čtyřproudové ulice s hromadnou dopravou).
Čtverce byly následně rozděleny do čtyř menších čtverců a opět se po hranách vytvořily ulice, tentokrát již užší a s menší dopravní kapacitou. Toto dělení pokračovalo dále až do stavu, kdy byly ty nejmenší čtverce (tvořící parcely pro blok několika domů) rozděleny ulicemi s nejmenší dopravní kapacitou; typicky se jednalo o obdobu našich obytných zón.
7. Fraktály a zpracování obrazu
S fraktály se můžeme setkat i při zpracování obrazu, například je možné použít Hilbertovu křivku (či podobný liniový objekt vyplňující plochu) při snižování počtu barevných odstínů pomocí ditheringu. V následujících dvou podkapitolách si však ukážeme dvě patrně nejznámější oblasti, ve které jsou fraktály prakticky použity.
7.1 Fraktální komprimace obrazů
Michael Barnsley je vědec, který se mimo jiné poměrně intenzivně zajímá o využití fraktálů a fraktální geometrie v praxi. Ve světě jsou proslulé především „jeho“ systémy iterovaných funkcí (Iterated Functions System – IFS), kterými jsme se v tomto seriálu poměrně intenzivně zabývali v části 30 až 37. Kromě přímé aplikace generativní metody používající IFS systémy pro tvorbu fraktálních obrazců (koláží) je možné IFS použít také v takzvané inverzní úloze – k nalezení soustavy jednoduchých lineárních funkcí (resp. lineárních transformací) popisujících nějaký rastrový obrázek. To je základní princip (obecně ztrátové) fraktální komprimace obrazů, kterou má Michael Barnsley a jeho spolupracovníci patentovanou.
Patenty na tuto technologii však měly na praktické využití fraktální komprimace obrazů negativní dopad, protože se místo ní začaly masivně aplikovat jiné technologie využívající ztrátovou komprimaci, zejména diskrétní kosinová transformace (DCT – discrete cosinus transformation, viz paralelně běžící seriál o grafických formátech) a později také vlnková transformace (WT – wavelet transformation). Je to samozřejmě škoda, protože fraktální komprimace obrazů v některých případech (například pro fotky většiny přírodních objektů) nabízí lepší poměr kvalita obrazu/objem dat než DCT a WT.
Fraktální komprimaci obrazů je možné použít i při přenosu videa po datových linkách s malou kapacitou přenosu. S využitím algoritmu pro generování minima pixelů (MPA:Minimum Plotting Algorithm – ten jsme si v tomto seriálu již popsali) je možné provádět přenos poměrně kvalitního videa v rozlišení QCIF i na lince s 64kbits-1, pro dekomprimaci postačuje i slabší PC či dokonce „pouze“ PDA (musíme si však uvědomit, že dnešní PDA mají větší výpočetní výkon než dřívější servery). Největší výpočetní nároky jsou tak požadovány od stroje, který video komprimuje; i tuto operaci je však možné provádět v reálném čase, což je důležité především pro telekonference provozované například na ISDN.
7.2 Rozpoznávání obrazů
Při studiu fraktální komprimace obrazů se ukázalo, že je tato metoda vhodná i pro rozpoznávání obrazů, tj. pro nalezení určitých struktur v rastrovém obrazu. Metod pro rozpoznávání obrazů existuje celá řada, od ad-hoc algoritmů používajících heuristiky přes neuronové sítě až po složité algoritmy snažící se obraz strukturovat a pochopit globálně. Při fraktální komprimaci obrazů se každý objekt či skupina objektů převede na řadu čísel, tj. nějaký vektor.
Ukazuje se, že pro stejné objekty (ale v jiné orientaci či velikosti) je mnoho číselných hodnot v tomto vektoru stejných nebo podobných. Právě tohoto poznatku je možné využít – budeme mít uloženy vektory grafických objektů, které potřebujeme nalézt, po provedené IFS komprimaci a při rozpoznávání neznámého obrazu budeme zkoumat, zda se v něm při komprimaci neobjeví podobné sekvence hodnot.

Princip této metody není nijak nový: existuje mnoho postupů, které analyzují předložený obrázek a vrátí vektor číselných hodnot, ve kterém jsou uloženy některé globální a strukturální informace o tomto obrázku: průměrná světlost, směrodatné odchylky od světlosti, hustota hran v různých směrech, „kulatost“ objektů v obrázku atd. Tento vektor může být také získán pro různé podobrázky: typicky se celý obrázek rozloží do pravidelné mřížky a vektor se vypočítá a pamatuje pro všechny bitmapy omezené každou buňkou této mřížky.
Takto vytvořené vektory s uloženou charakteristikou je možné použít například při vyhledávání typu: „vrať všechny obrázky, v jejichž levém horním rohu je slunce a spodní polovina je v průměru zelená (louka, les)“. Fraktální komprimace však do tohoto postupu přináší možnost analýzy geometrie objektů a to do velké míry nezávisle na jejich orientaci a velikosti.
Obrázek 13: Toto NEJSOU obrázky generované počítačem – jedná se o obrazy získané systémem se zpětnou vazbou: monitorem propojeným s kamerou. Podobný pokus si můžete udělat sami, pokud má váš fotoaparát výstup na televizi či „live“ video přenášené přes USB do počítače.
8. Odkazy na další informační zdroje
- Barnsley Michael: „Fractals Everywhere“,
Academic Press Inc., 1988, ISBN 0–12–079062–9 - Barnsley Michael, Devaney R. L., Mandelbrot Benoit B., Peitgenn Heinz-Otto, Saupe Dietmar, Voss Richard: „The Science of Fractal Images“,
Springer-Verlag, New York, 1988 - Barnsley Michael, Hurd Lyman P.: „Fractal Image Compression“,
A. K. Peters, 1993 - Devaney Robert L.: „A First Course In Chaotic Dynamical Systems“,
Addison-Wesley, Reading, MA, 1992 - Fischer Yuval (editor): „Fractal Image Compression: Theory and Application“,
Springer-Verlag, New York, 1995 - H. O. Peitgen, D. Saupe: „The Science of Fractal Images“,
Springer-Velag, 1988 - R. F. Cahalan and J. H. Joseph: „Fractal statistics of cloud fields“,
Mon. Wea.Rev. 117, 261–272, 1989 - R. F. Cahalan, W. Ridgway, W. J. Wiscombe, T. L. Bell and J. B. Snider: „The albedo of fractal stratocumulus clouds“,
Atmos. Sci. 51, 2434–2455, 1994
9. Obsah dalšího pokračování tohoto seriálu
Následující pokračování tohoto seriálu bude již poslední. Sepíšeme si v něm všechna témata, kterým jsme se věnovali v předchozích částech.































