Obsah
1. Lorenzův atraktor podruhé
2. První modifikace Lorenzova atraktoru
3. Druhá modifikace Lorenzova atraktoru
4. Třetí modifikace Lorenzova atraktoru
5. Rosslerův atraktor
6. Obsah dalšího pokračování tohoto seriálu
1. Lorenzův atraktor podruhé
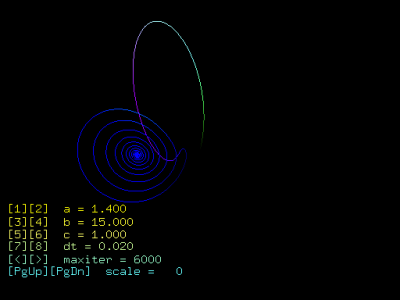
Lorenzův atraktor jsme si teoreticky popsali již v šesté části tohoto seriálu, procedura pro jeho vykreslení však ještě nebyla uvedena, protože se jedná o systém zobrazovaný v třírozměrném prostoru pomocí polyčar a většina předchozích příkladů byla zaměřena spíše na vykreslování bodů v rovině či 3D prostoru. Vzhledem k tomu, že jednotlivé body umístěné na orbitu Lorenzova atraktoru mohou být od sebe značně vzdálené (zejména při bližším přiblížení pozorovatele k atraktoru nebo při „vhodném“ zadání počátečních podmínek), jsou vždy dva po sobě vypočtené body při vykreslení propojeny úsečkou. V následujícím úryvku kódu je ukázán velmi jednoduchý a přímočarý způsob vykreslení Lorenzova atraktoru pomocí funkcí poskytovaných grafickou knihovnou OpenGL, jež podporují vykreslení libovolně dlouhé lomené čáry (polyčáry). V kódu se vychází z trojice vztahů pro iterativní výpočet pozic bodůPn=[xn, yn, zn] rozmístěných v prostoru:
xn+1 = xn + (-a × xn × dt) + (a × yn × dt)
yn+1 = yn + (b × xn × dt) – (yn × dt) – (zn × xn × dt)
zn+1 = zn + (-c × zn × dt) + (xn × yn × dt)
Původní diferenciální rovnice pro Lorenzův atraktor měly před svým převodem do diskrétní podoby tvar:
dx/dt = -ax+ay
dy/dt = bx-y-zx
dz/dt = -cz+xy
//-----------------------------------------------------------------------------
// Překreslení Lorenzova atraktoru v prostoru (původní Lorenzův atraktor)
//-----------------------------------------------------------------------------
void recalcLorenz( double a, // parametry fraktálu
double b,
double c,
double dt, // použito při numerické integraci
int maxiter, // maximální počet iterací
double scale) // měřítko obrazce
{
double x=0.1, y=0, z=0; // pozice bodu v prostoru
double x2, y2, z2;
int iter=maxiter;
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_LINE_STRIP); // začátek vykreslování polyčáry
while (iter--) { // iterační smyčka
glColor3f(x/10.0,y/10.0,z/10.0);
x2 = x+(-a*x*dt)+(a*y*dt);
y2 = y+(b*x*dt)-(y*dt)-(z*x*dt);
z2 = z+(-c*z*dt)+(x*y*dt);
x=x2; // přepis nových souřadnic
y=y2;
z=z2;
glVertex3d(x*scale, y*scale, z*scale); // vykreslení úsečky
}
glEnd(); // konec vykreslování polyčáry
} Obrázek 1: První varianta originálního Lorenzova atraktoru
Zdrojový kód demonstračního příkladu určeného pro vykreslení Lorenzova atraktoru je uložený ke stažení, HTML verze se zvýrazněním syntaxe je také dostupná. Při překladu a následném spuštění prvního demonstračního příkladu je možné měnit pohled na atraktor pomocí myši. Při stlačení levého tlačítka myši se atraktorem rotuje (zhruba) ve směru pohybu myši, při stlačení pravého tlačítka se atraktor přibližuje ke kameře (pozorovateli), nebo se od něj naopak vzdaluje (entity, které se nachází blízko ke kameře, jsou ořezány). Pomocí kláves [1] až [6] se mění vstupní parametry dynamického systému a, b, c, klávesami[7] a [8] je možné upravit hodnotu kroku dt. Čím menší je hodnota kroku, tím kratší jsou vykreslované úsečky a tím přesněji je atraktor vykreslován. Na druhou stranu se spolu se zmenšováním kroku musí zvětšovat počet iterací, protože je vykreslována menší část atraktoru. Klávesou [Esc] nebo [Q] se popisovaná demonstrační aplikace ukončí.
Obrázek 2: Druhá varianta originálního Lorenzova atraktoru
Obrázek 3: Třetí varianta originálního Lorenzova atraktoru
2. První modifikace Lorenzova atraktoru
Při použití původních rovnic pro Lorenzův atraktor je vykreslen obrazec, ve kterém jsou patrné dvě charakteristické smyčky, přičemž dráha počítaných bodů chaoticky mezi oběma smyčkami přeskakuje. Autoři Rick Miranda a Emily Stone vytvořili několik modifikací původních rovnic Lorenzova atraktoru tak, aby se při jejich aplikaci vytvořily obrazce s obecně různým počtem smyček. Při použití následující trojice modifikovaných rovnic se vytvoří atraktor, ve kterém je patrná pouze jedna smyčka:
xn+1 = xn + (-a × dt-dt) × xn+(a × dt – b × dt) × yn + (dt-a × dt) × norm + yn × dt × zn
yn+1 = yn + (b × dt-a × dt) × xn – (a × dt+dt) × yn + (b × dt+a × dt) × norm-xn × dt × zn – norm × zn × dt
zn+1 = zn + yn × dt/2.0 – c × dt × zn
Pomocná proměnná norm se vypočte z hodnot xn a yn:
norm = sqrt(xn2 + yn2)
Procedura, která využívá výše zmíněné vztahy, bude v céčku vypadat následovně:
//-----------------------------------------------------------------------------
// Překreslení modifikovaného Lorenzova atraktoru (první modifikace)
//-----------------------------------------------------------------------------
void recalcLorenz2( double a, // parametry fraktálu
double b,
double c,
double dt, // použito při numerické integraci
int maxiter, // maximální počet iterací
double scale) // měřítko obrazce
{
double x=1.0, y=1.0, z=1.0; // počáteční pozice bodu
double x2, y2, z2; // v prostoru
double norm;
int iter=maxiter;
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_LINE_STRIP); // začátek vykreslování polyčáry
while (iter--) { // iterační smyčka
glColor3f(x/10.0,y/10.0,z/10.0);
norm=sqrt(x*x+y*y); // výpočet pomocné proměnné
x2 = x+(-a*dt-dt)*x+(a*dt-b*dt)*y+(dt-a*dt)*norm+y*dt*z;
y2 = y+(b*dt-a*dt)*x-(a*dt+dt)*y+(b*dt+a*dt)*norm-x*dt*z-norm*z*dt;
z2 = z+y*dt/2.0-c*dt*z;
x=x2; // přepis nových souřadnic
y=y2;
z=z2;
glVertex3d(x*scale, y*scale, z*scale); // vykreslení úsečky
}
glEnd(); // konec vykreslování polyčáry
} Obrázek 4: První varianta modifikovaného Lorenzova atraktoru
Procedura recalcLorenz2() je použita ve druhém demonstračním příkladu, jehož zdrojový kód je uložen ke stažení, popř. jako HTML verze se zvýrazněnou syntaxí. Ovládání tohoto demonstračního příkladu je obdobné prvnímu demonstračnímu příkladu, tj. myš slouží k otáčení atraktoru a jeho přibližování či vzdalování od pozorovatele, klávesami [1] až [8] se mění parametry dynamického systému a klávesy [Esc] a[Q] aplikaci ukončí.
Obrázek 5: Druhá varianta modifikovaného Lorenzova atraktoru
3. Druhá modifikace Lorenzova atraktoru
Druhá modifikace Lorenzova atraktoru vytváří při vykreslení orbitů obrazec, ve kterém jsou patrné tři smyčky. Autoři této modifikace jsou opět Rick Miranda a Emily Stone. Modifikované rovnice pro výpočet bodů na orbitu mají tvar:
xn+1 = xn + (-(a × dt+dt) × xn + (a × dt – b × dt+zn × dt) × yn)/3 + ((dt – a × dt) × (xn2 – yn2) + 2 × (b × dt + a × dt – zn × dt) × xn × yn)/(3 × norm)
yn+1 = yn + ((b × dt-a × dt-zn × dt) × xn – (a × dt+dt) × yn)/3
+ (2 × (a × dt-dt) × xn × yn
+ (b × dt + a × dt – zn × dt) × (xn2 – yn2))/(3 × norm)
zn+1 = zn + (3 × xn × dt × xn × yn – yn × dt × yn2)/2 – c × dt × zn
Pomocná proměnná norm se, podobně jako v předchozím případě, vypočte z hodnot xn a yn:
norm = sqrt(xn2 + yn2)
A výsledná procedura pro výpočet bodů na orbitu má po převedení do céčka tvar:
//-----------------------------------------------------------------------------
// Překreslení modifikovaného Lorenzova atraktoru (druhá modifikace)
//-----------------------------------------------------------------------------
void recalcLorenz3( double a, // parametry fraktálu
double b,
double c,
double dt, // použito při numerické integraci
int maxiter, // maximální počet iterací
double scale) // měřítko obrazce
{
double x=1.0, y=1.0, z=1.0; // počáteční pozice bodu
double x2, y2, z2; // v prostoru
double norm;
int iter=maxiter;
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_LINE_STRIP); // začátek vykreslování polyčáry
while (iter--) { // iterační smyčka
glColor3f(x/10.0,y/10.0,z/10.0);
norm=sqrt(x*x+y*y);
x2 = x +(-(a*dt+dt)*x + (a*dt-b*dt+z*dt)*y)/3.0
+ ((dt-a*dt)*(x*x-y*y)
+ 2.0*(b*dt+a*dt-z*dt)*x*y)/(3.0*norm);
y2 = y +((b*dt-a*dt-z*dt)*x - (a*dt+dt)*y)/3.0
+ (2.0*(a*dt-dt)*x*y
+ (b*dt+a*dt-z*dt)*(x*x-y*y))/(3.0*norm);
z2 = z +(3.0*x*dt*x*y-y*dt*y*y)/2.0 - c*dt*z;
x=x2; // přepis nových souřadnic
y=y2;
z=z2;
glVertex3d((x+0.35)*scale, (y+1.5)*scale, (z-8.0)*scale); // vykeslení úsečky
}
glEnd(); // konec vykreslování polyčáry
} Obrázek 6: První varianta modifikovaného Lorenzova atraktoru
Procedura recalcLorenz3() je použita ve třetím demonstračním příkladu, k němuž je k dispozici opět jak zdrojový kód, tak i HTML verze se zvýrazněnou syntaxí. Ovládání třetího demonstračního příkladu je totožné s předchozími demonstračními příklady, takže ho zde již nebudu popisovat.
Obrázek 7: Druhá varianta modifikovaného Lorenzova atraktoru
Obrázek 8: Třetí varianta modifikovaného Lorenzova atraktoru
4. Třetí modifikace Lorenzova atraktoru
Třetí a současně poslední modifikace Lorenzova atraktoru vytváří při zobrazení orbitů obrazec, ve kterém jsou patrné čtyři charakteristické smyčky. Modifikované rovnice mají již dosti komplikovaný tvar:
z(0) = y(0) = z(0) = 1
xn+1 = xn +(-a × dt × xn3
+ (2 × a × dt+b × dt-zn × dt) × xn2 × yn + (a × dt-2 × dt) × xn × yn2
+ (zn × dt-b × dt) × yn3) / (2 × (xn2+yn2))
yn+1 = yn +((b × dt-zn × dt) × xn3 + (a × dt-2 × dt) × xn2 × yn
+ (-2 × a × dt-b × dt+zn × dt) × xn × yn2
– a × dt × yn3) / (2 × (xn2+yn2))
zn+1 = zn +(2 × xn × dt × xn2 × yn – 2 × xn × dt × yn3 – c × dt × zn)
A céčkovská implementace těchto rovnic v proceduře určené pro výpočet a vykreslení atraktoru může vypadat následovně:
//-----------------------------------------------------------------------------
// Překreslení modifikovaného Lorenzova atraktoru (třetí modifikace)
//-----------------------------------------------------------------------------
void recalcLorenz4( double a, // parametry fraktálu
double b,
double c,
double dt, // použito při numerické integraci
int maxiter, // maximální počet iterací
double scale) // měřítko obrazce
{
double x=1.0, y=1.0, z=1.0; // počáteční pozice bodu
double x2, y2, z2; // v prostoru
double norm;
int iter=maxiter;
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_LINE_STRIP); // začátek vykreslování polyčáry
while (iter--) { // iterační smyčka
glColor3f((x+5.0)/10.0, (y+5.0)/10.0, z/62.0);
norm=sqrt(x*x+y*y);
x2= x +(-a*dt*x*x*x
+ (2*a*dt+b*dt-z*dt)*x*x*y + (a*dt-2*dt)*x*y*y
+ (z*dt-b*dt)*y*y*y) / (2 * (x*x+y*y));
y2 = y +((b*dt-z*dt)*x*x*x + (a*dt-2*dt)*x*x*y
+ (-2*a*dt-b*dt+z*dt)*x*y*y
- a*dt*y*y*y) / (2 * (x*x+y*y));
z2= z +(2*x*dt*x*x*y - 2*x*dt*y*y*y - c*dt*z);
x=x2; // přepis nových souřadnic
y=y2;
z=z2;
glVertex3d((x-0.1)*scale, (y-0.1)*scale, (z-31)*scale);
}
glEnd(); // konec vykreslování polyčáry
} Obrázek 9: První varianta modifikovaného Lorenzova atraktoru
I aplikace třetí modifikace Lorenzova atraktoru je ukázána na demonstračním příkladu (zdrojový kód, HTML verze). Způsob ovládání tohoto demonstračního příkladu se v ničem neliší od předchozích příkladů.
Obrázek 10: Druhá varianta modifikovaného Lorenzova atraktoru
Obrázek 11: Třetí varianta modifikovaného Lorenzova atraktoru
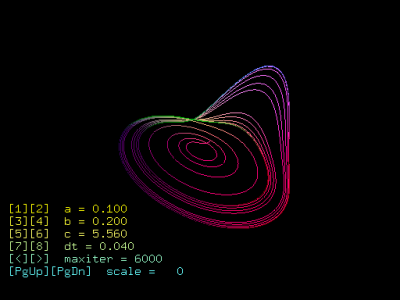
5. Rosslerův atraktor
Dynamický systém s velmi zajímavým atraktorem publikoval lékařOtto Rossler. Jeho dynamický systém je, podobně jako u Lorenzova atraktoru, tvořen trojicí diferenčních rovnic:
xn+1 = xn – yn × dt – zn × dt
yn+1 = yn + xn × dt + a yn × dt
zn+1 = zn + b × dt + xn × zn × dt – c × zn × dt
s počáteční podmínkou x0=y0=z0=1. Atraktor tohoto dynamického systému vytváří v prostoru zajímavý obrazec, který připomíná několik do sebe vložených a ohnutých smyček. Procedura, která provádí přepočet a následné vykreslení Rosslerova atraktoru, vypadá následovně:
//-----------------------------------------------------------------------------
// Překreslení Rosslerova atraktoru v prostoru
//-----------------------------------------------------------------------------
void recalcRossler( double a, // parametry fraktálu
double b,
double c,
double dt, // použito při numerické integraci
int maxiter, // maximální počet iterací
double scale) // měřítko obrazce
{
double x=1.0, y=1.0, z=1.0; // pozice bodu v prostoru
double x2, y2, z2;
int iter=maxiter;
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_LINE_STRIP); // začátek vykreslování polyčáry
while (iter--) { // iterační smyčka
glColor3f(x/15.0+(float)iter/maxiter, y/10.0, z/10.0+(float)iter/maxiter/2.0);
x2 = x-y*dt-z*dt;
y2 = y+x*dt+a*y*dt;
z2 = z+b*dt+x*z*dt-c*z*dt;
x=x2; // přepis nových souřadnic
y=y2;
z=z2;
glVertex3d(x*scale, y*scale, z*scale); // vykreslení úsečky
}
glEnd(); // konec vykreslování polyčáry
} Obrázek 12: První varianta Rosslerova atraktoru
Zdrojový kód programu provádějícího vykreslení Rosslerova atraktoru je uložen ke stažení, dostupná je i HTML verze se zvýrazněním syntaxe. Tento demonstrační příklad se ovládá naprosto stejným způsobem, jako všechny čtyři předešlé demonstrační příklady.
Obrázek 13: Druhá varianta Rosslerova atraktoru
Obrázek 14: Třetí varianta Rosslerova atraktoru
6. Obsah dalšího pokračování tohoto seriálu
V dalším pokračování tohoto seriálu se budeme zabývat velmi zajímavým tématem – zobrazováním map vybraných dynamických systémů v komplexní rovině. Mezi známé dynamické systémy, se kterými se pracuje v komplexní rovině, patří i Juliovy množiny a k nim příslušnáMandelbrotova množina, kterou je možné považovat za prakticky nejznámější fraktální útvar.