Obsah
1. Dynamický systém
2. Lineární dynamický systém
3. Nelineární dynamický systém
4. Dynamický systém se zpětnou vazbou
5. Jednodimenzionální dynamické systémy
6. Bifurkační diagram a logistická mapa
7. Demonstrační příklad – logistická funkce
8. Demonstrační příklady – bifurkační diagramy
9. Obsah dalšího pokračování tohoto seriálu
1. Dynamický systém
Dynamické systémy je možné použít v případech, ve kterých je zapotřebí vyjádřit dynamické chování, to znamená určitou změnu stavu systému v probíhajícím čase. Systém je většinou popsán soustavou diferenciálních rovnic, jež popisují tuto změnu (při implementaci na počítači se většinou diferenciální rovnice převádí na rovnice diferenční). Důležitou otázkou přitom zůstává, zda (a případně jak) lze předpovědět stav systému v budoucnosti. Také nás většinou zajímá, jakých stavů může systém nabýt – zjednodušeně řečeno nás zajímají vlastnosti množiny všech dosažitelných stavů. Přitom u některých dynamických systémů tento stavový prostor tvoří fraktální struktury. V následujících odstavcích si vysvětlíme některé základní pojmy, které souvisejí s dynamickými systémy.
Dynamický systém je, jak již víme z předchozích částí tohoto seriálu, popsán pomocí dynamických podmínek, které popisují změnu tohoto systému v čase. Stav systému v libovolném časovém okamžiku je potom reprezentován stavovým vektorem, který leží ve stavovém prostoru dynamického systému. Dynamické podmínky jsou zadány soustavou diferenciálních či diferenčních rovnic, které popisují změnu stavového vektoru v čase. Změna stavu dynamického systému se děje provedením těchto diferenciálních rovnic a nahrazením starého stavového vektoru vektorem novým.
Dynamický systém může být deterministický, nebo stochastický (náhodný). Deterministický dynamický systém lze poměrně přesně popsat pomocí diferenciálních rovnic a dalších matematických nástrojů, zatímco u systému stochastického jsme odkázáni pouze na statistické vlastnosti takového systému (například střední hodnotu, disperzi, směrodatnou odchylku, centrální moment a jiné).
V dalších kapitolách si stručně (a vzhledem k praktickému zaměření tohoto seriálu poněkud nepřesně) uvedeme některé pojmy, které se týkají dynamických systémů.
2. Lineární dynamický systém
Lineární dynamický systém je takový systém, v němž je možné uplatnit princip superpozice. To lze ilustrovat na následujícím velmi jednoduchém příkladu:
Jestliže je f(x)=0 a současně i f(y)=0, potom také platíf(x+y)=0 a obecně dokonce f(ax+by)=0 pro libovolné a,b z N.
Pro funkci f s těmito vlastnostmi lze potom využít principu superpozice.
Superpozice je v praxi často využívána při řešení velkého množství technicky orientovaných problémů, například při výpočtu průtoku elektrického proudu v elektronických obvodech s lineárními součástkami nebo ve fyzice při skládání působení sil na hmotný bod. Obecně platí, že je-li systém lineární a lze pro něj využít princip superpozice, je analytické řešení změny stavu takového systému často velmi jednoduché a jednoznačné. Chování takových systémů lze předpovědět i do budoucnosti. Z toho také vyplývá, že lineární dynamické systémy jsou pro nás z hlediska fraktálů nezajímavé, a proto se jimi nebudeme dále zabývat.
3. Nelineární dynamický systém
Nelineární dynamický systém je takový systém, kde pro obecné případy neplatí princip superpozice. To znamená že jestliže f(x)=0 a současněf(y)=0, není zaručeno, že také f(x+y)=0. V nelineárním systému může platit princip superpozice pouze pro malou množinu izolovaných bodů, které se díky této vlastnosti nazývají fixní body.
Je-li systém nelineární, a nelze tedy využít principu superpozice, je nutné při výpočtech změny stavu systému řešit diferenciální či diferenční rovnice, což je mnohdy velmi složité. Také není zaručeno, že se nám podaří předpovědět stav systému i do budoucnosti.
V případě elektrických obvodů je nelineárním prvkem například dioda. Pro diodu neplatí klasický Ohmův zákon (resp. platí za předpokladu, že R není konstantní, ale jedná se o funkci závislou buď na protékajícím proudu, nebo na přiloženém napětí), a je-li dioda zapojena ve složitějším elektrickém obvodu, nelze tento obvod řešit běžnými metodami (superpozice, smyčkové proudy). Někdy se takový systém pro snazší výpočty linearizuje, tj. nelineární závislost se nahradí závislostí lineární. To je ovšem možné pouze pro omezené počáteční podmínky (pro tranzistor se v některých případech předpokládá, že v jeho aktivní oblasti charakteristiky je zesílení konstantní apod.).
4. Dynamický systém se zpětnou vazbou
Dynamický systém se zpětnou vazbou tvoří základ prakticky všech algoritmů generujících fraktály. Princip zpětné vazby je velmi jednoduchý – výstup systému (či jeho část) je znovu přiveden na vstup systému, a ovlivňuje tak jeho chování i do budoucnosti. Programově je zpětnou vazbu možné vytvořit přímočarým způsobem, jak bude ostatně patrné z demonstračních příkladů. Jedním reálným dynamickým systémem, u nějž zpětná vazba tvoří za vhodných podmínek fraktální obrazce, je systém složený z televizoru (monitoru) a kamery (digitálního fotoaparátu), kdy je výstup z kamery přiveden na vstup televizoru a kamera přitom snímá právě generovaný (a zpožděný) obraz na stínítku. Při větší vzdálenosti kamery se na obrazovce postupně objeví opakující se vzorek (zajímavé je kamerou otáčet v ose obrazovky, jednotlivé zmenšené kopie původního obrazu se otáčí se zpožděním 1/25 sekundy), ale při větším přiblížení se začnou objevovat fraktální vzory ne nepodobné známé Mandelbrotově množině.

Obrázek 1: Dynamický systém se zpětnou vazbou
5. Jednodimenzionální dynamické systémy
V následujících kapitolách si popíšeme některé nejzajímavější jednodimenzionální nelineární dynamické systémy, které mají fraktální strukturu. Některé z těchto systémů mají uplatnění v počítačové grafice či jiných vědních i praktických oborech. Všechny dále popisované systémy vykazují velkou citlivost na počáteční podmínky a mají podivný atraktor.
6. Bifurkační diagram a logistická mapa
Při studiu populačního růstu v uzavřeném prostoru (například ryb žijících v rybníce) se pro jeho značně zjednodušený model došlo k závěru, že populační růst v určitém časovém období, například pro každý rok, závisí na populačním růstu v jednom předchozím časovém období. Systém tedy nemá dlouhodobou „paměť“, ve které by si pamatoval všechny předešlé stavy. Populační růst klesá, jakmile celková část populace dosáhne či přesáhne určitou hodnotu Xm (příliš mnoho organismů v uzavřeném prostoru), a v menší populaci naopak dochází k jejímu růstu. Tento dynamický proces (dynamický proto, že se mění v čase) je nelineární a vžil se pro něj také název Verhulstův proces. Výpočet vychází z velmi jednoduchého matematického modelu omezeného růstu populace po jednotlivých generacích:
xn+1=Gr × xn × (1-xn)
Kde se symbolem xn značí počet jedinců v n-té generaci a Gr je velikost růstu. Hodnoty xnse zadávají v rozmezí 0..1, kde 0 značí vymření populace a 1 plně saturovaný stav.
Pro zajímavost budeme sledovat chování systému pro různé hodnoty Gr, tj. pro různé velikosti růstu:
- Pro hodnotu růstu, která je menší než 200 procent (Gr<2.0), se po určité době stav populace ustálí na hodnotě xu a v jednotlivých generacích nenastávají žádné výraznější odchylky. Hodnota xu je tedy pro tuto hodnotu růstu atraktorem.
- Jestliže hodnota růstu dosahuje 200 procent (Gr=2.0), hodnoty xu se nikdy nedosáhne. Systém osciluje mezi hodnotou, která je menší než xu, a hodnotou, která je větší než xu. Existují tedy dvě velikosti populace, které se každý rok vyměňují. Tyto dvě hodnoty jsou atraktorem, který je periodický.
- Jestliže hodnota růstu dosáhne přesně 245 procent (Gr=2.45), nastává oscilace mezi čtyřmi stavy. Hodnoty xu se samozřejmě nikdy nedosáhne, tyto čtyři stavy jsou tedy atraktorem systému.
- Pro vybrané hodnoty větší než 245 procent nastává postupně oscilace mezi osmi, šestnácti, dvaatřiceti, … atd. stavy. Tato vlastnost se v literatuře nazývá zdvojování period (period doubling) a je to charakteristická vlastnost mnoha jednorozměrných i vícerozměrných dynamických systémů.
- Zajímavý efekt nastane, je-li hodnota růstu větší než 257 procent (Gr>2.57). Pro tyto hodnoty se systém stává chaotický, to znamená, že velikost populací v následujících letech je nepředvídatelná a nikdy se neustálí (samozřejmě ani pro dvě po sobě jdoucí generace) na nějaké konstantní hodnotě.
Vzdálenost parametrů intervalů, kde jsou periody stabilní (tedy například pro oněch zmíněných 245 procent, dále pak 300%, 345%, 354%, 356.4% atd.), se nazývá Feigenbaumovo číslo. Toto číslo (přesněji řečeno konstanta) je kupodivu pro všechny dynamické systémy vykazující zdvojování periody univerzální, stejně jako například číslo π v geometrii neboe v matematické analýze. Feigenbaumovo číslo se označuje symbolem δ a má přibližnou hodnotu δ= 4.669 201 609 102 990 671 853 203 8.
7. Demonstrační příklad – logistická funkce
Výše popsaný Verhulstův proces je možné velmi jednoduchým způsobem zobrazit na plošném grafu. Přímým zobrazením funkce f(x) získáme takzvanouLogistickou funkci (či logistickou mapu). Pro různé počáteční hodnoty x0 a zejména velikosti růstu Gr bude mít logistická mapa jeden z následujících průběhů: buď se po několika krocích hodnota ustálí a populace bude dosahovat konstantní hodnoty xu, hodnota bude oscilovat mezi dvěma, čtyřmi, osmi atd. stavy, nebo dojde k chaotickému chování celého systému (včetně divergence hodnot). Proceduru, která bude provádět vykreslení logistické funkce, je možné v programovacím jazyku C napsat následujícím způsobem:
//-----------------------------------------------------------------------------
// Procedura provádějící překreslení logistické funkce
//-----------------------------------------------------------------------------
void recalcLogistic(double x0, double gr, int yp)
{
int i; // čítač vykreslovací smyčky
double x=x0, y; // počáteční hodnota x0
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_LINE_STRIP); // začátek vykreslování lomené čáry
for (i=8; i<glutGet(GLUT_WINDOW_WIDTH)-16; i+=8) { // výpočet pro vybranou hodnotu Gr
x=gr*(x-x*x); // hodnota funkce v dalším kroku
y=yp+((1.0+x)*glutGet(GLUT_WINDOW_HEIGHT)/2.0);
glVertex2f(i, y); // připojení další části lomené čáry
}
glEnd(); // konec vykreslování lomené čáry
}
//-----------------------------------------------------------------------------
// Konec procedury
//----------------------------------------------------------------------------- Výše uvedená procedura recalcLogistic() akceptuje tři parametry. V prvním parametru typu double se předává počáteční hodnota nulté generace populace x0, ve druhém parametru (také typudouble) se předává hodnota růstu Gr a ve třetím parametru typu int posun grafu ve vertikálním směru.
Tato procedura je použita i v demonstračním příkladu 5.1, jehož zdrojový soubor je dostupný ke stažení (HTML verzi zdrojového souboru se zvýrazněním syntaxe si můžete také stáhnout). Po překladu a spuštění tohoto příkladu se zobrazí náhled na logistickou funkci s předem zadanými parametry Gr, x0 a yp. Parametry, pro něž je logistická mapa zobrazena, je možné v běžící aplikaci měnit pomocí několika kláves, jejichž funkce je uvedena v následující tabulce.
| Klávesa | Význam |
|---|---|
| Esc | ukončení aplikace |
| Q | ukončení aplikace |
| L | zmenšení velikosti růstu Gr o 5% |
| H | zvětšení velikosti růstu Gr o 5% |
| J | posun celého grafu o 5 pixelů směrem dolů |
| K | posun celého grafu o 5 pixelů směrem vzhůru |
| 1 | zmenšení počáteční hodnoty x0 o jednu setinu |
| 2 | zvýšení počáteční hodnoty x0 o jednu setinu |
Obrázek 2: Logistická funkce s konstantním atraktorem
Obrázek 3: Logistická funkce s periodickým atraktorem
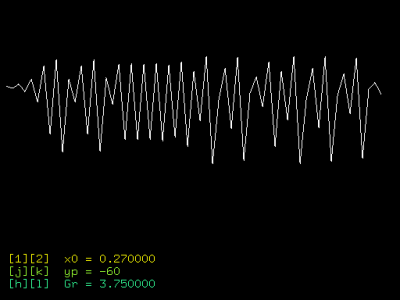
Obrázek 4: Logistická funkce s chaotickým atraktorem
8. Demonstrační příklady – bifurkační diagramy
Přímé zobrazení logistické funkce nám nedává zcela jasnou představu o tom, při jakých počátečních podmínkách je systém stabilní, kdy dochází ke zdvojování period a pro jaké hodnoty nastává chaotické chování systému. Pro jasnější představu o chování jednorozměrného dynamického systému se proto používá jiný vizuální nástroj – bifurkační diagram. V bifurkačním diagramu jsou na horizontální osu naneseny hodnoty některého vstupního parametru (v našem případě růstu Gr) a na vertikální osu vnitřní stavy dynamického systému, což je u logistické funkce hodnotaxn, jichž systém nabývá pro daný počet kroků (iterací). Hodnota xn je vykreslena triviálním způsobem pomocí jednoho bodu, nedochází tedy k tvorbě spojitého grafu. V některých případech se bifurkační diagram dále upravuje, například tak, že se vykreslují hodnoty až po předem zadaném počtu iterací, kdy je systém již částečně ustálen (jedná se o takzvané „počáteční“ nebo „startovní“ iterace). Procedura pro vykreslení bifurkačního diagramu vypadá v programovacím jazyku C následovně:
//-----------------------------------------------------------------------------
// Překreslení bifurkačního diagramu
//-----------------------------------------------------------------------------
void recalcBiffurcation(pixmap *pix,
double x0,
double gr0,
int yp,
int maxiter,
int iter0)
{
int grr, iter;
for (grr=0; grr<(int)pix->width; grr++) { // změna parametru Gr
double gr=3.0f*(double)grr/(double)pix->width+gr0;
double x=x0;
for (iter=0; iter<maxiter; iter++) { // výpočet pro vybranou hodnotu Gr
x=gr*(x-x*x); // logistická funkce
if (iter>iter0) { // pokud se překročila mez iterací
int y=yp+(((pix->height)+(int)(pix->height*x)) >> 1);
putpixel(pix, grr, y, 255, 255, 255); // vykreslení bodu
}
}
}
}
//-----------------------------------------------------------------------------
// Konec procedury
//----------------------------------------------------------------------------- V demonstračním příkladu 5.2 (zdrojový kód, obarvený zdrojový kód) je vykreslen bifurkační diagram výše uvedené logistické funkce xn+1=Gr × xn ×(1-xn). Klávesové zkratky pro ovládání tohoto příkladu jsou vypsány ve druhé tabulce.
| Klávesa | Význam |
|---|---|
| Esc | ukončení aplikace |
| Q | ukončení aplikace |
| S | uložení pixmapy s bifurkačním diagramem do souboru typu TGA |
| L | posun grafu směrem doleva (změna rozsahu velikosti růstu Gr) |
| H | posun grafu směrem doprava (změna rozsahu velikosti růstu Gr) |
| J | posun grafu o 5 pixelů směrem dolů |
| K | posun grafu o 5 pixelů směřem vzhůru |
| 1 | zmenšení počáteční hodnoty x0 o jednu setinu |
| 2 | zvýšení počáteční hodnoty x0 o jednu setinu |
| 3 | zmenšení maximálního počtu iterací o deset cyklů |
| 4 | zvětšení maximálního počtu iterací o deset cyklů |
| 5 | zmenšení počtu startovních iterací (při kterých nedochází k vykreslování) |
| 6 | zvětšení počtu startovních iterací |
Obrázek 5: Bifurkační diagram pro kladné hodnoty Gr
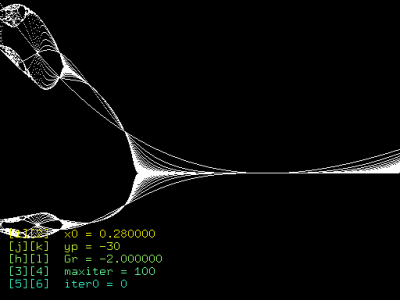
Obrázek 6: Bifurkační diagram pro záporné hodnoty Gr
Velmi zajímavé je, že i pokud se použije odlišná „jednorozměrná“ funkce, může její bifurkační diagram vypadat podobně jako bifurkační diagram logistické funkce. To je ukázáno v demonstračním příkladu 5.3, jehož zdrojový kód si můžete stáhnout, dostupný je i soubor se zvýrazněnou syntaxí. V tomto příkladu je použita odlišná funkce xn+1=Gr(x-sin x2), ostatní části programu jsou shodné s příkladem 5.2.
//-----------------------------------------------------------------------------
// Překreslení bifurkačního diagramu pro odlišnou funkci
//-----------------------------------------------------------------------------
void recalcBiffurcation(pixmap *pix,
double x0,
double gr0,
int yp,
int maxiter,
int iter0)
{
int grr, iter;
for (grr=0; grr<(int)pix->width; grr++) { // změna parametru Gr
double gr=3.0f*(double)grr/(double)pix->width+gr0;
double x=x0;
for (iter=0; iter<maxiter; iter++) { // výpočet pro vybranou hodnotu Gr
x=gr*(x-sin(x*x));
if (iter>iter0) { // pokud se překročila mez iterací
int y=yp+(((pix->height)+(int)(pix->height*x)) >> 1);
putpixel(pix, grr, y, 255, 255, 255); // vykreslení bodu
}
}
}
}
//-----------------------------------------------------------------------------
// Konec procedury
//----------------------------------------------------------------------------- Obrázek 7: Bifurkační diagram funkce xn+1=Gr(x-sin x2)
Obrázek 8: Bifurkační diagram funkce xn+1=Gr(x-cos x)
9. Obsah dalšího pokračování tohoto seriálu
V dalším pokračování tohoto seriálu si popíšeme dynamické nelineární systémy zobrazené ve dvojrozměrném a třírozměrném prostoru.