Fraktály v počítačové grafice XII

Obsah

1. Stručná historie Mandelbrotovy množiny
2. Kdo první vykreslil Mandelbrotovu množinu?
3. Mandelbrotova množina jako dynamický systém
4. Test na divergenci orbitu
5. Výpočet bodů ležících v Mandelbrotově množině
6. Obsah dalšího pokračování tohoto seriálu

1. Stručná historie Mandelbrotovy množiny

„[I have] had the privilege to enrich Fatou-Julia's theory by adding a new part, by suggesting what Douady and Hubbard (1982) have called "Mandelbrot set or M-set“ … I have proceeded in a way loathed by theoreticians… I have wandered, contemplated, dissected, with the astonishing equivalent of a microscope that the computer is… Unforgettable images, even with the primitive tools of 1980… I did this work in 1979–1980…"
Benoit B. Mandelbrot

Mandelbrotova množina byla, podobně jako Juliovy množiny, objevena při analýze některých zdánlivě jednoduchých dynamických systémů se zpětnou vazbou. Analýza dynamických systémů se zabývá otázkou budoucího stavu systému, pokud iterativně provádíme výpočet s tou samou funkcí (resp. skupinou funkcí). Některé výsledky z analytického i numerického výzkumu těchto systémů byly publikovány již počátkem minulého století (samozřejmě, že se bez pomoci počítačů jednalo o poměrně nezáživné matematické stati). Těmito dynamickými systémy se zabývali především matematikové Gaston Julia (1893–1978) a Pierre Fatou (1878–1929), o kterých jsme si pověděli v předcházejících dílech tohoto seriálu. Na jejich práce, které souvisely především s Juliovými množinami (tak však byly nazvány až o více než půlstoletí později) navázal v sedmdesátých letech minulého století matematik Benoit B. Mandelbrot.

Jako součást své výzkumné práce využil Benoit Mandelbrot možností tehdy dostupné počítačové grafiky – to ovšem bylo na matematika dosti nezvyklé. V tomto období byly v pracovní skupině Mandelbrota a prakticky ve stejném čase i dvojicí Brookse a Matelskiho vytvořeny první obrazy fraktálu dnes nazývaného Mandelbrotova množina. První rastrové obrázky byly, vzhledem k dané době a omezeným možnostem použité výpočetní techniky, pouze černobílé, vzbudily však velký zájem jak mezi odbornou, tak i laickou veřejností. Z matematického pohledu jsou samozřejmě korektní pouze černobílé (resp. monochromatické) obrázky, protože se rozlišují pouze dvě možnosti: divergence či konvergence posloupnosti hodnot z_n. V počítačové grafice se posléze došlo k barevnému „vylepšování“ obrázků, při kterém jsou barvy pixelům přiřazovány například podle počtu iterací, vzdálenosti čísla z_n od počátku atd.

Obrázek 1: Tímto způsobem zobrazovalo Mandelbrotovu množinu mnoho starších aplikací pro DOS a grafickou kartu VGA

2. Kdo první vykreslil Mandelbrotovu množinu?

The resulting revival makes the properties of iterations essential for the theory of fractals. The fact that the Fatou-Julia findings did not develop to become the source of this theory suggests that even classical analysis needs intuition to develop, and can be helped by the computer.
Benoit B. Mandelbrot

Na tuto zdánlivě jednoduchou otázku existuje překvapivě několik odpovědí. Mandelbrot vytvořil první obrázky Mandelbrotovy množiny v roce 1979. V roce 1981 byl na matematické konferenci prezentován článek od Brookse a Matelskiho, který také obsahoval obrázky množiny později pojmenované po Mandelbrotovi. Problém je, že tento článek i se všemi ilustracemi byl vytvořen již v roce 1978, tj. „těsně“ před Mandelbrotem, takže v tomto případě prvenství jasně připadá Brooksovi a Matelskimu.

Na druhou stranu je jasné, že Mandelbrot „svoji“ množinu studoval a také popsal (v přesné kanonické podobě, jako iteraci komplexního polynomu) mnohem důkladněji než pánové Brooks a Matelski, což také vedlo Johna Hubbarda k tomu, že v roce 1982 tuto množinu pojmenoval po Mandelbrotovi – ve skutečnosti dokonce Hubbard pravděpodobně o málo známé práci Brookse a Matelskiho nevěděl. Jak je z této příhody vidět, historie se již několikrát opakovala v tom, že jeden objev v prakticky stejnou dobu udělá více lidí. V tomto případě se sešlo více skutečností: hlubší zájem o iterativní procesy a také prudký rozvoj počítačů a počítačové grafiky.

Další verze o vzniku Mandelbrotovy množiny říká, že první obrázek byl vytvořen počítačovým odborníkem, který byl přítelem jak Mandelbrota, tak i Brookse a Matelskiho – to je do jisté míry pravděpodobné, protože v té době bylo počítačových odborníků poměrně málo a veškeré práce se prováděly na sálových počítačích dávkovým způsobem. Mandelbrot přitom v té době pracoval pro IBM a ta zase poskytovala výpočetní prostředky mnoha univerzitám, takže mezi počítačovými odborníky od IBM a vědci vznikaly poměrně rozsáhlé „družby“.

Aby se historie Mandelbrotovy množiny ještě více zamotala, byla poměrně nedávno objevena starodávná práce v dnešní době prakticky už neznámého všestranného umělce a vědce jménem Udo von Aachen. Tento nedoceněný vědec, který je v celoevropském měřítku srovnatelný snad pouze s Járou Cimrmanem, počítal konvergenci či divergenci bodů v Mandelbrotově množině ručně, pouze za pomoci papíru a husího brku. Takto prováděné výpočty samozřejmě trvaly několik let a „rozlišení“ vytvořeného obrazu Mandelbrotovy množiny bylo velmi nízké. Jak bylo ve středověku zvykem, nesměly se některé práce odporující tehdy platné doktríně přímo zveřejňovat, proto byl obrázek Mandelbrotovy množiny zakomponován do rozsáhlejší rytiny jako její nenápadná součást. Toto důležité poselství z minulosti rozluštili vědci až dnes s využitím moderní výpočetní techniky. Bližší informace o tomto důležitém objevu jsou uvedeny na stránce: http://www.ra­ygirvan.co.uk/a­poth/udo.htm.

Obrázek 2: Detail Mandelbrotovy množiny

3. Mandelbrotova množina jako dynamický systém

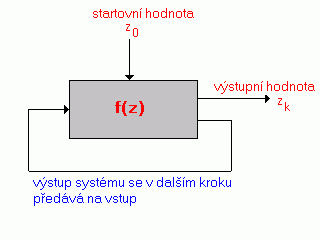
Mandelbrotova množina je vytvořena pomocí jednoduchého dynamického systému, který je založen na iteraci funkce komplexní paraboly:

z_n+1=z_n²+c

kde proměnné z a c leží v komplexní rovině.

Obrázek 3: Iterační výpočet bodů ležících v Mandelbrotově množině

V průběhu výpočtu se hodnota z postupně mění, zatímco hodnota c zůstává konstantní – tato se mění pouze při přesunu výpočtu na nový bod. Celý iterační proces začíná s určitou startovní hodnotou z₀, takže systém postupně generuje sekvenci hodnot z_k, které nazýváme orbit. Postup si ukážeme na prvních čtyřech iteracích:

z₁=(z₀)²+c
z₂=((z₀)²+c)^2­+c
z₃=(((z₀)²+c)­²+c)²+c
z₄=((((z₀)²+c­)²+c)²+c)²+c
 

Při práci se systémem popsaným v předchozím textu nás zajímá, zda pro danou startovní hodnotu z₀ a konstantu c posloupnost z_k konverguje či diverguje. Ukazuje se, že pro některé počáteční hodnoty nastává také oscilace – hodnoty z_k se opakují s určitou periodou, to znamená, že platí rovnost z_k=z_k+i, kde i je perioda oscilace. Bližším studiem vlivu počátečních podmínek na budoucí stav systému se zabýval právě Benoit B. Mandelbrot a před ním i Fatou.

Mandelbrot se omezil na případ, kdy počáteční hodnota z₀ je nulová a pro každý počítaný bod se mění pouze konstanta c. Iterativním výpočtem vzniknou pouze orbity nuly. Orbity nuly lze podle jejich vlastností rozdělit do dvou kategorií:

1. Pro některé hodnoty c je orbit konečný, tzn. všechny hodnoty z_k jsou konečné. Do této kategorie spadají také hodnoty, které oscilují.
2. Pro další hodnoty c je orbit nekonečný, tzn. po určité době rostou hodnoty z_k nade všechny meze.

Mandelbrotova množina je poté definována jako množina všech komplexních čísel c, které produkují konečný orbit nuly, tedy:

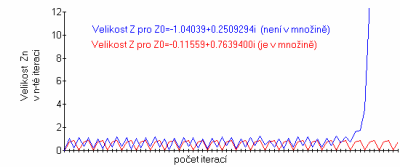
kde P_cⁿ(0) znamená hodnotu z_n pro danou konstantu c a z₀=0. Na dalším obrázku je ukázán příklad pro dvě počáteční hodnoty c (resp. z₀, protože po první iteraci je c rovno z₀). První orbit je konečný, zatímco hodnoty druhého orbitu po několika prvních iteracích rostou nade všechny meze.

Obrázek 5: Konvergence a divergence dvou různých hodnot z₀

Pro porovnání definice Mandelbrotovy množiny a Juliových množin uvádím ještě definici Juliových množin (ta již byla vysvětlena v desátém pokračování tohoto seriálu):

4. Test na divergenci orbitu

Abychom mohli úspěšně vykreslit hrubý obrázek Mandelbrotovy množiny, musíme zjistit, které body do této množiny zcela jistě nepatří. Jak již víme z předchozího textu, jedná se o ty body, jejichž orbit míří na Riemanově sféře (což je, zjednodušeně řečeno, komplexní rovina pouze s jedním nekonečnem) k nekonečnu. Je však možné jednoduše zjistit, že nějaký orbit míří k nekonečnu v konečném čase, resp. v konečném počtu kroků? Ukazuje se, že pro některé body je možné vytvořit jednoduchý test, jehož princip je ukázán na následujících řádcích.

Při testu na nekonečnost orbitu použijeme důkazu, že pro |c|<=|z| a |z|>2 posloupnost diverguje. Využije se přitom trojúhelníkové nerovnosti pro komplexní čísla:

|a+b| >= |a|-|b|,

kde za obecnou hodnotu a dosadíme z×z a za obecnou hodnotu b komplexní konstantu c:

|z×z+c| >= |z×z|-|c| = (|z|)²-|c|

Je nutné najít minimální hodnotu |z|, při jejímž překročení je |z×z+c|>|z|. Nazvěme tuto hodnotu r. Potom r×r-|c|=r resp. r×r-r-|c|=0 a dále z řešení kvadratické rovnice vyplývá:

r=(1+(1+4|c|)­^1/2)/2.

Známe tedy hodnotu r. Jestliže je velikost |z| větší než r, systém diverguje. Pokud iterace začíná s hodnotou z=0, je po první iteraci z=c. V předchozích vzorcích můžeme r nahradit |c| a dostaneme vztah:

|c|×|c|-2|c| = 0 tedy |c|=2 resp. |z|=2 protože z=c

Posloupnost tedy pro |z|>2 skutečně diverguje. V průběhu iteračního výpočtu tedy stačí testovat, zda je velikost |z_k|>2. Podmínka pro divergenci posloupnosti mimo jiné také znamená, že všechny body Mandelbrotovy množiny leží v komplexní rovině uvnitř kružnice o poloměru 2. Je to dáno tím, že pro |c|>2 je po první iteraci také |z|>2 a z podmínek uvedených výše vyplývá, že posloupnost diverguje.

Obrázek 7: Další detail Mandelbrotovy množiny

5. Výpočet bodů ležících v Mandelbrotově množině

Z předchozího textu vyplývá, že všechny body Mandelbrotovy množiny mají absolutní hodnotu menší než 2. Také víme, že jestliže v průběhu iteračního procesu absolutní hodnota z překročí 2, posloupnost diverguje a počítaný bod tudíž neleží v Mandelbrotově množině. Opačný test, tj. test na konvergenci posloupnosti, nelze přímo provést. Používá se proto metoda, při které se zvolí dostatečně velký počet iterací, přičemž v každém kroku je testováno, zda absolutní hodnota z nepřekročí 2. Pokud tato možnost nastane, bod uvnitř Mandelbrotovy množiny zcela jistě neleží. Pokud proběhne výpočet všech iterací, aniž by absolutní hodnota z překročila 2, je počítaný bod prohlášen za prvek Mandelbrotovy množiny. Tato metoda je sice nepřesná, ale lze ji v podstatě libovolně zpřesňovat zvyšováním maximálního počtu iterací. Hodnota 2 použitá v testu se v literatuře nazývá bailout.

Postup při výpočtu bodů ležících v Mandelbrotově množině lze zapsat pomocí jednoduchého algoritmu. Vstupem algoritmu je komplexní číslo c a konstanta určující maximální počet iterací MaxIter:

1. nastav iter:=0
2. nastav z:=0
3. pokud iter<MaxIter prováděj smyčku:
4.     nastav z:=z2+c
5.     jestliže |z|>2 bod neleží v Mandelbrotově množině; konec
6.     nastav iter:=iter+1
7. konec smyčky
8. bod leží uvnitř Mandelbrotovy množiny; konec

Tento algoritmus lze velmi jednoduše implementovat s tím, že proměnné z a c jsou komplexní čísla, tj. nabývají komplexních hodnot. Protože ve většině programovacích jazyků nejsou komplexní čísla zavedena jako základní datové typy, pomůžeme si tím, že každé komplexní číslo reprezentujeme jeho reálnou a imaginární složkou – prakticky stejným způsobem jsme ostatně postupovali při vykreslování Mandelbrotovy množiny. Proto například původní komplexní proměnná z bude reprezentována dvojicí reálných proměnných zx a zy a komplexní proměnná c bude reprezentována dvojicí cx a cy.

Absolutní hodnotu |z| lze rozepsat jako sqrt(zxzx+zyzy), kde sqrt() je matematická funkce provádějící druhou odmocninu. V reálných programech není použit přímo výpočet absolutní hodnoty, protože vyčíslení odmocniny je časově velmi náročné. Poměrně složitou podmínku ve tvaru sqrt(zxzx+zyzy)>2 lze na obou stranách umocnit (obě strany jsou vždy kladné) a použít novou podmínku, kde není zapotřebí provádět časově náročný výpočet odmocnin. Výsledný tvar podmínky má tvar: zxzx+zyzy>4. Výraz z:=z2+c, jenž je zapsán pomocí dvou komplexních proměnných z a c, lze rozepsat na jeho reálnou a imaginární část:

zx'=zxzx-zyzy+cx
zy'=2zxzy+cy 

Kde zx, zy, cx, cy, zx' a zy' jsou proměnné nabývající reálných hodnot. Aby nebylo nutné používat dvou nových proměnných zx' a zy', použijí se již předpočítané mocniny reálné a imaginární složky z (podle reakcí čtenářů pod předchozími díly tohoto seriálu se však ukazuje, že se v některých případech nemusí jednat o ideální řešení). Také je vhodné prohodit oba výrazy, aby nebylo nutné zavádět nové pomocné proměnné:

zx2=zxzx
zy2=zyzy
zy=2zxzy+cy
zx=zx2-zy2+cx 

Hodnoty v proměnných zx2 a zy2 budou použity při testu zx2+zy2>4. Nyní již můžeme celý algoritmus pro výpočet bodů Mandelbrotovy množiny přepsat do konkrétního programovacího jazyka. Jako příklad je uveden zápis v programovacím jazyce C:

/*
 * Parametrem této funkce je komplexní číslo C, pro které
 * probíhá test.
 */
int MandelbrotTest(double cx, double cy)
{
    double      zx,zy,zx2,zy2,cx,cy;    // komplexní proměnná Z
    int         iter;                   // počet iterací

    zx=0;                               // vynulovat komplexní proměnnou C
    zy=0;

    iter=0;                             // nastavit počitadlo iterací

    do {                                // iterační smyčka
        zx2=zx*zx;                      // zx^2
        zy2=zy*zy;                      // zy^2
        zy=2.0*zx*zy+cy;
        zx=zx2-zy2+cx;                  // z:=z^2+c
        iter++;                         // zvýšit hodnotu počitadla iterací
    } while (iter<maxiter && (zx2+zy2)<4.0);// test na počet iterací a bailout

    if (iter==maxiter)                  // bod leží uvnitř Mandelbrotovy množiny
        return LEZI_UVNITR;
    else                                // bod leží vně Mandelbrotovy množiny
        return LEZI_VNE;
} 

Výše uvedený algoritmus lze přímo použít pro vykreslení Mandelbrotovy množiny. Výsledek je vidět na přiloženém obrázku. Bílé pixely reprezentují body v komplexní rovině, jež neleží v Mandelbrotově množině, černé pixely naopak reprezentují body v Mandelbrotově množině ležící. Symetrie Mandelbrotovy množiny okolo reálné osy je způsobena tím, že změna znaménka cy způsobí pouze změnu znaménka proměnné zy, nikoliv zx. Na výpočet absolutní hodnoty |z| nemají znaménka reálné a imaginární složky žádný vliv. Funkce MandelbrotTest() je volaná pro každý počítaný (resp. zobrazovaný) pixel. Při větších velikostech pixelů může dojít ke znatelnému prodloužení výpočtu z důvodu častého volání této funkce. Proto je výhodnější vložit tělo funkce MandelbrotTest() přímo do hlavní výpočetní smyčky programu, kde se provádí nastavení jednotlivých pixelů.

Obrázek 8: Celkový pohled na Mandelbrotovu množinu

6. Obsah dalšího pokračování tohoto seriálu

V dalším pokračování tohoto seriálu si ukážeme demonstrační příklady pro vykreslování Mandelbrotovy množiny. Také si řekneme, jakým způsobem je možné generovat animaci „průletu“ tímto fraktálem.