Fraktály v počítačové grafice XIX

Obsah

1. Kubická Mandelbrotova množina s iteračním vztahem Z_n+1=Z_n³+C
2. Rozepsání komplexní hodnoty Z³ na reálnou a imaginární část
3. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě počtu iterací
4. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě reálné složky orbitu
5. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě imaginární složky orbitu
6. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě součtu reálné a imaginární složky orbitu
7. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě úhlu orbitu
8. Hodnota perturbation a její vztah ke kubické Mandelbrotově množině
9. Obsah dalšího pokračování tohoto seriálu

1. Kubická Mandelbrotova množina s iteračním vztahem Z_n+1=Z_n³+C

V předchozích několika částech tohoto seriálu jsme si ukázali, jakým způsobem (resp. několika způsoby) je možné vykreslovat „klasickou“ Mandelbrotovu množinu, při jejímž výpočtu se používal iterační vztah Z_n+1=Z_n²+C, ve kterém je původní hodnota Z v každé iteraci umocněna na druhou a k výsledku je přičtena konstanta C. Tuto Mandelbrotovu množinu budu zkráceně nazývat kvadratická Mandelbrotova množina. V dnešním a příštím pokračování si ukážeme, jak vypadá modifikovaná Mandelbrotova množina v případě, že je původní iterační vztah změněn na Z_n+1=Z_n³+C (takzvaná kubická Mandelbrotova množina), popř.  na Z_n+1=Z_n⁴+C. Další celočíselné mocniny se do iteračního vztahu aplikují podobným způsobem, dokonce je možné používat i mocniny neceločíselné, jejich implementace v reálných programech je však složitější, pokud ovšem není k dispozici dobrá matematická knihovna podporující práci s komplexními čísly. Nejprve začneme s popisem kubické Mandelbrotovy množiny, ve které je v iteračním vztahu použita třetí mocnina a nikoli mocnina druhá.

2. Rozepsání komplexní hodnoty Z³ na reálnou a imaginární část

Při výpočtech Mandelbrotovy množiny využíváme v demonstračních příkladech programovací jazyk C, který ve své starší a dnes prakticky nejrozšířenější normě (ANSI X3.159–1989, resp. ISO 9899:1990, zkráceně též C89) neobsahuje přímou podporu pro komplexní čísla. Novější překladače podporující normu C99 sice s komplexními čísly pracovat do jisté míry umí, ale vzhledem ke snaze o dosažení co největší přenositelnosti a také kvůli snadnějšímu převodu do jiných programovacích jazyků budeme v demonstračních programech stále používat pouze primitivní datové typy int (počitadla smyček) a double (složky komplexních čísel). Při rozepisování komplexní hodnoty Z³ na reálnou a imaginární složku můžeme postupovat stejným způsobem, jako při odvození hodnoty Z². Pro oživení si ukažme, jak byla reálná a imaginární část komplexní hodnoty Z² získána:

Z²=(z_re+iz_im)²=
=z_re²-z_im²+2iz_rez_im

Re(Z²): z_re²-z_im²
Im(Z²): 2z_rez_im 

Podobným odvozením je možné vyjádřit i složky hodnoty Z³:

Z³=(z_re+iz_im)³=
=(z_re+iz_im)²(z_re+i­z_im)=
=(z_re²-z_im²+2iz_rez_im)(z_re+i­z_im)=
=z_re³-iz_im³+3iz_re²z_im-3z_rez_im²

Re(Z³): z_re³-3z_rez_im²
Im(Z³): -z_im³+3z_re²z_im 

3. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě počtu iterací

Výše uvedené rozepsání hodnoty Z³ na reálnou a imaginární složku může být přímo použito v iterační smyčce provádějící výpočet a obarvení bodů ležících vně kubické Mandelbrotovy množiny. Bodům (resp. pixelům) ležícím uvnitř množiny je přiřazena černá barva. Funkce, která tento výpočet provádí, vypadá v čistě céčkovské implementaci následovně:

//-----------------------------------------------------------------------------
// Překreslení kubické Mandelbrotovy množiny. Pixely ležící uvnitř jsou vykre-
// sleny černou barvou, body ležící vně množiny jsou vykresleny na základě
// počtu iterací.
//-----------------------------------------------------------------------------
void recalcCubicMandelbrot1( pixmap *pix,       // pixmapa pro vykreslování
                  int    maxiter,               // maximální počet iterací
                  double scale,                 // měřítko obrazce
                  double xpos,                  // posun obrazce
                  double ypos,
                  int    palette,               // barvová paleta
                  int    rf, int gf, int bf)    // příznaky barvových složek
{
    double zx, zy, zx2, zy2, zx3, zy3;          // složky komplexní proměnné Z, Z^2 a Z^3
    double zxn, zyn;
    double cx, cy;                              // složky komplexní konstanty C
    double cx0, cy0;
    double xmin, ymin, xmax, ymax;              // rohy vykreslovaného obrazce v komplexní
                                                // rovině
    int    x, y;                                // počitadla sloupců a řádků v pixmapě
    int    iter;                                // počitadlo iterací
    unsigned char r, g, b;

    calcCorner(xpos, ypos, scale, &xmin, &ymin, &xmax, &ymax);
    cy0=ymin;
    for (y=0; y<pix->height; y++) {             // pro všechny řádky v pixmapě
        cx0=xmin;
        for (x=0; x<pix->width; x++) {          // pro všechny pixely na řádku
            cx=cy0;                             // nastavit počáteční hodnotu Z(0)
            cy=cx0;
            zx=zy=0.0;                          // nastavení nulového orbitu
            for (iter=0; iter<maxiter; iter++) {// iterační smyčka
                zx2=zx*zx;                      // zkrácený výpočet druhé mocniny složek Z
                zy2=zy*zy;
                zx3=zx2*zx;                     // zkrácený výpočet třetí mocniny složek Z
                zy3=zy2*zy;
                zxn= zx3-3.0*zx*zy2+cx;
                zyn=-zy3+3.0*zx2*zy+cy;
                if (zx2+zy2>4.0) break;         // kontrola překročení meze divergence
                zx=zxn;
                zy=zyn;
            }
            if (iter==maxiter)                  // pixely uvnitř Mandelbrotovy
                r=g=b=0;                        // množiny jsou černé
            else                                // výpočet barev podle počtu iterací
                mapPalette(palette, iter, &r, &g, &b);
            r=r*rf;                             // uživatelem řízené vynulování
            g=g*gf;                             // vybraných barvových složek
            b=b*bf;
            putpixel(pix, x, y, r, g, b);
            cx0+=(xmax-xmin)/pix->width;        // posun na další bod na řádku
        }
        cy0+=(ymax-ymin)/pix->height;           // posun na další řádek
    }
} 

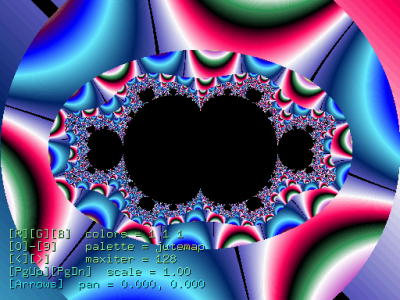
Výše uvedená funkce recalcCubicMan­delbrot1() je použita i v dnešním prvním demonstračním příkladu, screenshoty získané z tohoto demonstračního příkladu jsou zobrazeny na prvním, druhém a třetím obrázku.

Obrázek 1: Celkový pohled na kubickou Mandelbrotovu množinu

Obrázek 2: Detail kubické Mandelbrotovy množiny

Obrázek 3: Další detail kubické Mandelbrotovy množiny

4. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě reálné složky orbitu

Podobně jako u „klasické“ (tj. kvadratické) Mandelbrotovy množiny, i u množiny kubické je možné modifikovat výpočet barev tak, aby se lépe zvýraznila její geometrická struktura. Jednou z nejjednodušších modifikací je obarvení bodů (pixelů) ležících vně množiny na základě hodnoty orbitu, při kterém došlo ke splnění podmínky divergence. V následující funkci je ukázáno obarvení na základě reálné složky orbitu:

//-----------------------------------------------------------------------------
// Překreslení kubické Mandelbrotovy množiny s využitím reálné složky orbitu
// pro obarvení bodů ležících vně množiny.
//-----------------------------------------------------------------------------
void recalcCubicMandelbrot2( pixmap *pix,       // pixmapa pro vykreslování
                  int    maxiter,               // maximální počet iterací
                  double scale,                 // měřítko obrazce
                  double xpos,                  // posun obrazce
                  double ypos,
                  int    palette,               // barvová paleta
                  int    rf, int gf, int bf)    // příznaky barvových složek
{
    double zx, zy, zx2, zy2, zx3, zy3;          // složky komplexní proměnné Z, Z^2 a Z^3
    double zxn, zyn;
    double cx, cy;                              // složky komplexní konstanty C
    double cx0, cy0;
    double xmin, ymin, xmax, ymax;              // rohy vykreslovaného obrazce v komplexní
                                                // rovině
    int    x, y;                                // počitadla sloupců a řádků v pixmapě
    int    iter;                                // počitadlo iterací
    unsigned char r, g, b;

    calcCorner(xpos, ypos, scale, &xmin, &ymin, &xmax, &ymax);
    cy0=ymin;
    for (y=0; y<pix->height; y++) {             // pro všechny řádky v pixmapě
        cx0=xmin;
        for (x=0; x<pix->width; x++) {          // pro všechny pixely na řádku
            cx=cy0;                             // nastavit počáteční hodnotu Z(0)
            cy=cx0;
            zx=zy=0.0;                          // nastavení nulového orbitu
            for (iter=0; iter<maxiter; iter++) {// iterační smyčka
                zx2=zx*zx;                      // zkrácený výpočet druhé mocniny složek Z
                zy2=zy*zy;
                zx3=zx2*zx;                     // zkrácený výpočet třetí mocniny složek Z
                zy3=zy2*zy;
                zxn= zx3-3.0*zx*zy2+cx;
                zyn=-zy3+3.0*zx2*zy+cy;
                if (zx2+zy2>4.0) break;         // kontrola překročení meze divergence
                zx=zxn;
                zy=zyn;
            }
            if (iter==maxiter)                  // pixely uvnitř Mandelbrotovy
                r=g=b=0;                        // množiny jsou černé
            else                                // výpočet barev podle počtu iterací
                mapPalette(palette, iter+10.0*zx, &r, &g, &b);// a reálné části orbitu
            r=r*rf;                             // uživatelem řízené vynulování
            g=g*gf;                             // vybraných barvových složek
            b=b*bf;
            putpixel(pix, x, y, r, g, b);
            cx0+=(xmax-xmin)/pix->width;        // posun na další bod na řádku
        }
        cy0+=(ymax-ymin)/pix->height;           // posun na další řádek
    }
} 

Upravená funkce recalcCubicMan­delbrot2() je použita v dnešním druhém demonstračním příkladu.

Obrázek 4: Screenshot druhého demonstračního příkladu

5. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě imaginární složky orbitu

Ve třetím demonstračním příkladu je implementována metoda, ve které je k obarvení bodů ležících vně Mandelbrotovy množiny využita i imaginární složka orbitu. Ukázka množiny vypočtené pomocí tohoto demonstračního příkladu je zobrazena na pátém obrázku. Všimněte si, že barevné pruhy jsou vůči předchozímu obrázku pootočeny.

//-----------------------------------------------------------------------------
// Překreslení kubické Mandelbrotovy množiny s využitím imaginární složky
// orbitu pro obarvení bodů ležících vně množiny.
//-----------------------------------------------------------------------------
void recalcCubicMandelbrot3( pixmap *pix,       // pixmapa pro vykreslování
                  int    maxiter,               // maximální počet iterací
                  double scale,                 // měřítko obrazce
                  double xpos,                  // posun obrazce
                  double ypos,
                  int    palette,               // barvová paleta
                  int    rf, int gf, int bf)    // příznaky barvových složek
{
    double zx, zy, zx2, zy2, zx3, zy3;          // složky komplexní proměnné Z, Z^2 a Z^3
    double zxn, zyn;
    double cx, cy;                              // složky komplexní konstanty C
    double cx0, cy0;
    double xmin, ymin, xmax, ymax;              // rohy vykreslovaného obrazce v komplexní
                                                // rovině
    int    x, y;                                // počitadla sloupců a řádků v pixmapě
    int    iter;                                // počitadlo iterací
    unsigned char r, g, b;

    calcCorner(xpos, ypos, scale, &xmin, &ymin, &xmax, &ymax);
    cy0=ymin;
    for (y=0; y<pix->height; y++) {             // pro všechny řádky v pixmapě
        cx0=xmin;
        for (x=0; x<pix->width; x++) {          // pro všechny pixely na řádku
            cx=cy0;                             // nastavit počáteční hodnotu Z(0)
            cy=cx0;
            zx=zy=0.0;                          // nastavení nulového orbitu
            for (iter=0; iter<maxiter; iter++) {// iterační smyčka
                zx2=zx*zx;                      // zkrácený výpočet druhé mocniny složek Z
                zy2=zy*zy;
                zx3=zx2*zx;                     // zkrácený výpočet třetí mocniny složek Z
                zy3=zy2*zy;
                zxn= zx3-3.0*zx*zy2+cx;
                zyn=-zy3+3.0*zx2*zy+cy;
                if (zx2+zy2>4.0) break;         // kontrola překročení meze divergence
                zx=zxn;
                zy=zyn;
            }
            if (iter==maxiter)                  // pixely uvnitř Mandelbrotovy
                r=g=b=0;                        // množiny jsou černé
            else                                // výpočet barev podle počtu iterací
                mapPalette(palette, iter+10.0*zy, &r, &g, &b);// a imaginární částí orbitu
            r=r*rf;                             // uživatelem řízené vynulování
            g=g*gf;                             // vybraných barvových složek
            b=b*bf;
            putpixel(pix, x, y, r, g, b);
            cx0+=(xmax-xmin)/pix->width;        // posun na další bod na řádku
        }
        cy0+=(ymax-ymin)/pix->height;           // posun na další řádek
    }
} 

Obrázek 5: Screenshot třetího demonstračního příkladu

6. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě součtu reálné a imaginární složky orbitu

Ve čtvrtém demonstračním příkladu je ukázáno, že po součtu reálné a imaginární složky orbitu se zvýrazní symetrie kubické Mandelbrotovy množiny – tato množina je symetrická jak kolem reálné, tak i imaginární osy, na rozdíl od klasické kvadratické množiny, jež je symetrická pouze vůči reálné ose.

//-----------------------------------------------------------------------------
// Překreslení kubické Mandelbrotovy množiny s využitím součtu reálné
// a imaginární složky orbitu pro obarvení bodů ležících vně množiny.
//-----------------------------------------------------------------------------
void recalcCubicMandelbrot4( pixmap *pix,       // pixmapa pro vykreslování
                  int    maxiter,               // maximální počet iterací
                  double scale,                 // měřítko obrazce
                  double xpos,                  // posun obrazce
                  double ypos,
                  int    palette,               // barvová paleta
                  int    rf, int gf, int bf)    // příznaky barvových složek
{
    double zx, zy, zx2, zy2, zx3, zy3;          // složky komplexní proměnné Z, Z^2 a Z^3
    double zxn, zyn;
    double cx, cy;                              // složky komplexní konstanty C
    double cx0, cy0;
    double xmin, ymin, xmax, ymax;              // rohy vykreslovaného obrazce v komplexní
                                                // rovině
    int    x, y;                                // počitadla sloupců a řádků v pixmapě
    int    iter;                                // počitadlo iterací
    unsigned char r, g, b;

    calcCorner(xpos, ypos, scale, &xmin, &ymin, &xmax, &ymax);
    cy0=ymin;
    for (y=0; y<pix->height; y++) {             // pro všechny řádky v pixmapě
        cx0=xmin;
        for (x=0; x<pix->width; x++) {          // pro všechny pixely na řádku
            cx=cy0;                             // nastavit počáteční hodnotu Z(0)
            cy=cx0;
            zx=zy=0.0;                          // nastavení nulového orbitu
            for (iter=0; iter<maxiter; iter++) {// iterační smyčka
                zx2=zx*zx;                      // zkrácený výpočet druhé mocniny složek Z
                zy2=zy*zy;
                zx3=zx2*zx;                     // zkrácený výpočet třetí mocniny složek Z
                zy3=zy2*zy;
                zxn= zx3-3.0*zx*zy2+cx;
                zyn=-zy3+3.0*zx2*zy+cy;
                if (zx2+zy2>4.0) break;         // kontrola překročení meze divergence
                zx=zxn;
                zy=zyn;
            }
            if (iter==maxiter)                  // pixely uvnitř Mandelbrotovy
                r=g=b=0;                        // množiny jsou černé
            else                                // výpočet barev podle počtu iterací
                                                // a součtu reálné a imaginární části orbitu
                mapPalette(palette, iter+10.0*(zx+zy), &r, &g, &b);
            r=r*rf;                             // uživatelem řízené vynulování
            g=g*gf;                             // vybraných barvových složek
            b=b*bf;
            putpixel(pix, x, y, r, g, b);
            cx0+=(xmax-xmin)/pix->width;        // posun na další bod na řádku
        }
        cy0+=(ymax-ymin)/pix->height;           // posun na další řádek
    }
} 

Obrázek 6: Screenshot čtvrtého demonstračního příkladu

7. Obarvení bodů ležících vně kubické Mandelbrotovy množiny na základě úhlu orbitu

Podobně jako u kvadratické Mandelbrotovy množiny, i u množiny kubické je možné při obarvení pixelů brát v úvahu úhel orbitu, který se vypočítá jako arctan z_im/z_re. Tento vztah je použit v níže uvedené funkci/proceduře recalcCubicMan­delbrot5(), implementace je ukázána v pátém demonstračním příkladu. Screenshot z tohoto demonstračního příkladu je uveden na sedmém obrázku.

//-----------------------------------------------------------------------------
// Překreslení kubické Mandelbrotovy množiny s využitím úhlu orbitu
// pro obarvení bodů ležících vně množiny.
//-----------------------------------------------------------------------------
void recalcCubicMandelbrot5( pixmap *pix,       // pixmapa pro vykreslování
                  int    maxiter,               // maximální počet iterací
                  double scale,                 // měřítko obrazce
                  double xpos,                  // posun obrazce
                  double ypos,
                  int    palette,               // barvová paleta
                  int    rf, int gf, int bf)    // příznaky barvových složek
{
    double zx, zy, zx2, zy2, zx3, zy3;          // složky komplexní proměnné Z, Z^2 a Z^3
    double zxn, zyn;
    double cx, cy;                              // složky komplexní konstanty C
    double cx0, cy0;
    double xmin, ymin, xmax, ymax;              // rohy vykreslovaného obrazce v komplexní
                                                // rovině
    int    x, y;                                // počitadla sloupců a řádků v pixmapě
    int    iter;                                // počitadlo iterací
    unsigned char r, g, b;

    calcCorner(xpos, ypos, scale, &xmin, &ymin, &xmax, &ymax);
    cy0=ymin;
    for (y=0; y<pix->height; y++) {             // pro všechny řádky v pixmapě
        cx0=xmin;
        for (x=0; x<pix->width; x++) {          // pro všechny pixely na řádku
            cx=cy0;                             // nastavit počáteční hodnotu Z(0)
            cy=cx0;
            zx=zy=0.0;                          // nastavení nulového orbitu
            for (iter=0; iter<maxiter; iter++) {// iterační smyčka
                zx2=zx*zx;                      // zkrácený výpočet druhé mocniny složek Z
                zy2=zy*zy;
                zx3=zx2*zx;                     // zkrácený výpočet třetí mocniny složek Z
                zy3=zy2*zy;
                zxn= zx3-3.0*zx*zy2+cx;
                zyn=-zy3+3.0*zx2*zy+cy;
                if (zx2+zy2>4.0) break;         // kontrola překročení meze divergence
                zx=zxn;
                zy=zyn;
            }
            if (iter==maxiter)                  // pixely uvnitř Mandelbrotovy
                r=g=b=0;                        // množiny jsou černé
            else                                // výpočet barev podle počtu iterací
                                                // a úhlu orbitu
                mapPalette(palette, iter+5.0*atan2(zx, zy), &r, &g, &b);
            r=r*rf;                             // uživatelem řízené vynulování
            g=g*gf;                             // vybraných barvových složek
            b=b*bf;
            putpixel(pix, x, y, r, g, b);
            cx0+=(xmax-xmin)/pix->width;        // posun na další bod na řádku
        }
        cy0+=(ymax-ymin)/pix->height;           // posun na další řádek
    }
} 

Obrázek 7: Screenshot pátého demonstračního příkladu

8. Hodnota perturbation a její vztah ke kubické Mandelbrotově množině

V předchozích pokračováních tohoto seriálu jsme si ukázali, že samotný tvar Mandelbrotovy množiny je možné změnit pomocí takzvané hodnoty „perturbation“. Princip použitý u kvadratické Mandelbrotovy množiny lze implementovat i u množiny kubické, což je ukázáno na funkci recalcCubicMan­delbrot6(), jež je implementována v šestém demonstračním příkladu. Po spuštění tohoto příkladu se vedle sebe zobrazí dvojice kubických Mandelbrotových množin. Pohybem myši (se stlačeným tlačítkem) po levé množině se mění hodnota „perturbation“, která je následně použita při výpočtu a překreslení pravé Mandelbrotovy množiny. Výsledek (s nezměněnou množinou a množinou, na kterou je aplikována hodnota „perturbation“) je zobrazen na osmém obrázku.

//-----------------------------------------------------------------------------
// Překreslení kubické Mandelbrotovy množiny s možností změny hodnoty
// "perturbation", pomocí které se tvar Mandelbrotovy množiny modifikuje.
//-----------------------------------------------------------------------------
void recalcCubicMandelbrot6( pixmap *pix,       // pixmapa pro vykreslování
                  int    maxiter,               // maximální počet iterací
                  double scale,                 // měřítko obrazce
                  double xpos,                  // posun obrazce
                  double ypos,
                  int    palette,               // barvová paleta
                  int    rf, int gf, int bf,    // příznaky barvových složek
                  double pertx,
                  double perty)                 // aktuálně nastavená hodnota perturbace
{
    double zx, zy, zx2, zy2, zx3, zy3;          // složky komplexní proměnné Z, Z^2 a Z^3
    double zxn, zyn;
    double cx, cy;                              // složky komplexní konstanty C
    double cx0, cy0;
    double xmin, ymin, xmax, ymax;              // rohy vykreslovaného obrazce v komplexní
                                                // rovině
    int    x, y;                                // počitadla sloupců a řádků v pixmapě
    int    iter;                                // počitadlo iterací
    unsigned char r, g, b;

    calcCorner(xpos, ypos, scale, &xmin, &ymin, &xmax, &ymax);
    cy0=ymin;
    for (y=0; y<pix->height; y++) {             // pro všechny řádky v pixmapě
        cx0=xmin;
        for (x=0; x<pix->width; x++) {          // pro všechny pixely na řádku
            cx=cy0;                             // nastavit počáteční hodnotu Z(0)
            cy=cx0;
            zx=pertx;                           // nastavení hodnoty perturbace
            zy=perty;
            for (iter=0; iter<maxiter; iter++) {// iterační smyčka
                zx2=zx*zx;                      // zkrácený výpočet druhé mocniny složek Z
                zy2=zy*zy;
                zx3=zx2*zx;                     // zkrácený výpočet třetí mocniny složek Z
                zy3=zy2*zy;
                zxn= zx3-3.0*zx*zy2+cx;
                zyn=-zy3+3.0*zx2*zy+cy;
                if (zx2+zy2>4.0) break;         // kontrola překročení meze divergence
                zx=zxn;
                zy=zyn;
            }
            if (iter==maxiter)                  // pixely uvnitř Mandelbrotovy
                r=g=b=0;                        // množiny jsou černé
            else                                // výpočet barev podle počtu iterací
                                                // a úhlu orbitu
                mapPalette(palette, iter, &r, &g, &b);
            r=r*rf;                             // uživatelem řízené vynulování
            g=g*gf;                             // vybraných barvových složek
            b=b*bf;
            putpixel(pix, x, y, r, g, b);
            cx0+=(xmax-xmin)/pix->width;        // posun na další bod na řádku
        }
        cy0+=(ymax-ymin)/pix->height;           // posun na další řádek
    }
} 

Obrázek 8: Screenshot šestého demonstračního příkladu

9. Obsah dalšího pokračování tohoto seriálu

Ve dvacáté části tohoto seriálu si popíšeme kubické Juliovy množiny (viz devátý obrázek) a také Mandelbrotovy a Juliovy množiny, u kterých je použit iterační vztah Z_n+1=Z_n⁴+C.

Obrázek 9: Kubická Juliova množina