Neobvyklý vánoční dárek: skládačka z dlaždic

Obsah

1. Neobvyklý vánoční dárek – Penroseovy dlaždice
2. Periodické a aperiodické mozaiky
3. Mozaiky a L-systémy
4. Kites & Darts
5. Mozaiky a hra Life
6. Vytvoření obrazce v Inkscape
7. Obarvení jednotlivých dílů skládačky
8. Tisk výsledné skládačky
9. Odkazy na další informační zdroje

1. Neobvyklý vánoční dárek – Penroseovy dlaždice

Zajímavou úlohou z geometrie je tvorba takzvaných aperiodických vzorů, mezi které patří i Penroseovy dlaždice (Penrose tiles). Kromě vlastností dlaždic a jejich uspořádání, které jsou zkoumány ponejvíce matematiky, se jedná o i esteticky zajímavé vzory, které mohou sloužit pro výrobu netradičního vánočního dárku pro děti i dospělé. K vytvoření Penroseových dlaždic i dalších podobných vzorů nám poslouží počítač s vektorovým grafickým editorem Inkscape (primárně určeným pro Linux) a běžná tiskárna, která může tisknout pouze černou barvu, protože barevné dlaždice vytvoříme tiskem nebo kopií na různobarevné papíry. V následujících čtyřech kapitolách se seznámíme se způsobem tvorby aperiodických vzorů a posléze si řekneme, jak se dají jednoduchým způsobem vytvářet v Inkscape, který pro (nejenom) tyto účely disponuje generátorem obrazců definovaných pomocí takzvaných L-systémů.

Co tedy budeme potřebovat? Počítač s Linuxem či jiným operačním systémem, na kterém běží Inkscape verze alespoň 0.44, přístup k tiskárně popř. i do copy-centra a konečně nůžky.

Cena? cca jedna hodina strávená u počítače, náklady na papíry a kopírku do 50 korun, stříhání výsledných tvarů již můžete nechat na obdarovaném.

2. Periodické a aperiodické mozaiky

Poměrně značnou úlohu v počítačové grafice, geometrii, umění i architektuře hrají obrazce (říkejme jim dlaždice, z anglického termínu tiles), ze kterých je možné sestavovat mozaiky beze zbytku vyplňující nějakou předem známou plochu či dokonce celou (nekonečnou) rovinu. Dlaždicové vzory se mohou buď opakovat (tj. jsou periodické, například šestiúhelníky, nebo obraz zdi složené ze dvou typů cihel) resp. mohou být složeny z náhodných či nepravidelných tva­rů.

Speciální formou dlaždic, ideově ležící na pomezí mezi periodickými a nepravidelnými tvary jsou aperiodické vzory, které se sice skládají z konečného množství základních tvarů, ale tyto tvary jsou poskládány takovým způsobem, že se tvar vytvořené mozaiky nikdy neopakuje (je možné matematicky dokázat, že pro některé pečlivě vybrané základní tvary je možné sestavit nekonečné množství možností, jakými tyto tvary vyplňují rovinu).

Periodickými a aperiodickými vzory se zabývalo mnoho umělců i vědců, mezi jinými i slavný Johannes Kepler, který je známý zejména díky svým (Keplerovým) zákonům. Tento vědec si zaslouží obdiv nejenom kvůli dosaženým teoretickým výsledkům, ale především proto, že dokázal (jistě s těžkým srdcem) zahodit svoji představu vesmíru řízeného geometrií, zejména dokonalými tělesy (tyto tělesa vkládal mezi koule, na jejichž povrchu ležely dráhy planet), a tuto představu nahradil něčím na první pohled méně „ušlechtilým“ – drahami ve tvaru elips. Dokázal tak odvrhnout sice velmi propracovanou a z geometrického hlediska elegantní, ale mylnou teorii na základě měření, které ukazovaly, že skutečnost se od této teorie odlišuje.

Nicméně se vraťme k periodickým a aperiodickým mozaikám. Tyto mozaiky jsou typické tím, že se pro jejich vytváření používá omezený počet tvarů. Nejjednodušší (a vlastně také nejnudnější) jsou periodické mozaiky složené z pravidelných tvarů, například z trojúhelníků, čtverců, obdélníků či šestiúhelníků. Pokud se však použijí jiné základní tvary, vznikají zajímavější obrazce. Jeden z nich je zobrazen i na obrázcích v této kapitole, na kterých je vyobrazena postupná konstrukce mozaiky složené ze dvou typů kosočtverců. Tyto kosočtverce mají stejně dlouhé strany (aby na sebe navazovaly) a liší se pouze svými vnitřními úhly.

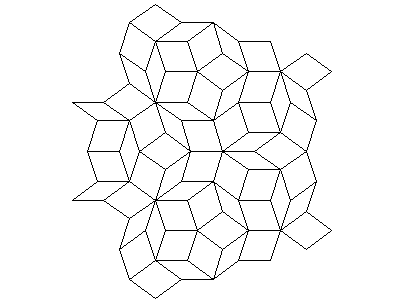
Podobným způsobem vytvořených vzorů je možné navrhnout bezpočet, ale jistě si kladete otázku, zda není možné celý postup nějakým způsobem zautomatizovat a použít pro jejich vykreslení počítač. Odpověď je samozřejmě kladná, existují poměrně jednoduché metody, které je možné použít pro vykreslení periodických i aperiodických vzorů, dokonce se jedná o z uživatelského hlediska jednoduché postupy, u kterých si vystačíme s „běžnými“ linuxovými programy, takže není potřeba nic doinstalovávat ani se učit složitou matematiku. Pro ty, kteří chtějí vědět více o teorii vytváření vzorů, je určena následující kapitola.

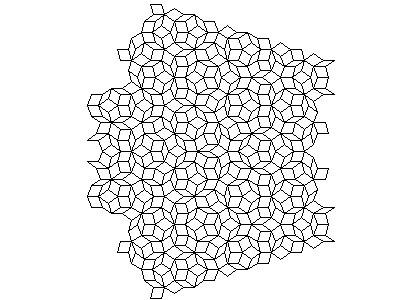
3. Mozaiky a L-systémy

Ukazuje se, že zejména periodické dlaždicové vzory je možné generovat pomocí takzvaných L-systémů, kterými jsem se podrobněji zabýval v seriálu o fraktálech [1] [2] [3] [4] [5]. Na obrázcích uvedených v předchozí kapitole byl zobrazen L-systém definovaný gramatikou popsanou v dalším odstavci. Tvar tohoto L-systému je vyobrazen po jedné až pěti iteracích, tj. přepisech axiomu. Úhel natáčení želvy je nastavený na 36°, což je, jak si povíme dále, úhel typický pro mnoho dlaždicovitých vzorů. Za povšimnutí stojí, že celý obrazec je složen pouze ze dvou typů kosočtverců, které mají stejně dlouhé hrany a odlišují se pouze svými vnitřními úhly. Gramatika tohoto L-systému má tvar:

Axiom +WF--XF---YF--ZF
W=YF++ZF----XF[-YF----WF]++
X=+YF--ZF[---WF--XF]+
Y=-WF++XF[+++YF++ZF]-
Z=--YF++++WF[+ZF++++XF]--XF
F=

Podobný L-systém je zobrazený i na dalším obrázku, tentokrát pro 1–6 iterací, tj. axiom je na základě přepisovací gramatiky přepsán jedenkrát až šestkrát. Gramatika tohoto L-systému je poněkud odlišná, základní úhel natočení želvy (36°) však zůstává zachován.

Axiom ++ZF----XF-YF----WF
W=YF++ZF----XF[-YF----WF]++
X=+YF--ZF[---WF--XF]+
Y=-WF++XF[+++YF++ZF]-
Z=--YF++++WF[+ZF++++XF]--XF
F=

Pomocí výše popsaných dvou tvarů kosočtverců je možné vytvořit i pravidelnější mozaiky. V následující kapitole si řekneme, jakým způsobem je možné na základě výzkumu Rogera Penrose vytvářet aperiodické mozaiky. Ten stejný vědec se však zabýval i mozaikami periodickými, které se mnohdy vyznačují značnou středovou symetrií, což je vidět i na další dvojici obrázků.

Všimněte si, že základní tvar zůstává stále stejný – jde o pět kosočtverců, které se dotýkají svými stranami a mají také společný jeden vrchol. Úhel svíraný stranami v tomto vrcholu je 2×36=72°, což pro pět kosočtverců dává 5×72=360°. Druhý typ kosočtverce má menší úhel svíraný stranami přesně poloviční, tj. 36°. Tento „magický“ úhel je použitý i u dále popsaných tvarů draka a šipky.

4. Kites & Darts

Známý vědec a mezi nevědeckou veřejností úspěšný spisovatel Roger Penrose zkoumal, pomocí jakých základních tvarů je možné vytvořit aperiodické mozaiky, tj. vzory, které se nikde (na nekonečné ploše/rovině) neopakují. Některé z jeho děl jsou zobrazeny na následujících obrázcích. Zpočátku Penrose používal sadu cca dvanácti základních tvarů (ty se trošku podobaly dnešním puzzle, ale měly rovné hrany), později počet základních tvarů neustále snižoval, až došel k překvapivému závěru – aperiodické mozaiky je možné vytvořit pouze skládáním dvou základních dlaždic. Ty lze získat rozdělením kosočtverce s vnitřními úhly 72° a 108° tak, jak to naznačuje schematický obrázek. Zajímavé přitom je, že jak 72°, tak i 108° jsou celočíselnými násobky 36°, tedy úhlu s pomocí kterého byly vytvořeny vzory vyobrazené v předchozích dvou kapitolách. Symbol Φ představuje hodnotu zlatého řezu (golden mean), který lze vyjádřit vztahem (1+5^1/2)/2.

Dva tvary dlaždic, pomocí kterých je možné vytvářet aperiodické mozaiky

Modrý tvar se nazývá kite (drak, podle podoby s papírovým drakem), fialový tvar dart (šipka). Vytvořené mozaiky se z tohoto důvodu souhrnně nazývají Kites and Darts. Jednoduchým tvarem, který je možné složit z draka a šipky je ace (eso) – to představuje základ pro tvorbu složitějších mozaik. Na dalších třech obrázcích je zobrazeno několik variant mozaik vytvořených pomocí tvarů kite a dart. Všimněte si neobyčejně vysoké variability při skládání těchto tvarů. Přepisovací gramatiky těchto mozaik mají tvar:

Axiom k
k=+[@.618034a]f@.618034---[-k]f-f---[-k]@i.618034f[@.618034|a]
a=[@.618034k]+f@.618034[|a]----f+f----[a]@i.618034f
f=g

Axiom [k]++[k]++[k]++[k]++[k]
k=+[@.618034a]f@.618034---[-k]f-f---[-k]@i.618034f[@.618034|a]
a=[@.618034k]+f@.618034[|a]----f+f----[a]@i.618034f
f=g

Axiom [a]++[a]++[a]++[a]++[a]
k=+[@.618034a]f@.618034---[-k]f-f---[-k]@i.618034f[@.618034|a]
a=[@.618034k]+f@.618034[|a]----f+f----[a]@i.618034f
f=g

kde symbol @ představuje změnu délky kreslených hran, což je rozšíření původních L-systémů.

5. Mozaiky a hra Life

O značné variabilitě na první pohled zdánlivě „nemožných“ tvarů draka a šipky svědčí i další tři obrázky. Všimněte si na nich, že jakoukoli mozaiku můžeme považovat za topologicky zdeformovanou šachovnici, ve které drak a šipka představují jednotlivá políčka. Stejně jako u normální šachovnice, i u těchto mozaik přísluší každému políčku čtyři sousedé, se kterými políčko sdílí svoji stranu (hranu). Jedná se o takzvané čtyřokolí.

K čemu to může být dobré? Většina i začínajících programátorů zná hru Life, což je vlastně na první pohled jednoduchá hříčka pro simulaci buněčného života (ve skutečnosti je princip této hry použit například v buněčných automatech, což žádné hříčky nejsou). Na základě algoritmu se vyhodnocuje, zda je nějaké políčko šachovnice obsazeno živou buňkou nebo je prázdné. V jednotlivých „generacích“ se tak mění obsazení jednotlivých políček.

Hru Life je možné upravit takovým způsobem, aby byla hratelná i na mozaikách vytvořených pomocí tvarů draka a šipky. Pravidla zůstávají stejná, pouze se mění topologie šachovnice, tj. pravidelné mřížky na počítačem vygenerovanou mozaiku. Lidé s velkou představivostí by možná na těchto mozaikách dokázali hrát i jiné hry, například dámu nebo piškvorky, pouze je nutné definovat, co znamená přímý a diagonální směr.

6. Vytvoření obrazce v Inkscape

Ve známém vektorovém grafickém editoru Inkscape je přítomen i modul pro vytváření objektů definovaných pomocí L-systémů. Jedná se o modul vytvořený v Pythonu, což znamená, že rychlostí určitě neoslní, což je patrné zejména při tvorbě rozsáhlejších mozaik – i několikaminutové výpočty nejsou vzácností. Nicméně spojení L-systémů a Inkscape je na druhou stranu výhodné, protože se s vytvořeným vzorem dají provádět všechny běžné manipulace, včetně obarvení či změny stylu.

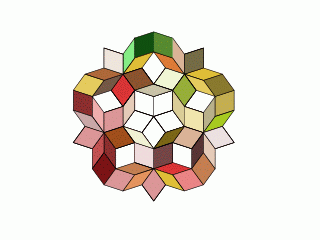
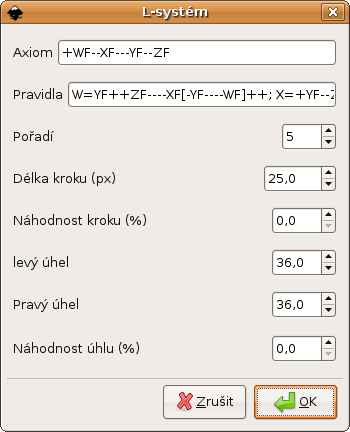
Pro práci s L-systémy je nutné vlastnit Inkscape verze alespoň 0.44. V násle­dujících odstavcích si popíšeme práci s L-systémy, která je velmi snadná, zejména v případě, kdy jsou připravena přepisovací pravidla i axiom, ze kterého se při přepisování vychází (blíže viz výše uvedené odkazy na seriál o fraktálech).

Po spuštění Inkscape se zobrazí prázdný dokument. Nyní je zapotřebí z hlavního menu vybrat položku Efekty a po vyjetí podnabídky zvolit položku Vykreslit a posléze L-systém:

Zobrazí se formulář, ve kterém je možné specifikovat všechny parametry L-systému. Při tvorbě mozaik nás nebudou zajímat položky Náhodnost kroku ani Náhodnost úhlu; zde je nutné ponechat nulové hodnoty. Položka Délka kroku ovlivňuje délku stran jednotlivých dlaždic, ale tu lze upravit i po vykreslení změnou měřítka. Levý i Pravý úhel bude při tvorbě dlaždic nastaven vždy shodně na 36°.

Položka pořadí je počeštěna nevhodně, jedná se vlastně o počet přepisů gramatiky L-systému, tj. počet iterací. Čím vyšší je číslo zde uložené, tím více dlaždic bude vygenerováno, ale roste samozřejmě i čas nutný pro vytváření objektů a alokovaná paměť. Určitě do tohoto políčka nezapisujte hodnoty vyšší než 10. Do položek Axiom a Pravidla se zapisuje gramatika L-systému, přičemž jednotlivá pravidla je nutné oddělit středníkem. Následuje několik typických L-systémů, které lze použít pro tvorbu dlaždicových vzorů. Při zápisu pravidel na jeden řádek nezapomeňte jednotlivá pravidla oddělit středníkem a počet iterací alespoň zpočátku ponechat na malé hodnotě 3–4:

Penrose1
  Axiom +WF--XF---YF--ZF
  W=YF++ZF----XF[-YF----WF]++
  X=+YF--ZF[---WF--XF]+
  Y=-WF++XF[+++YF++ZF]-
  Z=--YF++++WF[+ZF++++XF]--XF
  F=

Penrose2
  Axiom ++ZF----XF-YF----WF
  W=YF++ZF----XF[-YF----WF]++
  X=+YF--ZF[---WF--XF]+
  Y=-WF++XF[+++YF++ZF]-
  Z=--YF++++WF[+ZF++++XF]--XF
  F=

Penrose3
  Axiom [X]++[X]++[X]++[X]++[X]
  W=YF++ZF----XF[-YF----WF]++
  X=+YF--ZF[---WF--XF]+
  Y=-WF++XF[+++YF++ZF]-
  Z=--YF++++WF[+ZF++++XF]--XF
  F=

Penrose4
  Axiom [Y]++[Y]++[Y]++[Y]++[Y]
  W=YF++ZF----XF[-YF----WF]++
  X=+YF--ZF[---WF--XF]+
  Y=-WF++XF[+++YF++ZF]-
  Z=--YF++++WF[+ZF++++XF]--XF
  F=

DoublePenrose
  Axiom [X][Y]++[X][Y]++[X][Y]++[X][Y]++[X][Y]
  W=YF++ZF----XF[-YF----WF]++
  X=+YF--ZF[---WF--XF]+
  Y=-WF++XF[+++YF++ZF]-
  Z=--YF++++WF[+ZF++++XF]--XF
  F=

Vzhledem k tomu, že v generátoru L-systémů nejsou přítomny terminální symboly určené pro změnu délky kreslených čar, není možné přímo generovat mozaiky složené z dlaždic draka a šipky. To však není na škodu, v osmé kapitole si ukážeme, jak přesto vytvořit reálnou skládačku i s těmito tvary.

Stisk tlačítka OK zahájí generování obrázku:

7. Obarvení jednotlivých dílů skládačky

Jednotlivé dlaždice je možné před tiskem obarvit. Nejprve se musí celý objekt rozdělit na jednotlivé dlaždice či jejich části volbou položky menu Křivka-Rozdělit:

Posléze je možné provést obarvení jednotlivých dlaždic. To se provádí buď postupným výběrem dlaždic k tomu určeným nástrojem „šipka“ a následnou volbou barvy z barvové palety (barvy v paletě je možné přepínat). Další možností je „přetažení“ barvy z palety přímo na jednotlivé dlaždice.

8. Tisk výsledné skládačky

Posledním krokem je tisk celé skládačky. Pokud máte barevnou tiskárnu, tak není s tiskem žádný problém, jen je zapotřebí dodržet minimální rozumnou velikost stran jednotlivých dílků cca 2cm, pro menší děti spíše 5cm. Vyplatí se provést tisk na více papírů, potom je možné skládat rozsáhlejší mozaiky. V případě, že si chcete usnadnit stříhání (delší rovné střihy), je lepší si vytvořit „mřížku“ na sebe navazujících kosočtverců (ty jsou, jak jsme si již řekli, pouze dvou typů), a složité mozaiky si vytisknout pouze pro ukázku a inspiraci.

Nám ostatním, co nemáme barevnou tiskárnu, bude plně postačovat jeden výtisk neobarvené skládačky na jediný papír velikosti A4. S tímto listem zajdeme do většího copy-centra, kde určitě nabízí kopie na barevné papíry, ideálně s větší gramáží (tyto papíry sice kopírkou prolezou, ale běžnými tiskárnami již ne, proto je lepší jít do copy-centra). Barva papírů může být různá, většinou postačí šest základních barev (6× kopie té samé strany), popř. je možné použít i papíry s „gradientním“ barevným přechodem.

Stejným způsobem je možné vytisknout i dlaždice ve tvaru draka a šipky – viz ukázky mozaik v páté kapitole. Zde sice narazíme na problém s tím, že se L-systém s těmito tvary nedá v Inkscape vytvořit, nic nám však nezabrání v tom si v Inkscape nebo i jiném vektorovém editoru (popř. pouze pravítkem a úhloměrem) zkonstruovat tvar esa, což je jeden spojený drak a šipka (v kapitole 4 je zobrazen „okótovaný“ obrázek). Pokud si z es vytvoříte mřížku, usnadní se vám i stříhání, protože se povedou přímé střihy přes celý formát A4. Opět je vhodné provést kopii na několik papírů různých barev (minimálně čtyři barvy, ideálně barev šest) a k takto vytvořenému dárku přidat několik vytištěných vzorů výsledné mozaiky pro inspiraci.

9. Odkazy na další informační zdroje

1. Hill, F. S. jr.: „Computer Graphics using OpenGL“,
   Prentice Hall, 2001
2. Prusinkiewicz Przemyslaw and Hanan James: „Lindenmayer Systems, Fractals, and Plants“,
   Springer-Verlag, New York, 1989.
3. Prusinkiewicz Przemyslaw and Lindenmayer Aristid: „The Algorithmic Beauty of Plants“,
   Springer-Verlag, NY, 1990. ISBN 0–387–97297–8
4. Weber J., Penn J.: „Creation and Rendering of Realistic Trees“,
   Proceedings of SIGGRAPH '95, volume 22(4), ACM SIGGRAPH, New York, 1995
5. Wegner Timothy, Peterson Mark: „Fractal Creations, First Edition“,
   The Waite Group Press, 1991
6. Wegner Timothy, Tyler Bert: „Fractal Creations, Second Edition“,
   The Waite Group Press, 1993
7. Žára J., Beneš B., Felkel P.: „Moderní počítačová grafika“,
   Computer Press, Praha, 1998, ISBN 80–7226–049–9
8. Žára J., Limpouch A., Beneš B., Werner T.: „Počítačová grafika – principy a algoritmy“,
   Grada, 1992
9. Popis L-systémů implementovaných v Inkscape:
   http://tavmjon­g.free.fr/INKSCA­PE/MANUAL/html/Ef­fects-Render.html#Effects-Lindenmayer
10. Penrose Tiles:
    http://mathwor­ld.wolfram.com/Pen­roseTiles.html
11. Non Periodic Tiling of the Plane:
    http://local.was­p.uwa.edu.au/~pbou­rke/texture_co­lour/nonperio­dic/index.html
12. Roger Penrose na Wikipedii:
    http://en.wiki­pedia.org/wiki/Ro­ger_Penrose
13. Penrose Tiling:
    http://en.wiki­pedia.org/wiki/Pen­rose_tiling
14. Penrose Tiling 2:
    http://www.uw­gb.edu/DutchS/sym­metry/penrose­.htm
15. Johannes Kepler:
    http://en.wiki­pedia.org/wiki/Jo­hannes_Kepler
16. L-systémy: přírodní objekty i umělé artefakty:
    /clanky/l-systemy-prirodni-objekty-i-umele-artefakty/
17. Implementace L-systémů založená na želví grafice:
    /clanky/imple­mentace-l-systemu-zalozena-na-zelvi-grafice/
18. Závorkové a stochastické L-systémy:
    /clanky/zavorkove-a-stochasticke-l-systemy/
19. Paralelní přepisování řetězců v L-systémech:
    /clanky/paralelni-prepisovani-retezcu-v-l-systemech/
20. Mozaiky s L-systémy a trojrozměrné L-systémy:
    /clanky/mozaiky-s-l-systemy-a-trojrozmerne-l-systemy/
21. penrose(6) – Linux man page:
    http://linux.di­e.net/man/6/p­enrose
22. Polygon names apod.:
    http://joemaller­.com/2001/12/pa­ge/2/
23. Obrázky vytvořené v Inkscape::
    http://www.in­kscape.org/scre­enshots/galle­ry/inkscape-0.44-lindenmayer.png
24. Stránka programu LParser:
    http://home.wa­nadoo.nl/lauren­s.lapre/lparser­.html
25. Wikipedia: „Helge von Koch“,:
    http://cs.wiki­pedia.org/wiki/Hel­ge_von_Koch
26. Kolka Milan: „Spojování želv v jazyce založeném na L-systémech“,:
    http://www.elek­trorevue.cz/clan­ky/01010
27. Tuček Vít: „Implementace L-systému v Prologu“,:
    http://artax.kar­lin.mff.cuni.cz/~tu­cev2am/v0.9be­ta/
28. Mr. Zdeeck: „WWW L-System Explorer“ (česky),:
    http://zdeeck­.borg.cz/wlse/in­dex.php?lang=cz