Obsah
1. Paralelní přepisování řetězců v gramatikách
2. Fraktální křivka v podobě Sierpinského trojúhelníku
3. První demonstrační příklad – Sierpinského trojúhelník
4. Hilbertova křivka
5. Druhý demonstrační příklad – Hilbertova křivka vykreslená pomocí L-systémů
6. Třetí demonstrační příklad – Hilbertova křivka vykreslená rekurzivně
7. Dračí křivka
8. Obsah dalšího pokračování tohoto seriálu
1. Paralelní přepisování řetězců v gramatikách
V předchozí části tohoto seriálu jsme si ukázali tvorbu velmi jednoduchých L-systémů, které měly jednu společnou vlastnost – v jejich gramatice bylo použito pouze jedno přepisovací pravidlo, přičemž na jeho levé straně se většinou nacházel samotný symbol F. L-systémů s jedním přepisovacím pravidlem existuje celá řada, kromě toho je však mnoho systémů, které přepisovacích pravidel používají více, a právě zde přichází na řadu takzvané paralelní přepisování řetězců. To spočívá v současné aplikaci přepisovacích pravidel na všechny řetězce uvedené na pravé straně přepisovacích pravidel v jednom iteračním kroku.
Ve skutečnosti se samozřejmě nejedná o „pravý“ paralelní výpočet (už jen proto, že řetězce jsou uloženy v jedné paměti s technologicky vynuceným sekvenčním přístupem), pouze musíme zaručit, aby se přepsání řetězců v jednom kroku iterace projevilo až v kroku následujícím. Jinými slovy to znamená, že nezáleží na pořadí aplikace pravidel, můžeme je tedy začít přepisovat ve zcela libovolném pořadí. Praktická implementace paralelního přepisování řetězců je jednoduchá: nové řetězce vzniklé přepsáním zapisujeme do nové oblasti paměti tak, aby nedošlo k přepsání původních řetězců. Až po provedení všech přepisů se nové řetězce zkopírují na místo řetězců stávajících a výpočet může probíhat následujícím iteračním krokem.
Při implementaci paralelního přepisování řetězců narazíme, podobně jako v minulé části tohoto seriálu, na malou podporu řetězců v programovacím jazyku C. Proto je také dále uvedená funkce applyRules(), která se o přepisování stará, poměrně složitá (velký počet pomocných proměnných, vnořených smyček apod.), i když ve skutečnosti provádí jednoduchou činnost a v jiném programovacím jazyce by se jednalo o poměrně triviální úlohu. Funkce provádějící přepis řetězců v programovacím jazyku C může mít tvar:
//-----------------------------------------------------------------------------
// Aplikace přepisovacích pravidel na řetězec
//-----------------------------------------------------------------------------
void applyRules(
char *rules[], // pole přepisovacích pravidel
char *axiom, // axiom - prvotní naplnění řetězce
char *ret, // řetězec, do kterého se má uložit výsledek
int maxiters) // maximální počet iterací (aplikací pravidel)
{
int rulesCount; // počet pravidel
int rule; // právě aplikované pravidlo
char *leftSide; // pole levých částí přepisovacích pravidel
char **rightSideSrc; // pole pravých částí přepisovacích pravidel
char **rightSideDest;
int i, j, k, iter; // počitadla smyček a indexy znaků
// zjistit celkový počet přepisovacích pravidel
for (rulesCount=0; rules[rulesCount]; rulesCount++)
;
// nyní máme v proměnné rulesCount uložen počet přepisovacích pravidel
printf("celkový počet pravidel=%d\n", rulesCount);
// alokace paměti pro levou stranu přepisovacích pravidel
// a inicializace pole znaků
leftSide=(char *)malloc(rulesCount*sizeof(char));
for (i=0; i<rulesCount; i++)
leftSide[i]=rules[i][0];
// alokace paměti pro pravou stranu přepisovacích pravidel
// a inicializace pravých stran
rightSideSrc=(char **)malloc(rulesCount*sizeof(char *));
rightSideDest=(char **)malloc(rulesCount*sizeof(char *));
for (i=0; i<rulesCount; i++) {
rightSideSrc[i]=(char *)malloc(MAX_LENGTH);
rightSideDest[i]=(char *)malloc(MAX_LENGTH);
strcpy(rightSideSrc[i], rules[i]+2); // podřetězec za znakem '='
}
// nastavení axiomu
strcpy(ret, axiom);
// hlavní iterační smyčka
for (iter=0; iter<=maxiters; iter++) {
printf("iteration=%d\n", iter);
// pro všechna pravidla
for (rule=0; rule<rulesCount; rule++) {
// výpis pravidla před přepisem
printf("%c\t%s\t", leftSide[rule], rightSideSrc[rule]);
// projít celým řetězcem a zpracovat jednotlivé znaky
for (i=0, j=0; rightSideSrc[rule][i]; i++) {
int left;
int found=0;
// pro každý znak zjistit, zda pro něj neexistuje přepisovací pravidlo
// a pokud ano, provést přepis
for (left=0; left<rulesCount; left++) {
if (leftSide[left]==rightSideSrc[rule][i]) {
for (k=0; rightSideSrc[left][k]; k++) // provést přepis
rightSideDest[rule][j++]=rightSideSrc[left][k];
found=1;
}
}
// žádné pravidlo pro daný znak jsme nenašli, proto se znak
// pouze zkopíruje
if (!found) {
rightSideDest[rule][j]=rightSideSrc[rule][i];
j++;
}
}
// ukončení řetězce
rightSideDest[rule][j]=0;
// výpis pravidla po přepisu
printf("%s\n", rightSideDest[rule]);
}
// "paralelní" přepis nových řetězců namísto stávajících
// (leží mimo předchozí smyčku!)
for (rule=0; rule<rulesCount; rule++)
strcpy(rightSideSrc[rule], rightSideDest[rule]);
}
// přepis výsledku
strcpy(ret, rightSideSrc[1]);
// a doplnění posledního posunu želvy (pouze pro křivku Sierpinského trojúhelníka)
strcat(ret, "F");
puts("");
// výpis řetězce v podobě, kdy jsou vypsány pouze znaky ovládající želvu
for (i=0; i<strlen(ret); i++)
if (ret[i]=='F' || ret[i]=='+' || ret[i]=='-') putchar(ret[i]);
} Výše uvedená funkce potřebuje několik vysvětlení, zejména se to týká parametrů, které jsou před jejím zavoláním vyplněny:
Parametr rules – jedná se o pole přepisovacích pravidel, které musí být ukončeno ukazatelem nastaveným na hodnotu NULL, v opačném případě by nemohl být korektně spočítán počet položek uložených v poli (a prováděl by se přepis paměti za polem pravidel). V dále uvedeném demonstračním příkladu je pole inicializováno následovně:
char *rules[]={
"X=YF+XF+Y",
"Y=XF-YF-X",
NULL
}; Parametr axiom – opravdu se jedná o jakýsi axiom L-systému, tedy řetězec, ze kterého se při paralelním přepisování řetězců vychází.
Parametr ret – ukazatel na místo v paměti, od kterého se má uložit výsledný řetězec. Paměť pro řetězec musí být předem alokována na dostatečně velkou hodnotu, jinak by mohlo dojít k porušení ochrany paměti.
Parametr maxiters – maximální počet iterací, tj. aplikací přepisovacích pravidel. S rostoucím počtem iterací stoupá (mnohdy exponenciálně) počet znaků ve výsledném řetězci.
2. Fraktální křivka v podobě Sierpinského trojúhelníku
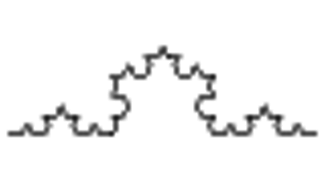
Sierpinského trojúhelník patří mezi jeden z nejčastěji zobrazovaných fraktálních útvarů. Možností jeho počítačem řízené konstrukce existuje celá řada, od využití systémů iterovaných funkcí (Iterated Function Systems – IFS) přes speciálně navržené dynamické systémy vytvářené v komplexní rovině až po L-systémy. Dnes si ukážeme tvorbu fraktální křivky, která vytváří útvar do značné míry podobný Sierpinskému trojúhelníku. Tato křivka, jež je zobrazena na následujícím obrázku, je zajímavá především tím, že je generována pomocí jednoduché gramatiky a při jejím zobrazení v rovině se nikde neprotíná, má tedy podobné vlastnosti jako křivka Helge von Kocha. Na rozdíl od dále popsané Hilbertovy křivky se však nejedná o útvar, který by pokrýval celou rovinu.

Obrázek 1: Fraktální křivka v podobě Sierpinského trojúhelníku
Přepisovací pravidla a axiom pro Sierpinského trojúhelník mají tvar:
X=YF+XF+Y
Y=XF-YF-X
axiom YF Ukázka aplikace této gramatiky L-systému bude ukázána v dnešním prvním demonstračním příkladu, který je popsán v následující kapitole.
3. První demonstrační příklad – Sierpinského trojúhelník
Výše uvedenou dvojici přepisovacích pravidel je možné použít pro konstrukci řetězce sloužícího pro vykreslení Sierpinského trojúhelníka. To je také ukázáno v dnešním prvním demonstračním příkladu, který křivku ve tvaru Sierpinského trojúhelníka nejprve vypočte (tj. vytvoří řetězec interpretovatelný želvou) a poté vykreslí. Při vytváření L-systému s touto křivkou je možné řetězce přepsat 1×, 2× či 3×, větší počet přepisů není možné provést (teoreticky samozřejmě ano, ale musí se zvýšit kapacita paměti alokovaná pro všechny tři řetězce).

Obrázek 2: Screenshot prvního demonstračního příkladu – jedna iterace
Ovládání první demonstrační aplikace je jednoduché, což ostatně dokládá i následující tabulka (podobná tabulce z demonstračního příkladu uvedeného v předchozí části tohoto seriálu):
| Klávesa | Význam |
|---|---|
| 1 | počet iterací (přepisu řetězce) je nastaven na 1 |
| 2 | počet iterací (přepisu řetězce) je nastaven na 2 |
| 3 | počet iterací (přepisu řetězce) je nastaven na 3 |
| Q | ukončení běhu aplikace |
| Esc | ukončení běhu aplikace |
| Page Up | zvýšení hodnoty kroku o 0,1 (zvětšení křivky) |
| Page Down | snížení hodnoty kroku o 0,1 (zmenšení křivky) |
| Left | změna počátečního umístění želvy směrem doleva o 5 pixelů |
| Right | změna počátečního umístění želvy směrem doprava o 5 pixelů |
| Up | změna počátečního umístění želvy směrem nahoru o 5 pixelů |
| Down | změna počátečního umístění želvy směrem dolů o 5 pixelů |

Obrázek 3: Screenshot prvního demonstračního příkladu – dvě iterace
Oproti příkladu uvedenému v předchozí části se však dynamicky nemění krok želvy při změně počtu iterací (přepsání řetězců), což znamená, že se při vysokém počtu iterací (3) nezobrazí celý obrázek, ale pouze jeho výřez. Proto je nutné provést korekci zvětšení pomocí kláves Page Up a Page Down. Zdrojový kód dnešní první demonstrační aplikace je dostupný jak v ASCII formátu, tak i jako HTML stránka se zvýrazněnou syntaxí.
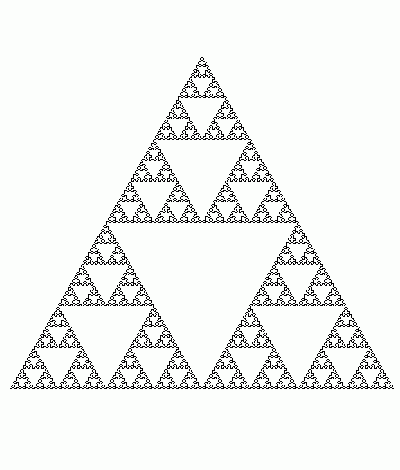
Obrázek 4: Screenshot prvního demonstračního příkladu – tři iterace
4. Hilbertova křivka
V předchozích dvou pokračováních tohoto seriálu jsme si ukázali nejznámější příklady fraktálních objektů, které je možné vytvořit pomocí L-systémů. Dalším známým fraktálním útvarem vytvořeným pomocí L-systémů je Hilbertova křivka. Ta je významná především tím, že se jedná o jeden z nejjednodušších deterministických fraktálů, který je sice tvořen pomocí na sebe navazujících jednorozměrných úseček, ale současně vyplňuje celou plochu. Z toho vyplývá, že topologická dimenze je rovna jedné, ale dimenze Hausdorffova je o celou jedničku vyšší (podobně jako u Mandelbrotovy množiny, ta však v žádném případě nevyplňuje celou plochu).
Konstrukce Hilbertovy křivky je již poněkud složitější, než konstrukce předešlých dvou typů fraktálů. Hilbertova křivka vytvořená v n-té iteraci (n>1) se získá ze čtyř Hilbertových křivek vytvořených v n-1 iteraci, přičemž tyto křivky jsou odpovídajícím způsobem orotovány a zmenšeny na polovinu (tím se dodrží velikost původního obrázku). Čtyři základní křivky A, B, C a D, ze kterých se v dalších iteracích skládá celkový obraz, je možné slovně popsat pomocí rekurze:
| A: | D (doleva) A (dolů) A (doprava) B |
| B: | C (nahoru) B (doleva) B (dolů) A |
| C: | B (doprava) C (nahoru) C (doleva) D |
| D: | A (dolů) D (doleva) D (nahoru) C |
Výše uvedený popis je možné přímo přepsat do algoritmu implementovaného v programovacím jazyce (bez použití gramatik), my si zde však nejprve ukážeme gramatiku, která tvoří řetězec interpretovatelný želvou.
Gramatika, pomocí níž se Hilbertova křivka tvoří, má tvar:
GHilbert=[V,P,S]
V={X,Y,F,+,–}
P={X→-YF+XFX+FY-, Y→+XF-YFY-FX+}
S=X

Obrázek 5: Postupná tvorba Hilbertovy křivky
Implementace algoritmu vytvářejícího Hilbertovu křivku pomocí přepisovacích gramatik bude uvedena v následující kapitole.
5. Druhý demonstrační příklad – Hilbertova křivka vykreslená pomocí L-systémů
V dnešním druhém demonstračním příkladu je předvedeno vykreslení Hilbertovy křivky pro zadaný počet iterací (1–3). Postup při tvorbě křivky je prakticky shodný s prvním demonstračním příkladem, pouze se liší tvar axiomu a přepisovacích pravidel; více změn není aplikováno. Zdrojový kód dnešní druhé demonstrační aplikace je dostupný jak v ASCII formátu, tak i jako HTML stránka se zvýrazněnou syntaxí.

Obrázek 6: Screenshot druhého demonstračního příkladu
6. Třetí demonstrační příklad – Hilbertova křivka vykreslená rekurzivně
Třetí demonstrační příklad taktéž slouží pro vykreslení Hilbertovy křivky, ale při jejím vytváření se nevyužívá paralelní přepisování řetězců ale jiná důležitá programovací technika – rekurze. Ve čtvrté kapitole bylo naznačeno, že se křivka na určité úrovni rekurze skládá ze čtyř částí, které jsou pojmenované symboly A, B, C a D. Vykreslení těchto částí je velmi jednoduché naprogramovat, protože víme, jaká úsečka se má vykreslit. Místo želví grafiky je použita technika založená na grafickém kurzoru, kterým je možné pohybovat buď se současným vykreslením úsečky nebo pouhým přesunem. Samotný grafický kurzor je však neviditelný. Funkce vykreslující čtyři části Hilbertovy křivky, mohou vypadat následovně:
//-----------------------------------------------------------------------------
// Vykreslení části 'A' Hilbertovy křivky
//-----------------------------------------------------------------------------
void hilbertA(int level)
{
if (level>0) {
hilbertB(level-1); lineRel(0,dist);
hilbertA(level-1); lineRel(dist,0);
hilbertA(level-1); lineRel(0,-dist);
hilbertC(level-1);
}
}
//-----------------------------------------------------------------------------
// Vykreslení části 'B' Hilbertovy křivky
//-----------------------------------------------------------------------------
void hilbertB(int level)
{
if (level>0) {
hilbertA(level-1); lineRel(dist,0);
hilbertB(level-1); lineRel(0,dist);
hilbertB(level-1); lineRel(-dist,0);
hilbertD(level-1);
}
}
//-----------------------------------------------------------------------------
// Vykreslení části 'C' Hilbertovy křivky
//-----------------------------------------------------------------------------
void hilbertC(int level)
{
if (level>0) {
hilbertD(level-1); lineRel(-dist,0);
hilbertC(level-1); lineRel(0,-dist);
hilbertC(level-1); lineRel(dist,0);
hilbertA(level-1);
}
}
//-----------------------------------------------------------------------------
// Vykreslení části 'D' Hilbertovy křivky
//-----------------------------------------------------------------------------
void hilbertD(int level) {
if (level>0) {
hilbertC(level-1); lineRel(0,-dist);
hilbertD(level-1); lineRel(-dist,0);
hilbertD(level-1); lineRel(0,dist);
hilbertB(level-1);
}
} Inicializaci překreslování vyvolává funkce, která vypočte krok, o který se má grafický kurzor posouvat jak ve směru horizontálním, tak i ve směru vertikálním. Tato funkce má tvar:
//-----------------------------------------------------------------------------
// Překreslení Hilbertovy křivky
//-----------------------------------------------------------------------------
void recalcHilbert(void)
{
int i;
int level=5;
xx=yy=0;
dist=dist0;
// získat krok pro zadaný počet iterací
for (i=level; i>0; i--)
dist/=2;
// první úroveň kreslení
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_LINES);
gotoXY(dist/2, dist/2);
hilbertA(level);
glEnd();
} Posun grafického kurzoru (bez kreslení i s kreslením) zajišťuje dvojice funkcí gotoXY() a lineRel(), které mění hodnotu „globálních“ proměnných xx a yy:
//-----------------------------------------------------------------------------
// Přesun grafického kurzoru na absolutní souřadnice [x, y]
//-----------------------------------------------------------------------------
void gotoXY(int x, int y)
{
xx=x;
yy=y;
}
//-----------------------------------------------------------------------------
// Přesun grafického kurzoru o vektor [deltaX, deltaY] spolu s kreslením
//-----------------------------------------------------------------------------
void lineRel(int deltaX, int deltaY)
{
// původní pozice grafického kurzoru
glVertex2i(xx, yy);
// přesun grafického kurzoru
xx+=deltaX;
yy+=deltaY;
// nová pozice grafického kurzoru
glVertex2i(xx, yy);
} Zdrojový kód dnešní třetí demonstrační aplikace je dostupný jak v ASCII formátu, tak i jako HTML stránka se zvýrazněnou syntaxí.
Obrázek 7: Screenshot třetího demonstračního příkladu
7. Dračí křivka
Dračí křivka je dalším známým typem fraktálního objektu vytvářeného pomocí L-systémů. Její význam tkví především v tom, že její první iterace je možné vytvořit pouze pomocí ohýbání proužku papíru, žádné další pomůcky nejsou zapotřebí. Postup tvorby dračí křivky je ukázán na následujícím animovaném obrázku. Začíná se s jednou úsečkou. Tato úsečka je ve své polovině ohnuta o pravý úhel doleva, takže vzniknou dvě úsečky navzájem svírající pravý úhel. Výsledkem je tvar zobrazený na zmíněné animaci.
Poté se již postupuje podobně jako u předchozích typů fraktálů, tj. iterativním způsobem. Obě úsečky jsou opět ohnuty, první o pravý úhel doleva, druhá o pravý úhel doprava. Výsledkem je čtveřice úseček tvořících lomenou čáru. Ohyb úseček probíhá podle popsaného principu dále a po několika iteracích se již začíná rýsovat tvar dračího těla i s ocasem a hlavou. Mimochodem, tento fraktál je velmi oblíbený například i mezi uživateli AutoCADu, kteří ho tvoří pomocí skriptů napsaných v LISPu.
Gramatika pro dračí křivku GDragon má tvar:
GDragon=[V,P,S]
V={X,Y,F,+,–}
P={Y→+FX–FY+, X→-FX++FY-}
S=FX

Obrázek 8: Animace postupné konstrukce dračí křivky zvyšováním počtu iterací
8. Obsah dalšího pokračování tohoto seriálu
Navzdory „předvolebním slibům” jsme se dnes nedostali až k vysvětlení závorkových L-systémů, tj. L-systémů, ve kterých má želva k dispozici lokální paměť ve formě zásobníku. Tímto tématem se tedy budeme zabývat až v následující části tohoto seriálu spolu s úvodními informacemi o trojrozměrných L-systémech, které mají pro počítačovou grafiku velký význam.