Obsah
1. Perlinova šumová funkce a její aplikace
2. Princip šumové funkce
3. Jednorozměrný šum
4. První demonstrační příklad – jednorozměrný šum
5. Dvourozměrný šum
6. Druhý demonstrační příklad – dvourozměrný šum
7. Aplikace Perlinovy šumové funkce
8. Odkazy na další informační zdroje
9. Obsah dalšího pokračování tohoto seriálu
1. Perlinova šumová funkce a její aplikace
V předchozí části tohoto seriálu jsme si popsali jeden neperiodický vzorek (moaré s kružnicovým vzorem, s možností rozšíření o další funkce při výpočtu moaré), který sice na první pohled vykazuje podobné charakteristiky jaké jsou typické pro fraktály, ve skutečnosti se však o fraktál nejedná, protože není splněna podmínka nezávislosti na změně měřítka ani podmínka soběpodobnosti. Dnes se budeme zabývat takzvanou Perlinovou šumovou funkcí, která je také do jisté míry podobná fraktálům, i když ani u ní není splněna podmínka soběpodobnosti (teoreticky je ovšem možné provést její rozšíření formou nekonečné řady). Vzhledem k tomu, že má Perlinova funkce v počítačové grafice široké možnosti využití, ukážeme si, jak se s pomocí ní dají generovat dvourozměrné textury i textury objemové (volumetric textures).

Perlinova šumová funkce byla s velkým úspěchem použita v mnoha aplikacích počítačové grafiky; například prakticky každý film, ve kterém je použita renderovaná grafika, tuto funkci nějakým způsobem použil. Její úspěch spočívá v tom, že se pomocí ní dají do původně přesných a „počítačově chladných“ modelů vnést náhodné prvky, takže se model či celá vytvářená scéna přiblíží realitě. Podobný princip vnesení náhodnosti ostatně umožňují i fraktály, zejména ty vytvářené na stochastickém základě (plasma, stochastické L-systémy apod.) Perlin šumovou funkci navrhl už v roce 1983, v roce 1985 o její aplikaci vznikl článek prezentovaný na SIGGRAPHu (jedna z nejvýznamnějších konferencí počítačové grafiky) a v letech 1986 až 1988 tuto funkci s některými modifikacemi používaly takové firmy, jako Pixar, Alias, SoftImage apod.

2. Princip šumové funkce
Při tvorbě textur, které by měly reprezentovat přírodní vzorky jako je mramor, dřevo či mraky není možné použít ani klasický generátor pseudonáhodných čísel RNG (tím je myšlena například například rand() ze standardní céčkové knihovny), ale ani základní matematické funkce. V minulosti byly prováděny pokusy o využití goniometrických funkcí, které posléze vyústily v úspěšnou metodu generování plasmy pomocí Fourierovy syntézy. Tuto metodu jsme si již popisovali v předcházejících částech tohoto seriálu, spolu s metodou přesouvání prostředního bodu (midpoint displacement). Při přímé aplikaci generátorů pseudonáhodných čísel sice získáme šum, ten je však příliš náhodný a vůbec se nehodí pro generování textur, a to ani po své filtraci.
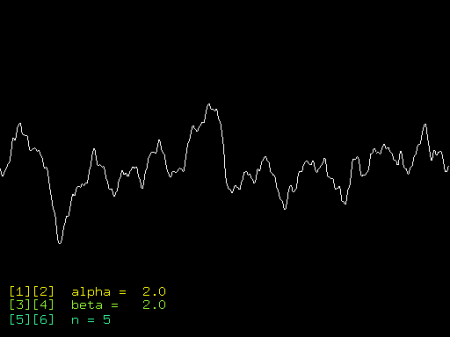
Obrázek 3: Jednorozměrná Perlinova šumová funkce s parametry alpha=2, beta=2, n=10 (obrázek získaný z prvního demonstračního příkladu)Perlin pro účely vytváření přírodních textur navrhl výpočet, který sice využívá generátor pseudonáhodných čísel, ale mezi jednotlivými vypočtenými náhodnými hodnotami je prováděna interpolace, která výsledný průběh funkce vyhladí, takže se již nebude jednat o zcela náhodný šum. Pro vyhlazení je možné použít velké množství matematických funkcí, od jednoduché lineární interpolace přes kvadratické a kubické funkce až po funkce goniometrické a jejich vzájemné kombinace. Perlin použil (pokud celý popis jeho postupu značně zjednodušíme) dvojici funkcí, první nazvanou s_curve() a druhou nazvanou lerp(). Při výpočtu šumu je nejdříve použita funkce s_curve(), posléze se získají dvě náhodné hodnoty a na výsledek je aplikována funkce lerp(). Funkce s_curve() má tvar:
s_curve(t)=(t2*(3–2t))
Obrázek 4: Průběh funkce s_curve(); na horizontální ose je použito jiné měřítko, než v originálních Perlinových zdrojových kódech. Ve skutečnosti je v praxi využit pouze rozsah vstupních hodnot 0..1 (na grafu 0..20), sestupná část již nikoli.Funkce lerp() má tvar:
lerp(t, a, b)=(a+t(b-a))
Všimněte si, že se v tomto případě nejedná o nic jiného, než o lineární interpolaci řízenou parametrem t. Pro t=0,0 je výsledkem funkce hodnota a, pro t=1,0 pak hodnota b. Konkrétní hodnota parametru t je získána výpočtem výše uvedené funkce s_curve().
3. Jednorozměrný šum
Jednorozměrný šum je vypočten v céčkové funkci noise1(), jejíž zdrojový kód je zobrazen níže:
//-----------------------------------------------------------------------------
double noise1(double arg)
{
int bx0, bx1;
double rx0, rx1, sx, t, u, v, vec[1];
vec[0] = arg;
if (start) {
start = 0;
init();
}
setup(0,bx0,bx1,rx0,rx1);
sx = s_curve(rx0);
u = rx0 * g1[ p[ bx0 ] ];
v = rx1 * g1[ p[ bx1 ] ];
return(lerp(sx, u, v));
} Takto vypočtený šum se však většinou nepoužívá přímo; místo toho je sečteno více těchto šumů s rozdílnou „frekvencí“ (nejedná se však o periodickou funkci, proto ty uvozovky). Čím vyšší je frekvence šumových průběhů, tím nižší je i jejich amplituda. Tento výpočet je prováděn v céčkové funkci PerlinNoise1D() s tvarem:
//-----------------------------------------------------------------------------
double PerlinNoise1D(double x, double alpha, double beta, int n)
{
int i;
double val,sum = 0;
double p,scale = 1;
p = x;
for (i=0;i<n;i++) {
val = noise1(p);
sum += val / scale;
scale *= alpha;
p *= beta;
}
return(sum);
} Parametrem n je určen počet šumových průběhů, které se sčítají. Parametr alpha řídí změnu amplitudy a tím i míru náhodnosti průběhu a parametrem beta, který je většinou nastaven na hodnotu 2 pak změna „frekvence“.
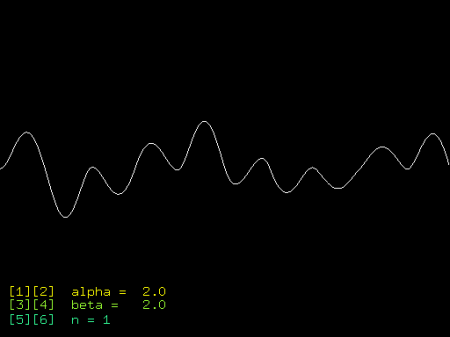
Obrázek 5: Jednorozměrná Perlinova šumová funkce s parametry alpha=2, beta=2, n=1 (obrázek získaný z prvního demonstračního příkladu)
4. První demonstrační příklad – jednorozměrný šum
Dnešní první demonstrační příklad, jehož zdrojový kód můžete získat pod tímto odkazem (popř. i jako HTML stránku se zvýrazněnou syntaxí), slouží k zobrazení jednorozměrné Perlinovy šumové funkce pomocí příkazů z grafické knihovny OpenGL. Pro překlad je ještě zapotřebí získat původní Perlinovy zdrojové kódy: perlin.c a perlin.h. Perlinova šumová funkce je vykreslena ve formě obyčejného plošného grafu; vlastní vykreslení pomocí lomené čáry (polyčáry) přitom zajišťuje céčkovská funkce nazvaná recalcPerlinNoise1D(), která má následující tvar:
//-----------------------------------------------------------------------------
// Prekresleni jednorozmerne Perlinovy sumove funkce
//-----------------------------------------------------------------------------
void recalcPerlinNoise1D(double alpha, double beta, int n)
{
int i;
double x=-5.0, y; // pocatecni hodnota souradnice x
int width=glutGet(GLUT_WINDOW_WIDTH); // sirka okna
int height=glutGet(GLUT_WINDOW_HEIGHT); // vyska okna
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_LINE_STRIP); // zacatek vykreslovani lomene cary (polycary)
for (i=0; i<width; i++) {
y=PerlinNoise1D(x, alpha, beta, n); // vypocet Perlinovy funkce
y*=(double)height/2.0; // zmena amplitudy podle vysky okna
y+=height>>1; // posun ve vertikalnim smeru do stredu okna
glVertex2f(i, y); // pripojeni dalsi casti lomene cary
x+=10.0/(double)width; // prechod na dalsi souradnici v horizontalnim smeru
}
glEnd(); // konec vykreslovani lomene cary
} Jak je z uvedeného výpisu patrné, jsou funkci recalcPerlinNoise1D() předány tři parametry. V prvním parametru je specifikován koeficient alpha (míra snižování amplitudy šumu s rostoucím n), ve druhém parametru koeficient beta a třetí parametr určuje počet volání šumové funkce (její jednotlivé hodnoty mají s rostoucím n nižší amplitudu). Hodnotu těchto koeficientů je možné změnit pomocí několika kláves, jejich konkrétní mapování je vypsáno v následující tabulce:
| Klávesa | Význam |
|---|---|
| Q | ukončení aplikace |
| F | přepnutí zobrazení grafu funkce na celou obrazovku (pokud to dovolí okenní manažer) |
| W | zpětné přepnutí zobrazení do okna o implicitní velikosti |
| 1 | snížení koeficientu alpha o hodnotu 0,5 |
| 2 | zvýšení koeficientu alpha o hodnotu 0,5 |
| 3 | snížení koeficientu beta o hodnotu 0,5 |
| 4 | zvýšení koeficientu beta o hodnotu 0,5 |
| 5 | snížení celočíselného koeficientu n o jedničku |
| 6 | zvýšení celočíselného koeficientu n o jedničku |
5. Dvourozměrný šum
Dvourozměrný šum je vypočten prakticky stejným způsobem jako šum jednorozměrný. Jediný podstatný rozdíl spočívá v tom, že se interpolace provádí ve dvou směrech a výsledek této interpolace je sečten. Céčková funkce navržená Perlinem má tvar:
//-----------------------------------------------------------------------------
double noise2(double vec[2])
{
int bx0, bx1, by0, by1, b00, b10, b01, b11;
double rx0, rx1, ry0, ry1, *q, sx, sy, a, b, t, u, v;
int i, j;
if (start) {
start = 0;
init();
}
setup(0, bx0,bx1, rx0,rx1);
setup(1, by0,by1, ry0,ry1);
i = p[ bx0 ];
j = p[ bx1 ];
b00 = p[ i + by0 ];
b10 = p[ j + by0 ];
b01 = p[ i + by1 ];
b11 = p[ j + by1 ];
sx = s_curve(rx0);
sy = s_curve(ry0);
q = g2[ b00 ] ; u = at2(rx0,ry0);
q = g2[ b10 ] ; v = at2(rx1,ry0);
a = lerp(sx, u, v);
q = g2[ b01 ] ; u = at2(rx0,ry1);
q = g2[ b11 ] ; v = at2(rx1,ry1);
b = lerp(sx, u, v);
return lerp(sy, a, b);
} V praxi se opět používá součet několika šumových funkcí s klesající amplitudou a rostoucí frekvencí

//-----------------------------------------------------------------------------
double PerlinNoise2D(double x,double y,double alpha,double beta,int n)
{
int i;
double val,sum = 0;
double p[2],scale = 1;
p[0] = x;
p[1] = y;
for (i=0;i<n;i++) {
val = noise2(p);
sum += val / scale;
scale *= alpha;
p[0] *= beta;
p[1] *= beta;
}
return(sum);
}
//-----------------------------------------------------------------------------
6. Druhý demonstrační příklad – dvourozměrný šum
V dnešním druhém demonstračním příkladu je ukázáno, jakým způsobem je možné použít dvourozměrnou Perlinovu šumovou funkci pro vytvoření velmi jednoduché textury. Po překladu a spuštění tohoto příkladu se vytvoří deset rastrových obrázků ve formátu TGA (neboli Targa – viz paralelně běžící seriál o grafických formátech). Změnou parametrů funkce recalcPerlinNoise2D() (viz její zdrojový kód zobrazený níže) je možné získat obrázky s různou hustotou šumu, různým barevným podáním atd. Zdrojový kód druhého demonstračního příkladu je dostupný zde, popř. jako HTML stránka se zvýrazněnou syntaxí.
//-----------------------------------------------------------------------------
// Funkce provadejici vypocet dvourozmerne Perlinovy sumove funkce
//-----------------------------------------------------------------------------
void recalcPerlinNoise2D(pixmap *pix, // pracovni pixmapa
int palette, // cislo barvove palety
double xmin, // meze fraktalu v rovine
double ymin,
double xmax,
double ymax,
double alpha, // koeficient alpha
double beta, // koeficient beta
int n) // koeficient n
{
int x, y, i; // pocitadla smycek
double x1, y1, z; // prepoctena pozice pixelu
init();
y1=ymin;
for (y=0; y<pix->height; y++) { // pro vsechny radky pixmapy
x1=xmin;
for (x=0; x<pix->width; x++) { // pro vsechny pixely na radku
unsigned char r, g, b;
x1+=(xmax-xmin)/pix->width; // pocatecni hodnota x1
z=PerlinNoise2D(x1, y1, alpha, beta, n); // vypocet sumove funkce
i=z*32.0+128; // aplikace zesileni a offsetu
mapPalette(palette, i & 0xff, &r, &g, &b); // mapovani na barvovou paletu
putpixel(pix, x, y, r, g, b); // a vytisteni pixelu
}
y1+=(ymax-ymin)/pix->height; // prechod na dalsi radek
}
} 


7. Aplikace Perlinovy šumové funkce
Perlinovu šumovou funkci je možné v počítačové grafice všestranně použít k vytváření mnoha různých přírodních vzorků, například mramoru, textury dřeva, ohně, mraků, kamenů hor. Všechny výše uvedené funkce je možné různými způsoby modifikovat, například do výpočtů prováděných ve funkcích PerlinNoise1D() a PerlinNoise2D přidávat další matematické funkce. Často se původní Perlinova funkce upravuje tak, že se sčítají absolutní hodnoty dílčích šumů, přidává se goniometrická funkce sinus atd.
Mnohem důležitější je však rozšíření výpočtů do trojrozměrného prostoru. Programově se nejedná o žádnou komplikaci (viz snadný a přímočarý přechod z 1D na 2D), ovšem dopad na možnosti využití je značný. Dvourozměrné textury mají několik vážných nevýhod, z nichž největší spočívá v obtížném mapování na nerovné povrchy. Například mapování obdélníkové textury na kouli vede k tomu, že se textura na pólech smrští a naopak na rovníku příliš roztáhne. Výsledek je většinou neuspokojivý, zvláště při aplikaci šumové funkce (ta by měla být směrově invariantní). Přechodem k výpočtům 3D (volumetrických) textur se tohoto problému zbavíme (viz obrázek číslo 2 zobrazený v první kapitole), protože pro každý bod v prostoru je možné zjistit hodnotu šumu bez nutnosti mapování.
3D textury se často používají v raytracerech, kde se projevuje i jejich další přednost – jejich hodnotu je možné vypočítat pro libovolný bod v prostoru, není tedy nutné nejprve provést výpočet textury v nějakém rastru. Tím ušetříme velké množství paměti (3D rastrové textury mají obrovské paměťové nároky), nebude docházet k aliasu a také je možné texturu animovat, například postupnou změnou některého z parametrů (barvové palety, parametru alpha, beta, n atd.)
8. Odkazy na další informační zdroje
- Perlin Noise and Turbulence:
http://local.wasp.uwa.edu.au/~pbourke/texture_colour/perlin/ - Perlin Ken:
An Image Synthesizer,
Computer Graphics, Volume 19, Number 3, 1985, pages 287–296 - Perlin Ken and Hoffert E. M.:
Hypertexture,
Computer graphics, Volume 23, Number 3, July 1989, pages 253–262 - WWW stránky raytraceru POV-Ray:
http://www.povray.org - POV-Team:
POV-Ray v3.1g User's documentation,
Elektronická dokumentace k programu POV-Ray, 1999
9. Obsah dalšího pokračování tohoto seriálu
V následujícím (pravděpodobně již předposledním) pokračování tohoto seriálu si ukážeme zajímavé krátké programy upravené do tvaru známých signatur (podpisů například e-mailů), které slouží pro výpočet a zobrazení fraktálů. Uvidíme, že fraktální obrázky může sama generovat i obyčejná tiskárna vybavená PostScriptem nebo je možné vykreslovat Mandelbrotovy a Juliovy množiny na konzoli.