Obsah
2. Vlastnosti programovacího jazyka APL
3. Je jazyk APL skutečně nečitelný?
4. Základní (primitivní) funkce
7. Obsah dalšího pokračování seriálu
1. Programovací jazyk APL
Historie programovacího jazyka APL se začala psát již v roce 1957. Právě tehdy Kenneth Iverson z Hardvardské university vytvořil notaci vhodnou pro jednotný zápis matematických funkcí i tvorbu funkcí nových. V roce 1962 byla tato notace popsána v knize „A Programming Language“ a o několik let později se začaly objevovat skutečné interpretry i překladače programovacího jazyka používajícího stejné symboly, jaké popsal Iverson ve své knize. Konkrétně se jednalo o jazyk IVSYS implementovaný v roce 1965, který byl následován jazykem APL\1130 z roku 1967, jenž pracoval na počítači IBM 1130. Další implementace tohoto jazyka vznikly na mainframech IBM/360 a IBM/370, později se různé (ve větší či menší míře modifikované) verze APL začaly používat i na minipočítačích a posléze i na mikropočítačích. Dnes existují implementace pro všechny rozšířené operační systémy mikropočítačů, takže APL je možné použít na Linuxu, Mac OS i Microsoft Windows (viz odkazy uvedené v deváté kapitole).

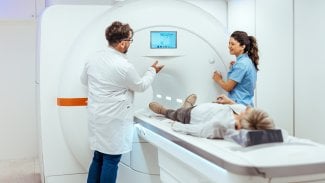
Obrázek 1: Rozložení znaků na klávesnici používané při programování v jazyku APL. Speciální znaky na klávesnici reprezentují základní (primitivní) funkce a operátory.
Kenneth Iverson se rozvoji a propagaci jazyka APL aktivně věnoval více než 20 let, za což mu byla v roce 1979 udělena Turingova cena (Turing Award). Později Iverson navrhl programovací jazyk J, v němž se místo speciálních symbolů (viz následující kapitoly) používají pouze znaky obsažené v ASCII tabulce. Popisu tohoto jazyka se budeme věnovat v některém z dalších dílů seriálu. Vraťme se však k programovacímu jazyku APL. Specifikace jazyka se od poloviny šedesátých let minulého století několikrát změnila (rozšířila). Jedním z nejvíce důležitých rozšíření je APL2 od J. Browna z IBM, které do jazyka zavedlo podporu pro rekurzivní datové struktury (pole jako prvky jiných polí). Většina dnešních implementací tohoto jazyka se snaží dodržovat specifikaci APL2, i když je jazyk dále rozšiřován (například v APLX verze 4 byla přidána podpora pro objektově orientované programování, i když v poněkud jiné podobě, než ji známe z mainstreamových programovacích jazyků).
2. Vlastnosti programovacího jazyka APL
„Real Programmers don't write in APL, unless the whole program can be written on one line“
Jedním z typických rysů programovacího jazyka APL je jeho orientace na zpracování vektorů a matic (obecně polí téměř libovolné dimenze, většina implementací povoluje definovat až 63dimenzionální struktury) bez nutnosti použití čítačů či programových smyček. Jazyk APL s těmito datovými strukturami pracuje z hlediska programátora prakticky stejně jako se skalárními hodnotami (čísly), takže například součet položek dvou polí je zapisován stejně jako součet dvou číselných hodnot. Dalším typickým rysem je způsob aplikace funkcí na hodnoty (obecně pole) a vzájemné kombinace funkcí pomocí operátorů (slovem operátor jsou v jazyce APL označovány funkce vyššího řádu, tj. funkce vracející jiné funkce; s funkcemi vyššího řádu se můžeme setkat i v mnoha dalších programovacích jazycích). Pomocí funkcí a operátorů, které jsou přímo v APL definovány, je možné nahradit i řídicí struktury – podmíněné příkazy a programové smyčky – které dokonce v prvních verzích jazyka ani nebylo možné zapisovat (v pozdějších verzích se pro usnadnění programování tyto řídicí struktury do APL přidaly).
Každá základní (primitivní) funkce a operátor je v jazyce zapisována formou nějakého symbolu, přičemž většina těchto symbolů (znaků) se nenachází v ASCII tabulce, ale jedná se buď o písmeno řecké abecedy nebo jiný (matematický) symbol zvolený Iversonem. Použití symbolů namísto kombinace alfanumerických znaků, tj. zápisu známého z většiny dalších vysokoúrovňových programovacích jazyků, je třetím a pro většinu programátorů nejtypičtějším rysem jazyka APL. V podstatě se jedná o zcela opačný přístup než jaký jsme mohli vidět v předchozí části tohoto seriálu při popisu programovacího jazyka COBOL. Zatímco v COBOLu se každá programová konstrukce popisovala jedním či několika klíčovými slovy (kterých existuje více než 300), jazyk APL žádná klíčová slova neobsahuje, ale nabízí programátorům sadu základních (primitivních) funkcí (cca 50) a operátorů (celkem šest), které je možné kombinovat a vytvářet tak nové uživatelské funkce i uživatelské operátory.
3. Je jazyk APL skutečně nečitelný?
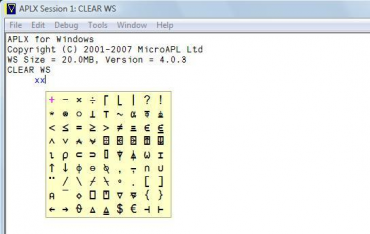
Vzájemná kombinace (zřetězení) primitivních funkcí a operátorů bez vytváření a pojmenování funkcí vlastních vede k velmi úspornému zápisu kódu, který je však pro většinu programátorů prakticky nečitelný (mnozí programátoři čtení podobných programů přirovnávají k luštění hieroglyfů), o čemž se můžete přesvědčit například z následujícího výpisu několika výrazů (vzhledem k tomu, že na některých systémech nemusí být všechny znaky zobrazeny korektně, byl z výpisu programu pořízen screenshot:

Obrázek 2: Užitečné a relativně často používané idiomy jazyka APL zapisované pomocí kombinace základních funkcí a operátorů.
Podobné programátorské praktiky, jaké byly ukázány na předchozím výpisu (ovšem vytvořené profesionálem, nejedná se o žádné nesmyslné demo, ale užitečné idiomy), vedly k tomu, že je jazyk APL považován, byť poněkud neoprávněně, za jazyk „write only“, podobně jako Forth. Ve skutečnosti je však i v jazyku APL možné poměrně snadno psát přehledné a srozumitelné programy, ve kterých navíc programátoři mohou využívat všechny výhody tohoto jazyka (jednoduchá práce s vektory, maticemi a poli, funkce vyššího řádu, velmi rychlé prototypování vhodné pro aplikace, ve kterých je důležitý co nejrychlejší nástup na trh atd.). Pokud jsou například nadefinovány základní řídicí příkazy (mnoho moderních implementací APL je obsahuje), lze programy v APL zapisovat prakticky stejným způsobem, jako v jiných programovacích jazycích (symbol ← značí přiřazení a symbol ⎕ neboli quad je primitivní funkce pro načtení libovolné hodnoty z klávesnice či obecně ze standardního vstupu):
GUESS;VAL
'Hadej cislo'
:Repeat
VAL ← ⎕
:If VAL=42
'Uhodl jsi!'
:Leave
:EndIf
'Tesne vedle, zkus to znovu...'
:EndRepeat

Obrázek 3: Moderní fonty (OpenType, PostScriptové) obsahují buď část nebo dokonce všechny znaky používané jazykem APL pro zápis základních funkcí a operátorů.
4. Základní (primitivní) funkce
Ve druhé kapitole jsme si řekli, že programovací jazyk APL obsahuje cca 50 základních (primitivních) funkcí. V APL se můžeme setkat se třemi typy funkcí. Jedná se o funkce bez argumentů (niladické funkce), tj. ve skutečnosti procedury, dále pak o funkce s jedním argumentem (monadické funkce) a konečně funkce se dvěma argumenty (dyadické funkce). V APL lze přímo ze zápisu zdrojového kódu určit, jakého typu je volaná funkce, což mj. Iversonovi umožnilo použít jeden symbol pro reprezentaci více funkcí – podle toho, jakým způsobem je symbol v programu použit, je zavolána určitá primitivní funkce. Na jednu stranu se může zdát, že toto „přetížení symbolů“ povede k větší nepřehlednosti programů, na stranu druhou jsou však symboly „přetížené“ s rozmyslem, takže například symbol - značí negaci (monadická funkce) či rozdíl (dyadická funkce), podobně jako v mnoha dalších programovacích jazycích. Symbol ÷ znamená v monadické formě výpočet převrácené hodnoty a ve formě dyadické podíl čísel, vektorů či korespondujících prvků polí. V následující tabulce jsou vypsány některé primitivní funkce jazyka APL (pro korektní zobrazení symbolů v tabulce je nutné použít fonty s podporou Unicode, například některý z řezů fontu DejaVu):
| Symbol | Jeden argument | Dva argumenty |
|---|---|---|
| + | identita | součet |
| – | negace | rozdíl |
| × | znaménko | součin |
| ÷ | převrácená hodnota | podíl |
| ᒥ | zaokrouhlení na celé číslo nahoru | vrátí větší argument |
| ᒪ | zaokrouhlení na celé číslo dolů | vrátí menší argument |
| | | absolutní hodnota | zbytek po dělení |
| ι | čítač | |
| * | ex | xy |
| < | menší než | |
| ≤ | menší nebo rovno | |
| = | rovno | |
| ≥ | větší nebo rovno | |
| > | větší než | |
| ≠ | nerovno | |
| ∈ | obsahuje (dotaz na existenci prvku v poli) | |
| ∈ | nalezení hodnoty (prvku v poli) | |
| ○ | π×hodnota | goniometrická funkce specifikovaná 2.argumentem |
| ! | 1×2×3×.. | kombinace |
| ⌹ | inverze matice | podíl matic |
| ⍉ | transpozice řádků za sloupce | transpozice specifikovaná 2.argumentem |
| ⌽ | obrácení pořadí položek | rotace položek (vektoru, matice) |
| ⍋ | setřídění položek vektoru vzestupně | setřídění podle zadaného argumentu |
| ⍒ | setřídění položek vektoru sestupně | setřídění podle zadaného argumentu |
Obrázek 4: Editory a integrovaná vývojová prostředí pro jazyk APL dnes většinou obsahují i dialog s nabídkou symbolů používaných při zápisu základních funkcí a operátorů.
5. Výrazy
Programy v jazyce APL se skládají z výrazů, při jejichž zápisu se musí dodržovat jen minimální množství syntaktických pravidel. Nejdůležitějším pravidlem je, že se jednotlivé funkce vyhodnocují zprava doleva, přičemž již vyhodnocená funkce (tj. její návratová hodnota) je použita jako argument funkce ležící nalevo od ní. Symboly monadických funkcí se zapisují vždy před svůj argument, naopak symboly funkcí dyadických jsou zapsány mezi oba argumenty (což je v matematice obvyklé, protože funkce v APL odpovídají v matematice operátorům). Při zápisu aritmetických výrazů je zapotřebí dát pozor na to, že všechny funkce mají stejné priority (bylo by totiž velmi složité definovat či zapamatovat si prioritu více než padesáti primitivních funkcí). Interpret jazyka APL vypisuje hodnotu vyhodnoceného výrazu (tj. návratovou hodnotu nejlevější funkce) na výstup:
aritmetický výraz 1+2×3 7 vyhodnocení zprava doleva, priority všech funkcí jsou stejné 2×3+1 8 argumentem funkce může být i vektor či pole (zde vektor šesti čísel) každá položka vektoru je vynásobena hodnotou 0.5 2 4 6 8 × 0.5 1 2 3 4 totéž platí pro monadickou funkci "převrácená hodnota" ÷1 2 3 4 5 1 0.5 0.3333333333 0.25 0.2 hodnota 10 je vydělena každou hodnotou z vektoru, výsledkem je též vektor 10÷1 2 3 4 5 10 10 5 3.33333333 2.5 2.0 1 ukázka kombinace více funkcí, vyhodnocování je stále zprava doleva ᒥ 10÷1 2 3 4 5 10 10 5 4 3 2 1 dtto pro funkci provádějící zaokrouhlení na celá čísla směrem dolů ᒪ 10÷1 2 3 4 5 10 10 5 3 2 2 1

Obrázek 5: Ukázka obrazovky integrovaného vývojového prostředí jazyka APL se zvýrazněním syntaxe, automatickým číslováním řádků při zápisu funkcí atd.
6. Práce s poli
Již v předchozí kapitole jsme si na příkladech ukázali základy práce s číselnými vektory. Jazyk APL podporuje i práci s vícedimenzionálními poli, kde hraje velkou roli monadická a dyadická funkce ρ (ró, reshape) a taktéž monadická funkce ι (jóta, index, též čítač). V následujících ukázkách si povšimněte způsobu přiřazení hodnoty (čísla, vektoru nebo pole) do proměnné pomocí funkce ←:
zjištění počtu prvků vektoru pomocí monadické funkce ρ ρ 1 2 3 4 4 přiřazení vektoru do proměnné VECTOR ← 1 2 3 4 5 6 zjištění počtu prvků vektoru pomocí monadické funkce ρ ρVECTOR 6 použití funkce ι, která vygeneruje vektor s prvky 1..n (Pythonisté zde mohou vidět souvislost s voláním range()) VECTOR ← ι10 VECTOR 1 2 3 4 5 6 7 8 9 10 jeden ze způsobů vytvoření prázdného vektoru (seznamu) pomocí funkce ι EMPTY_LIST ← ι0 EMPTY_LIST *** zde se nic nezobrazilo :-) *** zjištění počtu prvků vektoru pomocí monadické funkce ρ ρEMPTY_LIST vytvoření dvourozměrného pole pomocí dyadické funkce ρ nejdříve se zadá rozměr jako první argument (4×3), druhým argumentem je seznam, který je transformován do požadovaného pole 4 3 ρ 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 dvourozměrné pole lze taktéž naplnit pomocí funkce ι 4 3 ρ ι12 1 2 3 4 5 6 7 8 9 10 11 12 pokud nemá seznam dostatečnou délku pro naplnění pole, jsou jeho položky do pole vloženy opakovaně za sebou 4 3 ρ 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 výše uvedené vlastnosti lze snadno využít pro vytvoření pole s prvky o stejné hodnotě 4 3 ρ 0 0 0 0 0 0 0 0 0 0 0 0 0 naplnění proměnné hodnotou matice MATICE ← 3 3 ρ ι 9 MATICE 1 2 3 4 5 6 7 8 9 operace nad prvky matice MATICE × 10 10 20 30 40 50 60 70 80 90 vytvoření matice se třemi řádky a dvěma sloupci CENY ← 3 2 ρ 1 2 3 4 5 6 CENY 1 2 3 4 5 6 přeuspořádaní prvků v matici CENY ← 2 3 ρ CENY CENY 1 2 3 4 5 6 vytvoření matice 2×2 se všemi prvky = 1 M1 ← 2 2 ρ 1 vytvoření matice 2×6 se všemi prvky = 2 M2 ← 2 6 ρ 5 spojení matic (musí mít stejný počet řádků) VYSLEDEK ← M1,M2 výpis obsahu všech tří matic M1 1 1 1 1 M2 5 5 5 5 5 5 5 5 5 5 5 5 VYSLEDEK 1 1 5 5 5 5 5 5 1 1 5 5 5 5 5 5
7. Obsah dalšího pokračování seriálu
V následujícím pokračování seriálu o historii výpočetní techniky dokončíme popis programovacího jazyka APL. Ukážeme si tvorbu hierarchických datových struktur (tj. polí v polích), práci se znaky a řetězci, a především pak způsob použití operátorů, pomocí nichž lze například aplikovat nějakou funkci na všechny prvky pole, zkombinovat vzájemně všechny prvky v poli (z vektoru o n prvcích se stane matice velikosti n×n) atd. Právě díky operátorům nemusí programátoři tvořící aplikace v jazyku APL vytvářet programové smyčky, protože například součet (sumu) či součin (produkt) všech prvků vektoru lze velmi jednoduše zapsat pomocí dyadické funkce + aplikované postupně na všechny prvky vektoru s využitím operátoru / nazývaného „slash“ nebo také „reduce“:
+/ 1 2 3 4 10 ×/ 1 2 3 4 24
8. Literatura
- Ajay Askoolum, „System Building with APL + WIN,“
Wiley, ISBN: 0–470–03020–8, August 2006. - Brown et. al. „APL2 at a Glance,“
Prentice Hall, ISBN 0–13–038670–7. - T. Budd, „An APL Compiler,“
Springer-Verlag. - Maurice Dalois, „Introduction to APL*PLUS PC,“
- J. Ever and C. Fair, „Guidelines for APL Systems,“
DPD 22 IBM 037301, March 1976. - Gilman and Rose, „APL – An Interactive Approach,“
Wiley, ISBN 220–471–30022–5. - Ulf Grenander, „Mathematical Experiments on the Computer,“
Academic Press, 1982, ISBN 0–12–301750–5. - Kent Haralson, „Useful APL Defined Functions“,
IBM Technical Report, TR 00.2409, Feb. 8 1973. - Timothy Holls, „APL Programming Guide,“
IBM G320–6103, 1978, and G320–6735, 1981. - IBM, „APL2 Programming: Language Reference“
(Version 2, SH21–1061; Version 1, SH20–9227). - IBM, „The APL Handbook of Techniques“,
IBM publication number S320–5996, April 1978. - IBM, „The IBM System Journal, V. 30, No. 4 (1991)“,
Special Issue Devoted to APL. - MicroAPL, „Learning APL with APLX“,
Version 5.0 July 2009 - A.D. Falkoff, K.E Iverson, E.H Sussenguth, „A formal description of System/360,“
The IBM System Journal, V. 3, No. 3 (1964) - K. E. Iverson, „A Programming Language“,
Wiley, 1962. - K. E. Iverson, „Algebra : an algorithmic treatment“,
APL Press 1977, Copyright 1972 by Addison Wesley,
Preliminary Edition entitled „Elementary Algebra“
Copyright 1971 by IBM Corporation.
- K. E. Iverson, „Elementary analysis“,
APL press 1976, Preliminary Edition „Elementary Functions“
Copyright 1974 by IBM Corporation ISBN 0–917326–01–6
- K. E. Iverson, „An introduction to APL for Scientists and Engineers“,
APL Press 1976,
First published by IMB Corporation as Technical Report No 320–3019 March 1973 – ISBN 0–917326–04–0
- K. E. Iverson, „APL in exposition“,
APL Press 1976,
First published by IBM Corporation as Technical Report No 320–3010 March 1973 – ISBN 0–917326–02–4.
- K. E. Iverson, „Introduction To APL“,
(1984-APL Press Palo Alto) ISBN 0–917326–14–8. - K. E. Iverson, „A personal view of APL,“
IBM Systems Journal, - K. E. Iverson, „Concrete Mathematics Companion“.
- S. Kamin, „Programming Languages: An Interpreter-Based Approach,“
contains (among other things) toy implementations of Lisp, APL, Scheme, SASL, CLU, Smalltalk, and Prolog, Addison-Wesley, 1990, ISBN 0–201–06824–9. - Bernard LEGRAND, „Les APL Etendus,“
Masson, Paris, 1994. An introduction to modern APL (French). - Jon McGrew, „An Introduction to APL2,“
IBM (SH20–9229). - James A. Mason, „Learning APL: An Array Processing Language,“
Harper & Row Publishers Inc., New York, 1986, ISBN 0–06–044243–3 260 pp. - Peelle, „APL an Introduction“,
Holt, Rinehart & Winston, ISBN 0–03–004953–9. - Reiter & Jones, „APL with a Mathematical Accent“,
Brooks/Cole ISBN 0–534–12864–5, (now being distributed by Chapman & Hall). - C. Reiter, „Fractuals Visualization and J“,
Iverson Software, Inc, 1995 ISBN 1–895721–11–3. - Adrian Smith, „APL, A Design Handbook for Commercial Systems,“
Wiley series in information processing, Wiley & Sons, 1982, ISBN 0–471–10092–7. - D. Stiers, M.J. Goovaerts, J. De Kerf, „APL – The Language and its Actuarial Applications“
- Norman D. Thomson, Raymond P. Polivka, „APL2 in Depth,“
Springer-Verlag, 1995, ISBN 0–387–94213–0. - Jerry R. Turner, „APL IS EASY!,“
Manugistics, 1993. - „SHARP APL Reference Manual,“
2nd ed., Soliton Associates Limited PC Version: Iverson Software, 1993, ISBN 1–895721–07–5. - „A Source Book in APL,“
APL Press, 1981, ISBN 0–917326–10–5. - „J Phrases,“
Iverson Software, 1996, ISBN 1–895721–12–1 - „Exploring Math“, Iverson Software, 1996, ISBN 1–895721–13-X
- „J Primer,“
Iverson Software, 1996, ISBN 1–895721–14–8 - Linda Alvord and Norman Thomson, „Easy-J: An Introduction to the World's most Remarkable Programming Language“
October 2002
9. Odkazy na Internetu
- Vector (obsahuje odkazy na články, knihy a blogy o programovacích jazycích APL, J a K)
http://www.vector.org.uk/ - APL Interpreters
http://www.vector.org.uk/?… - APL_(programming_language
http://en.wikipedia.org/wiki/APL_(programming_language - APL FAQ
http://www.faqs.org/faqs/apl-faq/ - APL FAQ (nejnovější verze)
http://home.earthlink.net/…apl.faq.html - A+
http://www.aplusdev.org/ - APLX
http://www.microapl.co.uk/ - FreeAPL
http://www.pyr.fi/apl/index.htm - J: a modern, high-level, general-purpose, high-performance programming language
http://www.jsoftware.com/ - K, Kdb: an APL derivative for Solaris, Linux, Windows
http://www.kx.com - openAPL (GPL)
http://sourceforge.net/…ects/openapl - Parrot APL (GPL)
http://www.parrotcode.org/ - Learning J (Roger Stokes)
http://www.jsoftware.com/…contents.htm - Rosetta Code
http://rosettacode.org/wiki/Main_Page - Why APL
http://www.acm.org/…l/whyapl.htm