Využití POV-Raye pro vizualizaci

3. 3. 2009

Doba čtení: 13 minut

Líbí se vám článek?
Podpořte redakci

V poslední části seriálu o POV-Rayi si ukážeme, jak lze tento raytracer využít jak při vykreslování implicitních funkcí, tak i pro zobrazení objemových dat či výsledků různých simulací, například částicových systémů. Na závěr bude uvedena literatura, články na Internetu, stránky modelovacích programů aj.

Obsah

1. Využití POV-Raye pro vizualizaci
2. Zobrazení ploch zapsaných implicitní funkcí
3. Vizualizace obecných implicitních funkcí a objemových dat
4. POV-Ray jako back-end simulačních programů
5. Literatura
6. Články dostupné na Internetu
7. Modelovací programy a specializované 3D editory
8. Konverzní programy a utility pro POV-Ray
9. Další zajímavé odkazy na Internetu

1. Využití POV-Raye pro vizualizaci

V předchozích dílech tohoto seriálu jsme se zaměřili především na popis využití POV-Raye při vykreslování trojrozměrných scén, které byly buď vymodelovány v některém z modelovacích programů určených přímo pro POV-Ray (Moray, KPovModeler), importovány z jiného modelovacího programu (Blender, 3D Studio) či CAD/CAM (Rhinoceros, SurfCAM), popř. ručně zapsány přímo ve formě zdrojového kódu určeného pro POV-Ray. Dnes si řekneme, jakým způsobem lze POV-Ray použít pro vizualizaci dat získaných z různých simulačních programů (může se jednat i o objemová data) i různými způsoby zobrazení funkcí zapsaných v implicitní formě. Jedná se o jedno z poměrně častých použití tohoto raytraceru, především v akademické sféře – viz první obrázek, na kterém je zobrazen výsledek práce programu, který simulovat turbulentní proudění vzduchu. Ze simulačního programu byla data získána ve formě souboru typu VRML (Virtual Reality Modelling Language), který byl zkonvertován do formátu POV-Raye pomocí utility vrml2pov a následně v tomto raytraceru vykreslen.

Obrázek 1: Výsledek práce programu, který simuloval turbulentní proudění vzduchu. Vypočtená data byla převedeno do formátu POV-Raye a následně vykreslena.

2. Zobrazení ploch zapsaných implicitní funkcí

Moderní raytracery (POV-Ray samozřejmě nevyjímaje) se velmi často používají pro vizualizaci v těch případech, kdy je vypočtený či modelovaný objekt popsán implicitní funkcí, tj. funkcí nabývající tvaru f(x,y,z)=0. V případě, že je použitá implicitní funkce výpočetně složitá, například obsahuje goniometrické či logaritmické funkce atd., používají se pro vyobrazení (tj. výpočet průsečíků paprsků s plochou popsanou implicitní funkcí) numerické metody řešení, ovšem pro polynomy nižších stupňů lze použít řešení analytické, které je rychlejší a především přesnější. V páté části tohoto seriálu jsme si popsali základy modelování takzvaných kvadrik pomocí POV-Rayovského objektu nazvaného quadric. Jedná se o objekt definovaný pomocí deseti reálných čísel zapsaných ve formě tří třísložkových vektorů a jedné skalární hodnoty. Ve své podstatě se jedná o specifikaci parametrů implicitní funkce (polynomu), která je vykreslována tím způsobem, že jsou analyticky vypočteny všechny průsečíky paprsků s plochou tvořenou všemi body, které splňují rovnici:

A x² + B y² + C z² + D xy + E xz + F yz + G x + H y + I z + J = 0

(koeficienty A až J jsou specifikovány pomocí výše zmíněně trojice vektorů a jedné skalární hodnoty):

Obrázek 2: Sada kvadrik zapsaných implicitní rovnicí – válce, kužely, paraboloidy, hyperboloidy a elipsoid.

V POV-Rayi je však možné vytvářet i další objekty, jejichž plocha je specifikovaná implicitní funkcí definovanou pomocí polynomů vyšších řádů. Jedná se především o kubiky, kvartiky (pozor, neplést s kvadrikami, které jsou definovány polynomem nižšího stupně) a obecné polynomiální plochy. Nejprve si připomeňme práci s kubikami (demonstrační příklady byly uvedeny v desáté části seriálu), které byly do POV-Raye implementovány Alexandrem Enzmannem, jenž je mimochodem i autorem dnes již poněkud neprávem pozapomenutého raytraceru Polyray. Zatímco kvadriky byly zadány pomocí polynomu, ve kterém se vyskytovaly maximálně druhé mocniny souřadnic x, y, z a všechny kombinace prvních mocnin, jsou u kubik použity i třetí mocniny. To má samozřejmě za následek větší množství parametrů, které uživatel musí specifikovat, ale především je možné modelovat mnohem větší množství tvarů, než to bylo možné pomocí kvadrik. Parametrů (přesněji řečeno koeficientů polynomu) není v tomto případě pouze deset, ale hned dvacet (v rovnici uvedené níže jsou tyto koeficienty označeny symboly A₁ až A₂₀):

A₁x³ + A₂x²y + A₃x²z + A₄x² + A₅xy² + A₆xyz + A₇xy + A₈xz² + A₉xz + A₁₀x + A₁₁y³ + A₁₂y²z + A₁₃y² + A₁₄yz² + A₁₅yz + A₁₆y + A₁₇z³ + A₁₈z² + A₁₉z + A₂₀=0

Obrázek 3: Sada kubik zapsaných implicitní rovnicí. Každá kubika je specifikována pomocí dvaceti koeficientů dosazených do implicitní rovnice.

Zobecněním objektů typu quadric, cubic a quartic vznikl objekt nazvaný jednoduše poly (od slova polynom), který do POV-Raye implementoval opět výše zmíněný Alexander Enzmann. Jedná se o implicitní plochu definovanou polynomem n-tého stupně, přičemž stupeň polynomu může ležet v rozsahu 2 až 15. S vyšším stupněm polynomu samozřejmě roste i počet jeho členů, tj. i koeficientů, které se musí specifikovat. Například pro šestý stupeň se jedná o 84 koeficientů, jelikož polynom má v tomto případě tři nezávislé proměnné x, y a z. Objekt typu poly je sice možné použít i pro vytvoření kvadrik či kubik, ovšem rychlost výpočtu bude pomalejší než v případě, že se použijí specializované objekty quadric a cubic (podobně je možné například kouli či válec popsat obecnou kvadrikou, ale rychlejší i syntakticky přehlednější bude použití objektů sphere či cylinder). Syntaxe zápisu objektu poly je velmi jednoduchá:

poly {
        stupeň <A1, A2, A3,... Am>
    }

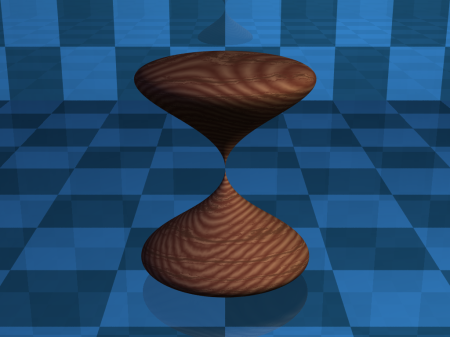
Obrázek 4: Implicitní plocha zapsaná obecným polynomem pátého stupně.

Obrázek 5: Implicitní plocha zapsaná obecným polynomem šestého stupně.

3. Vizualizace obecných implicitních funkcí a objemových dat

Poměrně často se v praxi můžeme setkat s potřebou vykreslení obecných implicitních funkcí. V POV-Rayi lze tyto funkce vykreslit hned několika různými způsoby. V případě, že nám postačuje zvýraznění pouze jedné či několika izoploch, tj. ploch, které spojují všechny body, pro které platí F(x,y,z)=c, kde c je vhodně zvolená konstanta (prahová hodnota), je možné použít objekt typu isosurface, pro který se kromě vlastní implicitní funkce specifikuje i její prahová hodnota, obalové těleso i některé další parametry, které POV-Rayi pomáhají při numerickém výpočtu průsečíku paprsku s izoplochou. Na šestém obrázku je vyobrazena izoplocha poměrně složité implicitní funkce, jejíž tvar je: y-cos(sqrt(xx + zz)3pi)0.1+sin(12atan2(x, z))sin(8atan2(y, sqrt(xx + zz)))*0.1. Vidíme, že POV-Ray může při zobrazování implicitních funkcí mnohdy nahradit i takové „těžkotonážní“ programy, jakými jsou například Maple či Mathematica (do vytvořeného 3D modelu lze samozřejmě přidat i souřadné osy, ořezové plochy, barevné zvýraznění minim a maxim pomocí procedurálních textur atd.). Na šestém obrázku je objekt popsaný následovně:

isosurface
{
    function
    {
        y-cos(sqrt(x*x + z*z)*3*pi)*0.1  // 2D funkce "vlny"
        +sin(12*atan2(x, z))*sin(radians(clock*360)+8*atan2(y, sqrt(x*x + z*z)))*0.1
    }
    threshold 0.0                        // hranice
    accuracy 1e-8                        // přesnost výpočtu
    max_gradient 10                      // maximální gradient
    contained_by
    {                                    // hraniční těleso
        box
        {
            -2.2, 2.2
        }
    }
    texture
    {                                    // textura povrchu implicitní plochy
        Solid
    }
    scale 1.7                            // lineární transformace aplikované na plochu
}

Obrázek 6: Objekt typu isosurface vykreslený POV-Rayem

Ovšem použití izoploch nepředstavuje jedinou možnost, jak lze implicitní funkce v POV-Rayi zobrazit. Ve třicáté části tohoto seriálu jsme si mj. řekli, že v POV-Rayi lze vnitřní část uzavřených těles vyplnit částicemi (particles) s proměnlivou hustotou a různými optickými vlastnostmi. Částice mohou absorbovat (pohlcovat) světelné záření, mohou ho naopak emitovat (vyzařovat, výsledkem je světélkující hmota) nebo – což je výpočetně nejsložitější případ – dokonce mohou rozptylovat procházející světlo. Hustotu těchto částic v prostoru je možné popsat i matematickou funkcí. Právě s využitím tohoto výpočetního aparátu lze zobrazit i implicitní funkce a to zcela odlišným způsobem, než v případě využití izoploch. Výsledek tohoto způsobu zobrazení implicitní funkce, jejíž vzorec byl uveden v předchozím odstavci, je ukázán na sedmém a osmém obrázku. U obou obrázků je použita stejná implicitní funkce, liší se pouze pozice kamery (pozorovatele) v prostoru – jednou se na funkci díváme z osy y, podruhé z osy z:

box
{
    -3,3                                 // hranice kvádru
    pigment
    {
        color rgbf <1,1,1,1>
    }
    interior                             // vlastnosti vnitřku kvádru
    {
        media
        {
            emission 0.55
            intervals 2                  // parametry pro algoritmus Monte Carlo
            samples 5
            method 3
            density
            {                            // změna hustoty částic
                function                 // na základě funkce
                {
                    y-cos(sqrt(x*x + z*z)*3*pi)*0.1  // 2D funkce "vlny"
                    +sin(12*atan2(x, z))*sin(radians(clock*360)+8*atan2(y, sqrt(x*x + z*z)))*0.1
                }
                color_map                // barvová mapa
                {
                    [0.0 color rgb <0, 0, 0>]
                    [0.5 color rgb <1, 0, 0>]
                    [1.0 color rgb <1, 1, 0>]
                }
            }
        }
    }
    hollow                               // Duležité! kvádr musí být "prázdný"
}

Obrázek 7: Implicitní funkce použitá pro nastavení hustoty části hmoty, která emituje světlo.

Obrázek 8: Odlišný pohled na kvádr vyplněný hmotou emitující světlo.

To však ještě není vše – zcela stejnou funkci je možné použít i jako základ pro procedurální texturu. Namapováním této prostorové textury na plochu dojde k výběru pouze jedné roviny z původně kontinuálního prostoru, přičemž rovina řezu může být libovolná. Tato technika byla použita pro získání devátého a desátého obrázku. Následuje výpis fragmentu kódu, ve kterém vidíme, jakým způsobem lze použít uživatelsky definovanou funkci pro vytvoření prostorové procedurální textury:

box
{
    <-3,-1,-3>, <3,0,3>
    pigment
    {
        function
        {
            y-cos(sqrt(x*x + z*z)*3*pi)*0.1  // 2D funkce "vlny"
            +sin(12*atan2(x, z))*sin(radians(clock*360)+8*atan2(y, sqrt(x*x + z*z)))*0.1

        }
        color_map                // barvová mapa
        {
            [0.0 color rgb <0, 0, 0>]
            [0.5 color rgb <1, 0, 0>]
            [1.0 color rgb <1, 1, 0>]
        }
    }
}

Obrázek 9: Řez prostorové textury (definované vlastní funkcí) rovinou y=-3.

Obrázek 10: Řez prostorové textury (definované vlastní funkcí) rovinou y=-2.

Raytracer POV-Ray dokáže ve vykreslovaných scénách použít i objekty reprezentované objemovými elementy (voxely), které tvoří pravidelnou rastrovou mřížku. Každý voxel je přitom zapsaný osmibitovou, šestnáctibitovou či dokonce třicetidvoubitovou hodnotou, kterou je možné považovat za „hustotu“ hmoty v daném objemu prostoru (ovšem tuto hodnotu voxelu lze mapovat i na barvu pomocí nám již známých barvových map). Tímto – z hlediska klasických modelovacích programů – poněkud nekonvenčním způsobem, kterým disponuje relativně malé množství aplikací, je možné v jedné scéně zkombinovat různé typy prostorových dat. Objemová data se v praxi začínají objevovat stále častěji, především z toho důvodu, že roste počet zařízení, která tato data produkují (počítačová tomografie, magnetická rezonance) a současně rostou i kapacity operačních pamětí a rychlosti mikroprocesorů, takže se tato data již dají poměrně snadno zpracovávat. Na následujících obrázcích jsou ukázky objemových dat vykreslených POV-Rayem.

Obrázek 11: CT mozku, vizualizováno POV-Rayem.

Obrázek 12: Výsledek simulace proudění po vizualizaci výsledných objemových dat.

Obrázek 13: Vesmír v makroskopickém měřítku.

Obrázek 14: Výsledek jednoduché simulace tepelného proudění.

Obrázek 15: Uměle vytvořená prostorová data.

4. POV-Ray jako back-end simulačních programů

Vzhledem k tomu, že zdrojový kód scény určené pro POV-Ray je možné poměrně jednoduše generovat v jiných aplikacích, používá se tento raytracer velmi často jako vizualizační back-end různých simulačních programů. Idea spolupráce POV-Raye a simulačního programu je v tom nejjednodušším případě založena na průběžném exportu dat ze simulačního programu do formátu, jaký dokáže POV-Ray zpracovat. Jednotlivé takto získané soubory jsou následně vyrendrovány a převedeny do animace. Tímto způsobem bylo získáno i následujících osm animací. Jedná se o výsledek práce jednoduchého programu, který dokáže simulovat změnu tvaru a polohy systému tvořeného hmotnými kuličkami spojenými elastickými vazbami (tyto systémy se nazývají mass and springs). Tento program v každém kroku simulace vytvořil jeden soubor pojmenovaný xxxx.inc, kde xxxx je číslo snímku. V souboru byly uloženy souřadnice jednotlivých kuliček i válců, které představují elastickou vazbu. Všechny další informace důležité pro POV-Ray (souřadnice kamery, pozice světelných zdrojů, deklarace textur atd.) byly uloženy v souboru simulation.pov, do kterého se vygenerované soubory vložily pomocí malého triku:

#include concat(str(frame_number, -4, 0), ".inc")

Vykreslení všech snímků je velmi jednoduché – postačí použít volbu -kffx, kde za x se dosadí celkový počet snímků. Interní proměnná frame_number je totiž korektně automaticky nastavena na číslo právě renderovaného snímku v animaci.

animace 1
animace 2
animace 3
animace 4
animace 5 (pozor, klouže to)
animace 6 (nestabilita)
animace 7 (pád ze schodů 1)
animace 8 (pád ze schodů 2)

Pro ilustraci si ještě ukažme čtyři snímky získané z jedné simulace.

5. Literatura

Barr, A.H.: Superquadrics and Angle Preserving Transformations,
IEEE Computer Graphics and Applications, January 1981
Bourke Paul: Quadrics,
July 1996
Bourke Paul: Superellipse and Superellipsoid,
January 1990
Faux, I.D. a Pratt, M.J.: Computational Geometry for Design and Manufacture,
Ellis Horwood Ltd., Wiley & Sons, 1979
Foley J., Dam van A., Feiner S., Hughes J.: Computer Graphics – Principles and Practice (Second Edition)
Addison-Wesley, Reading, Massachusetts, 1990, ISBN 0–201–12110–7
Hill, F. S. jr.: Computer Graphics using OpenGL,
Prentice Hall, 2001
Prusinkiewicz Przemyslaw and Hanan James: Lindenmayer Systems, Fractals, and Plants,
Springer-Verlag, New York, 1989.
Prusinkiewicz Przemyslaw and Lindenmayer Aristid: The Algorithmic Beauty of Plants,
Springer-Verlag, NY, 1990. ISBN 0–387–97297–8
http://algorithmicbotany.org/papers/abop/abop.lowquality.pdf
Wallace A.: Differential Topology,
Benjamin/Cummings Co., Reading, Massachussetts, USA, 1968
Weber J., Penn J.: Creation and Rendering of Realistic Trees,
Proceedings of SIGGRAPH '95, volume 22(4), ACM SIGGRAPH, New York, 1995
Žára J., Beneš B., Felkel P.: Moderní počítačová grafika
Computer Press, Praha, 1998, ISBN 80–7226–049–9
Žára J., Limpouch A., Beneš B., Werner T.: Počítačová grafika – principy a algoritmy
Grada, Praha, 1992, ISBN 80–85623–00–5