Obsah
1. Podmíněný příkaz typu ifelse a jeho varianty
2. Křivka Helge von Kocha
3. Sněhová vločka Helge von Kocha
4. Sierpinského trojúhelník
5. Odlišná forma Sierpinského trojúhelníku
6. Pythagorův strom
7. Obsah následující části tohoto seriálu
1. Podmíněný příkaz typu ifelse a jeho varianty
V předchozí části tohoto seriálu jsme si popsali a na demonstračních příkladech předvedli podmíněný příkaz typu if. Pomocí tohoto příkazu je možné zapisovat programy, ve kterých se na základě nějaké logické podmínky buď provede nebo naopak neprovede nějaká větev programu, která je v Logu zapsána jako seznam příkazů. V některých programech je však zapotřebí provést (opět na základě logického výrazu) výběr mezi dvěma větvemi, přičemž je vždy provedena pouze jedna větev (nikdy obě současně). I takovéto rozvětvení programu je sice možné zapsat pomocí dvojice příkazů if (druhý příkaz if používá negovaný logický výraz), v praxi je však běžnější využít jazykovou konstrukci typu if-else. Touto konstrukcí, která se někdy označuje jako úplný příkaz if, disponují prakticky všechny vyšší programovací jazyky, samozřejmě včetně Loga.
Příkaz typu ifelse se v mnohém podobá příkazu typu if, ovšem s tím rozdílem, že místo jednoho seznamu příkazů jsou uvedeny dva seznamy. Obsah prvního seznamu příkazů je spuštěn (resp. je interpretován) v případě, že je logický výraz vyhodnocen jako „pravda“ (true), ovšem pokud je výraz vyhodnocen jako „nepravda“ (false), je naopak spuštěn druhý seznam příkazů. Některé interpretery Loga požadují, aby konec prvního seznamu a začátek druhého seznamu byly umístěny na stejném programovém řádku, což také budeme ve všech dále uváděných demonstračních příkladech dodržovat (poznamenejme, že příkaz else, který v Logu také existuje, se používá v jiném kontextu a není ho možné kombinovat s příkazem if). Zápis celé programové konstrukce s podmíněným příkazem ifelse by měl vypadat následovně:
ifelse logický_výraz [
seznam příkazů větve "true"
][
seznam příkazů větve "false
]
2. Křivka Helge von Kocha
Rekurze se spolu s želví grafikou často používá pro vykreslování jednoduchých fraktálů. Bližší informace o fraktálech jsou uvedeny v seriálu Fraktály v počítačové grafice, který taktéž vycházel na Rootu, proto si zde nebudeme uvádět ani teorii fraktálů, ani způsoby jejich vykreslování v jiných programovacích jazycích. Ukážeme si však využití Loga, rekurze a želví grafiky při práci s fraktály známými pod souhrnným názvem L-systémy.
Jedním z nejznámějších fraktálních útvarů, který je možné velmi jednoduše pomocí Loga a jeho želvy vykreslit, je takzvaná křivka Helge von Kocha a sněhová vločka Helge von Kocha. Popišme si nejdříve křivku Helge von Kocha, sněhová vločka vzniká pouhou změnou počátečních podmínek. Vytváření křivky Helge von Kocha spočívá v provedení následujících kroků (nejedná se o popis programu, ale geometrické konstrukce této křivky):
- Nejprve se zkonstruuje vodorovná úsečka o zadané délce.
- Ve druhém kroku se tato úsečka rozdělí na (stejně dlouhé) třetiny. Prostřední třetina se vyjme a na jejím místě se sestrojí dvě ramena rovnoramenného trojúhelníku. Vznikne tedy obrazec, který se skládá z lomené úsečky (polyčáry), jejíž délka je rovna 4/3 délky původní úsečky, tj. celková délka takto zkonstruované křivky se o třetinu prodlouží.
- Na vzniklý obrazec se opakovaně aplikuje pravidlo uvedené v předchozím bodě, tj. každá úsečka je rozdělena na třetiny, prostřední třetina se vyjme a nahradí se dvojicí ramen rovnoramenného trojúhelníka.




Při implementaci programové procedury, která má pomocí želví grafiky vykreslit Kochovu křivku, se sice budeme řídit výše uvedenými pravidly pro geometrickou konstrukci křivky, vlastní implementace však bude dosti odlišná, protože odebírání částí úseček a náhrada odebraných částí úsečkami novými nejsou operace, které by bylo možné jednoduše provádět.
Zvolíme mnohem elegantnější řešení založené na rekurzi. Základem vznikající procedury bude vykreslení tvaru podobného první iteraci Kochovy křivky, tj. čtyř úseček, z nichž dvě krajní úsečky jsou vodorovné a prostřední úsečky tvoří dvojici ramen rovnostranného trojúhelníku (viz obrázek číslo 1). Tento tvar je možné vykreslit například následující sekvencí příkazů, ve kterých parametr :strana představuje celkovou délku původní (nerozdělené) úsečky:
forward :strana/3
right 60
forward :strana/3
left 120
forward :strana/3
right 60
forward :strana/3 Každá další iterace křivky Helge von Kocha spočívá v nahrazení všech úseček vzniklých v předchozí iteraci čtyřmi novými úsečkami s třetinovou délkou. Tato úvaha nás povede k vytvoření rekurzivně volané procedury nazvané kochova_krivka, která bude volat sebe samu pro každou vykreslovanou (a v dalších iteracích dělenou) úsečku.
To znamená, že se v předchozím fragmentu kódu nahradí příkaz forward rekurzivním voláním procedury kochova_krivka. Rekurzivní volání této procedury se zastaví ve chvíli, kdy je úsečka rozdělena na část kratší než zadaný limit. V tomto případě je úsečka přímo vykreslena a nedochází k jejímu dalšímu dělení. Test na délku úsečky je jednoduchý, protože se jedná o parametr předávaný proceduře. Pro zachování obecnosti pro různá rozlišení výsledných obrazců bude předáván ještě jeden parametr – délkový limit úsečky. Zdrojový kód procedury kochova_krivka má následující tvar:
to kochova_krivka :strana :limit
ifelse :strana>:limit [
kochova_krivka :strana/3 :limit
left 60
kochova_krivka :strana/3 :limit
right 120
kochova_krivka :strana/3 :limit
left 60
kochova_krivka :strana/3 :limit
][
forward :strana
]
end 
Výše uvedenou proceduru by bylo možné upravit tak, aby se Kochova křivka vykreslovala pro zadaný počet iterací a ne až do chvíle, kdy je překročen limit délky úsečky. Úprava je velmi jednoduchá – místo parametru limit se bude předávat číslo iterace, které bude postupně klesat k nule. Pokud dosáhne této hodnoty, rekurzivní dělení úsečky se ukončí a úsečka je vykreslena, stejně jako v předchozí proceduře. Celkový počet iterací zadá uživatel při volání procedury kochova_krivka2 jako druhý parametr (prvním je horizontální rozměr obrazce):
to kochova_krivka2 :strana :iterace
ifelse :iterace>0 [
kochova_krivka2 :strana/3 :iterace-1
left 60
kochova_krivka2 :strana/3 :iterace-1
right 120
kochova_krivka2 :strana/3 :iterace-1
left 60
kochova_krivka2 :strana/3 :iterace-1
][
forward :strana
]
end 
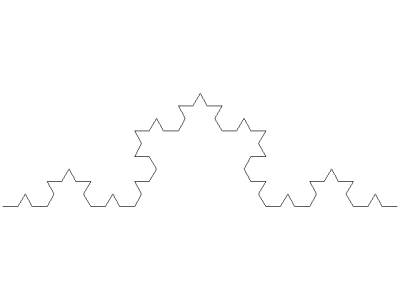
Seznam příkazů použitých při vykreslení sedmého obrázku:
; nastavení velikosti kreslicí plochy v Turtle Tracks
(draw 300 300)
; otočení želvy a posun k hornímu okraji kreslicí plochy
right 180
back 300
; smazání kreslicí plochy a skrytí želvy
clean
ht
; pět na sebe navazujících křivek
kochova_krivka2 100 0
kochova_krivka2 100 1
kochova_krivka2 100 2
kochova_krivka2 100 3
kochova_krivka2 100 4
3. Sněhová vločka Helge von Kocha
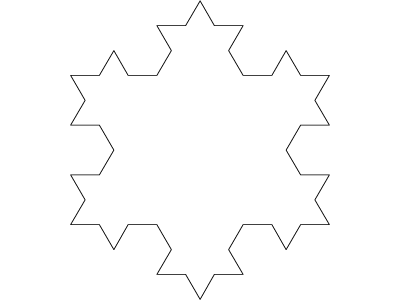
Sněhová vločka Helge von Kocha vzniká nepatrnou úpravou počáteční podmínky při generování křivky téhož matematika. Místo jedné úsečky, která se rekurzivně dělí na třetiny, se v případě sněhové vločky začíná s rovnostranným trojúhelníkem, u nějž se v každé iteraci dělí všechny tři strany stejným způsobem. Již po první iteraci je patrný základní tvar vločky, který se v dalších iteracích postupně zjemňuje a zpřesňuje. To je ostatně patrné i z následující pětice ukázkových obrázků:




Implementace konstrukce sněhové vločky Helge von Kocha v Logu je taktéž velmi jednoduchá, protože můžeme použít již naprogramovanou proceduru kochova_krivka či kochova_krivka2. Postačí vytvořit novou proceduru, která třikrát za sebou zavolá proceduru pro vykreslení Kochovy křivky, ovšem pokaždé se želva otočí doprava o 120°, aby vytvořila základní trojúhelník, na kterém je sněhová vločka postavena. Procedura pro vykreslení sněhové vločky může mít například tento tvar:
to kochova_vlocka :strana :iterace
repeat 3 [
kochova_krivka2 :strana :iterace
right 120
]
end A celý program pro vykreslení sněhové vločky Helge von Kocha v interpreteru Loga Turtle Tracks vypadá následovně:
to kochova_krivka2 :strana :iterace
ifelse :iterace>0 [
kochova_krivka2 :strana/3 :iterace-1
left 60
kochova_krivka2 :strana/3 :iterace-1
right 120
kochova_krivka2 :strana/3 :iterace-1
left 60
kochova_krivka2 :strana/3 :iterace-1
][
forward :strana
]
end
to kochova_vlocka :strana :iterace
repeat 3 [
kochova_krivka2 :strana :iterace
right 120
]
end
; nastavení velikosti kreslicí plochy v Turtle Tracks
(draw 300 300)
; skrytí želvy
ht
; vykreslení pěti iterací sněhové vločky Helge von Kocha
kochova_vlocka 100 5 
4. Sierpinského trojúhelník
Také Sierpinského trojúhelník patří mezi jeden z nejčastěji zobrazovaných fraktálních útvarů. Možností jeho počítačem řízené konstrukce existuje celá řada, od využití systémů iterovaných funkcí (Iterated Function Systems – IFS) přes speciálně navržené dynamické systémy vytvářené v komplexní rovině až po L-systémy. Vykreslení Sierpinského trojúhelníku v Logu taktéž vede na tvorbu rekurzivně volané procedury. Samotný Sierpinského trojúhelník je totiž definován jako rekurzivní dělení trojúhelníku na menší trojúhelníkové části, vždy s výjimkou prostřední čtvrtiny, která se dále nedělí. První čtyři iterace tohoto objektu jsou vyobrazeny na patnáctém obrázku:
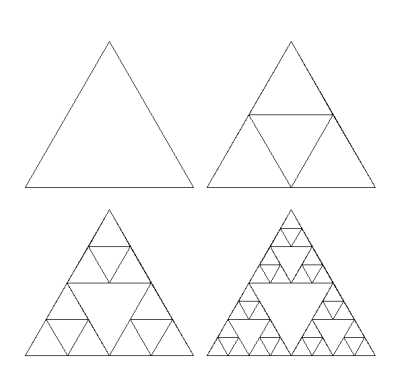
Z předchozího obrázku je patrné, jakým způsobem vykreslování probíhá. V každé iteraci se rekurzivně volá procedura pro vykreslení trojúhelníka, tento trojúhelník má však poloviční délku strany a je jinak natočený (to však není, vzhledem k jeho symetrii, patrné). Celé rekurzivní volání je možné zapsat do třikrát opakované programové smyčky, ve které želva postupně zavolá proceduru pro vytvoření „podtrojúhelníku“, vykreslí všechny tři strany a vrátí se do stejného bodu, v jakém vykreslování začala.
V případě, že je překročen zadaný počet iterací, vykreslí se pouze trojúhelník s určenou délkou strany. Pro jeho vykreslování je vytvořena pomocná procedura nazvaná trojuhelnik. Program, který posloužil pro vytvoření patnáctého obrázku, vypadá následovně:
to trojuhelnik :strana
repeat 3 [
forward :strana
left 120
]
end
to sierpinski :strana :iterace
ifelse :iterace>0 [
repeat 3 [
sierpinski :strana/2 :iterace-1
forward :strana
left 120
]
][
trojuhelnik :strana
]
end
; nastavení velikosti kreslicí plochy v Turtle Tracks
(draw 300 300)
; smazání grafické plochy, skrytí želvy a natočení do vodorovné polohy
cs
ht
right 90
; přesun želvy na zadanou absolutní pozici (bez kreslení) a následná tvorba Sierpinského trojúhelníku
pu
setpos [-260 0]
pd
sierpinski 250 0
; přesun želvy na zadanou absolutní pozici (bez kreslení) a následná tvorba Sierpinského trojúhelníku
pu
setpos [10 0]
pd
sierpinski 250 1
; přesun želvy na zadanou absolutní pozici (bez kreslení) a následná tvorba Sierpinského trojúhelníku
pu
setpos [-260 -250]
pd
sierpinski 250 2
; přesun želvy na zadanou absolutní pozici (bez kreslení) a následná tvorba Sierpinského trojúhelníku
pu
setpos [10 -250]
pd
sierpinski 250 3
5. Odlišná forma Sierpinského trojúhelníku
Existuje i odlišná forma Sierpinského trojúhelníku, která je tvořena jedinou lomenou čarou (polyčarou), přičemž úhel napojení sousedních úseček je roven 120° a délka všech úseček tvořících lomenou čaru je shodná. Způsobů vykreslení této formy existuje více, my si ukážeme způsob založený na nepřímé rekurzi, tj. na algoritmu, ve kterém nějaká procedura A volá proceduru B, ve které se rekurzivně volá opět procedura A (ve skutečnosti je v daném algoritmu přítomna i rekurze přímá, tj. procedura A volá jak sama sebe, tak i proceduru B).
Vytvořené procedury mají pro jednoduchost názvy x a y (tyto názvy jsou odvozeny z názvů nonterminálních symbolů v přepisovací gramatice L-systému, to však již zabíháme do podrobností) a výsledný tvar programu pro vykreslení lomené čáry ve tvaru Sierpinského trojúhelníka pro daný počet iterací a délku úseček vypadá takto:
to x :a :iter
if :iter>0 [
y :a :iter-1
forward :a
left 60
x :a :iter-1
forward :a
left 60
y :a :iter-1
]
end
to y :a :iter
if :iter>0 [
x :a :iter-1
forward :a
right 60
y :a :iter-1
forward :a
right 60
x :a :iter-1
]
end
(draw 300 300)
y 10 5
forward 10 
6. Pythagorův strom
Dalším zajímavým útvarem, který je možné vytvořit pomocí rekurzivně volané procedury, je takzvaný Pythagorův strom (tento termín jsem objevil ve starším vydání časopisu Elektronika, v angličtině pro něj existují i různá pojmenování, například Pythagoras tree nebo Pythagorean tree). Základem Pythagorova stromu je známý domeček kreslený jedním tahem. Pokud považujeme šířku domku a výšku jeho stěn za základní délku, pak mají úhlopříčné tahy délku rovnou odmocnině dvou (sqrt 2) a délka stran střechy je naopak rovná převrácené hodnotě odmocnině dvou (1/sqrt 2).
V proceduře nazvané domek se šířka domku a jeho výška předává v parametru strana. O výpočet druhé odmocniny se stará matematická funkce sqrt s parametrem 2 (i funkce je v Logu zapisována stejně jako procedura, tj. její parametry nemusí být uzavřeny do závorek ani nemusí být odděleny čárkami či jinými oddělovači kromě mezery).
V případě, že se vykreslení každé strany střechy nahradí rekurzivně volanou procedurou pro kreslení celého domečku, získáme charakteristický tvar vzdáleně podobný stromu či keři. Zajímavé je také sledování postupného vykreslování Pythagorova stromu, zejména na pomalejším počítači (Turtle Tracks je sám o sobě dostatečně pomalý interpreter, takže vykreslování pozdrží i na výkonném stroji :-)
Samozřejmě je nutné opět zavést podmínku pro ukončení rekurze, jinak by program skončil běhovou chybou (překročení volné kapacity paměti). Pokud je délka strany pro vykreslení domku menší než deset kroků želvy, je místo domku vykreslena pouze úsečka o této délce, čímž je zajištěno vykreslení střech domků ležících na konci „stromu“. Pokud však délka strany přesahuje tuto hodnotu (deset kroků želvy), je jedním tahem vykreslen celý domek. Výsledný program pro vykreslení Pythagorova stromu má tvar:
to domek :strana
ifelse :strana>10 [
; základna
forward :strana
; úhlopříčka
left 90+45
forward :strana*sqrt 2
; stěna
left 90+45
forward :strana
; úhlopříčka
left 90+45
forward :strana*sqrt 2
; úsečka pod střechou
left 90+45
forward :strana
; první část střechy
right 90+45
domek :strana/sqrt 2
; druhá část střechy
right 90
domek :strana/sqrt 2
; zbývající stěna
right 45
forward :strana
left 90
][
forward :strana
]
end
draw
clean
right 90
domek 70 

7. Obsah následující části tohoto seriálu
V další části seriálu o programovacím jazyku Logo si vysvětlíme práci s globálními i lokálními proměnnými a ukážeme si jejich použití při psaní složitějších programů.





























