Obsah
1. Pět způsobů provádění komprese obrazových dat dle standardu JPEG v sekvenčním režimu
2. Posloupnost operací při základní ztrátové kompresi pomocí JPEG
3. Transformace barev do barvového prostoru YCbCr
4. Redukce (podvzorkování) barvonosných složek
5. Dopředná diskrétní kosinová transformace
6. Kvantování DCT koeficientů pomocí kvantizačních tabulek
7. Kódování kvantovaných DCT koeficientů (aritmetické a Huffmanovo kódování)
8. Uložení zakódovaných dat do souboru typu JFIF
9. Obsah dalšího pokračování tohoto seriálu
1. Pět způsobů provádění komprese obrazových dat dle standardu JPEG v sekvenčním režimu
V předchozí části tohoto seriálu jsme se seznámili se základními charakteristikami standardu JPEG, pomocí kterého je možné provádět ztrátovou i bezeztrátovou kompresi rastrových obrazových dat, zejména plnobarevných (truecolor) fotografických materiálů, monochromatických rentgenových a ultrazvukových snímků, kopií naskenovaných dokumentů obsahujících obrázky apod. Ve standardu JPEG jsou definovány celkem čtyři režimy činnosti, které může kodér i dekodér podporovat (aplikace konkrétního režimu bývá nazývána kódování). Tyto režimy jsou sepsány a stručně charakterizovány v první tabulce:
| Režim | Ztrátové kódování? | Stručná charakteristika |
|---|---|---|
| sekvenční | ano | nejméně náročné na paměť, nejpoužívanější |
| progresivní | ano | poněkud více náročné na paměť, určeno pro přenos obrázků po síti |
| bezeztrátový | ne | predikční kódování, není příliš známé ani používané/podporované, kompresní poměr 1:2 |
| hierarchický | ano | mnoho rozlišení v jednom snímku, rychlé náhledy, podpora zobrazení, tisku, osvitu |
V dnešní části nás bude zajímat pouze první režim činnosti, při kterém jsou obrazová data zpracovávána sekvenčně, konkrétně po blocích 8×8 a 16×16 pixelů. Sekvenční zpracování přináší některé výhody. Jednoznačně přínosný je fakt, že se při kódování i dekódování využívá pouze minimum operační paměti, která může mít kapacitu v řádech několika desítek kilobytů. Jen díky tomu je možné konstruovat například digitální fotoaparáty vytvářející fotografie složené z několika milionů pixelů, i když kapacita operační paměti na čipech ve fotoaparátu je mnohdy několikanásobně menší (ve skutečnosti jsou ony miliony pixelů uváděných v letáčcích velmi zavádějící).
Také při dekódování obrázku z formátu JPEG do nekomprimovaného rastru je sekvenční režim výhodný – obrázek se například může při přenosu po síti či při načítání z pomalého paměťového média postupně zobrazovat v prohlížeči a i dekodér si vystačí pouze s malým množstvím paměti. Některé tiskárny s menším množstvím paměti také dokážou začít s tiskem obrázku ve formátu JPEG bez nutnosti ho celý načíst (provádí se současně tisk jedné části a dekódování a rasterizace části navazující). Takto sofistikovaných tiskáren však pravděpodobně bude ubývat na úkor win-tiskáren, u kterých se rastrování provádí přímo v počítači a tiskárna obsahuje pouze relativně malý buffer.
V sekvenčním režimu existuje celkem pět způsobů (resp. cest), kterými mohou být data zpracovávána. Způsoby zpracování se od sebe liší především bitovou hloubkou barevných vzorků na vstupu, způsobem výpočtu DCT spolu s kvantizací a konečně kódováním kvantizovaných vzorků. Na vstupu se mohou nacházet osmibitové či dvanáctibitové barvové vzorky (viz třetí kapitolu), výpočet DCT může být prováděn standardním (baseline) či rozšířeným (extended) algoritmem a kódování může být buď aritmetické či Huffmanovo. Všechny způsoby jsou přehledně zobrazeny na následujícím diagramu:
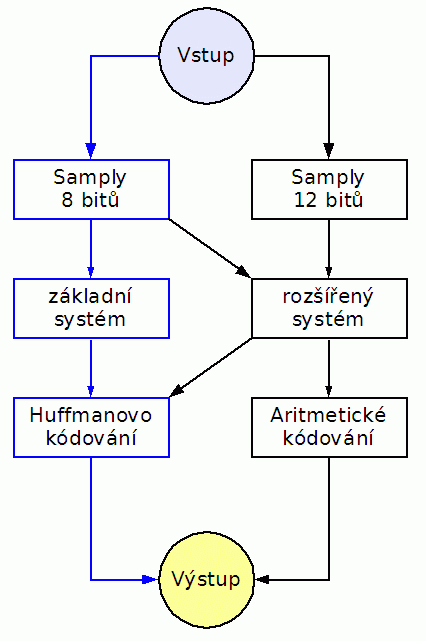
Obrázek 1: Pět způsobů zpracování dat při ztrátové kompresi
V dalším textu se budeme zabývat především nejpoužívanějším způsobem komprese: použitím osmibitových barevných vzorků, výpočet DCT (diskrétní kosinové transformace) a kvantizace se provádí pomocí standardního algoritmu (baseline) a výsledek tohoto zpracování je zakódován Huffmanovým kódem. Norma JPEG předepisuje, že tento způsob zpracování obrazových dat musí podporovat jakýkoli kodér i dekodér, ostatní způsoby jsou pouze volitelné, což také většina aplikací a aplikačních knihoven pro práci s JPEGem dodržuje. Většina obrázků uložených v JFIF/JPEG je vytvořena právě tímto způsobem.
2. Posloupnost operací při základní ztrátové kompresi pomocí JPEG
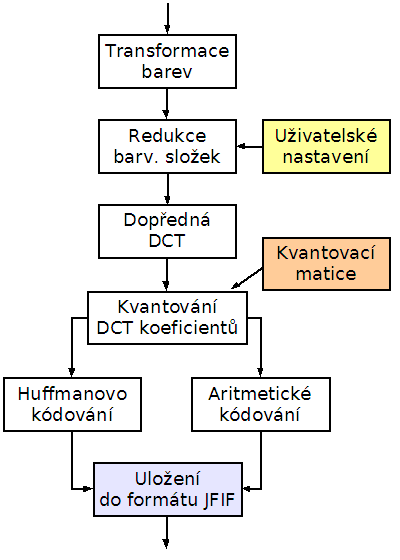
Při ztrátové kompresi obrazových dat pomocí standardu JPEG se vstupní rastrová data podrobují několika za sebou jdoucím operacím, jak je schematicky znázorněno na druhém obrázku:

Obrázek 2: Posloupnost operací při základní ztrátové kompresi pomocí JPEG
- Nejprve je provedena transformace barev z barvových prostorů RGB, CMYK či dalších (například CCD čipy mají vlastní barvový prostor) do barvového prostoru YCbCr. Tato transformace je bezeztrátová, tj. nedochází při ní k žádné ztrátě informací o obrázku.
- Dále může podle konfigurace kodéru docházet k podvzorkování barvonosných složek. V barvovém prostoru YCbCr nese složka Y informaci o světlosti pixelu a složky Cb a Cr informaci o barvě. Právě poslední dvě složky mohou být podvzorkovány, čímž dojde ke snížení objemu dat, ale i k určité (mnohdy zanedbatelné) ztrátě informace.
- Další kroky jsou odděleně prováděny pro složku Y a pro barvonosné složky. Na bloky 8×8 hodnot je aplikována diskrétní kosinová transformace (DCT), která je už z principu bezeztrátová. Výsledkem DCT jsou bloky 8×8 hodnot, tentokrát ležící ve frekvenční rovině.
- Bloky DCT o velikosti 8×8 hodnot jsou kvantovány pomocí vypočtených kvantizačních tabulek. Výsledkem je stav, kdy je mnoho hodnot v tomto bloku nulových, čehož se využívá v následujícím kroku zpracování. Právě při kvantizaci může docházet k největší ztrátě informace a tím i ke kýženému snížení bitové rychlosti (bitrate).
- Kvantované DCT koeficienty jsou následně kódovány pomocí aritmetického či Huffmanova kódování. Aritmetické kódování je sice účinnější o cca 10%, je však mnohem výpočetně i aritmeticky náročnější. Proto se u většiny obrázků používá Huffmanovo kódování, které je sice méně účinné, ale může být prováděno i na málo výkonných čipech (například v mobilních telefonech či fotoaparátech).
- Posledním krokem zpracování je uložení vytvořených dat do souboru typu JFIF/JPEG. V podstatě se jedná o „obalení“ vzniklého datového toku vhodnou hlavičkou, přidání dalších doplňujících informací (včetně populárního EXIF či náhledového obrázku) a zakončení celého souboru patičkou.
3. Transformace barev do barvového prostoru YCbCr
Prvním krokem, který se při komprimaci rastrových obrazových dat pomocí standardu JPEG provádí, je transformace barev ze zdrojového barvového prostoru (kterým může být například RGB, CMYK nebo barvový prostor CCD čipu umístěného v digitálním fotoaparátu) do barvového prostoru nazvaného poněkud záhadně YCbCr. Tento barvový prostor je odvozen z barvového prostoru YUV, který je použit například v některých normách televizního vysílání (konkrétně v normě PAL, zde popisovaný barvový model je použit v podceňované normě SECAM). Složka Y nese informaci o světlosti pixelů, složky Cb a Cr pak rozdílové hodnoty barev pixelů (rozdíl se počítá oproti složce Y).

Obrázek 3: Blok transformace barev do barvového prostoru YCbCr
Jedná se o barvový prostor navržený především pro přenos videosignálu nabízející kompatibilitu s černobílou televizí a plné využití šířky pásma televizního kanálu, proto se s ním NEsetkáme například v grafických editorech – ty jsou zaměřeny především na koncové uživatele, a proto jim nabízí buď intuitivně použitelné barvové prostory (zejména HSV a HLS) nebo barvové prostory odpovídající technologii zobrazení a tisku (RGB, CIE-xy, CMYK).
Pro přepočet barev pixelů z barvového prostoru RGB do barvového prostoru YCbCr je možné použít následující trojici vzorců. Ty se v literatuře většinou zapisují pomocí násobení transformační matice vektorem RGB, tato matematická operace se však v HTML formátu špatně zapisuje, proto jsem zvolil „programový“ zápis. Předpokladem je, že všechny barvové složky (R, G, B, Y, Cb, Cr) jsou uloženy jako celá čísla v rozsahu 0..255, tj. jako byty:
Y = 0,299 R + 0,587 G + 0,114 B Cb = - 0,1687 R - 0,3313 G + 0,5 B + 128 Cr = 0,5 R - 0,4187 G - 0,0813 B + 128
Zpětný přepočet (ten provádí dekodér umístěný například v prohlížečce obrázků) se provede pomocí vzorců:
R = Y + 1.402 (Cr-128) G = Y - 0.34414 (Cb-128) - 0.71414 (Cr-128) B = Y + 1.772 (Cb-128)
Některá literatura uvádí odlišné vzorce, ty ovšem platí pro normu YCbCr (konkrétně CCIR 601), ve které má signál Y rozsah <0, 1> a signály Cb a Cr rozsah ← 0.5, 0,5> (to je ovšem z hlediska zpracování na počítači nevýhodné). V následující části tohoto seriálu si ukážeme jednoduchý demonstrační příklad, který bude provádět přepočet obrázků z barvového prostoru RGB právě do prostoru YCbCr.
4. Redukce (podvzorkování) barvonosných složek
Dalším krokem, který zpracovává rastrová data, je redukce neboli podvzorkování barvonosných složek. Idea podvzorkování je následující: lidské oko obsahuje několik typů senzorů reagujících na dopadající světlo. Některé senzory snímají (a následně přenáší do mozku) informace o světlosti, další senzory jsou citlivé na různé barevné odstíny. Vzhledem k tomu, že senzorů, které snímají informace o světlosti, je více, může lidské oko rozpoznat jas objektů s větší přesností („rozlišením“) než barvu objektů. Právě tento poznatek je využit při podvzorkování barvonosných složek. Zdaleka se nejedná pouze o vlastnost JPEGu, velmi podobně (a někdy i mnohem drastičtěji) se podvzorkování provádí například při kódování digitální televize.

Obrázek 4: Blok redukce (podvzorkování) barvonosných složek
Podvzorkování pracuje následujícím způsobem: složka Y, která nese informaci o světlosti jednotlivých pixelů, není podvzorkována, protože světlost lidské oko rozpoznává ve větším rozlišení. Naproti tomu barvonosné složky Cb a Cr mohou být podvzorkovány, a to tak, že se jejich hodnota vypočítá jako průměr buď ze dvou sousedních pixelů na řádku, nebo ze čtyř pixelů tvořících čtverec 2×2 pixely. Při výpočtu průměru ze dvou sousedních pixelů dochází ke zmenšení objemu dat (pro tyto dva pixely) ze 6 bytů na 4 byty, tj. na cca 66%. Větší úspory objemu se dosáhne při použití čtyř pixelů tvořících informaci o barvě, kde se původních 12 bytů sníží na 6 bytů, tj. na 50%. Je důležité si uvědomit, že se zde jedná o ztrátový převod, protože už nemáme informace o barvách všech pixelů samostatně, ale pouze sousedů v blocích buď 2×1 pixel nebo 2×2 pixely.
5. Dopředná diskrétní kosinová transformace
Následujícím krokem definovaným v normě JPEG je provedení diskrétní kosinové transformace (DCT – Discrete Cosinus Transformation). DCT se provádí odděleně pro jednotlivé barvové složky barvového modelu YCbCr. Pro každou barvovou složku je nejprve provedeno rozdělení celého obrázku na pravidelné bloky o velikosti 8×8 hodnot. Rozdělování se provádí postupně, tj. není zapotřebí, aby byl celý obrázek uložen v operační paměti (to je výhodné zejména při implementaci JPEGu na specializovaných čipech). Pokud šířka či výška obrázku není dělitelná osmi (popř. šestnácti v případě barvonosných složek – nesmíme zapomenout na podvzorkování barev), jsou zbylé hodnoty, které se v obrázku nenacházejí, dopočítány tak, aby se co nejvíce snížil podíl energie ve vyšších frekvencích (viz následující odstavec).

Obrázek 5: Blok dopředné diskrétní kosinové transformace
DCT je jednoznačná transformace v tom smyslu, že se žádná informace při jejím provedení neztrácí. Daný blok o velikosti 8×8 hodnot se převádí na jiný blok o téže velikosti 8×8 hodnot, tyto hodnoty se ovšem nenacházejí v „časové“ doméně jako pixely v komprimovaném obrázku, ale v doméně „frekvenční“. První vypočtený koeficient představuje stejnosměrnou složku (DC), tj. ve skutečnosti průměrnou hodnotu celého vstupního bloku. V dalších transformovaných koeficientech jsou uloženy amplitudy střídavých kosinových složek (AC) různých celočíselných frekvencí.
Jak si ukážeme na vzorcích v následující části tohoto seriálu, je diskrétní kosinová transformace obdobou rychlé Fourierovy transformace (FFT), ovšem s tím rozdílem, že jsou vypočteny pouze kosinové složky, které mají jeden význačný rys: kosinus je sudá funkce, tj. při transformaci barevných přechodů (typických pro mnoho obrázků) nedochází po zpětné transformaci k zákmitům jako v případě FFT. Zákmity by se projevily nežádoucími dvojitými hranami (duchy) na ukládaných obrázcích. Plynulý barevný přechod je možné považovat za 2D variantu jednorozměrného signálu tvořícího pilovitý průběh.
6. Kvantování DCT koeficientů pomocí kvantizačních tabulek
Ústřední částí ztrátové komprimace JPEG je kvantování koeficientů vypočtených pomocí diskrétní kosinové transformace. V předchozí kapitole jsme si řekli, že výsledkem DCT jsou bloky o velikosti 8×8 hodnot. U typických obrázků se největší hodnoty nachází v koeficientech reprezentujících stejnosměrnou složku a také amplitudy kosinových průběhů malých frekvencí. Vyšší frekvence se v obrázcích samozřejmě také vyskytují (například na hranách nebo u textu), tyto části obrázku jsou však nejvíce postiženy ztrátovou komprimací a dochází k jejich mnohdy na první pohled viditelnému rozmazání. Tato ztráta je způsobena právě kvantováním koeficientů. Každý blok 8×8 hodnot je celočíselně vydělen hodnotami uloženými v takzvaných kvantizačních tabulkách (jedná se o dělení typu „položka po položce“).

Obrázek 6: Blok kvantování DCT koeficientů pomocí kvantizačních tabulek
Kvantizační tabulky jsou vytvořeny tak, aby obsahovaly nízké hodnoty u stejnosměrné složky i koeficientů amplitud nízkých frekvencí a naopak vysoké hodnoty u koeficientů amplitud vysokých frekvencí. Výsledkem dělení je nový blok 8×8 hodnot, který většinou obsahuje u vysokých frekvencí nulové hodnoty (nezapomeňme, že se používá celočíselné dělení, právě zde dochází k největší ztrátě informace). Ve vytvoření nulových hodnot spočívá význam DCT a kvantování: sady nulových hodnot jsou velmi dobře kódovatelné pomocí Huffmanova i aritmetického kódování. Blok se navíc prochází metodou cik-cak (zig-zag), takže se nulové hodnoty nachází za sebou, což dále zefektivňuje kódovací rutiny a nabízí použití slovníkových metod. Na správné volbě kvantizačních tabulek závisí jak komprimační poměr, tak i kvalita výsledného obrázku.
7. Kódování kvantovaných DCT koeficientů (aritmetické a Huffmanovo kódování)
Z předchozího bloku (kvantování DCT koeficientů) přichází datový tok, který obsahuje mnoho nulových hodnot. Tento datový tok je podroben buď aritmetickému nebo Huffmanovu kódování. Huffmanovo kódování, které musí podporovat každý kodér i dekodér JPEGu, spočívá ve výstavbě slovníku často se opakujících číselných posloupností a zápisu těchto posloupností pomocí kratších kódů. Naopak, méně často se opakující posloupnosti mohou být zapsány pomocí delších kódů. V navazujících částech se tímto kódováním budeme zabývat podrobněji.
Místo Huffmanova kódování je možné použít i kódování aritmetické, které v průměru vytváří soubory, jež jsou o cca 10% menší. Aritmetické kódování, ve kterém jsou posloupnosti považovány za binárně zapsaná čísla menší než 1 roztříděná do intervalů (která je možné po úpravách zaokrouhlovat), je časově náročnější a také bylo zatíženo několika patenty a patrně z těchto důvodu se příliš často nepoužívá. I aritmetickým kódováním se budeme podrobněji zabývat v navazujících částech tohoto seriálu.

Obrázek 7: Blok kódování kvantovaných DCT koeficientů pomocí aritmetického nebo Huffmanova kódování
8. Uložení zakódovaných dat do souboru typu JFIF
Posledním krokem je uložení zakódovaných dat do souboru typu JFIF. Tento krok již není v normě JPEG popsán, neboť se jedná o proces závislý na použitém systému. JPEG je totiž možné vkládat do mnoha diametrálně odlišných souborových formátů, například PostScriptu, PDF, TIFFu, MJPEG (některé soubory s koncovkou MOV vytvářené digitálními fotoaparáty) apod. Pravděpodobně nejpopulárnější jsou však soubory ve formátu JFIF, které obsahují rastrová data komprimovaná pomocí metody JPEG. Aby byla situace o něco málo zamotanější, mají tyto soubory většinou koncovku „.jpeg“ resp. „.jpg“ a nikoli „.jfif“. JFIF obaluje zkomprimovaná rastrová data informační hlavičkou, koncovkou souboru, náhledovým obrázkem (nemusí být vždy přítomen) a dalšími rozšiřujícími bloky, například dnes populárním blokem EXIF. Opět se jedná o téma, kterým se budeme blíže zabývat v některé navazující části.
Obrázek 8: Blok ukládání zakódovaných dat do souborů typu JFIF
9. Obsah dalšího pokračování tohoto seriálu
V následující části tohoto seriálu si podrobněji popíšeme způsob výpočtu dopředné diskrétní kosinové transformace spolu s kvantováním DCT koeficientů pomocí kvantizačních tabulek. Tyto dva funkční bloky tvoří ústřední část celé ztrátové komprimace pomocí JPEGu, proto je pochopení jejich funkce pro další výklad klíčové.



























