Fraktály v počítačové grafice XXIX

Obsah

1. Urychlení vykreslování fraktálů v komplexní rovině
2. Detekce periodické posloupnosti
3. Eliminace počtu zpracovávaných pixelů a rychlý náhled na generovaný fraktál
4. Metoda nazvaná „boundary tracing“
5. Metoda nazvaná „tesseral“
6. Metoda nazvaná „solid-guessing“
7. Metoda nazvaná „diffusion scan“
8. Urychlení výpočtů při animaci průletu fraktálními množinami
9. Obsah dalšího pokračování tohoto seriálu

1. Urychlení vykreslování fraktálů v komplexní rovině

V předchozích devatenácti dílech tohoto seriálu jsme si popisovali principy vytváření fraktálních obrazců v komplexní rovině. Některé z těchto fraktálů, zejména světoznámá Mandelbrotova množina, byly definovány pomocí velmi jednoduchých iteračních vztahů (v případě Mandelbrotovy množiny vztahem z_n+1=z_n²+c), avšak jiné popisované typy fraktálních množin, například fraktály typu Newton, Magnet 1, Magnet 2, Barnsley 1, Barnsley 2 a Phoenix byly určeny pomocí vztahů mnohem složitějších, ve kterých se buď vyskytovaly vyšší mocniny komplexní hodnoty z_i nebo se ve vztahu nacházely podmínky či dokonce dělení komplexních čísel. Vzhledem k tomu, že pro každý pixel odpovídající jednomu bodu v komplexní rovině je zapotřebí provést až několik stovek iteračních kroků pro rozhodnutí, zda posloupnost hodnot z_i konverguje, diverguje či se periodicky opakuje, objevily se již v poměrně vzdálené minulosti snahy o urychlení těchto časově velmi náročných výpočtů.

Vzpomínám si, že na domácím počítači Atari 800XL s osmibitovým mikroprocesorem MOS 6502C a 64kB operační paměti RAM (samozřejmě bez matematického koprocesoru) trval výpočet rastrového obrazu Mandelbrotovy množiny v rozlišení 320×192 pixelů při maximálně šestnácti iteracích zhruba osm hodin! Dnes jde sice o záležitost, kterou moderní mikroprocesory podporované optimalizujícími překladači dokončí za několik desítek milisekund, na druhou stranu se však prudce zvýšily požadavky na vygenerované obrázky, například se řádově zvýšilo jejich rozlišení (tj. počet generovaných pixelů) a některé aplikace také provádí výpočet barev jednotlivých bodů přímo za běhu jiných výpočtů – to se děje zejména při vykreslování trojrozměrných scén pomocí raytracingu, při kterém jsou stěny těles pokryty vhodnými fraktálními či procedurálními obrazci místo rastrových textur (to s sebou přináší odstranění aliasu a velkou úsporu operační a texturovací paměti). V dalších kapitolách si popíšeme některé techniky, které byly v minulosti vyvinuty pro urychlení výpočtů fraktálů v komplexní rovině. Urychlení se dá obecně provést ve třech oblastech:

1. Zrychlení výpočtu barvy jednoho pixelu (nezávisle na pixelech ostatních), například rychlým nalezením periodické či konvergující posloupnosti hodnot z_i.
2. Redukce celkového počtu pixelů, u kterých je nutné barvu získat iterativním výpočtem.
3. Redukce celkového počtu pixelů nových při dynamické změně pohledu na fraktální obrázek – průlet fraktálem.

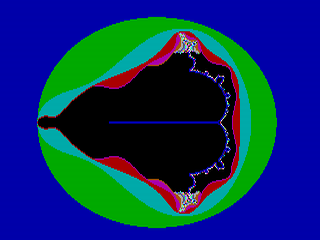
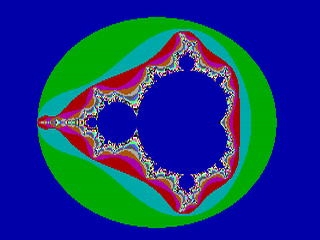
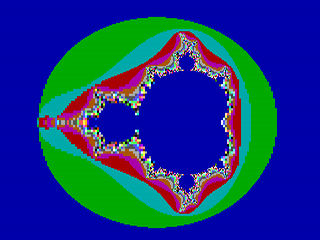
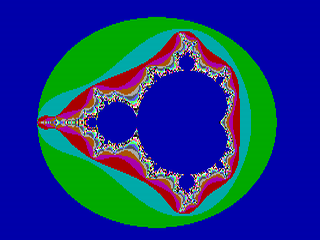
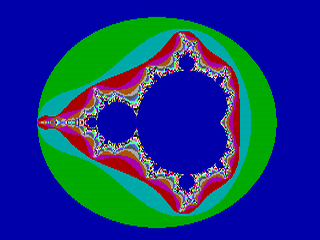
Všechny tři vyjmenované způsoby urychlení si popíšeme v dalším textu. Ve druhé kapitole se budeme zabývat detekcí periodické posloupnosti, třetí až sedmá kapitola je věnována metodám sloužícím k redukci počtu pixelů, u kterých je nutné použít iterativní výpočet a konečně se v osmé kapitole dozvíme, jak výrazně zredukovat počet pixelů při „průletu“ fraktálem. Ve všech případech se budou výpočty provádět s klasickou Mandelbrotovou množinou zobrazenou v základním pohledu, vygenerované obrázky mají rozlišení 320×240 pixelů (QCIF), 256 barev (odpovídajících maximálně 256 iteracím) a standardní VGA paletu. Mandelbrotova množina s těmito parametry je zobrazena na prvním obrázku.

Obrázek 1: Základní pohled na Mandelbrotovu množinu v rozlišení 320×240 pixelů a standardní VGA paletě

2. Detekce periodické posloupnosti

Základní metodou, která slouží pro urychlení výpočtu barvy jednoho pixelu, a to nezávisle na pixelech ostatních, je metoda detekce periodické posloupnosti. Pokud totiž při iteračním výpočtu dojde k situaci, že se nějaká hodnota z_i bude po několika iteracích opakovat, tj. bude platit z_i+p=z_i, je jasné, že daný bod musí ležet uvnitř dané fraktální množiny. Jestliže tedy nalezneme cestu, jak tuto periodu co nejrychleji detekovat, můžeme mnohdy výrazným způsobem urychlit celý iterační výpočet, který by v opačném případě dosáhl až maximálního počtu iterací – to platí pro všechny body ležící uvnitř fraktálu. Jednou z možností, jak periodickou posloupnost najít, je zapamatování si všech již vypočtených hodnot z_i a porovnávání nově vypočtené hodnoty se všemi hodnotami předešlými. To je však poměrně náročné, a to jak paměťově, tak i díky nutnosti prohledávání pole s předchozími hodnotami při každé iteraci (jednalo by se o smyčku uvnitř iterační smyčky, vnořené smyčky většinou nebývají tím nejrychlejším řešením).

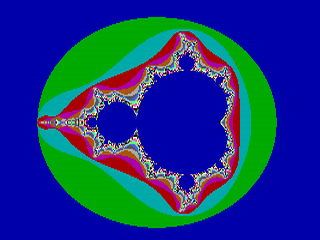
Z tohoto důvodu byl nalezen jiný způsob, který sice nemusí být vždy účinný (nalezne pouze periody o menší hodnotě a to ne v minimálním počtu kroků), jedná se však o způsob rychlý a současně paměťově nenáročný. Při tomto způsobu se vlastně počítají dvě posloupnosti, můžeme je označit Z_i a Z'_i. Hodnota prvků z první posloupnosti je počítána v každém iteračním kroku, avšak hodnota posloupnosti druhé je počítána s mnohem nižší frekvencí, například každý šestnáctý iterační krok. V každém iteračním kroku jsou obě hodnoty navzájem porovnány a v případě, že jsou si velmi blízké, znamená to, že jsme našli periodickou posloupnost. Na druhém obrázku je zobrazena Mandelbrotova množina, ve které jsou barevně zvýrazněny vnitřní oblasti obsahující periodické posloupnosti; body nacházející se vně množiny jsou vybarveny černou barvou. Periodické posloupnosti jsou nalezeny po poměrně malém počtu iterací (20–30), což je mnohem méně, než nastavený maximální počet iterací (255). Pod obrázkem je uveden fragment kódu, který provádí výpočet pixelů v Mandelbrotově množině s detekcí periodické posloupnosti.

Obrázek 2: Mandelbrotova množina se zvýrazněnými vnitřními oblastmi, ve kterých byla nalezena periodická posloupnost

#define MAXITER    1000                 // maximální počet iterací
#define PER_PERIOD 16                   // frekvence výpočtu posloupnosti Z'
#define PER_CHECK  0.0001               // minimální vzdálenost z'(i) a z(i)

    do {                                // iterační smyčka
        if (period==PER_PERIOD) {       // výpočet z'(i)
          zzx2=zzx*zzx;
          zzy2=zzy*zzy;
          zzy=2.0*zzx*zzy+ccy;
          zzx=zzx2-zzy2+ccx;
          period=0;                     // nulování počitadla kontroly periody
        }
        zx2=zx*zx;                      // výpočet z(i)
        zy2=zy*zy;
        zy=2.0*zx*zy+ccy;
        zx=zx2-zy2+ccx;
        i++;                            // zvýšit počitadlo iterací
        period++;
        dst=ldabs(zx-zzx)+ldabs(zy-zzy);// výpočet vzdálenosti z'(i) a z(i)
        if (dst<PER_CHECK) {            // pokud byla nalezena perioda
          i=MAXITER;                    // ukončit iterační smyčku
          result2=1;
        }
    } while (i<MAXITER && zx2+zy2<4.0); 

3. Eliminace počtu zpracovávaných pixelů a rychlý náhled na generovaný fraktál

Dalším způsobem vedoucím ke znatelnému urychlení výpočtů obrazů fraktálních množin v komplexní rovině je eliminace počtu pixelů, u kterých musí být proveden celý iterační výpočet. Je totiž možné využít faktu, že většina fraktálů v komplexní rovině je spojitá a dokonce, že body o stejném počtu iterací tvoří souvislé izoplochy. Nemusí být tedy nutné složitě a především zdlouhavě počítat barvy všech bodů, ale pouze bodů, které fraktál nějakým význačným způsobem reprezentují. Toho využívají další popisované metody, které současně umožňují provést rychlý náhled na vznikající fraktální obrazec, jeho tvar je možné rozeznat například již po výpočtu a vykreslení pouhé jedné desetiny všech pixelů. V následujících čtyřech kapitolách budou stručně popsány čtyři metody, které umožňují vytvoření rychlého náhledu na vznikající fraktál, první tři metody (nazvané boundary tracing, tesseral a solid-guessing) dokonce mohou snížit počet pixelů, pro které je nutné provádět časově náročný iterativní výpočet.

4. Metoda nazvaná „boundary tracing“

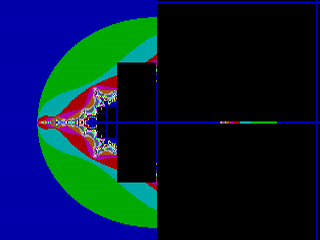
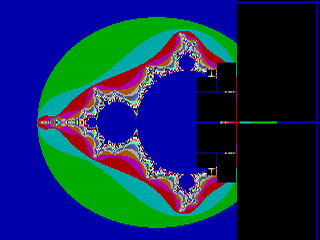
Při aplikaci metody boundary tracing je použit následující postup: nejprve je pomocí iterativního výpočtu získán počet iterací pro všechny pixely, které tvoří okraj obrázku. Posléze je ve vertikálním nebo horizontálním směru nalezen jeden pixel, který má nastaven nejnižší počet iterací a dále je iterativně prohledáváno čtyřokolí či (častěji) osmiokolí tohoto pixelu a v něm je nalezen pixel se stejnou hodnotou iterace. Pro fraktální obrazce, které tvoří spojité izoplochy (mezi tyto obrazce patří i Mandelbrotova množina) je zaručeno, že se tímto postupem dostaneme zpět do původního pixelu a vnější oblast vymezenou příslušnou osmispojitou či čtyřspojitou cestou je možné vybarvit konstantní barvou. Takto se postupuje dále ke středu obrazce až do chvíle, kdy jsou vybarveny všechny pixely; naposledy jsou přitom vybarveny body ležící uvnitř fraktálu. Metodu je možné aplikovat pouze na ty fraktální množiny, jejichž izoplochy jsou spojité a neobsahují izolované „ostrůvky“, ty by totiž nebyly nalezeny a byly by chybně vybarveny konstantní barvou. Mezi fraktály, pro které dává tato metoda špatné výsledky, patří například Newtonova fraktální množina. Postup výpočtu rastrového obrazce Mandelbrotovy množiny při použití metody boundary tracing je zobrazený na třetím až šestém obrázku.

Obrázek 3: Metoda „boundary tracing“: počáteční fáze výpočtu

Obrázek 4: Metoda „boundary tracing“: pokročilejší fáze výpočtu

Obrázek 5: Metoda „boundary tracing“: již byly nalezeny hraniční body ležící uvnitř fraktálu

Obrázek 6: Metoda „boundary tracing“: obrazec Mandelbrotovy množiny po dokončení všech výpočtů

5. Metoda nazvaná „tesseral“

Jednou z nejrychlejších a současně i nejčastěji používaných metod vedoucích k urychlení vykreslení obrazce fraktálu v komplexní rovině, je metoda nazývaná tesseral. Název této metody přesně vystihuje i její funkci. Nejprve jsou vyčísleny počty iterací pro body (pixely) ležící na okrajích rastrového obrazu. Posléze se obraz rekurzivně dělí na stejně velké čtvrtiny (podobrazy) a pro každý podobraz jsou opět vypočteny počty iterací všech jeho okrajových bodů. V případě, že jsou všem bodům na okraji přiřazeny stejné počty iterací, je celý podobraz vyplněn barvou odpovídající tomuto počtu iterací. Pokud se naopak i jediný z vypočtených bodů liší, je proveden další krok rekurze a daná oblast je rozdělena na čtyři stejně velké podoblasti. V nejhorším, tj. nejpomalejším případě dělení rastrového obrázku končí až na úrovni jednoho pixelu, který se již samozřejmě dále nedělí. Metoda je použitelná pouze pro spojité fraktály, jelikož u fraktálů nespojitých by se mohlo stát, že by mohly být vynechány části ležící uvnitř nějaké podoblasti, přičemž by všechny body této podoblasti měly přiřazenu jednu hodnotu počtu iterací. Postup metody tesseral je zobrazený na sedmém, osmém a devátém obrázku.

Obrázek 7: Metoda „tesseral“: první fáze výpočtu

Obrázek 8: Metoda „tesseral“: druhá fáze výpočtu

Obrázek 9: Metoda „tesseral“: obrazec Mandelbrotovy množiny po dokončení všech výpočtů

6. Metoda nazvaná „solid-guessing“

Metoda nazvaná solid-guessing je v některých svých aspektech podobná metodě tesseral. I zde je obrázek dělen na menší části, zde však na pravidelné čtverce o velikosti začínající na hodnotě 2×2 pixely do cca 16×16 pixelů (velikost se mění v závislosti na rozlišení výsledného obrázku). Nejprve jsou vypočteny barvy všech pixelů na okrajích čtverců a pokud jsou všechny barvy okolo čtverce stejné, je daný čtverec vybarven konstantní barvou. Pokud barvy (resp. počty iterací) stejné nejsou, je po dokončení první fáze přistoupeno k fázi druhé, kdy je čtverec rozdělen na čtyři menší čtverce, pro které je provedena stejná operace – vyčíslení pixelů na okrajích s případným vybarvením čtverce. Takto se postupuje v několika krocích až do chvíle, kdy mají zbylé (tj. dosud nevybarvené) čtverce velikost 1×1 pixel – zde se jejich barvy musí zjistit klasickým iteračním výpočtem. Tato metoda sice může vést k chybně vyplněným čtvercům u některých typů fraktálů, na druhou stranu se jedná o jednu z mála metod, kde se již při vyčíslení nepatrného množství pixelů může zobrazit hrubý náhled na tvar celého fraktálního obrace, což je také demonstrováno na obrázcích 10 – 14.

Obrázek 10: Metoda „solid-guessing“: hrubě vypočtený obrazec

Obrázek 11: Metoda „solid-guessing“: pokračování první fáze výpočtu

Obrázek 12: Metoda „solid-guessing“: těsně před dokončením první fáze

Obrázek 13: Metoda „solid-guessing“: druhá fáze výpočtu

Obrázek 14: Metoda „solid-guessing“: obrazec Mandelbrotovy množiny po dokončení všech výpočtů

7. Metoda nazvaná „diffusion scan“

Výše uvedené tři metody boundary tracing, tesseral a solid-guessing byly navrženy tak, aby se v co největší míře redukoval počet pixelů, pro něž bylo nutné provádět časově zdlouhavé iterativní výpočty. Kromě toho všechny tyto metody vybíraly pixely v obrázku takovým způsobem, že se i po krátké době ukázal hrubý tvar výsledného fraktálního obrazce, takže uživatel mohl i před dokreslením celého obrázku výpočet přerušit a například pozměnit parametry fraktálu (zvětšení, barvovou paletu apod.). Zde popisovaná metoda nazvaná diffusion scan slouží především k vytvoření rychlého náhledu na fraktální obrazec, ale na rozdíl od předešlých metod se ve výsledku přesně spočítají barvy všech pixelů v obrázku pomocí iterativního výpočtu. To znamená, že doba výpočtu se od klasické metody „pixel po pixelu“ nijak nemění, ale prvotní náhled na obrázek je možný již po výpočtu cca jedné setiny všech pixelů. Metoda pracuje následujícím způsobem: nejprve jsou vyčísleny pouze barvy pixelů, které se nachází v poměrně řídké mřížce se vzdálenostmi sousedů např. 16×16 pixelů. Vždy je však vybarveno celé políčko mřížky, tj. po první fázi je vykreslen obrázek s bloky o velikosti 16×16 pixelů. Ve druhém kroku je mřížka zjemněna tak, že obsahuje bloky o velikosti 8×8 pixelů (již vypočtené pixely se však nemusí znovu počítat), ve třetím kroku jsou vytvořeny bloky 4×4 pixely atd. až do konečné fáze, ve které je vypočítán každý pixel. Ukázka aplikace metody diffusion scan je zobrazena na obrázcích 15 až 18.

Obrázek 15: Metoda „diffusion scan“: první zobrazení mřížky

Obrázek 16: Metoda „diffusion scan“: zjemňování mřížky

Obrázek 17: Metoda „diffusion scan“: další zjemnění

Obrázek 18: Metoda „diffusion scan“: obrazec Mandelbrotovy množiny po dokončení všech výpočtů

8. Urychlení výpočtů při animaci průletu fraktálními množinami

Při vytváření animací průletu fraktálními množinami, kdy je dynamicky měněn pohled na fraktální obrázek (přiblížení resp. oddalování čili zoom) je možné výpočet urychlit až tisícinásobně a to tak, že se provede výpočet barev pouze těch pixelů, které jsou při přiblížení či naopak oddálení opravdu změněny. Na tomto místě si stručně popíšeme metodu, která je použita například ve známé aplikaci XaoS (http://xaos.sou­rceforge.net/blac­k/index.php), jejímž hlavním vývojářem je Honza Hubička. Podle dokumentace k tomuto programu se při zvětšování zoomu výpočet provádí pouze pro necelé jedno procento pixelů, což při rychlosti dnešních počítačů, které dokážou provést výpočet cca 100 000 pixelů za sekundu (pro Mandelbrotovu množinu), znamená, že je možné bez problémů vytvářet plynulé animace o rozlišení 1024×768 pixelů s 25 snímky za sekundu. Popíšeme si postup při přibližování i vzdalování se od fraktálu:

1. Nejprve se zaměříme na postup aplikovaný při oddalování se od fraktálu, který je poněkud méně efektivní než algoritmus použitý při přibližování. Oddálení vlastně v praxi probíhá tak, že se část původního rastrového obrázku pouze zmenší (tj. hodnoty některých pixelů jsou zahozeny) a posléze se dopočítají nové pixely na okrajích obrázku, protože tyto pixely nebyly v původním obrázku obsaženy. Výpočet nových pixelů probíhá buď klasickým způsobem pixel po pixelu, nebo je možné použít libovolnou z urychlujících metod popsaných v předchozích kapitolách. Zmenšení původního obrázku (ten bude v novém obrázku vycentrován) může probíhat buď prostým přepočtením pozic pixelů, například celočíselným algoritmem DDA či Bresenhamovým algoritmem, nebo se pro každý nový pixel vyčíslí vektor ukazující na barvu některého z pixelů původního obrázku a následně se provede přemapování pixelů na jejich nové pozice (prakticky se však přemapování provádí inverzně, tj. pro každý pixel nového obrázku je zjištěna pozice pixelu z obrázku původního, jehož barva se má získat). Při dostatku výpočetního výkonu je možné při zmenšování obrázku uplatnit také nějaký konvoluční filtr určený pro resampling.
2. Postup použitý při přiblížení fraktálního obrazce je mnohem zajímavější a také efektivnější. Přiblížení spočívá v tom, že se již vypočtené pixely posunou ve vytvářeném obrázku do nových pozic, takže se pro každý pixel může vypočítat vektor posunu směřující z jeho staré pozice do pozice nové (vektory míří od středu obrázku). Vzhledem k tomu, že se provádí přibližování, jsou pixely původně umístěné blízko okrajů obrázku zahozeny a v novém obrázku tak vzniknou „díry“ (černé pixely), které je zapotřebí zaplnit. Oněch děr je necelé jedno procento, tj. pro obrázek o rozlišení 1024×768 pixelů je při každém přiblížení nutné dopočítat zhruba 8000 pixelů, spíše to však bude řádově méně. Uvedené hodnoty jsou platné pouze v případě, že se jedná o malé přiblížení (zvětšení), to je však při provádění plynulých animací vždy zaručeno. V případě, že by bylo přiblížení větší, znamenalo by to i větší rozdíly mezi oběma obrázky, což by způsobilo nárůst počtu pixelů, které je zapotřebí dopočítat.

9. Obsah dalšího pokračování tohoto seriálu

Od jubilejního třicátého pokračování tohoto seriálu se začneme zabývat takzvanými systémy iterovaných funkcí (IFS), které je možné použít pro vytváření procedurálních modelů těles s fraktální charakteristikou, zejména soběpodobností a invariancí ke změně měřítka. Nejprve bude stručně uvedena teorie IFS systémů, poté způsob vytváření IFS kódu, generování koláží pomocí IFS systémů a využití IFS systémů pro vytváření trojrozměrných procedurálních modelů těles většinou složených z bezrozměrných částic či plošných elementů (surfelů).

Obrázek 19: Kapradina vytvořená pomocí systémů iterovaných funkcí IFS