Obsah
1. Iterační vztah platný pro fraktální množinu Phoenix
2. Mandelbrotova varianta fraktální množiny Phoenix
3. Demonstrační příklad vykreslující Mandelbrotovu variantu fraktální množiny Phoenix
4. Juliova varianta fraktální množiny Phoenix
5. Demonstrační příklad vykreslující Juliovu variantu fraktální množiny Phoenix
6. Hodnota perturbace a její vliv na tvar fraktální množiny Phoenix
7. Demonstrační příklad vykreslující množinu Phoenix ovlivněnou hodnotou perturbace
8. Obsah dalšího pokračování tohoto seriálu
1. Iterační vztah platný pro fraktální množinu Phoenix
Fraktální množina nazvaná Phoenix byla vytvořena autorem, který se jmenuje Shigehiro Ushiki. Iterační vzorec, pomocí kterého je tato množina vytvořena, byl poprvé zveřejněn v časopise IEEE Transactions on Circuits and Systems, Volume 35, číslo 7, červenec 1988 na stranách 788–789. Za povšimnutí stojí, že se ještě v roce 1988 zveřejňovaly odborné články o počítačové grafice v „nepočítačových“ časopisech – dnes je díky SIGGRAPHu samozřejmě všechno jinak a na světě vychází cca dvě desítky specializovaných časopisů o počítačové grafice. Vraťme se však k iteračnímu vzorci, kterým jsou popsány body ležící uvnitř fraktální množiny Phoenix. Zajímavé je, že vzorec je vlastně tvořen dvěma částmi. První část určuje změnu posloupnosti hodnot zi, druhá část potom posloupnost hodnot pomocné komplexní proměnné nazývané podle notace použité ve výše uvedeném článku yi. Vzorec (resp. oba dva vzorce) je možné zapsat následujícím způsobem:
zn+1=zn2+Re©+Im©yn
yn+1=zn
Přičemž zn představuje n-tý člen posloupnosti zi, yn n-tý člen řady yi a c je komplexní konstanta, jež je před vstupem do iterační smyčky nastavena v závislosti na poloze právě obarvovaného pixelu v komplexní rovině. Počáteční podmínky při vstupu do iterační smyčky jsou nastaveny takto:
z0=c
y0=0+0i
Oba uvedené iterační vzorce je možné rozepsat na jejich reálné a imaginární složky a po přepsání takto získaných vztahů do programovacího jazyka C získáme posloupnost příkazů, kterou je možné použít ve funkcích počítajících Mandelbrotovy i Juliovy varianty fraktální množiny Phoenix:
// proměnné použité v iterační smyčce
double zx, zy, zx2, zy2, zxn, zyn; // složky komplexní proměnné Z a Z^2
double cx0, cy0; // hodnota komplexní konstanty C
double xmin, ymin, xmax, ymax; // rohy vykreslovaného obrazce v komplexní
// rovině
double ynx, yny; // jeden prvek posloupnosti Y(n)
// nastavení počátečních podmínek před vstupem do iterační smyčky
zx=cx0; // nastavit počáteční hodnotu Z(0)
zy=cy0;
ynx=0.0; // nastavit počáteční hodnotu Y(0)
yny=0.0;
// rozepsaný iterační vztah prováděný uvnitř iterační smyčky
zx2=zx*zx; // zkrácený výpočet druhé mocniny složek Z
zy2=zy*zy;
zxn=zx2-zy2+cx0+cy0*ynx; // výpočet reálné části Z(n+1)
zyn=2.0*zx*zy+cy0*yny; // výpočet imaginární části Z(n+1)
ynx=zx; // provedení přiřazení Y(n+1)=Z(n)
yny=zy;
zx=zxn; // převod vypočtených hodnot
zy=zyn; // do Z(n+1) pro další iteraci
2. Mandelbrotova varianta fraktální množiny Phoenix
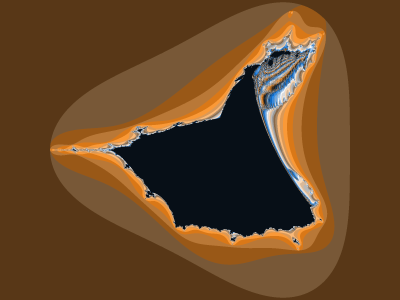
Mandelbrotova varianta fraktální množiny Phoenix má netypický a poněkud nudný tvar, což je také patrné z prvního obrázku, na kterém je vyobrazen celkový pohled na tuto fraktální množinu (celá množina je umístěna v obdélníku omezeném body -2–2i, -2+2i, 2–2i a 2+2i, což je stejný rozsah, jaký platí i pro originální Mandelbrotovu množinu). Při bližší prohlídce detailů na hranici mezi body ležícími uvnitř a vně množiny však můžeme nalézt i velmi zajímavé tvary; některé z nich jsou vyobrazeny na druhém, třetím a čtvrtém obrázku.
Obrázek 1: Celkový pohled na Mandelbrotovu variantu fraktální množiny Phoenix
S využitím všech částí kódu uvedeného v první kapitole je možné vytvořit céčkovskou funkci recalcPhoenixM(), která slouží pro výpočet a následné barevné odlišení pixelů (bodů) ležících vně i uvnitř Mandelbrotovy varianty fraktální množiny Phoenix. Všimněte si, že v této funkci je použita stejná podmínka pro ukončení iterační smyčky jako v případě „klasické“ Mandelbrotovy množiny.
//-----------------------------------------------------------------------------
// Výpočet a následné překreslení Mandelbrotovy varianty fraktální množiny
// typu Phoenix
//-----------------------------------------------------------------------------
void recalcPhoenixM(pixmap *pix, // pixmapa pro vykreslování
int maxiter, // maximální počet iterací
double scale, // měřítko obrazce
double xpos, // posun obrazce
double ypos,
int palette, // barvová paleta
int rf, int gf, int bf) // příznaky barvových složek
{
double zx, zy, zx2, zy2, zxn, zyn; // složky komplexní proměnné Z a Z^2
double cx0, cy0;
double xmin, ymin, xmax, ymax; // rohy vykreslovaného obrazce v komplexní
double ynx, yny; // rovině
int x, y; // počitadla sloupců a řádků v pixmapě
int iter; // počitadlo iterací
unsigned char r, g, b;
calcCorner(xpos, ypos, scale, &xmin, &ymin, &xmax, &ymax);
cy0=ymin;
for (y=0; y<pix->height; y++) { // pro všechny řádky v pixmapě
cx0=xmin;
for (x=0; x<pix->width; x++) { // pro všechny pixely na řádku
zx=cx0; // nastavit počáteční hodnotu Z(0)
zy=cy0;
ynx=0.0; // nastavit počáteční hodnotu Y(0)
yny=0.0;
for (iter=0; iter<maxiter; iter++) {// iterační smyčka
zx2=zx*zx; // zkrácený výpočet druhé mocniny složek Z
zy2=zy*zy;
zxn=zx2-zy2+cx0+cy0*ynx;
zyn=2.0*zx*zy+cy0*yny;
ynx=zx;
yny=zy;
zx=zxn;
zy=zyn;
if (zx2+zy2>4) break;
}
iter++;
mapPalette(palette, iter, &r, &g, &b);
r=r*rf; // uživatelem řízené vynulování
g=g*gf; // vybraných barvových složek
b=b*bf;
putpixel(pix, x, y, r, g, b);
cx0+=(xmax-xmin)/pix->width; // posun na další bod na řádku
}
cy0+=(ymax-ymin)/pix->height; // posun na další řádek
}
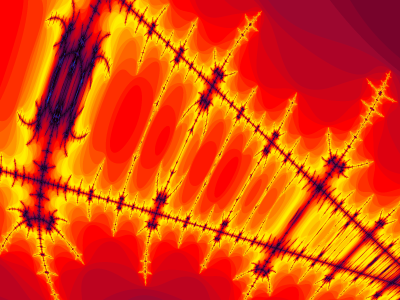
} Obrázek 2: Detail Mandelbrotovy varianty fraktální množiny Phoenix
Obrázek 3: Další detail Mandelbrotovy varianty fraktální množiny Phoenix
Obrázek 4: Poslední ukázka detailu Mandelbrotovy varianty fraktální množiny Phoenix
3. Demonstrační příklad vykreslující Mandelbrotovu variantu fraktální množiny Phoenix
V předchozí kapitole byl uveden výpis céčkovské funkce recalcPhoenixM(). Tato funkce je použita v dnešním prvním demonstračním příkladu. Po překladu tohoto příkladu a jeho následném spuštění se zobrazí rastrový obrázek Mandelbrotovy varianty fraktální množiny Phoenix o rozlišení 512×384 pixelů. Způsob výpočtu i zobrazení tohoto fraktálu je možné ovlivnit pomocí klávesnice, seznam všech kláves, které je možné použít, je uvedený v následující tabulce. Screenshot prvního demonstračního příkladu je zobrazený na pátém obrázku.
| Klávesa | Význam |
|---|---|
| , | snížení počtu iterací o jednotku s okamžitým překreslením obrázku |
| . | zvýšení počtu iterací o jednotku s okamžitým překreslením obrázku |
| < | snížení počtu iterací o deset jednotek s okamžitým překreslením obrázku |
| > | zvýšení počtu iterací o deset jednotek s okamžitým překreslením obrázku |
| S | uložení rastrového obrázku s fraktálem do externího souboru typu TGA |
| Q | ukončení tohoto demonstračního příkladu |
| Esc | má stejný význam jako klávesa Q – ukončení aplikace |
| kurzorové šipky | posun obrazce ve směru šipek (o cca pět procent velikosti obrázku) |
| Page Up | změna měřítka (zvětšení výřezu o deset procent) |
| Page Down | změna měřítka (zmenšení výřezu o deset procent) |
| 0 | nastavení barvové palety „Blues“ |
| 1 | nastavení barvové palety „Gold“ |
| 2 | nastavení barvové palety „Greens“ |
| 3 | nastavení barvové palety „Ice“ |
| 4 | nastavení barvové palety „Juteblue“ |
| 5 | nastavení barvové palety „Jutemap“ |
| 6 | nastavení barvové palety „Jutes“ |
| 7 | nastavení barvové palety „Mandmap“ |
| 8 | nastavení barvové palety „Phong“ |
| 9 | nastavení barvové palety „Rose“ |
Obrázek 5: Screenshot prvního demonstračního příkladu s Mandelbrotovou variantou fraktální množiny Phoenix
4. Juliova varianta fraktální množiny Phoenix
V případě, že se vhodným způsobem změní počáteční podmínky a tvar iterační smyčky, je možné provést úpravu funkce počítající Mandelbrotovu verzi fraktální množiny Phoenix na funkci, jež vypočte a zobrazí Juliovu verzi téže množiny. Počáteční podmínky se změní tím způsobem, že se hodnota z0 nastaví podle pozice počítaného bodu/pixelu v komplexní rovině. V iteračním vzorci se však použije jiná hodnota konstanty c – tato hodnota zůstane zachována pro všechny počítané body jednoho obrázku. Juliovy varianty této fraktální množiny jsou ukázány na šestém, sedmém a osmém obrázku; funkce, která tyto obrázky počítá, se jmenuje recalcPhoenixJ() a má následující tvar:
//-----------------------------------------------------------------------------
// Výpočet a následné překreslení fraktální množiny typu Phoenix
// v Juliově variantě
//-----------------------------------------------------------------------------
void recalcPhoenixJ(pixmap *pix, // pixmapa pro vykreslování
int maxiter, // maximální počet iterací
double scale, // měřítko obrazce
double xpos, // posun obrazce
double ypos,
double cx,
double cy, // poloha bodu v komplexní rovině
int palette, // barvová paleta
int rf, int gf, int bf) // příznaky barvových složek
{
double zx, zy, zx2, zy2, zxn, zyn; // složky komplexní proměnné Z, Z^2 a Z^3
double cx0, cy0;
double xmin, ymin, xmax, ymax; // rohy vykreslovaného obrazce v komplexní
double ynx, yny; // rovině
int x, y; // počitadla sloupců a řádku v pixmapě
int iter; // počitadlo iterací
unsigned char r, g, b;
calcCorner(xpos, ypos, scale, &xmin, &ymin, &xmax, &ymax);
cy0=ymin;
for (y=0; y<pix->height; y++) { // pro všechny řádky v pixmapě
cx0=xmin;
for (x=0; x<pix->width; x++) { // pro všechny pixely na řádku
zx=cx0; // nastavit počáteční hodnotu Z(0)
zy=cy0;
ynx=0.0;
yny=0.0;
for (iter=0; iter<maxiter; iter++) {// iterační smyčka
zx2=zx*zx; // zkrácený výpočet druhé mocniny složek Z
zy2=zy*zy;
zxn=zx2-zy2+cx+cy*ynx;
zyn=2.0*zx*zy+cy*yny;
ynx=zx;
yny=zy;
zx=zxn;
zy=zyn;
if (zx2+zy2>4) break;
}
iter++;
mapPalette(palette, iter, &r, &g, &b);
r=r*rf; // uživatelem řízené vynulování
g=g*gf; // vybraných barvových složek
b=b*bf;
putpixel(pix, x, y, r, g, b);
cx0+=(xmax-xmin)/pix->width; // posun na další bod na řádku
}
cy0+=(ymax-ymin)/pix->height; // posun na další řádek
}
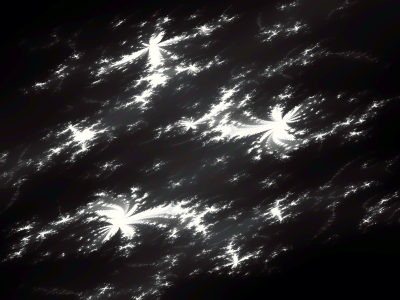
} Všimněte si, že tvar Juliovy varianty fraktální množiny Phoenix se opravdu může podobat tomuto bájnému tvorovi – to je ostatně důvod, který vedl k jejímu pojmenování a proč je tento fraktál tak populární (to můžeme soudit podle četnosti jeho použití v aplikacích generujících fraktály i podle mnoha obrázků zveřejněných na Internetu).
Obrázek 6: Juliova verze fraktální množiny Phoenix
Obrázek 7: Další typ Juliovy verze fraktální množiny Phoenix
Obrázek 8: Juliova verze fraktální množiny Phoenix s odlišnou hodnotou konstanty c
5. Demonstrační příklad vykreslující Juliovu variantu fraktální množiny Phoenix
Výše uvedená funkce recalcPhoenixJ() je implementována v dnešním druhém demonstračním příkladu. Po úspěšném překladu a následném spuštění tohoto příkladu se vytvoří okno, v jehož levé části se zobrazuje Mandelbrotova varianta fraktální množiny Phoenix a v pravé části je naopak zobrazena varianta Juliova. Pohybem myši po levé části okna (přitom musí být stlačeno levé tlačítko myši) se mění hodnota komplexní konstanty c a tím se ovlivňuje tvar Juliovy varianty fraktální množiny zobrazené v pravé části okna. Screenshot ze druhého demonstračního příkladu je zobrazen na devátém obrázku.
Obrázek 9: Screenshot druhého demonstračního příkladu s Juliovou variantou fraktální množiny Phoenix
6. Hodnota perturbace a její vliv na tvar fraktální množiny Phoenix
Tvar Mandelbrotovy varianty fraktální množiny Phoenix je možné změnit nastavením nenulové hodnoty perturbace podobným způsobem, jaký známe i z předchozích funkcí pro generování fraktálů v komplexní rovině. Zde se bude konkrétně jednat o změnu počátečních podmínek ze tvaru:
zx=cx0; // nastavit počáteční hodnotu Z(0)
zy=cy0;
ynx=0.0; // nastavit počáteční hodnotu Y(0)
yny=0.0; na nový tvar zohledňující perturbaci, jejíž komplexní hodnota je uložena v proměnných pcx a pcy:
zx=cx0+pcx; // nastavit počáteční hodnotu Z(0)
zy=cy0+pcy;
ynx=0.0; // nastavit počáteční hodnotu Y(0)
yny=0.0; Výsledné tvary fraktálu po aplikaci nenulové hodnoty perturbace mohou být dosti různorodé, což názorně ilustrují obrázky 10 a 11.
Obrázek 10: Mandelbrotova verze fraktální množiny Phoenix s nenulovou hodnotou perturbace
Obrázek 11: Odlišný pohled na Mandelbrotovu verzi fraktální množiny Phoenix s nenulovou hodnotou perturbace
Funkce, která provádí výpočet a překreslení Mandelbrotovy varianty tohoto fraktálu s nastavenou nenulovou hodnotou perturbace, může vypadat takto:
//-----------------------------------------------------------------------------
// Překreslení Mandelbrotovy verze fraktální množiny typu Phoenix s možností
// nastavení nenulové hodnoty perturbace
//-----------------------------------------------------------------------------
void recalcPhoenixMP(pixmap *pix, // pixmapa pro vykreslování
int maxiter, // maximální počet iterací
double scale, // měřítko obrazce
double xpos, // posun obrazce
double ypos,
double pcx, // nastavená hodnota perturbace
double pcy,
int palette, // barvová paleta
int rf, int gf, int bf) // příznaky barvových složek
{
double zx, zy, zx2, zy2, zxn, zyn; // složky komplexní proměnné Z a Z^2
double cx0, cy0;
double xmin, ymin, xmax, ymax; // rohy vykreslovaného obrazce v komplexní
double ynx, yny; // rovině
int x, y; // počitadla sloupců a řádků v pixmapě
int iter; // počitadlo iterací
unsigned char r, g, b;
calcCorner(xpos, ypos, scale, &xmin, &ymin, &xmax, &ymax);
cy0=ymin;
for (y=0; y<pix->height; y++) { // pro všechny řádky v pixmapě
cx0=xmin;
for (x=0; x<pix->width; x++) { // pro všechny pixely na řádku
zx=cx0+pcx; // nastavit počáteční hodnotu Z(0)
zy=cy0+pcy;
ynx=0.0; // nastavit počáteční hodnotu Y(0)
yny=0.0;
for (iter=0; iter<maxiter; iter++) {// iterační smyčka
zx2=zx*zx; // zkrácený výpočet druhé mocniny složek Z
zy2=zy*zy;
zxn=zx2-zy2+cx0+cy0*ynx;
zyn=2.0*zx*zy+cy0*yny;
ynx=zx;
yny=zy;
zx=zxn;
zy=zyn;
if (zx2+zy2>4) break;
}
iter++;
mapPalette(palette, iter, &r, &g, &b);
r=r*rf; // uživatelem řízené vynulování
g=g*gf; // vybraných barvových složek
b=b*bf;
putpixel(pix, x, y, r, g, b);
cx0+=(xmax-xmin)/pix->width; // posun na další bod na řádku
}
cy0+=(ymax-ymin)/pix->height; // posun na další řádek
}
}
7. Demonstrační příklad vykreslující množinu Phoenix ovlivněnou hodnotou perturbace
Funkce recalcPhoenixMP() je použita i v dnešním třetím demonstračním příkladu. Ovládání tohoto příkladu je shodné s příkladem druhým, jediný rozdíl spočívá v tom, že se v pravé části okna zobrazuje Mandelbrotova verze fraktální množiny Phoenix s hodnotou perturbace, která je vypočtena z pozice kurzoru myši. Screenshot ze třetího demonstračního příkladu je zobrazen na dvanáctém obrázku.
Obrázek 12: Screenshot třetího demonstračního příkladu s Mandelbrotovou verzí fraktální množiny Phoenix s nastavenou nenulovou hodnotou perturbace
8. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování tohoto seriálu dokončíme poměrně objemnou část celé série (o délce celých dvaceti dílů!) věnovanou fraktálním množinám počítaným v komplexní rovině. Rozebereme si další dosud nepopsané možnosti, jakými je možné urychlit výpočet bodů ležících vně či uvnitř těchto fraktálních množin. Také si ukážeme některé pokročilejší vykreslovací techniky, pomocí nichž je možné vytvářet zajímavé variace k obrázkům založených na vyčíslení počtu iterací nutných k rozhodnutí konvergence či divergence posloupnosti zi.