Fraktály v počítačové grafice XXX

Obsah

1. Úvodní informace o systémech iterovaných funkcí
2. Využití systémů iterovaných funkcí v počítačové grafice
3. Teorie systémů iterovaných funkcí
4. Algoritmus náhodné procházky
5. Matematický popis IFS systémů a práce s těmito systémy
6. Literatura
7. Odkazy na Internetu
8. Obsah dalšího pokračování tohoto seriálu

1. Úvodní informace o systémech iterovaných funkcí

V předchozích částech tohoto seriálu jsme se zabývali zejména popisem dynamických systémů s fraktální strukturou a velkou pozornost jsme přitom věnovali dynamickým systémům vytvářeným v komplexní rovině (mezi tyto systémy patří i známá Mandelbrotova množina, množiny Juliovy a také Newtonova fraktální množina). Od dnešní části se zaměříme na systémy iterovaných funkcí, které jsou v anglické literatuře označovány zkratkou IFS. Pozornost budeme věnovat především různým způsobům vytváření fraktálních obrazců pomocí systémů IFS a metodám pro výpočet pravděpodobnosti jednotlivých transformací v IFS systému, protože rozdělení pravděpodobností jednotlivých transformací má velký vliv na celkový počet operací, které je zapotřebí provést v průběhu vytváření koláže (tj. plošného obrazce IFS systému) či procedurálního modelu trojrozměrného tělesa. Také si popíšeme některé algoritmy používané pro generování koláží spolu s uvedením předností a záporů jednotlivých výpočetních postupů.

Název IFS systémů je odvozen z původního anglického označení Iterated Function System, česky lze tento název přeložit jako systém iterovaných funkcí. První publikace, které se týkaly IFS systémů, vydali už v roce 1985 Demko a následně pak v roce 1987 Michael Barnsley [L-1] [L-2] [L-3]. Tvorba obrázků pomocí IFS systémů patří mezi generativní metody vytváření fraktálů, kterou řadíme mezi metody deterministické (viz popsané metody pro vytváření fraktálních objektů v komplexní rovině, které byly stručně uvedeny v předchozích dílech tohoto seriálu). Algoritmus pro generování IFS fraktálů však může být jak deterministický, tak nedeterministický (tj. stochastický – viz v dalších dílech uvedený algoritmus RWA).

Obrázek 1: Dvojrozměrný IFS systém vykazující základní znak fraktálů – soběpodobnost

2. Využití systémů iterovaných funkcí v počítačové grafice

Systémy iterovaných funkcí tvoří velmi důležitou skupinu lineárních deterministických fraktálů, které mají v počítačové grafice více uplatnění. Jejich nejdůležitější aplikací je v současné době takzvaná fraktální komprimace (rastrových) obrazových dat, jejíž podrobnější popis je uveden v publikacích pana Barnsleyho [L-1] [L-2] [L-3] a kterou se samozřejmě ještě budeme zabývat. Jak už bylo napsáno v předchozím textu, první publikace o systémech IFS publikoval Demko v roce 1985 a Michael Barnsley v roce 1987. V obou publikacích, zejména však v publikaci druhé, autoři předkládají praktický návod, jak používat IFS pro generování rastrových textur s rozmanitým použitím. IFS se skutečně pro tuto činnost používají a to i v běžných aplikacích, kterými jsou například počítačové hry.

IFS systémy jsou implementovány v některých aplikacích, které slouží k tvorbě procedurálních modelů těles. Ve velkém množství případů se však jedná o pouhý podpůrný nástroj bez další návaznosti na celé trojrozměrné scény. Existuje také poměrně velké množství aplikací, které používají IFS systémy v rovině pro vytváření rastrových obrázků. Jedná se jak o specializované aplikace (FDesign, IFS CAD [L-8] [L-9]), tak i o nadstavby nad univerzálními grafickými editory – příkladem z oblasti GNU software může být plugin nazvaný IFS Composer, jenž je určen pro grafický editor GIMP.

V pozdější době se metoda uspořádání transformací do IFS systému ukázala jako mimořádně výhodná pro komprimaci dat rastrových obrázků zobrazujících reálné předměty, jelikož jedna transformace je v tomto případě zapsána pouze pomocí vektoru osmi čísel (šest reálných čísel na zapsání transformace a dvě reálná čísla na změnu kontrastu a jasu, což lze také považovat za transformaci, tentokrát však v barvové oblasti). Metodu IFS komprimace využívá mimo jiné i grafický formát FIF. V porovnání s ostatními grafickými formáty dosahuje většinou lepších výsledků nebo výsledků alespoň srovnatelných se ztrátovou metodou JPEG (komprimace pomocí IFS je také ztrátová metoda).

Grafický formát FIF se prozatím příliš nerozšířil, protože proces komprimace je stále příliš náročný na výpočetní výkon, zejména pro použití ve spotřební elektronice (digitální fotoaparáty, kamery, mobilní zařízení s CCD čipem atd.) – komprimace je totiž až o několik řádů pomalejší než zpětná dekomprimace. Dalším faktorem, který negativně ovlivnil rozšíření FIF, jsou patenty, které na tuto technologii (zejména na postup hledání transformací) vlastní Michael Barnsley a jeho spolupracovníci. Kvůli poplatkům za FIF se nakonec začaly masivně šířit jiné technologie využívající ztrátovou komprimaci, zejména se jedná o technologie založené na diskrétní kosinové transformaci (DCT – discrete cosinus transformation), použité u známého „formátu“ JPEG, a později také o metody využívající vlnkovou transformaci (WT – wavelet transformation). Určitě je škoda, že se FIF více nerozšířil, protože fraktální komprimace obrazů může v některých případech, například u fotek většiny přírodních objektů, nabízet lepší poměr kvality obrazu ku objemu dat, než „konkurenční“ diskrétní kosinová transformace popř. transformace vlnková.

Patent na komprimaci použitou v grafickém formátu typu FIF drží v současné době firma Iteration Systems, která také dodává hardwarové akcelerátory ve formě zásuvných karet do osobních počítačů typu IBM PC a Apple. Dříve se tyto karty připojovaly přes sběrnici ISA, dnes jde o mnohem kvalitnější a zejména rychlejší sběrnici PCI. Dekompresní algoritmy jsou dostatečně rychlé pro programovou implementaci a jsou (kupodivu) volně dostupné. Například pro HTML prohlížeč Netscape a jeho následovníky existuje zásuvný modul (plug-in) určený pro zobrazování rastrových obrázků komprimovaných metodou FIF. Velkou výhodou tohoto formátu je možnost zobrazení obrázku ve velkém zvětšení bez viditelné ztráty kvality. To představuje znatelný rozdíl oproti JPEG komprimaci, kde je při velkém zvětšení jasně viditelné rozdělení rastrového obrázku na bloky 8×8 resp. 16×16 pixelů, které se samostatně transformují pomocí DCT.

Třetí možností, kde lze v počítačové grafice využít systémy IFS, je procedurální konstrukce třídimenzionálních objektů, například stromů či rostlin, s následnou možností jejich vizualizace či animace. V této oblasti se využívají jak systémy IFS, tak i dále popsané L-systémy. Každá z těchto metod pro vytváření fraktálních obrazců se hodí pro jiný účel. Pomocí L-systémů lze vytvářet polygonové objekty nabízející možnost dalšího zpracování v CAD systémech či jejich vykreslování pomocí současných grafických akcelerátorů, například přes knihovnu OpenGL. Pomocí IFS systémů se naopak vytvoří jednotlivé pixely v rovině či body v prostoru. Body rozmístěné v prostoru lze pro účely dalšího zpracování a následného zobrazení na obrazovce považovat buď za neorientované částice (particles) nebo za prostorově orientované elementární plošky – surfely (surface element).

Obrázek 2: 3D scéna vytvořená pomocí IFS systémů

3. Teorie systémů iterovaných funkcí

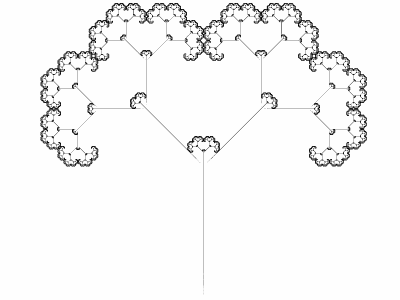
V předchozích částech tohoto seriálu (zejména v úvodních dílech) bylo řečeno, že soběpodobnost je hlavním znakem většiny fraktálních útvarů. Pokud je fraktál soběpodobný, můžeme najít zobrazení, které transformuje (mapuje) celek na jednotlivé části. Iterace tohoto zobrazení má za výsledek konvergenci k atraktoru fraktálu. Systémy iterovaných funkcí jsou z matematického hlediska vlastně množiny několika zobrazení (resp. v rovině R² či prostoru R³ transformacemi x->F(x); tyto transformace jsou většinou afinní). Celý IFS fraktál je poté popsán množinou několika zobrazení (transformací), které budeme označovat symboly φ₁ až φ_n. Většinou se jedná o lineární transformace, tj. změnu měřítka, posun, rotaci a zkosení, v některých případech se však používají i transformace nelineární, jakými jsou ohyb, zkrut, zborcení apod. Ve čtvrté kapitole bude stručně popsán algoritmus náhodné procházky, matematickým popisem systémů IFS se budeme věnovat v kapitole páté.

Obrázek 3: Další známý dvojrozměrný soběpodobný IFS systém – Sierpinského trojúhelník

4. Algoritmus náhodné procházky

Princip generování IFS fraktálu je v nejjednodušším případě založený na takzvaném algoritmu náhodné procházky, který iterativně provádí následující výpočet: na bod P_iter, který se nachází v rovině R² nebo v prostoru R³, jsou buď deterministicky nebo náhodně (oním algoritmem náhodné procházky) aplikovány jednotlivé transformace φ_n. Výsledkem je nová pozice bodu P_iter+1. IFS fraktál je poté zobrazen jako koláž složená ze všech vygenerovaných bodů P_i, i=(1..maxiter).

Před vlastním generováním je zapotřebí určit počáteční pozici startovního bodu P₀. V předchozí sekci bylo řečeno, že všechny transformace jsou zároveň i transformacemi změny měřítka s koeficientem menším než 1 – jde tedy o kontrahující transformace zajišťující směřování systému ke svému atraktoru. Proto je možné pozici startovního bodu P₀ zvolit libovolně, protože po několika počátečních iteracích se díky kontrahujícím transformacím posloupnost generovaných bodů P_i samovolně dostane do atraktoru IFS. Většinou se volí P₀=[0, 0] v rovině R² resp. P₀=[0, 0, 0] v prostoru R³.

Transformace, které se budou v daném iteračním kroku aplikovat na bod P_i, lze vybírat buď deterministicky, nebo náhodně. Rozbory obou těchto metod a jejich různých variant budou uvedeny v dalším textu. Na čtvrtém obrázku jsou zobrazeny ukázky IFS fraktálů generovaných algoritmem náhodné procházky (random walk). Na obrázku pátém je zobrazena třídimenzionální scéna, která je sestrojena pouze z IFS fraktálů. Na vysvětlení, proč algoritmus náhodné procházky funguje, si musíme počkat do dalšího pokračování tohoto seriálu.

Obrázek 4: Ukázka dvojrozměrných IFS systémů

Obrázek 5: 3D scéna vygenerovaná pomocí IFS

5. Matematický popis IFS systémů a práce s těmito systémy

Při matematickém popisu systémů iterovaných funkcí IFS se vychází z matematické teorie pevných bodů (fixed points). Celá tato teorie, která se ostatně objevuje v jiném kontextu i v teoretické informatice, je ve své podstatě aplikací věty o Banachově pevném bodu:

Nechť U je metrický prostor s metrikou d. Dále, nechť f je funkce mapující množinu A na množinu U:

f: A → U

přičemž A je podmnožinou množiny U.

Jestliže dále pro funkci f existuje bod x₀ takový, že platí:

f(x₀)=x₀

tj. bod x₀ je funkcí f mapován na sám sebe, pak se bod (jsme v metrickém prostoru) x₀ nazývá pevný bod. Pro funkci f s existujícím pevným bodem x₀ platí mimo jiné i následující věta:

Jestliže je množina A podmnožinou množiny U a f je taková funkce, která mapuje množinu A do sebe sama (tj.  f: A → A), přičemž existuje určitá konstanta δ (nazývaná kvůli své geometrické interpretaci kontrakční faktor), pro kterou platí 0<δ<1, potom:

d[f(x), f(y)]<=δd[x,y]

a funkce f se nazývá kontrakce.

Poznámka: symbol d v našem případě znamená vzdálenost, ať už jakkoliv definovanou. Z toho mimo jiné vyplývá, že IFS systémy mohou být definovány nad jakýmkoliv prostorem, který má definován pojem vzdálenosti. Například pro Euklidovu metriku platí:

d=(x_n²+y_n²)^-2

Pomocí vektoru kontrakcí a vektoru pravděpodobností (ten si popíšeme příště) je možné popsat celý IFS systém, a to v jakémkoli metrickém prostoru, včetně roviny R² či trojrozměrného prostoru R³. Podrobnější výklad takto pojatého IFS systému bude uveden v dalším pokračování tohoto seriálu.

Obrázek 6: Pomocí množiny kontrakcí o poměrně malém počtu prvků je možné sestrojit i takovýto soběpodobný nápis

6. Literatura

[L-1] Barnsley Michael: ''Fractals Everywhere '',
        Academic Press Inc., 1988, ISBN 0–12–079062–9

[L-2] Barnsley Michael, Devaney R. L., Mandelbrot Benoit B., Peitgenn Heinz-Otto, Saupe Dietmar, Voss Richard: ''The Science of Fractal Images '',
        Springer-Verlag, New York, 1988

[L-3] Barnsley Michael, Hurd Lyman P.: ''Fractal Image Compression '',
        A. K. Peters, 1993

[L-4] Bowman Richard L.: ''Fractal Metamorphosis: A Brief Student Tutorial '',
        Computer and Graphics, 19, strany 157–164, 1995

[L-5] Gröller Eduard: ''Interactive design of Nonlinear Functions for Iterated Function System '',
        Technical University Vienna, 1995

[L-6] Lauwerier Hans: ''Fractals '',
        Princeton University Press, 1991

[L-7] Peitgen Heinz-Otto, Jurgens Hartmut, Saupe Dietmar: ''Fractals For The Classroom '',
        Springer-Verlag, New York, 1988

[L-8] Tišnovský Pavel: ''Návrh editoru IFS '',
        Vysoké učení technické v Brně, Fakulta elektrotechniky a informatiky, 1998

[L-9] Tišnovský Pavel: ''Interaktivní editor afinních transformací '',
        Vysoké učení technické v Brně, Fakulta elektrotechniky a informatiky, 1999

[L-10] Wegner Timothy, Peterson Mark: ''Fractal Creations, First Edition '',
        The Waite Group Press, 1991

[L-11] Wegner Timothy, Tyler Bert: ''Fractal Creations, Second Edition '',
        The Waite Group Press, 1993

[L-12] Wegner Timothy, Tyler Bert, Peterson Mark, Branderhorst Pierer: ''Fractals for Windows '',
        The Waite Group Press, 1992

[L-13] Žára J., Beneš B., Felkel P.: ''Moderní počítačová grafika '',
        Computer Press, Praha, 1998, ISBN 80–7226–049–9

[L-14] Žára J., Limpouch A., Beneš B., Werner T.: ''Počítačová grafika – principy a algoritmy '',
        Grada, 1992

Obrázek 7: Ukázka nelineárního 3D IFS systému, viz [I-13]

7. Odkazy na Internetu

[I-1] Taylor Michael Charles: ''Frequently Asked Questions about Fractals '',
        http://spanky­.triumf.ca/pub/frac­tals/docs/SCI_FRAC­TALS.FAQ   (2.5.2005)

[I-2] Giffin Noel a kol.: ''The Spanky Fractal Database '',
        http://spanky­.triumf.ca/   (2.5.2005)

[I-3] Tyler Bert, Wegner Tim a kol.: ''Fractint (fractal generator for DOS) '',
        http://www.frac­tint.org   (2.5.2005)

[I-4] Letbetter Jason: ''Set Surfer '',
        http://www.flash­.net/~redbeard   (2.5.2005)

[I-5] Chardonnet David: ''IFS Fractals Digital Encyclopedy '',
        http://www.chez­.com/fractals/ga­leries/gb_index­.html   (2.5.2005)

[I-6] Bowman Richard L.: ''IFS Fractal Generation Exercise '',
        http://www.brid­gewater.edu/de­partments/phy­sics/ISAW/Frac­talGenEx.html   (2.5.2005)

[I-7] Devaney Bob: ''Dynamical systems and Iterated Function Systems '',
        http://math.bu­.edu/people/bob/   (2.5.2005)

[I-8] Freeland Graham C., Durrani Tariq S.: ''An Introduction to Multiscale Defined Systems: Self-Organising IFS Fractal Networks '',
        http://www.spd­.eee.strath.ac­.uk/users/gcf/pa­pers/icassp98fsp­.pdf   (2.5.2005)

[I-9] Pulcini, Verrando, Meloni Rossi: ''IFS: Fractal Image Compression '',
        http://mathfo­rum.org/libra­ry/view/6165.html   (2.5.2005)

[I-10] Lartigue Ghislain: ''Hydrodynamical Instabilities: The Iterative Function System '',
        http://www.en­seeiht.fr/hmf/tra­vaux/CD9900/tra­vaux/optmfn/hi/00pa­/mfn11/pa01.htm   (2.5.2005)

[I-11] Henstridge James: ''What is an IFS fractal '',
        http://www.da­a.com.au/~james/frac­tals/ifs/intro­.html   (2.5.2005)

[I-12] Pulcini Giovambattista: ''Fractal Image Compression Software (for Windows) '',
        http://www.ve­rrando.com/pul­cini/gp-ifs1.html   (2.5.2005)

[I-13] Thornton Sterling: ''XenoDream (Interactive IFS Editor) '',
        http://xenodre­am.com   (2.5.2005)

Obrázek 8: Další nelineární IFS systém

8. Obsah dalšího pokračování tohoto seriálu

I v následujícím pokračování tohoto seriálu budeme pokračovat v popisu systémů iterovaných funkcí. Popíšeme si způsob vytvoření základního obrazce a jeho následného pokrytí jeho menšími kopiemi. Dále si ukážeme některé způsoby výpočtu pravděpodobností jednotlivých transformací, což je důležitá informace, která se používá především pro urychlení algoritmu náhodné procházky.