Obsah
1. Význam řídicích bodů Ci a poměru dělení úsečky ξ na tvar vytvářeného objektu
2. Postup specifikace parametrů systémů L-IFS
3. Matice posloupnosti transformací
4. Test korektnosti matice posloupnosti transformací
5. Algoritmus výběru dalšího řídicího bodu posloupnosti
6. Interaktivní vytváření obrazců pomocí linearizovaných systémů iterovaných funkcí
7. Demonstrační aplikace pro vytváření fraktálů pomocí L-IFS systémů
8. Algoritmy použité v demonstrační aplikaci
9. Obsah dalšího pokračování tohoto seriálu
1. Význam řídicích bodů Ci a poměru dělení úsečky ξ na tvar vytvářeného objektu
Pomocí množiny řídicích bodů C={C1,… Cn} se určuje zejména konvexní obálka, ve které je umístěn atraktor generovaného fraktálního obrazce. Vzhledem k tomu, že každá (byť nepřímo zadaná) transformace v systému L-IFS je kontrahující (vzdálenost libovolných dvou nestejnolehlých bodů se po provedení transformace zmenší), je zaručena soběpodobnost generovaného obrazce či objektu. Díky této soběpodobnosti se tvar obálky v obrazci opakuje v nekonečném počtu kopií, které se od sebe liší pouze svým měřítkem.
Na tvar generovaného obrazce má přímý vliv i volba poměru dělení úsečky ξ. Zatímco změna polohy řídicího bodu Ci měla za následek pouze lokální změny ve výsledném obrazci (které se však díky soběpodobnosti v obrázku opakují v menších detailech), má změna hodnoty ξ význam globální, protože se podle něj mění těsnost vazby generovaných bodů k atraktoru systému. Parametr ξ musí, jak již víme z předchozí části tohoto seriálu, nabývat hodnot v rozsahu (0, 1), protože jen v tomto rozsahu je zaručeno, že každá prováděná transformace bude současně transformací kontrahující.
Pro hodnoty ξ>1/2 a libovolný bod P0 platí, že po několika iteracích (řádově se jedná o desítky iterací v závislosti na poloze bodu P0 vůči atraktoru) systém konverguje ke svému atraktoru. Prováděním dalších iterací se nové body tvoří pouze uvnitř tohoto atraktoru. Konvergence systému k atraktoru je zaručena díky faktu, že v každé iteraci se zkracuje průměrná vzdálenost bodu Piter od řídicích bodů Ci o poměr ξ. Pro hodnoty ξ<1/2 je sice zaručena konvergence systému, protože generovaná posloupnost bodů Pi leží uvnitř konvexního obalu sestaveného z řídicích bodů C, ale výsledný tvar atraktoru není ve vygenerovaném objektu patrný.

Obrázek 1: Systém L-IFS zadaný pomocí šesti řídicích bodů
2. Postup specifikace parametrů systémů L-IFS
Postup aplikovaný při interaktivním zadávání parametrů fraktálních obrazců (koláží) pomocí linearizovaného systému iterovaných funkcí je poměrně jednoduchý a lze ho popsat v několika bodech:
- Uživateli se zobrazí předem definovaný obrazec, který se skládá z několika řídicích bodů Ci. Poloha těchto bodů je zadána buď v E2 (rovinné obrazce v Euklidově rovině), nebo v E3 (prostorové objekty v třírozměrném prostoru). Řídicí body mohou být pro větší přehlednost navzájem propojeny úsečkami.
- Uživatel má možnost interaktivně měnit polohu řídicích bodů Ci. Polohu bodů je vhodné zadávat v interaktivním grafickém editoru s možností zpětné editace. Editor by také měl pro větší komfort umožnit přidávat a ubírat řídicí body.
- Posléze uživatel, například pomocí posuvníku (scrollbaru), zadá poměr dělení úsečky ξ v rozsahu (0, 1), volba krajních bodů intervalu není povoleno. Vzhledem k velkému vlivu tohoto poměru na charakter generovaného objektu je žádoucí, aby se změna ihned promítla do vykreslované scény. Je také možné zadávat poměr dělení úsečky nezávisle v jednotlivých osách (ξx, ξy), čímž lze dosáhnout další variability vykreslovaných tvarů.
- Uživatel (opět pomocí scrollbaru) specifikuje maximální počet iterací itermax a počet startovních iterací iterstart (popř. lze ponechat automatické nastavení na aplikaci).
- Program následně vykreslí výslednou L-IFS koláž a umožní uživateli modifikovat všechny parametry generování (tj. opakování bodů 2–4).
Řídicí body Ci určují hranici, ve které se nachází atraktor celého systému. Poměr dělení úsečky ξ udává, ve kterém místě bude vytvořen nový bod Piter+1. Poloha tohoto nového bodu závisí na vybraném řídicím bodu Ci a na poloze předchozího bodu Piter:
Piter+1=ξ×Ci + (1-ξ)×Piter
Nový bod tedy leží na úsečce u=PiterCi. Parametr ξ určuje poměr, podle kterého je úsečka rozdělena. Na místě tohoto rozdělení leží nový bod Piter+1.

Obrázek 2: Systém L-IFS ve tvaru sněhové vločky
3. Matice posloupnosti transformací
V této části článku si popíšeme rozšíření L-IFS systémů o takzvanou matici posloupnosti transformací. Vytvořením a následnou editací této matice může uživatel radikálně změnit tvar výsledného obrazce. Pro interaktivní práci je důležité, že změna matice může probíhat s okamžitou zpětnou odezvou systému (překreslením obrazce).
Pomocí matice posloupnosti transformací lze povolit nebo naopak zakázat určité posloupnosti výběru transformací (resp. posloupnosti řídicích bodů Ci, protože vybraný řídicí bod přímo určuje transformaci která se má s body Piter provést). V předchozí části tohoto seriálu jsme si popsali základní systém L-IFS, ve kterém mohly být transformace prováděny v libovolném pořadí. Příklad takového systému je zobrazen na následujícím obrázku. Zobrazený systém obsahuje tři řídicí body C1, C2 a C3. Transformace specifikované výběrem řídicích bodů se mohou provádět v libovolném pořadí, což je naznačeno orientovanými šipkami.
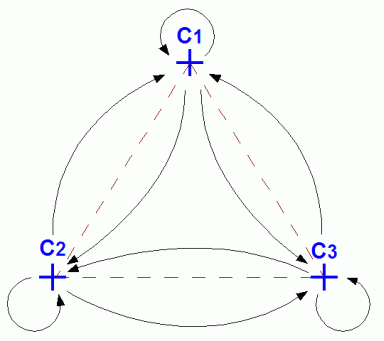
Obrázek 3: Ukázka systému L-IFS, ve kterém jsou povoleny všechny kombinace transformací
Předchozí obrázek lze chápat i jako zobrazení orientovaného grafu (orgrafu), kde uzly odpovídají řídicím bodům Ci a orientované hrany určují možnou posloupnost výběru těchto řídicích bodů. Konfiguraci orientovaného grafu lze popsat takzvanou maticí sousednosti. Tato matice má rozměr n × n, kde n je počet řídicích bodů. Prvky matice vrcholů mají hodnotu buď 0 nebo 1. Pokud má prvek matice aij hodnotu rovnu jedné, znamená to, že existuje orientovaná hrana z vrcholu i do vrcholu j. Pokud má naopak tento prvek hodnotu nulovou, orientovaná hrana v daném grafu neexistuje. Grafu zobrazeném na prvním obrázku odpovídá matice sousednosti s rozměry 3 × 3, jejíž všechny prvky mají hodnotu 1.
V případě systémů L-IFS budeme matici sousednosti podle jejího konkrétního významu nazývat maticí posloupnosti transformací. Tato matice bude mít rozměry n × n, kde n je počet řídicích bodů systému. Pokud má prvek matice aij hodnotu rovnou 1, lze pro transformace vybrat posloupnost řídicích bodů (Ci, Cj). Pokud má tento prvek hodnotu nulovou, nelze posloupnost (Ci, Cj) vybrat – druhý řídicí bod musí být odlišný od Cj. Příklad systému L-IFS s maticí posloupnosti transformací, kde jsou některé posloupnosti transformací zakázány, je zobrazen na čtvrtém obrázku.
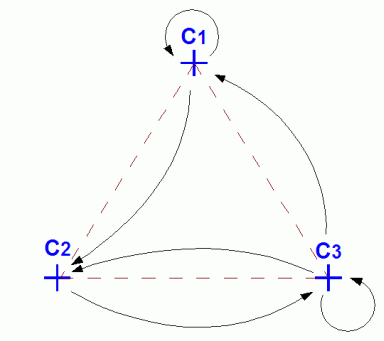
Obrázek 4: Ukázka systému L-IFS, který má zakázány některé posloupnosti transformací
Na matici posloupnosti transformací klademe určitá omezení. Prvním omezením je, že by neměl existovat takový řídicí bod, do kterého nevedou žádné orientované hrany. Tento řídicí bod by se na generování fraktálu podílel maximálně v jedné iteraci a to pouze v případě, že by byl vybrán již v první iteraci. V dalších iteracích tento bod vzhledem k funkci matice nemůže být nikdy vybrán. Příklad systému L-IFS, jenž obsahuje bod, do kterého nevedou žádné orientované hrany, je zobrazen na následujícím obrázku. Inkriminovaný bod C1 je vyznačen červenou barvou.

Obrázek 5: Ukázka systému L-IFS, který obsahuje bod (C1), do kterého nevedou žádné orientované hrany
Druhým omezením kladeným na matici posloupnosti transformací je, aby neexistoval žádný řídicí bod, ze kterého by nevedly žádné orientované hrany. Takový řídicí bod by zapříčinil zacyklení běhu algoritmu, protože po dosažení tohoto bodu by již neexistovala žádná povolená posloupnost transformací. Interaktivní aplikace, pomocí které se konstruují a vykreslují systémy L-IFS, by měla takovou skutečnost detekovat a vyzvat uživatele ke změně parametrů modelu, aby nedošlo k nekonečné smyčce. Příklad systému L-IFS, který obsahuje bod, ze kterého nevedou žádné orientované hrany, je zobrazen na čtvrtém obrázku. Inkriminovaný bod C2 je opět vyznačen červenou barvou.

Obrázek 6: Ukázka systému L-IFS, který obsahuje bod (C2), ze kterého nevedou žádné orientované hrany
Nyní již zbývá popsat algoritmus testu korektnosti matice posloupnosti transformací (detekce bodu, ze kterého nevedou žádné orientované hrany) a algoritmus výběru dalšího řídicího bodu posloupnosti s ohledem na aktuální obsah matice posloupnosti transformací.
4. Test korektnosti matice posloupnosti transformací
Nejprve si slovně popišme, jakým způsobem algoritmus pracuje. Cílem algoritmu je najít takové uzly v orientovaném grafu, ze kterých nevedou žádné orientované hrany. Tyto uzly se v matici posloupnosti transformací projeví sloupcem se samými nulami. Algoritmus tedy v matici posloupnosti transformací jednoduše detekuje tyto sloupce a pokud alespoň jeden takový sloupec najde, ukončí svůj běh. Poznamenejme, že dále uvedený algoritmus nebude detekovat všechny případy, kdy graf není tranzitivní. Pro tyto případy je možné použít konstrukci tranzitivního uzávěru grafu, například pomocí Warnockova algoritmu.
- vstupní data: matice posloupnosti transformací – prvky aij
- výstupní data: pravdivostní hodnota true, pokud je matice posloupnosti transformací v pořádku, jinak hodnota false
- proveď smyčku s počitadlem i pro všechny sloupce matice
- nastav proměnnou columnOK na hodnotu false
- proveď smyčku s počitadlem j pro všechny prvky v daném sloupci
- pokud je prvek aij roven 1, nastav columnOK na true
- konec vnitřní smyčky
- pokud je columnOK rovno false konec algoritmu s návratovou hodnotou false
- konec vnější smyčky
- konec algoritmu s návratovou hodnotou true
Implementace tohoto algoritmu v programovacím jazyce Java může vypadat například následovně:
boolean isTransformationMatrixValid() {
boolean columnOK;
for (int i=0; i<activeVertexes; i++) {
columnOK=false;
for (int j=0; j<activeVertexes; j++)
if (matrix[i][j]==1) columnOK=true;
if (!columnOK) return false;
}
return true;
}
5. Algoritmus výběru dalšího řídicího bodu posloupnosti
Pro výběr dalšího řídicího bodu Ci je možné použít následující postup:
- vstupní data: matice posloupnosti transformací (prvky aij), seznam řídicích bodů Ci a číslo řídicího bodu vybraného v předchozí iteraci oldPoint
- výstupní data: číslo dalšího řídicího bodu posloupnosti newPoint
- začátek smyčky
- vygeneruj náhodné číslo v rozsahu 0..n, kde n je počet řídicích bodů, číslo ulož do proměnné newPoint
- pokud je prvek a(oldPoint newPoint) roven 1, konec s návratovou hodnotou newPoint
- opakuj smyčku od bodu 4
- konec algoritmu
Implementace tohoto algoritmu v programovacím jazyce Java může vypadat například následovně:
Random r=new Random(0);
do {
newPoint=(int)(r.nextDouble()*activeVertexes);
} while (!matrix[oldPoint][newPoint]);
return newPoint; Na následujícím obrázku jsou zobrazeny L-IFS fraktály, které se liší pouze obsahem matice posloupnosti transformací.
Obrázek 7: Ukázka systémů L-IFS, které se liší pouze obsahem matice posloupnosti transformací
6. Interaktivní vytváření obrazců pomocí linearizovaných systémů iterovaných funkcí
V úvodu tohoto článku jsme napsali, že pro úspěšné používání IFS systémů za účelem generování koláží (například dekorativní či umělecká činnost) je důležitá názornost zadávání parametrů a interaktivita. Názornost znamená, že uživatel by měl intuitivně dopředu odhadnout výsledek operací, které se při editaci IFS provádí. Interaktivitou je zde myšlena okamžitá zpětná odezva systému na požadavky uživatele.
Zavedení systémů L-IFS umožnilo splnit oba požadavky. Názornost je dosažena zejména způsobem editace řídicích bodů. Řídicí body Ci přímo ovlivňují tvar atraktoru generovaného L-IFS systému. Při každé změně polohy některého z řídicích bodů lze ihned provést přepočet výsledného obrazce. I na výpočetně slabších počítačích platformy PC, které se dnes běžně používají (frekvence procesoru cca 800 MHz, kapacita RAM 128 MB), lze již dosáhnout uspokojivé rychlosti výpočtu. Je možné například vygenerovat pouze tisíc bodů, jejichž počet je dostatečný pro získání základního přehledu o tvaru výsledného fraktálu. Vykreslení tohoto tisíce bodů by nemělo trvat déle než 50ms, aby byla dosažena snímková frekvence (FPS) alespoň 20Hz, která je pro interaktivní práci již uspokojivá.
Druhý způsob interakce se systémem, tedy úprava matice posloupnosti transformací, již není pro uživatele tak přímočará jako editace řídicích bodů. Po určité praxi je však uživatel schopen dopředu odhadnout výsledek změny této matice na tvar výsledného obrazce. I zde musí být samozřejmě zajištěna interaktivita, kdy se po každé změně matice přepočítá výsledný obrazec.
Pro ilustraci interaktivní editace systémů L-IFS jsme (autor tohoto článku a Petr „Pety“ Petyovský) vytvořili demonstrační aplikaci, která může být spuštěna přímo v okně internetového prohlížeče. Tato aplikace pracuje jako takzvaný applet a je naprogramována v jazyce Java. V další kapitole bude popsáno ovládání této aplikace.
7. Demonstrační aplikace pro vytváření fraktálů pomocí L-IFS systémů
Dnešní demonstrační aplikace, která se od všech předchozích aplikací liší tím, že je vytvořená v Javě a nikoli v Céčku, slouží k vytváření, editaci a následnému zobrazení plošných fraktálních objektů generovaných pomocí linearizovaných systémů iterovaných funkcí (L–IFS). Aplikace je z důvodu maximálního zjednodušení a zpřehlednění upravena tak, že vytváří fraktální objekty pouze v rovině E2 s tím, že rozšíření do prostoru E3 (či pro speciální případy i do dalších rozměrů) je možné provést mírnou modifikací generujícího algoritmu a současně úplným přepisem funkce pro vykreslení jednotlivých bodů (viz další pokračování tohoto seriálu).
Ukázka grafického uživatelského rozhraní (GUI) tohoto demonstračního příkladu i s vytvořeným fraktálním obrazcem je uvedena na dalším obrázku, zdrojový kód si můžete prohlédnout či stáhnout z této stránky.
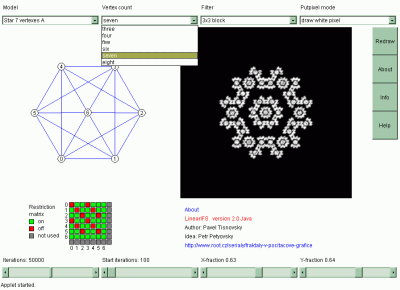
Obrázek 8: Ukázka grafického uživatelského rozhraní demonstračního příkladu
Vzhledem k určitým omezením, která jsou kladena na grafická uživatelská rozhraní appletů, je celá aplikace tvořena jednou pracovní plochou rozdělenou do několika částí. Na jednotlivých částech jsou umístěny ovládací prvky grafického uživatelského rozhraní. Pracovní plocha aplikace může být zobrazena přímo na ploše WWW stránky v internetovém prohlížeči – to znamená, že se nevytváří žádná další okna ani dialogy. Alternativně lze použít prohlížeč appletů AppletViewer, který je dodávaný k některým vývojovým prostředím založeným na jazyku Java a také k Sunovskému JDK.
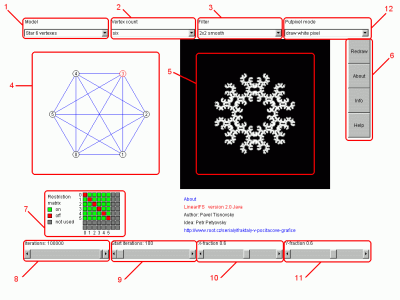
Obrázek 9: Ovládací prvky demonstračního příkladu
Následuje vysvětlující text k jednotlivým ovládacím prvkům, které jsou očíslovány podle devátého obrázku:
- Z výběrového seznamu (list boxu) Model lze vybrat jeden z předdefinovaných L–IFS systémů. Výběrem se změní poloha řídicích bodů Ci, počet aktivních řídicích bodů n, prvky matice posloupnosti transformací A, poměry dělení úseček ξx, ξy a mezní hodnoty iterací iterstart a itermax.
- Pomocí výběrového seznamu Vertex count lze změnit počet aktivních řídicích bodů. Aplikace umožňuje práci s minimálně třemi řídicími body, maximálně s body osmi.
- Z výběrového seznamu Filter lze vybrat jeden konvoluční filtr, který se aplikuje na výsledný rastrový obrázek s fraktálem. Tento filtr vždy provede rozmazání obrazu, čímž lze vizuálně vylepšit výsledný fraktál, neboť přestanou být patrné jednotlivé body či pixely vygenerované algoritmem pro vytváření L–IFS systému. Jméno filtru udává velikost a tvar konvoluční masky. Čím větší je maska, tím větší rozmazání výsledného obrazu se provede. Následuje popis jednotlivých druhů filtrů:
- 2×2 smooth: konvoluční filtr s velikostí konvolučního jádra 2×2 pixely a s konstantními váhami všech jeho koeficientů, které mají shodnou hodnotu 1/4. Součet vah všech koeficientů dává hodnotu 1, stejně jako i u všech následujících filtrů.
- 3×3 diamond: konvoluční filtr s velikostí konvolučního jádra 3×3 pixely, kde nenulové koeficienty tvoří tvar diamantu. Tyto koeficienty (jež jsou čtyři) mají hodnotu 1/4, ostatní koeficienty jsou nulové.
- 3×3 cross: konvoluční filtr s velikostí konvolučního jádra 3×3 pixely, kde nenulové koeficienty tvoří tvar osového kříže. Těchto pět koeficientů má hodnotu 1/5, ostatní koeficienty jsou nulové.
- 3×3 X-cross: konvoluční filtr s velikostí konvolučního jádra 3×3 pixely, kde nenulové koeficienty tvoří úhlopříčný kříž. Těchto pět koeficientů má hodnotu 1/5, ostatní koeficienty jsou nulové, podobně jako u předchozího typu filtru.
- 3×3 block: konvoluční filtr s velikostí konvolučního jádra 3×3 pixely s hodnotami všech koeficientů nastavenými na 1/9.
- 5×5 diamond: konvoluční filtr s velikostí konvolučního jádra 5×5 pixelů, kde nenulové koeficienty tvoří tvar diamantu. Tyto koeficienty, jichž je osm, mají hodnotu 1/8, ostatní koeficienty mají hodnotu nulovou.
- 5×5 cross: konvoluční filtr s velikostí konvolučního jádra 5×5 pixelů, kde nenulové koeficienty tvoří tvar osového kříže. Tyto koeficienty, kterých je celkem devět, mají hodnotu 1/9, ostatní koeficienty mají hodnotu opět nulovou.
- 5×5 X-cross: konvoluční filtr s velikostí konvolučního jádra 5×5 pixelů, kde nenulové koeficienty tvoří úhlopříčný kříž. Tyto koeficienty mají hodnotu 1/9, ostatní koeficienty mají hodnotu nulovou, podobně jako u předchozího typu filtru.
- 5×5 block: konvoluční filtr s velikostí konvolučního jádra 5×5 pixelů, kde všechny koeficienty mají váhu rovnou hodnotě 1/25.
- 3 pixels horizontal: konvoluční filtr s velikostí konvolučního jádra 3×1 pixel. Všechny koeficienty mají váhu rovnou 1/3. Maska tohoto filtru je orientována vodorovně, zvýrazňuje tedy horizontální směry v obraze.
- 5 pixels horizontal: konvoluční filtr s velikostí konvolučního jádra 5×1 pixel. Všechny koeficienty mají váhu rovnou hodnotě 1/5.
- 3 pixels vertical: konvoluční filtr s velikostí konvolučního jádra 1×3 pixely. Všechny koeficienty mají váhu rovnou hodnotě 1/3. Maska tohoto filtru je orientována svisle, zvýrazňuje tedy vertikální směry v obraze.
- 5 pixels vertical: konvoluční filtr s velikostí konvolučního jádra 5×1 pixel. Všechny koeficienty mají váhu rovnou hodnotě 1/5.
- V této pracovní oblasti lze měnit polohu řídicích bodů, čímž se změní i tvar atraktoru vytvářeného linearizovaného systému iterovaných funkcí L–IFS. Změna polohy se provede přesunutím některého z řídicích bodů se stlačeným levým tlačítkem myši. Při změně polohy bodu se v oblasti 5 provádí rychlé překreslení s malým počtem iterací.
- Zde se zobrazuje vygenerovaný fraktální obrazec (tj. atraktor systému L–IFS). Jedná se o rastrový obraz (pixmapu) s pevně nastavenými rozměry 384×384 pixelů, který zobrazuje pixely v 256ti stupních šedi.
- Na pravé straně plochy aplikace se nachází několik tlačítek (buttons), které slouží k překreslení fraktálu (tlačítko Redraw) a k zobrazení různých informativních textů o běžící aplikaci (tlačítka About, Info a Help). Informativní texty jsou zobrazeny pod pixmapou (rastrovým obrázkem) s fraktálním obrazcem.
- V této tabulce lze interaktivně měnit prvky matice posloupnosti transformací aij. Změna se provede kliknutím levého tlačítka myši na daném prvku. Zelená barva značí, že prvek má hodnotu 1 (povolená transformace), červená barva značí prvek s hodnotou 0 (zakázaná transformace).
- Na spodní části plochy demonstrační aplikace se nachází několik posuvníků (sliders). Posuvníkem umístěným po levém okraji lze měnit maximální počet iterací – itermax. Čím větší je počet iterací, tím větší počet bodů bude ve výsledném obrazci vygenerován. S rostoucím počtem iterací však roste i výpočetní čas na jeden snímek. Při interaktivní práci (například posunu řídicích bodů) se vždy generuje a zobrazuje pouze tisíc bodů a neprovádí se filtrace.
- Zde lze měnit počet startovních iterací – iterstart. První iterace probíhají „naprázdno“ – bez zobrazování bodů. Až po dosažení zadaného počtu startovních iterací je prováděno vykreslování vypočtených bodů. Malý počet startovních iterací může mít za příčinu vykreslení bodů které neleží v atraktoru systému. Příliš velký počet startovních iterací zbytečně zpomaluje výpočet a na tvar výsledného obrazce nemá prakticky žádný výraznější vliv. Počet startovních iterací by proto neměl v praxi přesáhnout hodnoty 1000.
- Posuvníkem X-fraction lze měnit poměr dělení úsečky ve směru x-ové osy – ξx, který musí ležet v rozsahu (0, 1). Čím je tato hodnota vyšší (blíží se k 1), tím více se budou vygenerované body přimykat k řídicím bodům.
- Ovládací prvek Y-fraction má podobnou funkci jako prvek předchozí s tím rozdílem, že se mění poměr dělení úsečky ve směru y-ové osy – ξy.
- Nakonec je možné zvolit způsob vykreslování jednotlivých pixelů. Buď se pixel vykreslí bílou barvou (na černém pozadí), nebo se zvýší jeho intenzita o zadanou hodnotu.
Překlad této aplikace se provádí pomocí překladače jazyka Java do bytekódu virtuálního stroje jazyka Java. V průběhu vývoje aplikace jsem používal překladač, který je dodávaný s vývojovým prostředím JavaTM 2 SDK, Standard Edition ve verzi 1.4.1, je však možné použít i jiné překladače (včetně jikes apod.). Pro překlad je nutné zadat následující příkaz:
javac LinearIFS.java Po úspěšném překladu vznikne soubor LinearIFS.class, který lze spustit buď otevřením příslušné stránky s odkazem v internetovém prohlížeči, nebo pomocí programu AppletViewer následovně:
appletviewer LinearIFS.html Pro bezproblémové spuštění této aplikace je zapotřebí, aby byla korektně nainstalován a povolen JRE (Java Runtime Environment). Pokud se aplikace nespustí korektně, je nutno buď povolit používání JVM, nebo JVM doinstalovat. Instalaci JRE lze (spolu s JDK) provést například ze stránek firmy Sun Microsystems (http://java.sun.com/).
Pokud je použita starší JVM veze 1.0 či 1.1 (starší prohlížeče), je nutné při překladu aplikace specifikovat verzi používané JVM:
javac -target 1.1 LinearIFS.java Výsledný bytekód, zejména jeho hlavička, je upraven tak, aby pracoval na JRE specifikované verze a samozřejmě i na všech novějších verzích JRE.
8. Algoritmy použité v demonstrační aplikaci
V navazujících odstavcích jsou stručně uvedeny a popsány zdrojové kódy nejdůležitějších metod:
isTransformationMatrixValid1() – první kontrola matice posloupnosti transformací. Cílem aplikovaného algoritmu je najít takové body (uzly) v orientovaném grafu (orgrafu), ze kterých nevedou žádné orientované hrany. Tyto uzly se v matici posloupnosti transformací projeví sloupcem, který obsahuje pouze nulové hodnoty. Algoritmus tedy v matici posloupnosti transformací jednoduše detekuje tyto sloupce a pokud alespoň jeden takový sloupec nalezne, ukončí svůj běh.
isTransformationMatrixValid2() – druhá kontrola matice posloupnosti transformací. Cílem tohoto algoritmu je nalézt takové uzly v orientovaném grafu (orgrafu), ze kterých nevedou žádné orientované hrany kromě povolených jednoduchých smyček. Oproti předchozímu algoritmu pro detekci uzlů bez výstupních hran (jehož implementace byla uvedena v předchozí metodě) je přidána podmínka, která zamezí nalezení jednoduché smyčky, tj. orientované hrany, která začíná a končí ve stejném uzlu orientovaného grafu.
isTransformationMatrixValid3() – třetí kontrola matice posloupnosti transformací. Ve zde uvedeném algoritmu se provádí test, zda orientovaný graf představovaný maticí posloupnosti transformací systému L–IFS, neobsahuje uzly, do kterých nevedou žádné hrany. Takové uzly (resp. jim příslušné lineární transformace v matici transformací) by se při generování fraktálních objektů na vytváření těchto objektů nepodílely. Jedinou výjimkou by mohla být první iterace, ovšem pouze za předpokladu, že by se transformace začaly vybírat právě z uzlu bez vstupních hran.
chooseControlPoint() – výběr dalšího řídicího bodu posloupnosti. Cílem zde prezentovaného algoritmu je nalézt další řídicí bod posloupnosti, se kterým se bude provádět výpočet nového bodu generovaného systému s fraktální strukturou. Posloupnost řídicích bodů není možné vybírat náhodně, je nutné se omezit pouze na takovou posloupnost, která odpovídá zadané matici posloupnosti transformací. Zastavení běhu algoritmu je zaručeno pouze v případě, že zadaná matice posloupnosti transformací je korektní.
recalcFractal() – překreslení celého fraktálu. V této metodě je názorně ukázáno, jakým způsobem může být provedeno vykreslení linearizovaného systému iterovaných funkcí L–IFS. Nejprve je provedena kontrola na korektnost zadané matice posloupnosti transformací, poté je vybrán index první transformace pro provedení počáteční iterace a posléze je smazána pixmapa, do které se bude obrázek vznikajícího fraktálního objektu vykreslovat.
initModel() – inicializace modelu vytvořeného z L–IFS systému. V této metodě je názorně ukázáno, jakým způsobem se provádí inicializace modelu v návaznosti na GUI celého appletu či aplikace.
9. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování tohoto seriálu si řekneme, jakým způsobem je možné provádět „morfing“ mezi několika obrázky IFS systémů.