Obsah
1. Animace změny tvaru systému iterovaných funkcí
2. Princip morfingu IFS systémů
3. Demonstrační příklad umožňující změnu tvaru IFS systému
4. Výpis nejdůležitějších metod použitých v demonstračním příkladu
4.1 Vykreslení vygenerovaného bodu do pixmapy
4.2 Vykreslení jednoho pixelu do pixmapy v závislosti na nastaveném režimu
4.3 Implementovaný algoritmus vykreslení IFS koláže
5. Literatura
6. Odkazy na Internetu
7. Obsah dalšího pokračování tohoto seriálu
1. Animace změny tvaru systému iterovaných funkcí
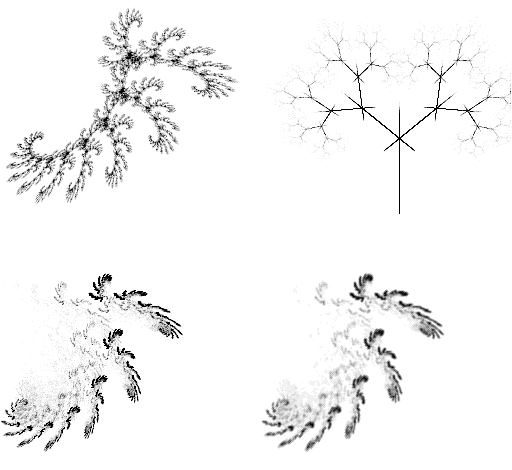
V několika předchozích částech tohoto seriálu jsme si ukázali, jakým způsobem je možné vytvářet zajímavě vypadající koláže pomocí systémů iterovaných funkcí IFS. Původně statické obrázky je však možné poměrně jednoduchým způsobem „rozpohybovat“ a vygenerovat z nich působivou animaci. Dnes si ukážeme způsob vycházející z klasického morfingu. Na rozdíl od morfingu prováděného s libovolnými tvary však při práci s iterovanými funkcemi použijeme jednoduchý trik: nebudeme přímo pohybovat vygenerovanými body v rovině obrazovky, což by bylo náročné a ve výsledku nezajímavé, ale budeme měnit přímo parametry systému iterovaných funkcí (přesněji řečeno transformační matici A). Vzhledem k tomu, že se má jednat o morfing, tj. plynulou změnu tvaru mezi dvojicí tvarů zadaných, bude do „morfovacího“ procesu vstupovat dvojice systémů iterovaných funkcí IFS. Výsledkem morfingu bude plynulá animace mezi dvojicí koláží odpovídajících oběma zadaným IFS systémům. Ukázka morfingu mezi dvěma známými IFS systémy (Sierpinského trojúhelníkem a binárním stromem) je zobrazena na obrázcích 1 – 7.
Obrázek 1: Postupná změna Sierpinského trojúhelníka na binární strom (100%:0%)
Obrázek 2: Postupná změna Sierpinského trojúhelníka na binární strom (80%:20%)
Obrázek 3: Postupná změna Sierpinského trojúhelníka na binární strom (60%:40%)
2. Princip morfingu IFS systémů
Jak již bylo řečeno v předchozí kapitole, spočívá princip morfingu IFS systémů v tom, že se postupně mění hodnoty uložené v transformační matici A. V nejjednodušším případě je možné postupovat tak, že se provede vážený součet odpovídajících koeficientů ai,j prvního a druhého systému:
ai,j=(1-morphRatio)×a1i,j + morphRatio×a2i,j
Kde parametr morphRatio nabývá hodnot z intervalu <0, 1>. Výše uvedený výpočet je samozřejmě nutné použít pro všechny transformace příslušející zadaným IFS systémům. Prakticky může aplikace výpočtu transformačních matic vypadat následovně (jedná se o zdrojový kód napsaný v programovacím jazyce Java):
double a[][]=new double [Size][MatSize]; // matice s koeficienty IFS systému
for (int j=0; j<Size; j++) { // přenos koeficientů IFS systému
for (int i=0; i<MatSize; i++) { // a smíchání prvního a druhého systému
a[j][i]=(1.0-morphRatio)*data1[j+firstIFS*Size][i] // do výsledné matice
+(morphRatio)*data2[j+secondIFS*Size][i];
}
} Pozorný čtenář se může zeptat, co se stane v případě, že první IFS systém bude mít jiný počet transformací než systém druhý. Zde přichází na řadu drobná úprava toho systému, který má nižší počet transformací – jejich počet je uměle zvýšen, a to tak, že přidané transformace obsahují identitu, tj. jednotkovou matici, která po své aplikaci vrátí původní souřadnice bodu. Pravděpodobnost těchto uměle přidaných transformací je nastavena na jedničku, a to z toho důvodu, že po provedení výše uvedeného vzorce se mohou pravděpodobnosti předchozích transformací snížit tak, že by jejich součet již nebyl roven jedné, což je samozřejmě chyba, která by způsobila nekorektní práci algoritmu. Pod další čtveřicí obrázků je uveden příklad zápisu množiny transformací dvou IFS systémů; všimněte si posledních řádků s uměle přidanými transformacemi s identitami.
Obrázek 4: Postupná změna Sierpinského trojúhelníka na binární strom (40%:60%)
Obrázek 5: Postupná změna Sierpinského trojúhelníka na binární strom (20%:80%)
Obrázek 6: Postupná změna Sierpinského trojúhelníka na binární strom (10%:90%)
Obrázek 7: Postupná změna Sierpinského trojúhelníka na binární strom (0%:100%)
// fern
{ 0.850000, 0.040000,-0.040000, 0.850000, 0.000000, 1.600000, 0.850000},
{ 0.200000,-0.260000, 0.230000, 0.220000, 0.000000, 1.600000, 0.070000},
{-0.150000, 0.280000, 0.260000, 0.240000, 0.000000, 0.440000, 0.070000},
{ 0.000000, 0.000000, 0.000000, 0.160000, 0.000000, 0.000000, 0.010000},
{ 1.000000, 0.000000, 0.000000, 1.000000, 0.000000, 0.000000, 1.000000},
// triangle
{ 0.500000, 0.000000, 0.000000, 0.500000,-0.500000, 0.000000, 0.333333},
{ 0.500000, 0.000000, 0.000000, 0.500000, 0.500000, 0.000000, 0.333333},
{ 0.500000, 0.000000, 0.000000, 0.500000, 0.000000, 0.860000, 0.333334},
{ 1.000000, 0.000000, 0.000000, 1.000000, 0.000000, 0.000000, 1.000000},
{ 1.000000, 0.000000, 0.000000, 1.000000, 0.000000, 0.000000, 1.000000},
3. Demonstrační příklad umožňující změnu tvaru IFS systému
Dnešní demonstrační aplikace slouží k vytvoření a následnému zobrazení fraktálů, které vznikají postupnou aplikací transformací systému iterovaných funkcí (IFS) na počáteční bod ležící v rovině. Po spuštění aplikace je možné nastavit celkový počet provedených iterací, počet startovních iterací (při nichž se neprovádí vykreslování, pouze nastavování hranice opsaného obdélníku), tvar generovaného obrazce (tj. parametry dvou IFS systémů) a procentuelní poměr mezi těmito dvěma IFS systémy při výpočtu jednotlivých transformací. Také je možná specifikace typu vykreslovaných bodů a konvolučního filtru, který se na výsledný obrázek může aplikovat.
Vzhledem k tomu, že uživatel může specifikovat parametry dvou IFS systémů, provede aplikace nejprve sloučení těchto systémů podle předem zadaných koeficientů. Sloučení se provádí váženým součtem odpovídajících koeficientů transformačních matic IFS systémů podle principu popsaného v předchozí kapitole.
Každý vygenerovaný bod může být reprezentován buď jedním pixelem, což je nejjednodušší případ použitý prakticky ve všech ostatních aplikacích pro práci s IFS systémy, nebo malým obrazcem, jež může být složen až z několika desítek pixelů. Aplikací konvolučního filtru je možné obrázek vyhladit, aby v něm nebyly patrné stopy jednotlivých bodů; ovšem na úkor částečného rozmazání obrázku.
Ukázka grafického uživatelského rozhraní (GUI) tohoto demonstračního příkladu i s vytvořeným fraktálním obrazcem je uvedena na dalším obrázku, zdrojový kód si můžete prohlédnout či stáhnout z této stránky a po překladu pomocí překladače jazyka Java je možné aplikaci spustit přes AppletViewer.
Obrázek 8: Screenshot demonstračního příkladu
Vzhledem k určitým omezením, která jsou kladena na grafická uživatelská rozhraní appletů, je celá aplikace tvořena jednou pracovní plochou rozdělenou do několika částí. Na jednotlivých částech jsou umístěny ovládací prvky grafického uživatelského rozhraní. Pracovní plocha aplikace může být zobrazena přímo na ploše WWW stránky v internetovém prohlížeči – to znamená, že se nevytváří žádná další okna ani dialogy. Alternativně lze použít prohlížeč appletů AppletViewer, který je dodáván k některým vývojovým prostředím založeným na jazyku Java a také k Sunovskému JDK.
4. Výpis nejdůležitějších metod použitých v demonstračním příkladu
V této kapitole, resp. v jejích podkapitolách, budou stručně uvedeny a popsány zdrojové kódy nejdůležitějších metod dnešní demonstrační aplikace.
4.1 Vykreslení vygenerovaného bodu do pixmapy
Metoda sloužící k vykreslení jednoho vygenerovaného bodu do pixmapy se ve své podstatě skládá z několika volání metody putPixel(), jež je popsána v navazující podkapitole. Tvar bodu v rastru (pixmapě) je závislý na volbě uživatele; podle zvoleného tvaru se mění i volání a parametry funkce putPixel(). Také způsob vykreslení bodu (přímý zápis barvy či snížení jasu) se volí z grafického uživatelského rozhraní aplikace:
// -----------------------------------------------------------------------
// Vykreslení vygenerovaného bodu do pixmapy
// -----------------------------------------------------------------------
private void putPoint(int x, int y) {
if (x<4) x=4; // kontrola mezí pixmapy
if (x>=width-3) x=width-4;
if (y<4) y=4;
if (y>=height-3) y=height-4;
y=height-1-y;
if (pointShape!=PointShape.Diamond3x3 &&
pointShape!=PointShape.Diamond5x5) {
putPixel(x, y); // prostřední pixel
}
if (pointShape==PointShape.Cross3x3 ||
pointShape==PointShape.Diamond3x3 ||
pointShape==PointShape.Block3x3 ||
pointShape==PointShape.Cross5x5 ||
pointShape==PointShape.Block5x5 ||
pointShape==PointShape.Horizontal3 ||
pointShape==PointShape.Horizontal5) {
putPixel(x-1,y); // pixel nalevo
putPixel(x+1,y); // pixel napravo
}
if (pointShape==PointShape.Horizontal5 ||
pointShape==PointShape.Cross5x5 ||
pointShape==PointShape.Diamond5x5 ||
pointShape==PointShape.Block5x5) {
putPixel(x-2,y); // druhý pixel nalevo
putPixel(x+2,y); // druhý pixel napravo
}
if (pointShape==PointShape.Cross3x3 ||
pointShape==PointShape.Diamond3x3 ||
pointShape==PointShape.Block3x3 ||
pointShape==PointShape.Cross5x5 ||
pointShape==PointShape.Block5x5 ||
pointShape==PointShape.Vertical3 ||
pointShape==PointShape.Vertical5) {
putPixel(x, y-1); // pixel nahoře
putPixel(x, y+1); // pixel dole
}
if (pointShape==PointShape.Vertical5 ||
pointShape==PointShape.Cross5x5 ||
pointShape==PointShape.Diamond5x5 ||
pointShape==PointShape.Block5x5) {
putPixel(x, y-2); // druhý pixel nahoře
putPixel(x, y+2); // druhý pixel dole
}
if (pointShape==PointShape.XCross3x3 ||
pointShape==PointShape.Block3x3 ||
pointShape==PointShape.XCross5x5 ||
pointShape==PointShape.Diamond5x5 ||
pointShape==PointShape.Block5x5) {
putPixel(x-1, y-1); // diagonální pixely
putPixel(x-1, y+1);
putPixel(x+1, y-1);
putPixel(x+1, y+1);
}
if (pointShape==PointShape.XCross5x5 ||
pointShape==PointShape.Block5x5) {
putPixel(x-2, y-2);
putPixel(x-2, y+2);
putPixel(x+2, y-2);
putPixel(x+2, y+2);
}
if (pointShape==PointShape.Block5x5) {
putPixel(x-1, y-2);
putPixel(x-1, y+2);
putPixel(x+1, y-2);
putPixel(x+1, y+2);
putPixel(x-2, y-1);
putPixel(x-2, y+1);
putPixel(x+2, y-1);
putPixel(x+2, y+1);
}
} Obrázek 9: Obrazec vzniklý morfingem mezi kapradinou a binárním stromem
4.2 Vykreslení jednoho pixelu do pixmapy v závislosti na nastaveném režimu
Tuto metodu využívá i výše uvedená metoda putPoint() pro vykreslování jednotlivých bodů do obrázku. V závislosti na nastaveném režimu se pixel buď přímo vykreslí (černou barvou na bílém pozadí), nebo se sníží intenzita pixelu tak, že se postupně blíží od původní bílé barvy k barvě černé. Také je prováděn test na přetečení aktuální hodnoty pixelu pod hodnotu 0×ff000000, což je kód černé neprůhledné barvy. Pixmapa, do které se má vykreslování provádět, je vytvořena velmi jednoduše jako jednorozměrné pole položek typu int. Takto vytvořená pixmapa je posléze použita jako zdroj dat pro obrázek typu Image, který je možné vykreslovat do grafického uživatelského rozhraní aplikace:
private int pixmap[]=new int[width*height]; // alokace paměti pro pixmapu
private MemoryImageSource imageSource=new MemoryImageSource(width, height, pixmap, 0, height);
private Image image=createImage(imageSource); // vytvoření obrázku // -----------------------------------------------------------------------
// Vykreslení jednoho pixelu podle nastaveného režimu
// -----------------------------------------------------------------------
private void putPixel(int x, int y) {
switch (putpixelMode) {
case 0:
pixelSrc[x+y*width]=0xff000000;
break;
case 1:
if (pixelSrc[x+y*width]>0xff040404)
pixelSrc[x+y*width]-=0x00040404;
break;
case 2:
if (pixelSrc[x+y*width]>0xff080808)
pixelSrc[x+y*width]-=0x00080808;
break;
case 3:
if (pixelSrc[x+y*width]>0xff0c0c0c)
pixelSrc[x+y*width]-=0x000c0c0c;
break;
case 4:
if (pixelSrc[x+y*width]>0xff101010)
pixelSrc[x+y*width]-=0x00101010;
break;
case 5:
if (pixelSrc[x+y*width]>0xff141414)
pixelSrc[x+y*width]-=0x00141414;
break;
default:
break;
}
} 
Obrázek 10: Další obrazec vzniklý morfingem
4.3 Implementovaný algoritmus vykreslení IFS koláže
V posledním výpisu je uveden implementovaný algoritmus pro vykreslení IFS koláže zapsané pomocí dvou „klasických“ systémů iterovaných funkcí IFS. Nejprve je proveden výpočet koeficientů IFS systému pomocí smíchání koeficientů obou vstupních systémů. Potom přichází na řadu iterační smyčka. V prvních několika iteracích (specifikovaných parametrem startIter) se pouze provádí výpočet polohy bodu v rovině a stanovují se hranice opsaného obdélníka (ten se svými hranami těsně dotýká IFS koláže). Jakmile čítač iterací dojde k hodnotě startIter, jsou hranice opsaného obdélníka zafixovány a v průběhu výpočtu jednoho snímku se již nemění. Ve všech dalších iteracích se již provádí vykreslení generovaných bodů, ovšem s tím, že souřadnice bodů jsou transformovány tak, aby ležely uvnitř opsaného obdélníku.
// -----------------------------------------------------------------------
// Vlastní aplikace algoritmu pro vykreslení IFS koláže
// -----------------------------------------------------------------------
private void generateIFS(double data1[][], // předávaná data prvního IFS systému
double data2[][], // předávaná data druhého IFS systému
int maxIter, // maximální počet iterací
int startIter, // počet startovních iterací
int width, // horizontální rozlišení obrázku
int height) { // vertikální rozlišení obrázku
double x1=0, y1=0, x2=0, y2=0; // generované souřadnice
double xmin=1e10, xmax=-1e10; // obdélník opsaný IFS fraktálu
double ymin=1e10, ymax=-1e10;
int x, y, k;
double pp, sum;
double delitel=1.0;
Random r=new Random(0); // generátor náhodných čísel
double a[][]=new double [5][7]; // matice s koeficienty IFS systému
for (int j=0; j<5; j++) { // přenos koeficientů IFS systému
for (int i=0; i<7; i++) { // a smíchání prvního a druhého systému
a[j][i]=(1.0-morphRatio)*data1[j+firstIFS*5][i] // do výsledné matice
+(morphRatio)*data2[j+secondIFS*5][i];
}
}
for (int i=0; i<maxIter; i++) { // pro všechny iterace
pp=r.nextDouble();
sum=0; // na základě náhodného čísla
for (k=0; sum<=pp; k++) // najít transformaci
sum+=a[k][6];
k--;
x2=x1*a[k][0] + y1*a[k][1] + a[k][4]; // aplikovat transformaci
y2=x1*a[k][2] + y1*a[k][3] + a[k][5];
x1=x2; y1=y2;
if (i>startIter) { // pokud byl překročen počet
x2=(x1-xmin)*(double)width/delitel; // startovních iterací
y2=(y1-ymin)*(double)height/delitel;
x=(int)x2; y=(int)y2; // vypočítat a zobrazit pozice pixelu
putPoint(x, y);
}
else { // pokud se jedná o startovní iterace
if (x1<xmin) xmin=x1; // provést výpočet opsaného obdélníka
if (y1<ymin) ymin=y1;
if (x1>xmax) xmax=x1;
if (y1>ymax) ymax=y1;
}
if (i==startIter) { // zafixovat opsaný obdélník
xmin*=1.1; // pro jistotu přidat 10% plochy
xmax*=1.1;
ymin*=1.1;
ymax*=1.1;
delitel=(xmax-xmin);
if (ymax-ymin>xmax-xmin) delitel=ymax-ymin;
}
}
} Obrázek 11: Další obrazec vzniklý morfingem
5. Literatura
[1] Barnsley Michael: ''Fractals Everywhere '',
Academic Press Inc., 1988, ISBN 0–12–079062–9
[2] Barnsley Michael, Devaney R. L., Mandelbrot Benoit B., Peitgenn Heinz-Otto, Saupe Dietmar, Voss Richard: ''The Science of Fractal Images '',
Springer-Verlag, New York, 1988
[3] Barnsley Michael, Hurd Lyman P.: ''Fractal Image Compression '',
A. K. Peters, 1993
[4] Devaney Robert L.: ''A First Course In Chaotic Dynamical Systems '',
Addison-Wesley, Reading, MA, 1992
[5] Fischer Yuval (editor): ''Fractal Image Compression: Theory and Application '',
Springer-Verlag, New York, 1995
[6] Gröller Eduard: ''Interactive design of Nonlinear Functions for Iterated Function System '',
Technical University Vienna, 1995
[7] Lauwerier Hans: ''Fractals '',
Princeton University Press, 1991
[8] Tišnovský Pavel: ''Návrh editoru IFS '',
Vysoké učení technické v Brně, Fakulta elektrotechniky a informatiky, 1998
[9] Tišnovský Pavel: ''Interaktivní editor afinních transformací '',
Vysoké učení technické v Brně, Fakulta elektrotechniky a informatiky, 1999
6. Odkazy na Internetu
[10] Tyler Bert, Wegner Tim a kol.: ''Fractint (fractal generator for DOS) '',
http://www.fractint.org (3.6.2006)
[11] Cygnus software: ''Fractal eXtreme (fractal generator for Windows) '',
http://www.cygnus-software.com (3.6.2006)
[12] Slijkerman Frederik: ''Ultra Fractal (fractal generator for Windows) '',
http://www.ultrafractal.com (3.6.2006)
[13] Gintz Terry W.: ''Zplot (fractal generator) '',
http://www.geocities.com/SoHo/Lofts/5601/gallery.htm (3.6.2006)
[14] Chardonnet David: ''IFS Fractals Digital Encyclopedy '',
http://www.chez.com/fractals/galeries/gb_index.html (3.6.2006)
[15] Bowman Richard L.: ''IFS Fractal Generation Exercise '',
http://www.bridgewater.edu/departments/physics/ISAW/FractalGenEx.html (3.6.2006)
[16] Devaney Bob: ''Dynamical systems and Iterated Function Systems '',
http://math.bu.edu/people/bob/ (3.6.2006)
[17] Thornton Sterling: ''XenoDream (Interactive IFS Editor) '',
http://xenodream.com (3.6.2006)
7. Obsah dalšího pokračování tohoto seriálu
V následující části tohoto seriálu si popíšeme velmi zajímavou skupinu fraktálů, která úzce souvisí se systémy iterovaných funkcí. Jedná se o fraktály nazývané „Fractal Flame“, které vznikají několikerou generalizací původních IFS systémů.
Obrázek 12: Ukázka fraktálu typu „Fractal Flame“







































