Obsah
1. Praktické použití nástroje Cython při překladu Pythonu do nativního kódu
2. Postupné úpravy jednoduché funkce pro součet dvou celých čísel
3. Soubor Makefile pro řízení překladu funkcí z Pythonu do nativního kódu
4. Přímý překlad Pythonovské funkce bez přidání typových informací
5. Proč Cython používá PyObject * aneb problematika dynamického typového systému
6. Použití deklarace cdef namísto def
7. Přidání informace o typech parametrů funkce pro součet celých čísel
8. Přidání informace o návratovém typu funkce pro součet celých čísel
9. Zákaz volání funkcí souvisejících s GILem
10. Náhrada Pythonovské funkce print za funkci printf
11. Pythonovské seznamy a céčková pole
12. Předchozí varianta benchmarku a oblasti, kde je možné provést optimalizace
13. Použití pole s barvovou paletou
14. Odstranění kontrol při dělení
17. Finální podoba benchmarku, srovnání s variantou naprogramovanou v céčku
19. Repositář s demonstračními příklady
1. Praktické použití nástroje Cython při překladu Pythonu do nativního kódu
V dnešním článku, který poměrně úzce navazuje na článek porovnávající RPython s Cythonem, si ukážeme, jak se Cython používá prakticky. Připomeňme si, že tento nástroj slouží k převodu (takzvané transkompilaci/transpřekladu) zdrojových kódů napsaných v Pythonu (popř. nadmnožině tohoto jazyka) do zdrojového kódu určeného pro překlad standardními překladači céčka. Výsledkem může být buď dynamická knihovna plně využitelná v CPythonu (standardním interpretru jazyka Python) nebo spustitelná aplikace, kterou je možné dále používat popř. distribuovat (ovšem s některými omezeními popsanými dále). Cython sice přeloží i běžné zdrojové kódy Pythonu, ovšem jak uvidíme v dalších kapitolách, přináší to s sebou některá omezení – výsledný kód není příliš efektivní, a to ani z hlediska jeho velikosti ani z pohledu rychlosti. Pro zajištění lepší efektivity je zapotřebí zdrojové kódy upravit – a právě tato problematika je ústředním tématem dnešního článku.

Obrázek 1: Porovnání doby výpočtu Mandelbrotovy množiny RPythonem, Cythonem (bez i s type hinty) a variantou naprogramovanou přímo v ANSI C. Z tohoto grafu je dobře patrné, jak důležité je pro Cython mít k dispozici informace o typech proměnných, parametrů a návratových kódů funkcí.
2. Postupné úpravy jednoduché funkce pro součet dvou celých čísel
Základní koncepty, na kterých je založeno mnoho optimalizací prováděných Cythonem (pokud ovšem tomuto transpřekladači vhodným způsobem pomůžeme), je možné vysvětlit na funkci sloužící pro součet dvou celých čísel. Programovací jazyk Python většina programátorů používá mj. i kvůli jeho jednouše použitelnému typovému systému, takže funkci pro součet mohou bez větší námahy zapsat například takto:
def add_two_numbers(x, y):
return x + y
Ve skutečnosti však samozřejmě tato funkce může provádět i mnoho dalších operací na základě konkrétních typů parametrů, které jsou funkci předávány. A právě zde leží základní problém, který musí řešit jak Cython, tak i již zmíněný RPython – aby byla tato funkce skutečně přeložena optimálně (v podstatě jen jedinou instrukcí add následovanou instrukcí ret), musíme dynamický typový systém Pythonu v tomto konkrétním případě omezit a stanovit jak typy parametrů, tak i návratový typ. Navíc, jak uvidíme dále, je možné v této funkci zcela vyloučit GIL (Global Interpreter Lock) a tak výslednou céčkovou funkci ještě zkrátit a zrychlit.
Postupně si tedy ukážeme vliv těchto dílčích kroků:
- Deklarace typů parametrů funkce
- Deklarace návratového typu
- Odstranění použití GIL (prolog a epilog ve funkci)
3. Soubor Makefile pro řízení překladu funkcí z Pythonu do nativního kódu
Před popisem jednotlivých (celkem šesti) variant funkce určené pro součet dvou čísel si ukažme, jakým způsobem vlastně budeme provádět překlad. Již víme, že celý překlad probíhá ve třech krocích:
- Transpřeklad zdrojového kódu napsaného v Pythonu do programovacího jazyka C
- Překlad kódu z jazyka C do tzv. objektového kódu (de facto strojový kód s relativními adresami)
- Slinkování objektového kódu s knihovnami a vytvoření spustitelné aplikace
Ze zdrojového kódu napsaného v Pythonu (či jeho nadstavbě) postupně vzniknou tři další soubory:
soubor.py → soubor.c → objektový_kód.o → nativní spustitelná aplikace
Celý řetězec zpracování bude řízen souborem Makefile, který vypadá následovně (jeho jednotlivé části budou popsány pod výpisem):
PYTHON=python3
COMPILER=gcc
LINKER=gcc
CFLAGS=-O9
INCLUDE_DIR:=$(shell $(PYTHON) -c "from distutils import sysconfig; print(sysconfig.get_python_inc())")
LIBRARY_DIR:=$(shell $(PYTHON) -c "from distutils import sysconfig; print(sysconfig.get_config_var('LIBDIR'))")
PYTHON_LIB:=$(shell $(PYTHON) -c "from distutils import sysconfig; print(sysconfig.get_config_var('LIBRARY')[3:-2])")
SYSLIBS:=$(shell $(PYTHON) -c "from distutils import sysconfig; print(sysconfig.get_config_var('SYSLIBS'))")
all: add_numbers_1 \
add_numbers_2 \
add_numbers_3 \
add_numbers_4 \
add_numbers_5 \
add_numbers_7
.PHONY: clean
# Výsledky překladu do C chceme ponechat i po doběhnutí Make
.PRECIOUS: %.c
clean:
rm -f *.o \
rm -f *.c \
rm -f add_numbers_[1-5]
# Pravidlo pro slinkovani vsech objektovych souboru a vytvoreni
# vysledne spustitelne aplikace.
%: %.o
$(LINKER) -o $@ -L$(LIBRARY_DIR) -l$(PYTHON_LIB) $(SYSLIBS) $<
# Pravidlo pro preklad kazdeho zdrojoveho souboru v C do prislusneho
# objektoveho souboru.
%.o: %.c
$(COMPILER) $(CFLAGS) -I$(INCLUDE_DIR) -c $< -o $@
# Pravidlo pro preklad kazdeho zdrojoveho souboru v Pythonu nebo Cythonu
# do prislusneho souboru C
%.c: %.py
cython -a --embed $<
%.c: %.pyx
cython -a --embed $<
Některé části Makefile jsou snadno pochopitelné. Jedná se zejména o pravidla pro transpřeklad zdrojových kódů s koncovkou .py nebo .pyx do céčkových souborů s koncovkou .c. Přepínač –embed zajistí vygenerování kódu funkce main, přepínač -a pak vytvoření HTML souboru, jehož význam si ukážeme dále.
Podobně je zde deklarováno pravidlo pro překlad céčkových souborů .c do objektového kódu .o. Zde musíme použít informaci o tom, kde se nachází hlavičkové soubory Pythonu – důvod jsme si vysvětlili zde. Další pravidlo určuje slinkování .o do spustitelné aplikace, opět s přidáním všech důležitých informací (umístění systémových knihoven apod.)
Následující deklarace zajistí, že nástroj make nebude mazat soubory *.c, které vznikly aplikací implicitních pravidel. Pokud tuto deklaraci zakomentujete, smaže utilita make na závěr nejenom všechny objektové soubory, ale i transpřeložené zdrojové kódy v céčku, které sice již nebudou zapotřebí, ale my je budeme chtít později prozkoumat:
.PRECIOUS: %.c
4. Přímý překlad Pythonovské funkce bez přidání typových informací
Pokusme se nyní přeložit první variantu funkce pro součet dvou celých čísel. Zdrojový kód s deklarací této funkce i s příkladem jejího volání naleznete na adrese https://github.com/tisnik/cython-examples/blob/master/add_numbers/add_numbers1.py:
def add_two_numbers(x, y):
return x + y
z = add_two_numbers(123, 456)
print(z)
Výsledkem překladu bude spustitelný soubor „add_numbers1“, ovšem nás nyní budou zajímat další dva vytvořené soubory nazvané „add_numbers1.c“ a „add_numbers1.html“. První z těchto souborů obsahuje zdrojový kód v céčku, jehož překladem a slinkováním vznikla výsledná spustitelná aplikace, druhý soubor pak obsahuje zajímavé informace o tom, jakým způsobem Cython program přeložil a především pak, na kterých místech by bylo vhodné provést úpravy s určením datových typů atd. Obsah tohoto souboru vypadá takto:
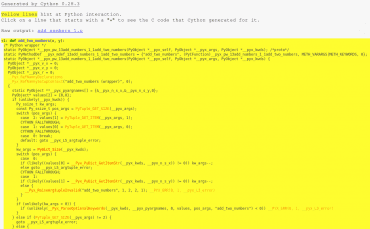
Obrázek 2: Část HTML souboru „add_numbers1.html“ vytvořeného Cythonem. Žlutě označené řádky označují ty bloky kódu, o nichž Cython nemá typové informace a které musel přeložit dosti neefektivním způsobem simulujícím chování interpretru Pythonu.
Lepší však bude, když si celý soubor přímo otevřete v prohlížeči, protože umožňuje interaktivní rozbalování jednotlivých přeložených řádků (kliknutím na znak + umístěný v prvním sloupci, popř. na libovolný řádek se žlutým podsvícením).
5. Proč Cython používá PyObject * aneb problematika dynamického typového systému
Zdrojový (céčkový) kód vygenerovaný Cythonem je poměrně nečitelný (alespoň prozatím!), a to mj. i z toho důvodu, že oba dva parametry funkce add_two_numbers i její návratová hodnota jsou představovány ukazateli na struktury typu PyObject. Cython totiž nemá k dispozici žádné informace o tom, jakého typu parametry budou a tak musí předpokládat, že se funkce bude volat s celými čísly, čísly s plovoucí řádovou čárkou, seznamy, n-ticemi, řetězci či dokonce s instancemi tříd, které mají předefinovánu speciální metodu __add__ (jinými slovy se všemi typy, u kterých má smysl používat operátor +).
Ostatně se stačí podívat na následující demonstrační příklad, v němž je naše funkce volána s různými typy parametrů (z čehož mj. plyne i to, že její název je dosti zavádějící):
def add_two_numbers(x, y):
return x + y
class Foo:
def __init__(self, value):
self._value = value
def __add__(self, other):
return Foo(self._value + other._value)
def __str__(self):
return "*" * self._value
def test_adding():
f1 = Foo(1)
f2 = Foo(2)
print(add_two_numbers(123, 456))
print(add_two_numbers("foo", "bar"))
print(add_two_numbers([1,2,3], [4,5,6]))
print(add_two_numbers((1,2,3), (4,5,6)))
print(add_two_numbers(f1, f2))
test_adding()
Po spuštění příkladu dostaneme následující řádky, které ukazují, že se + skutečně dá použít s různými datovými typy:
579 foobar [1, 2, 3, 4, 5, 6] (1, 2, 3, 4, 5, 6) ***
Zkusme si příklad ještě dále upravit – podíváme se na bajtkód, který bude interpretován Pythonem (bajtkód se vytváří vždy, i když se nemusí ukládat na disk):
import dis dis.dis(add_two_numbers) dis.dis(test_adding)
Funkce add_two_numbers je přeložena do čtyř instrukcí, které ovšem neobsahují řádné informace o typech operandů (na rozdíl od bajtkódu JVM, kde existuje například instrukce IADD, FADD, DADD apod.):
4 0 LOAD_FAST 0 (x)
3 LOAD_FAST 1 (y)
6 BINARY_ADD
7 RETURN_VALUE
Příklad volání funkce s předáním dvou celočíselných parametrů. Toto je varianta bajtkódu pro Python 2, který obsahuje print jako příkaz a tudíž pro něj existuje i odpovídající instrukce v bajtkódu:
22 24 LOAD_GLOBAL 1 (add_two_numbers)
27 LOAD_CONST 3 (123)
30 LOAD_CONST 4 (456)
33 CALL_FUNCTION 2
36 PRINT_ITEM
37 PRINT_NEWLINE
Celý bajtkód pro Python 2 vypadá následovně (poznámky jsem dopsal ručně):
# tělo funkce add_two_numbers()
4 0 LOAD_FAST 0 (x)
3 LOAD_FAST 1 (y)
6 BINARY_ADD
7 RETURN_VALUE
# f1 = Foo(1)
19 0 LOAD_GLOBAL 0 (Foo)
3 LOAD_CONST 1 (1)
6 CALL_FUNCTION 1
9 STORE_FAST 0 (f1)
# f2 = Foo(2)
20 12 LOAD_GLOBAL 0 (Foo)
15 LOAD_CONST 2 (2)
18 CALL_FUNCTION 1
21 STORE_FAST 1 (f2)
# součet dvou celých čísel
22 24 LOAD_GLOBAL 1 (add_two_numbers)
27 LOAD_CONST 3 (123)
30 LOAD_CONST 4 (456)
33 CALL_FUNCTION 2
36 PRINT_ITEM
37 PRINT_NEWLINE
# spojení dvou řetězců
23 38 LOAD_GLOBAL 1 (add_two_numbers)
41 LOAD_CONST 5 ('foo')
44 LOAD_CONST 6 ('bar')
47 CALL_FUNCTION 2
50 PRINT_ITEM
51 PRINT_NEWLINE
# konstrukce dvou seznamů s jejich následným spojením
24 52 LOAD_GLOBAL 1 (add_two_numbers)
55 LOAD_CONST 1 (1)
58 LOAD_CONST 2 (2)
61 LOAD_CONST 7 (3)
64 BUILD_LIST 3
67 LOAD_CONST 8 (4)
70 LOAD_CONST 9 (5)
73 LOAD_CONST 10 (6)
76 BUILD_LIST 3
79 CALL_FUNCTION 2
82 PRINT_ITEM
83 PRINT_NEWLINE
# konstrukce dvou n-tic s jejich následným spojením
25 84 LOAD_GLOBAL 1 (add_two_numbers)
87 LOAD_CONST 11 ((1, 2, 3))
90 LOAD_CONST 12 ((4, 5, 6))
93 CALL_FUNCTION 2
96 PRINT_ITEM
97 PRINT_NEWLINE
# "spojení" dvou instancí třídy Foo
26 98 LOAD_GLOBAL 1 (add_two_numbers)
101 LOAD_FAST 0 (f1)
104 LOAD_FAST 1 (f2)
107 CALL_FUNCTION 2
110 PRINT_ITEM
111 PRINT_NEWLINE
# ukončení funkce main
112 LOAD_CONST 0 (None)
115 RETURN_VALUE
Příklad volání funkce s předáním dvou celočíselných parametrů. Toto je varianta bajtkódu pro Python 3, v němž je print běžnou funkcí:
22 24 LOAD_GLOBAL 1 (print)
27 LOAD_GLOBAL 2 (add_two_numbers)
30 LOAD_CONST 3 (123)
33 LOAD_CONST 4 (456)
36 CALL_FUNCTION 2 (2 positional, 0 keyword pair)
39 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
42 POP_TOP
Opět si ukažme celý bajtkód pro Python 3 (poznámky jsem dopsal ručně):
# tělo funkce add_two_numbers()
4 0 LOAD_FAST 0 (x)
3 LOAD_FAST 1 (y)
6 BINARY_ADD
7 RETURN_VALUE
# f1 = Foo(1)
19 0 LOAD_GLOBAL 0 (Foo)
3 LOAD_CONST 1 (1)
6 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
9 STORE_FAST 0 (f1)
# f2 = Foo(2)
20 12 LOAD_GLOBAL 0 (Foo)
15 LOAD_CONST 2 (2)
18 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
21 STORE_FAST 1 (f2)
# součet dvou celých čísel
22 24 LOAD_GLOBAL 1 (print)
27 LOAD_GLOBAL 2 (add_two_numbers)
30 LOAD_CONST 3 (123)
33 LOAD_CONST 4 (456)
36 CALL_FUNCTION 2 (2 positional, 0 keyword pair)
39 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
42 POP_TOP
# spojení dvou řetězců
23 43 LOAD_GLOBAL 1 (print)
46 LOAD_GLOBAL 2 (add_two_numbers)
49 LOAD_CONST 5 ('foo')
52 LOAD_CONST 6 ('bar')
55 CALL_FUNCTION 2 (2 positional, 0 keyword pair)
58 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
61 POP_TOP
# konstrukce dvou seznamů s jejich následným spojením
24 62 LOAD_GLOBAL 1 (print)
65 LOAD_GLOBAL 2 (add_two_numbers)
68 LOAD_CONST 1 (1)
71 LOAD_CONST 2 (2)
74 LOAD_CONST 7 (3)
77 BUILD_LIST 3
80 LOAD_CONST 8 (4)
83 LOAD_CONST 9 (5)
86 LOAD_CONST 10 (6)
89 BUILD_LIST 3
92 CALL_FUNCTION 2 (2 positional, 0 keyword pair)
95 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
98 POP_TOP
# konstrukce dvou n-tic s jejich následným spojením
25 99 LOAD_GLOBAL 1 (print)
102 LOAD_GLOBAL 2 (add_two_numbers)
105 LOAD_CONST 11 ((1, 2, 3))
108 LOAD_CONST 12 ((4, 5, 6))
111 CALL_FUNCTION 2 (2 positional, 0 keyword pair)
114 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
117 POP_TOP
# "spojení" dvou instancí třídy Foo
26 118 LOAD_GLOBAL 1 (print)
121 LOAD_GLOBAL 2 (add_two_numbers)
124 LOAD_FAST 0 (f1)
127 LOAD_FAST 1 (f2)
130 CALL_FUNCTION 2 (2 positional, 0 keyword pair)
133 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
136 POP_TOP
# ukončení funkce main
137 LOAD_CONST 0 (None)
140 RETURN_VALUE
6. Použití deklarace cdef namísto def
První úpravou našeho zdrojového kódu funkce add_two_numbers, která povede k menšímu a rychlejšímu strojovému (nativnímu) kódu, bude použití klíčového slova cdef namísto pythonovského def. Zdrojový kód uložíme do souboru s koncovkou .pyx namísto .py, a to především z toho důvodu, že se již nejedná o běžný kód zpracovatelný Pythonem (pro připomenutí: Cython používá nadmnožinu Pythonu zatímco RPython jeho podmnožinu). Žádné další úpravy kromě náhrady s/def/cdef prozatím nebudou provedeny:
cdef add_two_numbers(x, y):
return x + y
z = add_two_numbers(123, 456)
print(z)
Vzhledem k tomu, že v Makefile voláme Cython s parametrem -a, vygeneruje se mj. i HTML stránka, na níž je patrné, jak byla naše funkce přeložena do céčka tentokrát. Celý kód je již citelně kratší, i když je stále velmi neefektivní: cython_add_numbers2.
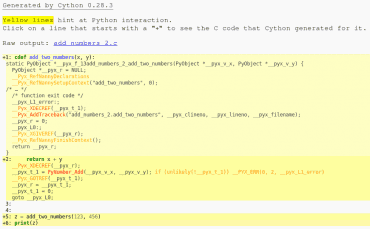
Obrázek 3: Část HTML souboru „add_numbers2.html“ vytvořeného Cythonem. Žlutě označené řádky opět označují ty bloky kódu, o nichž Cython nemá typové informace a které musel přeložit dosti neefektivním způsobem simulujícím chování interpretru Pythonu.
Hlavička céčkové funkce vzniklé transpřekladem vypadá takto:
static PyObject *__pyx_f_13add_numbers_2_add_two_numbers(PyObject *__pyx_v_x, PyObject *__pyx_v_y) {}
Potenciálně neefektivní části kódu:
- __Pyx_RefNannyDeclarations a __Pyx_RefNannySetupContext() na začátku funkce
- __Pyx_RefNannyFinishContext() na konci funkce
- vlastní výpočet je ovšem implementován voláním další funkce PyNumber_Add(__pyx_v_x, __pyx_v_y)
7. Přidání informace o typech parametrů funkce pro součet celých čísel
První výraznější úpravou, kterou můžeme provést, je přidání informace o typech parametrů funkce. Zápis je v tomto případě naprosto stejný, jako v klasickém céčku, tj. používá se pořadí datový_typ jméno_parametru. V našem případě budeme vyžadovat, aby parametry byly typu celé číslo, tj. v céčku se jedná o základní typ pojmenovaný int. Změněná funkce bude vypadat následovně:
cdef add_two_numbers(int x, int y):
return x + y
z = add_two_numbers(123, 456)
print(z)
Pokud se podíváme na vygenerovanou HTML stránku (cython_add_numbers3), popř. raději přímo na céčkový kód, uvidíme, že došlo k několika zásadním změnám. Zejména se pochopitelně změnila hlavička céčkové funkce vzniklé transpřekladem, která nyní vypadá následovně:
static PyObject *__pyx_f_13add_numbers_3_add_two_numbers(int __pyx_v_x, int __pyx_v_y) {
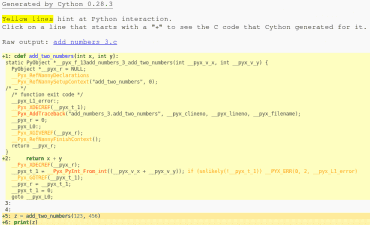
Obrázek 4: Část HTML souboru „add_numbers3.html“ vytvořeného Cythonem..
Dále se – pokud prozatím budeme ignorovat kód na začátku a konci funkce – celý výpočet pozměnil, protože se namísto volání PyNumber_Add již používá běžný součet. Ovšem následně se vypočtené celé číslo opět konvertuje na pythonovský objekt s využitím __Pyx_PyInt_From_int, protože jsme prozatím naschvál nespecifikovali návratový typ funkce:
__pyx_t_1 = __Pyx_PyInt_From_int((__pyx_v_x + __pyx_v_y))
Úplný céčkový kód je tedy již nepatrně lepší, ovšem k optimálnosti má stále daleko:
static PyObject *__pyx_f_13add_numbers_3_add_two_numbers(int __pyx_v_x, int __pyx_v_y) {
PyObject *__pyx_r = NULL;
__Pyx_RefNannyDeclarations
PyObject *__pyx_t_1 = NULL;
__Pyx_RefNannySetupContext("add_two_numbers", 0);
__Pyx_XDECREF(__pyx_r);
__pyx_t_1 = __Pyx_PyInt_From_int((__pyx_v_x + __pyx_v_y)); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 2, __pyx_L1_error)
__Pyx_GOTREF(__pyx_t_1);
__pyx_r = __pyx_t_1;
__pyx_t_1 = 0;
goto __pyx_L0;
/* function exit code */
__pyx_L1_error:;
__Pyx_XDECREF(__pyx_t_1);
__Pyx_AddTraceback("add_numbers_3.add_two_numbers", __pyx_clineno, __pyx_lineno, __pyx_filename);
__pyx_r = 0;
__pyx_L0:;
__Pyx_XGIVEREF(__pyx_r);
__Pyx_RefNannyFinishContext();
return __pyx_r;
}
8. Přidání informace o návratovém typu funkce pro součet celých čísel
Další úprava naší funkce se již přímo nabízí – musíme specifikovat typ návratové hodnoty. Pokud totiž tento typ není zadán, považuje Cython za nutné vracet PyObject *, aby byly výsledky kompatibilní s běžnými pythonovskými funkcemi a metodami. Specifikace návratové hodnoty se opět provádí stejným způsobem, jako v programovacím jazyku C, tj. zápisem příslušného typu před jméno funkce:
cdef int add_two_numbers(int x, int y):
return x + y
z = add_two_numbers(123, 456)
print(z)
Při transpřekladu do céčka získáme i HTML stránku s podrobnějšími informacemi o tom, jak byl Cython úspěšný. Tato stránka nyní vypadá takto a z jejího obsahu je patrné, že jsme se již velmi přiblížili k takové deklaraci, kterou by použil céčkový programátor (až na prolog a epilog):
static int __pyx_f_13add_numbers_4_add_two_numbers(int __pyx_v_x, int __pyx_v_y) {
int __pyx_r;
__Pyx_RefNannyDeclarations
__Pyx_RefNannySetupContext("add_two_numbers", 0);
__pyx_r = (__pyx_v_x + __pyx_v_y);
goto __pyx_L0;
/* function exit code */
__pyx_L0:;
__Pyx_RefNannyFinishContext();
return __pyx_r;
}

Obrázek 5: Část HTML souboru „add_numbers4.html“ vytvořeného Cythonem. Zde již není žádná část těla funkce podbarvena, protože Cython má k dispozici všechny potřebné informace o použitých datových typech.
9. Zákaz volání funkcí souvisejících s GILem
Zbývá nám udělat ještě poslední krok, a to odstranit přípravu takzvaného kontextu na začátku těla funkce a naopak odstranění kontextu na jejím konci. Jedná se o tuto trojici řádků:
__Pyx_RefNannyDeclarations
__Pyx_RefNannySetupContext("add_two_numbers", 0);
...
...
...
__Pyx_RefNannyFinishContext();
Zjednodušeně řečeno – kontext úzce souvisí s GIL (Global Interpreter Lock), který prozatím tvoří neoddělitelnou část klasického interpretru CPythonu (ovšem například v Jythonu ho nenajdeme, i když tento interpret má zase jiné problémy). GIL je zapotřebí nastavit tehdy, pokud naše (nyní vlastně céčková) funkce bude interně volat funkce naprogramované v Pythonu popř. funkce z jeho interní knihovny. To my ovšem nepotřebujeme – pouze sčítáme dvě celá čísla a vracíme výsledek součtu – takže můžeme práci s GILem zcela zakázat, a to použitím specifikace nogil. Finální podoba naší funkce bude vypadat následovně:
cdef int add_two_numbers(int x, int y) nogil:
return x + y
z = add_two_numbers(123, 456)
print(z)
Pokud se podíváme na výsledek překladu, zjistíme, že až na již výše zmíněné goto získáme čistý a čitelný céčkový kód:
static int __pyx_f_13add_numbers_5_add_two_numbers(int __pyx_v_x, int __pyx_v_y) {
int __pyx_r;
__pyx_r = (__pyx_v_x + __pyx_v_y);
goto __pyx_L0;
/* function exit code */
__pyx_L0:;
return __pyx_r;
}
Podívat se můžete i na HTML stránku vygenerovanou při transpřekladu: cython_add_numbers5. Ta ovšem nyní nebude obsahovat příliš zajímavé informace, protože jsme postupně (ve třech krocích) v nadmnožině Pythonu vlastně naprogramovali ekvivalent céčkovské funkce.
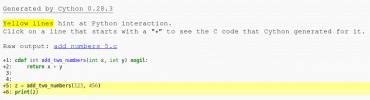
Obrázek 6: Část HTML souboru „add_numbers5.html“ vytvořeného Cythonem. Zde již není žádná část těla funkce podbarvena, protože Cython má k dispozici všechny potřebné informace o použitých datových typech.
10. Náhrada Pythonovské funkce print za funkci printf
Odstranění GILu z naší funkce bylo zcela korektní a nebude způsobovat žádné nepříjemnosti (pokud kratší a rychlejší kód nebudeme považovat za nepříjemnost). Ovšem zajímavé bude zjistit, co se stane ve chvíli, kdy se budeme snažit v takto upravené funkci volat jakýkoli Pythonovský kód (například print). Zkusme si tedy funkci upravit takovým způsobem, aby před provedením součtu vypsala hodnotu svého prvního parametru:
cdef int add_two_numbers(int x, int y) nogil:
print(x)
return x + y
z = add_two_numbers(123, 456)
print(z)
Při pokusu o transpřeklad s využitím Cythonu dojde k několika chybám:
$ cython -a --embed add_numbers_6.pyx
Error compiling Cython file:
------------------------------------------------------------
...
cdef int add_two_numbers(int x, int y) nogil:
print(x)
^
------------------------------------------------------------
add_numbers_6.pyx:2:4: Python print statement not allowed without gil
Error compiling Cython file:
------------------------------------------------------------
...
cdef int add_two_numbers(int x, int y) nogil:
print(x)
^
------------------------------------------------------------
add_numbers_6.pyx:2:4: Constructing Python tuple not allowed without gil
Error compiling Cython file:
------------------------------------------------------------
...
cdef int add_two_numbers(int x, int y) nogil:
print(x)
^
------------------------------------------------------------
add_numbers_6.pyx:2:10: Converting to Python object not allowed without gil
Proč tomu tak je? Problém spočívá v tom, že se sice naše funkce bez GILu zdánlivě obejde, ovšem běžné Pythonovské funkce a operace z ní volané s ním počítají. Proto pokud použijeme nogil, budeme se muset v tomto bloku obejít bez podpory pythoních funkcí. V našem případě to nebude nic složitého – prostě použijeme funkci printf ze standardní céčkové knihovny (ta se stejně bude linkovat). Řešení může vypadat následovně (pozor na slovo cimport a ne import):
from libc.stdio cimport printf
cdef int add_two_numbers(int x, int y) nogil:
printf("%i\n", x)
return x + y
z = add_two_numbers(123, 456)
print(z)
Podívejme se na vygenerovaný céčkový kód, který sice působí trochu uměle (explicitní (void), generované názvy identifikátorů atd.), ale v podstatě stejně, jako ručně psaný kód. Ono zbytečné goto bude odstraněno optimalizujícím překladačem céčka:
static int __pyx_f_13add_numbers_7_add_two_numbers(int __pyx_v_x, int __pyx_v_y) {
int __pyx_r;
(void)(printf(((char const *)"%i\n"), __pyx_v_x));
__pyx_r = (__pyx_v_x + __pyx_v_y);
goto __pyx_L0;
/* function exit code */
__pyx_L0:;
return __pyx_r;
}
11. Pythonovské seznamy a céčková pole
Seznamy a n-tice jsou sice v Pythonu základními a současně i velmi užitečnými složenými datovými typy, ovšem kvůli tomu, že jsou nehomogenní, se s nimi musí zacházet poměrně neefektivně. Navíc je neefektivní i samotné uložení těchto datových typů v operační paměti. Řešením je použití klasických céčkových polí s případným převodem seznamů na pole. To lze provést například vytvořením klasického céčkového pole s prvky zadaného typu:
cdef array.array byte_array = array.array('B')
cdef array.array int_array = array.array('i')
cdef array.array a = array.array('i', [1, 2, 3])
Důležité je specifikovat typ prvků pole:
| Signatura | Typ v C |
|---|---|
| b | signed char |
| B | unsigned char |
| u | Py_UNICODE |
| h | signed short |
| H | unsigned short |
| i | signed int |
| I | unsigned int |
| l | signed long |
| L | unsigned long |
| q | signed long long |
| Q | unsigned long long |
| f | float |
| d | double |
Ve skutečnosti není takto vytvořené pole přesnou obdobou céčkového pole, protože s ním můžeme provádět i operace, které spíše odpovídají dynamicky alokovanému poli:
// změna velikosti int resize(array self, Py_ssize_t n) // přidání nových prvků do pole (musí ovšem odpovídat jejich datový typ) cdef inline int extend_buffer(array self, char* stuff, Py_ssize_t n) // připojení obsahu druhého pole (opět musí odpovídat datový typ prvků) cdef inline int extend(array self, array other)
Takto vytvořené pole lze do funkcí předat přes ukazatel (referencí) příslušného typu, tj. například:
cdef void test(char *byte_array) nogil:
...
...
...
12. Předchozí varianta benchmarku a oblasti, kde je možné provést optimalizace
Nyní již máme k dispozici všechny potřebné informace nutné pro úpravu našeho benchmarku pro výpočet Mandelbrotovy množiny. Naším cílem bude dosažení rychlosti srovnatelné s variantou naprogramovanou v čistém ANSI C. Jen pro připomenutí – předchozí varianta, s níž jsme končili minulý článek, vypadala následovně. Nejedná se o špatné řešení, ovšem již nyní je nutné říct, že ho můžeme vylepšit a cca dvojnásobně urychlit:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
import palette_mandmap
from sys import argv, exit
cdef calc_mandelbrot(int width, int height, int maxiter, palette):
cdef double zx
cdef double zy
cdef double zx2
cdef double zy2
cdef double cx
cdef double cy
cdef int r
cdef int g
cdef int b
cdef int i
print("P3")
print("{w} {h}".format(w=width, h=height))
print("255")
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
r = palette[i][0]
g = palette[i][1]
b = palette[i][2]
print("{r} {g} {b}".format(r=r, g=g, b=b))
cx += 3.0/width
cy += 3.0/height
if __name__ == "__main__":
if len(argv) < 4:
print("usage: python mandelbrot width height maxiter")
exit(1)
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
calc_mandelbrot(width, height, maxiter, palette_mandmap.palette)
13. Použití pole s barvovou paletou
Nyní budeme muset provést ve zdrojovém kódu benchmarku několik úprav. První úprava se týká přístupu k n-tici s barvovou paletou. Jedná se konkrétně o tento kód:
cdef calc_mandelbrot(int width, int height, int maxiter, palette):
...
...
...
r = palette[i][0]
g = palette[i][1]
b = palette[i][2]
Problém spočívá v tom, že přístup k pythonovské n-tici nebo seznamu nebude nikdy optimální a bude se zbytečně provádět převod z PyObject * na číslo atd. atd. Tento kód se sice nevolá v nejvnitřnější smyčce, ale i tak může výpočet zdržovat – pro obrázek o rozlišení 1000×1000 pixelů se bude do seznamu nebo n-tice přistupovat 3 000 000×. Úprava spočívá v použití jednorozměrného pole:
cdef array.array palette = array.array('B')
for color in palette_mandmap.palette:
for component in color:
palette.append(component)
k jehož prvkům se bude přistupovat takto:
cdef unsigned char r cdef unsigned char g cdef unsigned char b cdef int index index = i * 3 r = palette[index] g = palette[index+1] b = palette[index+2]
Výsledkem bude kód minimálně srovnatelný s variantou naprogramovanou v ANSI C:
__pyx_v_index = (__pyx_v_i * 3); __pyx_v_r = (__pyx_v_palette[__pyx_v_index]); __pyx_v_g = (__pyx_v_palette[(__pyx_v_index + 1)]); __pyx_v_b = (__pyx_v_palette[(__pyx_v_index + 2)]);
14. Odstranění kontrol při dělení
Jen krátce se zmiňme o tom, že Cython implicitně vkládá do céčkového kódu testy na dělení nulou. V našem konkrétním případě vypadají takto (kód jsem pro větší čitelnost upravil):
/*
* cy += 3.0/height
*/
if (unlikely(__pyx_v_width == 0)) {
PyErr_SetString(PyExc_ZeroDivisionError, "float division");
__PYX_ERR(0, 56, __pyx_L1_error)
}
__pyx_v_cx = (__pyx_v_cx + (3.0 / __pyx_v_width));
}
/*
* cy += 3.0/height
*/
if (unlikely(__pyx_v_height == 0)) {
PyErr_SetString(PyExc_ZeroDivisionError, "float division");
__PYX_ERR(0, 57, __pyx_L1_error)
}
Sice se nejedná o implementačně příliš složité operace, ale i tak je můžeme odstranit, a to velmi jednoduše úpravou hlavičky funkce, resp. přesněji přidáním anotace před hlavičku:
@cython.cdivision(True) cdef void calc_mandelbrot(int width, int height, int maxiter, unsigned char *palette):
15. Náhrada print za printf
Další úprava je vyžádána tím, že budeme chtít z celé funkce pro výpočet Mandelbrotovy množiny odstranit GIL. Proto nahradíme veškeré volání funkce print za céčkovou funkci printf.
Původní kód:
print("P3")
print("{w} {h}".format(w=width, h=height))
print("255")
...
...
...
r = palette[i][0]
g = palette[i][1]
b = palette[i][2]
print("{r} {g} {b}".format(r=r, g=g, b=b))
...
...
...
Nový kód:
printf("P3\n%d %d\n255\n", width, height)
...
...
...
r = palette[index]
g = palette[index+1]
b = palette[index+2]
printf("%d %d %d\n", r, g, b)
...
...
...
Odměnou nám bude mnohem kratší a čitelnější výsledek.
16. Odstranění GIL
Tímto tématem jsme se již zabývali v deváté kapitole, takže jen krátce – volání jakýchkoli funkcí souvisejících s GILem můžeme odstranit, protože jsme mj. provedli náhradu print za printf. Změní se tedy hlavička funkce pro výpočet Mandelbrotovy množiny na finální podobu:
@cython.cdivision(True) cdef void calc_mandelbrot(int width, int height, int maxiter, unsigned char *palette) nogil:
17. Finální podoba benchmarku, srovnání s variantou naprogramovanou v céčku
Nyní si již můžeme ukázat výslednou verzi benchmarku upraveného takovým způsobem, aby byl výsledkem jeho transpřekladu do céčka co nejlepší kód. Zda se nám to skutečně povedlo se dozvíme po spuštění benchmarku a porovnání výsledků s výsledky předchozími. V kódu jsou zvýrazněny všechny speciality Cythonu:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
import palette_mandmap
from sys import argv, exit
import cython
from cpython cimport array
from libc.stdio cimport printf
@cython.cdivision(True)
cdef void calc_mandelbrot(int width, int height, int maxiter, unsigned char *palette) nogil:
cdef double zx
cdef double zy
cdef double zx2
cdef double zy2
cdef double cx
cdef double cy
cdef unsigned char r
cdef unsigned char g
cdef unsigned char b
cdef int i
cdef int index
printf("P3\n%d %d\n255\n", width, height)
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
index = i * 3
r = palette[index]
g = palette[index+1]
b = palette[index+2]
printf("%d %d %d\n", r, g, b)
cx += 3.0/width
cy += 3.0/height
cdef array.array palette = array.array('B')
if __name__ == "__main__":
if len(argv) < 4:
print("usage: python mandelbrot width height maxiter")
exit(1)
for color in palette_mandmap.palette:
for component in color:
palette.append(component)
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
calc_mandelbrot(width, height, maxiter, palette.data.as_uchars)
Jen pro porovnání – takto vypadá varianta benchmarku naprogramovaná v ANSI C:
#include <stdlib.h>
#include <stdio.h>
#include "palette_mandmap.h"
void calc_mandelbrot(unsigned int width, unsigned int height, unsigned int maxiter, unsigned char palette[][3])
{
puts("P3");
printf("%d %d\n", width, height);
puts("255");
double cy = -1.5;
int y;
for (y=0; y<height; y++) {
double cx = -2.0;
int x;
for (x=0; x<width; x++) {
double zx = 0.0;
double zy = 0.0;
unsigned int i = 0;
while (i < maxiter) {
double zx2 = zx * zx;
double zy2 = zy * zy;
if (zx2 + zy2 > 4.0) {
break;
}
zy = 2.0 * zx * zy + cy;
zx = zx2 - zy2 + cx;
i++;
}
unsigned char *color = palette[i];
unsigned char r = *color++;
unsigned char g = *color++;
unsigned char b = *color;
printf("%d %d %d\n", r, g, b);
cx += 3.0/width;
}
cy += 3.0/height;
}
}
int main(int argc, char **argv)
{
if (argc < 4) {
puts("usage: ./mandelbrot width height maxiter");
return 1;
}
int width = atoi(argv[1]);
int height = atoi(argv[2]);
int maxiter = atoi(argv[3]);
calc_mandelbrot(width, height, maxiter, palette);
return 0;
}
18. Výsledky všech benchmarků
Výsledky prezentované v následující tabulce hovoří jasně – optimalizace vysvětlené v předchozích kapitolách mají velký význam pro rychlost výsledného kódu a navíc je možné dosáhnout (a to relativně snadno) rychlosti plně srovnatelné s ANSI C. Přitom je Cythoní kód kratší a většinou i čitelnější:
| Rozlišení | CPython 2 | CPython 3 | Jython | RPython | ANSI C | Cython | Cython (typy) | Cython (optim) |
|---|---|---|---|---|---|---|---|---|
| 16×16 | 0,01 | 0,03 | 2,25 | 0,00 | 0,00 | 0,03 | 0,03 | 0,02 |
| 24×24 | 0,01 | 0,03 | 1,87 | 0,00 | 0,00 | 0,02 | 0,02 | 0,02 |
| 32×32 | 0,02 | 0,03 | 1,95 | 0,00 | 0,00 | 0,03 | 0,02 | 0,02 |
| 48×48 | 0,03 | 0,04 | 2,14 | 0,00 | 0,00 | 0,03 | 0,02 | 0,02 |
| 64×64 | 0,05 | 0,06 | 2,02 | 0,00 | 0,00 | 0,04 | 0,03 | 0,02 |
| 96×96 | 0,09 | 0,10 | 2,17 | 0,01 | 0,00 | 0,06 | 0,03 | 0,02 |
| 128×128 | 0,16 | 0,16 | 2,52 | 0,02 | 0,00 | 0,10 | 0,04 | 0,02 |
| 192×192 | 0,34 | 0,34 | 2,73 | 0,05 | 0,01 | 0,20 | 0,05 | 0,03 |
| 256×256 | 0,57 | 0,59 | 2,79 | 0,07 | 0,02 | 0,34 | 0,08 | 0,03 |
| 384×384 | 1,27 | 1,34 | 3,93 | 0,16 | 0,04 | 0,74 | 0,16 | 0,06 |
| 512×512 | 2,26 | 2,34 | 5,48 | 0,29 | 0,07 | 1,32 | 0,27 | 0,09 |
| 768×768 | 5,08 | 5,52 | 9,41 | 0,65 | 0,16 | 2,89 | 0,60 | 0,18 |
| 1024×1024 | 9,32 | 9,69 | 13,70 | 1,17 | 0,29 | 5,17 | 1,03 | 0,32 |
| 1536×1536 | 24,48 | 21,99 | 28,50 | 2,61 | 0,67 | 11,63 | 2,28 | 0,69 |
| 2048×2048 | 36,27 | 36,70 | 54,22 | 4,62 | 1,19 | 21,39 | 4,15 | 1,21 |
| 3072×3072 | 84,82 | 83,41 | 104,16 | 10,53 | 2,68 | 46,42 | 10,14 | 2,74 |
| 4096×4096 | 150,31 | 152,21 | 203,18 | 18,64 | 4,75 | 88,67 | 16,42 | 4,80 |
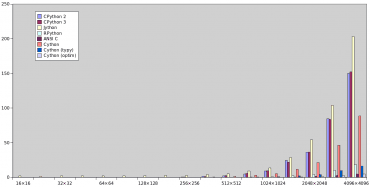
Obrázek 7: Porovnání doby výpočtu Mandelbrotovy množiny všemi sedmi variantami: CPython 2, CPython 3, Jython, RPython, ANSI C, Cython bez type hintů, Cython s type hinty a plně optimalizovaný kód v Cythonu.
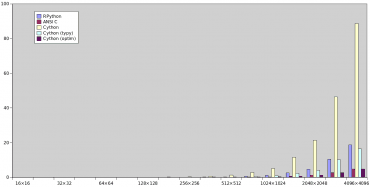
Obrázek 8: Porovnání doby výpočtu Mandelbrotovy množiny RPythonem, Cythonem (bez i s type hinty + plně optimalizovaná varianta) a verzí naprogramovanou přímo v ANSI C.
18. Repositář s demonstračními příklady
Všechny demonstrační příklady, které jsme si v dnešním článku ukázali, naleznete na adrese https://github.com/tisnik/cython-examples. Následují odkazy na jednotlivé příklady (pro jejich spuštění je nutné mít nainstalován Cython a jeho závislosti, především tedy překladač céčka a taktéž vývojové varianty knihoven pro Python včetně jejich hlavičkových souborů):
20. Odkazy na Internetu
- Cython (home page)
http://cython.org/ - Cython (wiki)
https://github.com/cython/cython/wiki - Cython (Wikipedia)
https://en.wikipedia.org/wiki/Cython - Cython (GitHub)
https://github.com/cython/cython - Python Implementations: Compilers
https://wiki.python.org/moin/PythonImplementations#Compilers - EmbeddingCython
https://github.com/cython/cython/wiki/EmbeddingCython - The Basics of Cython
http://docs.cython.org/en/latest/src/tutorial/cython_tutorial.html - Overcoming Python's GIL with Cython
https://lbolla.info/python-threads-cython-gil - GlobalInterpreterLock
https://wiki.python.org/moin/GlobalInterpreterLock - The Magic of RPython
https://refi64.com/posts/the-magic-of-rpython.html - RPython: Frequently Asked Questions
http://rpython.readthedocs.io/en/latest/faq.html - RPython’s documentation
http://rpython.readthedocs.io/en/latest/index.html - RPython (Wikipedia)
https://en.wikipedia.org/wiki/PyPy#RPython - Getting Started with RPython
http://rpython.readthedocs.io/en/latest/getting-started.html - PyPy (home page)
https://pypy.org/ - PyPy (dokumentace)
http://doc.pypy.org/en/latest/ - Localized Type Inference of Atomic Types in Python (2005)
http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.90.3231 - Numba
http://numba.pydata.org/ - Tutorial: Writing an Interpreter with PyPy, Part 1
https://morepypy.blogspot.com/2011/04/tutorial-writing-interpreter-with-pypy.html - List of numerical analysis software
https://en.wikipedia.org/wiki/List_of_numerical_analysis_software - Pixie: lehký skriptovací jazyk s „kouzelnými“ schopnostmi
https://www.root.cz/clanky/pixie-lehky-skriptovaci-jazyk-s-kouzelnymi-schopnostmi/ - Programovací jazyk Pixie: funkce ze základní knihovny a použití FFI
https://www.root.cz/clanky/programovaci-jazyk-pixie-funkce-ze-zakladni-knihovny-a-pouziti-ffi/ - The future can be written in RPython now (článek z roku 2010)
http://blog.christianperone.com/2010/05/the-future-can-be-written-in-rpython-now/ - PyPy is the Future of Python (článek z roku 2010)
https://alexgaynor.net/2010/may/15/pypy-future-python/ - Portal:Python programming
https://en.wikipedia.org/wiki/Portal:Python_programming - RPython Frontend and C Wrapper Generator
http://www.codeforge.com/article/383293 - PyPy’s Approach to Virtual Machine Construction
https://bitbucket.org/pypy/extradoc/raw/tip/talk/dls2006/pypy-vm-construction.pdf - Tutorial: Writing an Interpreter with PyPy, Part 1
https://morepypy.blogspot.com/2011/04/tutorial-writing-interpreter-with-pypy.html - A simple interpreter from scratch in Python (part 1)
http://www.jayconrod.com/posts/37/a-simple-interpreter-from-scratch-in-python-part-1 - Brainfuck Interpreter in Python
https://helloacm.com/brainfuck-interpreter-in-python/


























