Obsah
1. PyTorch: problematika rozpoznávání a klasifikace obrázků
2. První verze generátoru trénovacích obrázků číslic od 0 do 9
3. Konstrukce dvourozměrné matice 8×8 bodů pro vybranou číslici
4. Kooperace mezi knihovnami Matplotlib a NumPy: vizualizace obsahu 2D matice
5. Vizualizace matic s obrazy číslic v rastru 8×8
6. Vizualizace všech deseti matic s číslicemi
7. Problém rozpoznávání číslic na reálných obrázcích
8. Vliv šumu na kvalitu predikcí neuronové sítě
9. Vizualizace matice reprezentující zašuměnou číslici
10. Vizualizace vlivu parametru level na způsob zašumění matice s číslicí
12. Posun číslic v matici pro přípravu trénovacích dat
13. Zobrazení všech variant posunů matice s číslicí 2 o &plusm; jeden nebo dva pixely
14. Numerické ohodnocení klasifikační neuronové sítě pro rozpoznávání obrázků
16. Příklad klasifikační neuronové sítě se dvěma výstupy
18. Vrstvy v konvolučních neuronových sítích
19. Repositář s demonstračními příklady
1. PyTorch: problematika rozpoznávání a klasifikace obrázků
Na předchozí tři části [1] [2] [3] seriálu o knihovně PyTorch, v nichž jsme se seznámili se základními postupy, které se používají při tvorbě umělých neuronových sítí s pravidelnou strukturou tvořenou jednotlivými vrstvami, u nichž učení probíhá s využitím takzvaného backpropagation algoritmu (algoritmu zpětného šíření), dnes navážeme. Začneme se totiž zabývat problematikou rozpoznávání a klasifikace rastrových obrázků. Ty sice budou zpočátku velmi malé a budou obsahovat poměrně dobře predikovatelná data, ovšem i takto malé obrázky nám umožní ukázat některé nevýhody klasických obecných neuronových sítí při jejich aplikaci na rastrová data.
Ve druhé části dnešního článku se ve stručnosti seznámíme s neuronovými sítěmi provádějícími klasifikaci (a nikoli regresi). Právě tento typ neuronových sítí nám umožní realizovat rozpoznávání obrázků stylem „zde je pes“ nebo „tady jsou tři stromy“. S tímto tématem souvisí i problematika vyjádření kvality sítě s využitím matice záměn (confusion matrix).
V závěru článku se navíc seznámíme s principy, na nichž jsou postaveny takzvané konvoluční neuronové sítě. Ty jsou v současnosti velmi populární, a to hned z několika důvodů – po jejich natrénování sítě (to je sice časově náročné, ovšem s moderními GPU již většinou uspokojivě řešitelné) jsou již konvoluční sítě poměrně rychlé a především se rozšiřují možnosti, kde je možné tyto sítě prakticky použít (doprava, tedy například automatické řízení vozidel, průmysl atd.).
Tím získáme všechny dílky potřebné k tomu, abychom příště vytvořili skutečnou konvoluční síť, natrénovali ji a nakonec ověřili její kvalitu s využitím matice záměn.
2. První verze generátoru trénovacích obrázků číslic od 0 do 9
Jak jsme si již řekli v úvodní kapitole, budeme se snažit s využitím jednoduchých neuronových sítí rozpoznávat objekty na velmi malých obrázcích. Konkrétně se bude zpočátku jednat o vstupní obrázky s pevným rozlišením pouhých 8×8 pixelů, což nám mj. umožní velmi rychlý tréning sítě a samozřejmě i její následnou validaci (a to bez nutnosti zdlouhavého tréninku s využitím GPU; prozatím si vystačíme s výpočty na CPU).
Rastrové obrázky budou reprezentovány ve stupních šedi a úkolem postupně vytvářené neuronové sítě bude na těchto obrázcích rozpoznat číslice 0 až 9 zapsané pro jednoduchost předem známým fontem (příště už budeme mít horší úkol, protože číslice budou napsány rukou, navíc mnoha autory). Abychom získali představu, jak tyto číslice vypadají, necháme si vygenerovat testovací obrázky, a to z následujících vstupních dat:
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
# triviální výpis
print(digits)
Každá číslice, jejíž tvar je zakódován v n-tici digits, je reprezentována osmicí bajtů, protože každý bajt reprezentuje osm sousedních pixelů. Celkem tedy vstupní data obsahují osmdesát bajtů, protože máme deset číslic, každou uloženou v osmi bajtech:
((0, 60, 102, 118, 110, 102, 60, 0), (0, 24, 28, 24, 24, 24, 126, 0), (0, 60, 102, 48, 24, 12, 126, 0), (0, 126, 48, 24, 48, 102, 60, 0), (0, 48, 56, 60, 54, 126, 48, 0), (0, 126, 6, 62, 96, 102, 60, 0), (0, 60, 6, 62, 102, 102, 60, 0), (0, 126, 96, 48, 24, 12, 12, 0), (0, 60, 102, 60, 102, 102, 60, 0), (0, 60, 102, 124, 96, 48, 28, 0))
3. Konstrukce dvourozměrné matice 8×8 bodů pro vybranou číslici
Výše uvedený způsob uložení bitových map s číslicemi je sice velmi úsporný, ovšem příliš se nehodí pro trénink neuronových sítí (minimálně ne v takové formě, jakou nám nabízí knihovna PyTorch). Proto musíme mít k dispozici pomocnou funkci, která pro zadanou číslici 0–9 vrátí matici o rozměrech 8×8 prvků obsahující hodnoty 0,0 nebo 1,0, v závislosti na tom, zda příslušný prvek odpovídá černému pixelu nebo naopak pixelu bílému. Povšimněte si, že i když by bylo možné vytvořit matici s pravdivostními hodnotami True/False nebo celočíselnými hodnotami 0/1, použijeme hodnoty s plovoucí řádovou čárkou. To nám později umožní nejenom simulovat šum, ale i přímo takové matice použít pro vstup do neuronových sítí.
Převodní funkce může vypadat následovně:
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
Ověřme si, jak například bude vypadat výsledná dvourozměrná matice s reprezentací číslice 2 (ta je nesymetrická, takže si ověříme korektnost převodu):
import numpy as np
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
# vytvoření matice, kterou budeme vizualizovat
array = digit_to_array(digits, 2)
# výpis pole s reprezentací číslice 2
print(array)
Výsledná matice by měla vypadat následovně:
[[0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 1. 1. 1. 0. 0.] [0. 1. 1. 0. 0. 1. 1. 0.] [0. 0. 0. 0. 1. 1. 0. 0.] [0. 0. 0. 1. 1. 0. 0. 0.] [0. 0. 1. 1. 0. 0. 0. 0.] [0. 1. 1. 1. 1. 1. 1. 0.] [0. 0. 0. 0. 0. 0. 0. 0.]]
Pro zajímavost si můžeme doplnit krátký kód, který matici převede do tisknutelné podoby a navíc výslednou „bitmapu“ orámuje:
# převod na tisknutelnou podobu
print("+--------+")
for row in array:
print("|", end="")
for item in row:
print(" " if item==0.0 else "*", end="")
print("|")
print("+--------+")
Nyní bude výsledek vypadat následovně:
+--------+ | | | **** | | ** ** | | ** | | ** | | ** | | ****** | | | +--------+
4. Kooperace mezi knihovnami Matplotlib a NumPy: vizualizace obsahu 2D matice
V praxi, když začneme pracovat s obrázky ve stupních šedi, se zašuměnými obrázky atd., již není zobrazení obrázku na konzoli ideální. Pokusme se tedy využitím kooperace mezi knihovnami Matplotlib a NumPy. Konkrétně si ukážeme vizualizaci obsahu dvourozměrné matice (NumPy podporuje obecná n-rozměrná pole a matice jsou tedy pouze podtypem). Vytvoříme si matici o rozměrech 10×10 prvků a naplníme ji náhodnými hodnotami. Výsledek si necháme zobrazit na grafu a tento graf taktéž uložíme do souboru (formát PNG):
#!/usr/bin/env python
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
import numpy as np
# vytvoření matice, kterou budeme vizualizovat
array = np.random.rand(10, 10)
# vykreslení
plt.matshow(array)
# uložení vizualizované matice
plt.savefig("random.png")
# vizualizace na obrazovku
plt.show()
# finito
Výsledek bude vypadat následovně:
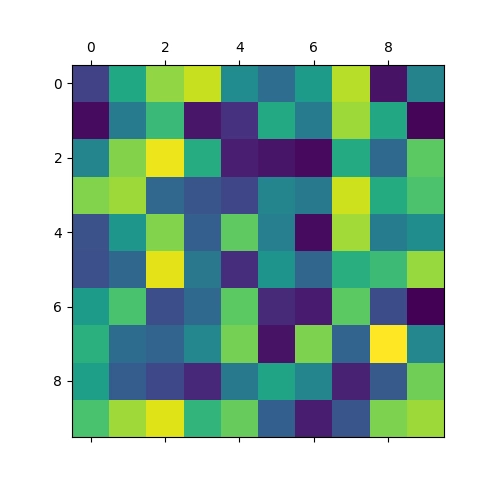
Obrázek 1: Vizualizace pole s náhodným obsahem.
Povšimněte si, že se při vizualizaci použily nepravé barvy. Těch se později zbavíme, protože nás budou spíše mást. Prozatím jsou však užitečné.
5. Vizualizace matic s obrazy číslic v rastru 8×8
Podívejme se nyní na způsob vizualizace matic s rozměry 8×8, jejichž prvky mají hodnoty 0,0 nebo 1,0. Tyto matice mohou obsahovat bitmapy číslic v rastru 8×8 pixelů. Nejdříve při vizualizaci použijeme nepravé barvy, přesněji řečeno barvovou paletu, která provádí mapování mezi hodnotami uloženými v matici na barvovou škálu. Algoritmus nejdříve zjistí minimální a maximální hodnoty prvků (což jsou v našem případě hodnoty 0,0 a 1,0) a následně určí měřítko použité při hledání barev:
import matplotlib.pyplot as plt
import numpy as np
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
# vytvoření matice, kterou budeme vizualizovat
array = digit_to_array(digits, 2)
# vykreslení matice
plt.matshow(array)
# uložení vizualizované matice
plt.savefig("conv_nn_03.png")
# vizualizace matice na obrazovce
plt.show()
Opět jsme si nechali zobrazit matici odpovídající číslici 2:

Obrázek 2: Matice číslice 2 zobrazená v nepravých barvách.
Alternativně je možné zavoláním plt.gray() dosáhnout převodu na stupně šedi, což může být v tomto případě výhodnější způsob vizualizace matice s de facto černobílým obrázkem. Opět si to ukažme:
import matplotlib.pyplot as plt
import numpy as np
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
# vytvoření matice, kterou budeme vizualizovat
array = digit_to_array(digits, 2)
# vykreslení matice
plt.matshow(array)
# převod na stupně šedi
plt.gray()
# uložení vizualizované matice
plt.savefig("conv_nn_04.png")
# vizualizace matice na obrazovce
plt.show()
Výsledek:
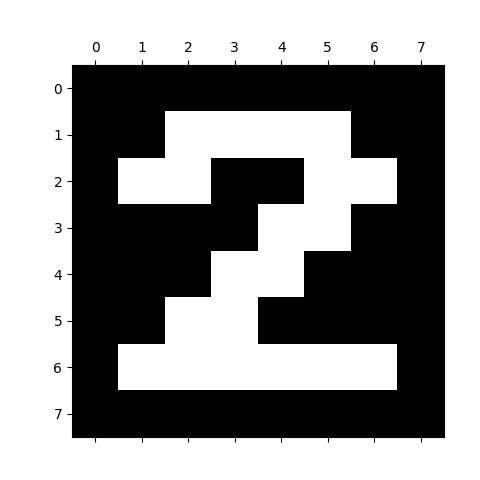
Obrázek 3: Matice číslice 2 zobrazená ve stupních šedi.
6. Vizualizace všech deseti matic s číslicemi
V navazujícím článku budeme zobrazovat velké množství číslic, resp. přesněji řečeno vizualizaci jejich matic. Pravděpodobně by nebylo praktické každou číslici vykreslit do samostatného grafu. Můžeme však využít další vlastností Matplotlibu – jeho schopnosti do jediné plochy grafu přidat více menších grafů. Plocha je rozdělena na pomyslnou mřížku, jejíž rozměry zadáváme při přidávání menšího grafu do jednotlivých políček:
ax = plt.subplot(počet řádků, počet sloupců, pozice/index v rámci mřížky)
Snadno tak můžeme zobrazit všech deset číslic do mřížky se třemi sloupci a čtyřmi řádky. Dvě políčka nebudou obsazena, což nám umožňuje simulovat rozložení numerických kláves na číselníku telefonu:
import matplotlib.pyplot as plt
import numpy as np
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 6.4))
plt.axis("off")
# vykreslení číslic 1-9
for digit in range(1, 10):
array = digit_to_array(digits, digit)
ax = plt.subplot(4, 3, digit)
plt.gray()
ax.matshow(array)
# dokreslení číslice 0
array = digit_to_array(digits, 0)
ax = plt.subplot(4, 3, 11)
plt.gray()
ax.matshow(array)
# uložení vizualizované matice
plt.savefig("conv_nn_05.png")
# vizualizace matice na obrazovce
plt.show()
Výsledky:

Obrázek 4: Vizualizace matic všech deseti číslic.
7. Problém rozpoznávání číslic na reálných obrázcích
Mohlo by se zdát, že pro rozpoznání obrázků nám stačí si natrénovat běžnou neuronovou síť se 64 vstupy a deseti výstupy. Jednalo by se o klasifikační síť, na jejíž vstup by se přivedly hodnoty všech 64 pixelů a na výstupu by se (ideálně) měla objevit hodnota 1,0 na jednom z výstupů a naopak hodnoty 0,0 na ostatních devíti výstupech. Ve skutečnosti je však nutné přiznat, že je to v praxi mnohem složitější, a to minimálně ze tří důvodů:
- Takto natrénovaná neuronová síť dokáže rozpoznat pouze jeden font, což obecně bude vadit, například ve chvíli, kdy namísto námi připravených trénovacích dat použijeme například ručně psané číslice z již zmíněné databáze MNIST. A raději ji vůbec nepouštějte na obrázky získané ze systémů CAPTCHA :-)
- Klasickou neuronovou síť je možné velmi snadno zmást i při použití stále stejného fontu. Postačuje pouze obraz číslice posunout o jeden jediný pixel (jakýmkoli směrem)!
- Síť nemusí být dobře připravena na klasifikaci zašuměných obrázků, tedy například obrázků číslic získaných z fotografií, po naskenování číslic z papíru, ale například číslic uložených do formátů se ztrátovou komprimací (JPEG) atd.
8. Vliv šumu na kvalitu predikcí neuronové sítě
Po natrénování neuronové sítě s využitím pouhých deseti vstupních obrázků by se mohlo stát, že by síť prakticky vůbec nebyla schopna rozeznat i nepatrně změněná vstupní data. Proto funkci pro vytvoření trénovacích obrázků vhodně pozměníme takovým způsobem, že se do obrázků zanese šum. Pro vytvoření šumu používám pro jednoduchost funkci np.random.rand, ovšem v případě potřeby samozřejmě můžete využít i funkci pro generování náhodných hodnot s normálním rozložením atd.:
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
Povšimněte si dále, že i zašuměné obrázky mají přesně stanovenou hranici mezi pixely, které tvoří číslici a pixely tvořícími pozadí (záleží na hodnotě level v rozsahu od 0,0 do 1,0). Tuto část si samozřejmě můžete upravit, a to i takovým způsobem, aby tato hranice byla z obou stran překračována. Ovšem takto obecně naučená síť nebude dávat jednoznačné výsledky – ostatně si to vyzkoušíme příště.
9. Vizualizace matice reprezentující zašuměnou číslici
Skript, po jehož spuštění se provede „zašumění“ matice s reprezentací číslice 2 a následné vykreslení takto upravené matice, vypadá takto:
import matplotlib.pyplot as plt
import numpy as np
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
# vytvoření matice, kterou budeme vizualizovat
array = digit_to_array(digits, 2)
array = add_noise(array, 0.2)
# vykreslení matice
plt.matshow(array)
# převod na stupně šedi
plt.gray()
# uložení vizualizované matice
plt.savefig("conv_nn_06.png")
# vizualizace matice na obrazovce
plt.show()
Zašuměný obraz číslice 2 nyní vypadá následovně:
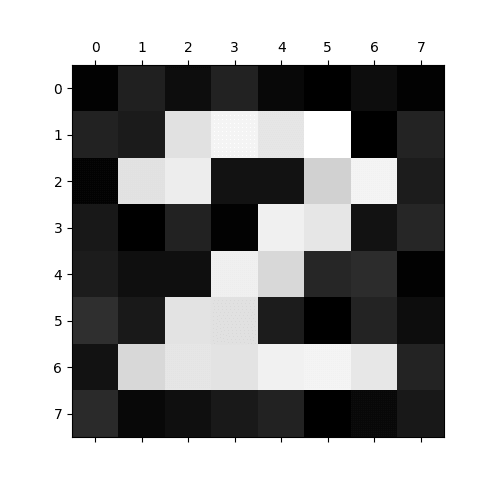
Obrázek 5: Vizualizace matice se zašuměnou číslicí 2.
10. Vizualizace vlivu parametru level na způsob zašumění matice s číslicí
Jak jsme si již řekli v předchozím textu, může parametr level, který ovlivňuje výpočet šumu, nabývat hodnot od 0,0 do 1,0. Vyzkoušejme si tedy, jak budou vypadat matice číslic v případě, kdy postupně úroveň šumu zvyšujeme v tomto rozsahu. Opět využijeme možnost vykreslení více grafů do jedné plochy:
import matplotlib.pyplot as plt
import numpy as np
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 6.4))
plt.axis("off")
for i in range(1, 17):
array = digit_to_array(digits, 2)
level = (i - 1.0) / 16.0
array = add_noise(array, level)
ax = plt.subplot(4, 4, i)
# plt.gray()
ax.matshow(array)
# uložení vizualizované matice
plt.savefig("conv_nn_07.png")
# vizualizace matice na obrazovce
plt.show()
Z vizualizace je patrné, že pro úrovně vyšší než 0,5 je výsledná číslice prakticky nerozeznatelná (ovšem to je logický důsledek):
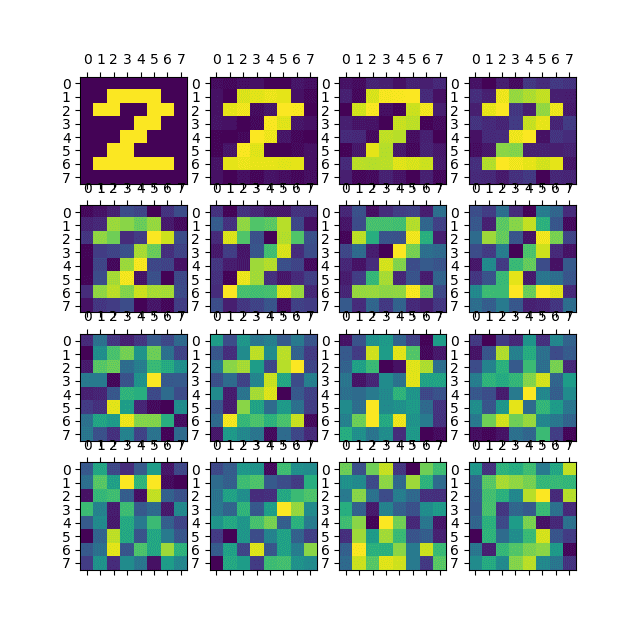
Obrázek 6: Vizualizace matice se zašuměnou číslicí 2, úroveň šumu se postupně zvyšuje.
11. Rozeznání číslic 5, 6 a 8
Font s číslicemi, který používáme, má jednu zajímavou vlastnost – rozdíly mezi číslicemi 5, 6 a 8 jsou pouze několika pixelové (a to existují i fonty, ve kterých je rozdíl jen jednopixelový). Bude tedy zajímavé zjistit, jak dobře budeme moci rozlišit tyto tři číslice v případě, že se postupně bude zvyšovat úroveň zašumění. Další demonstrační příklad zobrazí tři sloupce s vizualizovanými maticemi s číslicemi 5, 6 a 8. Úroveň šumu postupně roste od 0,0 do 1,0:
import matplotlib.pyplot as plt
import numpy as np
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
# velikost obrázku s grafem
plt.subplots(figsize=(3.2, 9.8))
plt.axis("off")
for j, digit in enumerate([5, 6, 8]):
for i in range(1, 12):
level = (i - 1.0) / 12.0
array = digit_to_array(digits, digit)
array = add_noise(array, level)
ax = plt.subplot(12, 3, j + 1 + i * 3)
ax.matshow(array)
ax.axis("off")
# uložení vizualizované matice
plt.savefig("conv_nn_08.png")
# vizualizace matice na obrazovce
plt.show()
Schválně si sami vyzkoušejte, jak dobře dokážete číslice rozeznat. Vaše vlastní neuronová síť je přitom mnohem výkonnější, než budou konvoluční umělé sítě, které si otestujeme příště:
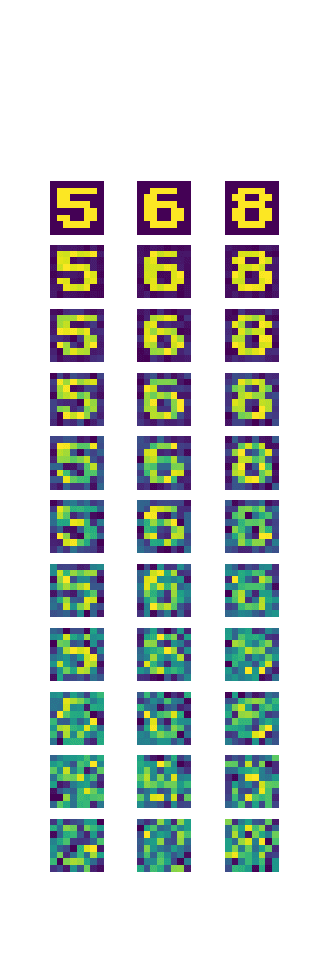
Obrázek 7: Matice číslic 5, 6 a 8 s postupně rostoucí úrovní šumu.
12. Posun číslic v matici pro přípravu trénovacích dat
Neuronovou síť je nutné natrénovat i na takových číslicích, které jsou v libovolném směru posunuty. Vzhledem k tomu, že možnosti posunu číslic v rastru 8×8 pixelů jsou velmi malé, bude mít v našem případě význam pouze posun o ±2 pixely v libovolném směru: horizontálním, vertikálním a/nebo šikmém. Pro posun v rámci matice kupodivu v knihovně NumPy neexistuje specializovaná funkce, ale to nevadí, protože posun lze nasimulovat rotací realizovanou funkcí numpy.roll zkombinovanou s výplní těch částí matice, které byly orotovány na její druhou stranu. Implementace funkce pro posun může vypadat takto (posun může být jak kladný, tak i záporný):
def shift(arr, x_shift, y_shift):
# horizontální posun
arr = np.roll(arr, x_shift, axis=1)
# výplně těch částí, které byly orotovány na druhou stranu
if x_shift < 0:
arr[:, x_shift:] = 0.0
elif x_shift > 0:
arr[:, :x_shift] = 0.0
# vertikální posun
arr = np.roll(arr, y_shift, axis=0)
# výplně těch částí, které byly orotovány na druhou stranu
if y_shift < 0:
arr[y_shift:] = 0.0
elif y_shift > 0:
arr[:y_shift] = 0.0
return arr
Začlenění této funkce do skriptu, který vykreslí matici posunuté číslice 2, vypadá takto:
import matplotlib.pyplot as plt
import numpy as np
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def shift(arr, x_shift, y_shift):
# horizontální posun
arr = np.roll(arr, x_shift, axis=1)
# výplně těch částí, které byly orotovány na druhou stranu
if x_shift < 0:
arr[:, x_shift:] = 0.0
elif x_shift > 0:
arr[:, :x_shift] = 0.0
# vertikální posun
arr = np.roll(arr, y_shift, axis=0)
# výplně těch částí, které byly orotovány na druhou stranu
if y_shift < 0:
arr[y_shift:] = 0.0
elif y_shift > 0:
arr[:y_shift] = 0.0
return arr
# vytvoření matice, kterou budeme vizualizovat
array = digit_to_array(digits, 2)
array = shift(array, 1, 1)
# vykreslení matice
plt.matshow(array)
# převod na stupně šedi
# plt.gray()
# uložení vizualizované matice
plt.savefig("conv_nn_09.png")
# vizualizace matice na obrazovce
plt.show()
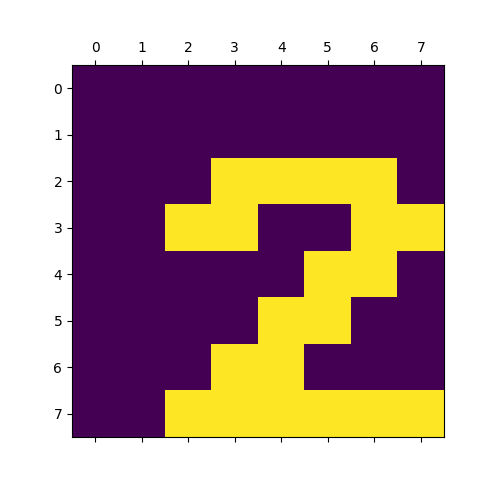
Obrázek 8: Vizualizovaná matice s posunutou číslicí 2.
13. Zobrazení všech variant posunů matice s číslicí 2 o &plusm; jeden nebo dva pixely
Nyní si vizuálně ověříme, jak vypadá matice s číslicí 2, která je posunutá o jeden či dva pixely v libovolném směru. Spuštěním skriptu, jehož zdrojový kód je zobrazen pod tímto odstavcem, získáme celkem 24 obrázků (dvacátý pátý je obrázek původní číslice), které jsou vloženy do jediného grafu:
import matplotlib.pyplot as plt
import numpy as np
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def shift(arr, x_shift, y_shift):
# horizontální posun
arr = np.roll(arr, x_shift, axis=1)
# výplně těch částí, které byly orotovány na druhou stranu
if x_shift < 0:
arr[:, x_shift:] = 0.0
elif x_shift > 0:
arr[:, :x_shift] = 0.0
# vertikální posun
arr = np.roll(arr, y_shift, axis=0)
# výplně těch částí, které byly orotovány na druhou stranu
if y_shift < 0:
arr[y_shift:] = 0.0
elif y_shift > 0:
arr[:y_shift] = 0.0
return arr
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 6.4))
plt.axis("off")
i = 1
for y_shift in range(-2, 3):
for x_shift in range(-2, 3):
array = digit_to_array(digits, 2)
array = shift(array, x_shift, y_shift)
ax = plt.subplot(5, 5, i)
i += 1
ax.matshow(array)
# převod na stupně šedi
plt.gray()
# uložení vizualizované matice
plt.savefig("conv_nn_10.png")
# vizualizace matice na obrazovce
plt.show()
Takto by měly vypadat výsledky:
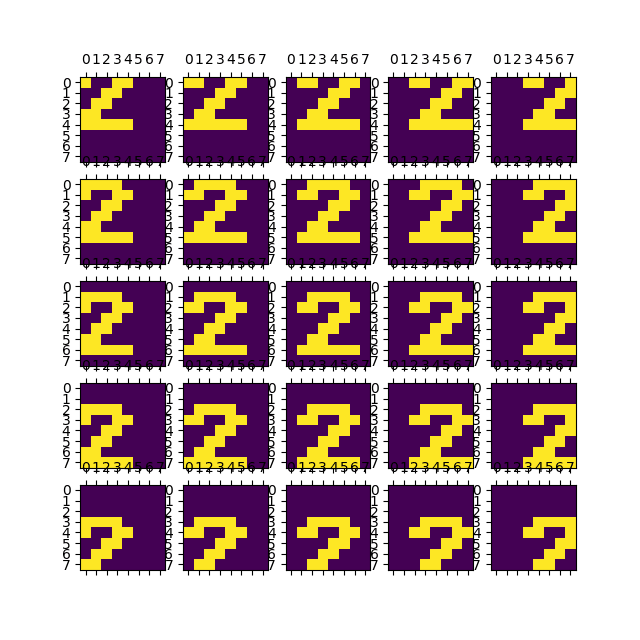
Obrázek 9: Číslice 2, která je posunutá o jeden až dva pixely v libovolném směru.
14. Numerické ohodnocení klasifikační neuronové sítě pro rozpoznávání obrázků
Pro klasifikační neuronové sítě si nevystačíme s výpočtem absolutní či relativní odchylky výsledku od korektní hodnoty. Typicky se pro tyto účely používá matice záměn zmíněná v následující kapitole. Ovšem pomoci nám může i funkce classification_report z knihovny Scikit-learn (již jsme se s ní setkali). Vyzkoušejme tedy, jaké výsledky získáme pro simulované odpovědi (prozatím neexistující) neuronové sítě pro rozpoznávání číslic s odpověďmi očekávanými. Tyto hodnoty jsou uloženy v seznamech y_pred a y_test:
from sklearn.metrics import classification_report y_pred = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9] y_test = [0, 1, 2, 8, 4, 5, 6, 7, 6, 9, 0, 1, 2, 2, 4, 5, 8, 7, 8, 9] # tisk zprávy o výsledcích klasifikace print(classification_report(y_test, y_pred))
Z výsledků získáme informace o tom, které číslice jsou z pohledu predikce sítě nejvíce problematické. Jedná se o číslici 3 a dále o dvojici 6 a 8, které se zaměňují:
precision recall f1-score support
0 1.00 1.00 1.00 2
1 1.00 1.00 1.00 2
2 1.00 0.67 0.80 3
3 0.00 0.00 0.00 0
4 1.00 1.00 1.00 2
5 1.00 1.00 1.00 2
6 0.50 0.50 0.50 2
7 1.00 1.00 1.00 2
8 0.50 0.33 0.40 3
9 1.00 1.00 1.00 2
accuracy 0.80 20
macro avg 0.80 0.75 0.77 20
weighted avg 0.88 0.80 0.83 20
15. Matice záměn
Při zjišťování kvality modelů, které provádí klasifikaci, se s úspěchem používá takzvaná matice záměn neboli confusion matrix. Jedná se o matici, která ve sloupcích obsahuje očekávané hodnoty a v řádcích pak předpovědi/odpovědi modelu (popř. je matice transponovaná, to však nevadí). Pokud model odpoví ve všech případech správně, bude matice obsahovat nenulové hodnoty pouze na hlavní diagonále a tyto hodnoty budou znamenat „očekávalo se X odpovědí A a model takto odpověděl skutečně X-krát“. Ovšem ve chvíli, kdy se model splete, vypíše se tato hodnota mimo hlavní diagonálu; tj. hodnoty mimo hlavní diagonálu znamenají chyby a navíc můžeme zjistit, které odpovědi způsobují modelu největší problémy (tj. například které číslice se nejčastěji zaměňují).
Podívejme se na příklad modelu, který vždy odpoví korektně:
| A B C --+------------ A | 10 0 0 B | 0 20 0 C | 0 0 30
Model pro 10 očekávaných odpovědí A skutečně desetkrát odpověděl „A“ atd. Celkem se provedlo 10+20+30 testů.
Naopak může model nesprávně rozlišovat mezi odpověďmi A a B. Potom může matice vypadat například takto:
| A B C --+------------ A | 7 3 0 B | 0 20 0 C | 0 0 30
Nebo takto:
| A B C --+------------ A | 10 0 0 B | 10 10 0 C | 0 0 30
Zkoumáním obsahu matice záměn můžeme zjistit nejenom citlivost modelu, ale i specificitu modelu (což je mnohdy důležitější atribut – ještě se k němu vrátíme).
Matice záměn může obsahovat i relativní hodnoty, které jsou nezávislé na počtu měření. Maximální hodnota prvku v takové matici je rovna 1.0 a minimální pochopitelně 0.0.
Ukažme si nyní využití matice záměn pro vizualizaci kvality (prozatím neexistující) neuronové sítě rozpoznávající číslice. Správné odpovědi jsou uloženy v seznamu y_test, odpovědi sítě pak v seznamu y_pred. Skript po svém spuštění vypočítá a zobrazí matici záměn:
import matplotlib.pyplot as plt
from sklearn.metrics import ConfusionMatrixDisplay
y_pred = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
y_test = [0, 1, 2, 8, 4, 5, 6, 7, 6, 9, 0, 1, 2, 2, 4, 5, 8, 7, 8, 9]
# výpočet matice záměn
disp = ConfusionMatrixDisplay.from_predictions(
y_test, y_pred,
cmap=plt.cm.Blues,
normalize=None,
)
# zobrazení matice záměn
print(disp.confusion_matrix)
# uložení výsledků
plt.savefig("confusion_matrix.png")
# vykreslení matice záměn
plt.show()
Výsledky, které získáme po spuštění tohoto skriptu:
[[2 0 0 0 0 0 0 0 0 0] [0 2 0 0 0 0 0 0 0 0] [0 0 2 1 0 0 0 0 0 0] [0 0 0 0 0 0 0 0 0 0] [0 0 0 0 2 0 0 0 0 0] [0 0 0 0 0 2 0 0 0 0] [0 0 0 0 0 0 1 0 1 0] [0 0 0 0 0 0 0 2 0 0] [0 0 0 1 0 0 1 0 1 0] [0 0 0 0 0 0 0 0 0 2]]
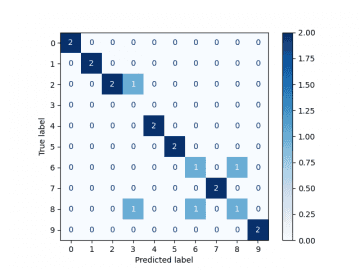
Obrázek 10: Vizualizovaná matice záměn.
Nejvíce problémů tedy způsobuje záměna číslic 6 a 8.
16. Příklad klasifikační neuronové sítě se dvěma výstupy
V dnešním posledním demonstračním příkladu je ukázána velmi jednoduchá klasifikační neuronová síť, která pro dvě vstupní hodnoty v rozsahu 0,0 až 1,0 vrátí informaci o tom, jaký je vztah mezi těmito hodnotami. Síť se naučí do jisté míry rozpoznávat relaci „menší než“ a „rovnost“ (rozšíření na číslice bude snadné):
import torch
from torch import nn
from torch import optim
from torch.utils.data import Dataset, DataLoader
import numpy as np
class NeuralNetwork(nn.Module):
"""Třída reprezentující neuronovou síť."""
def __init__(self, input_dim, hidden_dim, output_dim):
super().__init__()
# vrstvy neuronové sítě
self.layer_1 = nn.Linear(input_dim, hidden_dim)
self.layer_2 = nn.Linear(hidden_dim, hidden_dim)
self.layer_3 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# propagace hodnot přes neuronovou síť
x = torch.nn.functional.sigmoid(self.layer_1(x))
x = torch.nn.functional.sigmoid(self.layer_2(x))
x = torch.nn.functional.sigmoid(self.layer_3(x))
return x
# konfigurace vrstev neuronové sítě
input_dim = 2
hidden_dim = 4
output_dim = 2
# konstrukce neuronové sítě
nn1 = NeuralNetwork(input_dim, hidden_dim, output_dim)
# výpis základních informací o neuronové síti
print(nn1)
# příprava na trénink neuronové sítě
learning_rate = 0.1
loss_fn = nn.BCELoss()
optimizer = optim.SGD(nn1.parameters(), lr=learning_rate)
# konverze původních dat z NumPy do tenzorů
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
# příprava trénovacích dat
X_train = []
y_train = []
for a in np.linspace(0, 1.0, 101):
for b in np.linspace(0, 1.0, 101):
# vstupy
X_train.append([a, b])
# očekávané výstupy
y_train.append([1.0 if a>b else 0.0, 1.0 if abs(a-b)<0.2 else 0.0])
train_data = Data(np.array(X_train), np.array(y_train))
# zpracovat trénovací data
batch_size = 64
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)
print("Batches: ", len(train_dataloader))
# vlastní trénink
print("Training started")
num_epochs = 100
loss_values = []
for epoch in range(num_epochs):
print(f" Epoch {epoch}: ", end="")
last_lost_value = None
for X, y in train_dataloader:
optimizer.zero_grad()
# dopředný tok + zpětný tok + optimalizace
pred = nn1(X)
# výpočet účelové funkce
loss = loss_fn(pred, y)#.unsqueeze(-1))
loss_values.append(loss.item())
loss.backward()
optimizer.step()
last_lost_value = loss.item()
print(".", end="")
print(last_lost_value)
print("Training completed")
# naivní otestování neuronové sítě
for x in np.linspace(0, 1, 11):
X = torch.tensor([float(x), 1.0-float(x)])
y = nn1(X)
gt = y[0] >= 0.5
eq = y[1] >= 0.5
relation = "?"
if eq:
relation = "=="
elif gt:
relation = "> "
else:
relation = "< "
print(f"{x:4.3} {relation} {1.0-x:4.3}")
Výsledky po natrénování této sítě:
0.0 < 1.0 0.1 < 0.9 0.2 < 0.8 0.3 < 0.7 0.4 < 0.6 0.5 == 0.5 0.6 > 0.4 0.7 > 0.3 0.8 > 0.2 0.9 > 0.1 1.0 > 0.0
17. Konvoluční neuronové sítě
Jak je tedy možné zlepšit odhad sítě i v případě, že očekáváme, že obrázky posílané na její vstup budou posunuty, nepatrně otočeny, zkoseny atd.? Máme k dispozici více řešení. Buď udělat síť mnohem víc robustní, což znamená výrazně zvětšit počet skrytých vrstev, zvětšit počet neuronů v těchto vrstvách a o několik řádů zvětšit i množství trénovacích dat (různé formy offsetu, posun jen některých pixelů atd.). To je sice skutečně možné zařídit (ostatně zaplatíme za to „jen“ strojovým časem), ovšem stále zde narážíme na principiální omezení klasických vrstvených neuronových sítí – jednotlivé neurony se učí izolovaně od ostatních neuronů, zatímco na vstupu máme „plovoucí“ obrázek. Bylo by tedy výhodnější se zaměřit na vylepšení samotné architektury neuronové sítě specializované právě na to, že na vstupu bude mít bitmapy a tudíž by sousední neurony měly nějakým způsobem sdílet své váhy na vstupech. Taková architektura již ve skutečnosti byla dávno vymyšlena a jmenuje se konvoluční neuronová sít.
18. Vrstvy v konvolučních neuronových sítích
V konvolučních neuronových sítích se používají vrstvy se speciálním významem i chováním. Jedná se především o takzvané konvoluční vrstvy, které jsou napojeny přímo na vstupní vrstvu popř. na subsamplingové vrstvy. Konvoluční vrstvy se skládají z obecně libovolného množství příznakových map, podle toho, jaké objekty nebo vlastnosti vlastně v obrázku rozpoznáváme. Zpracovávaná bitmapa se zde rozděluje na podoblasti, které se vzájemně překrývají. Neurony přitom mohou sdílet své váhy přiřazené vstupům. Jak přesně to funguje si řekneme příště. Mezi jednotlivé konvoluční vrstvy se vkládají subsamplingové vrstvy, které jsou z výpočetního hlediska jednodušší, protože neurony zde obsahují jen dvě váhy (součet vstupů+práh). Tyto vrstvy získaly svoje jméno podle toho, že umožňují provádět podvzorkování založené většinou na velmi jednoduchých funkcích aplikovaných na okolí každého pixelu (maximální hodnota, střední hodnota…).
Typicky se vrstvy střídají takto:
- Vstupní vrstva
- Konvoluční vrstva #1
- Subsamplingová vrstva #1
- Konvoluční vrstva #2
- Subsamplingová vrstva #2
- …
- …
- Klasická skrytá vrstva
- Výstupní vrstva
Existují ovšem i další možnosti, opět se o nich zmíníme příště.
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu PyTorch lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady:
20. Odkazy na Internetu
- Seriál Programovací jazyk Lua na Rootu:
https://www.root.cz/serialy/programovaci-jazyk-lua/ - PDM: moderní správce balíčků a virtuálních prostředí Pythonu:
https://www.root.cz/clanky/pdm-moderni-spravce-balicku-a-virtualnich-prostredi-pythonu/ - PyTorch Tutorial: Building a Simple Neural Network From Scratch
https://www.datacamp.com/tutorial/pytorch-tutorial-building-a-simple-neural-network-from-scratch - Interní reprezentace numerických hodnot: od skutečného počítačového pravěku po IEEE 754–2008:
https://www.root.cz/clanky/interni-reprezentace-numerickych-hodnot-od-skutecneho-pocitacoveho-praveku-po-ieee-754–2008/ - Interní reprezentace numerických hodnot: od skutečného počítačového pravěku po IEEE 754–2008 (dokončení):
https://www.root.cz/clanky/interni-reprezentace-numerickych-hodnot-od-skutecneho-pocitacoveho-praveku-po-ieee-754–2008-dokonceni/ - Brain Floating Point – nový formát uložení čísel pro strojové učení a chytrá čidla:
https://www.root.cz/clanky/brain-floating-point-ndash-novy-format-ulozeni-cisel-pro-strojove-uceni-a-chytra-cidla/ - Stránky projektu PyTorch:
https://pytorch.org/ - Informace o instalaci PyTorche:
https://pytorch.org/get-started/locally/ - Tenzor (Wikipedia):
https://cs.wikipedia.org/wiki/Tenzor - Introduction to Tensors:
https://www.youtube.com/watch?v=uaQeXi4E7gA - Introduction to Tensors: Transformation Rules:
https://www.youtube.com/watch?v=j6DazQDbEhQ - Tensor Attributes:
https://pytorch.org/docs/stable/tensor_attributes.html - Tensors Explained Intuitively: Covariant, Contravariant, Rank :
https://www.youtube.com/watch?v=CliW7kSxxWU - What is the relationship between PyTorch and Torch?:
https://stackoverflow.com/questions/44371560/what-is-the-relationship-between-pytorch-and-torch - What is a tensor anyway?? (from a mathematician):
https://www.youtube.com/watch?v=K7f2pCQ3p3U - Visualization of tensors – part 1 :
https://www.youtube.com/watch?v=YxXyN2ifK8A - Visualization of tensors – part 2A:
https://www.youtube.com/watch?v=A95jdIuUUW0 - Visualization of tensors – part 2B:
https://www.youtube.com/watch?v=A95jdIuUUW0 - What the HECK is a Tensor?!?:
https://www.youtube.com/watch?v=bpG3gqDM80w - Stránka projektu Torch
http://torch.ch/ - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - An Introduction to Tensors
https://math.stackexchange.com/questions/10282/an-introduction-to-tensors - Differences between a matrix and a tensor
https://math.stackexchange.com/questions/412423/differences-between-a-matrix-and-a-tensor - Qualitatively, what is the difference between a matrix and a tensor?
https://math.stackexchange.com/questions/1444412/qualitatively-what-is-the-difference-between-a-matrix-and-a-tensor? - Tensors for Neural Networks, Clearly Explained!!!:
https://www.youtube.com/watch?v=L35fFDpwIM4 - Tensor Processing Unit:
https://en.wikipedia.org/wiki/Tensor_Processing_Unit - Třída Storage:
http://docs.pytorch.wiki/en/storage.html - Funkce torch.dot
https://pytorch.org/docs/stable/generated/torch.dot.html#torch.dot - Funkce torch.narrow
https://pytorch.org/docs/stable/generated/torch.narrow.html - Funkce torch.matmul
https://pytorch.org/docs/stable/generated/torch.matmul.html - Funkce torch.reshape
https://pytorch.org/docs/stable/generated/torch.reshape.html - Funkce torch.arange
https://pytorch.org/docs/stable/generated/torch.arange.html - Funkce torch.range
https://pytorch.org/docs/stable/generated/torch.range.html - Třída torch.Tensor
https://pytorch.org/docs/stable/tensors.html - Atributy tenzorů
https://pytorch.org/docs/stable/tensor_attributes.html - Pohledy vytvořené nad tenzory
https://pytorch.org/docs/stable/tensor_view.html - Broadcasting v knihovně
https://numpy.org/doc/stable/user/basics.broadcasting.html - Broadcasting semantics (v knihovně PyTorch)
https://pytorch.org/docs/stable/notes/broadcasting.html - Dot Product In Physics: What Is The Physical Meaning of It?
https://profoundphysics.com/dot-product-in-physics-what-is-the-physical-meaning-of-it/ - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/ - Třída torch.nn.Linear
https://pytorch.org/docs/stable/generated/torch.nn.Linear.html - Třída torch.nn.Parameter
https://pytorch.org/docs/stable/generated/torch.nn.parameter.Parameter.html - Třída torch.nn.Sigmoid
https://pytorch.org/docs/stable/generated/torch.nn.Sigmoid.html