Obsah
1. PyTorch: problematika rozpoznávání a klasifikace obrázků (2. část)
2. Klasifikace rastrových obrázků sítí běžnou neuronovou sítí s „vektorovým“ vstupem a výstupem
3. První skript: příprava datové sady pro trénink neuronové sítě s vektorovým vstupem a výstupem
4. Příprava vstupních dat, která mohou být zašuměna popř. posunuta
5. Druhý skript: příprava zašuměných a posunutých vstupních dat pro neuronovou síť
6. Náhodné rozdělení datové sady funkcí train_test_split
7. Realizace rozdělení datové sady na trénovací a testovací data
8. Třetí skript: rozdělení datové sady na trénovací a testovací data
9. Konstrukce neuronové sítě s vektorovým vstupem i výstupem
11. Čtvrtý skript: trénink neuronové sítě pro rozpoznávání rastrových obrázků
12. Zašuměné obrázky v trénovacích a testovacích datech
14. Posunuté obrázky v trénovacích a testovacích datech
15. Šestý skript: trénink neuronové sítě pro rozpoznání posunutých obrázků
16. Matice záměn pro síť, která odpovídá vždy korektně
17. Matice záměn pro zašuměné obrázky
18. Matice záměn pro posunuté obrázky
19. Repositář s demonstračními příklady
1. PyTorch: problematika rozpoznávání a klasifikace obrázků (2. část)
Na předchozí článek o neuronových sítích realizovaných s využitím knihovny PyTorch dnes navážeme. Ukážeme si trénink sítí, na jejichž vstupu budou rastrové obrázky s číslicemi a na výstupu konkrétní informace o číslici, kterou síť rozezná (nebo naopak nerozezná).
Připomeňme si, že vstupní data s číslicemi zakódovanými do bitmap s rozlišením 8×8 pixelů, vypadají takto:
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
Dále máme k dispozici pomocnou funkci, která tato data převede do formy dvourozměrného pole (NumPy):
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
Výsledek lze vizualizovat s využitím knihovny Matplotlib:

Obrázek 1: Matice číslice 2 zobrazená v nepravých barvách.
Abychom zjistili, do jaké míry bude neuronová síť naučena na rozlišení reálných obrázků, budeme ji trénovat a validovat s využitím obrázků zašuměných, a to s mírou šumu od 0% do 100%:
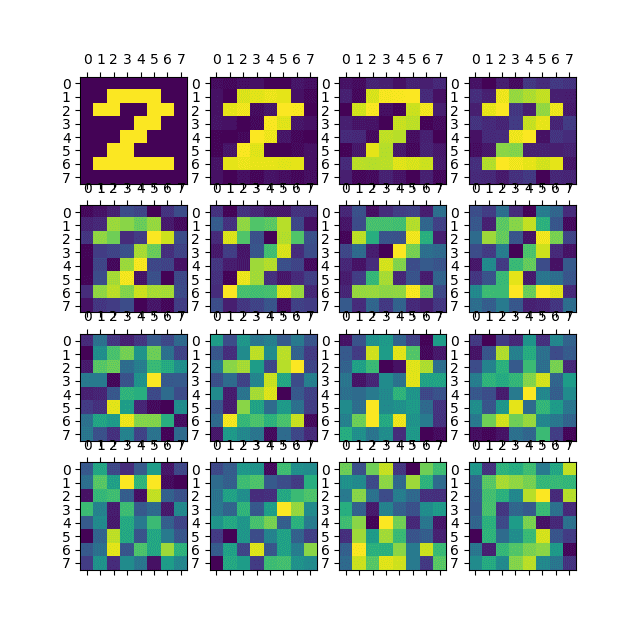
Obrázek 2: Vizualizace matice se zašuměnou číslicí 2, úroveň šumu se postupně zvyšuje.
Navíc budeme síť učit a následně validovat i na posunutých obrázcích, což se ukazuje být pro klasické neuronové sítě větším problémem, než šum:
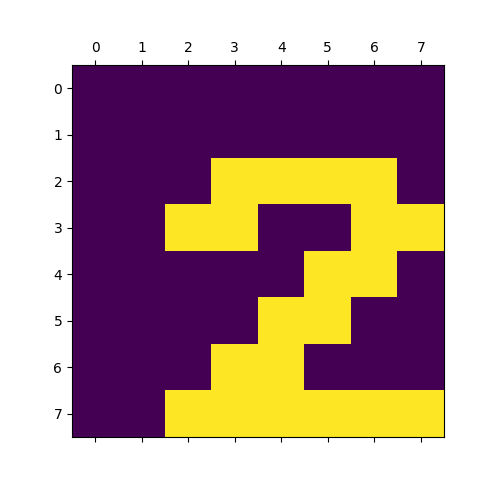
Obrázek 3: Vizualizovaná matice s posunutou číslicí 2.
2. Klasifikace rastrových obrázků sítí běžnou neuronovou sítí s „vektorovým“ vstupem a výstupem
Abychom zjistili limity klasických neuronových sítí pro klasifikaci rastrových obrázků, pokusíme se je skutečně pro klasifikaci použít. Zkonstruujeme tedy neuronovou síť, která bude jak na vstupu, tak i na výstupu obsahovat vektorová data. Konkrétně bude vstupem sítě 64prvkový vektor (s prvky typu float32), který obsahuje pixely původní bitmapy 8×8 pixelů, ovšem v „ploché“ podobě (z matice vytvoříme vektor). A na výstupu sítě bude taktéž vektor. Ten bude obsahovat deset prvků, přičemž pozice (index) největšího prvku určí číslici, kterou síť nalezla ve vstupním obrázku. Ideálně bude tento vektor vypadat například takto:
tensor([0., 0., 1., 0., 0., 0., 0., 0., 0., 0.]))
což odpovídá číslici 2.
V praxi však síť může odpovědět i takto:
tensor([0.1872, 0.1687, 0.9529, 0.0941, 0.0442, 0.1684, 0.0257, 0.0000, 0.0612, 0.2341])
což stále poměrně přesně určuje číslici 2 (prvek 0,9529).
Trénovací a testovací data budou reprezentována instancí třídy Data, která je odvozena od třídy torch.utils.data.Dataset. Tuto třídu jsme již několikrát použili, ovšem pro úplnost si ji ještě jednou ukažme:
# konverze původních dat z NumPy do tenzorů
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
Podívejme se nyní na pomocnou funkci, která trénovací a/nebo testovací data připraví. Tato funkce využívá jak vstupní matici 8×8 pixelů digits, tak i funkci nazvanou digit_to_array a popsanou minule. Povšimněte si způsobu tvorby vektorů x_vector a y_vector, jejichž délka i hodnoty prvků odpovídají popisu uvedeném výše:
def prepare_data(digits, length):
# příprava dat pro trénink a testování
X = []
y = []
for i in range(length):
# cislice
digit = i % 10
# vstupy
array = digit_to_array(digits, digit)
# prevod na vektor
x_vector = array.flatten()
X.append(x_vector)
# očekávané výstupy
y_vector = [0.0] * 10
y_vector[digit] = 1.0
y.append(y_vector)
return Data(np.array(X), np.array(y))
3. První skript: příprava datové sady pro trénink neuronové sítě s vektorovým vstupem a výstupem
Postup popsaný v předchozí kapitole nyní použijeme ve skriptu, jehož úkolem je příprava datové sady (což je instance třídy Data odvozené od třídy torch.utils.data.Dataset), která bude z vnějšího pohledu obsahovat sekvenci dvojic tenzorů. První tenzor z těchto dvojic bude jednorozměrným vektorem se 64 prvky typu float32, jejichž hodnoty odpovídají intenzitě pixelů původní bitmapy. A druhý tenzor bude taktéž jednorozměrným vektorem, nyní ovšem s deseti prvky typu float32. Takový vektor bude mít devět prvků nulových a jeden z prvků nastavený na jedničku – pozice jedničky odpovídá číslici 0 až 9:
import torch
from torch.utils.data import Dataset
import numpy as np
# konverze původních dat z NumPy do tenzorů
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def prepare_data(digits, length):
# příprava dat pro trénink a testování
X = []
y = []
for i in range(length):
# cislice
digit = i % 10
# vstupy
array = digit_to_array(digits, digit)
# prevod na vektor
x_vector = array.flatten()
X.append(x_vector)
# očekávané výstupy
y_vector = [0.0] * 10
y_vector[digit] = 1.0
y.append(y_vector)
return Data(np.array(X), np.array(y))
data = prepare_data(digits, 1000)
print(len(data))
for i in range(10):
print(data[i])
Skript po svém spuštění připraví data pro neuronovou síť, poté vytiskne jejich počet a nakonec i obsah prvních deseti dvojic. Povšimněte si, jak se ve druhém tenzoru „posunuje“ jednička, která určuje cifru na obrázku:
1000
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 0., 0., 0., 1.,
1., 0., 0., 1., 1., 0., 0., 1., 1., 0., 1., 1., 1., 0., 0., 1., 1., 1.,
0., 1., 1., 0., 0., 1., 1., 0., 0., 1., 1., 0., 0., 0., 1., 1., 1., 1.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]), tensor([1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]))
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0.,
1., 1., 1., 0., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0., 0., 1.,
1., 0., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 1., 1., 1., 1., 1.,
1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]), tensor([0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]))
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 0., 0., 0., 1.,
1., 0., 0., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0., 1.,
1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1.,
1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]), tensor([0., 0., 1., 0., 0., 0., 0., 0., 0., 0.]))
...
...
...
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 0., 0., 0., 1.,
1., 0., 0., 1., 1., 0., 0., 0., 1., 1., 1., 1., 0., 0., 0., 1., 1., 0.,
0., 1., 1., 0., 0., 1., 1., 0., 0., 1., 1., 0., 0., 0., 1., 1., 1., 1.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]), tensor([0., 0., 0., 0., 0., 0., 0., 0., 1., 0.]))
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 0., 0., 0., 1.,
1., 0., 0., 1., 1., 0., 0., 0., 1., 1., 1., 1., 1., 0., 0., 0., 0., 0.,
0., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 1., 1., 1., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]), tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]))
4. Příprava vstupních dat, která mohou být zašuměna popř. posunuta
V praxi však nebudou vstupní obrázky pro neuronovou síť ideální. Ostatně kdyby byly, stačilo by nám naprogramovat jednoduché mapování přesný_vstup→přesný_výstup. Na vstupní data tedy budeme aplikovat šum a popř. i operaci posunu obrázku ve směru horizontální a/nebo vertikální osy. Všechny potřebné pomocné funkce jsme si již vysvětlili v předchozím článku, takže jen ve stručnosti:
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
a:
def shift(arr, x_shift, y_shift):
# horizontální posun
arr = np.roll(arr, x_shift, axis=1)
# výplně těch částí, které byly orotovány na druhou stranu
if x_shift < 0:
arr[:, x_shift:] = 0.0
elif x_shift > 0:
arr[:, :x_shift] = 0.0
# vertikální posun
arr = np.roll(arr, y_shift, axis=0)
# výplně těch částí, které byly orotovány na druhou stranu
if y_shift < 0:
arr[y_shift:] = 0.0
elif y_shift > 0:
arr[:y_shift] = 0.0
return arr
Funkci pro přípravu dat upravíme takovým způsobem, že bude tyto dvě funkce volat a předávat jim vstupní parametry nastavené uživatelem – tedy úroveň šumu a maximální posun obrázků uvedený v pixelech:
def prepare_data(digits, length, noise_level=0.0, x_shift_amount=0, y_shift_amount=0):
# příprava dat pro trénink a testování
X = []
y = []
for i in range(length):
# cislice
digit = i % 10
# vstupy
array = digit_to_array(digits, digit)
# zasumeni
array = add_noise(array, noise_level)
# posuny
x_shift = random.randint(-x_shift_amount, x_shift_amount)
y_shift = random.randint(-y_shift_amount, y_shift_amount)
array = shift(array, x_shift, y_shift)
# prevod na vektor
x_vector = array.flatten()
X.append(x_vector)
# očekávané výstupy
y_vector = [0.0] * 10
y_vector[digit] = 1.0
y.append(y_vector)
return Data(np.array(X), np.array(y))
5. Druhý skript: příprava zašuměných a posunutých vstupních dat pro neuronovou síť
Opět se podívejme, jak by mohl vypadat skript, který připraví data pro trénink a testování klasické neuronové sítě s 64prvkovými vektory na vstupu a desetiprvkovými vektory na výstupu. Tentokrát však budou vstupní vektory obsahovat hodnoty, které jsou zašuměné, nebo mohou být obrázky posunuté v libovolném směru. Asi správně odhadnete, že právě posun bude kritický, protože jsme ztratili informaci o dvou rozměrech a vstupem je jen jednorozměrný vektor. Ukažme si zdrojový kód upraveného skriptu:
import random
import torch
from torch.utils.data import Dataset
import numpy as np
# konverze původních dat z NumPy do tenzorů
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
def shift(arr, x_shift, y_shift):
# horizontální posun
arr = np.roll(arr, x_shift, axis=1)
# výplně těch částí, které byly orotovány na druhou stranu
if x_shift < 0:
arr[:, x_shift:] = 0.0
elif x_shift > 0:
arr[:, :x_shift] = 0.0
# vertikální posun
arr = np.roll(arr, y_shift, axis=0)
# výplně těch částí, které byly orotovány na druhou stranu
if y_shift < 0:
arr[y_shift:] = 0.0
elif y_shift > 0:
arr[:y_shift] = 0.0
return arr
def prepare_data(digits, length, noise_level=0.0, x_shift_amount=0, y_shift_amount=0):
# příprava dat pro trénink a testování
X = []
y = []
for i in range(length):
# cislice
digit = i % 10
# vstupy
array = digit_to_array(digits, digit)
# zasumeni
array = add_noise(array, noise_level)
# posuny
x_shift = random.randint(-x_shift_amount, x_shift_amount)
y_shift = random.randint(-y_shift_amount, y_shift_amount)
array = shift(array, x_shift, y_shift)
# prevod na vektor
x_vector = array.flatten()
X.append(x_vector)
# očekávané výstupy
y_vector = [0.0] * 10
y_vector[digit] = 1.0
y.append(y_vector)
return Data(np.array(X), np.array(y))
data = prepare_data(digits, 1000, noise_level=0.0, x_shift_amount=2, y_shift_amount=2)
print(len(data))
for i in range(10):
print(data[i])
Po spuštění skriptu se opět zobrazí počet prvků v trénovací/testovací sadě a posléze hodnoty prvních deseti prvků. Nyní je patrné, že první vektor už neobsahuje pouze hodnoty 0,0 a 1,0, ale více či méně odlišné hodnoty:
1000
(tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0991, 0.1470,
0.0453, 0.1430, 0.0893, 0.0821, 0.0000, 0.0000, 0.9793, 0.8072, 0.9616,
0.8820, 0.0053, 0.0436, 0.0000, 0.0000, 0.9762, 0.0246, 0.0278, 0.8587,
0.9291, 0.0374, 0.0000, 0.0000, 0.9698, 0.0695, 0.8725, 0.8903, 0.9781,
0.0564, 0.0000, 0.0000, 0.9405, 0.9431, 0.1012, 0.9844, 0.9339, 0.1723,
0.0000, 0.0000, 0.8720, 0.1137, 0.1474, 0.8364, 0.8673, 0.0288, 0.0000,
0.0000]), tensor([1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]))
(tensor([0.1282, 0.1286, 0.9159, 0.9999, 0.0604, 0.0830, 0.1627, 0.0000, 0.0997,
0.8669, 0.8799, 0.9667, 0.1710, 0.0166, 0.1434, 0.0000, 0.1858, 0.0872,
0.9059, 0.8710, 0.1191, 0.1385, 0.0505, 0.0000, 0.0617, 0.0100, 0.9928,
0.9849, 0.1692, 0.1496, 0.0553, 0.0000, 0.0863, 0.0691, 0.9267, 0.8241,
0.1422, 0.1098, 0.0381, 0.0000, 0.8753, 0.8869, 0.9612, 0.8800, 0.9099,
0.8483, 0.0810, 0.0000, 0.1768, 0.1332, 0.1881, 0.1756, 0.0358, 0.1965,
0.1333, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000]), tensor([0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]))
...
...
...
(tensor([0.0000, 0.0000, 0.0733, 0.1337, 0.9931, 0.9026, 0.8485, 0.9472, 0.0000,
0.0000, 0.1810, 0.8931, 0.8541, 0.0940, 0.1297, 0.1427, 0.0000, 0.0000,
0.1165, 0.9050, 0.8881, 0.8289, 0.9612, 0.9271, 0.0000, 0.0000, 0.0582,
0.8934, 0.9511, 0.1421, 0.0801, 0.8987, 0.0000, 0.0000, 0.1779, 0.8515,
0.8020, 0.1619, 0.0649, 0.8573, 0.0000, 0.0000, 0.1445, 0.1342, 0.9168,
0.8039, 0.9018, 0.9114, 0.0000, 0.0000, 0.1518, 0.0960, 0.0952, 0.0685,
0.1568, 0.1162, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000]), tensor([0., 0., 0., 0., 0., 0., 1., 0., 0., 0.]))
(tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0170,
0.1181, 0.1175, 0.0079, 0.0321, 0.1954, 0.0000, 0.0000, 0.8095, 0.9161,
0.9373, 0.9020, 0.1813, 0.1592, 0.0000, 0.0000, 0.9597, 0.1631, 0.1652,
0.8400, 0.9894, 0.1514, 0.0000, 0.0000, 0.8719, 0.8249, 0.9083, 0.8364,
0.1119, 0.0627, 0.0000, 0.0000, 0.8413, 0.0157, 0.0148, 0.8373, 0.9239,
0.1173, 0.0000, 0.0000, 0.9013, 0.0727, 0.0251, 0.8195, 0.8519, 0.0888,
0.0000, 0.0000, 0.8526, 0.8314, 0.8749, 0.9900, 0.1544, 0.1514, 0.0000,
0.0000]), tensor([0., 0., 0., 0., 0., 0., 0., 0., 1., 0.]))
(tensor([0.0936, 0.9051, 0.9126, 0.1106, 0.0446, 0.8483, 0.9484, 0.1938, 0.1982,
0.0617, 0.9297, 0.8475, 0.8500, 0.9321, 0.9868, 0.1909, 0.1818, 0.0986,
0.0904, 0.1327, 0.0302, 0.8697, 0.8073, 0.0833, 0.0850, 0.1306, 0.0666,
0.1750, 0.8532, 0.8485, 0.0680, 0.0881, 0.0256, 0.0323, 0.9974, 0.9051,
0.9478, 0.1259, 0.0662, 0.0194, 0.0463, 0.1651, 0.0389, 0.0865, 0.0547,
0.1028, 0.0711, 0.1404, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000]), tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]))
6. Náhodné rozdělení datové sady funkcí train_test_split
Pro rozdělení dat, která byla získána postupem popsaným v předchozích kapitolách (dvojice 64prvkový vektor+desetiprvkový vektor) na data trénovací a validační (resp. testovací), použijeme funkci train_test_split. Tato funkce ve svém prvním parametru akceptuje přímo datovou sadu (nemusíme se tedy snažit o ruční získání naměřených dat a očekávaných výsledků), dále velikost testovacích a trénovacích dat (buď jako celé číslo, což je počet záznamů nebo hodnotu typu float, což bude zlomek od 0 do 1, nepovinnou hodnotu, která zamezí různým výsledkům pro několik volání této funkce a dále parametr povolující zamíchání dat (ve výchozím nastavení je povolen, což nám opět vyhovuje):
train_test_split(*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)
Split arrays or matrices into random train and test subsets.
Quick utility that wraps input validation,
``next(ShuffleSplit().split(X, y))``, and application to input data
into a single call for splitting (and optionally subsampling) data into a
one-liner.
Read more in the :ref:`User Guide <cross_validation>`.
Parameters
----------
*arrays : sequence of indexables with same length / shape[0]
Allowed inputs are lists, numpy arrays, scipy-sparse
matrices or pandas dataframes.
test_size : float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion
of the dataset to include in the test split. If int, represents the
absolute number of test samples. If None, the value is set to the
complement of the train size. If ``train_size`` is also None, it will
be set to 0.25.
train_size : float or int, default=None
If float, should be between 0.0 and 1.0 and represent the
proportion of the dataset to include in the train split. If
int, represents the absolute number of train samples. If None,
the value is automatically set to the complement of the test size.
random_state : int, RandomState instance or None, default=None
Controls the shuffling applied to the data before applying the split.
Pass an int for reproducible output across multiple function calls.
See :term:`Glossary <random_state>`.
shuffle : bool, default=True
Whether or not to shuffle the data before splitting. If shuffle=False
then stratify must be None.
stratify : array-like, default=None
If not None, data is split in a stratified fashion, using this as
the class labels.
Read more in the :ref:`User Guide <stratification>`.
7. Realizace rozdělení datové sady na trénovací a testovací data
Nyní si funkci pro přípravu dat, s nimiž budeme při konstrukci, tréninku a validaci neuronové sítě pracovat, rozšíříme o volání funkce train_test_split. Vstupem této funkce jsou hodnoty X a y převedené ze seznamů na n-rozměrná pole typu np.array (ale vlastně už nyní by bylo možné použít tenzory). Výsledkem je čtveřice n-rozměrných polí X_train, X_test, y_train a y_test, která jsou použita pro konstrukci dvou objektů typu Data. Tím máme přípravné práce za sebou:
def prepare_data(digits, length, noise_level=0.0, x_shift_amount=0, y_shift_amount=0, test_size=1/2):
# příprava dat pro trénink a testování
X = []
y = []
for i in range(length):
# cislice
digit = i % 10
# vstupy
array = digit_to_array(digits, digit)
# zasumeni
array = add_noise(array, noise_level)
# posuny
x_shift = random.randint(-x_shift_amount, x_shift_amount)
y_shift = random.randint(-y_shift_amount, y_shift_amount)
array = shift(array, x_shift, y_shift)
# prevod na vektor
x_vector = array.flatten()
X.append(x_vector)
# očekávané výstupy
y_vector = [0.0] * 10
y_vector[digit] = 1.0
y.append(y_vector)
X_train, X_test, y_train, y_test = train_test_split(
np.array(X), np.array(y),
test_size=test_size, random_state=26
)
# trénovací sada
train_data = Data(X_train, y_train)
# testovací sada
test_data = Data(X_test, y_test)
return train_data, test_data
8. Třetí skript: rozdělení datové sady na trénovací a testovací data
Celý skript, který připraví data pro neuronovou síť na základě bitmap s číslicemi, se „natáhl“ na délku přibližně tří kilobajtů, ovšem stále by mělo být zřejmé, jaké operace se v něm provádí a proč:
import random
from sklearn.model_selection import train_test_split
import torch
from torch.utils.data import Dataset
import numpy as np
# konverze původních dat z NumPy do tenzorů
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
def shift(arr, x_shift, y_shift):
# horizontální posun
arr = np.roll(arr, x_shift, axis=1)
# výplně těch částí, které byly orotovány na druhou stranu
if x_shift < 0:
arr[:, x_shift:] = 0.0
elif x_shift > 0:
arr[:, :x_shift] = 0.0
# vertikální posun
arr = np.roll(arr, y_shift, axis=0)
# výplně těch částí, které byly orotovány na druhou stranu
if y_shift < 0:
arr[y_shift:] = 0.0
elif y_shift > 0:
arr[:y_shift] = 0.0
return arr
def prepare_data(digits, length, noise_level=0.0, x_shift_amount=0, y_shift_amount=0, test_size=1/2):
# příprava dat pro trénink a testování
X = []
y = []
for i in range(length):
# cislice
digit = i % 10
# vstupy
array = digit_to_array(digits, digit)
# zasumeni
array = add_noise(array, noise_level)
# posuny
x_shift = random.randint(-x_shift_amount, x_shift_amount)
y_shift = random.randint(-y_shift_amount, y_shift_amount)
array = shift(array, x_shift, y_shift)
# prevod na vektor
x_vector = array.flatten()
X.append(x_vector)
# očekávané výstupy
y_vector = [0.0] * 10
y_vector[digit] = 1.0
y.append(y_vector)
X_train, X_test, y_train, y_test = train_test_split(
np.array(X), np.array(y),
test_size=test_size, random_state=26
)
# trénovací sada
train_data = Data(X_train, y_train)
# testovací sada
test_data = Data(X_test, y_test)
return train_data, test_data
train, test = prepare_data(digits, 1000, noise_level=0.0, x_shift_amount=2, y_shift_amount=2)
print(len(train))
print(len(test))
for i in range(10):
print(train[i])
Z prvních dvou vypsaných řádků je patrné, že jak trénovací data, tak i data pro otestování, mají shodně 500 prvků. Ovšem tyto prvky se pochopitelně od sebe odlišují:
500 500
Skript navíc vypíše prvních deset prvků trénovacích dat:
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
1., 1., 1., 1., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0.,
1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 1., 1., 0., 0.,
1., 1., 0., 0., 0., 1., 1., 1., 1., 0.]), tensor([0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]))
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 1., 0., 0., 0., 1., 1., 0., 0., 1., 1., 0., 0., 0., 0.,
0., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0.,
0., 0., 0., 0., 1., 1., 1., 1., 1., 1.]), tensor([0., 0., 1., 0., 0., 0., 0., 0., 0., 0.]))
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 1., 0., 0., 0., 1., 1., 0., 0., 1., 1., 0., 0., 0., 1.,
1., 1., 1., 1., 0., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0., 1.,
1., 0., 0., 0., 0., 1., 1., 1., 0., 0.]), tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]))
...
...
...
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 1., 0., 0., 0., 1., 1., 0., 0., 1., 1., 0., 0., 0., 0.,
0., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0.,
0., 0., 0., 0., 1., 1., 1., 1., 1., 1.]), tensor([0., 0., 1., 0., 0., 0., 0., 0., 0., 0.]))
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 1., 0., 0., 0., 1., 1., 0., 0., 1., 1., 0., 0., 1., 1.,
0., 1., 1., 1., 0., 0., 1., 1., 1., 0., 1., 1., 0., 0., 1., 1., 0., 0.,
1., 1., 0., 0., 0., 1., 1., 1., 1., 0.]), tensor([1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]))
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
1., 1., 1., 1., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0.,
1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 1., 1., 0., 0.,
1., 1., 0., 0., 0., 1., 1., 1., 1., 0.]), tensor([0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]))
9. Konstrukce neuronové sítě s vektorovým vstupem i výstupem
V dalším kroku (konečně) zkonstruujeme neuronovou síť, na jejíž vstup budeme posílat 64prvkové vektory s hodnotami zašuměných a posunutých obrázků s číslicemi a na jejímž výstupu bude desetiprvkový vektor, jehož nejvyšší prvek určí index číslice rozeznané touto sítí. Pro jednoduchost a pro rychlé učení bude síť obsahovat pouze jednu skrytou vrstvu. Jako aktivační funkci mezi vstupy a skrytou vrstvou vybereme ReLU a pro dvojici vrstev naopak sigmoid (později tento výběr můžeme kdykoli modifikovat):
class NeuralNetwork(nn.Module):
"""Třída reprezentující neuronovou síť."""
def __init__(self, input_dim, hidden_dim, output_dim):
super().__init__()
# vrstvy neuronové sítě
self.layer_1 = nn.Linear(input_dim, hidden_dim)
self.layer_2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# propagace hodnot přes neuronovou síť
x = torch.nn.functional.relu(self.layer_1(x))
x = torch.nn.functional.sigmoid(self.layer_2(x))
return x
Vstupem jsou 64prvkové vektory, výstupem desetiprvkový vektor. Tím jsou přímo určeny počty neuronů na vstupu i neuronů ve výstupní vrstvě. Skrytá vrstva může mít libovolný počet neuronů. Zvolme hodnotu 10. Ta není ani velká (problém nedoučení) ani malá (problém „hloupé“ sítě s malým množstvím stavů):
# konfigurace vrstev neuronové sítě
input_dim = 64
hidden_dim = 10
output_dim = 10
nn_64_10_10 = NeuralNetwork(input_dim, hidden_dim, output_dim)
# výpis základních informací o neuronové síti
print("Neural network:")
print(nn_64_10_10)
Skript v této zkrácené podobě by měl vypsat strukturu neuronové sítě:
Neural network: NeuralNetwork( (layer_1): Linear(in_features=64, out_features=10, bias=True) (layer_2): Linear(in_features=10, out_features=10, bias=True) )
Pokud vás mate, že skrytá vrstva má stejný počet neuronů, jako vrstva výstupní, můžeme skrytou vrstvu rozšířit na 99 neuronů:
Neural network: NeuralNetwork( (layer_1): Linear(in_features=64, out_features=99, bias=True) (layer_2): Linear(in_features=99, out_features=10, bias=True) )
10. Trénink neuronové sítě
Neuronovou síť máme nyní zkonstruovanou, ovšem váhy na vstupech neuronů jsou prozatím nastaveny na náhodnou hodnotu. Síť je tedy nutné natrénovat. Pro tento účel si necháme vygenerovat trénovací a testovací data, což není nic nového, protože jsme se s tímto konceptem seznámili v šesté a sedmé kapitole:
train_data, test_data = prepare_data(digits, 1000, noise_level=0.0, x_shift_amount=0, y_shift_amount=0)
print("Train data:")
print(len(train_data))
print("Test data:")
print(len(test_data))
Povšimněte si, že si sice necháme vygenerovat 1000 záznamů, ale vzhledem k tomu, že úroveň šumu je nulová a obrázky se neposunují, vlastně bude datová sada obsahovat každý záznam ve 100 identických kopiích:
Train data: 666 Test data: 334
Samotný trénink neuronové sítě taktéž není nová metoda. Na vstup sítě předáme jeden vektor vybraný z trénovacích dat, na výstup očekávaný výstup (taktéž vektor) a zpětným šířením chyby se poupraví váhy na vstupech jednotlivých neuronů:
# příprava na trénink neuronové sítě
learning_rate = 0.1
loss_fn = nn.BCELoss()
optimizer = optim.SGD(nn_64_10_10.parameters(), lr=learning_rate)
# zpracovat trénovací data
batch_size = 64
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)
print("Batches: ", len(train_dataloader))
# vlastní trénink
print("Training started")
num_epochs = 100
loss_values = []
for epoch in range(num_epochs):
print(f" Epoch {epoch}: ", end="")
last_lost_value = None
for X, y in train_dataloader:
optimizer.zero_grad()
# dopředný tok + zpětný tok + optimalizace
pred = nn_64_10_10(X)
# výpočet účelové funkce
loss = loss_fn(pred, y)
#loss = loss_fn(pred, y.unsqueeze(-1))
loss_values.append(loss.item())
loss.backward()
optimizer.step()
last_lost_value = loss.item()
print(".", end="")
print(last_lost_value)
print("Training completed")
V průběhu učení by se postupně měla snižovat hodnota vypočtená účelovou funkcí. V ideálním případě by měla klesnout k nule:
Batches: 11
Training started
Epoch 0: ...........0.6447266936302185
Epoch 1: ...........0.6193460822105408
Epoch 2: ...........0.587082028388977
Epoch 3: ...........0.5465092658996582
Epoch 4: ...........0.4956221878528595
Epoch 5: ...........0.44743767380714417
Epoch 6: ...........0.38974180817604065
Epoch 7: ...........0.3594760000705719
Epoch 8: ...........0.3338333070278168
Epoch 9: ...........0.3175426423549652
Epoch 10: ...........0.32316410541534424
Epoch 11: ...........0.32127857208251953
Epoch 12: ...........0.3148137927055359
Epoch 13: ...........0.3114672899246216
Epoch 14: ...........0.316869854927063
Epoch 15: ...........0.3137578070163727
Epoch 16: ...........0.3157559633255005
Epoch 17: ...........0.3102682828903198
Epoch 18: ...........0.3075677454471588
Epoch 19: ...........0.30908656120300293
Epoch 20: ...........0.3039756715297699
Epoch 21: ...........0.3026908338069916
Epoch 22: ...........0.30455878376960754
Epoch 23: ...........0.30317121744155884
Epoch 24: ...........0.29968011379241943
Epoch 25: ...........0.2984805703163147
Epoch 26: ...........0.2998690903186798
Epoch 27: ...........0.2988283932209015
Epoch 28: ...........0.28817668557167053
Epoch 29: ...........0.2917144298553467
Epoch 30: ...........0.2874159812927246
Epoch 31: ...........0.2909078598022461
Epoch 32: ...........0.27771422266960144
Epoch 33: ...........0.2821337580680847
Epoch 34: ...........0.28642821311950684
Epoch 35: ...........0.276723176240921
Epoch 36: ...........0.2759454548358917
Epoch 37: ...........0.27059292793273926
Epoch 38: ...........0.2683849036693573
Epoch 39: ...........0.268013060092926
Epoch 40: ...........0.2737174928188324
Epoch 41: ...........0.2644055187702179
Epoch 42: ...........0.26093563437461853
Epoch 43: ...........0.2565652132034302
Epoch 44: ...........0.25182580947875977
Epoch 45: ...........0.2551380693912506
Epoch 46: ...........0.2450740933418274
Epoch 47: ...........0.24896760284900665
Epoch 48: ...........0.24437251687049866
Epoch 49: ...........0.24140697717666626
Epoch 50: ...........0.23914998769760132
Epoch 51: ...........0.23454098403453827
Epoch 52: ...........0.23361629247665405
Epoch 53: ...........0.23802918195724487
Epoch 54: ...........0.223032146692276
Epoch 55: ...........0.2397080361843109
Epoch 56: ...........0.21921715140342712
Epoch 57: ...........0.21958164870738983
Epoch 58: ...........0.22020205855369568
Epoch 59: ...........0.2035556137561798
Epoch 60: ...........0.21375465393066406
Epoch 61: ...........0.1982254534959793
Epoch 62: ...........0.19214391708374023
Epoch 63: ...........0.2059931755065918
Epoch 64: ...........0.1918933093547821
Epoch 65: ...........0.20608077943325043
Epoch 66: ...........0.19234557449817657
Epoch 67: ...........0.1903819739818573
Epoch 68: ...........0.1945323795080185
Epoch 69: ...........0.1832999587059021
Epoch 70: ...........0.18331988155841827
Epoch 71: ...........0.1699090152978897
Epoch 72: ...........0.1823926419019699
Epoch 73: ...........0.17585024237632751
Epoch 74: ...........0.16324113309383392
Epoch 75: ...........0.17733824253082275
Epoch 76: ...........0.17202644050121307
Epoch 77: ...........0.16952469944953918
Epoch 78: ...........0.15982866287231445
Epoch 79: ...........0.16450724005699158
Epoch 80: ...........0.15805110335350037
Epoch 81: ...........0.16729946434497833
Epoch 82: ...........0.14237038791179657
Epoch 83: ...........0.16939890384674072
Epoch 84: ...........0.15275999903678894
Epoch 85: ...........0.14588870108127594
Epoch 86: ...........0.15782424807548523
Epoch 87: ...........0.15238074958324432
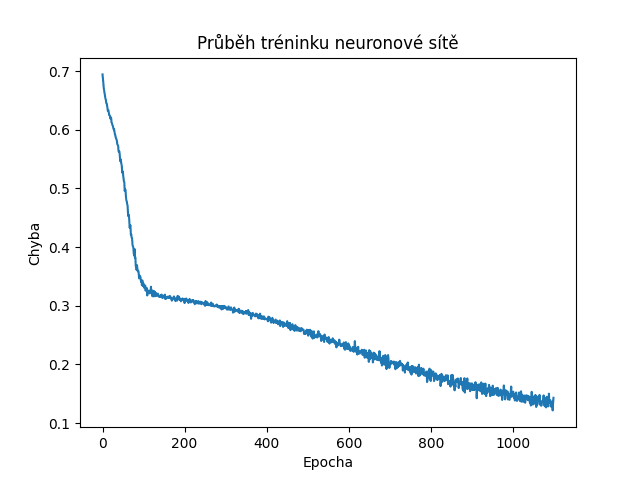
Obrázek 4: Postupně klesající hodnoty vypočítané účelovou funkcí naznačují korektní učení sítě – ovšem ne kvalitu jejich predikcí!
11. Čtvrtý skript: trénink neuronové sítě pro rozpoznávání rastrových obrázků
Postup popsaný v předchozích pěti kapitolách byl použit v dnešním čtvrtém skriptu, který vypadá takto:
import random
from sklearn.model_selection import train_test_split
import torch
from torch import nn
from torch import optim
from torch.utils.data import Dataset, DataLoader
import numpy as np
import matplotlib.pyplot as plt
class NeuralNetwork(nn.Module):
"""Třída reprezentující neuronovou síť."""
def __init__(self, input_dim, hidden_dim, output_dim):
super().__init__()
# vrstvy neuronové sítě
self.layer_1 = nn.Linear(input_dim, hidden_dim)
self.layer_2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# propagace hodnot přes neuronovou síť
x = torch.nn.functional.relu(self.layer_1(x))
x = torch.nn.functional.sigmoid(self.layer_2(x))
return x
# konfigurace vrstev neuronové sítě
input_dim = 64
hidden_dim = 10
output_dim = 10
nn_64_10_10 = NeuralNetwork(input_dim, hidden_dim, output_dim)
# výpis základních informací o neuronové síti
print("Neural network:")
print(nn_64_10_10)
# konverze původních dat z NumPy do tenzorů
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
def shift(arr, x_shift, y_shift):
# horizontální posun
arr = np.roll(arr, x_shift, axis=1)
# výplně těch částí, které byly orotovány na druhou stranu
if x_shift < 0:
arr[:, x_shift:] = 0.0
elif x_shift > 0:
arr[:, :x_shift] = 0.0
# vertikální posun
arr = np.roll(arr, y_shift, axis=0)
# výplně těch částí, které byly orotovány na druhou stranu
if y_shift < 0:
arr[y_shift:] = 0.0
elif y_shift > 0:
arr[:y_shift] = 0.0
return arr
def prepare_data(digits, length, noise_level=0.0, x_shift_amount=0, y_shift_amount=0, test_size=1/3):
# příprava dat pro trénink a testování
X = []
y = []
for i in range(length):
# cislice
digit = i % 10
# vstupy
array = digit_to_array(digits, digit)
# zasumeni
array = add_noise(array, noise_level)
# posuny
x_shift = random.randint(-x_shift_amount, x_shift_amount)
y_shift = random.randint(-y_shift_amount, y_shift_amount)
array = shift(array, x_shift, y_shift)
# prevod na vektor
x_vector = array.flatten()
X.append(x_vector)
# očekávané výstupy
y_vector = [0.0] * 10
y_vector[digit] = 1.0
y.append(y_vector)
X_train, X_test, y_train, y_test = train_test_split(
np.array(X), np.array(y),
test_size=test_size, random_state=26
)
# trénovací sada
train_data = Data(X_train, y_train)
# testovací sada
test_data = Data(X_test, y_test)
return train_data, test_data
train_data, test_data = prepare_data(digits, 1000, noise_level=0.0, x_shift_amount=0, y_shift_amount=0)
print("Train data:")
print(len(train_data))
print("Test data:")
print(len(test_data))
# příprava na trénink neuronové sítě
learning_rate = 0.1
loss_fn = nn.BCELoss()
optimizer = optim.SGD(nn_64_10_10.parameters(), lr=learning_rate)
# zpracovat trénovací data
batch_size = 64
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)
print("Batches: ", len(train_dataloader))
# vlastní trénink
print("Training started")
num_epochs = 100
loss_values = []
for epoch in range(num_epochs):
print(f" Epoch {epoch}: ", end="")
last_lost_value = None
for X, y in train_dataloader:
optimizer.zero_grad()
# dopředný tok + zpětný tok + optimalizace
pred = nn_64_10_10(X)
# výpočet účelové funkce
loss = loss_fn(pred, y)
#loss = loss_fn(pred, y.unsqueeze(-1))
loss_values.append(loss.item())
loss.backward()
optimizer.step()
last_lost_value = loss.item()
print(".", end="")
print(last_lost_value)
print("Training completed")
step = range(len(loss_values))
# příprava na vykreslení grafu
fig, ax = plt.subplots(figsize=(6.4, 4.8))
plt.plot(step, np.array(loss_values))
plt.title("Průběh tréninku neuronové sítě")
plt.xlabel("Epocha")
plt.ylabel("Chyba")
# uložení do souboru
plt.savefig("nn_16.png")
# vykreslení grafu
plt.show()
12. Zašuměné obrázky v trénovacích a testovacích datech
Naprosto stejnou neuronovou síť nyní natrénujeme s využitím zašuměných obrázků. A nutno říci, že úroveň šumu je nastavena poměrně vysoko – na 50%. To může v některých případech znamenat, že obrázky nebudou dobře rozeznatelné ani tou nejlepší neuronovou sítí pro rozpoznání obrazu – lidským mozkem:
train_data, test_data = prepare_data(digits, 1000, noise_level=0.5, x_shift_amount=0, y_shift_amount=0)
Průběh učení naznačuje, že hodnoty účelové funkce již neklesnou na hodnotu 0,15 tak, jako v příkladu předchozím:
Batches: 11
Training started
Epoch 0: ...........0.6567670106887817
Epoch 1: ...........0.6100022792816162
Epoch 2: ...........0.5560295581817627
Epoch 3: ...........0.491263747215271
Epoch 4: ...........0.4276190996170044
Epoch 5: ...........0.39090630412101746
Epoch 6: ...........0.3492359519004822
Epoch 7: ...........0.34494543075561523
Epoch 8: ...........0.3371904492378235
Epoch 9: ...........0.3227657973766327
Epoch 10: ...........0.32668638229370117
...
...
...
Epoch 90: ...........0.28734317421913147
Epoch 91: ...........0.28829020261764526
Epoch 92: ...........0.29428786039352417
Epoch 93: ...........0.27999159693717957
Epoch 94: ...........0.27175065875053406
Epoch 95: ...........0.2788369059562683
Epoch 96: ...........0.2692151367664337
Epoch 97: ...........0.28449100255966187
Epoch 98: ...........0.27109402418136597
Epoch 99: ...........0.28655123710632324
Training completed
Totéž je ostatně velmi dobře patrné i ve vizualizovaném průběhu účelové funkce:
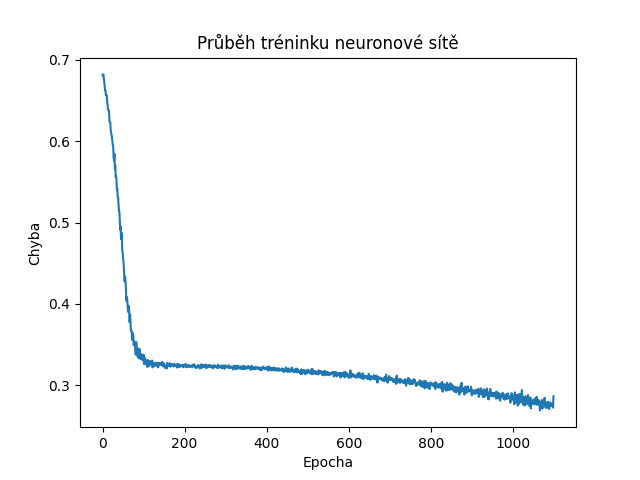
Obrázek 5: Postupně klesající hodnoty vypočítané účelovou funkcí naznačují korektní učení sítě. Nyní je ovšem učení pomalejší a model bude obsahovat chyby v predikci.
Vliv větší úrovně šumu (70%):
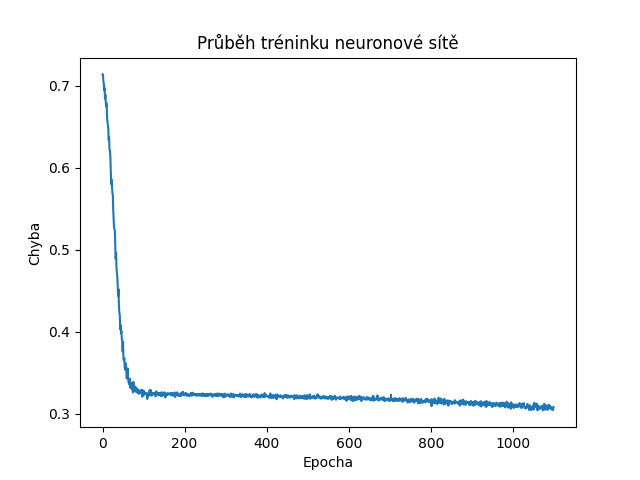
Obrázek 6: Postupně klesající hodnoty vypočítané účelovou funkcí naznačují korektní učení sítě.
13. Pátý skript: trénink neuronové sítě pro rozpoznávání rastrových obrázků s využitím zašuměných obrázků
Jen pro úplnost si ukažme celý skript, po jehož spuštění se neuronová síť natrénuje a následně i otestuje s využitím zašuměných obrázků:
import random
from sklearn.model_selection import train_test_split
import torch
from torch import nn
from torch import optim
from torch.utils.data import Dataset, DataLoader
import numpy as np
import matplotlib.pyplot as plt
class NeuralNetwork(nn.Module):
"""Třída reprezentující neuronovou síť."""
def __init__(self, input_dim, hidden_dim, output_dim):
super().__init__()
# vrstvy neuronové sítě
self.layer_1 = nn.Linear(input_dim, hidden_dim)
self.layer_2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# propagace hodnot přes neuronovou síť
x = torch.nn.functional.relu(self.layer_1(x))
x = torch.nn.functional.sigmoid(self.layer_2(x))
return x
# konfigurace vrstev neuronové sítě
input_dim = 64
hidden_dim = 10
output_dim = 10
nn_64_10_10 = NeuralNetwork(input_dim, hidden_dim, output_dim)
# výpis základních informací o neuronové síti
print("Neural network:")
print(nn_64_10_10)
# konverze původních dat z NumPy do tenzorů
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
def shift(arr, x_shift, y_shift):
# horizontální posun
arr = np.roll(arr, x_shift, axis=1)
# výplně těch částí, které byly orotovány na druhou stranu
if x_shift < 0:
arr[:, x_shift:] = 0.0
elif x_shift > 0:
arr[:, :x_shift] = 0.0
# vertikální posun
arr = np.roll(arr, y_shift, axis=0)
# výplně těch částí, které byly orotovány na druhou stranu
if y_shift < 0:
arr[y_shift:] = 0.0
elif y_shift > 0:
arr[:y_shift] = 0.0
return arr
def prepare_data(digits, length, noise_level=0.0, x_shift_amount=0, y_shift_amount=0, test_size=1/3):
# příprava dat pro trénink a testování
X = []
y = []
for i in range(length):
# cislice
digit = i % 10
# vstupy
array = digit_to_array(digits, digit)
# zasumeni
array = add_noise(array, noise_level)
# posuny
x_shift = random.randint(-x_shift_amount, x_shift_amount)
y_shift = random.randint(-y_shift_amount, y_shift_amount)
array = shift(array, x_shift, y_shift)
# prevod na vektor
x_vector = array.flatten()
X.append(x_vector)
# očekávané výstupy
y_vector = [0.0] * 10
y_vector[digit] = 1.0
y.append(y_vector)
X_train, X_test, y_train, y_test = train_test_split(
np.array(X), np.array(y),
test_size=test_size, random_state=26
)
# trénovací sada
train_data = Data(X_train, y_train)
# testovací sada
test_data = Data(X_test, y_test)
return train_data, test_data
train_data, test_data = prepare_data(digits, 1000, noise_level=0.5, x_shift_amount=0, y_shift_amount=0)
print("Train data:")
print(len(train_data))
print("Test data:")
print(len(test_data))
# příprava na trénink neuronové sítě
learning_rate = 0.1
loss_fn = nn.BCELoss()
optimizer = optim.SGD(nn_64_10_10.parameters(), lr=learning_rate)
# zpracovat trénovací data
batch_size = 64
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)
print("Batches: ", len(train_dataloader))
# vlastní trénink
print("Training started")
num_epochs = 100
loss_values = []
for epoch in range(num_epochs):
print(f" Epoch {epoch}: ", end="")
last_lost_value = None
for X, y in train_dataloader:
optimizer.zero_grad()
# dopředný tok + zpětný tok + optimalizace
pred = nn_64_10_10(X)
# výpočet účelové funkce
loss = loss_fn(pred, y)
#loss = loss_fn(pred, y.unsqueeze(-1))
loss_values.append(loss.item())
loss.backward()
optimizer.step()
last_lost_value = loss.item()
print(".", end="")
print(last_lost_value)
print("Training completed")
step = range(len(loss_values))
# příprava na vykreslení grafu
fig, ax = plt.subplots(figsize=(6.4, 4.8))
plt.plot(step, np.array(loss_values))
plt.title("Průběh tréninku neuronové sítě")
plt.xlabel("Epocha")
plt.ylabel("Chyba")
# uložení do souboru
plt.savefig("nn_17.png")
# vykreslení grafu
plt.show()
14. Posunuté obrázky v trénovacích a testovacích datech
Ověřme si, jak dobře či špatně se neuronová síť dokáže naučit a predikovat posunuté obrázky. Úroveň šumu vynulujeme a povolíme posun obrázků v obou směrech, ovšem maximálně o dva pixely:
train_data, test_data = prepare_data(digits, 1000, noise_level=0.0, x_shift_amount=2, y_shift_amount=2)
Průběh učení sítě:
Training started
Epoch 0: ...........0.662143349647522
Epoch 1: ...........0.6225242018699646
Epoch 2: ...........0.5437997579574585
Epoch 3: ...........0.47505685687065125
Epoch 4: ...........0.4151655435562134
Epoch 5: ...........0.3567219078540802
Epoch 6: ...........0.35883376002311707
Epoch 7: ...........0.3546479344367981
Epoch 8: ...........0.33377087116241455
Epoch 9: ...........0.33360761404037476
Epoch 10: ...........0.32562145590782166
...
...
...
Epoch 70: ...........0.31016451120376587
Epoch 71: ...........0.32512548565864563
Epoch 72: ...........0.3208373486995697
Epoch 73: ...........0.320453405380249
Epoch 74: ...........0.3224222660064697
Epoch 75: ...........0.30925461649894714
Epoch 76: ...........0.3184351325035095
Epoch 77: ...........0.3149249255657196
Epoch 78: ...........0.3213757276535034
Predikce sítě se pravděpodobně ještě více zhorší:
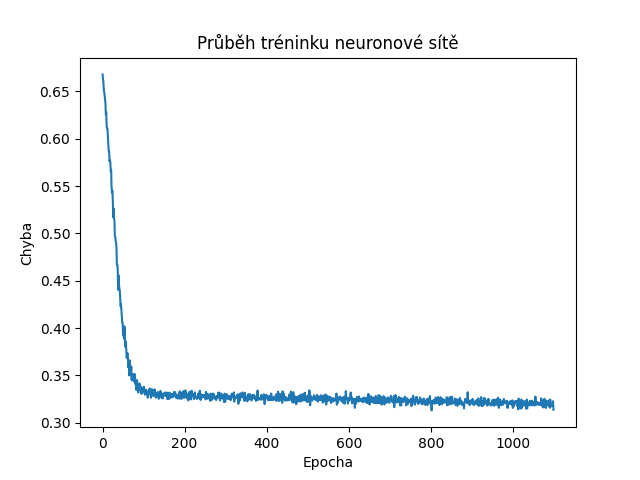
Obrázek 7: Postupně klesající hodnoty vypočítané účelovou funkcí naznačují korektní učení sítě. Nyní je učení ještě pomalejší a model bude obsahovat větší chyby v predikci.
Výsledky pro náhodný posun o ± tři pixely:
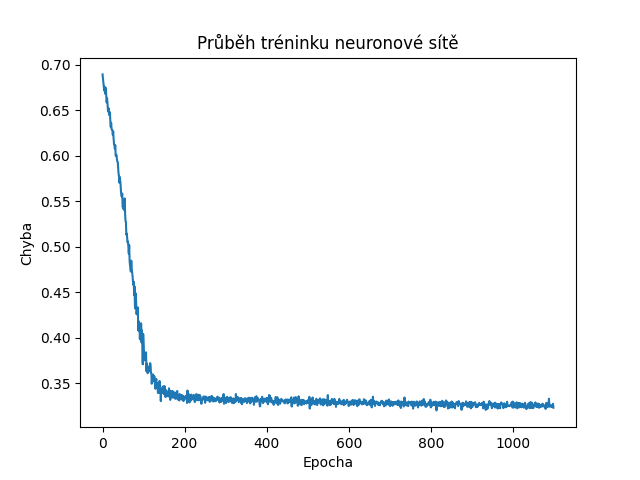
Obrázek 8: Postupně klesající hodnoty vypočítané účelovou funkcí naznačují korektní učení sítě.
15. Šestý skript: trénink neuronové sítě pro rozpoznání posunutých obrázků
Opět si, podobně jako ve třinácté kapitole, pro úplnost ukažme celý skript, po jehož spuštění se neuronová síť natrénuje a následně i otestuje s využitím zašuměných obrázků:
import random
from sklearn.model_selection import train_test_split
import torch
from torch import nn
from torch import optim
from torch.utils.data import Dataset, DataLoader
import numpy as np
import matplotlib.pyplot as plt
class NeuralNetwork(nn.Module):
"""Třída reprezentující neuronovou síť."""
def __init__(self, input_dim, hidden_dim, output_dim):
super().__init__()
# vrstvy neuronové sítě
self.layer_1 = nn.Linear(input_dim, hidden_dim)
self.layer_2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# propagace hodnot přes neuronovou síť
x = torch.nn.functional.relu(self.layer_1(x))
x = torch.nn.functional.sigmoid(self.layer_2(x))
return x
# konfigurace vrstev neuronové sítě
input_dim = 64
hidden_dim = 10
output_dim = 10
nn_64_10_10 = NeuralNetwork(input_dim, hidden_dim, output_dim)
# výpis základních informací o neuronové síti
print("Neural network:")
print(nn_64_10_10)
# konverze původních dat z NumPy do tenzorů
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
# číslice reprezentované v masce 8x8 pixelů
digits = (
(0x00, 0x3C, 0x66, 0x76, 0x6E, 0x66, 0x3C, 0x00),
(0x00, 0x18, 0x1C, 0x18, 0x18, 0x18, 0x7E, 0x00),
(0x00, 0x3C, 0x66, 0x30, 0x18, 0x0C, 0x7E, 0x00),
(0x00, 0x7E, 0x30, 0x18, 0x30, 0x66, 0x3C, 0x00),
(0x00, 0x30, 0x38, 0x3C, 0x36, 0x7E, 0x30, 0x00),
(0x00, 0x7E, 0x06, 0x3E, 0x60, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x06, 0x3E, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x7E, 0x60, 0x30, 0x18, 0x0C, 0x0C, 0x00),
(0x00, 0x3C, 0x66, 0x3C, 0x66, 0x66, 0x3C, 0x00),
(0x00, 0x3C, 0x66, 0x7C, 0x60, 0x30, 0x1C, 0x00),
)
def digit_to_array(digits, n):
digit = digits[n]
rows = []
# převod jednotlivých řádků na osmici bitů
for scanline in digit:
row = []
# převod bitmapy představující řádek na osmici bitů
for _ in range(8):
bit = scanline & 0x01
row.append(float(bit))
scanline >>= 1
rows.append(row)
# transformace na n-dimenzionální pole
return np.array(rows)
def add_noise(array, level):
return (1.0 - level) * array + level * np.random.rand(8, 8)
def shift(arr, x_shift, y_shift):
# horizontální posun
arr = np.roll(arr, x_shift, axis=1)
# výplně těch částí, které byly orotovány na druhou stranu
if x_shift < 0:
arr[:, x_shift:] = 0.0
elif x_shift > 0:
arr[:, :x_shift] = 0.0
# vertikální posun
arr = np.roll(arr, y_shift, axis=0)
# výplně těch částí, které byly orotovány na druhou stranu
if y_shift < 0:
arr[y_shift:] = 0.0
elif y_shift > 0:
arr[:y_shift] = 0.0
return arr
def prepare_data(digits, length, noise_level=0.0, x_shift_amount=0, y_shift_amount=0, test_size=1/3):
# příprava dat pro trénink a testování
X = []
y = []
for i in range(length):
# cislice
digit = i % 10
# vstupy
array = digit_to_array(digits, digit)
# zasumeni
array = add_noise(array, noise_level)
# posuny
x_shift = random.randint(-x_shift_amount, x_shift_amount)
y_shift = random.randint(-y_shift_amount, y_shift_amount)
array = shift(array, x_shift, y_shift)
# prevod na vektor
x_vector = array.flatten()
X.append(x_vector)
# očekávané výstupy
y_vector = [0.0] * 10
y_vector[digit] = 1.0
y.append(y_vector)
X_train, X_test, y_train, y_test = train_test_split(
np.array(X), np.array(y),
test_size=test_size, random_state=26
)
# trénovací sada
train_data = Data(X_train, y_train)
# testovací sada
test_data = Data(X_test, y_test)
return train_data, test_data
train_data, test_data = prepare_data(digits, 1000, noise_level=0.0, x_shift_amount=2, y_shift_amount=2)
print("Train data:")
print(len(train_data))
print("Test data:")
print(len(test_data))
# příprava na trénink neuronové sítě
learning_rate = 0.1
loss_fn = nn.BCELoss()
optimizer = optim.SGD(nn_64_10_10.parameters(), lr=learning_rate)
# zpracovat trénovací data
batch_size = 64
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)
print("Batches: ", len(train_dataloader))
# vlastní trénink
print("Training started")
num_epochs = 100
loss_values = []
for epoch in range(num_epochs):
print(f" Epoch {epoch}: ", end="")
last_lost_value = None
for X, y in train_dataloader:
optimizer.zero_grad()
# dopředný tok + zpětný tok + optimalizace
pred = nn_64_10_10(X)
# výpočet účelové funkce
loss = loss_fn(pred, y)
#loss = loss_fn(pred, y.unsqueeze(-1))
loss_values.append(loss.item())
loss.backward()
optimizer.step()
last_lost_value = loss.item()
print(".", end="")
print(last_lost_value)
print("Training completed")
step = range(len(loss_values))
# příprava na vykreslení grafu
fig, ax = plt.subplots(figsize=(6.4, 4.8))
plt.plot(step, np.array(loss_values))
plt.title("Průběh tréninku neuronové sítě")
plt.xlabel("Epocha")
plt.ylabel("Chyba")
# uložení do souboru
plt.savefig("nn_18.png")
# vykreslení grafu
plt.show()
16. Matice záměn pro síť, která odpovídá vždy korektně
To, že účelová funkce klesá k nule, sice znamená, že se síť učí (a to bez velkých problémů), ovšem její skutečné vlastnosti otestujeme jedině tak, že síti předáme pro ni neznámá testovací data, tedy v našem případě takové obrázky, která síť předtím „neviděla“. Tato testovací data již máme připravena v proměnné test_data, takže test sítě můžeme velmi snadno provést následujícím kódem. Povšimněte si, že se zde volá funkce torch.topk, která vrátí indexy k největších prvků v tenzoru. V našem případě potřebujeme index největšího prvku, protože síť vrací desetiprvkový vektor, jehož hodnoty říkají, do jaké míry se obrázek na vstupu podobá jednotlivým číslicím. Například pokud tento vektor bude roven [0.0, 0.9, 0.4, 0.3, …], velmi pravděpodobně je na vstupu obrázek číslice 1. Do seznamu y_pred se ukládají číslice predikované sítí, do seznamu y_test pak správné hodnoty:
# otestování neuronové sítě
test_dataloader = DataLoader(dataset=test_data, batch_size=1, shuffle=True)
y_pred = []
y_test = []
with torch.no_grad():
for X, y in test_dataloader:
outputs = nn_64_10_10(X)
correct_value = int(torch.topk(y, 1).indices[0][0])
predicted_value = int(torch.topk(outputs, 1).indices[0][0])
print(correct_value, predicted_value)
y_test.append(correct_value)
y_pred.append(predicted_value)
# výpočet matice záměn
disp = ConfusionMatrixDisplay.from_predictions(
y_test, y_pred,
cmap=plt.cm.Blues,
normalize=None,
)
# zobrazení matice záměn
print(disp.confusion_matrix)
# uložení výsledků
plt.savefig("confusion_matrix.png")
# vykreslení matice záměn
plt.show()
Pro síť, která je naučena na klasifikaci nezašuměných obrázků (a je na těchto obrázcích i otestována) bude matice záměn obsahovat nenulové prvky jen na hlavní diagonále. To značí, že je síť na 100% úspěšná:
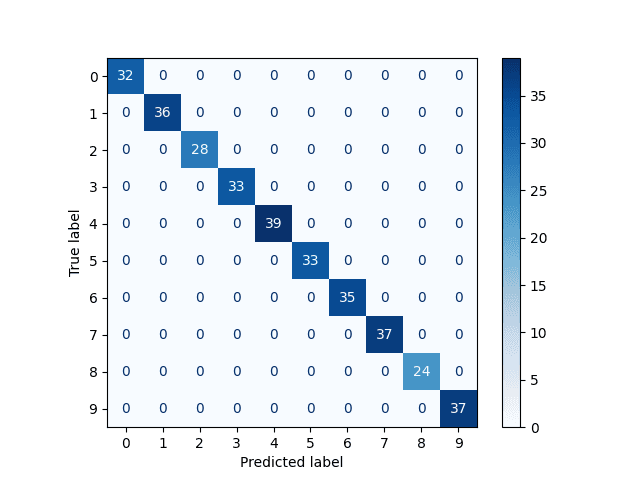
Obrázek 9: Matice záměn pro síť, která odpovídá vždy korektně.
Ovšem pozor – v případě, že budou trénovací data obsahovat malé množství obrázků (například jen 100 a nikoli 600), hrozí problém nedoučení sítě. Potom výsledky vypadají takto:
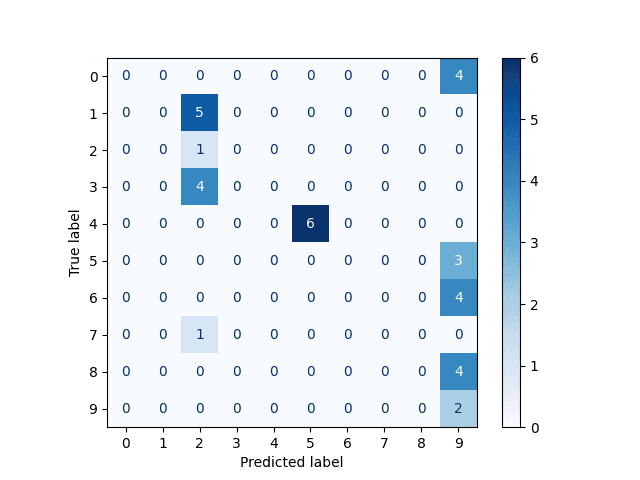
Obrázek 10: Matice záměn pro nedoučenou síť.
17. Matice záměn pro zašuměné obrázky
Nyní se podívejme, jak bude vypadat kvalita odpovědí sítě v případě, že obrázky v trénovací i testovací sadě budou zašuměny. Úroveň šumu se postupně zvyšuje od 25% přes 50% až do 75% (což je hodně – takové obrázky nerozpozná ani člověk – viz též obrázek z úvodní kapitoly).
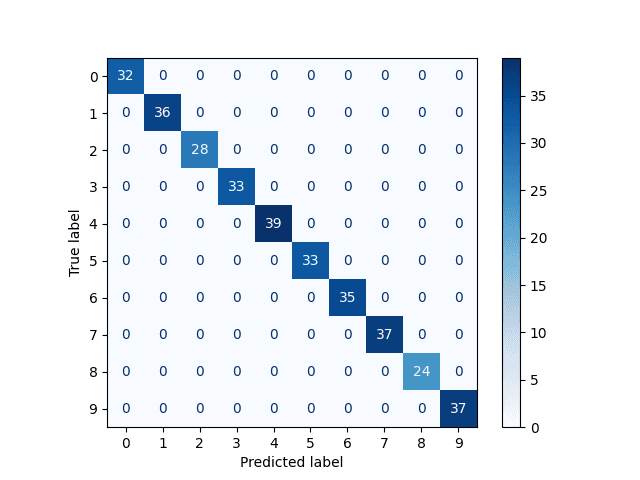
Obrázek 11: Matice záměn pro obrázky zašuměné z 25%. Síť odpovídá korektně.
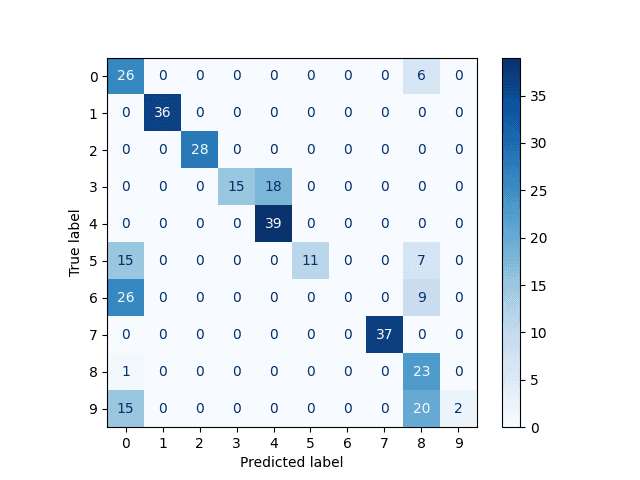
Obrázek 12: Matice záměn pro obrázky zašuměné z 50%. Vysoké hodnoty na hlavní diagonále značí korektní odpovědi, ovšem je patrné, že například číslice 6 není rozeznána nikdy. Nejlépe síť rozeznává číslice 1, 4 a 7.
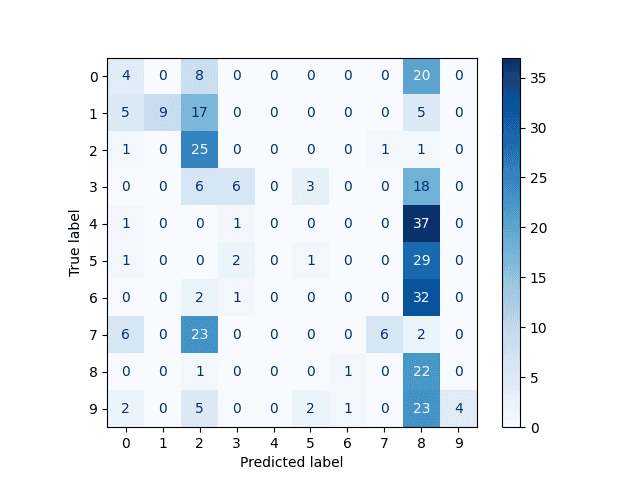
Obrázek 13: Matice záměn pro obrázky zašuměné ze 75%. Nyní jsou odpovědi zcela náhodné a tudíž nepoužitelné.
18. Matice záměn pro posunuté obrázky
Na závěr si ukažme matice záměn pro síť, která by měla umět predikovat obrázky posunuté o jeden či o dva pixely:
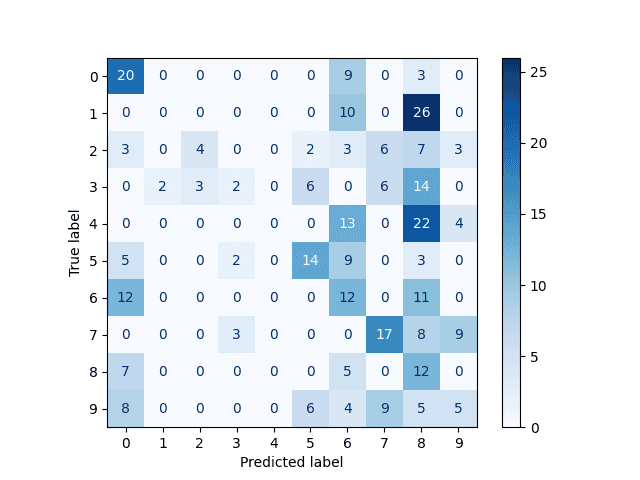
Obrázek 14: Matice záměn pro číslice posunuté maximálně o jeden pixel.
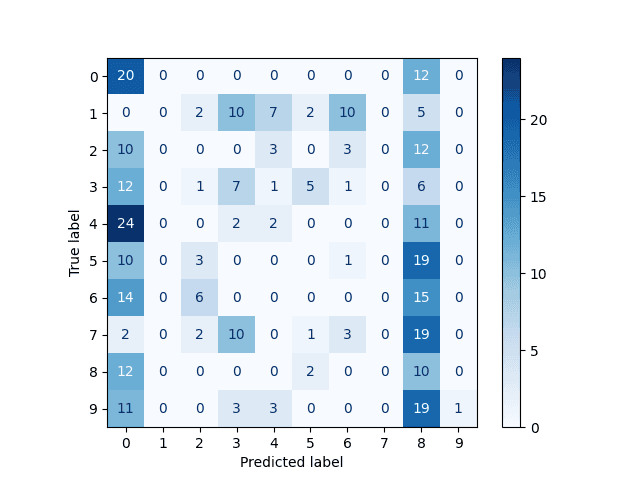
Obrázek 15: Matice záměn pro číslice posunuté maximálně o dva pixely.
Výsledky jsou zajímavé. Při pohledu na klesající účelovou funkci by se mohlo zdát, že je síť naučena relativně kvalitně, ovšem její odpovědi jsou opět prakticky zcela nepoužitelné. A právě zde se ukazuje teoretický i praktický limit běžných neuronových sítí při práci s jednorozměrnými nebo dvourozměrnými daty. Pro předpovědi na základě těchto dat potřebujeme lepší mechanismus – a tím jsou konvoluční neuronové sítě, které dokážou vliv posunu (a dalších transformací) do značné míry eliminovat.
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu PyTorch lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady:
20. Odkazy na Internetu
- Seriál Programovací jazyk Lua na Rootu:
https://www.root.cz/serialy/programovaci-jazyk-lua/ - PDM: moderní správce balíčků a virtuálních prostředí Pythonu:
https://www.root.cz/clanky/pdm-moderni-spravce-balicku-a-virtualnich-prostredi-pythonu/ - PyTorch Tutorial: Building a Simple Neural Network From Scratch
https://www.datacamp.com/tutorial/pytorch-tutorial-building-a-simple-neural-network-from-scratch - Interní reprezentace numerických hodnot: od skutečného počítačového pravěku po IEEE 754–2008:
https://www.root.cz/clanky/interni-reprezentace-numerickych-hodnot-od-skutecneho-pocitacoveho-praveku-po-ieee-754–2008/ - Interní reprezentace numerických hodnot: od skutečného počítačového pravěku po IEEE 754–2008 (dokončení):
https://www.root.cz/clanky/interni-reprezentace-numerickych-hodnot-od-skutecneho-pocitacoveho-praveku-po-ieee-754–2008-dokonceni/ - Brain Floating Point – nový formát uložení čísel pro strojové učení a chytrá čidla:
https://www.root.cz/clanky/brain-floating-point-ndash-novy-format-ulozeni-cisel-pro-strojove-uceni-a-chytra-cidla/ - Stránky projektu PyTorch:
https://pytorch.org/ - Informace o instalaci PyTorche:
https://pytorch.org/get-started/locally/ - Tenzor (Wikipedia):
https://cs.wikipedia.org/wiki/Tenzor - Introduction to Tensors:
https://www.youtube.com/watch?v=uaQeXi4E7gA - Introduction to Tensors: Transformation Rules:
https://www.youtube.com/watch?v=j6DazQDbEhQ - Tensor Attributes:
https://pytorch.org/docs/stable/tensor_attributes.html - Tensors Explained Intuitively: Covariant, Contravariant, Rank :
https://www.youtube.com/watch?v=CliW7kSxxWU - What is the relationship between PyTorch and Torch?:
https://stackoverflow.com/questions/44371560/what-is-the-relationship-between-pytorch-and-torch - What is a tensor anyway?? (from a mathematician):
https://www.youtube.com/watch?v=K7f2pCQ3p3U - Visualization of tensors – part 1 :
https://www.youtube.com/watch?v=YxXyN2ifK8A - Visualization of tensors – part 2A:
https://www.youtube.com/watch?v=A95jdIuUUW0 - Visualization of tensors – part 2B:
https://www.youtube.com/watch?v=A95jdIuUUW0 - What the HECK is a Tensor?!?:
https://www.youtube.com/watch?v=bpG3gqDM80w - Stránka projektu Torch
http://torch.ch/ - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - An Introduction to Tensors
https://math.stackexchange.com/questions/10282/an-introduction-to-tensors - Differences between a matrix and a tensor
https://math.stackexchange.com/questions/412423/differences-between-a-matrix-and-a-tensor - Qualitatively, what is the difference between a matrix and a tensor?
https://math.stackexchange.com/questions/1444412/qualitatively-what-is-the-difference-between-a-matrix-and-a-tensor? - Tensors for Neural Networks, Clearly Explained!!!:
https://www.youtube.com/watch?v=L35fFDpwIM4 - Tensor Processing Unit:
https://en.wikipedia.org/wiki/Tensor_Processing_Unit - Třída Storage:
http://docs.pytorch.wiki/en/storage.html - Funkce torch.dot
https://pytorch.org/docs/stable/generated/torch.dot.html#torch.dot - Funkce torch.narrow
https://pytorch.org/docs/stable/generated/torch.narrow.html - Funkce torch.matmul
https://pytorch.org/docs/stable/generated/torch.matmul.html - Funkce torch.reshape
https://pytorch.org/docs/stable/generated/torch.reshape.html - Funkce torch.arange
https://pytorch.org/docs/stable/generated/torch.arange.html - Funkce torch.range
https://pytorch.org/docs/stable/generated/torch.range.html - Třída torch.Tensor
https://pytorch.org/docs/stable/tensors.html - Atributy tenzorů
https://pytorch.org/docs/stable/tensor_attributes.html - Pohledy vytvořené nad tenzory
https://pytorch.org/docs/stable/tensor_view.html - Broadcasting v knihovně
https://numpy.org/doc/stable/user/basics.broadcasting.html - Broadcasting semantics (v knihovně PyTorch)
https://pytorch.org/docs/stable/notes/broadcasting.html - Dot Product In Physics: What Is The Physical Meaning of It?
https://profoundphysics.com/dot-product-in-physics-what-is-the-physical-meaning-of-it/ - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/ - Třída torch.nn.Linear
https://pytorch.org/docs/stable/generated/torch.nn.Linear.html - Třída torch.nn.Parameter
https://pytorch.org/docs/stable/generated/torch.nn.parameter.Parameter.html - Třída torch.nn.Sigmoid
https://pytorch.org/docs/stable/generated/torch.nn.Sigmoid.html
























