Scratch - plnohodnotný programovací jazyk nebo jen dětské puzzle? (4. část: pokročilá práce s BYOB)

Obsah

1. Scratch – plnohodnotný programovací jazyk nebo jen dětské puzzle? (4. část: pokročilá práce s BYOB)

2. Kreslíme domek aneb základní obrazec Pythagorova stromu

3. Využití rekurze při vykreslování Pythagorova stromu

4. Rozdělení programu na podprogramy a zobecnění algoritmu pro vykreslení Pythagorova stromu

5. Problematika vzájemného volání dvou podprogramů

6. Demonstrační příklad – Sierpinského trojúhelník vykreslený rekurzivním algoritmem

7. Algoritmus vykreslení Sierpinského trojúhelníku v projektu BYOB

8. Od Scratche přes BYOB až k vizuální tvorbě programů ve Smalltalku s využitím bloků

9. Odkazy na Internetu

1. Scratch – plnohodnotný programovací jazyk nebo jen dětské puzzle? (4. část: pokročilá práce s BYOB)

V předchozí části seriálu o programovacích jazycích navržených s ohledem na výuku programování jsme se seznámili s projektem BYOB, neboli plným názvem Build Your Own Block. Tento poměrně zajímavý projekt vznikl rozšířením projektu Scratch o relativně velké množství nových funkcí. Z hlediska uživatelů je nejdůležitější novinkou možnost tvorby nových příkazových bloků (podprogramů), u nichž je možné specifikovat jejich parametry, určit typ parametrů, jejich implicitní hodnoty atd. Každý nově vytvořený blok může být umístěn do jedné z osmi kategorií bloků – pohyb, vzhled, zvuk, pero, ovládání, vnímání, operátory a proměnné. Minule jsme si taktéž ukázali, jakým způsobem se bloky vytváří. Dnes si na několika demonstračních příkladech vysvětlíme použití uživatelsky definovaných bloků při vykreslování rekurzivních obrazců a taktéž si řekneme, jak lze (i když poněkud nešikovně) vyřešit problém, který nastane ve chvíli, když má blok A volat blok B a současně se z bloku B volá blok A (je ostatně zajímavé sledovat, jak je tento problém řešen v ostatních programovacích jazycích, ať již se jedná o překladače, nebo o interpretry).

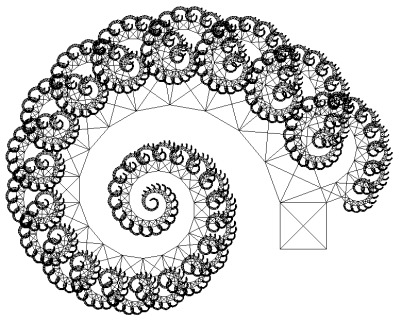
Obrázek 1: Zobecněná forma takzvaného Pythagorova stromu, která byla vykreslena programem, v němž byla využita rekurze. Finální verze tohoto programu je ukázána ve čtvrté kapitole.

Ve druhé části dnešního článku si popíšeme projekt s názvem Elements, jenž je součástí BYOBu (i když součástí poněkud nenápadnou, pravděpodobně proto, že se prozatím jedná o testovací verzi). Projekt Elements, jehož autorem Jens Mönig, se snaží využít stejnou techniku vizuální tvorby programů pomocí příkazových bloků, jaká je použita ve Scratchi, ovšem aplikuje ji na samotný programovací jazyk Smalltalk, v němž je Scratch a samozřejmě i BYOB naprogramován. Vzhledem k tomu, že v jazyku Smalltalk jsou prakticky všechny elementy jazyka považovány za objekty, a to včetně pravdivostních hodnot, čísel, programových bloků, programových smyček atd., obsahuje projekt Elements jen velmi málo typů základních stavebních bloků (konkrétně pouze sedm). Pokud by podobný projekt vznikl například pro mainstreamové jazyky (od céčka přes JavaScript až k Pythonu), bylo by nutné navrhnout mnohem větší počet stavebních bloků, čímž by se celé ovládání (i způsob „vykreslení zdrojových kódů“) mohlo zkomplikovat.

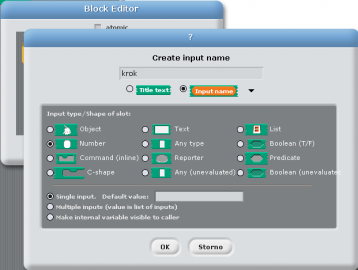
Obrázek 2: U parametrů podprogramů lze zavést kontrolu na správný typ předávaných parametrů. V demonstračních příkladech, které si dnes budeme ukazovat, je vždy použit numerický datový typ. Povšimněte si možnosti zadání implicitní hodnoty parametru ve spodní části formuláře.

2. Kreslíme domek aneb základní obrazec Pythagorova stromu

V úvodní části dnešního článku se budeme zabývat problematikou návrhu a implementace rekurzivních algoritmů, protože se jedná o poměrně důležitou část algoritmizace. Díky tomu, že projekt Scratch (a samozřejmě i na něj navazující projekt BYOB) umožňuje využití takzvané „želví grafiky“, je možné problematiku rekurzivních algoritmů vysvětlit na rekurzivně tvořených obrazcích, což je názorné a současně je na grafickém výstupu vidět jakákoli chyba vzniklá špatně navrženým algoritmem (například je ihned patrné, kdy se zapomene uvést ukončující podmínka rekurze atd.). Prvním programem, který v několika krocích vytvoříme, bude program na vykreslení takzvaného Pythagorova stromu. Základem Pythagorova stromu je známý domeček kreslený jedním tahem, jenž je zobrazen na třetím obrázku. Pokud považujeme šířku domku a výšku jeho stěn za základní jednotkovou délku, pak mají úhlopříčné tahy délku rovnou odmocnině dvou (sqrt 2) a délka stran střechy je naopak rovná převrácené hodnotě odmocnině dvou (1/sqrt 2). Obě hodnoty samozřejmě vychází ze známého vztahu pro délky stran pravoúhlého rovnoramenného trojúhelníku:

2a²=c²

Obrázek 3: Známá dětská hádanka – domeček vykreslený jediným tahem – tvoří základ jedné varianty Pythagorova stromu.

Původní implementace vykreslení domku jedním tahem je zapsána v syntaxi programovacího jazyka Logo:

to domek :strana
    ; základna
    forward :strana
 
    ; úhlopříčka
    left 90+45
    forward :strana*sqrt 2
 
    ; stěna
    left 90+45
    forward :strana
 
    ; úhlopříčka
    left 90+45
    forward :strana*sqrt 2
 
    ; úsečka pod střechou
    left 90+45
    forward :strana
 
    ; první část střechy
    right 90+45
    forward :strana/sqrt 2
 
    ; druhá část střechy
    right 90
    forward :strana/sqrt 2
 
    ; zbývající stěna
    right 45
    forward :strana
    left 90
end
 
; zobrazení pracovní plochy a její smazání
draw
clean
right 90
; vykreslení domku
domek 70

Převedení výše uvedeného programu na sekvenci do sebe zapojených příkazových bloků v projektu Scratch či BYOB je v tomto případě přímočaré – viz též screenshot zobrazený pod tímto odstavcem. Jak si můžete všimnout, nejsou ve variantě programu pro Scratch zapsány poznámky, protože Scratch kupodivu neumožňuje jejich tvorbu, což je škoda (poznámky by se například mohly zobrazit v bublinové nápovědě, podobně jako je tomu v některých textových procesorech či tabulkových kalkulátorech). V případě potřeby je možné v projektu BYOB namísto poznámky použít prázdný uživatelsky definovaný blok s jedním řetězcovým parametrem.

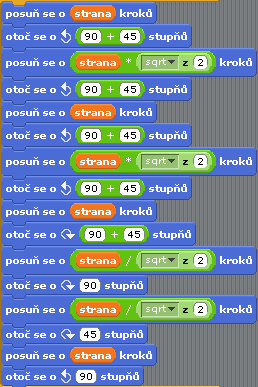
Obrázek 4: Sekvence příkazů pro vykreslení domku jedním tahem. Před provedením těchto příkazů je nutné nastavit hodnotu proměnné strana.

3. Využití rekurze při vykreslování Pythagorova stromu

V případě, že se vykreslení každé strany střechy nahradí rekurzivním voláním podprogramu pro vykreslení celého domku, získáme charakteristický tvar vzdáleně podobný stromu či keři – viz též obrázek číslo 5. Díky tomu, že oba segmenty střechy jsou kratší než základna původního domku, jsou další rekurzivně vykreslované domky menší (o odmocninu ze dvou), čehož lze využít při konstrukci podmínky pro zastavení rekurze. Při ladění programu je zajímavé taktéž sledování postupného vykreslování Pythagorova stromu, zejména na pomalejším počítači (ve skutečnosti se však právě na rekurzivních algoritmech projevuje relativní pomalost interpretace programů ve Scratchi i BYOBu).

Obrázek 5: Pokud se namísto střechy domku rekurzivně vykreslí dva nové (menší) domky, je výsledkem obrazec Pythagorova stromu.

Samozřejmě je nutné opět zavést podmínku pro ukončení rekurze, jinak by program teoreticky nikdy neskončil (ve skutečnosti by byl ukončen běhovou chybou při překročení volné kapacity operační paměti). Podmínka pro ukončení rekurze může být zadána různým způsobem, ale zde můžeme využít již výše zmíněného faktu, že se domky postupně zmenšují. V případě, že je délka strany pro vykreslení domku menší než délka předaná v parametru min_delka, je namísto domku vykreslena pouze úsečka o této délce, čímž je zajištěno vykreslení střech domků ležících na konci větví „stromu“. Pokud však délka strany přesahuje tuto hodnotu, je jedním tahem vykreslen celý domek. Tato podmínka je použita i v podprogramu domek, jenž je zobrazen na šestém obrázku. Jedná se prozatím o nerekurzivní variantu.

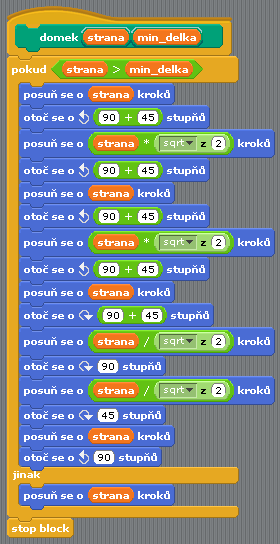
Obrázek 6: Nerekurzivní (testovací) varianta podprogramu domek, která již obsahuje podmínku na minimální délku strany domku.

Z výše uvedené nerekurzivní varianty programu je možné vytvořit rekurzivní variantu velmi snadno – namísto dvou příkazů pro vykreslení střechy postačuje rekurzivně zavolat samotný podprogram domek, samozřejmě s parametrem strana poděleným o odmocninu ze dvou. Nic dalšího není zapotřebí, protože podmínka pro ukončení rekurze automaticky zajistí, že program skončí v konečném čase.

Obrázek 7: Rekurzivní varianta podprogramu domek. Do programu jsou navíc přidány příkazy pro změnu barvy pera pro každý rekurzivně vykreslený domek.

Poznámka: v programovacím jazyce Logo by se vykreslení Pythagorova stromu mohlo řešit následujícím způsobe:

to domek :strana
    ifelse :strana>10 [
        ; základna
        forward :strana
 
        ; úhlopříčka
        left 90+45
        forward :strana*sqrt 2
 
        ; stěna
        left 90+45
        forward :strana
 
        ; úhlopříčka
        left 90+45
        forward :strana*sqrt 2
 
        ; úsečka pod střechou
        left 90+45
        forward :strana
 
        ; první část střechy
        right 90+45
        domek :strana/sqrt 2
 
        ; druhá část střechy
        right 90
        domek :strana/sqrt 2
 
        ; zbývající stěna
        right 45
        forward :strana
        left 90
    ][
        forward :strana
    ]
end
 
draw
clean
right 90
domek 70

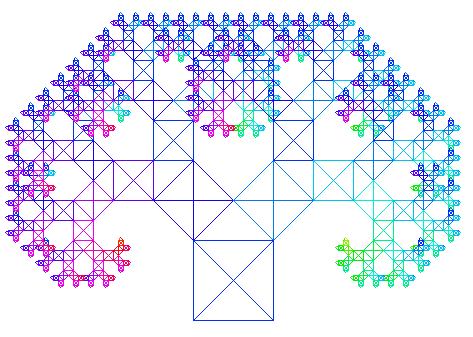
Obrázek 8: Výsledek běhu programu, jehož struktura byla zobrazena na předchozím obrázku.

4. Rozdělení programu na podprogramy a zobecnění algoritmu pro vykreslení Pythagorova stromu

Program, jehož struktura byla zobrazena na sedmém obrázku, sice pracuje korektně (pro správné parametry), ale není moc univerzální a ani přehledný. Program je však možné poměrně jednoduše rozdělit na menší a přehlednější podprogramy, což vede k jeho snadnější údržbě. Prvním krokem je vytvoření podprogramu (=uživatelského příkazového bloku) sloužícího pro vykreslení základny. Tento podprogram, jenž je nazvaný jednoduše zakladna, je velmi jednoduchý a bude volán přímo z upraveného podprogramu domek:

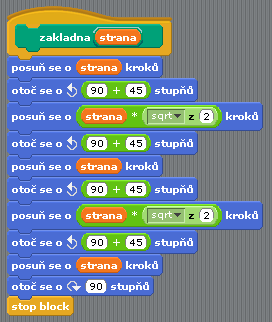
Obrázek 9: Podprogram nazvaný zakladna.

Další úprava programu může vést ke zobecnění Pythagorova stromu takovým způsobem, aby se větvení provádělo o libovolný úhel, nejenom pro 45°. Při kresbě zobecněného Pythagorova stromu je nutné vytvořit podprogram, který dokáže nakreslit pravoúhlý trojúhelník o zadané délce přepony (nejdelší strany) a úhlu mezi přeponou a jednou odvěsnou. Proč však potřebujeme vytvořit takový podprogram? Zobecněný Pythagorův strom se od pravidelného Pythagorova stromu, který jsme si popsali v předchozích dvou kapitolách, odlišuje především v tom, že je použit jiný úhel větvení, což jinými slovy znamená, že se změní tvar střechy z rovnoramenného pravoúhlého trojúhelníku na jiný pravoúhlý trojúhelník:

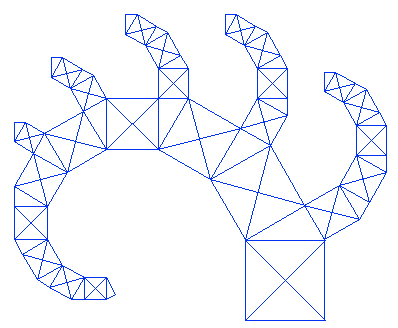
Obrázek 10: Zobecněný Pythagorův strom s odlišným úhlem rozvětvení.

Délka přepony v tomto trojúhelníku odpovídá šířce „domku“, který tvoří základ celého stromu, a odvěsny představují obě plochy střechy. Změnou úhlu odchylky první odvěsny se změní i tvar celého trojúhelníku.

Výpočet délky odvěsen je velmi jednoduchý. První odvěsna bude mít délku rovnou:
a=c×cos α
a druhá odvěsna:
b=c×sin α
kde α je úhel, který svírá odvěsna a s přeponou c.

Pokud již známe vzorce pro výpočet délky obou odvěsen, je již snadné napsat podprogram, který střechu skutečně vykreslí. Povšimněte si, že nový podprogram pojmenovaný strecha volá původní podprogram domek, ovšem museli jsme přidat nový parametr uhel. Teoreticky by se mohlo jednat o globální proměnnou, to však není z programátorského hlediska příliš čisté řešení, i když je to paměťově poněkud méně náročné:

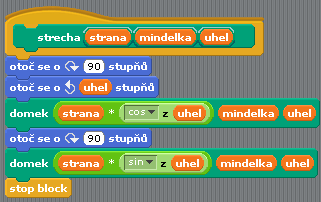
Obrázek 11: Podprogram nazvaný strecha.

Vlastní podprogram domek se nám značně zkrátil a zpřehlednil:

Obrázek 12: Podprogram domek se nám díky dekompozici programu značně zjednodušil.

A zde je vidět výsledek běhu celého programu pro úhel 20°:

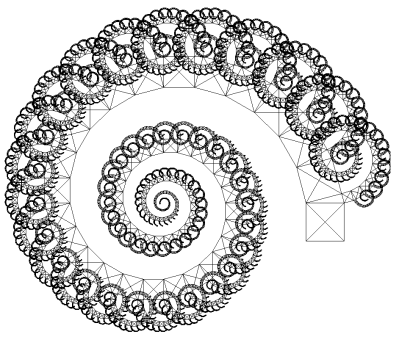
Obrázek 13: Zobecněný Pythagorův strom.

5. Problematika vzájemného volání dvou podprogramů

Jak jste se již mohli všimnout v poslední verzi programu pro vykreslení zobecněného Pythagorova stromu, můžeme se při implementaci některých rekurzivních algoritmů dostat do situace, kdy se má z bloku A volat blok B a současně se má z bloku B naopak volat blok A. U programu uvedeného v předchozí kapitole se tomuto stavu můžeme relativně snadno vyhnout (postačuje blok strecha přenést do bloku domek), ovšem existují i algoritmy, v nichž je nutné tuto nepřímou rekurzi použít a nelze se jí žádnou (rozumnou a čitelnou) úpravou programu zbavit. Ovšem v projektu BYOB se při tvorbě příkazových bloků nazvaných A a B dostaneme do situace, kdy není zdánlivě možné první blok A celý naprogramovat, protože ještě neexistuje druhý blok B, jehož box by se mohl přemístit do těla bloku A.

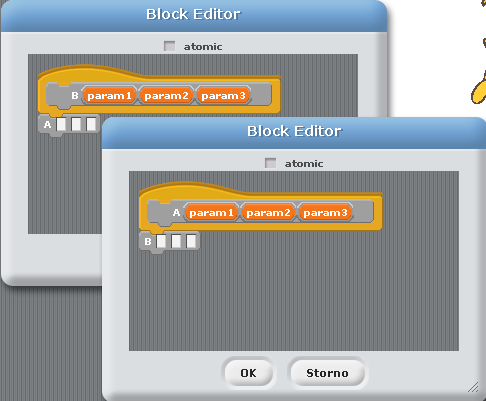
Obrázek 14: Současně otevřená okna s definicemi uživatelských příkazových bloků A a B.

V běžných programovacích jazycích, v nichž se program zapisuje formou textových souborů, se tato situace řeší různým způsobem. V Pascalu se například využívá předběžná deklarace druhého bloku s klíčovým slovem forward. Podobné je to ve Forthu a v jazyku C je nutné alespoň nadeklarovat hlavičky volaných funkcí. Některé interpretované programovací jazyky dokážou příslušnou funkci či metodu vyhledat až v čase běhu programu, nezávisle na tom, kde je ve skutečnosti deklarována. V projektu BYOB můžeme využít techniku, která se v určitém ohledu podobná předběžným deklaracím. Nejprve se totiž vytvoří hlavičky obou bloků A a B, tj. vytvoří se prázdné bloky, u nichž je zadán jejich název a počet i typ parametrů. V této chvíli je již možné nechat současně otevřená okna pro editaci obou bloků a z levé části uživatelského prostředí BYOBu do těchto oken přetáhnout boxy obou bloků A a B – viz též obrázek číslo 14.

6. Demonstrační příklad – Sierpinského trojúhelník vykreslený rekurzivním algoritmem

Využití nepřímé rekurze si můžeme snadno odzkoušet na rekurzivním algoritmu pro vykreslení jedné z forem Sierpinského trojúhelníku. Tato forma Sierpinského trojúhelníku je vytvořena pomocí jediné lomené čáry (polyčáry), přičemž úhel napojení sousedních úseček (které se stýkají ve společném vrcholu) je roven 120° a délka všech úseček tvořících lomenou čáru je konstantní.

Obrázek 15: Sierpinského trojúhelník vykreslený jedinou nepřerušovanou lomenou čarou.

Existuje hned několik způsobů vykreslení této formy Sierpinského trojúhelníku. My si v dnešním článku ukážeme způsob založený na nepřímé rekurzi, tj. na algoritmu, ve kterém nějaká procedura A volá proceduru B, ve které se rekurzivně volá opět procedura A (ve skutečnosti je v použitém algoritmu přítomna i rekurze přímá, tj. procedura A volá jak sama sebe, tak i proceduru B). Obě vytvořené procedury mají pro jednoduchost názvy sierpinsky_x a sierpinsky_y (tyto názvy jsou odvozeny z názvů nonterminálních symbolů v přepisovací gramatice L-systému, to však již zabíháme do podrobností, které s dnešním článkem souvisí jen částečně) a výsledný tvar programu pro vykreslení lomené čáry ve tvaru Sierpinského trojúhelníka pro daný počet iterací a délku úseček vypadá v programovacím jazyku Logo následovně:

 
to sierpinsky_x :strana :iter
    if :iter>0 [
        sierpinsky_y :strana :iter-1
        forward :strana
        left 60
        sierpinsky_x :strana :iter-1
        forward :strana
        left 60
        sierpinsky_y :strana :iter-1
    ]
end
 
to sierpinsky_y :strana :iter
    if :iter>0 [
        sierpinsky_x :strana :iter-1
        forward :strana
        right 60
        sierpinsky_y :strana :iter-1
        forward :strana
        right 60
        sierpinsky_x :strana :iter-1
    ]
end
 
(draw 300 300)
y 10 5
forward 10
 

Obrázek 16: Sierpinského trojúhelník vykreslený jedinou nepřerušovanou lomenou čarou. Oproti předchozímu obrázku se zmenšil krok, zvětšil počet iterací a do bloku sierpinsky_x byl přidán příkaz pro změnu barvy kreslicího pera.

7. Algoritmus vykreslení Sierpinského trojúhelníku v projektu BYOB

Při implementaci tohoto programu v projektu BYOB můžeme nejprve vytvořit kostru bloku sierpinsky_x, který je zde nazvaný sierpinsky-x a prozatím obsahuje pouze přímou rekurzi:

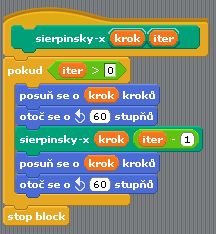
Obrázek 17: Prozatím neúplné tělo bloku nazvaného sierpinsky-x.

Dále je již možné vytvořit celý blok y (resp. sierpinsky-y), protože druhý blok sierpinsky-x již existuje, i když jeho tělo není úplné (to nás však nemusí v tomto okamžiku trápit, protože se program nebude ihned spouštět):

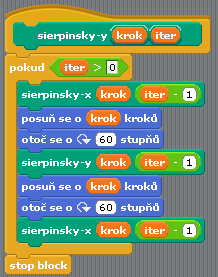
Obrázek 18: Úplné tělo bloku nazvaného sierpinsky-y.

Ve třetím kroku dokončíme tělo bloku sierpinsky-x:

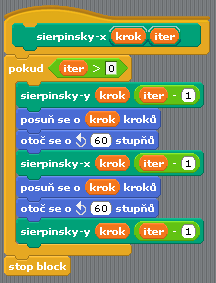
Obrázek 19: Nyní je již možné dokončit blok sierpinsky-x.

Hlavní program (blok) pouze vhodně nastaví sprite i pracovní plochu a posléze spustí vykreslování:

Obrázek 20: Hlavní program s inicializací spritu i pracovní plochy.

8. Od Scratche přes BYOB až k vizuální tvorbě programů ve Smalltalku s využitím bloků

V projektu BYOB je ve skutečnosti ukryt (a to poměrně dokonale :-) ještě jeden zajímavý projekt, který se nazývá Elements. Autorem tohoto projektu, jenž se v současnosti nachází v testovací, nicméně stabilní fázi, je Jens Mönig. Jens byl podle svých vlastních slov doslova fascinován jednoduchostí a současně i názorností tvorby programů ve Scratchi a rozhodl se k zajímavému počinu – vytvořit podobný systém vizuální tvorby programů i pro programovací jazyk Smalltalk.

Obrázek 21: Projekty Scratch i BYOB jsou naprogramované ve Squeaku, což je velmi zdařilá implementace jazyka Smalltalk a vlastního grafického uživatelského prostředí Morphic. Se Squeakem jsme se už seznámili v předchozích částech tohoto seriálu.

Vytvořením projektu Elements vlastně došlo k uzavření kruhu, protože projekty Scratch i BYOB jsou naprogramovány právě ve Smalltalku, což mj. znamená, že se v Elements mohou upravovat jak základní třídy Smalltalku i Squeaku, tak i třídy Scratche a BYOBu – to vše samozřejmě v „živém“ systému, jak je to ostatně v případě Smalltalku zvykem (pokud dojde ke změně nějaké třídy, ihned se v systému projeví její nové chování a současně je možné měnit chování jakékoli třídy, například i třídy Boolean, Number atd., i když to může být v těchto případech poněkud nebezpečné).

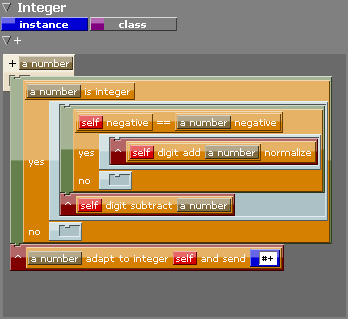
Obrázek 22: Tímto způsobem se v projektu Elements zobrazuje tělo zprávy + (součet) pro třídu Integer.

Díky tomu, že programovací jazyk Smalltalk má ve skutečnosti velmi jednoduchou syntaxi, vyskytuje se v projektu Elements pouze sedm základních typů bloků: objekt, zpráva, literál (konstanta), uzávěr, blok představující jeden krok – příkaz, primitivum a návratová hodnota. Pro zjednodušení jsou pseudoproměnné (a současně i objekty-jedináčci) true a false společně se speciálními objekty self a super reprezentovány vlastními bloky s odlišnou barvou pozadí. Stejně tak existuje i speciální blok pro přiřazení a taktéž blok reprezentující strukturovanou podmínku typu if-then-else, který je překládán na smalltalkovské zprávy #iftrue, #iffalse a jejich varianty (je to mnohem přehlednější a navíc se tím tvar vizuálně zobrazených algoritmů přibližuje tvaru algoritmů zapsaných přímo ve Scratchi či BYOBu).

Obrázek 23: Základní typy bloků, s nimiž se pracuje v projektu Elements.

V kontextovém menu přiřazeném ke každému příkazovému bloku v programu BYOB se nově nachází i příkaz Edit Elements. Tento příkaz vede k otevření nového okna projektu Elements, kde se vizuálně zobrazí programový kód vybraného bloku. Ovšem po rozkliknutí šipky zobrazené vlevo nahoře vedle jména bloku se zobrazí squeakovské menu s výběrem všech tříd, které se v systému nachází, včetně objektů Scratche, Squaku, projektu Elements i základních objektů typu Boolean, Number, Integer atd. Z tohoto menu lze vybrat kteroukoli třídu a z menu o řádek níže pak libovolnou metodu této třídy.

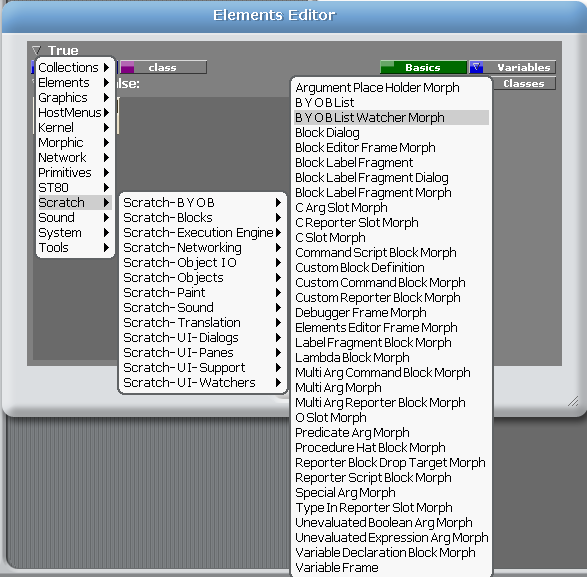
Obrázek 24: Menu s výběrem všech tříd.

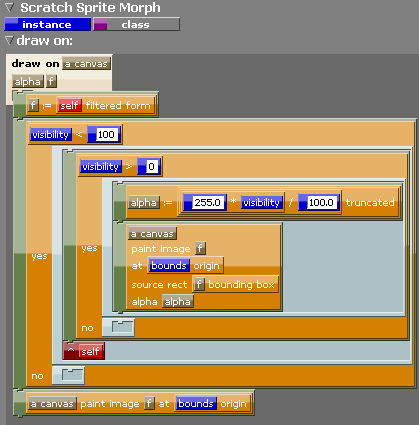
Obrázek 25: Projekt Elements by mohl odstranit určitou averzi k programovacímu jazyku Smalltalk, kterou někteří programátoři cítí kvůli neobvyklému zápisu programů. Vizuální tvar programů je velmi přehledný a skrývá některé „speciality“ Smalltalku.

9. Odkazy na Internetu

1. Scratch: oficiální stránka projektu
   http://scratch­.mit.edu/
2. Scratch: galerie projektů vytvořených ve Scratchi
   http://scratch­.mit.edu/galle­ries/browse/ne­west
3. Scratch: nápověda
   file:///usr/sha­re/scratch/Hel­p/en/index.html
4. Scratch: obrazovky nápovědy
   file:///usr/sha­re/scratch/Hel­p/en/allscreen­s.html
5. Scratch (Wikipedie CZ)
   http://cs.wiki­pedia.org/wiki/Scrat­ch
6. Scratch (programming language)
   http://en.wiki­pedia.org/wiki/Scrat­ch_(programmin­g_language)
7. Mitchel Resnick (Wikipedia EN)
   http://en.wiki­pedia.org/wiki/Mit­chel_Resnick
8. Domácí stránka Mitchela Resnicka
   http://web.me­dia.mit.edu/~mres/
9. BASIC-256 – BASIC256 – An easy to use BASIC language and IDE
   http://www.ba­sic256.org/
10. PythonTurtle
    http://python­turtle.org/
11. Turtle graphics for Tk
    http://docs.pyt­hon.org/libra­ry/turtle.html
12. Scratch Lowers Resistance to Programming
    http://www.wi­red.com/gadge­tlab/2009/03/scrat­ch-lowers/
13. Stopařův průvodce jedním převážně neškodným programovacím jazykem
    http://www.squ­eak.cz/
14. CamelCase
    http://en.wiki­pedia.org/wiki/Ca­mel_case
15. Smalltalk tutorial chapter 5 – Variables
    http://www.tu­torials4u.com/sma­lltalk/smalltalk-tutorial-05.htm
16. History around Pascal Casing and Camel Casing
    http://blogs.msdn­.com/b/brada/ar­chive/2004/02/0­3/67024.aspx
17. Xerox Alto
    http://en.wiki­pedia.org/wiki/Xe­rox_Alto
18. WIMP (computing)
    http://en.wiki­pedia.org/wiki/WIM­P_(computing)
19. Graphical user interface
    http://en.wiki­pedia.org/wiki/GUI
20. Xerox Star
    http://en.wiki­pedia.org/wiki/Xe­rox_Star
21. The Xerox Star 8010 „Dandelion“
    http://www.di­gibarn.com/co­llections/sys­tems/xerox-8010/index.html
22. Fibonacci number
    http://en.wiki­pedia.org/wiki/Fi­bonacci_number
23. Squeak home page
    http://www.squ­eak.org/
24. XO: The Children's Machine
    http://wiki.lap­top.org/go/The_Chil­dren's_Machine
25. Squeak na Wikipedii EN
    http://en.wiki­pedia.org/wiki/Squ­eak
26. Squeak na Wikipedii CZ
    http://cs.wiki­pedia.org/wiki/Squ­eak
27. Squeak by Example
    http://squeak­byexample.org/
28. Squeak Land
    http://www.squ­eakland.org/
29. SqueakNotes
    http://squeak­.zwiki.org/Squ­eakNotes
30. Squeak FAQ
    http://wiki.squ­eak.org/squeak/471
31. Learning Squeak
    http://c2.com/cgi/wi­ki?LearningSqu­eak
32. Lazarus (Software)
    http://en.wiki­pedia.org/wiki/La­zarus_%28softwa­re%29
33. FreePascal
    http://www.fre­epascal.org/
34. „Why I Love Python“ slides
    http://www.min­dviewinc.com/dow­nloads/pub/ec­kel/LovePython­.zip
35. „Why I love Python“ (presentation)
    http://www.sli­deshare.net/di­dip/why-i-love-python
36. První jazyk: Python
    http://macek.san­dbox.cz/texty/prvni-jazyk-python/
37. Programovací jazyk Python
    http://www.py­.cz/FrontPage
38. Python – Wikipedia CS
    http://cs.wiki­pedia.org/wiki/Pyt­hon
39. IPython
    http://en.wiki­pedia.org/wiki/I­python
40. IPython: an interactive computing environment
    http://ipython­.scipy.org/mo­in/
41. Category:Python
    http://rosetta­code.org/wiki/Ca­tegory:Python
42. Educational programming language
    http://en.wiki­pedia.org/wiki/E­ducational_pro­gramming_langu­age
43. Seriál Letní škola programovacího jazyka Logo
    http://www.ro­ot.cz/serialy/let­ni-skola-programovaciho-jazyka-logo/
44. Logo Tree Project:
    http://www.eli­ca.net/downlo­ad/papers/Logo­TreeProject.pdf
45. Language Poster (O'Reilly):
    http://www.ore­illy.com/news/grap­hics/prog_lan­g_poster.pdf
46. Informace o Comenius Logu:
    http://www.com­logo.input.sk/in­dex.html
47. Stránka nabízející stažení Comenius Loga:
    http://www.com­logo.input.sk/nas­tiahnutie.html
48. Seminární práce o Comenius Logu:
    http://nwit.ped­f.cuni.cz/rotal9ap/lo­go/
49. Informace o LEGO/Logu:
    http://educati­on.otago.ac.nz/nzlnet/L­ogo/legologo.html
50. Informace o systému Elica:
    http://www.eli­ca.net/site/in­dex.html
51. Informace o systému NetLogo:
    http://ccl.nor­thwestern.edu/ne­tlogo/
52. Stažení NetLoga:
    http://ccl.nor­thwestern.edu/ne­tlogo/download­.shtml
53. Uživatelský manuál NetLoga ve formátu PDF:
    http://ccl.nor­thwestern.edu/ne­tlogo/docs/Net­Logo%20User%20Ma­nual.pdf
54. NetLogo FAQ:
    http://ccl.nor­thwestern.edu/ne­tlogo/docs/faq­.html
55. Domácí stránka Daniela Azumy (autora implementace Turtle Tracks):
    http://alumnus­.caltech.edu/~da­zuma/home/
56. Informace o aUCBLogu:
    http://www.phy­sik.uni-augsburg.de/~miche­ler/
57. Domácí stránka MSW Loga:
    http://www.sof­tronix.com/lo­go.html
58. Karel online
    http://karel.ol­dium.net/
59. EDU-SIG: Python in Education
    http://www.pyt­hon.org/commu­nity/sigs/curren­t/edu-sig/
60. Guido van Robot
    http://en.wiki­pedia.org/wiki/Gu­ido_van_Robot
61. The Guido van Robot Programming Language
    http://gvr.sou­rceforge.net/
62. An Introduction to Programming with Karel J. Robot
    http://blog.thin­goid.com/2003/10­/karel-intro/
63. Teaching a young robot new tricks
    http://blog.thin­goid.com/2003/11­/karel-new-tricks/
64. Karel and Company – More Robots
    http://blog.thin­goid.com/2003/12­/karel-and-company/
65. Karel heads for the stars
    http://blog.thin­goid.com/2004/03­/karel-star/
66. Karel programming language documentation
    http://mormegil­.wz.cz/prog/ka­rel/prog_doc.htm
67. Karel J. Robot
    http://www.ma­inlandregional­.net/dklipp/Ho­nors%20Computer%20Sci­ence%20Java.htm
68. Karel (programming language)
    http://en.wiki­pedia.org/wiki/Ka­rel_(programmin­g_language)
69. Richard E. Pattis
    http://en.wiki­pedia.org/wiki/Richar­d_E._Pattis
70. XKarel home page
    http://xkarel­.sourceforge.net/en­g/
71. XKarel – screenshoty oken
    http://xkarel­.sourceforge.net/en­g/program.php#Ok­na
72. Greenfoot
    http://www.gre­enfoot.org/abou­t/whatis.html
73. Computer programming – Educational programming languages
    http://www.kid­slike.info/com­puter_program­ming_educatio­nal_programmin­g_languages
74. Making Great Programmers: Why BASIC is Still Relevant
    http://kidbasic­.sourceforge.net/en/why­.html
75. Gambas Wiki
    http://en.wiki­books.org/wiki/Gam­bas
76. Free tool offers ‚easy‘ coding
    http://news.bbc­.co.uk/2/hi/tec­hnology/6647011­.stm
77. Základy želví grafiky
    http://www.ro­ot.cz/clanky/za­klady-zelvi-grafiky/
78. Bill Kendrick's Web Turtle
    http://www.so­nic.net/~nbs/web­turtle/