Obsah
1. Perl Art a Mandelbrotova množina
2. Fraktály v Pythonu
3. Basic opět na scéně
3.1 Orbity dynamického systému nazvaného „Chip“
3.2 Orbity dynamického systému nazvaného „Gingerbreadman“
3.3 Orbity dynamického systému nazvaného „Hopalong“
3.4 Orbity dynamického systému nazvaného „Latoocarfian“
3.5 Orbity dynamického systému nazvaného „Pickover“
3.6 Orbity dynamického systému nazvaného „QuadrupTwo“
3.7 Zobrazení stavů systému „Dynamic“
3.8 Výpočet obrazce difůze
4. Fraktály vytvořené v LISPu
4.1 Dračí křivka
4.2 C-křivka
5. Perlička na závěr: Mandelbrotova množina generovaná Vimem
6. Odkazy na další informační zdroje
7. Obsah dalšího pokračování tohoto seriálu
1. Perl Art a Mandelbrotova množina
V předchozí části tohoto seriálu jsme si ukázali velké množství e-mailových signatur, tj. dvou až pětiřádkových programů vytvořených v céčku, pomocí kterých se dala v konzoli vykreslit Mandelbrotova množina (samozřejmě ne graficky, ale pomocí ASCII znaků). Podobné signatury je možné napsat i v Perlu. S ohledem na celkovou velikost programového kódu signatury má Perl výhodu v tom, že není zapotřebí deklarovat proměnné, na druhou stranu však musí být všechny skalární proměnné uvedeny s prefixem $, což může kód prodloužit.
Signatura s poměrně jednoduchým a přímočarým kódem pro vykreslení Mandelbrotovy množiny je ukázána na následujícím výpisu. Vzhledem k tomu, že nelze indexovat znaky v řetězci pomocí operátoru [], musela být použita konstrukce substr, která program prodloužila o cca 10 znaků oproti minule uvedenému céčkovému řešení. Vykreslený fraktál má „rozlišení“ 80×50 znaků, tj. na konzoli s 25 řádky bude viditelná pouze jeho spodní polovina. Rozlišení je možné změnit úpravou konstant .06 a .05 na prvním řádku:
#!/usr/bin/perl
for($g=-1.5;$g<1.439;$g+=.06){for($w=-2;$w<1.94;$w+=.05){$e=$
r=$t=0;while($e*$e+($v=$r*$r)<4&&$t++<13){$r=2*$e*$r+$g;$e=$e
*$e-$v+$w}print substr" .,`-:;+=:..: H\n",$w>-1.96?$t:15,1}} Níže vypsaný kód signatury sloužící taktéž k vykreslení Mandelbrotovy množiny, jehož autorem je Alun Jones, je již mnohem zajímavější a ukazuje velkou dynamičnost perlovských programů. Všimněte si způsobu doplnění prefixového znaku $ před skalární proměnné a toho, že větší část kódu je po své konverzi pomocí regulárního výrazu spuštěna/vyhodnocena příkazem eval (řetězec s touto částí programu začíná na konci druhého řádku a končí před zápisem regulárního výrazu). Zdrojový kód této netradiční signatury má tvar:
#!perl -i(X,Y,S,U,V,$_)=(-2,-2,4,80,40,"\n");if($#a>1){(X,Y,S)=@a}for((B,I)=Y+
@a=@ARGV,split('',' Alun Jones, IBS UW Aberystwyth, auj@aber.ac.uk ');$_=$^I.'
S;I++<V;B-=S/V){for((A,J)=X;J++<U;A+=S/U){(G,H,N)=(A,B);while((C=G*G)+(D=H*H)<
4&&++N<$#_){H=2*G*H+B,G=C-D+A}print$_[N]}print;A+=S/U}';s/([A-Z])/\$\1/g;eval;
2. Fraktály v Pythonu
Stále oblíbenější programovací jazyk Python je z hlediska programování signatur v některých ohledech problematický. Jeho sémantika je například pro matematické operace poněkud slabší než například v céčku (podobně jako použití 2D syntaxe), avšak pro jiné operace (seznamy, hashmapy, řetězce) se jedná o jazyk velmi mocný.
To ostatně dokazuje i následující program, který slouží k vykreslení křivky Helge von Kocha. Pro vykreslování je použita knihovna umožňující práci s takzvanou želví grafikou – turtle graphics. Celý výpočet má rekurzivní charakter, nejsou tedy použity klasické L-systémy (pomocí nich jsme křivku Helge von Kocha a další podobné fraktální objekty vykreslovali v předchozích částech tohoto seriálu). V programech psaných v Pythonu je nutné používat „2D syntaxi“ (bílé znaky na začátku řádku mají význam), proto je kód uvnitř rekurzivní funkce odsazený a nelze ho zapsat na jeden řádek.
from turtle import *;a=60;b=120
def f(_):
if _:f(_-1);left(a);f(_-1);right(b);f(_-1);left(a);f(_-1)
else:forward(10)
reset();up();backward(b);down();f(3);raw_input('') 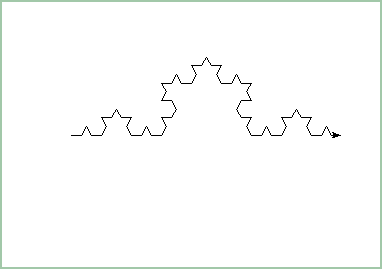
Po spuštění druhé signatury napsané v Pythonu se vykreslí takzvaná dračí křivka (Dragon Curve). Opět je použita želví grafika, tentokrát je však rekurzivní výpočet nahrazen počítanou smyčkou, ve které se provádí rozhodování, zda se má želva natočit doprava či doleva o 90°. Výraz provádějící rozhodnutí, kterým směrem se má želva pro danou hodnotu proměnné _ natočit, je založen na analýze řetězce získaného přepisovacími pravidly platnými pro dračí křivku. Přepsané řetězce mají pro první čtyři iterace tvar:
| Iterace | Řetězec pro ovládání želvy |
|---|---|
| 1 | R |
| 2 | R R L |
| 3 | R R L R R L L |
| 4 | R R L R R L L R R R L L R L L |
from turtle import *;
reset();tracer(0);left(90)
for _ in range(0,5000):
if((_&-_)<<1)&_:left(90)
else:right(90)
forward(2)
raw_input('') 
Obě dvě uvedené signatury jsou mými „prvotinami“ v Pythonu, proto je možné, že lze celý kód zapsat i kratším způsobem (i když si myslím, že vykreslení dračí křivky na 150 bytech kódu a Kochovy křivky na 170 bytech není špatný výsledek, hodně práce zde ovšem zastala knihovna implementující želví grafiku).
Následující program pravděpodobně není nutné Pythonistům zvlášť představovat, protože je součástí dokumentace tohoto programovacího jazyka (sekce FAQ). V programu je ukázáno použití funkcionálního stylu programování (převzatého z LISPu), které je zde charakterizováno funkcemi map(), reduce() a konstrukcí lambda:
# Mandelbrot set
print (lambda Ru,Ro,Iu,Io,IM,Sx,Sy:reduce(lambda x,y:x+y,map(lambda y,
Iu=Iu,Io=Io,Ru=Ru,Ro=Ro,Sy=Sy,L=lambda yc,Iu=Iu,Io=Io,Ru=Ru,Ro=Ro,i=IM,
Sx=Sx,Sy=Sy:reduce(lambda x,y:x+y,map(lambda x,xc=Ru,yc=yc,Ru=Ru,Ro=Ro,
i=i,Sx=Sx,F=lambda xc,yc,x,y,k,f=lambda xc,yc,x,y,k,f:(k<=0)or (x*x+y*y
>=4.0) or 1+f(xc,yc,x*x-y*y+xc,2.0*x*y+yc,k-1,f):f(xc,yc,x,y,k,f):chr(
64+F(Ru+x*(Ro-Ru)/Sx,yc,0,0,i)),range(Sx))):L(Iu+y*(Io-Iu)/Sy),range(Sy
))))(-2.1, 0.7, -1.2, 1.2, 30, 80, 24)
# \___ ___ \___ ___ | | |__ lines on screen
# V V | |______ columns on screen
# | | |__________ maximum of "iterations"
# | |_________________ range on y axis
# |____________________________ range on x axis
3. Basic opět na scéně
V předchozí části tohoto seriálu jsme si kromě céčkových signatur také ukázali několik programů napsaných v programovacím jazyku QBasic. K tomuto nepříliš povedenému, zato však populárnímu jazyku se dnes ještě vrátíme a ukážeme si signatury, po jejichž spuštění se vykreslí některý dynamický systém s fraktální charakteristikou (samotné prostředí QBasicu však není špatné – IDE i s nápovědou a konfiguračním souborem bylo možné uložit na 360kB disketu a kontrola syntaxe i sémantiky ihned po zapsání programového řádku je pro příležitostné uživatele, kterým je QBasic primárně určen, také výborná věc). Při použití DOSovského textového editoru EDIT se mimochodem vlastně volá vývojové prostředí QBasicu, pouze se při spouštění použije volba /EDITOR, pomocí níž se upraví menu prostředí a vyvolá se jiný soubor s nápovědou.
Ve všech dále uvedených basicovských signaturách je použit grafický režim karty VGA s rozlišením 640×480 pixelů a šestnácti barvami. Je ponechána implicitní barevná paleta karty VGA, což pro některé obrázky znamená určitou vizuální degradaci, ale QBasic neumožňuje jednoduchou změnu této palety (pouze přes vkládaný assembler, to by však signatury neúměrně prodloužilo).
3.1 Orbity dynamického systému nazvaného „Chip“
Dnešní první basicovská signatura po svém spuštění vykreslí orbity dynamického systému známého pod názvem „Chip“. Takto je systém pojmenovaný například v programu FractInt. Ve zdrojovém kódu programu ponechávám i přebytečné mezery; ty byly automaticky vytvořeny integrovaným editorem QBasicu, i když by program byl správně zapsaný i bez těchto mezer (IDE mezery automaticky doplňuje při načítání zdrojového kódu).
SCREEN 12: FOR i = 0 TO 50000: v = LOG(ABS(-19 * x - 1)): c = i / 5000
w = LOG(ABS(x + 19)): u = x: x = y - SGN(x) * COS(v * v) * ATN(w * w)
y = -15 - u: PSET (x + 320, y + 240), c: NEXT 
3.2 Orbity dynamického systému nazvaného „Gingerbreadman“
Dynamický systém „Gingerbreadman“ patří mezi ty nejjednodušší systémy s fraktální charakteristikou. Jednoduchost je patrná jak z délky celého programu, tak i ze zápisu iterační funkce:
SCREEN 12: x = -.1: y = 0!: FOR i = 0 TO 30000: u = x: x = 1! - y + ABS(x)
y = u: PSET (x * 35! + 180, y * 35! + 170), i / 5000: NEXT 
3.3 Orbity dynamického systému nazvaného „Hopalong“
Tento dynamický systém je vykreslován například ve starším programu HOP (pro DOS) nebo v demonstračním prográmku xmartin (pro Unixy). Iterační funkce je již složitější než v předchozím dynamickém systému, protože je v každém iteračním kroku proveden rozeskok na základě znaménka hodnoty xi.
SCREEN 12: y = .05: FOR i = 0 TO 30000: u = x: c = i / 2000
IF x > 0 THEN x = y - SQR(ABS(x)) ELSE x = y + SQR(ABS(x))
y = .4 - u: PSET (x * 100! + 325, y * 100! + 185), c: NEXT 
3.4 Orbity dynamického systému nazvaného „Latoocarfian“
Tento typ dynamického systému s fraktální charakteristikou popsal Clifford Pickover ve své knize „Chaos in Wonderland“. V iteračním výpočtu jsou použity goniometrické funkce a i výsledný obrázek s orbity obsahuje zaoblené tvary.
SCREEN 12: y = 1: a = -.966: b = 2.879: c = .744: FOR i = 0 TO 90000
u = SIN(b * y) + .765 * SIN(x * b): v = SIN(a * x) + c * SIN(y * a)
x = u: y = v: PSET (x * 120 + 320, y * 120 + 240), i / 8000: NEXT 
3.5 Orbity dynamického systému nazvaného „Pickover“
I tento dynamický systém popsal Clifford Pickover v knize „Chaos in Wonderland“. Iterační funkce je podobná té z předchozího fraktálu, jsou však použity jiné konstanty a místo funkcí sin() jsou použity funkce cos(). Konstanty a a c by samozřejmě nemusely být vůbec použity, takto je však možné celou signaturu zapsat se zhruba stejně dlouhými programovými řádky (QBasic neumožňuje rozdělení výrazu na více řádků, na rozdíl od některých jiných Basiců, které pro tento účel používají znak _).
SCREEN 12: FOR i = 0 TO 80000: a = 2.24: c = -.65: q = i / 5000
u = SIN(a * y) - z * COS(.43 * x): v = z * SIN(c * x) - COS(-2.43 * y)
z = SIN(x): x = u: y = v: PSET (x * 99 + 320, y * 99 + 240), q: NEXT 
3.6 Orbity dynamického systému nazvaného „QuadrupTwo“
Dynamický systém „QuadrupTwo“ je podobný systému „Hopalong“. Malou změnou konstanty 19 na prvním a druhém řádku je možné měnit i celkový tvar tohoto velmi zajímavého fraktálu.
SCREEN 12: FOR i = 0 TO 50000: u = x: v = LOG(ABS(x + 19))
x = y - SGN(x) * SIN(LOG(ABS(-19 * x - 1!))) * ATN(v * v)
y = -15 - u: PSET (x * 4 + 320, y * 4 + 240), i / 5000: NEXT 
3.7 Zobrazení stavů systému „Dynamic“
Dynamický systém nazvaný jednoduše „Dynamic“ se od předchozích systémů liší tím, že se na jednom obrázku zobrazuje velké množství orbitů, v našem případě 40×40. Změnou počítaných smyček for pro proměnné a a b se mění hustota „ok“ ve výsledném obrázku:
SCREEN 12: FOR a = -20 TO 20: FOR b = -20 TO 20: x = b
y = a: FOR i = 0 TO 5000: u = x - .01 * SIN(y + SIN(3 * y))
c = i / 400: y = y + .01 * SIN(x + SIN(3 * x)): x = u
PSET (x * 9 + 320, y * 9 + 240), c: NEXT: NEXT: NEXT 
3.8 Výpočet obrazce difůze
Poslední program napsaný v QBasicu je nejsložitější a také mnohem pomalejší než předchozí příklady. Generuje se totiž obrazec difůze v bitmapě o velikosti 150×150 pixelů, jejíž výpočet je založen na vytváření bodů na náhodném místě s následným testem, zda se bod nepřipojil k již vygenerovanému obrazci (větší obrazec nelze vytvořit kvůli paměťovým omezením QBasicu a vzhledem k době trvání výpočtu by to ani nebylo vhodné). Generování obrazce začíná s takzvaným semínkem (seed), které má v našem případě podobu jediného bodu umístěného na souřadnicích [75, 147]. Po připojení 1000 bodů program skončí.
DIM p(150, 150) AS INTEGER: SCREEN 12: p(75, 147) = 1
FOR d = 0 TO 999: x = INT(RND * 75) + 37: y = 10: h = 1: DO
x = x + INT(RND * 3) - 1 - (x < 2) + (x > 148)
y = y + INT(RND * 3) - 1 - (y < 2) + (y > 148)
i = p(x - 1, y - 1) OR p(x, y - 1) OR p(x + 1, y - 1) OR p(x - 1, y)
j = p(x + 1, y) OR p(x - 1, y + 1) OR p(x, y + 1) OR p(x + 1, y + 1)
IF i OR j THEN h = 0: p(x, y) = 1: PSET (x, y), 15
LOOP WHILE h: NEXT d 
4. Fraktály vytvořené v LISPu
Zajímavé signatury je možné vytvořit i v tak exotickém jazyku, jakým je LISP (osobně však mám LISP velmi rád, pro mnoho úkolů se jedná o ideální jazyk). V následujících dvou programech jsou využity funkce AutoLISPu, který slouží pro skriptování krátkých utilit i velkých aplikací ve známém grafickém programu AutoCAD. Dále uvedené signatury tedy mohou využít všech grafických možností AutoCADu, konkrétně se bude jednat o vytvoření grafické entity „polyline“, tj. polyčáry.
4.1 Dračí křivka
První signatura definuje nový AutoCADovský příkaz „drak“, po jehož zadání se vykreslí známá dračí křivka. Změnou hodnot proměnných l a m je možné měnit celkovou velikost draka a délku úseček, ze kterých je drak složen. Výpočet je založen na rekurzivním volání funkce „d“. Jak lze tuto signaturu spustit? Nejprve je zapotřebí načíst skript do AutoCADu a potom z příkazové řádky zadat příkaz „drak“. Načtení AutoLISPovských programů zajišťuje funkce LOAD:
(load "c:\\dragon.lsp")
drak Zdrojový kód signatury:
(defun C:drak(/ p l m)(setq p '(0 0)l 99 m 2)(setvar "cmdecho" 0)
(setvar "blipmode" 0)(command "_pline" p)(d l 0 1 m)(command "")(
setvar "cmdecho" 1)(command "_zoom" "m"))(defun d(l u s m)(cond((
< l m)(command(polar(getvar "lastpoint")u l)))(T(d(/ l(sqrt 2.))(+
u(* s(/ pi 4.)))1. m)(d(/ l(sqrt 2.))(- u(* s(/ pi 4.)))-1. m)))) 
4.2 C-křivka
Druhá LISPovská signatura po svém spuštění v AutoCADu vytvoří takzvanou C-křivku (C-curve). Název je odvozen od tvaru této křivky po jejím natočení o 90°. Opět se jedná o rekurzivní výpočet, tentokrát s funkcí „q“. V této signatuře jsou také použity proměnné l a m, které mají stejný význam jako v signatuře předešlé. Tvar signatury je možné změnit i modifikací výrazu (/ pi 4.), čímž dojde ke změně úhlu lomu polyčáry a tím pádem i k modifikaci tvaru celé křivky. Spuštění signatury v AutoCADu zajistí následující dvojice příkazů:
(load "c:\\c-curve.lsp")
c (defun C:C(/ p l m)(setq p '(0 0)l 100 m 2)(setvar "cmdecho"
0)(setvar "blipmode" 0)(command "_pline" p)(q l 0 m)(command
"")(setvar "cmdecho" 1)(command "_zoom" "m"))(defun q (l u m)
(cond((< l m)(command(polar(getvar "lastpoint")u l)))(T(q(/ l
(sqrt 2.))(+ u(/ pi 4.))m)(q(/ l(sqrt 2.))(- u(/ pi 4.))m)))) 
5. Perlička na závěr: fraktál generovaný Vimem
Fraktály nemusí být generovány pouze programy psanými v běžných programovacích jazycích, ale i pomocí maker textových editorů. Následující „program“, který je doslova geniální (jedná se o jediný kód, u kterého jsem nepřišel na to, jakým způsobem vlastně pracuje :-), využívá možností textového editoru Vim pro generování Mandelbrotovy množiny, vykreslované samozřejmě opět pomocí ASCII Artu. Vzhledem k tomu, že výpočet trvá dlouhou dobu, uvádím jak tvar textového zdrojového souboru před spuštěním (originál), tak i po dokončení celého výpočtu:
Originální zdrojový soubor se zápisem „programu“ pro výpočet Mandelbrotovy množiny:
- - --- ------.-----------> http://www.df.lth.se/~lft
.-- m a n d e l b r 0 t
`----------------> 0
by 0 l
Linus Akesson o t
. bb
fOo fgh
jfBjfbjfbjjmv jmwpbP Type GY@"
bbfRactalB21G42|"dy$b32G"dy$pi
@obticBtaCbtoeBmu29G4|fblyfn@" and watch...
xxkbABlblBibSBtbiBxxfwm`hpl24x
`hjbbbBbBBbbBBbBbBBbhF@fBlyljh
jULiabbbbbbbbbbbbbbbbbbBbbbbbb
9G9|fBlyf$@"26G9|fblyf$@"kewl.
bbbbbbbbbbbbbbbbbbbbbbbb'liThp
@@fM@fF@f9@ff@fl@fi@fw@fm@f.@n
20G"ay57l`nmb`erb`hD@a27Gmijmj
`iy24l`fpl24x`g"tpl24x@g`h"ty$
`m24~`gl24rb~@g`hy$`fpl24xabcd
`byl`cpX`bjyl`dpX0y10l@""byllyl'h31|p`e"bpX`bhmb2hf@y2l@"nOemax
18G"ay30l`nlFB2lF@y2l@"`j"zP24lx`ix22lp@c`ky$`fpl24x@o`mye`kPlD
15G"tye`kD@c`k"tpx10G"ay2l`ffb4hf@y2l@"BBBBBBBBBBBBBBBbbbbbbbbb
@v31G7|yl'a$p13G6|y24l`fpl24x`g"spl24x@g`h"sy$fishyl"zPfbp2Fbxl
22G40|"sy$23Gy46l17@"@w13G7|y24l`fpl24x`g"rpl24x@g`h"ry$'ajmadt
16Gy30l31G7|PlD15G"ly24l"my24l31G8|y2l@"m@u`mye`iP`jPl24xk24x@h
@r`vmplmuB21G42|"ey$b32G"ey$B@nBBBbBbbbbbbbbbbbbbbbbbbb@aBbgrey
bbBbbbbbbbbbbbbbbbbbbbbb@maNdelbbbbbbbbbbbbbbbbbbbbbbbBroTbrot
bbbbbbbbbbbbbbbbbbbbbbbb`quAckDBBBbBbbablblbhbabiblbebrbibs
b`''B@nb31G7|3xly2l@"@n21G"ay41l`jy24l`fpl24xFBf@y2l@"
iaMafNorDBBBBBBBBBBbBbbbbbbbbbbbbbbbbbbb
faTesw@@fM@fF@f9@ff@fl@fi@fw@fm@f.@n
9G"zyl17G"gy22l
v24lcat23G51|y$'a$"zp33|15@"49|x
x@u`mye`iPl24x`jye`fpl24x@u`mye`jPl24x@h@d@e
paRatHEoa.dog`iyl14G6|pX`jyl14G19|pX0y25l@"`iye`fpl24
26G55|mn32|mmhmfjmgjlmh8G3|mc3lmd3lme19G"oy26l30G10|mkufo'
35G20|y$j$p24|"iy$64|Dbe8G32|D2jlD3Gma22G40|"ry$24Gy61l16@"gg
`f"lpl24x`g"rpl24x@g`h"ly$`f"mpl24x`g"spl24x@g`h"my$`f"lpl24x@j
`kh`k"py24l`f"mpl24x@j`k"qy24l`i"lPl24x`j"mPl24x@i`kx8P`k"my24l
llhlkl`f"qpl24x@o`hy24l`gpl24x`f"ppl24x@g`hx9P`h"ly24l`f"ppl24x
k`g"qpl24x@g`hy$`fpl24x@o`gl24rb18h~@g`hyl10G24|pX18|y13l@"gg0l
22G"hy17l19|"uy21l29G24|"cy31l25G"vy40l42|"jy$34G39|"wy$39G"f4Y
7k6|yfk@"17G23|y8l@"33G49|y$@"43GY@":se ul=-1|se cpo-=E|se tw=0
lft---------------------------44GY@"32G"ny038G3|yfD@"38G27|y$@" Výsledek práce programu
- - --- ------.-----------> http://www.df.lth.se/~lft
.-- m a n d e l b r 0 t
`----------------> 0 @@@@@@@@@@@@@@@@.@@@@@@@@@@@@@@@
by 0 l @@@@@@@@@MMFFF99.99FFFMM@@@@@@@@
Linus Akesson o t @@@@@@MMMFFFF9fi.if9FFFFMMM@@@@@
. bb @@@@MMMFFFFF9.m...m.9FFFFFMMM@@@
fOo fgh @@@MMMMFFFF9fw.....wf9FFFFMMMM@@
jfbjfbjfbjjmv jmwpbP @@MMMMFFF99flw.....wlf99FFFMMMM@
bbfRactalB21G42|"dy$b32G"dy$pi @MMMMMFF99l...........l99FFMMMMM
@obticBtaCbtoeBmu29G4|fBlyfn@" @MMMMMFfl...............lfFMMMMM
xxkbABlblBibSBtbiBxxfwm`hpl24x MMMMMMM9.m.............m.9MMMMMM
`hjbbbBbBBbbBBbBbBBbhF@fBlyljh @MMMMMMF99f...........f99FMMMMMM
jULiabbbbbbbbbbbbbbbbbbBbbbbbb @MMMMMMMMFF9fffffffff9FFMMMMMMMM
9G9|fblyf$@"26G9|fblyf$@"kewl. @@MMMMMMMMMFFFFFFFFFFFMMMMMMMMM@
bbbbbbbbbbbbbbbbbbbbbbbb'liThp @@@MMMMMMMMMMMMMFMMMMMMMMMMMMM@@
@@fM@fF@f9@ff@fl@fi@fw@fm@f.@n @@@@MMMMMMMMMMMMMMMMMMMMMMMMM@@@
20G"ay57l`nmb`erb`hD@a27Gmijmj @@@@@@MMMMMMMMMMMMMMMMMMMMM@@@@@
`iy24l`fpl24x`g"tpl24x@g`h"ty$ @@@@@@@@@MMMMMMMMMMMMMMM@@@@@@@@
`m24~`gl24rb~@g`hy$`fpl24xabcd
`byl`cpX`bjyl`dpX0y10l@""byllyl'h31|p`e"bpX`bhmb2hf@y2l@"nOemax
18G"ay30l`nlFB2lF@y2l@"`j"zP24lx`ix22lp@c`ky$`fpl24x@o`mye`kPlD
15G"tye`kD@c`k"tpx10G"ay2l`ffb4hf@y2l@"BBBBBBBBBBBBBBBbbbbbbbbb
@v31G7|yl'a$p13G6|y24l`fpl24x`g"spl24x@g`h"sy$fishyl"zPfbp2Fbxl
22G40|"sy$23Gy46l17@"@w13G7|y24l`fpl24x`g"rpl24x@g`h"ry$'ajmadt
16Gy30l31G7|PlD15G"ly24l"my24l31G8|y2l@"m@u`mye`iP`jPl24xk24x@h
@r`vmplmuB21G42|"ey$b32G"ey$B@nbbbbbbbbbbbbbbbbbBbbbbbb@aBbgrey
bbbbbbbbbbbbbBbbBBbBbbbb@maNdelbbbbbbbbbbbbbbbBBBbbbbbbroTbrot
bbbbbbbbbbbbbbbbbbbbbbbb`quAckDbbbbbbbbbbbbbbBbbbbbbbbb
b`''B@nb31G7|3xly2l@"@n21G"ay41l`jy24l`fpl24xFBf@y2l@"
iaMafNorDbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb
faTeswM@fF@f9@ff@fl@fi@fw@fm@f.@n
9G"zyl17G"gy22l
v24lcat23G51|y$'a$"zp33|15@"49|x
x@u`mye`iPl24x`jye`fpl24x@u`mye`jPl24x@h@d@e
paRatHEoa.dog`iyl14G6|pX`jyl14G19|pX0y25l@"`iye`fpl24
26G55|mn32|mmhmfjmgjlmh8G3|mc3lmd3lme19G"oy26l30G10|mkufo'
35G20|y$j$p24|"iy$64|Dbe8G32|D2jlD3Gma22G40|"ry$24Gy61l16@"gg
`f"lpl24x`g"rpl24x@g`h"ly$`f"mpl24x`g"spl24x@g`h"my$`f"lpl24x@j
`kh`k"py24l`f"mpl24x@j`k"qy24l`i"lPl24x`j"mPl24x@i`kx8P`k"my24l
llhlkl`f"qpl24x@o`hy24l`gpl24x`f"ppl24x@g`hx9P`h"ly24l`f"ppl24x
k`g"qpl24x@g`hy$`fpl24x@o`gl24rb18h~@g`hyl10G24|pX18|y13l@"gg0l
22G"hy17l19|"uy21l29G24|"cy31l25G"vy40l42|"jy$34G39|"wy$39G"f4Y
7k6|yfk@"17G23|y8l@"33G49|y$@"43GY@":se ul=-1|se cpo-=E|se tw=0
lft---------------------------44GY@"32G"ny038G3|yfD@"38G27|y$@"
6. Odkazy na další informační zdroje
- AutoLISP Release 9, Programmer's reference,
Autodesk Ltd., Oct. 1987 - AutoLISP Release 10, Programmer's reference,
Autodesk Ltd., Sept. 1988 - Ing. Karel Mareš:
Učebnice AutoLISPu,
VUT v Brně, interní učební text - Kolář J., Muller K.:
Speciální programovací jazyky,
Praha 1981 - Wegner Timothy, Tyler Bert:
Fractal Creations, Second Edition,
The Waite Group Press, 1993 - Pickover Clifford:
Chaos in Wonderland,
ISBN 0–312–10743–9 St. Martin's Press - International Obfuscated C Code:
http://www.ioccc.org/ - Quines:
http://en.wikipedia.org/wiki/Quine_%28computing%29 - Polyglot:
http://ideology.com.au/polyglot/ - WWW stránky programu FractInt:
http://www.fractint.org
7. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování seriálu o fraktálech si ukážeme, jakým způsobem je možné fraktály vykreslovat pomocí krátkých programů napsaných v assembleru.






























