Obsah
1. Výpočty v systému pevné řádové čárky na platformě IBM PC (2. část)
2. Problémy, které nastávají při omezení výpočtů pouze na n-bitové hodnoty
3. Násobení příliš malých hodnot
4. Výpočty omezené na 2n-bitové hodnoty
5. Snížení počtu bitů reprezentujících numerické hodnoty při výpočtu Mandelbrotovy množiny
6. Původní výpočet s 32 bitovými hodnotami
7. Výpočet Mandelbrotovy množiny omezený na 16bitové hodnoty
8. Rozdíly ve zdrojových kódech
9. Rozdíly ve vypočtených obrázcích
10. Výpočty složitějších funkcí
11. Iterativní výpočet druhé odmocniny
12. Demonstrační příklad na výpočet druhé odmocniny ve formátu plovoucí řádové tečky
13. Demonstrační příklad na výpočet druhé odmocniny ve formátu pevné řádové tečky
14. Překlad jedné iterace pro výpočet druhé odmocniny do assembleru
15. Goniometrické funkce počítané pomocí číselných řad
16. Demonstrační příklad: výpočet sinu s využitím Taylorova rozvoje
17. Výsledky výpočtu hodnot funkce sin()
18. Univerzální algoritmus CORDIC
19. Repositář s demonstračními příklady
1. Výpočty v systému pevné řádové čárky na platformě IBM PC (2. část)
Na úvodní článek o realizaci aritmetických výpočtů bez využití matematického koprocesoru dnes navážeme. Opět se budeme zabývat matematickými výpočty, které využívají numerické hodnoty s pevnou řádovou binární tečkou (čárkou) – fixed point. Nejprve si na několika demonstračních příkladech ukážeme některé limity tohoto způsobu reprezentace numerických hodnot (pro vizualizaci opět použijeme Mandelbrotovu množinu), dále budeme realizovat výpočty některých často používaných funkcí (druhá odmocnina, goniometrické funkce) iteračními algoritmy a v závěru dnešního článku se taktéž seznámíme s univerzálním algoritmem nazvaným CORDIC (COordinate ROtation DIgital Computer), který je možné relativně snadno použít pro výpočet goniometrických funkcí, logaritmů atd.
2. Problémy, které nastávají při omezení výpočtů pouze na n-bitové hodnoty
Již v předchozím článku jsme se zmínili o problémech, které mohou nastat při provádění výpočtů s hodnotami s pevnou řádovou čárkou (tečkou) v případě, že všechny části výpočtu provádíme s n-bitovými hodnotami, kde n je bitová šířka operandů i výsledné hodnoty. Příkladem může být operace součinu, která v takovém případě vyžaduje, aby se operandy bitově posunuly doprava ještě před provedením instrukce MUL nebo IMUL. Ovšem pokud provádíme bitový posun doprava, ztrácíme (pochopitelně) vysunuté bity a tudíž ztrácíme i přesnost. To může vést až k tomu, že se jeden operand vynuluje a výsledkem součinu tedy bude nekorektní nulová hodnota.
Nejprve se podívejme na příklad, ve kterém ke ztrátě přesnosti nebo vynulování operandu nedochází. Využíváme formát 16.16, tedy šestnáct bitů před pevnou binární tečkou a šestnáct bitů za ní. A násobíme hodnoty 2.0 a 1/256 (zhruba 0.00390625):
;-----------------------------------------------------------------------------
org 0x100 ; zacatek kodu pro programy typu COM (vzdy se zacina na 256)
start:
jmp main ; skok na zacatek kodu
%include "io.asm" ; nacist symboly, makra a podprogramy
%include "print.asm" ; nacist symboly, makra a podprogramy
P equ 65536 ; poloha desetinne tecky v FX-pointu
x equ 2 * P ; konstanty, ktere se budou nasobit
y equ P / 256
main:
mov eax, x
print_hex eax ; vytisknout hodnotu prvni konstanty
mov eax, y
print_hex eax ; vytisknout hodnotu druhe konstanty
mov eax, x
mov ebx, y
shr eax, 8 ; posun jeste pred nasobenim (ztrata presnosti)
shr ebx, 8 ; posun jeste pred nasobenim (ztrata presnosti)
mul ebx ; nasobeni v FX-pointu do EDX:EAX
print_hex eax
finish:
wait_key ; cekani na klavesu
exit ; navrat do DOSu
; datova cast
section .data
section .bss
Výsledky i s jejich popisem:
operand: 00020000 ≅ 2.0 operand: 00000100 ≅ 1.0 / 256 ≅ 0.00390625 součin: 00000200 ≅ 2.0 / 256 ≅ 0.00781250
V tomto případě tedy výpočty dopadly podle očekávání.
3. Násobení příliš malých hodnot
V dalším kroku výpočet nepatrně upravíme. Nebudeme násobit hodnoty 2.0 a 1/256, ale hodnoty 2.0 a 1/512, což znamená, že druhý operand bude mít obsazeno pouze spodních osm bitů a vyšších 24 bitů bude nulových. Zde se již musí projevit fakt, že před instrukcí MUL či IMUL posunujeme operandy o osm bitů doprava:
;-----------------------------------------------------------------------------
org 0x100 ; zacatek kodu pro programy typu COM (vzdy se zacina na 256)
start:
jmp main ; skok na zacatek kodu
%include "io.asm" ; nacist symboly, makra a podprogramy
%include "print.asm" ; nacist symboly, makra a podprogramy
P equ 65536 ; poloha desetinne tecky v FX-pointu
x equ 2 * P ; konstanty, ktere se budou nasobit
y equ P / 512
main:
mov eax, x
print_hex eax ; vytisknout hodnotu prvni konstanty
mov eax, y
print_hex eax ; vytisknout hodnotu druhe konstanty
mov eax, x
mov ebx, y
shr eax, 8 ; posun jeste pred nasobenim (ztrata presnosti)
shr ebx, 8 ; posun jeste pred nasobenim (ztrata presnosti)
mul ebx ; nasobeni v FX-pointu do EDX:EAX
print_hex eax
finish:
wait_key ; cekani na klavesu
exit ; navrat do DOSu
; datova cast
section .data
section .bss
Opět se podívejme na zprávy vypsané tímto příkladem, ke kterým jsou doplněny vysvětlivky:
operand: 00020000 ≅ 2.0 operand: 00000080 ≅ 1.0 / 512 ≅ 0.001953125 součin: 00000000 = 0.0 ⇒ nekorektní!
V tomto případě tedy došlo k tomu, že byl druhý operand posunut o osm bitů doprava, čímž byl mezivýsledek vynulován. A operace součinu tedy podle očekávání vrátila nulu!
4. Výpočty omezené na 2n-bitové hodnoty
V případě, že CPU podporuje provádění operací součinu tak, že výsledkem součinu dvou n-bitových hodnot je hodnota 2n-bitová, je pochopitelně situace jednodušší a k žádným ztrátám přesnosti nebo vynulování výsledků vůbec nemusí dojít. Pouze je nutné zajistit bitový posun výsledku. Na platformě x86 (nebo x86–64) obecně platí, že operace součinu, tedy MUL a IMUL mají jako svůj vstup dvojici n-bitových registrů (n=8, 16, 32 nebo 64) a výsledek je uložen ve dvojici taktéž n-bitových registrů:
| Instrukce | Stručný popis |
|---|---|
| MUL r/m8 | AX := AL ∗ r/m8 |
| MUL r/m81 | AX := AL ∗ r/m8 |
| MUL r/m16 | DX:AX := AX ∗ r/m16 |
| MUL r/m32 | EDX:EAX := EAX ∗ r/m32 |
| MUL r/m64 | RDX:RAX := RAX ∗ r/m64 |
a:
| Instrukce | Stručný popis |
|---|---|
| IMUL r/m81 | AX:= AL ∗ r/m byte |
| IMUL r/m16 | DX:AX := AX ∗ r/m word |
| IMUL r/m32 | EDX:EAX := EAX ∗ r/m32 |
| IMUL r/m64 | RDX:RAX := RAX ∗ r/m64 |
| IMUL r16, r/m16 | word register := word register ∗ r/m16 |
| IMUL r32, r/m32 | doubleword register := doubleword register ∗ r/m32 |
| IMUL r64, r/m64 | Quadword register := Quadword register ∗ r/m64 |
| IMUL r16, r/m16, imm8 | word register := r/m16 ∗ sign-extended immediate byte |
| IMUL r32, r/m32, imm8 | doubleword register := r/m32 ∗ sign-extended immediate byte |
| IMUL r64, r/m64, imm8 | Quadword register := r/m64 ∗ sign-extended immediate byte |
| IMUL r16, r/m16, imm16 | word register := r/m16 ∗ immediate word |
| IMUL r32, r/m32, imm32 | doubleword register := r/m32 ∗ immediate doubleword |
| IMUL r64, r/m64, imm32 | Quadword register := r/m64 ∗ immediate doubleword |
Předchozí demonstrační příklad tedy můžeme upravit do této podoby:
;-----------------------------------------------------------------------------
org 0x100 ; zacatek kodu pro programy typu COM (vzdy se zacina na 256)
start:
jmp main ; skok na zacatek kodu
%include "io.asm" ; nacist symboly, makra a podprogramy
%include "print.asm" ; nacist symboly, makra a podprogramy
P equ 65536 ; poloha desetinne tecky v FX-pointu
x equ 2 * P ; konstanty, ktere se budou nasobit
y equ P / 512
main:
mov eax, x
print_hex eax ; vytisknout hodnotu prvni konstanty
mov eax, y
print_hex eax ; vytisknout hodnotu druhe konstanty
mov eax, x
mov ebx, y
mul ebx ; nasobeni v FX-pointu do EDX:EAX
mov ax, dx ; bity 16-32
ror eax, 16 ; prohodit horni a spodni polovinu registru
print_hex eax
finish:
wait_key ; cekani na klavesu
exit ; navrat do DOSu
; datova cast
section .data
section .bss
Výsledky nyní budou, na rozdíl od příkladu předchozího, zcela korektní:
operand: 00020000 ≅ 2.0 operand: 00000080 ≅ 1.0 / 512 ≅ 0.001953125 součin: 00000100 = 1.0 / 256 ⇒ korektní!
5. Snížení počtu bitů reprezentujících numerické hodnoty při výpočtu Mandelbrotovy množiny
V navazujících kapitolách si ukážeme (zejména ve vizuální podobě), jaké problémy může přinést snaha o provádění výpočtů s hodnotami s pevnou řádovou binární čárkou (fixed point) v případě, že není k dispozici dostatečný počet bitů pro zajištění potřebné přesnosti výpočtů a/nebo pro zajištění potřebného rozsahu hodnot (minimální a maximální reprezentovatelné hodnoty). Aby se nejednalo pouze o strohé numerické výpočty s výstupem ve formě tabulek, budeme provádět – podobně jako v předchozím článku – vizualizaci Mandelbrotovy množiny.
Výpočet bodů v této množině je dostatečně jednoduchý na implementaci a současně jsou všechny chyby (nedostatečná přesnost či rozsah) ihned viditelné na výsledných rastrových obrázcích. Pokusíme se o výpočet bodů Mandelbrotovy množiny s využitím pouze šestnáctibitových hodnot, přičemž (pochopitelně) je nutné několik bitů rezervovat pro celou část a zbytek bitů pro část za řádovou tečkou. K dispozici je tedy několik formátů, od formátu označovaného „16.0“ (celočíselné 16bitové hodnoty) přes „8.8“ (osm bitů pro celou část, osm bitů za tečkou) až po „0.16“ (pouze bity umístěné za řádovou tečkou).
6. Původní výpočet s 32 bitovými hodnotami
Jen pro krátké připomenutí, jak vypadal původní výpočet s 32bitovými hodnotami (a tedy i 32bitovými pracovními registry) si zopakujme zdrojový kód programu, který vypočítá body v Mandelbrotově množině a zobrazí je s využitím standardního grafického režimu s rozlišením 320×200 pixelů a s 256 barvami (karta VGA a všechny karty SVGA). Program je napsán pro reálný režim, ovšem kvůli 32bitovým operacím vyžaduje minimálně mikroprocesor 80386 nebo vyšší. Povšimněte si zejména pozice pevné řádové binární tečky mezi bitem číslo 11 a 12. Tím je určen jak rozsah hodnot, tak i jejich přesnost:
;-----------------------------------------------------------------------------
org 0x100 ; zacatek kodu pro programy typu COM (vzdy se zacina na 256)
; konstanty
P equ 4096 ; poloha desetinne tecky v X-pointu
K equ 4*P/256 ; vzdalenost mezi dvema body (krok smycky)
L equ 4*P/192
MIN equ -2*P ; minimalni a maximalni hodnota konstant fraktalu
; v komplexni rovine
MAXITER equ 40 ; maximalni pocet iteraci
BAILOUT equ 4
SLOUPCU equ 320 ; pocet sloupcu na obrazovce
section .text
start:
jmp main ; skok na zacatek kodu
%include "io.asm" ; nacist symboly, makra a podprogramy
main:
mov ax, 13h ; graficky rezim 320x200x256
int 10h
;:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
;: MANDELBROTOVA MNOZINA ::
;:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
push 0xa000
pop ES ; segment obrazove pameti karty VGA
xor DI, DI ; zacatek vykreslovani na obrazovce
mov CL, 6 ; posun pro FX format
mforx: mov dword [cx_], MIN ; od -2 (imaginarni osa)
mov SI, SLOUPCU ; x
mfory: mov CH, MAXITER ; pocet iteraci
xor EAX, EAX ;
mov EBP, EAX ; nastaveni real.casti zacatku
mov dword [zy1], EAX ; nastaveni imag.casti zacatku
iter_loop: ; *** iteracni smycka ***
mov EAX, EBP ;
sar EAX, CL ;
imul EAX ; zx2:=zx1^2 (v X-pointu)
mov dword [zx2], EAX ;
mov EAX, dword [zy1] ;
sar EAX, CL ;
imul EAX ; zy2:=zy1^2 (v X-pointu)
mov dword [zy2], EAX ;
mov EAX, EBP ;
sar EAX, CL ; zx1 div 256 (pro mul v X-pointu)
mov EBX, [zy1] ;
sar EBX, 5 ; zy1 div 256 * 2 (pro mul v X-pointu)
imul EBX ; zy1:=2*zx1*zy1
add EAX, [cy_] ; zy1:=2*zx1*zy1+CY (u Mandelbrota poc.iter.)
mov [zy1], EAX ; ulozit novou hodnotu zy1
mov EAX, [zx2] ;
sub EAX, [zy2] ; zx2:=zx2-zy2=zx1^2-zy1^2
add EAX, [cx_] ;
mov EBP, EAX ; zx1:=zx1^2-zy1^2+CX
dec CH ; pocitadlo iteraci
jz short mpokrac ; konec iteraci ?
mov EAX, [zx2] ;
add EAX, [zy2] ; ==zx1^2+zy1^2
cmp EAX, BAILOUT*P ; kontrola na bailout (abs[Z]<4)
jc short iter_loop ; abs[Z]<4 =>dalsi iterace
mpokrac:
mov AL, CH ; pocet iteraci
add AL, 32 ; posun na vhodne barvy v palete
stosb ; vykreslit pixel+posun na dalsi pixel
add dword [cx_], K ; cy_:=cy_+K
dec si
jnz short mfory ; Y!=0 ->dalsi radek
add dword [cy_], L ; cx_:=cx_+K
cmp di, 64000 ; konec obrazku ?
jne mforx
finish:
wait_key ; cekani na klavesu
exit ; navrat do DOSu
section .data
cy_ dd MIN ; poloha v komplexni rovine rovine
section .bss
cx_ resd 1 ;
zy1 resd 1 ; aktualni poloha v komplexni rovine
zx2 resd 1 ; zx2=zx1^2 (aby se to nemuselo pocitat 2x)
zy2 resd 1 ; zy2=zy1^2
; finito
7. Výpočet Mandelbrotovy množiny omezený na 16bitové hodnoty
Relativně snadným způsobem můžeme dosáhnout toho, že všechny výpočty budou probíhat pouze se šestnáctibitovými hodnotami (a navíc je program napsán pro zaručení kompatibility s čipem 80286). V tomto případě je vhodné si velmi dobře rozmyslet, na které místo umístit binární řádovou tečku. Můžeme bez dalších odhadů použít formát 8.8, tedy osm bitů před binární tečkou a osm bitů za tečkou, ovšem to nemusí být ideální, protože může docházet k velké ztrátě přesnosti nebo naopak k přetečení hodnot (mezivýsledků). Proto může být výhodnější omezit počet bitů před tečkou a naopak zvýšit počet bitů za ní (například realizovat formát 5.11 nebo dokonce 4.12). Podívejme se nejdříve na příklad použití formátu, ve kterém je tečka umístěna mezi jedenáctým a dvanáctým bitem:
;-----------------------------------------------------------------------------
org 0x100 ; zacatek kodu pro programy typu COM (vzdy se zacina na 256)
; konstanty
P equ 4096 ; poloha desetinne tecky v X-pointu
K equ 4*P/256 ; vzdalenost mezi dvema body (krok smycky)
L equ 4*P/192
MIN equ -2*P ; minimalni a maximalni hodnota konstant fraktalu
; v komplexni rovine
MAXITER equ 40 ; maximalni pocet iteraci
BAILOUT equ 4
SLOUPCU equ 320 ; pocet sloupcu na obrazovce
section .text
start:
jmp main ; skok na zacatek kodu
%include "io.asm" ; nacist symboly, makra a podprogramy
main:
mov ax, 13h ; graficky rezim 320x200x256
int 10h
;:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
;: MANDELBROTOVA MNOZINA ::
;:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
push 0xa000
pop ES ; segment obrazove pameti karty VGA
xor DI, DI ; zacatek vykreslovani na obrazovce
mov CL, 6 ; posun pro FX format
mforx: mov word [cx_], MIN ; od -2 (imaginarni osa)
mov SI, SLOUPCU ; x
mfory: mov CH, MAXITER ; pocet iteraci
xor AX, AX ;
mov BP, AX ; nastaveni real.casti zacatku
mov word [zy1], AX ; nastaveni imag.casti zacatku
iter_loop: ; *** iteracni smycka ***
mov AX, BP ;
sar AX, CL ;
imul AX ; zx2:=zx1^2 (v X-pointu)
mov word [zx2], AX ;
mov AX, [zy1] ;
sar AX,CL ;
imul AX ; zy2:=zy1^2 (v X-pointu)
mov word [zy2], AX ;
mov AX, BP ;
sar AX,CL ; zx1 div 256 (pro mul v X-pointu)
mov BX, [zy1] ;
sar BX,5 ; zy1 div 256 * 2 (pro mul v X-pointu)
imul BX ; zy1:=2*zx1*zy1
add AX, [cy_] ; zy1:=2*zx1*zy1+CY (u Mandelbrota poc.iter.)
mov [zy1], AX ; ulozit
mov AX, [zx2] ;
sub AX, [zy2] ; zx2:=zx2-zy2=zx1^2-zy1^2
add AX, [cx_] ;
mov BP, AX ; zx1:=zx1^2-zy1^2+CX
dec CH ; pocitadlo iteraci
jz short mpokrac ; konec iteraci ?
mov AX, [zx2] ;
add AX, [zy2] ; ==zx1^2+zy1^2
cmp AX, BAILOUT*P ; kontrola na bailout (abs[Z]<4)
jc short iter_loop ; abs[Z]<4 =>dalsi iterace
mpokrac:
mov AL, CH ; pocet iteraci
add AL, 32 ; posun na vhodne barvy v palete
stosb ; vykreslit pixel+posun na dalsi pixel
add word [cx_], K ; cy_:=cy_+K
dec si
jnz short mfory ; Y!=0 ->dalsi radek
add word [cy_], L ; cx_:=cx_+L
cmp di, 64000 ; konec obrazku ?
jne short mforx
finish:
wait_key ; cekani na klavesu
exit ; navrat do DOSu
section .data
cy_ dw MIN ; poloha v komplexni rovine rovine
section .bss
cx_ resw 1 ;
zy1 resw 1 ; aktualni poloha v komplexni rovine
zx2 resw 1 ; zx2=zx1^2 (aby se to nemuselo pocitat 2x)
zy2 resw 1 ; zy2=zy1^2
; finito
Můžeme se ovšem pokusit o „poladění“ pozice binární tečky. Příkladem může být odlišná realizace posunu, která vyžaduje pouze změnu tří konstant v kódu:
;-----------------------------------------------------------------------------
org 0x100 ; zacatek kodu pro programy typu COM (vzdy se zacina na 256)
; konstanty
P equ 4096/4 ; poloha desetinne tecky v X-pointu
K equ 4*P/256 ; vzdalenost mezi dvema body (krok smycky)
L equ 4*P/192
MIN equ -2*P ; minimalni a maximalni hodnota konstant fraktalu
; v komplexni rovine
MAXITER equ 40 ; maximalni pocet iteraci
BAILOUT equ 4
SLOUPCU equ 320 ; pocet sloupcu na obrazovce
section .text
start:
jmp main ; skok na zacatek kodu
%include "io.asm" ; nacist symboly, makra a podprogramy
main:
mov ax, 13h ; graficky rezim 320x200x256
int 10h
;:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
;: MANDELBROTOVA MNOZINA ::
;:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
push 0xa000
pop ES ; segment obrazove pameti karty VGA
xor DI, DI ; zacatek vykreslovani na obrazovce
mov CL, 5 ; posun pro FX format
mforx: mov word [cx_], MIN ; od -2 (imaginarni osa)
mov SI, SLOUPCU ; x
mfory: mov CH, MAXITER ; pocet iteraci
xor AX, AX ;
mov BP, AX ; nastaveni real.casti zacatku
mov word [zy1], AX ; nastaveni imag.casti zacatku
iter_loop: ; *** iteracni smycka ***
mov AX, BP ;
sar AX, CL ;
imul AX ; zx2:=zx1^2 (v X-pointu)
mov word [zx2], AX ;
mov AX, [zy1] ;
sar AX,CL ;
imul AX ; zy2:=zy1^2 (v X-pointu)
mov word [zy2], AX ;
mov AX, BP ;
sar AX,CL ; zx1 div 256 (pro mul v X-pointu)
mov BX, [zy1] ;
sar BX,4 ; zy1 div 256 * 2 (pro mul v X-pointu)
imul BX ; zy1:=2*zx1*zy1
add AX, [cy_] ; zy1:=2*zx1*zy1+CY (u Mandelbrota poc.iter.)
mov [zy1], AX ; ulozit
mov AX, [zx2] ;
sub AX, [zy2] ; zx2:=zx2-zy2=zx1^2-zy1^2
add AX, [cx_] ;
mov BP, AX ; zx1:=zx1^2-zy1^2+CX
dec CH ; pocitadlo iteraci
jz short mpokrac ; konec iteraci ?
mov AX, [zx2] ;
add AX, [zy2] ; ==zx1^2+zy1^2
cmp AX, BAILOUT*P ; kontrola na bailout (abs[Z]<4)
jc short iter_loop ; abs[Z]<4 =>dalsi iterace
mpokrac:
mov AL, CH ; pocet iteraci
add AL, 32 ; posun na vhodne barvy v palete
stosb ; vykreslit pixel+posun na dalsi pixel
add word [cx_], K ; cy_:=cy_+K
dec si
jnz short mfory ; Y!=0 ->dalsi radek
add word [cy_], L ; cx_:=cx_+L
cmp di, 64000 ; konec obrazku ?
jne short mforx
finish:
wait_key ; cekani na klavesu
exit ; navrat do DOSu
section .data
cy_ dw MIN ; poloha v komplexni rovine rovine
section .bss
cx_ resw 1 ;
zy1 resw 1 ; aktualni poloha v komplexni rovine
zx2 resw 1 ; zx2=zx1^2 (aby se to nemuselo pocitat 2x)
zy2 resw 1 ; zy2=zy1^2
; finito
8. Rozdíly ve zdrojových kódech
Přechod z 32bitových hodnot s pevnou řádovou čárkou na použití pouze šestnáctibitových hodnot ve skutečnosti vyžaduje relativně malé zásahy do zdrojových kódů. Modifikovaných programových řádků je sice velké množství, ovšem jen kvůli tomu, že v assembleru nemáme k dispozici „centrální místo“ pro specifikaci datových typů proměnných (tedy obdobu céčkovských deklarací proměnných a parametrů funkcí). Podívejme se tedy, jaké úpravy bylo nutné provést (výstup je proveden formou unifikovaného diffu):
--- fx_mandel_2.asm 2025-07-02 13:00:19.307893801 +0200
+++ fx_mandel_3.asm 2025-07-02 13:20:35.772896137 +0200
@@ -33,55 +33,51 @@
xor DI, DI ; zacatek vykreslovani na obrazovce
mov CL, 6 ; posun pro FX format
-mforx: mov dword [cx_], MIN ; od -2 (imaginarni osa)
+mforx: mov word [cx_], MIN ; od -2 (imaginarni osa)
mov SI, SLOUPCU ; x
mfory: mov CH, MAXITER ; pocet iteraci
- xor EAX, EAX ;
- mov EBP, EAX ; nastaveni real.casti zacatku
- mov dword [zy1], EAX ; nastaveni imag.casti zacatku
+ xor AX, AX ;
+ mov BP, AX ; nastaveni real.casti zacatku
+ mov word [zy1], AX ; nastaveni imag.casti zacatku
iter_loop: ; *** iteracni smycka ***
- mov EAX, EBP ;
- sar EAX, CL ;
- imul EAX ; zx2:=zx1^2 (v X-pointu)
- mov dword [zx2], EAX ;
-
- mov EAX, dword [zy1] ;
- sar EAX, CL ;
- imul EAX ; zy2:=zy1^2 (v X-pointu)
- mov dword [zy2], EAX ;
-
- mov EAX, EBP ;
- sar EAX, CL ; zx1 div 256 (pro mul v X-pointu)
-
- mov EBX, [zy1] ;
- sar EBX, 5 ; zy1 div 256 * 2 (pro mul v X-pointu)
-
- imul EBX ; zy1:=2*zx1*zy1
- add EAX, [cy_] ; zy1:=2*zx1*zy1+CY (u Mandelbrota poc.iter.)
- mov [zy1], EAX ; ulozit novou hodnotu zy1
-
- mov EAX, [zx2] ;
- sub EAX, [zy2] ; zx2:=zx2-zy2=zx1^2-zy1^2
- add EAX, [cx_] ;
- mov EBP, EAX ; zx1:=zx1^2-zy1^2+CX
-
+ mov AX, BP ;
+ sar AX, CL ;
+ imul AX ; zx2:=zx1^2 (v X-pointu)
+ mov word [zx2], AX ;
+ mov AX, [zy1] ;
+ sar AX,CL ;
+ imul AX ; zy2:=zy1^2 (v X-pointu)
+ mov word [zy2], AX ;
+
+ mov AX, BP ;
+ sar AX,CL ; zx1 div 256 (pro mul v X-pointu)
+ mov BX, [zy1] ;
+ sar BX,5 ; zy1 div 256 * 2 (pro mul v X-pointu)
+ imul BX ; zy1:=2*zx1*zy1
+ add AX, [cy_] ; zy1:=2*zx1*zy1+CY (u Mandelbrota poc.iter.)
+ mov [zy1], AX ; ulozit
+
+ mov AX, [zx2] ;
+ sub AX, [zy2] ; zx2:=zx2-zy2=zx1^2-zy1^2
+ add AX, [cx_] ;
+ mov BP, AX ; zx1:=zx1^2-zy1^2+CX
dec CH ; pocitadlo iteraci
jz short mpokrac ; konec iteraci ?
- mov EAX, [zx2] ;
- add EAX, [zy2] ; ==zx1^2+zy1^2
- cmp EAX, BAILOUT*P ; kontrola na bailout (abs[Z]<4)
+ mov AX, [zx2] ;
+ add AX, [zy2] ; ==zx1^2+zy1^2
+ cmp AX, BAILOUT*P ; kontrola na bailout (abs[Z]<4)
jc short iter_loop ; abs[Z]<4 =>dalsi iterace
mpokrac:
mov AL, CH ; pocet iteraci
add AL, 32 ; posun na vhodne barvy v palete
stosb ; vykreslit pixel+posun na dalsi pixel
- add dword [cx_], K ; cy_:=cy_+K
+ add word [cx_], K ; cy_:=cy_+K
dec si
jnz short mfory ; Y!=0 ->dalsi radek
- add dword [cy_], L ; cx_:=cx_+K
+ add word [cy_], L ; cx_:=cx_+L
cmp di, 64000 ; konec obrazku ?
- jne mforx
+ jne short mforx
finish:
wait_key ; cekani na klavesu
@@ -90,14 +86,14 @@
section .data
-cy_ dd MIN ; poloha v komplexni rovine rovine
+cy_ dw MIN ; poloha v komplexni rovine rovine
section .bss
-cx_ resd 1 ;
-zy1 resd 1 ; aktualni poloha v komplexni rovine
-zx2 resd 1 ; zx2=zx1^2 (aby se to nemuselo pocitat 2x)
-zy2 resd 1 ; zy2=zy1^2
+cx_ resw 1 ;
+zy1 resw 1 ; aktualni poloha v komplexni rovine
+zx2 resw 1 ; zx2=zx1^2 (aby se to nemuselo pocitat 2x)
+zy2 resw 1 ; zy2=zy1^2
9. Rozdíly ve vypočtených obrázcích
Výpočty Mandelbrotovy množiny ve formátu s minimálně šestnácti bity před binární tečkou a šestnácti bity za binární tečkou jsou sice nepřesné, ovšem (pokud nedojde k velkému zvětšení nebo nepoužijeme příliš velký maximální počet iterací) nejsou tyto nepřesnosti příliš patrné. Ovšem naprosto odlišná je situace v případě, že celá hodnota má pouze šestnáct bitů, přičemž se do těchto bitů musí „vejít“ jak celá část hodnoty, tak i desetinná část. Nejlépe jsou chyby viditelné po vykreslení Mandelbrotovy množiny:
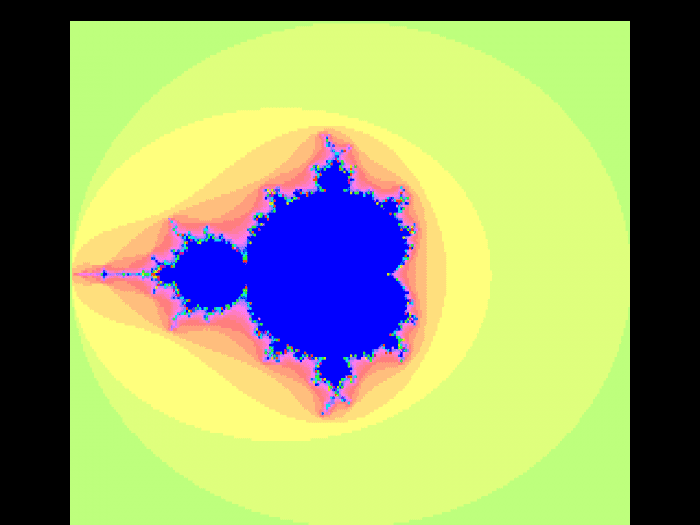
Obrázek 1: Mandelbrotova množina vykreslená s využitím kódu používajícího pouze FX operace. Základní neoptimalizovaná varianta s 32bitovými hodnotami.
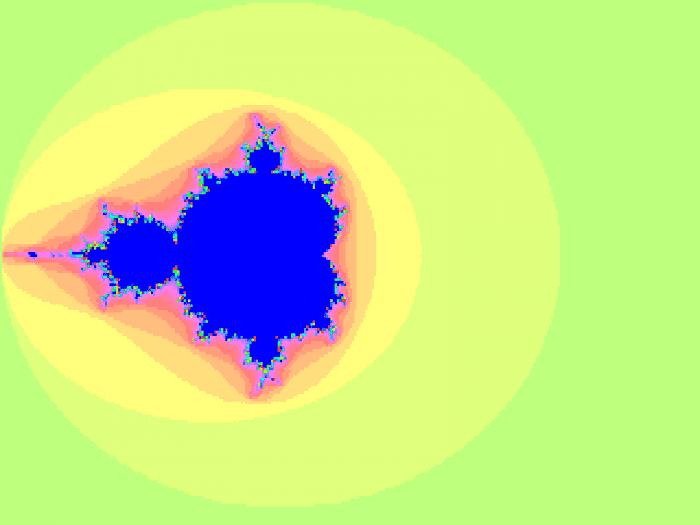
Obrázek 2: Mandelbrotova množina vykreslená s využitím kódu používajícího pouze FX operace. Optimalizovaná varianta s 32bitovými hodnotami.
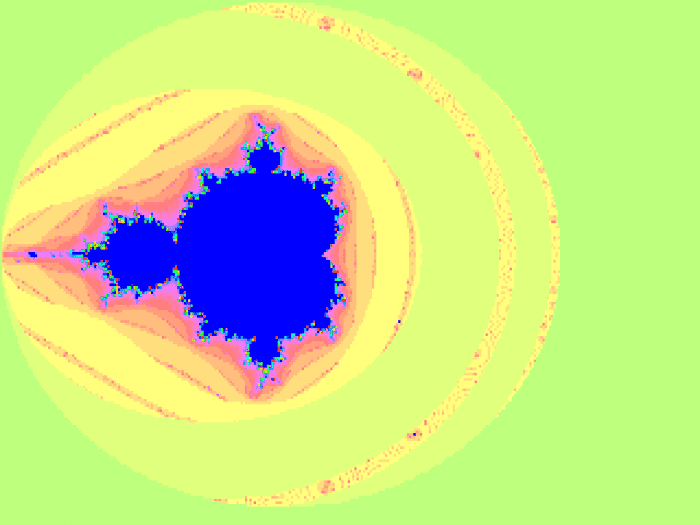
Obrázek 3: Mandelbrotova množina vykreslená s využitím kódu používajícího pouze FX operace. Varianta se šesnáctibitovými hodnotami, ovšem použitý formát nabízí omezenou přesnost, takže dochází k viditelným chybám při výpočtu.
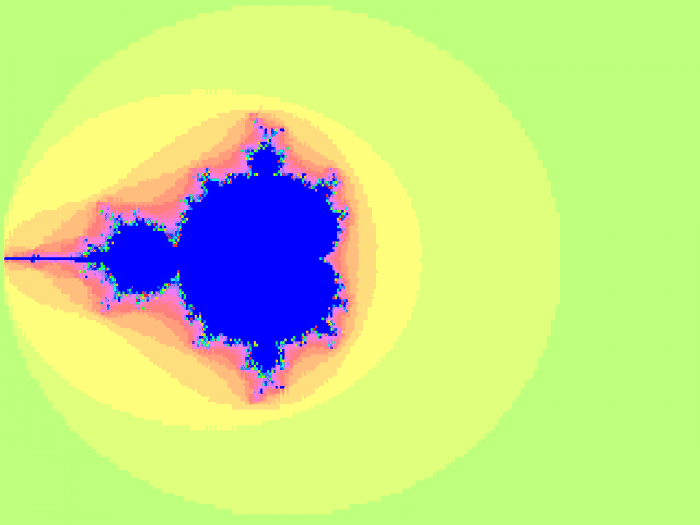
Obrázek 4: Mandelbrotova množina vykreslená s využitím kódu používajícího pouze FX operace. Oproti předchozí variantě je pro část hodnoty za binární tečkou použit jeden bit navíc, takže chyb zde vidíme méně.

Obrázek 5: Mandelbrotova množina vykreslená s využitím kódu používajícího pouze FX operace. Další zvyšování počtu bitů za řádovou tečkou vede k omezenému rozsahu, takže obrázek bylo nutné zvětšit a navíc dochází k přetečení přes hodnotu bailout (4.0).
10. Výpočty složitějších funkcí
V praxi se kromě čtyř základních aritmetických operací (součet, rozdíl, součin, podíl) pochopitelně používají i další operace a matematické funkce. V případě matematického koprocesoru je množství těchto funkcí implementováno formou instrukcí (nebo jejich kombinací), ovšem v případě, že namísto FP formátu (a přímého volání instrukcí koprocesoru) budeme chtít použít numerický formát s pevnou řádovou tečkou (čárkou), bude nutné nějakým způsobem implementovat i všechny požadované funkce. Některé z těchto funkcí lze realizovat triviálně; příkladem je výpočet absolutní hodnoty. Ovšem většina často používaných funkcí nemá triviální implementaci a výpočty jsou více či méně komplikované. Proto se často setkáme i s tím, že jsou hodnoty funkcí předvypočteny (například pro 256 vstupních hodnot) a zbylé hodnoty se dopočítají lineární či jinou interpolací.
V dalších kapitolách se zaměříme na dvojici často volaných matematických funkcí. V první řadě se jedná o výpočet druhé odmocniny, který nalezneme v grafických algoritmech (normalizace vektorů, výpočet vzdálenosti) a v řadě druhé o goniometrické funkce (rotace apod.).
11. Iterativní výpočet druhé odmocniny
Výpočet druhé odmocniny (square root) je v praxi velmi často používaný (počítačová grafika, dnes například zpracování přirozeného jazyka atd.) a i z tohoto důvodu je implementován ve většině FPU, ale i GPU. My si v tomto článku ukážeme jednu z možností implementace, která spočívá v iterativním zpřesňování odhadu výsledku. Nyní se tedy povězme, jakým způsobem se může iterativní výpočet druhé odmocniny provádět. Vstupní hodnotou algoritmu je původní číslo y, výstupem je (po i-té iteraci) odhad výsledku xi. V každé iteraci se provádí poměrně jednoduchá operace vyžadující dělení:
xi+1=1/2 (xi+y/xi)
Zbývá nám pouze nastavit počáteční odhad x1. Většinou se volí hodnota x1=y/2, protože je ji možné velmi jednoduše spočítat prostým bitovým posunem mantisy nebo snížením hodnoty exponentu (a u FX operací ještě jednodušeji pouhým bitovým posunem). Přesnější (a tím pádem i rychlejší, jelikož se provede méně iterací) je však odhad vypočtený z mantisy a exponentu vstupující hodnoty y, což lze ovšem provést jen u FP hodnot:
x1=m×2e/2
tj. hodnota exponentu se sníží na polovinu. Důkaz pro korektnost takto vytvořeného prvního odhadu je poměrně přímočarý. Vstupní hodnota y může být rozepsána na mantisu a exponent:
y=m×2e
Znaménko můžeme ignorovat, protože odmocniny se počítají pouze pro kladné hodnoty. Prvotní odhad vychází z aplikace odmocniny na výše uvedený rozepsaný vztah:
y1/2=m1/2×2e/2
Hodnotu mantisy je možné (resp. nutné) ignorovat, protože normalizovaná mantisa představuje hodnoty z intervalu <1, 2-ε> a tento interval se aplikací odmocniny nijak nemění.
12. Demonstrační příklad na výpočet druhé odmocniny ve formátu plovoucí řádové tečky
Pro ilustraci iterativního výpočtu druhé odmocniny a zejména faktu, že řešení poměrně rychle (jen po několika iteracích) spěje ke korektnímu výsledku, si ukažme demonstrační příklad napsaný pro jednoduchost v programovacím jazyku C. Po překladu a spuštění tohoto příkladu se zobrazí tabulka s postupně zpřesňovaným výpočtem druhé odmocniny hodnoty 10 000. Kromě průběžných výsledků je zobrazována i absolutní a relativní chyba výpočtu:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
/* tato funkce provede jednu iteraci
* se zlepšeným odhadem výsledku x_i
*/
float sqrt_step(float xi, float y)
{
return 1.0 / 2.0 * (xi + y / xi);
}
int main(void) {
/* vstupní hodnota, ze které se počítá odmocnina */
double y = 10000;
/* postupně zpřesňovaný odhad výsledku */
double xi = y;
/* hodnota pro porovnání výsledků */
double sqr = sqrt(y);
/* počitadlo iterací */
int i;
/* iterativní výpočet */
for (i = 0; i < 20; i++) {
double abs_error, rel_error;
xi = sqrt_step(xi, y); /* zpřesnění odhadu */
abs_error = fabs(xi - sqr); /* absolutní chyba */
rel_error = 100.0f * fabs(xi - sqr) / sqr; /* relativní chyba */
printf("%d\t%11.5f\t%11.5f\t%10.2f%%\n", i + 1, xi, abs_error, rel_error);
}
return 0;
}
/* finito */
Podívejme se nyní na výsledky vypočtené a vypsané tímto příkladem. Všimněte si, že již po deseti iteracích klesá relativní chyba pod setinu procenta (alespoň v rámci dané přesnosti FP formátu), takže iterační metoda je zvolena vhodně, protože řešení konverguje velmi rychle:
iterace mezivýsledek absolutní chyba relativní chyba ---------------------------------------------------------- 1 5000.50000 4900.50000 4900.50% 2 2501.25000 2401.25000 2401.25% 3 1252.62402 1152.62402 1152.62% 4 630.30365 530.30365 530.30% 5 323.08450 223.08450 223.08% 6 177.01808 77.01808 77.02% 7 116.75475 16.75475 16.75% 8 101.20218 1.20218 1.20% 9 100.00714 0.00714 0.01% 10 100.00000 0.00000 0.00% 11 100.00000 0.00000 0.00% 12 100.00000 0.00000 0.00% 13 100.00000 0.00000 0.00% 14 100.00000 0.00000 0.00% 15 100.00000 0.00000 0.00% 16 100.00000 0.00000 0.00% 17 100.00000 0.00000 0.00% 18 100.00000 0.00000 0.00% 19 100.00000 0.00000 0.00% 20 100.00000 0.00000 0.00%
13. Demonstrační příklad na výpočet druhé odmocniny ve formátu pevné řádové tečky
Demonstrační příklad z předchozí kapitoly si můžeme relativně snadno přepsat do varianty používající formát pevné řádové tečky (čárky). Namísto FP výpočtů tedy využijeme celočíselné operace a pouze zajistíme, aby byla zachována pozice řádové tečky. Konkrétně budou všechny výpočty probíhat s hodnotami int32_t (C99 a vyšší) a pozice řádové tečky bude nastavena mezi bit s indexem 15 a 16:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
/* počet míst před a za binární řádovou tečkou */
#define A 16
#define B 16
/* datový typ, se kterým budeme pracovat */
typedef int32_t fx;
/* hlavičky použitých funkcí */
void fx_print(fx x);
fx fp2fx(double x);
double fx2fp(fx x);
/*
* Tisk numerické hodnoty uložené ve formátu pevné
* řádové binární čárky (FX)
*/
void fx_print(fx x)
{
int i;
int val = x; /* pomocná proměnná pro převod do dvojkové soustavy */
printf("bin: ");
for (i = 0; i < A + B; i++) { /* převod na řetězec bitů (do dvojkové soustavy) */
putchar(!!(val & (1 << (A + B - 1))) + '0'); /* výpis hodnoty aktuálně nejvyššího bitu */
if (i == B - 1)
putchar('.'); /* po řádové binární čárce vypsat značku */
val = val << 1; /* posun na další (méně významný) bit */
}
printf(" hex: %08x fp: %+11.5f\n", x, fx2fp(x));
}
/*
* Převod z formátu plovoucí řádové binární čárky (FP)
* do formátu pevné řádové binární čárky (FX)
*/
fx fp2fx(double x)
{
return (fx) (x * (2 << (B - 1)));
}
/*
* Převod z celočíselného formátu (integer)
* do formátu pevné řádové binární čárky (FX)
*/
fx int2fx(int x)
{
return (fx) (x << B);
}
/*
* Převod z formátu pevné řádové binární čárky (FX)
* do formátu plovoucí řádové binární čárky (FP)
*/
double fx2fp(fx x)
{
return (double) x / (2 << (B - 1));
}
/*
* Součet dvou hodnot uložených ve shodném formátu
* pevné binární řádové čárky (FX)
*/
fx fx_add(fx x, fx y)
{
return x + y;
}
/*
* Rozdíl dvou hodnot uložených ve shodném formátu
* pevné binární řádové čárky (FX)
*/
fx fx_sub(fx x, fx y)
{
return x - y;
}
/*
* Součin dvou hodnot uložených ve shodném formátu
* pevné binární řádové čárky (FX)
*/
fx fx_mul(fx x, fx y)
{
fx result = (x >> (B / 2)) * (y >> (B / 2));
return result;
}
/*
* Podíl dvou hodnot uložených ve shodném formátu
* pevné binární řádové čárky (FX)
*/
fx fx_div(fx x, fx y)
{
fx result = x / (y >> (B / 2));
return result << (B / 2);
}
/* jeden krok odhadu druhé odmocniny */
fx sqrt_step_calc(fx f1, fx f2, fx xi, fx y)
{
return fx_mul(fx_div(f1, f2), xi + fx_div(y, xi));
}
/* tato funkce provede jednu iteraci
* se zlepšeným odhadem výsledku x_i
*/
fx sqrt_step(fx xi, fx y)
{
fx f1 = fp2fx(1.0);
fx f2 = fp2fx(2.0);
return sqrt_step_calc(f1, f2, xi, y);
}
int main(void) {
double orig_y = 10000.0;
/* vstupní hodnota, ze které se počítá odmocnina */
fx y = fp2fx(orig_y);
/* postupně zpřesňovaný odhad výsledku */
fx xi = y;
/* hodnota pro porovnání výsledků */
double sqr = sqrt(orig_y);
/* počitadlo iterací */
int i;
/* iterativní výpočet */
for (i = 0; i < 20; i++) {
double abs_error, rel_error;
double xf;
xi = sqrt_step(xi, y); /* zpřesnění odhadu */
xf = fx2fp(xi); /* převést na FP pro výpočty a tisk */
abs_error = fabs(xf - sqr); /* absolutní chyba */
rel_error = 100.0f * fabs(xf - sqr) / sqr; /* relativní chyba */
printf("%d\t%11.5f\t%11.5f\t%10.2f%%\n", i + 1, xf, abs_error, rel_error);
}
return 0;
}
/* finito */
Výsledky ukazují, že ke korektní hodnotě opět dospějeme relativně rychle; po deseti iteracích:
iterace mezivýsledek absolutní chyba relativní chyba ---------------------------------------------------------- 1 5000.50000 4900.50000 4900.50% 2 2501.24805 2401.24805 2401.25% 3 1252.62109 1152.62109 1152.62% 4 630.30078 530.30078 530.30% 5 323.08203 223.08203 223.08% 6 177.01562 77.01562 77.02% 7 116.75391 16.75391 16.75% 8 101.20117 1.20117 1.20% 9 100.00586 0.00586 0.01% 10 100.00000 0.00000 0.00% 11 100.00000 0.00000 0.00% 12 100.00000 0.00000 0.00% 13 100.00000 0.00000 0.00% 14 100.00000 0.00000 0.00% 15 100.00000 0.00000 0.00% 16 100.00000 0.00000 0.00% 17 100.00000 0.00000 0.00% 18 100.00000 0.00000 0.00% 19 100.00000 0.00000 0.00% 20 100.00000 0.00000 0.00%
14. Překlad jedné iterace pro výpočet druhé odmocniny do assembleru
Výpočty jsme sice ve formátu FX realizovali relativně snadno, ovšem ještě se musíme podívat na to, jak kvalitně nebo nekvalitně byl kód přeložen do assembleru. Při vypnutí optimalizací (-O0) bude výsledkem otrocký překlad původních příkazů zapsaných v jazyku C a výsledek bude dlouhý a pomalý (ostatně přesně podle předpokladů):
sqrt_step_calc(int, int, int, int):
push rbp
mov rbp, rsp
push rbx
sub rsp, 16
mov DWORD PTR [rbp-12], edi
mov DWORD PTR [rbp-16], esi
mov DWORD PTR [rbp-20], edx
mov DWORD PTR [rbp-24], ecx
mov edx, DWORD PTR [rbp-20]
mov eax, DWORD PTR [rbp-24]
mov esi, edx
mov edi, eax
call fx_div(int, int)
mov edx, DWORD PTR [rbp-20]
lea ebx, [rax+rdx]
mov edx, DWORD PTR [rbp-16]
mov eax, DWORD PTR [rbp-12]
mov esi, edx
mov edi, eax
call fx_div(int, int)
mov esi, ebx
mov edi, eax
call fx_mul(int, int)
mov rbx, QWORD PTR [rbp-8]
leave
ret
Při použití optimalizací (-O9) bude výsledek nepatrně lepší:
sqrt_step_calc(int, int, int, int):
mov eax, ecx
mov r9d, edx
mov r8d, edx
sar esi, 8
sar r9d, 8
cdq
idiv r9d
mov ecx, eax
mov eax, edi
cdq
sal ecx, 8
idiv esi
add ecx, r8d
sar ecx, 8
mov edi, eax
mov eax, ecx
sal edi, 8
sar edi, 8
imul eax, edi
ret
I zde však máme prostor pro další optimalizace. Například není nutné předávat konstanty 1 a 2 ve formátu FX. Ovšem důležitější je, že lze využít odlišný algoritmus, který výsledek odhadne rychleji. Podrobnosti si řekneme příště.
15. Goniometrické funkce počítané pomocí číselných řad
Goniometrické funkce, které jsou velmi důležité například v počítačové grafice, je možné počítat více způsoby. V navazující části tohoto seriálu si ukážeme výpočet goniometrických funkcí pomocí algoritmu CORDIC, dnes si pouze řekneme, jakým způsobem je možné použít číselné řady. Uvažujme například funkci sin(), která je, jak víme už ze střední školy, funkcí periodickou s periodou 2π (pro další goniometrické funkce platí podobné vztahy a závěry, tj. v dalším textu se jimi nebudu zabývat).
Na první pohled to vypadá, že se můžeme omezit pouze na výpočet této funkce pro vstupní hodnoty z intervalu <0, 2π>. Ve skutečnosti však můžeme využít velké symetrie této funkce, a to dokonce dvakrát. V intervalu <π, 2π> je funkce zrcadlově otočena vůči vzoru z intervalu <0, π>. Kromě toho je funkce na intervalu <0, π/2> vertikálně symetrická s intervalem <π/2, π>. Z obou těchto symetrií vyplývá, že je zapotřebí přímým výpočtem zjistit hodnoty funkce sin() pouze na intervalu <0, π/2>, hodnoty v ostatních intervalech se dopočítají buď změnou znaménka výsledku, nebo změnou vstupní hodnoty. Daný interval jednoho „kvadrantu“ má i další přednost: funkce sin() je v něm neustále rostoucí bez nežádoucích zákmitů a lokálních minim či maxim.
Všechny goniometrické funkce je možné na určitém intervalu (typicky kvadrantu) rozepsat s využitím Taylorova rozvoje. V případě funkce sin() dostaneme nekonečný rozvoj, který vypadá následovně:
sin(x)=x1/1! – x3/3! + x5/5! – x7/7! + …
16. Demonstrační příklad: výpočet sinu s využitím Taylorova rozvoje
Taylorův rozvoj sice na první pohled vypadá výpočetně velmi náročně, ve skutečnosti je však v praxi zapotřebí pro dosažení relativně dobré přesnosti vypočítat poměrně malé množství jeho členů, o čemž nás přesvědčí demonstrační příklad uvedený pod tímto odstavcem, který pro výpočet funkce sin() na intervalu <0, π/2> používá pouze první tři nenulové členy posloupnosti (což se může zdát jako pouze velmi hrubé přiblížení):
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif
#define EPSILON 10.0e-20
/* tato funkce provede výpočet funkce
* sin() pomocí tří nenulových členů
* Taylorova rozvoje
*/
double compute_sin(double x)
{
double t1=x/1.0;
double t3=x*x*x/6.0;
double t5=x*x*x*x*x/120.0;
return t1-t3+t5;
}
int main(void)
{
/* počitadlo iterací */
double alfa;
for (alfa=0.0; alfa<=M_PI/2.0; alfa+=M_PI/40.0) {
/* korektní výpočet */
double sin1=sin(alfa);
/* náš odhad */
double sin2=compute_sin(alfa);
/* absolutní chyba */
double abs_error = fabs(sin2-sin1);
/* relativní chyba */
double rel_error = fabs(sin1)<EPSILON ? 0.0 : 100.0*fabs(sin2-sin1)/sin1;
/* tisk řádku tabulky */
printf("%5.3f\t%8.6f\t%8.6f\t%8.6f\t%6.2f%%\n",
alfa,
sin1,
sin2,
abs_error,
rel_error);
}
return 0;
}
/* finito */
17. Výsledky výpočtu hodnot funkce sin()
Po překladu a spuštění příkladu z předchozí kapitoly se zobrazí následující tabulka (bez prvního řádku), s vyčíslenými hodnotami funkce sin() pro 21 úhlů z prvního kvadrantu. Ve druhém sloupci je výsledek standardní matematické operace sin(), třetí sloupec obsahuje hodnoty vypočtené pomocí tří členů Taylorova rozvoje a v posledních dvou sloupcích je spočtena a zobrazena absolutní a relativní chyba. Všimněte si, že chyba postupně stoupá od prakticky nulové hodnoty (přesný výsledek) až po cca 0,5%. To je jedna z vlastností Taylorova rozvoje; při vzdalování se od počáteční hodnoty chyba obecně roste. Pokud by bylo zapotřebí použít vyšší přesnosti, není nic jednoduššího, než přidat další jeden či dva členy rozvoje.
úhel sin() Taylorův rozvoj absolutní chyba relativní chyba 0.000 0.000000 0.000000 0.000000 0.00% 0.079 0.078459 0.078459 0.000000 0.00% 0.157 0.156434 0.156434 0.000000 0.00% 0.236 0.233445 0.233445 0.000000 0.00% 0.314 0.309017 0.309017 0.000000 0.00% 0.393 0.382683 0.382684 0.000000 0.00% 0.471 0.453990 0.453992 0.000001 0.00% 0.550 0.522499 0.522502 0.000003 0.00% 0.628 0.587785 0.587793 0.000008 0.00% 0.707 0.649448 0.649465 0.000017 0.00% 0.785 0.707107 0.707143 0.000036 0.01% 0.864 0.760406 0.760477 0.000071 0.01% 0.942 0.809017 0.809146 0.000129 0.02% 1.021 0.852640 0.852866 0.000226 0.03% 1.100 0.891007 0.891386 0.000379 0.04% 1.178 0.923880 0.924493 0.000613 0.07% 1.257 0.951057 0.952017 0.000961 0.10% 1.335 0.972370 0.973834 0.001464 0.15% 1.414 0.987688 0.989867 0.002178 0.22% 1.492 0.996917 1.000088 0.003170 0.32% 1.571 1.000000 1.004525 0.004525 0.45%
18. Univerzální algoritmus CORDIC
CORDIC neboli COordinate ROtation DIgital Computer je výpočetní metoda používající specializovaný iterativní algoritmus, který slouží v první řadě k výpočtu trigonometrických funkcí s předem známou přesností, tj. funkcí sin(), cos(), tan() atd. Po malých úpravách je možné tento algoritmus využít i pro další výpočty, například fáze (úhlu) a velikosti komplexních čísel, vyčíslení logaritmických funkcí, hyperbolických funkcí (sinh(), cosh(), tanh()) atd.
Jednou ze základních vlastností metody CORDIC, která se snad nejvíce v minulosti postarala o jeho velké rozšíření, je jednoduchost operací, které se v každé iteraci provádí – používá se zde totiž pouze sečítání, odečítání a bitové posuny, žádné další operace nejsou zapotřebí; dokonce není ani nutné implementovat násobičku (přesněji řečeno, u některých „odvozených“ funkcí, například tan() je zapotřebí dělička k vydělení vypočtených hodnot sin() a cos(), viz další článek). Díky této vlastnosti bylo možné CORDIC využít i ve velmi (z pohledu moderních CPU) omezených zařízeních, například kalkulačkách či osmibitových mikrořadičích (omezením zde mám na mysli relativně malý počet logických členů i ALU bez násobiček a děliček). Podrobnější informace o této velmi zajímavé metodě budou uvedeny v následujícím pokračování tohoto seriálu.
19. Repositář s demonstračními příklady
Demonstrační příklady napsané v assembleru, které jsou určené pro překlad s využitím assembleru NASM, byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/8bit-fame. Jednotlivé demonstrační příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý (dnes již poměrně rozsáhlý) repositář:
| # | Příklad | Stručný popis | Adresa |
|---|---|---|---|
| 1 | hello.asm | program typu „Hello world“ naprogramovaný v assembleru pro systém DOS | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hello.asm |
| 2 | hello_shorter.asm | kratší varianta výskoku z procesu zpět do DOSu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hello_shorter.asm |
| 3 | hello_wait.asm | čekání na stisk klávesy | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hello_wait.asm |
| 4 | hello_macros.asm | realizace jednotlivých částí programu makrem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hello_macros.asm |
| 5 | gfx4_putpixel.asm | vykreslení pixelu v grafickém režimu 4 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_putpixel.asm |
| 6 | gfx6_putpixel.asm | vykreslení pixelu v grafickém režimu 6 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_putpixel.asm |
| 7 | gfx4_line.asm | vykreslení úsečky v grafickém režimu 4 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_line.asm |
| 8 | gfx6_line.asm | vykreslení úsečky v grafickém režimu 6 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_line.asm |
| 9 | gfx6_fill1.asm | vyplnění obrazovky v grafickém režimu, základní varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_fill1.asm |
| 10 | gfx6_fill2.asm | vyplnění obrazovky v grafickém režimu, varianta s instrukcí LOOP | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_fill2.asm |
| 11 | gfx6_fill3.asm | vyplnění obrazovky instrukcí REP STOSB | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_fill3.asm |
| 12 | gfx6_fill4.asm | vyplnění obrazovky, synchronizace vykreslování s paprskem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_fill4.asm |
| 13 | gfx4_image1.asm | vykreslení rastrového obrázku získaného z binárních dat, základní varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_image1.asm |
| 14 | gfx4_image2.asm | varianta vykreslení rastrového obrázku s využitím instrukce REP MOVSB | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_image2.asm |
| 15 | gfx4_image3.asm | varianta vykreslení rastrového obrázku s využitím instrukce REP MOVSW | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_image3.asm |
| 16 | gfx4_image4.asm | korektní vykreslení všech sudých řádků bitmapy | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_image4.asm |
| 17 | gfx4_image5.asm | korektní vykreslení všech sudých i lichých řádků bitmapy | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_image5.asm |
| 18 | gfx4_image6.asm | nastavení barvové palety před vykreslením obrázku | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_image6.asm |
| 19 | gfx4_image7.asm | nastavení barvové palety před vykreslením obrázku, snížená intenzita barev | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_image7.asm |
| 20 | gfx4_image8.asm | postupná změna barvy pozadí | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx4_image8.asm |
| 21 | gfx6_putpixel1.asm | vykreslení pixelu, základní varianta se 16bitovým násobením | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_putpixel1.asm |
| 22 | gfx6_putpixel2.asm | vykreslení pixelu, varianta s osmibitovým násobením | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_putpixel2.asm |
| 23 | gfx6_putpixel3.asm | vykreslení pixelu, varianta bez násobení | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_putpixel3.asm |
| 24 | gfx6_putpixel4.asm | vykreslení pixelu přes obrázek, nekorektní chování (přepis obrázku) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_putpixel4.asm |
| 25 | gfx6_putpixel5.asm | vykreslení pixelu přes obrázek, korektní varianta pro bílé pixely | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/gfx6_putpixel5.asm |
| 26 | cga_text_mode1.asm | standardní textový režim s rozlišením 40×25 znaků | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/cga_text_mode1.asm |
| 27 | cga_text_mode3.asm | standardní textový režim s rozlišením 80×25 znaků | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/cga_text_mode3.asm |
| 28 | cga_text_mode_intensity.asm | změna významu nejvyššího bitu atributového bajtu: vyšší intenzita namísto blikání | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/cga_text_mode_intensity.asm |
| 29 | cga_text_mode_cursor.asm | změna tvaru textového kurzoru | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/cga_text_mode_cursor.asm |
| 30 | cga_text_gfx1.asm | zobrazení „rastrové mřížky“: pseudografický režim 160×25 pixelů (interně textový režim) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/cga_text_gfx1.asm |
| 31 | cga_text_mode_char_height.asm | změna výšky znaků | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/cga_text_mode_char_height.asm |
| 32 | cga_text_160×100.asm | grafický režim 160×100 se šestnácti barvami (interně upravený textový režim) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/cga_text_160×100.asm |
| 33 | hercules_text_mode1.asm | využití standardního textového režimu společně s kartou Hercules | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hercules_text_mode1.asm |
| 34 | hercules_text_mode2.asm | zákaz blikání v textových režimech | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hercules_text_mode2.asm |
| 35 | hercules_turn_off.asm | vypnutí generování video signálu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hercules_turn_off.asm |
| 36 | hercules_gfx_mode1.asm | přepnutí karty Hercules do grafického režimu (základní varianta) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hercules_gfx_mode1.asm |
| 37 | hercules_gfx_mode2.asm | přepnutí karty Hercules do grafického režimu (vylepšená varianta) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hercules_gfx_mode2.asm |
| 38 | hercules_putpixel.asm | subrutina pro vykreslení jediného pixelu na kartě Hercules | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/hercules_putpixel.asm |
| 39 | ega_text_mode_80×25.asm | standardní textový režim 80×25 znaků na kartě EGA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_text_mode_80×25.asm |
| 40 | ega_text_mode_80×43.asm | zobrazení 43 textových řádků na kartě EGA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_text_mode_80×43.asm |
| 41 | ega_gfx_mode_320×200.asm | přepnutí do grafického režimu 320×200 pixelů se šestnácti barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_gfx_mode_320×200.asm |
| 42 | ega_gfx_mode_640×200.asm | přepnutí do grafického režimu 640×200 pixelů se šestnácti barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_gfx_mode_640×200.asm |
| 43 | ega_gfx_mode_640×350.asm | přepnutí do grafického režimu 640×350 pixelů se čtyřmi nebo šestnácti barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_gfx_mode_640×350.asm |
| 44 | ega_gfx_mode_bitplanes1.asm | ovládání zápisu do bitových rovin v planárních grafických režimech (základní způsob) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_gfx_mode_bitplanes1.asm |
| 45 | ega_gfx_mode_bitplanes2.asm | ovládání zápisu do bitových rovin v planárních grafických režimech (rychlejší způsob) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_gfx_mode_bitplanes2.asm |
| 46 | ega_320×200_putpixel.asm | vykreslení pixelu v grafickém režimu 320×200 pixelů se šestnácti barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_320×200_putpixel.asm |
| 47 | ega_640×350_putpixel.asm | vykreslení pixelu v grafickém režimu 640×350 pixelů se šestnácti barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_640×350_putpixel.asm |
| 48 | ega_standard_font.asm | použití standardního fontu grafické karty EGA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_standard_font.asm |
| 49 | ega_custom_font.asm | načtení vlastního fontu s jeho zobrazením | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_custom_font.asm |
| 50 | ega_palette1.asm | změna barvové palety (všech 16 barev) v grafickém režimu 320×200 se šestnácti barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_palette1.asm |
| 51 | ega_palette2.asm | změna barvové palety (všech 16 barev) v grafickém režimu 640×350 se šestnácti barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_palette2.asm |
| 52 | ega_palette3.asm | změna všech barev v barvové paletě s využitím programové smyčky | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_palette3.asm |
| 53 | ega_palette4.asm | změna všech barev, včetně barvy okraje, v barvové paletě voláním funkce BIOSu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ega_palette4.asm |
| 54 | vga_text_mode_80×25.asm | standardní textový režim 80×25 znaků na kartě VGA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_text_mode_80×25.asm |
| 55 | vga_text_mode_80×50.asm | zobrazení 50 a taktéž 28 textových řádků na kartě VGA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_text_mode_80×50.asm |
| 56 | vga_text_mode_intensity1.asm | změna chování atributového bitu pro blikání (nebezpečná varianta změny registrů) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_text_mode_intensity1.asm |
| 57 | vga_text_mode_intensity2.asm | změna chování atributového bitu pro blikání (bezpečnější varianta změny registrů) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_text_mode_intensity2.asm |
| 58 | vga_text_mode_9th_column.asm | modifikace způsobu zobrazení devátého sloupce ve znakových režimech (720 pixelů na řádku) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_text_mode_9th_column.asm |
| 59 | vga_text_mode_cursor_shape.asm | změna tvaru textového kurzoru na grafické kartě VGA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_text_mode_cursor_shape.asm |
| 60 | vga_text_mode_custom_font.asm | načtení vlastního fontu s jeho zobrazením | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_text_mode_custom_font.asm |
| 61 | vga_gfx_mode_640×480.asm | přepnutí do grafického režimu 640×480 pixelů se šestnácti barvami, vykreslení vzorků | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_640×480.asm |
| 62 | vga_gfx_mode_320×200.asm | přepnutí do grafického režimu 320×200 pixelů s 256 barvami, vykreslení vzorků | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_320×200.asm |
| 63 | vga_gfx_mode_palette.asm | změna všech barev v barvové paletě grafické karty VGA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_palette.asm |
| 64 | vga_gfx_mode_dac1.asm | využití DAC (neočekávané výsledky) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_dac1.asm |
| 65 | vga_gfx_mode_dac2.asm | využití DAC (očekávané výsledky) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_dac2.asm |
| 66 | vga_640×480_putpixel.asm | realizace algoritmu pro vykreslení pixelu v grafickém režimu 640×480 pixelů se šestnácti barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_640×480_putpixel.asm |
| 67 | vga_320×200_putpixel1.asm | realizace algoritmu pro vykreslení pixelu v grafickém režimu 320×200 s 256 barvami (základní varianta) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_putpixel1.asm |
| 68 | vga_320×200_putpixel2.asm | realizace algoritmu pro vykreslení pixelu v grafickém režimu 320×200 s 256 barvami (rychlejší varianta) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_putpixel2.asm |
| 69 | vga_gfx_mode_dac3.asm | přímé využití DAC v grafickém režimu 13h | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_dac3.asm |
| 70 | vga_gfx_mode_unchained_step1.asm | zobrazení barevných pruhů v režimu 13h | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_unchained_step1.asm |
| 71 | vga_gfx_mode_unchained_step2.asm | vypnutí zřetězení bitových rovin a změna způsobu adresování pixelů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_unchained_step2.asm |
| 72 | vga_gfx_mode_unchained_step3.asm | vykreslení barevných pruhů do vybraných bitových rovin | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_unchained_step3.asm |
| 73 | vga_gfx_mode_320×400.asm | nestandardní grafický režim s rozlišením 320×400 pixelů a 256 barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_gfx_mode_320×400.asm |
| 74 | vga_320×200_image.asm | zobrazení rastrového obrázku ve standardním grafickém režimu 320×200 pixelů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_image.asm |
| 75 | vga_320×200_unchained_image1.asm | zobrazení rastrového obrázku v režimu s nezřetězenými rovinami (nekorektní řešení) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_unchained_image1.asm |
| 76 | vga_320×200_unchained_image2.asm | zobrazení rastrového obrázku v režimu s nezřetězenými rovinami (korektní řešení) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_unchained_image2.asm |
| 77 | vga_320×400_unchained_image.asm | zobrazení rastrového obrázku v nestandardním režimu 320×400 pixelů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×400_unchained_image.asm |
| 78 | vga_vertical_scroll1.asm | vertikální scrolling na kartě VGA v režimu s rozlišením 320×200 pixelů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_vertical_scroll1.asm |
| 79 | vga_vertical_scroll2.asm | vertikální scrolling na kartě VGA v režimu s rozlišením 320×400 pixelů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_vertical_scroll2.asm |
| 80 | vga_split_screen1.asm | režim split-screen a scrolling, nefunční varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_split_screen1.asm |
| 81 | vga_split_screen2.asm | režim split-screen a scrolling, plně funkční varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_split_screen2.asm |
| 82 | vga_horizontal_scroll1.asm | horizontální scrolling bez rozšíření počtu pixelů na virtuálním řádku | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_horizontal_scroll1.asm |
| 83 | vga_horizontal_scroll2.asm | horizontální scrolling s rozšířením počtu pixelů na virtuálním řádku | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_horizontal_scroll2.asm |
| 84 | vga_horizontal_scroll3.asm | jemný horizontální scrolling s rozšířením počtu pixelů na virtuálním řádku | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_horizontal_scroll3.asm |
| 85 | vga_320×240_image.asm | nastavení grafického režimu Mode-X, načtení a vykreslení obrázku, scrolling | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×240_image.asm |
| 86 | io.asm | knihovna maker pro I/O operace | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/io.asm |
| 87 | vga_lib.asm | knihovna maker a podprogramů pro programování karty VGA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_lib.asm |
| 88 | vga_320×240_lib.asm | nastavení grafického režimu Mode-X, tentokrát knihovními funkcemi | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×240_lib.asm |
| 89 | vga_bitblt1.asm | první (naivní) implementace operace BitBLT | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_bitblt1.asm |
| 90 | vga_bitblt2.asm | operace BitBLT s výběrem bitových rovin pro zápis | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_bitblt2.asm |
| 91 | vga_bitblt3.asm | operace BitBLT s výběrem bitových rovin pro čtení i zápis | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_bitblt3.asm |
| 92 | vga_bitblt4.asm | korektní BitBLT pro 16barevný režim, realizace makry | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_bitblt4.asm |
| 93 | vga_bitblt5.asm | korektní BitBLT pro 16barevný režim, realizace podprogramem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_bitblt5.asm |
| 94 | vga_bitblt_rotate.asm | zápisový režim s rotací bajtu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_bitblt_rotate.asm |
| 95 | vga_bitblt_fast.asm | rychlá korektní 32bitová operace typu BitBLT | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_bitblt_fast.asm |
| 96 | vga_320×400_bitblt1.asm | přenos obrázku v režimu 320×400 operací BitBLT (neúplná varianta) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×400_bitblt1.asm |
| 97 | vga_320×400_bitblt2.asm | přenos obrázku v režimu 320×400 operací BitBLT (úplná varianta) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×400_bitblt2.asm |
| 98 | vga_write_modes1.asm | volitelné zápisové režimy grafické karty VGA, zápis bez úpravy latche | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_write_modes1.asm |
| 99 | vga_write_modes2.asm | volitelné zápisové režimy grafické karty VGA, zápis s modifikací latche | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_write_modes2.asm |
| 100 | vga_write_modes3.asm | volitelné zápisové režimy grafické karty VGA, cílená modifikace latche vzorkem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_write_modes3.asm |
| 101 | instruction_jump.asm | použití instrukce JMP | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_jump.asm |
| 102 | instruction_jnz.asm | použití instrukce JNZ pro realizaci programové smyčky | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_jnz.asm |
| 103 | instruction_jz_jmp.asm | použití instrukcí JZ a JMP pro realizaci programové smyčky | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_jz_jmp.asm |
| 104 | instruction_loop.asm | použití instrukce LOOP pro realizaci programové smyčky | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_loop.asm |
| 105 | instruction_template.asm | šablona všech následujících demonstračních příkladů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_template.asm |
| 106 | instruction_print_hex.asm | tisk osmibitové hexadecimální hodnoty | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_print_hex.asm |
| 107 | instruction_xlat.asm | využití instrukce XLAT pro získání tisknutelné hexadecimální cifry | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_xlat.asm |
| 108 | instruction_daa.asm | operace součtu s využitím binární i BCD aritmetiky | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_daa.asm |
| 109 | instruction_daa_sub.asm | instrukce DAA po provedení operace rozdílu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_daa_sub.asm |
| 110 | instruction_das.asm | instrukce DAS po provedení operace rozdílu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_das.asm |
| 111 | instruction_aaa.asm | korekce výsledku na jedinou BCD cifru operací AAA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_aaa.asm |
| 112 | instruction_mul.asm | ukázka výpočtu součinu dvou osmibitových hodnot | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_mul.asm |
| 113 | instruction_aam.asm | BCD korekce po výpočtu součinu instrukcí AAM | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_aam.asm |
| 114 | instruction_stosb.asm | blokový zápis dat instrukcí STOSB | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_stosb.asm |
| 115 | instruction_rep_stosb.asm | opakované provádění instrukce STOSB | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_rep_stosb.asm |
| 116 | instruction_lodsb.asm | čtení dat instrukcí LODSB | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_lodsb.asm |
| 117 | instruction_movsb.asm | přenos jednoho bajtu instrukcí MOVSB | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_movsb.asm |
| 118 | instruction_rep_movsb.asm | blokový přenos po bajtech instrukcí MOVSB | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_rep_movsb.asm |
| 119 | instruction_rep_scas.asm | vyhledávání v řetězci instrukcí SCAS | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_rep_scas.asm |
| 120 | vga_320×200_image_0B.asm | výsledek blokového přenosu ve chvíli, kdy je CX=0 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_image_0B.asm |
| 121 | vga_320×200_image_64kB.asm | výsledek blokového přenosu ve chvíli, kdy je CX=0×ffff | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_image_64kB.asm |
| 122 | vga_320×200_image_movsb.asm | blokový přenos v rámci obrazové paměti instrukcí REP MOVSB | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_image_movsb.asm |
| 123 | vga_320×200_image_movsw.asm | blokový přenos v rámci obrazové paměti instrukcí REP MOVSW | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_image_movsw.asm |
| 124 | vga_320×200_image_movsd.asm | blokový přenos v rámci obrazové paměti instrukcí REP MOVSD | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_image_movsd.asm |
| 125 | vga_320×200_image_movsb_forward.asm | blokový přenos překrývajících se bloků paměti (zvyšující se adresy) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_image_movsb_forward.asm |
| 126 | vga_320×200_image_movsb_backward1.asm | blokový přenos překrývajících se bloků paměti (snižující se adresy, nekorektní nastavení) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_image_movsb_backward1.asm |
| 127 | vga_320×200_image_movsb_backward2.asm | blokový přenos překrývajících se bloků paměti (snižující se adresy, korektní nastavení) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_image_movsb_backward2.asm |
| 128 | sound_bell.asm | přehrání zvuku pomocí tisku ASCII znaku BELL | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_bell.asm |
| 129 | sound_beep.asm | přehrání zvuku o zadané frekvenci na PC Speakeru | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_beep.asm |
| 130 | sound_play_pitch.asm | přehrání zvuku o zadané frekvenci na PC Speakeru, použití maker | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_play_pitch.asm |
| 131 | sound_opl2_basic.asm | přehrání komorního A na OPL2 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl2_basic.asm |
| 132 | sound_opl2_table.asm | přehrání komorního A na OPL2, použití tabulky s hodnotami registrů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl2_table.asm |
| 133 | sound_opl2_table2.asm | přepis tabulky s obsahy registrů pro přehrání komorního A | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl2_table2.asm |
| 134 | sound_key_on.asm | přímé ovládání bitu KEY ON mezerníkem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_key_on.asm |
| 135 | sound_adsr.asm | nastavení obálky pro tón přehrávaný prvním kanálem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_adsr.asm |
| 136 | sound_modulation.asm | řízení frekvence modulátoru klávesami 1 a 0 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_modulation.asm |
| 137 | keyboard_basic.asm | přímá práce s klávesnicí IBM PC | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/keyboard_basic.asm |
| 138 | sound_stereo_opl2.asm | stereo zvuk v konfiguraci DualOPL2 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_stereo_opl2.asm |
| 139 | sound_opl2_multichannel.asm | vícekanálový zvuk na OPL2 (klávesy), delší varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl2_multichannel.asm |
| 140 | sound_opl2_multichannel2.asm | vícekanálový zvuk na OPL2 (klávesy), kratší varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl2_multichannel2.asm |
| 141 | sound_opl3_stereo1.asm | stereo výstup na OPL3 (v kompatibilním režimu) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl3_stereo1.asm |
| 142 | sound_opl3_stereo2.asm | stereo výstup na OPL3 (v režimu OPL3) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl3_stereo2.asm |
| 143 | sound_opl3_multichannel.asm | vícekanálový zvuk na OPL3 (klávesy) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl3_multichannel.asm |
| 144 | sound_opl3_waveform1.asm | interaktivní modifikace tvaru vlny u prvního operátoru | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl3_waveform1.asm |
| 145 | sound_opl3_waveform2.asm | oprava chyby: povolení režimu kompatibilního s OPL3 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl3_waveform2.asm |
| 146 | sound_opl3_waveform3.asm | vliv tvaru vln na zvukový kanál s FM syntézou | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl3_waveform3.asm |
| 147 | sound_opl3_waveform4.asm | modifikace tvaru vlny nosné vlny i modulátoru | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl3_waveform4.asm |
| 148 | sound_opl3_4operators1.asm | výběr AM/FM režimu ve čtyřoperátorovém nastavení | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl3_4operators1.asm |
| 149 | sound_opl3_4operators2.asm | výběr AM/FM režimu ve čtyřoperátorovém nastavení | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sound_opl3_4operators2.asm |
| 150 | timer_basic.asm | základní obsluha přerušení od časovače/čítače | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/timer_basic.asm |
| 151 | timer_restore.asm | obnovení původní obsluhy přerušení při ukončování aplikace | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/timer_restore.asm |
| 152 | timer_restore_better_structure.asm | refaktoring předchozího demonstračního příkladu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/timer_restore_better_structure.asm |
| 153 | timer_faster_clock.asm | zrychlení čítače na 100 přerušení za sekundu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/timer_faster_clock.asm |
| 154 | instruction_push_imm.asm | instrukce PUSH s konstantou | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_push_imm.asm |
| 155 | instruction_imul_imm.asm | instrukce IMUL s konstantou | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_imul_imm.asm |
| 156 | instruction_into1.asm | instrukce INTO s obsluhou přerušení | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_into1.asm |
| 157 | instruction_into2.asm | instrukce INTO s obsluhou přerušení | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_into2.asm |
| 158 | instruction_bound1.asm | instrukce BOUND s obsluhou přerušení (nekorektní řešení) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_bound1.asm |
| 159 | instruction_bound2.asm | instrukce BOUND s obsluhou přerušení (korektní řešení) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_bound2.asm |
| 160 | vga_320×200_putpixel286.asm | instrukce bitového posunu s konstantou větší než 1 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_putpixel286.asm |
| 161 | instruction_push_pop.asm | instrukce PUSH a POP se všemi pracovními registry | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_push_pop.asm |
| 162 | instruction_push_pop_B.asm | instrukce s novými segmentovými registry | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_push_pop_B.asm |
| 163 | instruction_near_jz_jmp.asm | blízké skoky | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_near_jz_jmp.asm |
| 164 | instruction_bsf.asm | nová instrukce BSF | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_bsf.asm |
| 165 | instruction_bsr.asm | nová instrukce BSR | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_bsr.asm |
| 166 | instruction_add_32bit.asm | 32bitový součet | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_add_32bit.asm |
| 167 | instruction_inc_32bit.asm | 32bitová instrukce INC v šestnáctibitovém režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_inc_32bit.asm |
| 168 | instruction_inc_32bit_B.asm | 32bitová instrukce INC v 32bitovém režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/instruction_inc_32bit_B.asm |
| 169 | ems_status.asm | zjištění stavu (emulace) paměti EMS | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ems_status.asm |
| 170 | ems_total_mem.asm | získání celkové kapacity paměti EMS v blocích | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ems_total_mem.asm |
| 171 | ems_free_mem.asm | získání volné kapacity paměti EMS v blocích | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/ems_free_mem.asm |
| 172 | xms_free_mem.asm | získání volné kapacity paměti XMS v blocích | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/xms_free_mem.asm |
| 173 | vga_320×200_short_address1.asm | blokový přenos provedený v rámci prostoru segmentu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_short_address1.asm |
| 174 | vga_320×200_short_address2.asm | rozepsaný blokový přenos provedený v rámci prostoru segmentu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_short_address2.asm |
| 175 | vga_320×200_short_address3.asm | přenos nelze provést přes hranici offsetu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_short_address3.asm |
| 176 | vga_320×200_short_address4.asm | přenos nelze provést přes hranici offsetu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_short_address4.asm |
| 177 | vga_320×200_long_address1.asm | 32bitový blokový přenos | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_long_address1.asm |
| 178 | vga_320×200_long_address2.asm | rozepsaný 32bitový blokový přenos provedený v rámci prostoru segmentu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_long_address2.asm |
| 179 | vga_320×200_long_address3.asm | přístup do obrazové paměti přes segment 0×0000 a 32bitový offset | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_long_address3.asm |
| 180 | vga_320×200_long_address4.asm | otestování, jak lze přenášet data s využitím 32bitového offsetu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/vga_320×200_long_address4.asm |
| 181 | print_msw.asm | přečtení a zobrazení obsahu speciálního registru MSW | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/print_msw.asm |
| 182 | print_cr0.asm | přečtení a zobrazení obsahu speciálního registru CR0 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/print_cr0.asm |
| 183 | prot_mode286.asm | přechod do chráněného režimu na čipech Intel 80286 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/prot_mode286.asm |
| 184 | prot_mode386.asm | přechod do chráněného režimu na čipech Intel 80386 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/prot_mode386.asm |
| 185 | prot_mode_back_to_real_mode286.asm | přechod mezi reálným režimem a chráněným režimem i zpět na čipech Intel 80286 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/prot_mode_back_to_real_mode286.asm |
| 186 | prot_mode_back_to_real_mode386.asm | přechod mezi reálným režimem a chráněným režimem i zpět na čipech Intel 80386 | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/prot_mode_back_to_real_mode386.asm |
| 187 | prot_mode_check.asm | test, zda se mikroprocesor již nachází v chráněném režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/prot_mode_check.asm |
| 188 | unreal_mode.asm | nastavení nereálného režimu (platné pro Intel 80386) | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/unreal_mode.asm |
| 189 | float32_constants.asm | vytištění základních FP konstant typu single | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/float32_constants.asm |
| 190 | float64_constants.asm | vytištění základních FP konstant typu double | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/float64_constants.asm |
| 191 | fpu_arithmetic.asm | základní aritmetické operace prováděné matematickým koprocesorem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_arithmetic.asm |
| 192 | fpu_divide_by_zero.asm | dělení nulou matematickým koprocesorem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_divide_by_zero.asm |
| 193 | fpu_divide_by_neg_zero.asm | dělení záporné hodnoty nulou matematickým koprocesorem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_divide_by_neg_zero.asm |
| 194 | fpu_divide_by_neg_zero2.asm | dělení hodnoty zápornou nulou matematickým koprocesorem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_divide_by_neg_zero2.asm |
| 195 | fpu_divide_zero_by_zero.asm | výpočet 0/0 matematickým koprocesorem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_divide_zero_by_zero.asm |
| 196 | io.asm | pomocná makra pro komunikaci s DOSem a BIOSem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/io.asm |
| 197 | print.asm | pomocná makra pro tisk FPU hodnot typu single a double v hexadecimálním tvaru | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/print.asm |
| 198 | fpu_divide.asm | operace podílu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_divide.asm |
| 199 | fpu_divide_r.asm | operace podílu s prohozenými operandy | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_divide_r.asm |
| 200 | fpu_sqrt.asm | výpočet druhé odmocniny | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_sqrt.asm |
| 201 | fpu_sqrt_neg_value.asm | výpočet druhé odmocniny ze záporné hodnoty | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_sqrt_neg_value.asm |
| 202 | fpu_check.asm | detekce typu matematického koprocesoru | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_check.asm |
| 203 | fpu_compare.asm | porovnání dvou hodnot s vyhodnocením výsledku | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_compare.asm |
| 204 | fpu_status_word.asm | tisk obsahu stavového slova koprocesoru | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_status_word.asm |
| 205 | fpu_status_word_stack.asm | tisk obsahu stavového slova koprocesoru | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fpu_status_word_stack.asm |
| 206 | svga_info1.asm | zjištění, zda je VBE dostupný | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_info1.asm |
| 207 | svga_info2.asm | zobrazení základních informací o grafické kartě | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_info2.asm |
| 208 | svga_info3.asm | výpis OEM řetězce s další informací o kartě | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_info3.asm |
| 209 | svga_info4.asm | zjištění a výpis čísel všech podporovaných grafických režimů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_info4.asm |
| 210 | svga_info5.asm | získání rozlišení, bitové hloubky a struktury obrazových řádků zvoleného grafického režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_info5.asm |
| 211 | svga_info6.asm | základní informace o čtecích a zápisových oknech pro reálný režim | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_info6.asm |
| 212 | svga_info7.asm | informace o oknech podporovaných grafickým režimem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_info7.asm |
| 213 | svga_mode0.asm | přepnutí do zvoleného grafického režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_mode0.asm |
| 214 | svga_mode1.asm | vyplnění jediného okna barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_mode1.asm |
| 215 | svga_mode2.asm | vyplnění čtyř banků barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_mode2.asm |
| 216 | svga_mode3.asm | otestování, jakým způsobem jsou uloženy pixely v režimu s bitovou hloubkou 24/32 bitů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_mode3.asm |
| 217 | svga_pixel_formats1.asm | zjištění formátu uložení pixelů v grafickém režimu s bitovou hloubkou 15 bitů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_pixel_formats1.asm |
| 218 | svga_pixel_formats2.asm | zjištění formátu uložení pixelů v grafickém režimu s bitovou hloubkou 16 bitů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_pixel_formats2.asm |
| 219 | svga_pixel_formats3.asm | zjištění formátu uložení pixelů v grafickém režimu s bitovou hloubkou 24 nebo 32 bitů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_pixel_formats3.asm |
| 220 | svga_palette.asm | nastavení barvové palety v režimu s 256 barvami | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_palette.asm |
| 221 | svga_640×480_image1.asm | vykreslení rastrového obrázku bez modifikace offsetů na řádcích | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_640×480_image1.asm |
| 222 | svga_640×480_image2.asm | vykreslení rastrového obrázku s modifikací offsetů na řádcích | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_640×480_image2.asm |
| 223 | svga_640×480_image3.asm | první realizace subrutiny typu BitBLT | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_640×480_image3.asm |
| 224 | svga_640×480_image4.asm | vykreslení všech 200 řádků rastrového obrázku | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_640×480_image4.asm |
| 225 | svga_640×480_image5.asm | vycentrování rastrového obrázku | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_640×480_image5.asm |
| 226 | svga_640×480_image6.asm | změna počtu pixelů na obrazovém řádku | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_640×480_image6.asm |
| 227 | svga_text_mode1.asm | nastavení rozšířeného textového režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_text_mode1.asm |
| 228 | svga_text_mode2.asm | přímý přístup do paměti rozšířeného textového režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_text_mode2.asm |
| 229 | svga_text_mode3.asm | nastavení odlišného rozšířeného textového režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_text_mode3.asm |
| 230 | svga_text_mode4.asm | změna tvaru kurzoru v rozšířeném textovém režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_text_mode4.asm |
| 231 | svga_text_mode_info.asm | získání základních informací o textovém režimu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_text_mode_info.asm |
| 232 | svga_text_modes.asm | tisk všech dostupných textových režimů karet SVGA | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/svga_text_modes.asm |
| 233 | fx_add1.asm | operace součtu ve formátu s pevnou řádovou tečkou | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_add1.asm |
| 234 | fx_add2.asm | operace součtu ve formátu s pevnou řádovou tečkou, realizace makrem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_add2.asm |
| 235 | fx_mul1.asm | naivní (nekorektní) implementace součinu ve formátu s pevnou řádovou tečkou | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mul1.asm |
| 236 | fx_mul2.asm | korektní implementace součinu ve formátu s pevnou řádovou tečkou, úprava výsledku | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mul2.asm |
| 237 | fx_mul3.asm | korektní implementace součinu ve formátu s pevnou řádovou tečkou, úprava operandů | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mul3.asm |
| 238 | fx_mul4.asm | násobení malých hodnot s korektním výsledkem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mul4.asm |
| 239 | fx_mul5.asm | násobení příliš malých hodnot s nekorektním výsledkem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mul5.asm |
| 240 | fx_mul6.asm | násobení malých hodnot omezené na 2n-bitové hodnoty | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mul6.asm |
| 241 | fx.c | implementace základních operací ve formátu s pevnou řádovou tečkou v jazyku C | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx.c |
| 242 | fx_O0.asm | překlad příkladu fx.c s vypnutím optimalizací | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_O0.asm |
| 243 | fx_O9.asm | překlad příkladu fx.c se zapnutím optimalizací na výkon | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_O9.asm |
| 244 | fx_Os.asm | překlad příkladu fx.c se zapnutím optimalizací na velikost kódu | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_Os.asm |
| 245 | fx_mandel1.asm | výpočet Mandelbrotovy množiny; základní varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mandel1.asm |
| 246 | fx_mandel2.asm | výpočet Mandelbrotovy množiny; optimalizovaná varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mandel2.asm |
| 247 | fx_mandel3.asm | výpočet Mandelbrotovy množiny; základní šestnáctibitová varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mandel3.asm |
| 248 | fx_mandel4.asm | výpočet Mandelbrotovy množiny; šestnáctibitová varianta s vyšší přesností | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mandel4.asm |
| 249 | fx_mandel5.asm | výpočet Mandelbrotovy množiny; šestnáctibitová varianta s vyšší přesností, ale malým rozsahem | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_mandel5.asm |
| 250 | fx_julia.asm | výpočet animace Juliovy množiny | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/fx_julia.asm |
| 251 | sqrt_fp.c | iterativní výpočet druhé odmocniny, FP varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sqrt_fp.c |
| 252 | sqrt_fx.c | iterativní výpočet druhé odmocniny, FX varianta | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sqrt_fx.c |
| 253 | sin_fp.c | výpočet hodnoty sinu na základě prvních členů Taylorova rozvoje | https://github.com/tisnik/8bit-fame/blob/master/pc-dos/sin_fp.c |
20. Odkazy na Internetu
- VESA BIOS Extensions
https://en.wikipedia.org/wiki/VESA_BIOS_Extensions - Video Electronics Standards Association
https://en.wikipedia.org/wiki/Video_Electronics_Standards_Association - DJGPP (Wikipedia)
https://cs.wikipedia.org/wiki/DJGPP - DJGPP home page
http://www.delorie.com/djgpp/ - DJGPP Zip File Picker
http://www.delorie.com/djgpp/zip-picker.html - The Intel 8088 Architecture and Instruction Set
https://people.ece.ubc.ca/~edc/464/lectures/lec4.pdf - x86 Opcode Structure and Instruction Overview
https://pnx.tf/files/x86_opcode_structure_and_instruction_overview.pdf - x86 instruction listings (Wikipedia)
https://en.wikipedia.org/wiki/X86_instruction_listings - x86 assembly language (Wikipedia)
https://en.wikipedia.org/wiki/X86_assembly_language - Intel Assembler (Cheat sheet)
http://www.jegerlehner.ch/intel/IntelCodeTable.pdf - 25 Microchips That Shook the World
https://spectrum.ieee.org/tech-history/silicon-revolution/25-microchips-that-shook-the-world - Chip Hall of Fame: MOS Technology 6502 Microprocessor
https://spectrum.ieee.org/tech-history/silicon-revolution/chip-hall-of-fame-mos-technology-6502-microprocessor - Chip Hall of Fame: Intel 8088 Microprocessor
https://spectrum.ieee.org/tech-history/silicon-revolution/chip-hall-of-fame-intel-8088-microprocessor - Jak se zrodil procesor?
https://www.root.cz/clanky/jak-se-zrodil-procesor/ - Apple II History Home
http://apple2history.org/ - The 8086/8088 Primer
https://www.stevemorse.org/8086/index.html - flat assembler: Assembly language resources
https://flatassembler.net/ - FASM na Wikipedii
https://en.wikipedia.org/wiki/FASM - Fresh IDE FASM inside
https://fresh.flatassembler.net/ - MS-DOS Version 4.0 Programmer's Reference
https://www.pcjs.org/documents/books/mspl13/msdos/dosref40/ - DOS API (Wikipedia)
https://en.wikipedia.org/wiki/DOS_API - Bit banging
https://en.wikipedia.org/wiki/Bit_banging - IBM Basic assembly language and successors (Wikipedia)
https://en.wikipedia.org/wiki/IBM_Basic_assembly_language_and_successors - X86 Assembly/Bootloaders
https://en.wikibooks.org/wiki/X86_Assembly/Bootloaders - Počátky grafiky na PC: grafické karty CGA a Hercules
https://www.root.cz/clanky/pocatky-grafiky-na-pc-graficke-karty-cga-a-hercules/ - Co mají společného Commodore PET/4000, BBC Micro, Amstrad CPC i grafické karty MDA, CGA a Hercules?
https://www.root.cz/clanky/co-maji-spolecneho-commodore-pet-4000-bbc-micro-amstrad-cpc-i-graficke-karty-mda-cga-a-hercules/ - Karta EGA: první použitelná barevná grafika na PC
https://www.root.cz/clanky/karta-ega-prvni-pouzitelna-barevna-grafika-na-pc/ - RGB Classic Games
https://www.classicdosgames.com/ - Turbo Assembler (Wikipedia)
https://en.wikipedia.org/wiki/Turbo_Assembler - Microsoft Macro Assembler
https://en.wikipedia.org/wiki/Microsoft_Macro_Assembler - IBM Personal Computer (Wikipedia)
https://en.wikipedia.org/wiki/IBM_Personal_Computer - Intel 8251
https://en.wikipedia.org/wiki/Intel_8251 - Intel 8253
https://en.wikipedia.org/wiki/Intel_8253 - Intel 8255
https://en.wikipedia.org/wiki/Intel_8255 - Intel 8257
https://en.wikipedia.org/wiki/Intel_8257 - Intel 8259
https://en.wikipedia.org/wiki/Intel_8259 - Support/peripheral/other chips – 6800 family
http://www.cpu-world.com/Support/6800.html - Motorola 6845
http://en.wikipedia.org/wiki/Motorola_6845 - The 6845 Cathode Ray Tube Controller (CRTC)
http://www.tinyvga.com/6845 - CRTC operation
http://www.6502.org/users/andre/hwinfo/crtc/crtc.html - The 6845 Cathode Ray Tube Controller (CRTC)
http://www.tinyvga.com/6845 - Motorola 6845 and bitwise graphics
https://retrocomputing.stackexchange.com/questions/10996/motorola-6845-and-bitwise-graphics - IBM Monochrome Display Adapter
http://en.wikipedia.org/wiki/Monochrome_Display_Adapter - Color Graphics Adapter
http://en.wikipedia.org/wiki/Color_Graphics_Adapter - Color Graphics Adapter and the Brown color in IBM 5153 Color Display
https://www.aceinnova.com/en/electronics/cga-and-the-brown-color-in-ibm-5153-color-display/ - The Modern Retrocomputer: An Arduino Driven 6845 CRT Controller
https://hackaday.com/2017/05/14/the-modern-retrocomputer-an-arduino-driven-6845-crt-controller/ - flat assembler: Assembly language resources
https://flatassembler.net/ - FASM na Wikipedii
https://en.wikipedia.org/wiki/FASM - Fresh IDE FASM inside
https://fresh.flatassembler.net/ - MS-DOS Version 4.0 Programmer's Reference
https://www.pcjs.org/documents/books/mspl13/msdos/dosref40/ - DOS API (Wikipedia)
https://en.wikipedia.org/wiki/DOS_API - IBM Basic assembly language and successors (Wikipedia)
https://en.wikipedia.org/wiki/IBM_Basic_assembly_language_and_successors - X86 Assembly/Arithmetic
https://en.wikibooks.org/wiki/X86_Assembly/Arithmetic - Art of Assembly – Arithmetic Instructions
http://oopweb.com/Assembly/Documents/ArtOfAssembly/Volume/Chapter6/CH06–2.html - ASM Flags
http://www.cavestory.org/guides/csasm/guide/asm_flags.html - Status Register
https://en.wikipedia.org/wiki/Status_register - Linux assemblers: A comparison of GAS and NASM
http://www.ibm.com/developerworks/library/l-gas-nasm/index.html - Programovani v assembleru na OS Linux
http://www.cs.vsb.cz/grygarek/asm/asmlinux.html - Is it worthwhile to learn x86 assembly language today?
https://www.quora.com/Is-it-worthwhile-to-learn-x86-assembly-language-today?share=1 - Why Learn Assembly Language?
http://www.codeproject.com/Articles/89460/Why-Learn-Assembly-Language - Is Assembly still relevant?
http://programmers.stackexchange.com/questions/95836/is-assembly-still-relevant - Why Learning Assembly Language Is Still a Good Idea
http://www.onlamp.com/pub/a/onlamp/2004/05/06/writegreatcode.html - Assembly language today
http://beust.com/weblog/2004/06/23/assembly-language-today/ - Assembler: Význam assembleru dnes
http://www.builder.cz/rubriky/assembler/vyznam-assembleru-dnes-155960cz - Programming from the Ground Up Book – Summary
http://savannah.nongnu.org/projects/pgubook/ - DOSBox
https://www.dosbox.com/ - The C Programming Language
https://en.wikipedia.org/wiki/The_C_Programming_Language - Hercules Graphics Card (HCG)
https://en.wikipedia.org/wiki/Hercules_Graphics_Card - Complete 8086 instruction set
https://content.ctcd.edu/courses/cosc2325/m22/docs/emu8086ins.pdf - Complete 8086 instruction set
https://yassinebridi.github.io/asm-docs/8086_instruction_set.html - 8088 MPH by Hornet + CRTC + DESiRE (final version)
https://www.youtube.com/watch?v=hNRO7lno_DM - Area 5150 by CRTC & Hornet (Party Version) / IBM PC+CGA Demo, Hardware Capture
https://www.youtube.com/watch?v=fWDxdoRTZPc - 80×86 Integer Instruction Set Timings (8088 – Pentium)
http://aturing.umcs.maine.edu/~meadow/courses/cos335/80×86-Integer-Instruction-Set-Clocks.pdf - Colour Graphics Adapter: Notes
https://www.seasip.info/VintagePC/cga.html - Restoring A Vintage CGA Card With Homebrew HASL
https://hackaday.com/2024/06/12/restoring-a-vintage-cga-card-with-homebrew-hasl/ - Demoing An 8088
https://hackaday.com/2015/04/10/demoing-an-8088/ - Video Memory Layouts
http://www.techhelpmanual.com/89-video_memory_layouts.html - Screen Attributes
http://www.techhelpmanual.com/87-screen_attributes.html - IBM PC Family – BIOS Video Modes
https://www.minuszerodegrees.net/video/bios_video_modes.htm - EGA Functions
https://cosmodoc.org/topics/ega-functions/#the-hierarchy-of-the-ega - Why the EGA can only use 16 of its 64 colours in 200-line modes
https://www.reenigne.org/blog/why-the-ega-can-only-use-16-of-its-64-colours-in-200-line-modes/ - How 16 colors saved PC gaming – the story of EGA graphics
https://www.custompc.com/retro-tech/ega-graphics - List of 16-bit computer color palettes
https://en.wikipedia.org/wiki/List_of16-bit_computer_color_palettes - Why were those colors chosen to be the default palette for 256-color VGA?
https://retrocomputing.stackexchange.com/questions/27994/why-were-those-colors-chosen-to-be-the-default-palette-for-256-color-vga - VGA Color Palettes
https://www.fountainware.com/EXPL/vga_color_palettes.htm - Hardware Level VGA and SVGA Video Programming Information Page
http://www.osdever.net/FreeVGA/vga/vga.htm - Hardware Level VGA and SVGA Video Programming Information Page – sequencer
http://www.osdever.net/FreeVGA/vga/seqreg.htm - VGA Basics
http://www.brackeen.com/vga/basics.html - Introduction to VGA Mode ‚X‘
https://web.archive.org/web/20160414072210/http://fly.srk.fer.hr/GDM/articles/vgamodex/vgamx1.html - VGA Mode-X
https://web.archive.org/web/20070123192523/http://www.gamedev.net/reference/articles/article356.asp - Mode-X: 256-Color VGA Magic
https://downloads.gamedev.net/pdf/gpbb/gpbb47.pdf - Instruction Format in 8086 Microprocessor
https://www.includehelp.com/embedded-system/instruction-format-in-8086-microprocessor.aspx - How to use „AND,“ „OR,“ and „XOR“ modes for VGA Drawing
https://retrocomputing.stackexchange.com/questions/21936/how-to-use-and-or-and-xor-modes-for-vga-drawing - VGA Hardware
https://wiki.osdev.org/VGA_Hardware - Programmer's Guide to Yamaha YMF 262/OPL3 FM Music Synthesizer
https://moddingwiki.shikadi.net/wiki/OPL_chip - Does anybody understand how OPL2 percussion mode works?
https://forum.vcfed.org/index.php?threads/does-anybody-understand-how-opl2-percussion-mode-works.60925/ - Yamaha YMF262 OPL3 music – MoonDriver for OPL3 DEMO [Oscilloscope View]
https://www.youtube.com/watch?v=a7I-QmrkAak - Yamaha OPL vs OPL2 vs OPL3 comparison
https://www.youtube.com/watch?v=5knetge5Gs0 - OPL3 Music Crockett's Theme
https://www.youtube.com/watch?v=HXS008pkgSQ - Bad Apple (Adlib Tracker – OPL3)
https://www.youtube.com/watch?v=2lEPH6Y3Luo - FM Synthesis Chips, Codecs and DACs
https://www.dosdays.co.uk/topics/fm_synthesizers.php - The Zen Challenge – YMF262 OPL3 Original (For an upcoming game)
https://www.youtube.com/watch?v=6JlFIFz1CFY - [adlib tracker II techno music – opl3] orbit around alpha andromedae I
https://www.youtube.com/watch?v=YqxJCu_WFuA - [adlib tracker 2 music – opl3 techno] hybridisation process on procyon-ii
https://www.youtube.com/watch?v=daSV5mN0sJ4 - Hyper Duel – Black Rain (YMF262 OPL3 Cover)
https://www.youtube.com/watch?v=pu_mzRRq8Ho - IBM 5155–5160 Technical Reference
https://www.minuszerodegrees.net/manuals/IBM/IBM_5155_5160_Technical_Reference_6280089_MAR86.pdf - a ymf262/opl3+pc speaker thing i made
https://www.youtube.com/watch?v=E-Mx0lEmnZ0 - [OPL3] Like a Thunder
https://www.youtube.com/watch?v=MHf06AGr8SU - (PC SPEAKER) bad apple
https://www.youtube.com/watch?v=LezmKIIHyUg - Powering devices from PC parallel port
http://www.epanorama.net/circuits/lptpower.html - Magic Mushroom (demo pro PC s DOSem)
http://www.crossfire-designs.de/download/articles/soundcards//mushroom.rar - Píseň Magic Mushroom – originál
http://www.crossfire-designs.de/download/articles/soundcards/speaker_mushroom_converted.mp3 - Píseň Magic Mushroom – hráno na PC Speakeru
http://www.crossfire-designs.de/download/articles/soundcards/speaker_mushroom_speaker.mp3 - Pulse Width Modulation (PWM) Simulation Example
http://decibel.ni.com/content/docs/DOC-4599 - Resistor/Pulse Width Modulation DAC
http://www.k9spud.com/traxmod/pwmdac.php - Class D Amplifier
http://en.wikipedia.org/wiki/Electronic_amplifier#Class_D - Covox Speech Thing / Disney Sound Source (1986)
http://www.crossfire-designs.de/index.php?lang=en&what=articles&name=showarticle.htm&article=soundcards/&page=5 - Covox Digital-Analog Converter (Rusky, obsahuje schémata)
http://phantom.sannata.ru/konkurs/netskater002.shtml - PC-GPE on the Web
http://bespin.org/~qz/pc-gpe/ - Keyboard Synthesizer
http://www.solarnavigator.net/music/instruments/keyboards.htm - FMS – Fully Modular Synthesizer
http://fmsynth.sourceforge.net/ - Javasynth
http://javasynth.sourceforge.net/ - Software Sound Synthesis & Music Composition Packages
http://www.linux-sound.org/swss.html - Mx44.1 Download Page (software synthesizer for linux)
http://hem.passagen.se/ja_linux/ - Software synthesizer
http://en.wikipedia.org/wiki/Software_synthesizer - Frequency modulation synthesis
http://en.wikipedia.org/wiki/Frequency_modulation_synthesis - Yamaha DX7
http://en.wikipedia.org/wiki/Yamaha_DX7 - Wave of the Future
http://www.wired.com/wired/archive/2.03/waveguides_pr.html - Analog synthesizer
http://en.wikipedia.org/wiki/Analog_synthesizer - Minimoog
http://en.wikipedia.org/wiki/Minimoog - Moog synthesizer
http://en.wikipedia.org/wiki/Moog_synthesizer - Tutorial for Frequency Modulation Synthesis
http://www.sfu.ca/~truax/fmtut.html - An Introduction To FM
http://ccrma.stanford.edu/software/snd/snd/fm.html - John Chowning
http://en.wikipedia.org/wiki/John_Chowning - I'm Impressed, Adlib Music is AMAZING!
https://www.youtube.com/watch?v=PJNjQYp1ras - Milinda- Diode Milliampere ( OPL3 )
https://www.youtube.com/watch?v=oNhazT5HG0E - Dune 2 – Roland MT-32 Soundtrack
https://www.youtube.com/watch?v=kQADZeB-z8M - Interrupts
https://wiki.osdev.org/Interrupts#Types_of_Interrupts - Assembly8086SoundBlasterDmaSingleCycleMode
https://github.com/leonardo-ono/Assembly8086SoundBlasterDmaSingleCycleMode/blob/master/sbsc.asm - Interrupts in 8086 microprocessor
https://www.geeksforgeeks.org/interrupts-in-8086-microprocessor/ - Interrupt Structure of 8086
https://www.eeeguide.com/interrupt-structure-of-8086/ - A20 line
https://en.wikipedia.org/wiki/A20_line - Extended memory
https://en.wikipedia.org/wiki/Extended_memory#eXtended_Memory_Specification_(XMS) - Expanded memory
https://en.wikipedia.org/wiki/Expanded_memory - Protected mode
https://en.wikipedia.org/wiki/Protected_mode - Virtual 8086 mode
https://en.wikipedia.org/wiki/Virtual_8086_mode - Unreal mode
https://en.wikipedia.org/wiki/Unreal_mode - DOS memory management
https://en.wikipedia.org/wiki/DOS_memory_management - Upper memory area
https://en.wikipedia.org/wiki/Upper_memory_area - Removing the Mystery from SEGMENT : OFFSET Addressing
https://thestarman.pcministry.com/asm/debug/Segments.html - Segment descriptor
https://en.wikipedia.org/wiki/Segment_descriptor - When using a 32-bit register to address memory in the real mode, contents of the register must never exceed 0000FFFFH. Why?
https://stackoverflow.com/questions/45094696/when-using-a-32-bit-register-to-address-memory-in-the-real-mode-contents-of-the - A Brief History of Unreal Mode
https://www.os2museum.com/wp/a-brief-history-of-unreal-mode/ - Segment Limits
https://wiki.osdev.org/Segment_Limits - How do 32 bit addresses in real mode work?
https://forum.osdev.org/viewtopic.php?t=30642 - The LOADALL Instruction by Robert Collins
https://www.rcollins.org/articles/loadall/tspec_a3_doc.html - How do you put a 286 in Protected Mode?
https://retrocomputing.stackexchange.com/questions/7683/how-do-you-put-a-286-in-protected-mode - Control register
https://en.wikipedia.org/wiki/Control_register - CPU Registers x86
https://wiki.osdev.org/CPU_Registers_x86 - x86 Assembly/Protected Mode
https://en.wikibooks.org/wiki/X86_Assembly/Protected_Mode - MSW: Machine Status Word
https://web.itu.edu.tr/kesgin/mul06/intel/intel_msw.html - 80×87 Floating Point Opcodes
http://www.techhelpmanual.com/876–80×87_floating_point_opcodes.html - Page Translation
https://pdos.csail.mit.edu/6.828/2005/readings/i386/s05_02.htm - 80386 Paging and Segmenation
https://stackoverflow.com/questions/38229741/80386-paging-and-segmenation - 80386 Memory Management
https://tldp.org/LDP/khg/HyperNews/get/memory/80386mm.html - DOSEMU
http://www.dosemu.org/ - Intel 80386, a revolutionary CPU
https://www.xtof.info/intel80386.html - PAI Unit 3 Paging in 80386 Microporcessor
https://www.slideshare.net/KanchanPatil34/pai-unit-3-paging-in-80386-microporcessor - 64 Terabytes of virtual memory for 32-bit x86 using segmentation: how?
https://stackoverflow.com/questions/5444984/64-terabytes-of-virtual-memory-for-32-bit-x86-using-segmentation-how - Pi in the Pentium: reverse-engineering the constants in its floating-point unit
http://www.righto.com/2025/01/pentium-floating-point-ROM.html - Simply FPU
http://www.website.masmforum.com/tutorials/fptute/ - Art of Assembly language programming: The 80×87 Floating Point Coprocessors
https://courses.engr.illinois.edu/ece390/books/artofasm/CH14/CH14–3.html - Art of Assembly language programming: The FPU Instruction Set
https://courses.engr.illinois.edu/ece390/books/artofasm/CH14/CH14–4.html - INTEL 80387 PROGRAMMER'S REFERENCE MANUAL
http://www.ragestorm.net/downloads/387intel.txt - x86 Instruction Set Reference: FLD
http://x86.renejeschke.de/html/file_module_x86_id100.html - x86 Instruction Set Reference: FLD1/FLDL2T/FLDL2E/FLDPI/FLDLG2/FLDLN2/FLDZ
http://x86.renejeschke.de/html/file_module_x86_id101.html - X86 Assembly/Arithmetic
https://en.wikibooks.org/wiki/X86_Assembly/Arithmetic - 8087 Numeric Data Processor
https://www.eeeguide.com/8087-numeric-data-processor/ - Data Types and Instruction Set of 8087 co-processor
https://www.eeeguide.com/data-types-and-instruction-set-of-8087-co-processor/ - 8087 instruction set and examples
https://studylib.net/doc/5625221/8087-instruction-set-and-examples - GCC documentation: Extensions to the C Language Family
https://gcc.gnu.org/onlinedocs/gcc/C-Extensions.html#C-Extensions - GCC documentation: Using Vector Instructions through Built-in Functions
https://gcc.gnu.org/onlinedocs/gcc/Vector-Extensions.html - SSE (Streaming SIMD Extentions)
http://www.songho.ca/misc/sse/sse.html - Timothy A. Chagnon: SSE and SSE2
http://www.cs.drexel.edu/~tc365/mpi-wht/sse.pdf - Intel corporation: Extending the Worldr's Most Popular Processor Architecture
http://download.intel.com/technology/architecture/new-instructions-paper.pdf - SIMD architectures:
http://arstechnica.com/old/content/2000/03/simd.ars/ - Tour of the Black Holes of Computing!: Floating Point
http://www.cs.hmc.edu/~geoff/classes/hmc.cs105…/slides/class02_floats.ppt - 3Dnow! Technology Manual
AMD Inc., 2000 - Intel MMXTM Technology Overview
Intel corporation, 1996 - MultiMedia eXtensions
http://softpixel.com/~cwright/programming/simd/mmx.phpi - AMD K5 („K5“ / „5k86“)
http://www.pcguide.com/ref/cpu/fam/g5K5-c.html - Sixth Generation Processors
http://www.pcguide.com/ref/cpu/fam/g6.htm - Great Microprocessors of the Past and Present
http://www.cpushack.com/CPU/cpu1.html - Very long instruction word (Wikipedia)
http://en.wikipedia.org/wiki/Very_long_instruction_word - CPU design (Wikipedia)
http://en.wikipedia.org/wiki/CPU_design - Grafické karty a grafické akcelerátory (14)
https://www.root.cz/clanky/graficke-karty-a-graficke-akceleratory-14/ - Grafické karty a grafické akcelerátory (15)
https://www.root.cz/clanky/graficke-karty-a-graficke-akceleratory-15/ - Grafické karty a grafické akcelerátory (16)
https://www.root.cz/clanky/graficke-karty-a-graficke-akceleratory-16/ - VESA Video Modes
https://wiki.osdev.org/VESA_Video_Modes - Introduction to VESA programming
http://www.monstersoft.com/tutorial1/VESA_intro.html - Guide: VBE 2.0 graphics modes
https://delorie.com/djgpp/doc/ug/graphics/vbe20.html - NASM instruction list
https://userpages.cs.umbc.edu/chang/cs313/nasmdoc/html/nasmdocb.html - BitBlt function (wingdi.h)
https://learn.microsoft.com/en-us/windows/win32/api/wingdi/nf-wingdi-bitblt - SetDIBitsToDevice function (wingdi.h)
https://learn.microsoft.com/en-us/windows/win32/api/wingdi/nf-wingdi-setdibitstodevice - Why did line printers have 132 columns?
https://retrocomputing.stackexchange.com/questions/7838/why-did-line-printers-have-132-columns - Tabulating machine
https://en.wikipedia.org/wiki/Tabulating_machine - Why do printers print 132 columns on 14 7/8″ paper? It’s history
https://blog.adafruit.com/2019/01/22/why-do-printers-print-132-columns-on-14–7–8-paper-its-history-vintagecomputing-kenshirriff-ibm/ - IBM 1403 (Wikipedia)
https://en.wikipedia.org/wiki/IBM_1403

























