Obsah
1. Mikrořadiče a DSP společnosti Infineon
2. Osmibitové mikrořadiče založené na 8051
4. Moduly mikrořadičů řady XC800
7. Multiplication/Division Unit (MDU)
8. Field Oriented Control (FOC)
9. Algoritmus CORDIC (COrdinate Rotation DIgital Computer)
10. Princip CORDICu: rotace vektoru r okolo počátku souřadného systému
11. Úprava vztahu rotace vektoru pro algoritmus CORDIC
12. Hodnoty úhlů, po kterých se provádí rotace
13. Ukázka: výpočet funkcí sin a cos algoritmem CORDIC
14. CORDIC a formát pevné řádové čárky
1. Mikrořadiče a DSP společnosti Infineon
Dalším výrobcem (nejenom) digitálních signálových procesorů je německá společnost Infineon, která se zaměřuje na čipy určené pro automobilový průmysl a taktéž pro různé řídicí systémy v průmyslu (průmyslová automatizace, diagnostika atd.). Spektrum čipů, které Infineon vyráběl či vyrábí, je poměrně široké: od osmibitových mikrořadičů (například řady C505, nověji XC800) založených na dnes již pravěké, ale stále používané architektuře 8051 přes čipy s některým ARMovským mikrořadičovým jádrem Cortex-M (řada XMC1000 používá Cortex-M0 a řada XMC4000 Cortex-M4) až po 32bitové čipy s architekturou TriCore, v nichž se kombinují možnosti RISCových procesorů, digitálních signálových procesorů a mikrořadičů. Vzhledem k tomu, pro jaké typy aplikací jsou čipy společnosti Infineon určeny, asi nepřekvapí, že jsou v naprosté většině případů vybaveny rozhraním pro sběrnici CAN (CAN Bus) popř. jednodušší sběrnice LIN a u mnoha mikrořadičů nalezneme i pomocné „koprocesory“ určené například pro řízení elektrických motorů apod.

Obrázek 1: Dobový vývojový kit s původním mikrořadičem Intel 8051 (MCS-51).
2. Osmibitové mikrořadiče založené na 8051
Některé významné čipy Infineon si v tomto seriálu postupně popíšeme. Začneme přitom těmi nejméně výkonnými osmibitovými mikrořadiči, které jsou postaveny na architektuře 8051. Aby byly tyto mikrořadiče použitelné i pro řídicí účely, jsou vybaveny pomocnými moduly, typicky samostatnou násobičkou a děličkou, modulem pro algoritmus CORDIC atd. (s velkou pravděpodobností tyto moduly zabírají větší plochu čipu, než samotné jádro 8051). Díky přidání pomocných modulů a taktéž navýšením kapacity pamětí pro programový kód a data je možné čipy s jádrem 8051 nasadit i v těch oblastech, kde by jinak byl vyžadován výkonnější mikrořadič, ať již osmibitový (H8, S08), šestnáctibitový (H8–300H, MSP430) či 32bitový (Cortex-M0, Cortex-M3, Cortex-M4, Cortex-M7, SuperH).

Obrázek 2: Připojení LCD s rozlišením 128×64 pixelů k mikrořadiči 8051.
Již na tomto místě si však musíme říct, že největší nevýhody 8051 vlastně vůbec nebyly odstraněny, což se týká jak omezeného adresního prostoru, tak i malého množství pracovních registrů (jedná se akumulátorovou architekturu, takže často musí docházet k přesunům dat, i když se další výrobci klonů 8051 snažili rozšířit instrukční soubor a toto omezení obejít), nízké kapacity zásobníku a jen velmi jednoduchých adresovacích režimů (zejména se to týká použití šestnáctibitových adres, kde lze použít jediný adresní registr). To vše se negativně projevuje především při programování v céčku či v dalších vyšších programovacích jazycích.

Obrázek 3: „Zbastlený“ video výstup založený na přímém programovém ovládání tří signálů – LUMINANCE (světlost), BLANK (interval v němž je obraz zatemněný – okraje a návrat paprsku) a SYNC (synchronizační impuls) mikrořadičem 8051 (resp. přesněji řečeno jeho rychlejší variantou). Všechny tři signály jsou pomocí čtveřice rezistorů smíchány a tvoří tak vstup (kompozitní video bez barvonosné složky) pro televizor pracující v normě PAL, SECAM či NTSC.
3. Řada XC800, rodina A a I
Mezi mikrořadiče s jádry založenými na 8051 patří především řada čipů nazvaná XC800. Tyto čipy jsou rozděleny do dvou velkých rodin: XC800 A-Family a XC800 I-Family. A-Family obsahuje mikrořadiče určené pro automobilový průmysl (A značí automotive), zatímco do I-Family patří čipy pro průmyslovou automatizaci (I značí industry). Jak jsme si již řekli v předchozí kapitole, jsou tyto mikrořadiče postaveny na jádru 8051, které ovšem bylo vylepšeno a při shodné hodinové frekvenci by bylo šestkrát výkonnější, než původní Intel 8051 (ve skutečnosti však čipy Infineon používají vyšší hodinové frekvence, typicky 24 až 27 MHz podle konkrétního typu čipu). Okolo vylepšeného jádra 8051 byly přidány další moduly, které na původních mikrořadičích Intel 8051 a Intel 8052 nenajdeme. Typicky se jedná o sériové sběrnice a porty SPI, I2C, většinou i CAN Bus (Controller Area Network) a/nebo poněkud jednodušší a levnější LIN (Local Interconnect Network). Dále většina čipů řady XC800 obsahuje i vícekanálový A/D převodník s rozlišením deseti bitů, větší kapacitu RAM i ROM a možnost použít paměť Flash jak pro program, tak i pro data (viz navazující kapitoly). Nesmíme zapomenout ani na „koprocesory“, jejichž popisu je věnována druhá polovina dnešního článku.
Čipy XC800 mohou být na jedné straně připojeny ke sběrnici CAN, na straně druhé pak mohou přímo ovládat k nim připojená zařízení, a to přes SPI, SSI, I2C a paralelní porty, číst stav čidel (jak digitálních, tak i analogových) apod.
4. Moduly mikrořadičů řady XC800
Na následujícím obrázku jsou zobrazeny všechny základní moduly mikrořadičů XC800 postavené okolo mikroprocesorového jádra založeného na 8051. Moduly jsou rozděleny podle své funkce, nikoli podle toho, jakým způsobem jsou interně zapojeny (interně čip obsahuje několik sběrnic atd.). Povšimněte si mnohých rozšíření oproti „klasickým“ starodávným mikrořadičům 8051. Nalezneme zde více bloků paměti (navíc s mnohem vyšší kapacitou), větší množství časovačů včetně šestnáctibitového watchdogu, sériové sběrnice a porty, A/D převodníky, dva paralelní porty navíc a taktéž koprocesory nazvané MDU a CORDIC:

Obrázek 4: Základní moduly mikrořadičů XC800.
Význam některých použitých zkratek:
- BootROM jediná skutečná ROM s uloženým programovým kódem pro inicializaci MCU, spuštění ladění atd. Zbylá část programu je uložena v paměti Flash. Typická velikost BootROM je 8KB.
- Flash je význačná tím, že se v ní používají ECC umožňující opravit jednobitovou chybu v každém bajtu a odhalit dva chybné bity. Typická kapacita dosahuje 52 až 64 KB.
- XRAM je běžný blok paměti RAM, která může být adresovaná buď jako programová paměť nebo jako externí datová paměť. Jedná se o jediný blok paměti, který je však dostupný jak přes instrukci MOVX, tak i instrukcí MOVC. Původní význam zkratky XRAM je External RAM, zde se však jedná o RAM umístěnou přímo na mikrořadiči.
- UART klasický sériový port s asynchronním přenosem dat a konfigurovatelným počtem datových bitů, délky stop bitu, výpočtu parity atd.
- SSP (Synchronous Serial Port) řadič podporující sběrnici SPI i sériové rozhraní SSI.
- SPI (Serial Peripheral Interface) standardní sériová sběrnice.
- SSI (Synchronous Serial Interface) jednodušší sériové rozhraní pro jednosměrný přenos dat.
- CAN (Controller Area Network) je průmyslová sběrnice často používaná v automotive i v průmyslových aplikacích.
- MDU (Multiplication/Division Unit) je koprocesor, který bude popsán v sedmé kapitole.
- CORDIC (COrdinate Rotation DIgital Computer) je koprocesor, který bude popsán v deváté kapitole.
5. Vylepšené jádro 8051
Vylepšené jádro použité v mikrořadičích XC800, které je označováno názvem „E-warp“, zachovává kompatibilitu s původními čipy Intel 8051/Intel 8052 jak na binární úrovni, tak i na úrovni zdrojových kódů. Došlo ovšem k vylepšení interní struktury, takže běžné instrukce se namísto dvanácti cyklů provedou jen ve dvou cyklech (šestinásobné urychlení při použití stejné hodinové frekvence). Existují ovšem i delší instrukce, konkrétně instrukce provedené za čtyři cykly (INC DPTR protože chybí 16bitová ALU) o dokonce i za osm cyklů (MUL AB a DIV AB, mimochodem tyto instrukce na původním 8051 trvaly 48 cyklů, takže se stále jedná o šestinásobné urychlení). Nová a tím pádem i zpětně nekompatibilní instrukce existuje jen jedna: MOVC @(DPTR++), A, která je mapována na kód 0×A5, který původně nebyl použit (v tabulce umístěné pod tímto odstavcem je tento kód reprezentován prázdnou červenou buňkou).
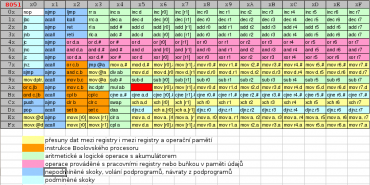
Obrázek 5: Instrukční sada mikrořadiče MCS-51.
U mikrořadičů 8051 se velké množství operací provádí s osmibitovým akumulátorem A, jedním z pracovních registrů R0 až R7, popř. s buňkou paměti adresovanou registrem R0 či R1. Navíc je však možné mnoho operací provádět přímo s paměťovými buňkami v interní paměti údajů nebo s registry speciálních funkcí (SFR); existuje například instrukce typu MOV adresa, #osmibitová_data, kterou lze naplnit libovolnou buňku interní RAM (ležící na adresách 0×00 až 0×7f) popř. SFR.
Kvůli tomu, že rozsah takzvané „externí paměti“ RAM může v případě původního 8051 nabývat až kapacity 64 kB, je množina pracovních registrů doplněna o šestnáctibitový registr DPTR (Data Pointer), do něhož lze přímo načíst šestnáctibitovou konstantu instrukcí MOV DPTR, #šestnáctibitová_data, popř. zvýšit jeho hodnotu o jedničku pomocí instrukce INC DPTR, což je užitečné například při procházení polem.
6. Paměťový subsystém
Paměťový subsystém čipů XC800 je poměrně složitý, což vyplývá z omezení samotné architektury 8051. Relativní složitost uspořádání pamětí a adresovacích režimů vynikne zejména při porovnání s některými dalšími (novějšími) osmibitovými mikrořadiči, například s čipy H8. Původní mikrořadiče 8051 totiž obsahovaly interní paměť údajů o kapacitě pouhých 128 bajtů (v případě modelu 8052 dokonce „celých“ 256 bajtů), ke které byla navíc připojena paměťová oblast o velikosti taktéž 128 bajtů, do níž byly mapovány registry speciálních funkcí (SFR). Prvních 128 bajtů RAM je dostupných přímo; z pohledu programátora se jedná o adresy 0×00 až 0×7f.
Do adresového rozsahu 0×80 až 0×ff, tj. do 128 bajtů ležících za pamětí údajů, je namapována oblast takzvaných registrů speciálních funkcí neboli SFR (Special Function Registers). Jedná se o registry, pomocí nichž se konfigurují různé moduly mikrořadiče Intel 8051, například čítače/časovače, sériový port a paralelní porty, nebo jsou v nich naopak uloženy různé příznaky a data naplňovaná samotným mikrořadičem, zejména příznak přetečení čítače/časovače, znak přijatý sériovým portem, stav jednotlivých přerušení atd. Mezi registry speciálních funkcí patří i samotný akumulátor A/ACC uložený na adrese 0×e0, pomocný registr B na adrese 0×f0, který je používán při násobení a dělení, stavové slovo programu PSW či ukazatel na vrchol zásobníku SP. Některé registry speciálních funkcí jsou dostupné pouze jako celistvé bajty, tj. jejich obsah lze načíst například instrukcí mov A,direct, ovšem několik těchto registrů lze alternativně adresovat i po jednotlivých bitech, podobně jako oblast 128 bitů (16 bajtů) v paměti údajů (tyto registry jsou součástí Boolovského procesoru).
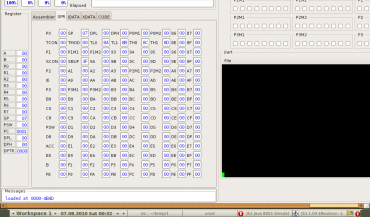
Obrázek 6: Obsah speciálních funkčních registrů zobrazený v emulátoru J51.
Přístup k paměti údajů (tj. ke 128 bajtům na adresách 0×00 až 0×7f) i k registrům speciálních funkcí (128 bajtů na adresách 0×80 až 0×ff) je jednoznačný v případě mikrořadiče Intel 8051, ovšem u mikrořadiče Intel 8052 museli jeho konstruktéři vyřešit, jakým způsobem bude adresování probíhat ve chvíli, kdy má paměť údajů kapacitu 256 bajtů namísto 128 bajtů, a adresy v instrukčních slovech mají pouze osmibitovou délku. Řešení tohoto problému spočívá v tom, že horních 128 bajtů paměti údajů je dostupných pouze při nepřímé adresaci (tj. použití instrukcí s operandy @R0 a @R1), zatímco dolních 128 bajtů paměti údajů a 128 bajtů se SFR je dostupných při adresaci přímé.
Situace se dále komplikuje v případě, že je k interní paměti údajů navíc připojena paměť externí, musí se použít plná šestnáctibitová adresa, která je uložená v šestnáctibitovém registru DPTR (Data Pointer), popř. osmibitová adresa uložená v registru R0 či R1, ovšem horních osm bitů adresy musí být při provedení instrukce „vystaveno“ na portu číslo 2.
Poznámka: „externí paměť“ je sice stále používaný termín, ovšem na XC800 je i tato paměť umístěna na stejném čipu.
Programová paměť je z tohoto hlediska jednodušší, protože se může jednat o jediný blok o velikosti 64 kB (původně jen 4 kB).
Konstruktéři čipů XC800 museli tyto vlastnosti původních mikrořadičů 8051 a 8052 brát v úvahu aby dodrželi zpětnou kompatibilitu. Proto navrhli systém paměťových banků, který vlastně známe i z mnoha dalších typů mikroprocesorů. Čipy XC800 totiž adresují až 1 MB paměti, která je rozdělena do banků o velikosti 64 kB (takových banků je šestnáct). Banky se používají jak pro programovou paměť, tak i pro paměť datovou. O přepínání banků se stará modul MMU neboli Memory Management Unit, který obsahuje trojici čtyřbitových registrů: CB (Current Bank), NB (Next Bank) a IB (Interrupt Bank).
Navíc se musí dodržet zpětná kompatibilita při přechodu mezi paměťovými banky, což znamená, že relativní skoky nikdy bank nemění (pro tyto skoky paměť stále končí na hranici 64 kB; chudáci programátoři překladačů). Jediné instrukce, které bank mohou přepnout, jsou instrukce LJMP, LCALL a ACALL, u datové paměti je přepnutí vždy explicitní. Navíc došlo k další změně – zásobník o velikosti 128 bajtů může být umístěn kdekoli v paměťovém rozsahu 1 MB, není tedy nutné, aby zabíral cenné bajty v prvních dvou oblastech RAM (to sice není zpětně kompatibilní chování, ale v případě potřeby lze zajistit původní umístění zásobníku).
O bloku XRAM jsme se již zmínili – ta je namapována do datového prostoru v banku 2 a v programovém prostoru v posledním šestnáctém banku. Lze ji tedy zpřístupnit jak instrukcí MOVX (přes DPTR či R0 R1) tak i MOVC.
7. Multiplication/Division Unit (MDU)
Vzhledem k tomu, že instrukce MUL AB akceptuje osmibitové operandy se šestnáctibitovým výsledkem a instrukce DIV AB počítá jen osmibitové výsledky, jsou čipy XC800 doplněny o samostatně pracující koprocesor nazvaný MDU neboli Multiplication/Division Unit. Tento obvod tvoří násobička a dělička pracující nezávisle na CPU, která je doplněna o sadu dvanácti datových registrů, jednoho řídicího registru a jednoho registru stavového (všechny registry jsou samozřejmě osmibitové). Kromě operací násobení a dělení dokáže MDU provést i bitové posuny doleva a doprava a taktéž operaci „normalizace“ vstupní hodnoty tak, aby nejvyšší bit byl vždy jedničkový. Tato operace vrací i počet provedených posunů, takže ji lze využít například při softwarové implementaci FP operací.
MDU podporuje tyto operace:
| Operace | Typ | Operand 1 | Operand 2 | Výsledek | Zbytek | Počet hodinových cyklů |
|---|---|---|---|---|---|---|
| Násobení | signed | 16bit | 16bit | 32bit | × | 16 |
| Dělení | signed | 32bit | 16bit | 32bit | 16bit | 33 |
| Dělení | signed | 16bit | 16bit | 16bit | 16bit | 17 |
| Násobení | unsigned | 16bit | 16bit | 32bit | × | 16 |
| Dělení | unsigned | 32bit | 16bit | 32bit | 16bit | 32 |
| Dělení | unsigned | 16bit | 16bit | 16bit | 16bit | 16 |
| Normalizace | × | × | × | × | × | 1–32 |
| Posun L/R | × | × | × | × | × | 1–32 |
Tento modul obsahuje následující registry:
| Registr | Význam |
|---|---|
| MDUSTAT | stavový registru modulu |
| MDUCON | řídicí registr, obsahuje mj. i kód prováděné operace a příznak, že se operace provádí (nuluje se automaticky) |
| MD0 | registr pro vstupní operand |
| MR0 | registr pro uložení výsledku |
| MD1 | -//- |
| MR1 | -//- |
| MD2 | -//- |
| MR2 | -//- |
| MD3 | -//- |
| MR3 | -//- |
| MD4 | -//- |
| MR4 | -//- |
| MD5 | -//- |
| MR5 | -//- |
Příklady použití těchto registrů:
násobení 16bit × 16bit → 32bit: MD1:MD0 × MD5:MD4 → MR3:MR2:MR1:MR0 dělení: 32bit ÷ 16bit → 16bit (+zbytek): MD3:MD2:MD1:MD0 ÷ MD5:MD5 → MR5:MR4 zbytek MR3:MR0
Poznámka: MDU lze zcela vypnout a snížit tak spotřebu celého čipu.
8. Field Oriented Control (FOC)
Důležitou součástí většiny mikrořadičů řady XC800 je modul nazvaný FOC neboli (Sensorless) Field Oriented Control*. Tento modul je, jak již jeho název napovídá, určený pro přesné řízení synchronních elektrických motorů (či mnohdy spíše motorků) s permanentními magnety v rotoru (PMSM – Permanent Magnet Synchronous Motor). Na rozdíl od krokových motorků vyžadují PMSM pro přesné řízení bez vzniku vibrací a zbytečně velkého namáhání hřídele vytvoření točivého magnetického pole ideálně se sinusovým průběhem. A právě pro vytvoření trojice analogových signálů se sinusovým průběhem a vzájemným fázovým posunem 120°, které navíc reaguje na zatížení atd. je určen FOC. Interní struktura tohoto modulu je poměrně složitá, ovšem nám postačuje vědět, že na vstupu je zapotřebí specifikovat referenční rychlost a na výstupu modulu FOC se analogové signály generují s využitím PWM (pulsně-šířkové modulace). Modul navíc musí zjišťovat aktuální polohu rotoru měřením proudu protékajícího statorem, takže obsahuje rychlý A/D převodník zapojený na výstup operačního zesilovače.
9. Algoritmus CORDIC (COrdinate Rotation DIgital Computer)
Velmi zajímavé je zařazení koprocesoru s implementovaným algoritmem CORDIC (COrdinate Rotation DIgital Computer). I zde se ukazuje, že autoři mikrořadičů XC800 zvolili řešení založené na relativně primitivním jádře 8051 vybaveném specializovanými moduly oproti obecnému rychlejšímu jádru, které by výpočty řešilo programově. Vraťme se však k CORDICu.
Jedná se o výpočetní metodu využívající iteraci, kterou pro účely jednoduchého a rychlého výpočtu goniometrických funkcí bez použití násobiček a děliček navrhl a zpopularizoval Jack Volder už v polovině minulého století. Později se ukázalo, že tuto metodu je možné po malých úpravách použít i pro výpočty dalších matematických funkcí, například arkustangenty, arkussinu, arkuskosinu, ale i pro vyčíslení délky vektoru či jeho rychlou rotaci o libovolný úhel; včetně transformace bodu či vektoru z polárních souřadnic do souřadnic kartézských. Již větší úpravy si vyžádala aplikace metody CORDIC pro výpočet hyperbolických funkcí (sinh(), cosh(), tanh()) a funkcí logaritmických, základní myšlenka a princip práce však zůstává stejný.
Vzhledem k tomu, že se při aplikaci algoritmu CORDIC využívají pouze ty nejzákladnější matematické operace (bitový posun doleva a doprava, sečítání, odečítání a porovnání dvou hodnot), je možné CORDIC využít ve všech číslicových systémech, ve kterých je zapotřebí šetřit použitými prostředky, tj. počtem logických hradel, kapacitou obsazené paměti, možnostmi použitých čipů atd. CORDIC tak byl implementován a s úspěchem používán například v kalkulačkách, osmibitových mikrořadičích (řada Intel 8051 a Motorola 68HC11), osmibitových domácích počítačích (Atari, Sinclair ZX Spectrum atd.) a mnoha specializovaných obvodech vytvořených pomocí programovatelných polí FPGA. Zajímavá je implementace CORDICu na mikrořadičové stavebnici Basic STAMP. V největší míře však bylo CORDICu využito v některých matematických koprocesorech (FPU), protože bylo zjištěno, že některé funkční bloky zabezpečující chod CORDICu zůstávají stále stejné, bez ohledu na to, jaká funkce je počítána, což do značné míry zjednodušilo (a tím pádem i zlevnilo) výrobu FPU. Samozřejmě se také snížil počet hradel nutných pro implementaci goniometrických, hyperbolických a logaritmických funkcí.
- Andraka, Ray: „A survey of CORDIC algorithms for FPGA based computers“,
ACM, 1998 - Despain, A.M.:„Fourier Transform Computations Using CORDIC Iterations“,
IEEE Transactions on Computers, Volume 23, strany 993–1001, 1974 - Mazenc C., Merrheim, X., Muller, J.M.: „Computing Functions Arccos and Arcsin Using CORDIC“,
IEEE Transactions on Computers, Volume 42, strany 118–122, 1993 - Volder, Jack: „Binary computation algorithms for coordinate rotation and function generation“,
Convair Report IAR-1, 1956 - Volder, Jack: „The CORDIC Trigonometric Computing Technique“,
IRE Transactions on Electronic Computing, Vol EC-8, strany 330–334, 1959 - NVIDIA Corporation: „Floating-Point Specials on the GPU“,
2005
10. Princip CORDICu: rotace vektoru r okolo počátku souřadného systému
Princip práce algoritmu CORDIC vychází z vyjádření rotace vektoru o určitý úhel δ a z následné úpravy vzorce pro rotaci tak, aby se eliminovaly zbytečně složité a časově náročné multiplikativní operace. Nejprve si napišme vzorce pro hodnoty funkcí sinus a kosinus součtu dvou úhlů. Jedná se o známé středoškolské vztahy používané pro úpravu výrazů s goniometrickými funkcemi:
sin(α+β)=sin α cos β + cos α sin β
cos(α+β)=cos α cos β – sin α sin β
Jak si ukážeme o několik odstavců níže, je možné tyto vzorečky použít pro vyjádření rotace vektoru. Vektor r, kterým budeme rotovat, může být vyjádřen souřadnicemi [x0, y0], přičemž je možné provést převod z kartézských souřadnic do souřadnic polárních:
x0=r cos φ
y0=r sin φ
kde r představuje délku vektoru r a φ je úhel vektoru měřený od kladné horizontální poloosy souřadného systému. Pokud bude vektor r rotován o úhel δ, změní se koncový bod vektoru tak, že bude ležet na kružnici o stejném poloměru r, ale úhel vektoru (opět měřený od kladné horizontální poloosy) se zvětší o δ. Tuto skutečnost je možné vyjádřit vztahy:
xr=r cos (φ+δ)
yr=r sin (φ+δ)
Dále je možné rozepsat výrazy cos (φ+δ) a sin (φ+δ) podle prvních dvou uvedených vzorečků a následně zpětně dosadit za výrazy r cos φ a r sin φ původní souřadnice vektoru r, tj. x0 a y0:
xr=r (cos φ cos δ – sin φ sin δ)=x0 cos δ – y0 sin δ
yr=r (sin φ cos δ + cos φ sin δ)=x0 sin δ + y0 cos δ
Všimněte si, že se ve výsledných vztazích nevyskytuje ani hodnota r ani úhel původního vektoru φ. To znamená, že převod na polární souřadnice pro nás byl pouze matematickou pomůckou při odvozování vzorce pro rotaci a ve skutečnosti se nebude nikdy provádět.
11. Úprava vztahu rotace vektoru pro algoritmus CORDIC
Pro účely algoritmu CORDIC se tento vztah dále upravuje. První úprava spočívá v tom, že se obě rovnice vydělí hodnotou cos δ, takže dostaneme vztahy:
xr /cos δ=x0 – y0 sin δ/cos δ
yr /cos δ=x0 sin δ/cos δ + y0
Pokud si uvědomíme skutečnost, že sin δ/cos δ=tan δ, můžeme pokračovat v úpravách:
xr /cos δ=x0 – y0 tan δ
yr /cos δ=y0 + x0 tan δ
a následně:
xr=cos δ(x0 – y0 tan δ)
yr=cos δ(y0 + x0 tan δ)
Nyní přichází základní myšlenka, na které je CORDIC postaven. Pokud budeme volit úhel δ takovým způsobem, aby jeho tangenta nabývala hodnot 2-i (pro i>0), je možné tangentu ve vzorci nahradit násobením zvolenou hodnotou 2-i; v tomto případě je však možné násobení nahradit jednoduchým a přitom rychlým bitovým posunem. Omezení hodnoty tangenty na zvolenou sadu hodnot však znamená, že se vektor nemůže rotovat o libovolný úhel, ale pouze o úhel odpovídající tangentě z dané sady. To však není problém, protože rotaci o libovolný je možné zapsat pomocí série rotací (doprava či doleva), například:
δ=δ1+δ2-δ3+…
Naproti tomu, že se parciální rotace mohou provádět v obou směrech (tj. jak doprava, tak i doleva), můžeme místo hodnoty cos δ dosadit konstantu Ki, protože platí cos δ=cos -δ. Nakonec místo tan δ přímo dosadíme mocninu dvojky 2-i a pomocí parametru di směr rotace (parametr di nabývá pouze hodnot +1 a –1):
xr=Ki (x0 – y0 di 2-i)
yr=Ki (y0 + x0 di 2-i)
Zbývá nám zjistit hodnotu konstanty Ki. Platí:
Ki=cos (arctan 2-i)=1/(1+2-2i)1/2
Limitně se součin hodnot Ki (po nekonečně mnoha iteracích) blíží k 0,6073, to znamená, že touto hodnotou bude v některých případech nutné vydělit výsledek (v jiných případech nám naopak toto zesílení při rotaci vadit nebude).
Veškerá práce algoritmu CORDIC spočívá v tom, že se nastaví počáteční souřadnice vektoru r a iterativně se provádí rotace o předem známé úhly δ1…δn tak, aby se dosáhlo požadované hodnoty rotace δ.
12. Hodnoty úhlů, po kterých se provádí rotace
Jak jsme si uvedli v předchozí kapitole, musí tangenty úhlů použitých v CORDICu splňovat podmínku tan δ=2-i. Pokud budeme veškeré výpočty provádět v prvním kvadrantu (ve skutečnosti však může počítat i ve čtvrtém kvadrantu), začíná se s úhlem 45°, tj. π/4, protože tan π/4=1. Další úhly jsou samozřejmě menší; o jaké hodnoty se konkrétně jedná, nám dá přehled následující tabulka:
| i | 21-i | úhel δ |
|---|---|---|
| 1 | 1.0000000000 | 45.000000000 |
| 2 | 0.5000000000 | 26.565051177 |
| 3 | 0.2500000000 | 14.036243468 |
| 4 | 0.1250000000 | 7.125016349 |
| 5 | 0.0625000000 | 3.576334375 |
| 6 | 0.0312500000 | 1.789910608 |
| 7 | 0.0156250000 | 0.895173710 |
| 8 | 0.0078125000 | 0.447614171 |
| 9 | 0.0039062500 | 0.223810500 |
| 10 | 0.0019531250 | 0.111905677 |
13. Ukázka: výpočet funkcí sin a cos algoritmem CORDIC
Nyní si na jednoduchém příkladu ukážeme, jakým způsobem je možné algoritmus CORDIC použít pro výpočet funkcí sinus a kosinus. Nejprve jsou spočteny tabulky úhlů a hodnota druhých záporných mocnin hodnoty 2. Při implementaci CORDICu na FPU, MCU či FPGA by se tyto tabulky samozřejmě znovu nevytvářely: tabulka úhlů by byla uložena v paměti (či masce obvodu) a tabulka mocnin hodnoty 2 by se implementovala pomocí bitových posunů.
Po vytvoření tabulek je již možné CORDIC spustit. Počáteční souřadnice vektoru r jsou nastaveny na hodnotu [1, 0]. Vektor je posléze v iterační smyčce rotován tak dlouho, dokud neproběhne daný počet iterací. Úhel vektoru r se přitom neustále přibližuje k zadanému úhlu δ, jelikož se v iterační smyčce adaptivně zadaný úhel buď zmenšuje či zvětšuje o hodnotu uloženou v tabulce atans[]. Výsledek, tj. hodnoty funkcí sinus a kosinus, je uložen v nových souřadnicích vektoru r (vynásobený o konstantu K) a to z toho důvodu, že vektor rotoval na jednotkové kružnici a souřadnice jakéhokoli bodu ležícího na jednotkové kružnici přímo odpovídají hodnotám sinu a kosinu úhlu tohoto bodu počítaného od kladné horizontální poloosy.
// --------------------------------------------------------
// Výpočet hodnot funkcí sin() a cos() pomocí iteračního
// algoritmu CORDIC.
// --------------------------------------------------------
#include <stdio.h>
#include <math.h>
#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif
// maximální počet iterací při běhu algoritmu
#define MAX_ITER 10
// "zesílení" při rotacích
#define K 0.6073
// tabulka arkustangentu úhlů
double atans[MAX_ITER];
// tabulka záporných celočíselných mocnin hodnoty 2
double pows[MAX_ITER];
// naplnění tabulek atans[] a pows[]
void createTables(void)
{
int i;
for (i=0; i<MAX_ITER; i++) {
double p=pow(2.0, -i);
atans[i]=atan(p);
pows[i]=p;
}
}
// výpočet funkcí sin() a cos() pro zadaný úhel delta
void sincos(double delta, double *sinval, double *cosval)
{
int i;
double x0=1.0; // nastavení počátečních podmínek
double y0=0.0;
double xn;
for (i=0; i<MAX_ITER; i++) { // iterační smyčka
if (delta<0) { // úhel je záporný => rotace doleva
xn=x0+y0*pows[i];
y0-=x0*pows[i];
delta+=atans[i];
}
else { // úhel je kladný => rotace doprava
xn=x0-y0*pows[i];
y0+=x0*pows[i];
delta-=atans[i];
}
x0=xn;
}
*sinval=y0*K; // opravit "zesílení" výsledku
*cosval=x0*K;
}
int main(void)
{
int i;
createTables();
for (i=0; i<=90; i++) { // výpočetní smyčka
double delta; // úhel, ze kterého se počítá sin a cos
double sinval; // vypočtené hodnoty
double cosval;
double sinerr; // absolutní chyby
double coserr;
delta=i*M_PI/180.0; // převod úhlu na radiány
sincos(delta, &sinval, &cosval); // výpočet sinu a kosinu
sinerr=fabs(sinval-sin(delta)); // výpočet absolutních chyb
coserr=fabs(cosval-cos(delta));
// tisk výsledků
printf("%02d\t%12.10f\t%12.10f\t%12.10f\t%12.10f\t%8.3f%%\t%8.3f%%\n",
i,
sinval, cosval,
sinerr, coserr,
100.0*sinerr/sinval, 100.0*coserr/cosval);
}
return 0;
}
// finito
Výsledek běhu předchozího programu je zobrazen v následující tabulce. Kromě vypočtených hodnot sinů a kosinů zadaného úhlu je spočtena i absolutní a relativní chyba, přičemž je zapotřebí upozornit na to, že relativní chyba pro obě krajní hodnoty (ty by měly vyjít nulové) je poněkud zavádějící. V každém případě však výsledky běhu algoritmu pro deset iterací nejsou špatné, zvláště když si uvědomíme, že se v každé iteraci provádělo pouze několik základních operací, konkrétně dva bitové posuvy a tři součty (či rozdíly):
-------------------------------------------------------------------------------------------------- vstupní vypočtená vypočtená sin cos sin cos úhel hodnota sin() hodnota cos() absolutní chyba absolutní chyba rel.chyba rel.chyba -------------------------------------------------------------------------------------------------- 00 0.0011726802 1.0000761814 0.0011726802 0.0000761814 100.000% 0.008% 01 0.0167806202 0.9999360752 0.0006717863 0.0000883801 4.003% 0.009% 02 0.0363058568 0.9994176447 0.0014063601 0.0000268177 3.874% 0.003% 03 0.0519144682 0.9987285075 0.0004214880 0.0000989728 0.812% 0.010% 04 0.0714093909 0.9975241564 0.0016529171 0.0000398938 2.315% 0.004% 05 0.0858859660 0.9963821278 0.0012697767 0.0001874297 1.478% 0.019% 06 0.1053286152 0.9945147694 0.0008001519 0.0000071260 0.760% 0.001% 07 0.1208522102 0.9927479474 0.0010171332 0.0002017957 0.842% 0.020% 08 0.1401999641 0.9902008452 0.0010268631 0.0000672235 0.732% 0.007% 09 0.1556537948 0.9878894877 0.0007806702 0.0002011471 0.502% 0.020% ... 40 0.6418729918 0.7669112114 0.0009146178 0.0008667682 0.142% 0.113% 41 0.6567280845 0.7542293861 0.0006690555 0.0004801942 0.102% 0.064% 42 0.6684306187 0.7438778473 0.0006999876 0.0007330218 0.105% 0.099% 43 0.6828308344 0.7306817333 0.0008324743 0.0006719683 0.122% 0.092% 44 0.6941513412 0.7199358716 0.0005070292 0.0005960713 0.073% 0.083% 45 0.7062435465 0.7080775359 0.0008632347 0.0009707547 0.122% 0.137% 46 0.7199358716 0.6941513412 0.0005960713 0.0005070292 0.083% 0.073% 47 0.7306817333 0.6828308344 0.0006719683 0.0008324743 0.092% 0.122% 48 0.7438778473 0.6684306187 0.0007330218 0.0006999876 0.099% 0.105% 49 0.7542293861 0.6567280845 0.0004801942 0.0006690555 0.064% 0.102% 50 0.7669112114 0.6418729918 0.0008667682 0.0009146178 0.113% 0.142% ... 81 0.9878894877 0.1556537948 0.0002011471 0.0007806702 0.020% 0.502% 82 0.9902008452 0.1401999641 0.0000672235 0.0010268631 0.007% 0.732% 83 0.9927479474 0.1208522102 0.0002017957 0.0010171332 0.020% 0.842% 84 0.9945147694 0.1053286152 0.0000071260 0.0008001519 0.001% 0.760% 85 0.9963821278 0.0858859660 0.0001874297 0.0012697767 0.019% 1.478% 86 0.9975241564 0.0714093909 0.0000398938 0.0016529171 0.004% 2.315% 87 0.9987285075 0.0519144682 0.0000989728 0.0004214880 0.010% 0.812% 88 0.9994176447 0.0363058568 0.0000268177 0.0014063601 0.003% 3.874% 89 0.9999360752 0.0167806202 0.0000883801 0.0006717863 0.009% 4.003% 90 1.0000761814 0.0011726802 0.0000761814 0.0011726802 0.008% 100.000%
14. CORDIC a formát pevné řádové čárky
Ve skutečnosti se CORDIC prakticky vždy implementuje takovým způsobem, že se nepoužívají hodnoty typu double, ale formát s pevnou řádovou čárkou. Násobení hodnotami z tabulky pows se nahradí bitovým posunem, takže se v iterační smyčce používají jen základní operace: součet, rozdíl a bitové posuny, zhruba takto:
/* datový typ, se kterým budeme pracovat */
typedef signed int fx;
/* výpočet funkce sin() pro zadaný úhel delta */
fx fx_sin_cordic_optim_iter(fx delta, int iter)
{
int i;
static fx K_fx=(fx)(K_float*(2<<(B-1)));
/* nastavení počátečních podmínek */
fx x0=int2fx(1);
fx y0=0;
fx xn;
for (i=0; i<iter; i++) { /* iterační smyčka */
if (delta<0) { /* úhel je záporný => rotace doleva */
xn=x0 + y0>>i; /* místo násobení bitový posuv */
y0-=x0>>i;
delta+=atans[i];
}
else { /* úhel je kladný => rotace doprava */
xn=x0 - y0>>i;
y0+=x0>>i;
delta-=atans[i];
}
x0=xn;
}
return fx_mul(y0, K_fx); /* opravit "zesílení" výsledku */
}
Podobným způsobem je CORDIC implementován v koprocesoru mikrořadiče XC800.
15. CORDIC na čipech XC800
Mikrořadiče XC800 obsahují koprocesor pro výpočet hodnot různých funkcí s využitím algoritmu CORDIC, který je zde parametrizovatelný a umožňuje používat nejenom předpočítané hodnoty funkce atan (rotace tak, jak je chápána v Euklidovské geometrii), ale atanh (rotace v hyperbolické geometrii) a lineární funkci (ta se hodí při násobeních a děleních). Počet iterací při výpočtu dosahuje šestnácti kroků, což je pro většinu použití plně dostačuje, a to jak z hlediska přesnosti výsledku, tak i doby trvání výpočtu. Navíc je možné zvolit rychlost výpočtů – buď se použije původní hodinový signál či signál vynásobený dvěma (pravděpodobně se provede synchronizace na obě hrany signálu). Při použití dvojnásobné rychlosti výpočtu a šestnácti iterací je výpočet dokončen v přibližně 41 cyklech, což je hodnota, která by nebyla čistě softwarovými prostředky vůbec možná, zvláště s ohledem na to, že výsledek je 16bitový a mezivýpočty jsou prováděny s přesností 20 bitů.
Hodnoty ei jsou vybírány z tabulky hodnot funkcí atan či atanh podle postupu popsaného v předchozích kapitolách. Pro klasický CORDIC je m=1, pro hyperbolickou geometrii je m=-1.
Tabulky hodnot funkcí atan a atanh obsahují slova široká dvacet bitů; interně je použit formát FX (fixed point) s devatenácti bity za řádovou čárkou (tečkou).
Komunikace s koprocesorem CORDIC probíhá přes několik registrů. Samotný koprocesor pracuje nezávisle na CPU (který může jednoduše zjistit, zda již došlo k dokončení výpočtu či zda je dostupný pouze mezivýsledek):
| Registr | Význam |
|---|---|
| CD_CORDxL | použit pro zápis prvotní hodnoty X pro algoritmus CORDIC |
| CD_CORDxH | dtto, ovšem obsahuje horních osm bitů |
| CD_CORDYL | podobný význam, ovšem pro hodnotu Y |
| CD_CORDYH | podobný význam, ovšem pro hodnotu Y |
| CD_CORDZL | podobný význam, ovšem pro hodnotu Z |
| CD_CORDZH | podobný význam, ovšem pro hodnotu Z |
| CD_STATC | stavový a datový registr |
| CD_CON | řídicí registr |
16. Odkazy na Internetu
- XC800 family
https://en.wikipedia.org/wiki/XC800_family - Permanent Magnet Synchronous Motor
https://en.wikipedia.org/wiki/Synchronous_motor#Permanent_magnet_motors - Implementing field oriented control of a brushless DC motor
http://www.eetimes.com/document.asp?doc_id=1279321 - Vector control (motor)
https://en.wikipedia.org/wiki/Vector_control_(motor) - Motorola DSP56k
https://www.rockbox.org/wiki/MotorolaDSP56k - Motorola 56000 (Wikipedia)
http://en.wikipedia.org/wiki/Motorola_56000 - Using the Motorola DSP56002EVM for Amateur Radio DSP Projects
http://www.johanforrer.net/EVM/article.html - The Atari Falcon030 „Personal Integrated Media System“
http://www.atarimuseum.com/computers/16bits/falcon030.html - Turtle Beach Corporation (stránky společnosti)
http://www.turtlebeach.com/ - Turtle Beach Corporation (Wikipedia)
https://en.wikipedia.org/wiki/Turtle_Beach_Corporation - Atari Falcon 030 DSP 3D engine test
http://www.digiti.info/video/WHQwMjNRaExfLWs=/atari_falcon030_dsp_3d_engine_test - Atari Falcon030 (německy)
http://www.maedicke.de/atari/hardware/falcon.htm - Old-computers.com: Atari Falcon030
http://www.old-computers.com/museum/computer.asp?c=125&st=1 - Atari Falcon030 (Wikipedia)
http://en.wikipedia.org/wiki/Atari_Falcon - Past and current projects (including Falcon stuff)
http://os.inf.tu-dresden.de/~nf2/projects/projects.html - Atari Falcon 030: The Case For The Defence
http://www.soundonsound.com/sos/1994_articles/sep94/atarifalcon.html - DaVinci processor family
http://www.ti.com/general/docs/datasheetdiagram.tsp?genericPartNumber=TMS320DM365&diagramId=64193 - Texas Instruments DaVinci
https://en.wikipedia.org/wiki/Texas_Instruments_DaVinci - TMS320DM6446 (DaVinci)
http://www.ti.com/product/tms320dm6446 - Digital Media Video Processors (TI)
http://www.ti.com/lsds/ti/processors/dsp/media_processors/davinci/products.page# - TI Wiki
http://processors.wiki.ti.com/index.php/Main_Page - C5000 ultra-low-power DSP
http://www.ti.com/lsds/ti/processors/dsp/c5000_dsp/overview.page - OMAP (Wikipedia)
https://en.wikipedia.org/wiki/OMAP - OMAP – TI Wiki
http://processors.wiki.ti.com/index.php/OMAP - Why OMAP can't compete in smartphones
http://www.eetimes.com/author.asp?section_id=40&doc_id=1286602 - Applications Processors – The Heart of the Smartphone
http://www.engineering.com/ElectronicsDesign/ElectronicsDesignArticles/ArticleID/5791/Applications-Processors-The-Heart-of-the-Smartphone.aspx - TI cuts 1,700 jobs in OMAP shift
http://www.eetimes.com/document.asp?doc_id=1262782 - VLIW: Very Long Instruction Word: Texas Instruments TMS320C6×
http://www.ecs.umass.edu/ece/koren/architecture/VLIW/2/ti1.html - An Introduction To Very-Long Instruction Word (VLIW) Computer Architecture
Philips Semiconductors - VLIW Architectures for DSP: A Two-Part Lecture (PDF, slajdy)
http://www.bdti.com/MyBDTI/pubs/vliw_icspat99.pdf - Very long instruction word (Wikipedia)
https://en.wikipedia.org/wiki/Very_long_instruction_word - A VLIW Approach to Architecture, Compilers and Tools
http://www.vliw.org/book/ - VEX Toolchain (VEX = VLIW Example)
http://www.hpl.hp.com/downloads/vex/ - Elbrus (computer)
https://en.wikipedia.org/wiki/Elbrus_%28computer%29 - Super Harvard Architecture Single-Chip Computer
https://en.wikipedia.org/wiki/Super_Harvard_Architecture_Single-Chip_Computer - Digital Signal Processors (stránky TI)
http://www.ti.com/lsds/ti/processors/dsp/overview.page - C674× Low Power DSP (stránky TI)
http://www.ti.com/lsds/ti/processors/dsp/c6000_dsp/c674×/overview.page - TMS320C30 (stránky TI)
http://www.ti.com/product/tms320c30 - TMS320C6722B
http://www.ti.com/product/tms320c6722b/description - Introduction to DSP
http://www.ti.com/lit/wp/spry281/spry281.pdf - The Evolution of TMS (Family of DSPs)
http://www.slideshare.net/moto_modx/theevo1 - Datasheet k TMS32010
http://www.datasheetarchive.com/dlmain/49326c32a52050140abffe6f0ac4894aa09889/M/TMS32010 - 1979: Single Chip Digital Signal Processor Introduced
http://www.computerhistory.org/siliconengine/single-chip-digital-signal-processor-introduced/ - The TMS32010. The DSP chip that changed the destiny of a semiconductor giant
http://www.tihaa.org/historian/TMS32010–12.pdf - Texas Instruments TMS320 (Wikipedia)
https://en.wikipedia.org/wiki/Texas_Instruments_TMS320 - Great Microprocessors of the Past and Present: Part IX: Signetics 8×300, Early cambrian DSP ancestor (1978):
http://www.cpushack.com/CPU/cpu2.html#Sec2Part9 - Great Microprocessors of the Past and Present (V 13.4.0)
http://jbayko.sasktelwebsite.net/cpu.html - Introduction to DSP – DSP processors:
http://www.bores.com/courses/intro/chips/index.htm - The Scientist and Engineer's Guide to Digital Signal Processing:
http://www.dspguide.com/ - Digital signal processor (Wikipedia EN)
http://en.wikipedia.org/wiki/Digital_signal_processor - Digitální signálový procesor (Wikipedia CZ)
http://cs.wikipedia.org/wiki/Digitální_signálový_procesor - Digital Signal Processing FAQs
http://dspguru.com/dsp/faqs - Reprezentace numerických hodnot ve formátech FX a FP
http://www.root.cz/clanky/fixed-point-arithmetic/ - IEEE 754 a její příbuzenstvo: FP formáty
http://www.root.cz/clanky/norma-ieee-754-a-pribuzni-formaty-plovouci-radove-tecky/ - Čtyři základní způsoby uložení čísel pomocí FX formátů
http://www.root.cz/clanky/binarni-reprezentace-numerickych-hodnot-v-fx-formatu/ - Základní aritmetické operace prováděné v FX formátu
http://www.root.cz/clanky/zakladni-aritmeticke-operace-provadene-ve-formatu-fx/ - Aritmetické operace s hodnotami uloženými ve formátu FP
http://www.root.cz/clanky/aritmeticke-operace-s-hodnotami-ve-formatu-plovouci-radove-carky/ - FIR Filter FAQ
http://dspguru.com/dsp/faqs/fir - Finite impulse response (Wikipedia)
http://en.wikipedia.org/wiki/Finite_impulse_response - DSPRelated
http://www.dsprelated.com/ - Addressing mode (Wikipedia)
https://en.wikipedia.org/wiki/Addressing_mode - Orthogonal instruction set
https://en.wikipedia.org/wiki/Orthogonal_instruction_set - TI 16-bit and 32-bit microcontrollers
http://www.ti.com/lsds/ti/microcontrollers16-bit32-bit/overview.page - TMS 32010 Assembly Language Programmer's Guide (kniha na Amazonu)
https://www.amazon.com/32010-Assembly-Language-Programmers-Guide/dp/0904047423 - COSC2425: PC Architecture and Machine Language, PC Assembly Language
http://www.austincc.edu/rblack/courses/COSC2425/index.html




























