Obsah
1. Realizace neuronových sítí s využitím knihovny PyTorch
2. Idealizovaný model neuronu používaný v umělých neuronových sítích
3. Role biasu ve výpočtech prováděných neurony
4. Malá odbočka: neuronové sítě a operace skalárního součinu
5. Aktivační funkce ve výpočtech prováděných neurony
6. Vytvoření feed-forward sítě z jednotlivých neuronů
7. Vstupní vrstva, výstupní vrstva a skryté vrstvy neuronů
8. Trénink (učení) sítě s využitím trénovacích dat
10. Aktivační funkce vypočtené knihovnou NumPy
11. Aktivační funkce vypočtené knihovnou PyTorch
12. Porovnání průběhu aktivačních funkcí
13. Vygenerování dat funkcí make_circles
15. Náhodné rozdělení datové sady funkcí train_test_split
16. Realizace rozdělení datové sady na trénovací a testovací množinu
17. Konverze původních dat z n-dimenzionálních polí do tenzorů
19. Repositář s demonstračními příklady
1. Realizace neuronových sítí s využitím knihovny PyTorch
V dnešním pokračování seriálu o knihovně PyTorch si ukážeme tu nejdůležitější funkcionalitu poskytovanou tímto balíčkem. PyTorch totiž umožňuje konstrukci neuronových sítí zvoleného typu a tvaru, trénink těchto sítí a jejich následné použití pro řešení konkrétních úloh (a samozřejmě podporuje i jejich validaci, i když zde si musíme vypomoci dalším kódem).
Zejména trénink neuronových sítí je přitom velmi náročný na výpočetní čas a z tohoto důvodu knihovna PyTorch umožňuje realizovat tyto výpočty na GPU, který je přesně pro tento typ úloh navržen (podporována je například CUDA apod). V první části článku se seznámíme se základními pojmy, které se vztahují k neuronovým sítím. Jedná se o krátké zopakování z článku o knihovně scikit-learn.
Druhá část článku bude zaměřena na praktické použití PyTorche společně s dalšími knihovnami. Připravíme si data ve formátu tenzorů, která budou následně použita pro natrénování i validaci neuronové sítě.
2. Idealizovaný model neuronu používaný v umělých neuronových sítích
Při práci s umělými neuronovými sítěmi je vhodné alespoň do jisté míry chápat, jakým způsobem je vlastně taková síť zkonstruována a z jakých prvků se interně skládá. Základním stavebním prvkem těchto sítí je takzvaný umělý neuron, resp. přesněji řečeno velmi zjednodušený a idealizovaný model skutečného neuronu (čím více rozumíme lidskému mozku, tím více je zřejmé, o jak primitivní model se vlastně jedná – to však zdá se v praxi nevadí).
Původní model neuronu byl navržen Warrenem McCullochem a Walterem Pittsem (MCP) již ve čtyřicátých letech minulého století, z čehož plyne, že neuronové sítě nejsou jen módním výstřelkem poslední doby (naopak, moderní GPU umožňují jejich nasazení i tam, kde to dříve nebylo možné, to je však téma na samostatný článek.). Na dalším obrázku jsou naznačeny prvky tohoto zjednodušeného modelu neuronu:

Obrázek 1: Idealizovaný model neuronu.
Z obrázku je patrné, že neuron může mít libovolný počet vstupů (na prvním obrázku jsou konkrétně zobrazeny tři vstupy x1, x2 a x3, ovšem může to být jen jeden vstup nebo naopak i sto vstupů) a má pouze jeden výstup y. Vstupem a výstupem jsou reálná čísla. Typicky přitom bývá výstup upraven aktivační funkcí takovým způsobem, že leží v rozsahu ← 1..1> nebo <0..1>. A i vstupy jsou typicky v rozsahu –1..1 nebo 0..1.
Dále na schématu zobrazeném na prvním obrázku vidíme váhy w1, w2 a w3. Těmito váhami jsou vynásobeny vstupní hodnoty. Váhy vlastně představují stav neuronu, tj. jde o funkci, na kterou byl neuron natrénován (naučen). Vstupní hodnoty x1 až xn jsou tedy postupně vynásobeny váhami w1 až wn a výsledky takto provedeného součinu jsou v neuronu sečteny, takže získáme jediné reálné číslo. Toto číslo je zpracováno aktivační funkcí (ta již většinou žádný stav nemá, ostatně stejně jako funkce pro výpočet sumy) výsledek této funkce je poslán na výstup neuronu.
Idealizovaný a značně zjednodušený model neuronu tedy provádí tento výpočet:
y = f(w1x1 + w2x2 + … + wnxn)
3. Role biasu ve výpočtech prováděných neurony
Ve skutečnosti není stav neuronu pro n vstupů x1 až xn určen pouze n vahami w1 až wn tak, jak jsme si to uvedli v předchozí kapitole. Navíc totiž musíme přidat ještě váhu w0, na kterou je připojena konstanta 1 (někdy se proto můžeme setkat s nákresem neuronové sítě, v níž se nachází speciální neurony bez vstupů a s jedničkou na výstupu). Idealizovaný model neuronu se přidáním nového vstupu nepatrně zkomplikuje:

Obrázek 2: Idealizovaný model neuronu s biasem.
I výpočet bude vypadat (nepatrně) odlišně, neboť do něho přidáme nový člen w0 (na začátku):
y = f(w0 + w1x1 + w2x2 + … + wnxn)
Tato přidaná váha se někdy nazývá bias, protože vlastně umožňuje posouvat průběh aktivační funkce nalevo a napravo, v závislosti na jeho hodnotě.
4. Malá odbočka: neuronové sítě a operace skalárního součinu
V paralelně běžícím seriálu o vektorových operacích podporovaných na moderních mikroprocesorech s architekturou x86 a x86–64 jsme si řekli, že s rozvojem neuronových sítí a umělé inteligence (ale nejenom zde) se začal masivně využívat známý algoritmus pro výpočet skalárního součinu (dot product, scalar product). Tento algoritmus se používá v oblasti velkých jazykových modelů (LLM) pro zjišťování podobnosti dlouhých vektorů s numerickými hodnotami (vector similarity). Kromě klasického skalárního součinu se v této oblasti používá i tzv. cosinus similarity, což je varianta skalárního součinu, v níž nezáleží na délce vektorů, ale pouze na jejich vzájemné orientaci (výpočet je tedy doplněn o normalizaci vektorů, ovšem základ zůstává stále stejný). A toto porovnávání vektorů se v LLM provádí neustále a většinou je optimalizováno a výpočty běží na GPU.
To však není zdaleka vše. Pokud se zaměříme na oblast klasických neuronových sítí (NN – neural networks), což je téma dnešního článku, zjistíme, že se tyto sítě skládají z takzvaných perceptronů, což je vlastně značně zjednodušený model neuronů s jejich složením do několika vrstev. A na vstup každého neuronu se přivádí nějaké množství numerických vstupů popsaných v předchozí kapitole. Každý z těchto vstupů je váhován, tj. vynásoben určitou konstantou a výsledky tohoto váhování jsou nakonec sečteny. Když se ovšem nad touto operací zamyslíme, zjistíme, že se vlastně nejedná o nic jiného, než opět o aplikaci výpočtu skalárního součinu. První z vektorů, který do tohoto součinu vstupuje jako operand, jsou vstupy do neuronu, druhým vektorem je pak vektor vah, které si neuron zapamatoval. A samotný trénink neuronové sítě vlastně není nic jiného, než rekonfigurace těchto vah – vektorů.
5. Aktivační funkce ve výpočtech prováděných neurony
Bez aktivační funkce by se neuron choval velmi jednoduše a především „lineárně “– spočítal by vážený součet vstupů a výsledek by poslal na svůj výstup. Aktivační funkce, kterou jsme v předchozích kapitolách označovali symbolem f, do celého výpočtu vnáší nelinearitu. Ta je přitom pro praktické využití sítě velmi důležitá. Nejjednodušší aktivační funkce může pro vstupní hodnoty <0 vracet –1 a pro hodnoty ≥0 vracet 1, což vlastně říká, že je nutné dosáhnout určité hraniční hodnoty váženého součtu vstupů, aby byl neuron aktivován (tj. na výstup vyslal jedničku a nikoli –1). Ostatně právě zde znovu vidíme význam biasu, který onu hraniční hodnotu posunuje.

Obrázek 3: Aktivační funkce ReLU.
V praxi je však aktivační funkce složitější, než zmíněný jednotkový skok. Často se používá ReLU, sigmoid nebo hyperbolický tangent. Pro specializovanější účely se však používají i další funkce, které dokonce nemusí mít monotonní průběh. S dalšími podporovanými funkcemi se seznámíme příště.

Obrázek 4: Aktivační funkce Tanh.
6. Vytvoření feed-forward sítě z jednotlivých neuronů
Samostatné neurony i s aktivační funkcí stále provádí velmi jednoduchou činnost, ovšem aby se mohly stát součástí složitějšího systému (řekněme automatického řízení auta nebo rozpoznávání obličejů), musíme z nich vytvořit síť. Jedna z nejjednodušších forem umělé neuronové sítě se nazývá feed-forward, a to z toho důvodu, že informace (tedy vstupní hodnoty, mezihodnoty i hodnoty výstupní) touto sítí tečou jen jedním směrem (při učení je tomu jinak, tehdy jsou naopak hodnoty posílány ve směru opačném). Neurony jsou typicky uspořádány pravidelně do vrstev:

Obrázek 5: Uspořádání neuronů do vrstev ve feed-forward síti.
Kolečka na obrázku představují jednotlivé neurony, přičemž žlutě jsou označeny neurony na vstupu, zeleně „interní“ (skryté) neurony a červeně neurony, které produkují kýžený výstup neuronové sítě.
Zcela nalevo jsou šipkami naznačeny vstupy. Jejich počet je prakticky zcela závislý na řešeném problému. Může se jednat jen o několik vstupů (viz naše testovací síť popsaná níže), ovšem pokud například budeme tvořit síť určenou pro rozpoznání objektů v rastrovém obrázku, může být počet vstupů roven počtu pixelů (což ovšem v praxi realizujeme odlišně – konkrétně takzvanými konvolučními sítěmi).
7. Vstupní vrstva, výstupní vrstva a skryté vrstvy neuronů
Vraťme se ještě jednou k obrázku číslo 5.
Povšimněte si, že vstupní neurony mají vlastně zjednodušenou funkci, protože mají jen jeden vstup. V mnoha typech sítí tyto neurony jen rozesílají vstup na další neurony a neprovádí žádný složitější výpočet, například u nich není použita aktivační funkce, ovšem to již záleží na konkrétní konfiguraci sítě. Dále stojí za povšimnutí, že neurony posílají svůj výstup neuronům na nejbližší další vrstvě; nejsou zde tedy žádné zkratky, žádné zpětné vazby atd.
Existují samozřejmě složitější typy sítí, těmi se teď ale nebudeme zabývat. Dále tato síť propojuje neurony na sousedních vrstvách systémem „každý s každým“. V našem konkrétním příkladu mají neurony na prostřední vrstvě dva vstupy, protože předchozí vrstva má jen dva neurony. Ovšem neurony na poslední vrstvě již musí mít tři vstupy.
První vrstva s jednoduchými („hloupými“) neurony se nazývá vstupní vrstva, poslední vrstva je vrstva výstupní. Vrstvy mezi vrstvou vstupní a výstupní, kterých může být teoreticky libovolné množství, se nazývají skryté vrstvy.
„Paměť“ neuronové sítě je tvořena vahami na vstupech neuronů (včetně biasu):
| Vrstva | Neuronů | Počet vstupů/neuron | Počet vah/neuron | Celkem |
|---|---|---|---|---|
| 1 | 2 | 1 | 2 | 4 |
| 2 | 3 | 2 | 3 | 9 |
| 3 | 2 | 3 | 4 | 8 |
| ∑ | 7 | 21 |
V praxi se používají sítě s více vrstvami a především s větším počtem neuronů v každé vrstvě. Stavový prostor a tím i schopnosti sítě se tak prudce rozšiřují (viz již zmíněná problematika rozpoznávání objektů v rastrových obrázcích).
8. Trénink (učení) sítě s využitím trénovacích dat
Nejzajímavější je proces tréninku (učení) sítě. Ten může probíhat několika způsoby, ovšem nejčastější je učení založené na tom, že na vstup sítě přivedeme data, u nichž dopředu známe očekávaný výsledek. Síť pro tato vstupní data provede svůj odhad a na základě rozdílů mezi odhadem sítě a očekávaným výsledkem se více či méně sofistikovanými algoritmy nepatrně pozmění váhy wi na vstupech do neuronů (včetně biasu, tedy w0).
Konkrétní míra změn váhy na vstupech neuronů je globálně řízena dalším parametrem či parametry, z nichž ten nejdůležitější ovlivňuje rychlost učení. Ta by neměla být příliš nízká (to vyžaduje objemná trénovací data nebo jejich opakování), ale ani příliš vysoká. Základní algoritmus učení sítě se jmenuje backpropagation, protože se váhy skutečně mění v opačném směru – od výstupů (na něž se přivede vypočtená chyba) ke vstupům. Asi nejlépe je tento koncept popsán v článku dostupném na adrese https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/.
9. Praktická část
Po teoretickém úvodu, ve kterém jsme si řekli skutečně jen základní, ale nezbytné informace o problematice neuronových sítí, přejdeme k praktické části, tj. postupně se pokusíme natrénovat neuronovou síť takovým způsobem, aby dokázala řešit jednoduché problémy. A pochopitelně taktéž budeme muset zvalidovat, jestli tato síť poskytuje korektní výsledky. Pokud výsledky validace nebudou uspokojivé, může to znamenat, že je neuronová síť příliš jednoduchá a nedokáže řešit složitější problémy; může být ale taktéž nedotrénovaná (málo trénovacích dat) nebo naopak přetrénovaná. Pro realizaci přípravy dat, trénink sítě a její validaci použijeme programovací jazyk Python a knihovny scikit-learn, PyTorch a částečně taktéž NumPy. Ovšem hlavní část řešení bude provedena v PyTorchi s tím, že výpočty (především fáze učení neuronové sítě) může probíhat buď na CPU (tedy čistě softwarově) nebo na GPU, tj. na grafickém procesoru.
10. Aktivační funkce vypočtené knihovnou NumPy
Začneme velmi pozvolna. Nejprve si necháme vypočítat a zobrazit všechny tři aktivační funkce, které byly popsány v páté kapitole. První verze skriptů je založena na knihovně NumPy a pro vizualizaci je použita knihovna Matplotlib.
# Výpočet a vykreslení aktivační funkce ReLU
# Výpočet je proveden knihovnou NumPy
import matplotlib.pyplot as plt
import numpy as np
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 4.8))
# hodnoty na x-ové ose
x = np.linspace(-5, 5, 100)
# výpočet aktivační funkce
y = [max(0, i) for i in x]
# vykreslení aktivační funkce
plt.plot(x, y, label="ReLU")
# zobrazení legendy
plt.legend()
# zobrazení mřížky
plt.grid()
# uložení do souboru
plt.savefig("activation_function_relu_numpy.png")
# zobrazení v novém okně
plt.show()
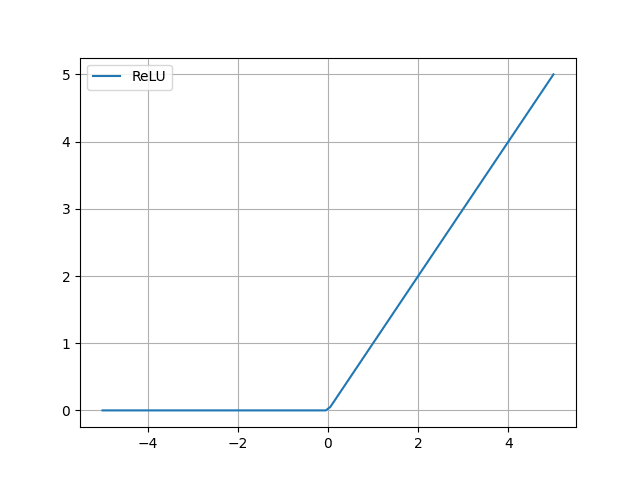
Obrázek 6: Aktivační funkce ReLU vypočtená knihovnou NumPy.
# Výpočet a vykreslení aktivační funkce sigmoid
# Výpočet je proveden knihovnou NumPy
import matplotlib.pyplot as plt
import numpy as np
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 4.8))
# hodnoty na x-ové ose
x = np.linspace(-5, 5, 100)
# výpočet aktivační funkce
y = 1/(1 + np.exp(-x))
# vykreslení aktivační funkce
plt.plot(x, y, label="Sigmoid")
# zobrazení legendy
plt.legend()
# zobrazení mřížky
plt.grid()
# uložení do souboru
plt.savefig("activation_function_sigmoid_numpy.png")
# zobrazení v novém okně
plt.show()

Obrázek 7: Aktivační funkce sigmoid vypočtená knihovnou NumPy.
# Výpočet a vykreslení aktivační funkce tanh
# Výpočet je proveden knihovnou NumPy
import matplotlib.pyplot as plt
import numpy as np
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 4.8))
# hodnoty na x-ové ose
x = np.linspace(-5, 5, 100)
# výpočet aktivační funkce
y = np.tanh(x)
# vykreslení aktivační funkce
plt.plot(x, y, label="Tanh")
# zobrazení legendy
plt.legend()
# zobrazení mřížky
plt.grid()
# uložení do souboru
plt.savefig("activation_function_tanh_numpy.png")
# zobrazení v novém okně
plt.show()

Obrázek 8: Aktivační funkce tanh vypočtená knihovnou NumPy.
11. Aktivační funkce vypočtené knihovnou PyTorch
Aktivační funkce jsou v oblasti neuronových sítí velmi důležité, takže asi nebude velkým překvapením, že podporu pro jejich výpočet nalezneme i přímo v PyTorchi. Pokusme se tedy vypočítat a zobrazit ty stejné funkce, nyní ovšem vypočtené PyTorchem s využitím tenzorů. Zdrojové kódy tedy vypadají podobně, ale interně se výpočty značně odlišují:
# Výpočet a vykreslení aktivační funkce ReLU
# Výpočet je proveden knihovnou PyTorch
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import numpy as np
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 4.8))
# hodnoty na x-ové ose
x = torch.linspace(-5, 5, 100)
# výpočet aktivační funkce
y = nn.ReLU()(x)
# vykreslení aktivační funkce
plt.plot(x, y, label="ReLU")
# zobrazení legendy
plt.legend()
# zobrazení mřížky
plt.grid()
# uložení do souboru
plt.savefig("activation_function_relu_pytorch.png")
# zobrazení v novém okně
plt.show()

Obrázek 9: Aktivační funkce ReLU vypočtená knihovnou PyTorch.
# Výpočet a vykreslení aktivační funkce sigmoid
# Výpočet je proveden knihovnou PyTorch
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import numpy as np
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 4.8))
# hodnoty na x-ové ose
x = torch.linspace(-5, 5, 100)
# výpočet aktivační funkce
y = nn.Sigmoid()(x)
# vykreslení aktivační funkce
plt.plot(x, y, label="Sigmoid")
# zobrazení legendy
plt.legend()
# zobrazení mřížky
plt.grid()
# uložení do souboru
plt.savefig("activation_function_sigmoid_pytorch.png")
# zobrazení v novém okně
plt.show()

Obrázek 10: Aktivační funkce sigmoid vypočtená knihovnou PyTorch.
# Výpočet a vykreslení aktivační funkce tanh
# Výpočet je proveden knihovnou PyTorch
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import numpy as np
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 4.8))
# hodnoty na x-ové ose
x = torch.linspace(-5, 5, 100)
# výpočet aktivační funkce
y = nn.Tanh()(x)
# vykreslení aktivační funkce
plt.plot(x, y, label="Tanh")
# zobrazení legendy
plt.legend()
# zobrazení mřížky
plt.grid()
# uložení do souboru
plt.savefig("activation_function_tanh_pytorch.png")
# zobrazení v novém okně
plt.show()

Obrázek 11: Aktivační funkce tanh vypočtená knihovnou PyTorch.
12. Porovnání průběhu aktivačních funkcí
Jednotlivé aktivační funkce mají stejný definiční obor, ale odlišný průběh i obor hodnot. Bude to patrné při zobrazení všech tří těchto funkcí na jediném grafu. Opět si uvedeme dvě varianty výpočtu a zobrazení. Jedna z variant je založená na knihovně NumPy, druhá na knihovně PyTorch:
# Výpočet a vykreslení všech aktivačních funkcí
# Výpočet je proveden knihovnou NumPy
import matplotlib.pyplot as plt
import numpy as np
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 4.8))
# hodnoty na x-ové ose
x = np.linspace(-5, 5, 100)
# výpočet všech tří aktivačních funkcí
relu = [max(0, i) for i in x]
tanh = np.tanh(x)
sigmoid = 1/(1 + np.exp(-x))
# vykreslení všech tří aktivačních funkcí
plt.plot(x, sigmoid, label="sigmoid")
plt.plot(x, tanh, label="tanh")
plt.plot(x, relu, label="ReLU")
plt.ylim(-1.5, 2)
# zobrazení legendy
plt.legend()
# zobrazení mřížky
plt.grid()
# uložení do souboru
plt.savefig("activation_functions_numpy.png")
# zobrazení v novém okně
plt.show()

Obrázek 12: Porovnání aktivačních funkcí; vypočteno pomocí knihovny NumPy.
# Výpočet a vykreslení všech aktivačních funkcí
# Výpočet je proveden knihovnou PyTorch
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 4.8))
# hodnoty na x-ové ose
x = torch.linspace(-5, 5, 100)
# výpočet všech tří aktivačních funkcí
relu = nn.ReLU()(x)
tanh = nn.Tanh()(x)
sigmoid = nn.Sigmoid()(x)
# vykreslení všech tří aktivačních funkcí
plt.plot(x, sigmoid, label="sigmoid")
plt.plot(x, tanh, label="tanh")
plt.plot(x, relu, label="ReLU")
plt.ylim(-1.5, 2)
# zobrazení legendy
plt.legend()
# zobrazení mřížky
plt.grid()
# uložení do souboru
plt.savefig("activation_functions_pytorch.png")
# zobrazení v novém okně
plt.show()

Obrázek 13: Porovnání aktivačních funkcí; vypočteno pomocí knihovny PyTorch.
13. Vygenerování dat funkcí make_circles
Pro trénink a validaci první verze jednoduché neuronové sítě použijeme data, která jsou vygenerovaná s využitím knihovny scikit-learn, která již byla (do určité míry) na Rootu popsána. V této knihovně nalezneme hned několik více či méně vhodných generátorů dat. My dnes použijeme funkci nazvanou make_circles. Jedná se o příhodný název, protože výsledek skutečně připomíná soustředné kružnice. Tuto funkci lze zavolat následovně:
samples, labels = make_circles(
n_samples=n_samples, factor=0.5, noise=0.05
)
kde parametr factor určuje rozdíl velikostí vnější a vnitřní kružnice a parametrem noise se nastavuje směrodatná odchylka při výpočtu pozice bodů.
Skript, který s využitím této funkce vygeneruje a následně zobrazí sadu bodů v rovině, vypadá následovně:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 6.4))
# testovací data
n_samples = 2000
samples, labels = make_circles(
n_samples=n_samples, factor=0.5, noise=0.05
)
# vykreslení bodů v rovině
plt.scatter(samples[:, 0], samples[:, 1], s=1.5, cmap=plt.cm.Set1)
# uložení grafu do souboru
plt.savefig("circles1.png")
# vykreslení na obrazovku
plt.show()
Výsledný graf s vygenerovanými body může vypadat následovně:

Obrázek 14: Graf s body vygenerovanými funkcí make_circles.
Jednotlivé body ovšem navíc spadají do nějaké skupiny (kategorie) určené návěštím (label). I tuto skupinu/kategorii si můžeme velmi snadno vizualizovat. Postačuje k tomu využít proměnnou labels, která je naplněna druhou návratovou hodnotou funkce make_circles. Výsledkem budou dvě skupiny bodů, přičemž z barvy je ihned patrné, do které skupiny bod spadá:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 6.4))
# testovací data
n_samples = 2000
samples, labels = make_circles(
n_samples=n_samples, factor=0.5, noise=0.05
)
# vykreslení bodů v rovině
plt.scatter(samples[:, 0], samples[:, 1], s=1.5, c=labels, cmap=plt.cm.Set1)
# uložení grafu do souboru
plt.savefig("circles2.png")
# vykreslení na obrazovku
plt.show()
Výsledek:

Obrázek 15: Graf s body vygenerovanými funkcí make_circles. Body jsou obarveny na základě své příslušnosti k první nebo druhé skupině.
14. Získání náhodnějších dat
Pokusme se nyní zvýšit směrodatnou odchylku a zjistit, jak se tato změna projeví ve výsledném obrazci složeném z bodů. Tím později poněkud ztížíme trénink neuronové sítě, resp. přesněji řečeno bude muset být neuronová síť naučena mnohem lépe v případě, kdy se budou body z obou skupin dotýkat:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
# velikost obrázku s grafem
plt.subplots(figsize=(6.4, 6.4))
# testovací data
n_samples = 2000
samples, labels = make_circles(
n_samples=n_samples, factor=0.5, noise=0.10
)
# vykreslení bodů v rovině
plt.scatter(samples[:, 0], samples[:, 1], s=1.5, c=labels, cmap=plt.cm.Set1)
# uložení grafu do souboru
plt.savefig("circles3.png")
# vykreslení na obrazovku
plt.show()
Výsledek:

Obrázek 16: Graf s body vygenerovanými funkcí make_circles. Body jsou obarveny na základě své příslušnosti k první nebo druhé skupině.
15. Náhodné rozdělení datové sady funkcí train_test_split
Pro rozdělení dat získaných voláním make_circles a data trénovací a validační použijeme funkci train_test_split. Tato funkce ve svém prvním parametru akceptuje přímo datovou sadu (nemusíme se tedy snažit o ruční získání naměřených dat a očekávaných výsledků), dále velikost testovacích a trénovacích dat (buď jako celé číslo, což je počet záznamů nebo hodnotu typu float, což bude zlomek od 0 do 1, nepovinnou hodnotu, která zamezí různým výsledkům pro několik volání této funkce a dále parametr povolující zamíchání dat (ve výchozím nastavení je povolen):
train_test_split(*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)
Split arrays or matrices into random train and test subsets.
Quick utility that wraps input validation,
``next(ShuffleSplit().split(X, y))``, and application to input data
into a single call for splitting (and optionally subsampling) data into a
one-liner.
Read more in the :ref:`User Guide <cross_validation>`.
Parameters
----------
*arrays : sequence of indexables with same length / shape[0]
Allowed inputs are lists, numpy arrays, scipy-sparse
matrices or pandas dataframes.
test_size : float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion
of the dataset to include in the test split. If int, represents the
absolute number of test samples. If None, the value is set to the
complement of the train size. If ``train_size`` is also None, it will
be set to 0.25.
train_size : float or int, default=None
If float, should be between 0.0 and 1.0 and represent the
proportion of the dataset to include in the train split. If
int, represents the absolute number of train samples. If None,
the value is automatically set to the complement of the test size.
random_state : int, RandomState instance or None, default=None
Controls the shuffling applied to the data before applying the split.
Pass an int for reproducible output across multiple function calls.
See :term:`Glossary <random_state>`.
shuffle : bool, default=True
Whether or not to shuffle the data before splitting. If shuffle=False
then stratify must be None.
stratify : array-like, default=None
If not None, data is split in a stratified fashion, using this as
the class labels.
Read more in the :ref:`User Guide <stratification>`.
16. Realizace rozdělení datové sady na trénovací a testovací množinu
Samotná realizace a rozdělení datové sady na část určenou pro trénink a na část určenou pro testování nebo validaci, je poměrně jednoduchá. Konkrétně použijeme výše popsanou funkci train_test_split následujícím způsobem:
samples, labels = make_circles(
n_samples=n_samples, factor=0.5, noise=0.05
)
# rozdělení na trénovací a testovací množinu
X_train, X_test, y_train, y_test = train_test_split(samples, labels, test_size=1/3, random_state=26)
Výsledný skript na konci zobrazí jak trénovací, tak i testovací množinu. Z obrázku by mělo být patrné, že jsou data vybrána skutečně náhodně (a nikoli například stylem první třetina, druhé dvě třetiny):
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
# testovací data
n_samples = 2000
samples, labels = make_circles(
n_samples=n_samples, factor=0.5, noise=0.05
)
# rozdělení na trénovací a testovací množinu
X_train, X_test, y_train, y_test = train_test_split(samples, labels, test_size=1/3, random_state=26)
# vizualizace
fig, (train_ax, test_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(10, 5))
train_ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.Set1)
train_ax.set_title("Trénovací data")
train_ax.set_xlabel("Feature #0")
train_ax.set_ylabel("Feature #1")
test_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=plt.cm.Set1)
test_ax.set_xlabel("Feature #0")
test_ax.set_title("Testovací data")
# uložení grafu do souboru
plt.savefig("circles4.png")
# vykreslení na obrazovku
plt.show()
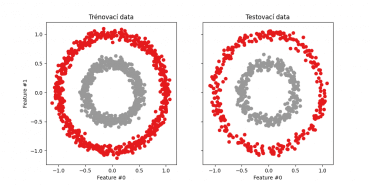
Obrázek 17: Trénovací a testovací data získaná rozdělením bodů získaných funkcí make_circles.
17. Konverze původních dat z n-dimenzionálních polí do tenzorů
V knihovně Pytorch se pracuje výhradně s tenzory, takže v dalším kroku musíme převést trénovací a testovací data do odlišné reprezentace. Prozatím máme obě sady dat uloženy ve formě n-dimenzionálních polí knihovny NumPy, výsledkem má být sada tenzorů. Převod provedeme následujícím skriptem (nejsem autorem „datové části“). Základem pro převody je funkce torch.from_numpy. Následně provedeme rozdělení dat na menší dávky, které využijeme příště pro trénink neuronové sítě:
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
import torch
import numpy as np
from torch.utils.data import Dataset, DataLoader
# konverze původních dat z NumPy do tenzorů
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
batch_size = 64
# testovací data
n_samples = 2000
samples, labels = make_circles(
n_samples=n_samples, factor=0.5, noise=0.05
)
# rozdělení na trénovací a testovací množinu
X_train, X_test, y_train, y_test = train_test_split(samples, labels, test_size=1/3, random_state=26)
# trénovací a testovací sada
# trénovací sada
train_data = Data(X_train, y_train)
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)
# testovací sada
test_data = Data(X_test, y_test)
test_dataloader = DataLoader(dataset=test_data, batch_size=batch_size, shuffle=True)
# otestování funkcionality
for batch, (X, y) in enumerate(train_dataloader):
print(f"Dávka: {batch+1}")
print(f"X shape: {X.shape}")
print(f"y shape: {y.shape}")
print()
18. Vygenerované sady tenzorů
Vytvořené sady (dávky) tenzorů by měly obsahovat tenzory s první dimenzí rovnou maximálně 64 (nebo méně). O tom se snadno přesvědčíme:
Dávka: 1 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 2 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 3 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 4 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 5 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 6 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 7 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 8 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 9 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 10 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 11 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 12 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 13 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 14 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 15 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 16 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 17 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 18 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 19 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 20 X shape: torch.Size([64, 2]) y shape: torch.Size([64]) Dávka: 21 X shape: torch.Size([53, 2]) y shape: torch.Size([53])
Proč je sad tolik? 20×64+53=1333. Toto číslo odpovídá 2000×2/3, kde 2000 je celkový počet bodů a 2/3 je koeficient rozdělení vstupních dat na trénovací část (1333) a testovací část (667).
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu PyTorch lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady:
20. Odkazy na Internetu
- Seriál Programovací jazyk Lua na Rootu:
https://www.root.cz/serialy/programovaci-jazyk-lua/ - PDM: moderní správce balíčků a virtuálních prostředí Pythonu:
https://www.root.cz/clanky/pdm-moderni-spravce-balicku-a-virtualnich-prostredi-pythonu/ - PyTorch Tutorial: Building a Simple Neural Network From Scratch
https://www.datacamp.com/tutorial/pytorch-tutorial-building-a-simple-neural-network-from-scratch - Interní reprezentace numerických hodnot: od skutečného počítačového pravěku po IEEE 754–2008:
https://www.root.cz/clanky/interni-reprezentace-numerickych-hodnot-od-skutecneho-pocitacoveho-praveku-po-ieee-754–2008/ - Interní reprezentace numerických hodnot: od skutečného počítačového pravěku po IEEE 754–2008 (dokončení):
https://www.root.cz/clanky/interni-reprezentace-numerickych-hodnot-od-skutecneho-pocitacoveho-praveku-po-ieee-754–2008-dokonceni/ - Brain Floating Point – nový formát uložení čísel pro strojové učení a chytrá čidla:
https://www.root.cz/clanky/brain-floating-point-ndash-novy-format-ulozeni-cisel-pro-strojove-uceni-a-chytra-cidla/ - Stránky projektu PyTorch:
https://pytorch.org/ - Informace o instalaci PyTorche:
https://pytorch.org/get-started/locally/ - Tenzor (Wikipedia):
https://cs.wikipedia.org/wiki/Tenzor - Introduction to Tensors:
https://www.youtube.com/watch?v=uaQeXi4E7gA - Introduction to Tensors: Transformation Rules:
https://www.youtube.com/watch?v=j6DazQDbEhQ - Tensor Attributes:
https://pytorch.org/docs/stable/tensor_attributes.html - Tensors Explained Intuitively: Covariant, Contravariant, Rank :
https://www.youtube.com/watch?v=CliW7kSxxWU - What is the relationship between PyTorch and Torch?:
https://stackoverflow.com/questions/44371560/what-is-the-relationship-between-pytorch-and-torch - What is a tensor anyway?? (from a mathematician):
https://www.youtube.com/watch?v=K7f2pCQ3p3U - Visualization of tensors – part 1 :
https://www.youtube.com/watch?v=YxXyN2ifK8A - Visualization of tensors – part 2A:
https://www.youtube.com/watch?v=A95jdIuUUW0 - Visualization of tensors – part 2B:
https://www.youtube.com/watch?v=A95jdIuUUW0 - What the HECK is a Tensor?!?:
https://www.youtube.com/watch?v=bpG3gqDM80w - Stránka projektu Torch
http://torch.ch/ - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - An Introduction to Tensors
https://math.stackexchange.com/questions/10282/an-introduction-to-tensors - Differences between a matrix and a tensor
https://math.stackexchange.com/questions/412423/differences-between-a-matrix-and-a-tensor - Qualitatively, what is the difference between a matrix and a tensor?
https://math.stackexchange.com/questions/1444412/qualitatively-what-is-the-difference-between-a-matrix-and-a-tensor? - Tensors for Neural Networks, Clearly Explained!!!:
https://www.youtube.com/watch?v=L35fFDpwIM4 - Tensor Processing Unit:
https://en.wikipedia.org/wiki/Tensor_Processing_Unit - Třída Storage:
http://docs.pytorch.wiki/en/storage.html - Funkce torch.dot
https://pytorch.org/docs/stable/generated/torch.dot.html#torch.dot - Funkce torch.narrow
https://pytorch.org/docs/stable/generated/torch.narrow.html - Funkce torch.matmul
https://pytorch.org/docs/stable/generated/torch.matmul.html - Funkce torch.reshape
https://pytorch.org/docs/stable/generated/torch.reshape.html - Funkce torch.arange
https://pytorch.org/docs/stable/generated/torch.arange.html - Funkce torch.range
https://pytorch.org/docs/stable/generated/torch.range.html - Třída torch.Tensor
https://pytorch.org/docs/stable/tensors.html - Atributy tenzorů
https://pytorch.org/docs/stable/tensor_attributes.html - Pohledy vytvořené nad tenzory
https://pytorch.org/docs/stable/tensor_view.html - Broadcasting v knihovně
https://numpy.org/doc/stable/user/basics.broadcasting.html - Broadcasting semantics (v knihovně PyTorch)
https://pytorch.org/docs/stable/notes/broadcasting.html - Dot Product In Physics: What Is The Physical Meaning of It?
https://profoundphysics.com/dot-product-in-physics-what-is-the-physical-meaning-of-it/ - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/

























