Obsah
1. Tvorba GUI v Pythonu: použití želví grafiky společně s knihovnou appJar
2. Úvodní informace o programovacím jazyku Logo
4. Kombinace knihoven appJar a turtle
5. Vytvoření a zobrazení jednoduchého obrazce vytvořeného přes modul turtle
7. Urychlení vykreslování – obnovení obsahu plátna až po 100 operacích
8. Explicitní obnovení obrazovky na konci kreslení
9. Želví grafika a složitější obrazec
10. Použití rekurze pro vykreslení sněhové vločky Helge von Kocha
11. Rekurzivní kreslení domku aneb Pythagorův strom
12. Zobecněný Pythagorův strom
13. Příkaz goto a jeho využití při kreslení na absolutní souřadnice plátna
15. Systémy iterovaných funkcí (IFS)
16. Vykreslení jednoduchého systému iterovaných funkcí krok za krokem
17. Zdrojový kód příkladu pro vykreslení IFS
18. Demonstrační příklad: galerie IFS, výběr a vykreslení vybraného IFS
19. Repositář s demonstračními příklady
1. Tvorba GUI v Pythonu: použití želví grafiky společně s knihovnou appJar
Vzhledem k tomu, že knihovna appJar byla navržena takovým způsobem, aby ji bylo možné použít při výuce programování (včetně návrhů GUI), se nabízí otázka, zda by nebylo možné nějakým způsobem spojit hned tři technologie používané na školách – programovací jazyk Python, knihovnu appJar a taktéž knihovnu turtle [1], která v Pythonu zajišťuje přístup k takzvané „želví grafice“ (turtle graphics), která byla nedílnou součástí programovacího jazyka Logo.
Poznámka: Python se pro potřeby výuky dnes používá dokonce i na MIT, kde nahradil Scheme, což byla změna, která byl přijata s rozpaky.
V navazující kapitole si řekneme základní informace o programovacím jazyku Logo i o želví grafice. Pokud vás ovšem primárně zajímá způsob integrace knihoven appJar a turtle v jediné aplikaci, klidně přeskočte přímo na čtvrtou kapitolu. Pokud vás naopak zaujme Logo, můžete si přečíst poněkud starší seriál, který na Rootu o tomto jazyku a jeho různých implementacích vyšel.

Obrázek 1: Historický screenshot pořízený v jedné z prvních verzí programovacího jazyka Logo.
2. Úvodní informace o programovacím jazyku Logo
Historicky jedním z prvních programovacích jazyků, který byl vyvinut s ohledem na snadnou a efektivní výuku programování, je jazyk Logo, jehož první verze vznikla již v roce 1967, tj. o celé desetiletí dříve, než začaly být dostupné první typy domácích osmibitových počítačů, jejichž vliv na výuku programování je značný. Někteří lidé sice považují tento jazyk za pouhou dětskou hračku (určitou obdobu počítačových her), ovšem ve skutečnosti se jedná o velmi zajímavý koncept, který je neustále zdokonalován a používán, zejména na základních ale i středních školách, kde je využíván jak pro výuku algoritmizace, tak i jako pomůcka při názorné výuce geometrie.
Obrázek 2: UCB Logo je jedním z představitelů tradičních interpretrů jazyka Logo, vybavený systémem pro práci se želví grafikou. Tento interpret je dostupný pro většinu platforem, samozřejmě včetně Linuxu.
Programovací jazyk Logo je postaven na takzvané konstruktivní vzdělávací filozofii a je navržen k podpoře konstruktivního učení. Konstruktivismus vysvětluje znalosti a dovednosti, jak jsou vytvořeny žáky v jejich vlastních myslích, prostřednictvím vzájemné interakce s jinými lidmi a okolím. Tato zajímavá teorie je spojena především se švýcarským psychologem Jeanem Piagetem, který strávil mnoho času studováním a zdokumentováním procesu učení malých dětí. S Piagetem spolupracoval i Seymour Papert, který později stál u vzniku Loga.
Obrázek 3: Obrazec vzniklý pomocí želví grafiky a programu obsahujícího dvojici vnořených programových smyček typu „repeat“.
Z programátorského hlediska je programovací jazyk Logo postaven na podobných principech jako například jazyk LISP (ostatně není bez zajímavosti, že první verze Loga byla implementována právě v LISPu), ovšem jeho syntaxe je odlišná, což v případě Loga vede k tvorbě čitelnějších programů, které se vizuálně odlišují od Lispovského „lesa závorek“. Navíc se matematické a logické výrazy v Logu zapisují v infixové podobě, na rozdíl od formy prefixové používané LISPem. Tvorba programů v Logu vede žáky k dekompozici problému na jednodušší podproblémy, ale i k opačnému postupu – tvorbě nových slov (což jsou pouze jinak pojmenované funkce), kterými se repertoár dostupných příkazů (slovník) postupně rozšiřuje – jazyk se „učí“ novým příkazům.
Příklady zápisu programu používajícího programovou smyčku repeat, dále zmíněnou želví grafiku a definici nových slov příkazem to:
to kruznice :krok
repeat 360 [
forward :krok
left 1
]
end
to kvet :pocet
repeat :pocet [
kruznice 1
left 360/:pocet
]
end
draw
kvet 10

Obrázek 4: Ukázka použití želví grafiky v Logu.
3. Želví grafika
Jednou z nejznámějších a pro výuku algoritmizace taktéž nejužitečnějších vlastností programovacího jazyka Logo je takzvaná želví grafika, anglicky turtle graphics. Právě želví grafika velkou mírou přispěla k poměrně značné oblíbenosti a také rozšíření tohoto programovacího jazyka, především v zahraničním školství. V USA se zpočátku Logo šířilo spolu s počítačem Apple II a později Commodore C64 i Apple Macintosh, zatímco v Evropě se děti poprvé s Logem seznámily na domácích osmibitových počítačích, především na Atari, Spectru, v tuzemsku na PMD, Didaktiku, IQ 151 atd.
Pojďme si nyní říci základní informace o této zajímavé součásti Loga a také o začlenění želví grafiky do dalších programovacích jazyků a aplikací.
Obrázek 5: Další ukázka možností želví grafiky.
Základem želví grafiky je virtuální želva (turtle), která se na základě poměrně malé množiny příkazů dodávaných napsaným programem (skriptem) či přímo pomocí interaktivního zápisu příkazů, pohybuje po obrazovce a přitom za sebou vykresluje stopu složenou z úseček. Tato virtuální želva se tedy chová podobně jako reálná želva, která se pohybuje po hladké pískové pláži a zanechává za sebou stopu. Původní Logo nedisponovalo pouze virtuální (vykreslovanou) želvou, ale skutečným malým robotem ve tvaru želvy, který byl radiovým spojením propojen s řídicím počítačem a reagoval na základní příkazy: pohyb vpřed, pohyb vzad, otočení doleva a otočení doprava. Navíc uměl tento robot reagovat i na jeden „multimediální“ příkaz – zapnutí zvonku. Je zřejmé, že pro výuku malých dětí je pohybující se reálný předmět mnohem zajímavější než pouhý obrázek, na druhou stranu však byl (prý) pohyb robota poměrně nepřesný, zejména při otáčení (což dnes již není problém, ostatně řiditelných a programovatelných robotů dnes existuje velké množství).

Obrázek 6: Při tvorbě tohoto obrázku se, na rozdíl od obrázků předchozích, již musely používat proměnné. Ovšem zajímavé je, že v Logu je možné programovat poměrně dlouho bez znalosti proměnných (protože jedinou „stavovou proměnnou“ je pozice a orientace želvy).
Dnešní implementace programovacího jazyka Logo většinou (kromě několika komerčních distribucí, například LEGO/Loga a několika amatérských projektů) touto možností již nedisponují, takže se budeme muset spokojit s virtuální želvou pohybující se na obrazovce. V některých implementacích Loga je želva zobrazena poměrně reálným obrázkem želvy viděné z ptačí perspektivy (jedná se například o Atari Logo, Commenius Logo, Imagine i dnes zmíněný modul turtle), většinou se však na obrazovce zobrazuje pouhý rovnoramenný trojúhelník, podobně jako ve hrách typu Xpilot nebo Asteroids. Jednotlivé implementace se od sebe také liší tím, zda za sebou želva stopu vykresluje „hlavičkou“, svým středem či „zadečkem“.
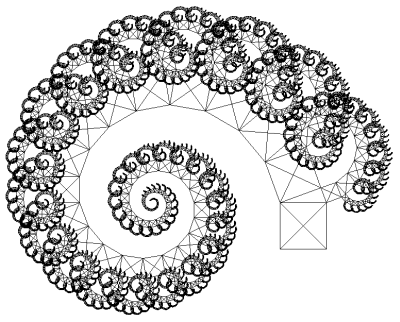
Obrázek 7: Zobecněný Pythagorův strom, jehož konstrukci si popíšeme v navazujících kapitolách.
4. Kombinace knihoven appJar a turtle
Želví grafika byla tak úspěšná a přitom implementačně jednoduchá, že se začala používat i mimo samotné Logo. To je mj. případ programovacího jazyka Python, který uživatelům nabízí standardní modul nazvaný turtle (o němž jsme se ostatně již zmínili), jenž má příkazy shodné s původním Logem. Modul turtle pro vykreslování používá Tkinter, tj. stejnou knihovnu, jako appJar, takže nám zbývá vyřešit problém, jak turtle a appJar použít společně v jedné aplikaci. Skutečně to možné je, i když (alespoň prozatím) nikoli oficiálně. Postup si ukážeme v dalších příkladech, v nichž vyřešíme i problematiku pomalého vykreslování celé scény, které sice nevadí při interaktivním ladění (tam naopak pomáhá), ale při kresbě složitějších obrazců již může být zpomalení neúnosné.

Obrázek 8: Želví grafika vykreslená v aplikaci, jejíž GUI bylo vytvořeno přes knihovnu appJar.
5. Vytvoření a zobrazení jednoduchého obrazce vytvořeného přes modul turtle
Postup umožňující použití modulu turtle společně s knihovnou appJar vychází z nám již známého postupu popsaného minule, v němž se používalo kreslicí plátno knihovny Tkinter neboli canvas. Nejprve tedy vytvoříme hlavní okno aplikace a následně na okno vložíme nové kreslicí plátno:
app = gui() canvas = tkinter.Canvas(app.topLevel, width=256, height=256) canvas.pack()
V dalším kroku získáme „želvu“, ovšem nikoli voláním konstruktoru turtle.Turtle() (tím by se vytvořilo nové okno), ale konstruktorem turtle.RawTurtle(), kterému předáme referenci na objekt představující plátno. Dále je již možné s „želvou“ manipulovat běžným způsobem, tj. skrýt její sprite, nastavit rychlost kreslení (0=nejvyšší rychlost :-) či barvu vykreslované křivky:
t = turtle.RawTurtle(canvas)
t.hideturtle()
t.speed(0)
t.pencolor("green")
Nakreslíme nějaký jednodušší obrazec, přitom nám postačí příkazy forward a right:
side = 0
angle = 117
for _ in range(160):
t.forward(side)
t.right(angle)
side += 1
Příkazem forward posuneme želvou o zadaný počet jednotek dopředu, tedy ve směru její hlavičky. V implicitním nastavení má území, na kterém se želva pohybuje, rozměry 200×200 jednotek s počátkem souřadnic uprostřed plátna. Příkazem right se želva otočí doprava o zadaný počet stupňů (nikoli radiánů).

Obrázek 9: Obrazec vykreslený přes modul turtle.
6. První demonstrační příklad
Úplný kód dnešního prvního demonstračního příkladu, v němž se používá želví grafika a výše uvedený postup pro získání kreslicího plátna, po kterém se želva pohybuje, vypadá takto:
#!/usr/bin/env python
from appJar import gui
import tkinter
import turtle
app = gui()
def onMenuItemSelect(menuItem):
if menuItem == "Quit":
app.stop()
app.setSticky("news")
fileMenu = ["Quit"]
app.addMenuList("File", fileMenu, onMenuItemSelect)
canvas = tkinter.Canvas(app.topLevel, width=256, height=256)
canvas.pack()
t = turtle.RawTurtle(canvas)
t.hideturtle()
t.speed(0)
t.pencolor("green")
t.home()
t.pd()
side = 0
angle = 117
for _ in range(160):
t.forward(side)
t.right(angle)
side += 1
app.go()

Obrázek 10: Nepatrná změna počátečních hodnot side a angle následovaná postprocessingem (zmenšení obrázku s filtrací).
7. Urychlení vykreslování – obnovení obsahu plátna až po 100 operacích
Jediný vážnější problém předchozího příkladu spočívá v tom, že vykreslování želví grafiky na kreslicí plátno je poměrně pomalé. Ostatně sami si vyzkoušejte, jaká je doba mezi spuštěním předchozího programu a zobrazením jeho okna s kresbou. Tento problém se při použití samostatného modulu turtle řešil jednoduše – zavoláním metody tracer objektu typu Screen, přičemž se v prvním parametru této metody předalo celé číslo udávající počet změn, které musí ve scéně proběhnout, než dojde k překreslení obrazovky. Druhý parametr udává rychlost želvy, přičemž nula znamená nejvyšší rychlost (žádné zpoždění). To například znamená, že pokud se zavolala metoda:
screen.tracer(100, 0)
znamená to, že k překreslení dojde až ve chvíli, kdy želva vykoná sto příkazů.
Aby bylo možné metodu tracer zavolat, je nutné příklad nepatrně změnit – musí se vytvořit instance třídy TurtleScreen (s předáním již vytvořeného kreslicího plátna) a při konstrukci želvy tuto instanci použít:
screen = turtle.TurtleScreen(canvas) t = turtle.RawTurtle(screen) screen.tracer(100, 0)
Upravený příklad vypadá takto:
#!/usr/bin/env python
from appJar import gui
import tkinter
import turtle
app = gui()
def onMenuItemSelect(menuItem):
if menuItem == "Quit":
app.stop()
app.setSticky("news")
fileMenu = ["Quit"]
app.addMenuList("File", fileMenu, onMenuItemSelect)
canvas = tkinter.Canvas(app.topLevel, width=256, height=256)
canvas.pack()
screen = turtle.TurtleScreen(canvas)
t = turtle.RawTurtle(screen)
screen.tracer(100, 0)
t.hideturtle()
t.speed(0)
t.pencolor("green")
t.home()
t.pd()
side = 0
angle = 117
for _ in range(160):
t.forward(side)
t.right(angle)
side += 1
app.go()

Obrázek 11: Obrazec vykreslený upraveným příkladem. Povšimněte si, že kresba není dokončena.
8. Explicitní obnovení obrazovky na konci kreslení
Příklad jsme sice s využitím instance třídy TurtleScreen a metody tracer několikanásobně urychlili, ovšem vyvstal nám další problém – obrazce nebudou dokresleny a některé obrazce, které se skládají jen z několika čar, nemusí být dokonce vykresleny vůbec! Je to pochopitelně způsobeno tím, že posledních až 100 příkazů předaných želvě zůstane uloženo v bufferu a nedojde k jejich skutečnému zobrazení v okně aplikace. Ovšem postačuje, když na konci vykreslování, v našem případě konkrétně těsně před příkaz app.go(), přidáme volání metody update, takže systém donutíme, aby okno aplikace překreslil i se všemi změnami, které želva na kreslicím plátně provedla:
screen.update()
Pro jistotu si ukažme, jak nyní vypadá zdrojový kód upraveného příkladu:
#!/usr/bin/env python
from appJar import gui
import tkinter
import turtle
app = gui()
def onMenuItemSelect(menuItem):
if menuItem == "Quit":
app.stop()
app.setSticky("news")
fileMenu = ["Quit"]
app.addMenuList("File", fileMenu, onMenuItemSelect)
canvas = tkinter.Canvas(app.topLevel, width=256, height=256)
canvas.pack()
screen = turtle.TurtleScreen(canvas)
t = turtle.RawTurtle(screen)
screen.tracer(100, 0)
t.hideturtle()
t.speed(0)
t.pencolor("green")
t.home()
t.pd()
side = 0
angle = 117
for _ in range(160):
t.forward(side)
t.right(angle)
side += 1
screen.update()
app.go()

Obrázek 12: Obrazec vykreslený upraveným příkladem. Povšimněte si, že kresba je již korektně dokreslena.
9. Želví grafika a složitější obrazec
Samozřejmě se můžeme pokusit o vykreslení složitějšího obrazce, například přepsáním následujícího programu z Loga:
repeat 36 [
left 10
repeat 10 [
left 36
forward 80
repeat 3 [
forward 30
left 120
]
]
]
Do Pythonu je možné tento program přepsat (prakticky příkaz po příkazu) například následujícím způsobem:
for i in range(36):
t.left(10)
for j in range(10):
t.left(36)
t.forward(80)
for k in range(3):
t.forward(30)
t.left(120)

Obrázek 13: Výsledek předchozí sekvence příkazů provedených ve třech vnořených programových smyčkách.
Výsledek zakomponujeme do aplikace, nyní již implicitně se „zrychleným“ vykreslováním a navíc s přidanou logikou pro změnu barev vykreslování:
#!/usr/bin/env python
from appJar import gui
import tkinter
import turtle
app = gui()
def setupTurtle(canvas):
screen = turtle.TurtleScreen(canvas)
t = turtle.RawTurtle(screen)
screen.tracer(100, 0)
t.hideturtle()
t.speed(0)
t.home()
t.pd()
return t, screen
def onMenuItemSelect(menuItem):
if menuItem == "Quit":
app.stop()
app.setSticky("news")
fileMenu = ["Quit"]
app.addMenuList("File", fileMenu, onMenuItemSelect)
canvas = tkinter.Canvas(app.topLevel, width=600, height=600)
canvas.pack()
t, screen = setupTurtle(canvas)
t.hideturtle()
t.speed(0)
t.pencolor("green")
t.home()
t.pd()
screen.colormode(255)
r = 0
g = 0
b = 0
rd = 1
for i in range(72):
t.left(5)
for j in range(10):
t.left(36)
t.forward(80)
for k in range(3):
r += rd
if r > 255 or r < 0:
b += 10
g += 10
rd = -rd
r += rd
t.pencolor((r, g, b))
t.forward(30)
t.left(120)
screen.update()
app.go()

Obrázek 14: Výsledek předchozího příkladu po úpravě barvy kreslení příkazem t.pencolor.
10. Použití rekurze pro vykreslení sněhové vločky Helge von Kocha
Mnohem silnější nástroj, než je pouhé opakování části kódu pomocí programové smyčky for, představuje rekurze. Jedním z nejčastěji ukazovaných a implementovaných rekurzivních algoritmů s grafickým výstupem používajícím želví grafiku je algoritmus pro vykreslení křivky Helge von Kocha, jejímž popisem jsme se již zabývali v seriálu Fraktály v počítačové grafice. Vytváření křivky Helge von Kocha spočívá v provedení následujících kroků (nejedná se o popis programu, ale geometrické konstrukce této křivky):
- Nejprve se zkonstruuje vodorovná úsečka o zadané délce.
- Ve druhém kroku se tato úsečka rozdělí na (stejně dlouhé) třetiny. Prostřední třetina se vyjme a na jejím místě se sestrojí dvě ramena rovnoramenného trojúhelníku. Vznikne tedy obrazec, který se skládá z lomené úsečky (polyčáry), jejíž délka je rovna 4/3 délky původní úsečky, tj. celková délka takto zkonstruované křivky se o třetinu prodlouží.
- Na vzniklý obrazec se opakovaně aplikuje pravidlo uvedené v předchozím bodě, tj. každá úsečka je rozdělena na třetiny, prostřední třetina se vyjme a nahradí se dvojicí ramen rovnoramenného trojúhelníka.
- Ze tří křivek lze pootočením o 120° vytvořit sněhovou vločku.

Obrázek 15: Sněhová vločka Helge von Kocha vykreslená z úseček kratších než 10 jednotek délky.
V následují dvojici funkcí je ukázáno, jak lze rekurzi použít spolu s želví grafikou pro vykreslení fraktální sněhové vločky Helge von Kocha. První funkce vykreslí jednu třetinu vločky:
def koch_curve(t, length, limit):
if length > limit:
koch_curve(t, length/3, limit)
t.right(60)
koch_curve(t, length/3, limit)
t.left(120)
koch_curve(t, length/3, limit)
t.right(60)
koch_curve(t, length/3, limit)
else:
t.forward(length)
O vykreslení třech navzájem pootočených třetin sněhové vločky se postará druhá funkce:
def koch_snowflake(t, limit):
t.home()
t.goto(-70, -70)
t.clear()
t.pencolor("blue")
for _ in range(3):
koch_curve(t, 150, limit)
t.left(120)

Obrázek 16: Sněhová vločka Helge von Kocha vykreslená z úseček kratších než 10 jednotek délky.
Alternativně je možné namísto testu na velikost úsečkových segmentů přímo počítat, kolikrát již byla úsečka (rekurzivně) rozdělena:
Verze psaná v Logu:
to koch_curve :length :iter
ifelse :iter>1 [
koch_curve :length/3 :iter-1
left 60
koch_curve :length/3 :iter-1
right 120
koch_curve :length/3 :iter-1
left 60
koch_curve :length/3 :iter-1
][
forward :length
]
end
Verze přepsaná do Pythonu:
def kochCurve(t, length, iter):
if iter > 1:
kochCurve(t, length/3, iter-1)
t.right(60)
kochCurve(t, length/3, iter-1)
t.left(120)
kochCurve(t, length/3, iter-1)
t.right(60)
kochCurve(t, length/3, iter-1)
else:
t.forward(length)
Tato funkce je zakomponována do dalšího demonstračního příkladu, který vám dává na výběr mezi vykreslením několika různých obrazců s využitím želví grafiky:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
from appJar import gui
import tkinter
import turtle
from math import *
app = gui()
def setupTurtle(canvas):
screen = turtle.TurtleScreen(canvas)
t = turtle.RawTurtle(screen)
screen.tracer(100, 0)
t.hideturtle()
t.speed(0)
t.home()
t.pd()
return t, screen
def onMenuItemSelect(menuItem):
if menuItem == "Quit":
app.stop()
def kochCurve(t, length, iter):
if iter > 1:
kochCurve(t, length/3, iter-1)
t.right(60)
kochCurve(t, length/3, iter-1)
t.left(120)
kochCurve(t, length/3, iter-1)
t.right(60)
kochCurve(t, length/3, iter-1)
else:
t.forward(length)
def kochSnowflake(t, iter):
for _ in range(3):
kochCurve(t, 200, iter)
t.left(120)
def prepareTurtle(t):
t.home()
t.goto(-100, -60)
t.clear()
def onKochSnowflakeSelect(command):
prepareTurtle(t)
t.pencolor("blue")
iter = int(command[0])
kochSnowflake(t, iter)
screen.update()
def onKochCombinationSelect(command):
prepareTurtle(t)
colors = ["red", "orange", "blue", "brown"]
for i in range(4):
t.pencolor(colors[i])
kochSnowflake(t, i+1)
screen.update()
app.setSticky("news")
fileMenu = ["Quit"]
kochMenu = ["1 iterarion", "2 iterations", "3 iterations",
"4 iterations", "5 iterations"]
specialMenu = ["Combine snowflakes"]
app.addMenuList("File", fileMenu, onMenuItemSelect)
app.addMenuList("Koch Snowflake", kochMenu, onKochSnowflakeSelect)
app.addMenuItem("Special", "Combine snowflakes", onKochCombinationSelect)
canvas = tkinter.Canvas(app.topLevel, width=256, height=256)
canvas.pack()
t, screen = setupTurtle(canvas)
app.go()

Obrázek 17: Sněhová vločka Helge von Kocha vykreslená z úseček kratších než 5 jednotek délky.
11. Rekurzivní kreslení domku aneb Pythagorův strom
Dalším zajímavým útvarem, který je možné vytvořit pomocí želví grafiky a rekurzivně volané procedury (funkce), je takzvaný Pythagorův strom (tento termín jsem objevil ve starším vydání časopisu Elektronika, v angličtině pro něj existují i různá nepatrně odlišná pojmenování, například Pythagoras tree nebo Pythagorean tree). Základem Pythagorova stromu je známý domek kreslený jedním tahem. Pokud považujeme šířku domku a výšku jeho stěn za základní délku, pak mají úhlopříčné tahy délku rovnou odmocnině dvou (√2) a délka stran střechy je naopak rovná převrácené hodnotě odmocnině dvou (1/√2):
def house(side):
# základna
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# stěna
t.left(90+45)
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# úsečka pod střechou
t.left(90+45)
t.forward(side)
# první část střechy
t.right(90)
t.right(90-45)
t.forward(side*math.cos(math.radians(45)))
# druhá část střechy
t.right(90)
t.forward(side*math.sin(math.radians(45)))
# zbývající stěna
t.right(45)
t.forward(side)
t.left(90)
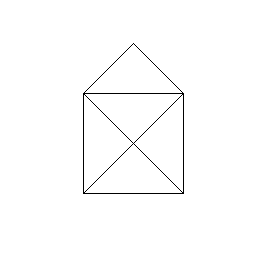
Obrázek 18: Domek jedním tahem vykreslený předchozí funkcí.
V proceduře nazvané house (domek) se šířka domku a jeho výška předává v parametru side. O výpočet druhé odmocniny se stará matematická funkce math.sqrt s parametrem 2. V případě, že se vykreslení každé strany střechy nahradí rekurzivně volanou procedurou pro kreslení celého domku, získáme charakteristický tvar vzdáleně podobný stromu či keři:
def house(side):
# základna
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# stěna
t.left(90+45)
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# úsečka pod střechou
t.left(90+45)
t.forward(side)
# první část střechy
t.right(90)
t.right(90-45)
house(side*math.cos(math.radians(45)))
# druhá část střechy
t.right(90)
house(side*math.sin(math.radians(45)))
# zbývající stěna
t.right(45)
t.forward(side)
t.left(90)
Samozřejmě je nutné opět zavést podmínku pro ukončení rekurze, jinak by program skončil běhovou chybou (překročení volné kapacity paměti). Pokud je délka strany pro vykreslení domku menší než čtyři kroky želvy, je místo domku vykreslena pouze úsečka o této délce, čímž je zajištěno vykreslení střech domků ležících na konci „stromu“. Pokud však délka strany přesahuje tuto hodnotu (deset kroků želvy), je jedním tahem vykreslen celý domek:
def house(side):
if side > 4:
# základna
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# stěna
t.left(90+45)
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# úsečka pod střechou
t.left(90+45)
t.forward(side)
# první část střechy
t.right(90)
t.right(90-45)
house(side*math.cos(math.radians(45)))
# druhá část střechy
t.right(90)
house(side*math.sin(math.radians(45)))
# zbývající stěna
t.right(45)
t.forward(side)
t.left(90)
else:
t.forward(side)
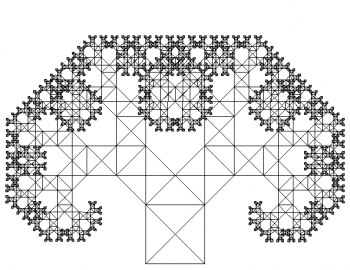
Obrázek 19: Rekurzivní kreslení domku jedním tahem aneb Pythagorův strom.
12. Zobecněný Pythagorův strom
Při kresbě zobecněného Pythagorova stromu je nutné vytvořit proceduru, která dokáže nakreslit pravoúhlý trojúhelník o zadané délce přepony (nejdelší strany) a úhlu mezi přeponou a jednou odvěsnou. Proč ale potřebujeme vytvořit takovou proceduru? Zobecněný Pythagorův strom se od pravidelného Pythagorova stromu, který jsme si popsali v předchozí kapitole, odlišuje především v tom, že je použit jiný úhel větvení, což jinými slovy znamená, že se změní tvar střechy z rovnoramenného pravoúhlého trojúhelníku na jiný pravoúhlý trojúhelník:

Délka přepony v tomto trojúhelníku odpovídá šířce „domku“, který tvoří základ celého stromu, a odvěsny představují obě plochy střechy. Změnou úhlu odchylky první odvěsny se změní i tvar celého trojúhelníku.
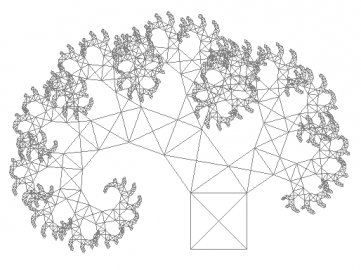
Obrázek 20: Zobecněný Pythagorův strom.
Úprava je jednoduchá; změněné řádky jsou zvýrazněny:
def house(side, angle):
if side > 4:
# základna
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# stěna
t.left(90+45)
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# úsečka pod střechou
t.left(90+45)
t.forward(side)
# první část střechy
t.right(90)
t.right(90-angle)
# původní příkaz: domek side/sqrt 2 :uhel
house(side*math.cos(math.radians(angle)), angle)
# druhá část střechy
t.right(90)
# původní příkaz: domek side/sqrt 2 :uhel
house(side*math.sin(math.radians(angle)), angle)
# zbývající stěna
t.right(angle)
t.forward(side)
t.left(90)
else:
t.forward(side)
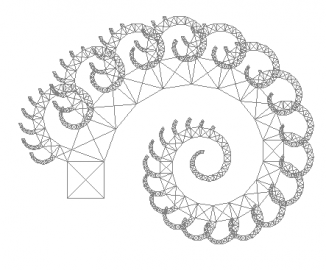
Obrázek 21: Zobecněný Pythagorův strom.
Následuje výpis zdrojového kódu příkladu, který dokáže zobrazit různé typy zobecněného Pythagorova stromu (typ vyberete z hlavního menu):
#!/usr/bin/env python
# vim: set fileencoding=utf-8
from appJar import gui
import math
import tkinter
import turtle
app = gui()
def setupTurtle(canvas):
screen = turtle.TurtleScreen(canvas)
t = turtle.RawTurtle(screen)
screen.tracer(100, 0)
t.hideturtle()
t.speed(0)
t.home()
t.pd()
return t, screen
def onMenuItemSelect(menuItem):
if menuItem == "Quit":
app.stop()
def onDrawMenuSelect(menuItem):
allParams = {
"Tree": (-50, -150, 100, 45),
"Bush": (40, -100, 80, 35),
"Spiral": (-200, -150, 50, 70),
"Spiral2": (-220, -50, 40, 80),
"Spiral3": (-300, -50, 30, 85)
}
params = allParams[menuItem]
t.hideturtle()
t.speed(0)
t.pencolor("gray")
t.goto(params[0], params[1])
t.pd()
t.clear()
house(params[2], params[3])
screen.update()
def house(side, angle):
if side > 4:
# základna
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# stěna
t.left(90+45)
t.forward(side)
# úhlopříčka
t.left(90+45)
t.forward(side*math.sqrt(2))
# úsečka pod střechou
t.left(90+45)
t.forward(side)
# první část střechy
t.right(90)
t.right(90-angle)
# původní příkaz: domek side/sqrt 2 :uhel
house(side*math.cos(math.radians(angle)), angle)
# druhá část střechy
t.right(90)
# původní příkaz: domek side/sqrt 2 :uhel
house(side*math.sin(math.radians(angle)), angle)
# zbývající stěna
t.right(angle)
t.forward(side)
t.left(90)
else:
t.forward(side)
app.setSticky("news")
fileMenu = ["Quit"]
app.addMenuList("File", fileMenu, onMenuItemSelect)
drawMenu = ["Tree", "Bush", "Spiral", "Spiral2", "Spiral3"]
app.addMenuList("Draw", drawMenu, onDrawMenuSelect)
canvas = tkinter.Canvas(app.topLevel, width=600, height=600)
canvas.pack()
t, screen = setupTurtle(canvas)
app.go()
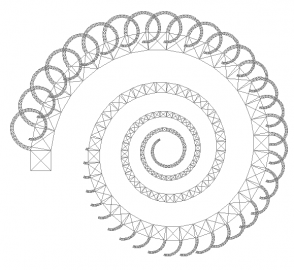
Obrázek 22: Další zobecněný Pythagorův strom.
13. Příkaz goto a jeho využití při kreslení na absolutní souřadnice plátna
Příkazy forward a backward, které jsou mnohdy zkracovány na fd a bk či back, slouží k relativnímu posunu želvy o zadaný počet kroků dopředu či dozadu, přičemž pojmy „dopředu“ a „dozadu“ jsou vztaženy k aktuálnímu natočení želvy. Ovšem existuje i příkaz, který donutí želvu skočit na zadané absolutní souřadnice a v závislosti na zvoleném stavu pera vykreslí či naopak nevykreslí úsečku mezi původní a novou pozicí želvy. Tento příkaz se jmenuje goto, alternativně je ale možné použít i příkaz setpos či setposition. Díky existenci těchto příkazů se želví grafika přibližuje klasické vektorové grafice, což si ukážeme na dalším demonstračním příkladu. Pro doplnění si ještě uveďme, že existují příkazy setx a sety, které nastavují jen x-ovou či naopak y-ovou souřadnici želvy (druhá souřadnice je ponechána na původní hodnotě).
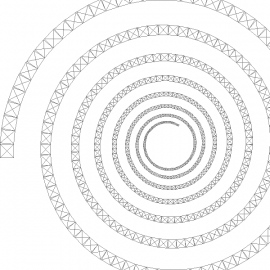
Obrázek 23: Ještě jeden zobecněný Pythagorův strom.
14. Fresnelův fraktál
V článku Fresnel Integral Coloring je popsána tvorba fraktálního útvaru založeného na Fresnelově integrálu. Tvorbu křivky (část z ní – klotoida – se používá na začátku oblouků kolejnic) je možné v Pythonu popsat kódem, v němž se nejdříve vypočítají krátké skoky ve směru daném úhlem představovaným proměnnou f. Povšimněte si, že se hodnota f používá ve druhé mocnině:
def drawFresnel():
x = 0.0
y = 0.0
f = 0.0
for i in range(maxiter+1):
f += fstep
x += cos(f * f)
y += sin(f * f)
t.goto(scale*x, scale*y)
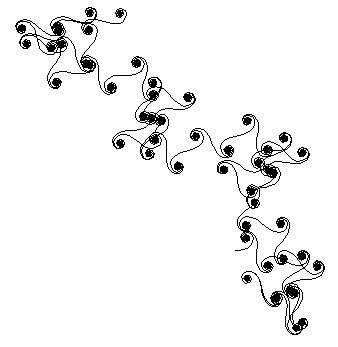
Obrázek 24: Fresnelův fraktál.
Na tomto příkladu se ukáže kombinace možností knihovny appJar a modulu Turtle, neboť přímo z aplikace je možné měnit základní parametry vykreslování – maximální počet iterací, hodnotu fstep i měřítko celého obrazce. Navíc se při výpočtu postupně aktualizuje „teploměr“ sledující, kdy má být výpočet dokončen. Tuto možnost jsme si již popsali v předchozích částech seriálu, nyní zde konečně dostává svůj význam:
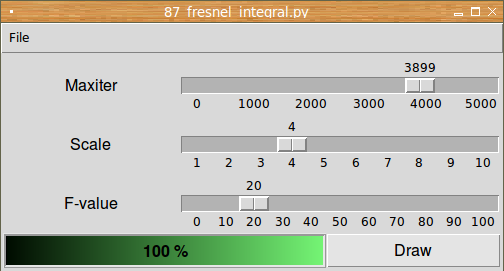
Obrázek 25: Ovládací prvky grafického uživatelského rozhraní aplikace.
#!/usr/bin/env python
from appJar import gui
import tkinter
import turtle
from math import *
app = gui()
def setupTurtle(canvas):
screen = turtle.TurtleScreen(canvas)
t = turtle.RawTurtle(screen)
screen.tracer(100, 0)
t.hideturtle()
t.speed(0)
t.home()
t.pd()
return t, screen
def onMenuItemSelect(menuItem):
if menuItem == "Quit":
app.stop()
def drawFresnel():
global progressBarValue
x = 0.0
y = 0.0
f = 0.0
for i in range(maxiter+1):
progressBarValue = 100.0 * i / maxiter
f += fstep
x += cos(f * f)
y += sin(f * f)
t.goto(scale*x, scale*y)
screen.update()
def updateMeter():
app.setMeter("progressBar", progressBarValue)
def onFresnelDraw(command):
t.home()
t.clear()
drawFresnel()
def onMaxiterChange(widgetName):
global maxiter
value = app.getScale(widgetName)
maxiter = int(value)
def onScaleChange(widgetName):
global scale
value = app.getScale(widgetName)
scale = float(value)
def onFValueChange(widgetName):
global fstep
value = app.getScale(widgetName)
fstep = float(value)/100.0
def createGui(app):
fileMenu = ["Quit"]
app.addMenuList("File", fileMenu, onMenuItemSelect)
app.addLabel("maxiter-label", "Maxiter", row=0, column=0)
app.addScale("maxiter", row=0, column=1, colspan=2)
app.showScaleIntervals("maxiter", 1000)
app.showScaleValue("maxiter")
app.setScaleRange("maxiter", 0, 5000, 1000)
app.setScaleChangeFunction("maxiter", onMaxiterChange)
app.addLabel("scale-label", "Scale", row=1, column=0)
app.addScale("scale", row=1, column=1, colspan=2)
app.showScaleIntervals("scale", 1)
app.showScaleValue("scale")
app.setScaleRange("scale", 1, 10, 4)
app.setScaleChangeFunction("scale", onScaleChange)
app.addLabel("f-value-label", "F-value", row=2, column=0)
app.addScale("f-value", row=2, column=1, colspan=2)
app.showScaleIntervals("f-value", 10)
app.showScaleValue("f-value")
app.setScaleRange("f-value", 0, 100, 20)
app.setScaleChangeFunction("f-value", onFValueChange)
app.addMeter("progressBar", row=3, column=0, colspan=2)
app.setMeterFill("progressBar", "green")
app.addButton("Draw", onFresnelDraw, row=3, column=2)
app.registerEvent(updateMeter)
progressBarValue = 0
scale = 4.0
maxiter = 1000
fstep = 0.2
app.setSticky("news")
createGui(app)
canvas = tkinter.Canvas(app.topLevel, width=500, height=500)
canvas.pack()
t, screen = setupTurtle(canvas)
app.go()
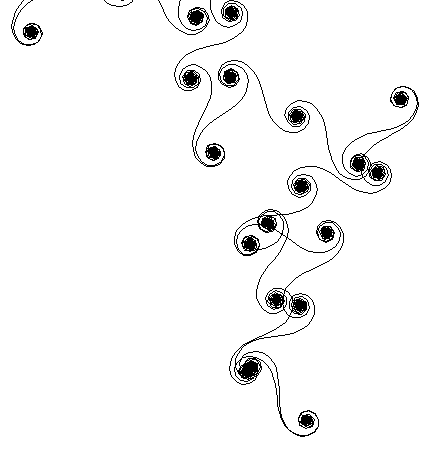
Obrázek 26: Fresnelův fraktál.
15. Systémy iterovaných funkcí (IFS)
V závěrečné části článku si ukážeme, jak je možné vykreslit různé obrazce s využitím systémů iterovaných funkcí (IFS). Tato problematika byla podrobněji popsána v článku Systémy iterovaných funkcí a algoritmus náhodné procházky , takže si dnes pouze řekneme, jak je možné IFS vykreslovat s využitím želví grafiky.
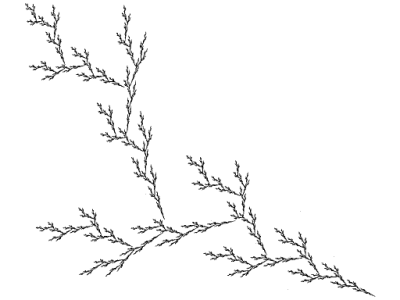
Obrázek 27: Model větvičky vytvořený pomocí IFS se třemi afinními transformacemi.
Vzhledem k tomu, že základní algoritmus náhodné procházky vykresluje jednotlivé body umisťované na absolutní souřadnice, použijeme pro vykreslování dvojici funkcí goto (přesun želvy na absolutní souřadnice) a dot (vykreslení bodu na pozici želvy). Samozřejmě je nutné, aby želva při svém pohybu řízeném funkcí goto nekreslila úsečku, takže před začátkem vykreslování zavoláme příkaz penup (či jen pu).
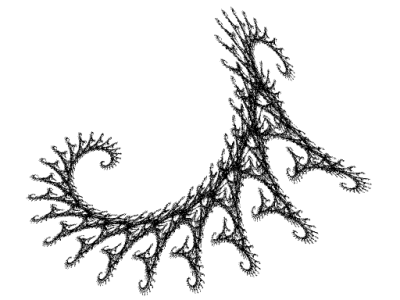
Obrázek 28: Fraktální drak vytvořený systémem iterovaných funkcí.
16. Vykreslení jednoduchého systému iterovaných funkcí krok za krokem
Každý IFS je popsán několika transformačními maticemi (ve 2D) a pravděpodobností aplikace té které transformace. Součet pravděpodobností by měl být roven jedné. Transformační matice by sice teoreticky měla mít velikost 3×3 prvky, ovšem poslední sloupec vždy obsahuje hodnotu [0, 0, 1]T, takže nám stačí uložit jen šest prvků matice. Celkem je tedy každá transformace reprezentována sedmi hodnotami – šest pro transformační matici, sedmá je pravděpodobnost:
ifs = (
(+0.85000, +0.04000, -0.04000, +0.85000, +0.00000, +1.60000, +0.85000),
(+0.20000, -0.26000, +0.23000, +0.22000, +0.00000, +1.60000, +0.07000),
(-0.15000, +0.28000, +0.26000, +0.24000, +0.00000, +0.44000, +0.07000),
(+0.00000, +0.00000, +0.00000, +0.16000, +0.00000, +0.00000, +0.01000))
Programová smyčka pro vykreslení IFS nejprve náhodně vybere transformaci. Povšimněte si, že čím má transformace vyšší pravděpodobnost, tím častěji bude vybrána (pokud se tedy můžeme spolehnout na generátor náhodných čísel):
# nahodne vybrat transformaci
pp = random()
sum = 0
k = 0
while sum <= pp:
sum += ifs[k][6]
k += 1
k -= 1
Dále se vybraná transformace aplikuje na bod [x1, y1]:
# aplikovat transformaci x2 = x1*ifs[k][0] + y1*ifs[k][1] + ifs[k][4] y2 = x1*ifs[k][2] + y1*ifs[k][3] + ifs[k][5] x1 = x2 y1 = y2
Poslední fáze – pokud byl překročen stanovený počet startovních iterací, vykreslí se bod:
# pokud byl prekrocen pocet startovnich iteraci
if i > start_iter:
x2 = x1 * scale - dx
y2 = y1 * scale - dy
t.goto(x2, y2)
t.dot(1)
Poznámka: tato podmínka nám prakticky zaručí, že bod [x1, y1] již leží v atraktoru systému.
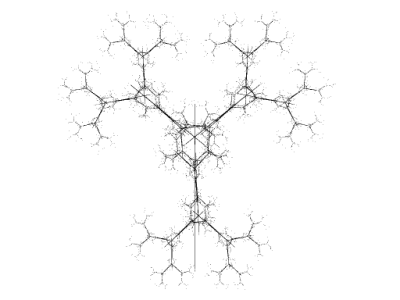
Obrázek 29: Variace na téma binárního stromu.
17. Zdrojový kód příkladu pro vykreslení IFS
Funkce popsané v předchozí kapitole jsou součástí dnešního předposledního demonstračního příkladu, jehož zdrojový kód najdete pod tímto odstavcem:
#!/usr/bin/env python
from appJar import gui
import tkinter
import turtle
import sys
from random import random
app = gui()
ifs = (
(+0.85000, +0.04000, -0.04000, +0.85000, +0.00000, +1.60000, +0.85000),
(+0.20000, -0.26000, +0.23000, +0.22000, +0.00000, +1.60000, +0.07000),
(-0.15000, +0.28000, +0.26000, +0.24000, +0.00000, +0.44000, +0.07000),
(+0.00000, +0.00000, +0.00000, +0.16000, +0.00000, +0.00000, +0.01000),
(+1.00000, +0.00000, +0.00000, +1.00000, +0.00000, +0.00000, +1.00000))
def setupTurtle(canvas):
screen = turtle.TurtleScreen(canvas)
t = turtle.RawTurtle(screen)
screen.tracer(100, 0)
t.hideturtle()
t.speed(0)
t.home()
t.pu()
return t, screen
def onMenuItemSelect(menuItem):
if menuItem == "Quit":
app.stop()
def onIFSItemSelect(menuItem):
global ifs
ifs = ifs_systems[menuItem]
def drawIFS(ifs):
global progressBarValue
start_iter = 100
# generovane souradnice
x1 = 0
y1 = 0
dy = 220
scale = 45
for i in range(maxiter+1):
progressBarValue = 100.0 * i / maxiter
# nahodne vybrat transformaci
pp = random()
sum = 0
k = 0
while sum <= pp:
sum += ifs[k][6]
k += 1
k -= 1
# aplikovat transformaci
x2 = x1*ifs[k][0] + y1*ifs[k][1] + ifs[k][4]
y2 = x1*ifs[k][2] + y1*ifs[k][3] + ifs[k][5]
x1 = x2
y1 = y2
# pokud byl prekrocen pocet startovnich iteraci
if i > start_iter:
x2 = x1 * scale
y2 = y1 * scale - dy
t.goto(x2, y2)
t.dot(1)
screen.update()
def updateMeter():
app.setMeter("progressBar", progressBarValue)
def onIFSDraw(command):
t.home()
t.clear()
drawIFS(ifs)
def onMaxiterChange(widgetName):
global maxiter
value = app.getScale(widgetName)
maxiter = int(value)
def createGui(app):
fileMenu = ["Quit"]
app.addMenuList("File", fileMenu, onMenuItemSelect)
app.addLabel("maxiter-label", "Maxiter", row=0, column=0)
app.addScale("maxiter", row=0, column=1, colspan=2)
app.showScaleIntervals("maxiter", 5000)
app.showScaleValue("maxiter")
app.setScaleRange("maxiter", 0, 25000, 5000)
app.setScaleChangeFunction("maxiter", onMaxiterChange)
app.addMeter("progressBar", row=3, column=0, colspan=2)
app.setMeterFill("progressBar", "green")
app.addButton("Draw", onIFSDraw, row=3, column=2)
app.registerEvent(updateMeter)
progressBarValue = 0
maxiter = 5000
app.setSticky("news")
createGui(app)
canvas = tkinter.Canvas(app.topLevel, width=500, height=500)
canvas.pack()
t, screen = setupTurtle(canvas)
app.go()
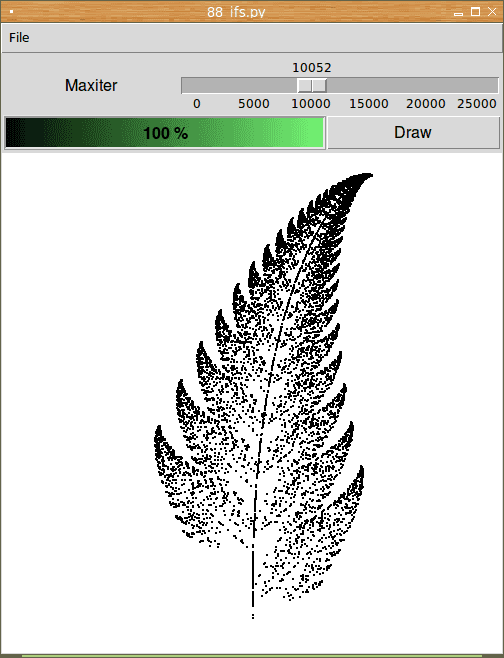
Obrázek 30: Barnsleyova kapradina je typickým představitelem IFS.
18. Demonstrační příklad: galerie IFS, výběr a vykreslení vybraného IFS
Poslední demonstrační příklad je vlastně pouze rozšířením příkladu předchozího o parametry dalších IFS. Konkrétní IFS je možné vybrat z hlavního menu, které obsahuje skupinu radiových tlačítek:
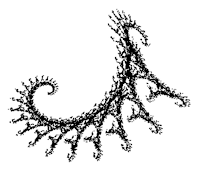
Obrázek 31: IFS vykreslený dnešním posledním demonstračním příkladem.
Zdrojový kód příkladu je již poměrně dlouhý, nicméně podstatnou část zabírají matice transformací, tedy „pouhá“ data:
#!/usr/bin/env python
from appJar import gui
import tkinter
import turtle
import sys
from random import random
app = gui()
ifs_systems = {
"binary": (
( 0.500000, 0.000000, 0.000000, 0.500000,-2.563477,-0.000003, 0.333333),
( 0.500000, 0.000000, 0.000000, 0.500000, 2.436544,-0.000003, 0.333333),
( 0.000000,-0.500000, 0.500000, 0.000000, 4.873085, 7.563492, 0.333333)),
"coral": (
( 0.307692,-0.531469,-0.461538,-0.293706, 5.401953, 8.655175, 0.400000),
( 0.307692,-0.076923, 0.153846,-0.447552,-1.295248, 4.152990, 0.150000),
( 0.000000, 0.545455, 0.692308,-0.195804,-4.893637, 7.269794, 0.450000)),
"crystal": (
( 0.696970,-0.481061,-0.393939,-0.662879, 2.147003,10.310288, 0.747826),
( 0.090909,-0.443182, 0.515152,-0.094697, 4.286558, 2.925762, 0.252174)),
"dragon": (
( 0.824074, 0.281482,-0.212346, 0.864198,-1.882290,-0.110607, 0.787473),
( 0.088272, 0.520988,-0.463889,-0.377778, 0.785360, 8.095795, 0.212527)),
"dragon2": (
( 0.824074, 0.281481,-0.212346, 0.864197,-1.772710, 0.137795, 0.771268),
(-0.138580, 0.283951,-0.670062,-0.279012, 2.930991, 7.338924, 0.228732)),
"feather": (
( 0.870370, 0.074074,-0.115741, 0.851852,-1.278016, 0.070331, 0.798030),
(-0.162037,-0.407407, 0.495370, 0.074074, 6.835726, 5.799174, 0.201970)),
"fern": (
( 0.850000, 0.040000,-0.040000, 0.850000, 0.000000, 1.600000, 0.850000),
( 0.200000,-0.260000, 0.230000, 0.220000, 0.000000, 1.600000, 0.070000),
(-0.150000, 0.280000, 0.260000, 0.240000, 0.000000, 0.440000, 0.070000),
( 0.000000, 0.000000, 0.000000, 0.160000, 0.000000, 0.000000, 0.010000)),
"koch": (
( 0.307692, 0.000000, 0.000000, 0.294118, 4.119164, 1.604278, 0.151515),
( 0.192308,-0.205882, 0.653846, 0.088235,-0.688840, 5.978916, 0.253788),
( 0.192308, 0.205882,-0.653846, 0.088235, 0.668580, 5.962514, 0.253788),
( 0.307692, 0.000000, 0.000000, 0.294118,-4.136530, 1.604278, 0.151515),
( 0.384615, 0.000000, 0.000000,-0.294118,-0.007718, 2.941176, 1.000000)),
"spiral": (
( 0.787879,-0.424242, 0.242424, 0.859848, 1.758647, 1.408065, 0.895652),
(-0.121212, 0.257576, 0.151515, 0.053030,-6.721654, 1.377236, 0.052174),
( 0.181818,-0.136364, 0.090909, 0.181818, 6.086107, 1.568035, 0.052174)),
"tree": (
( 0.000000, 0.000000, 0.000000, 0.500000, 0.000000, 0.000000, 0.050000),
( 0.420000,-0.420000, 0.420000, 0.420000, 0.000000, 0.200000, 0.400000),
( 0.420000, 0.420000,-0.420000, 0.420000, 0.000000, 0.200000, 0.400000),
( 0.100000, 0.000000, 0.000000, 0.100000, 0.000000, 0.200000, 0.150000)),
"triangle": (
( 0.500000, 0.000000, 0.000000, 0.500000,-0.500000, 0.000000, 0.333333),
( 0.500000, 0.000000, 0.000000, 0.500000, 0.500000, 0.000000, 0.333333),
( 0.500000, 0.000000, 0.000000, 0.500000, 0.000000, 0.860000, 0.333334)),
}
def setupTurtle(canvas):
screen = turtle.TurtleScreen(canvas)
t = turtle.RawTurtle(screen)
screen.tracer(100, 0)
t.hideturtle()
t.speed(0)
t.home()
t.pu()
return t, screen
def onMenuItemSelect(menuItem):
if menuItem == "Quit":
app.stop()
def onIFSItemSelect(menuItem):
global ifs
ifs = ifs_systems[menuItem]
def drawIFS(ifs):
global progressBarValue
start_iter = 100
# generovane souradnice
x1 = 0
y1 = 0
dy = 100
for i in range(maxiter+1):
progressBarValue = 100.0 * i / maxiter
# nahodne vybrat transformaci
pp = random()
sum = 0
k = 0
while sum <= pp:
sum += ifs[k][6]
k += 1
k -= 1
# aplikovat transformaci
x2 = x1*ifs[k][0] + y1*ifs[k][1] + ifs[k][4]
y2 = x1*ifs[k][2] + y1*ifs[k][3] + ifs[k][5]
x1 = x2
y1 = y2
# pokud byl prekrocen pocet startovnich iteraci
if i > start_iter:
x2 = x1 * 30
y2 = y1 * 30 - dy
t.goto(x2, y2)
t.dot(1)
screen.update()
def updateMeter():
app.setMeter("progressBar", progressBarValue)
def onIFSDraw(command):
t.home()
t.clear()
drawIFS(ifs)
def onMaxiterChange(widgetName):
global maxiter
value = app.getScale(widgetName)
maxiter = int(value)
def createGui(app):
fileMenu = ["Quit"]
app.addMenuList("File", fileMenu, onMenuItemSelect)
ifsMenu = sorted(ifs_systems.keys())
for ifsMenuItem in ifsMenu:
app.addMenuRadioButton("IFS", "ifs", ifsMenuItem,
lambda i, ifsMenuItem=ifsMenuItem: onIFSItemSelect(ifsMenuItem))
app.addLabel("maxiter-label", "Maxiter", row=0, column=0)
app.addScale("maxiter", row=0, column=1, colspan=2)
app.showScaleIntervals("maxiter", 5000)
app.showScaleValue("maxiter")
app.setScaleRange("maxiter", 0, 25000, 5000)
app.setScaleChangeFunction("maxiter", onMaxiterChange)
app.addMeter("progressBar", row=3, column=0, colspan=2)
app.setMeterFill("progressBar", "green")
app.addButton("Draw", onIFSDraw, row=3, column=2)
app.registerEvent(updateMeter)
progressBarValue = 0
maxiter = 5000
ifs = ifs_systems["binary"]
app.setSticky("news")
createGui(app)
canvas = tkinter.Canvas(app.topLevel, width=500, height=500)
canvas.pack()
t, screen = setupTurtle(canvas)
app.go()

Obrázek 32: IFS vykreslený dnešním posledním demonstračním příkladem.
19. Repositář s demonstračními příklady
Zdrojové kódy všech dvanácti dnes popsaných demonstračních příkladů byly opět uloženy do Git repositáře dostupného na adrese https://github.com/tisnik/presentations. Pokud nechcete klonovat celý repositář, můžete namísto toho použít odkazy na jednotlivé příklady, které naleznete v následující tabulce:
Poznámka: pro úspěšné spuštění těchto příkladů musíte mít v aktuálním adresáři rozbalenou knihovnu appJar!. Podrobnosti o instalaci jsme si řekli v úvodním článku.
20. Odkazy na Internetu
- Seriál Letní škola programovacího jazyka Logo
http://www.root.cz/serialy/letni-skola-programovaciho-jazyka-logo/ - Educational programming language
http://en.wikipedia.org/wiki/Educational_programming_language - Logo Tree Project:
http://www.elica.net/download/papers/LogoTreeProject.pdf - Hra Breakout napísaná v Tkinteri
https://www.root.cz/clanky/hra-breakout-napisana-v-tkinteri/ - Hra Snake naprogramovaná v Pythone s pomocou Tkinter
https://www.root.cz/clanky/hra-snake-naprogramovana-v-pythone-s-pomocou-tkinter/ - 24.1. turtle — Turtle graphics
https://docs.python.org/3.5/library/turtle.html#module-turtle - TkDND
http://freecode.com/projects/tkdnd - Python Tkinter Fonts
https://www.tutorialspoint.com/python/tk_fonts.htm - The Tkinter Canvas Widget
http://effbot.org/tkinterbook/canvas.htm - Ovládací prvek (Wikipedia)
https://cs.wikipedia.org/wiki/Ovl%C3%A1dac%C3%AD_prvek_%28po%C4%8D%C3%ADta%C4%8D%29 - Rezervovaná klíčová slova v Pythonu
https://docs.python.org/3/reference/lexical_analysis.html#keywords - TkDocs: Styles and Themes
http://www.tkdocs.com/tutorial/styles.html - Drawing in Tkinter
http://zetcode.com/gui/tkinter/drawing/ - Changing ttk widget text color (StackOverflow)
https://stackoverflow.com/questions/16240477/changing-ttk-widget-text-color - The Hitchhiker's Guide to Pyhton: GUI Applications
http://docs.python-guide.org/en/latest/scenarios/gui/ - 7 Top Python GUI Frameworks for 2017
http://insights.dice.com/2014/11/26/5-top-python-guis-for-2015/ - GUI Programming in Python
https://wiki.python.org/moin/GuiProgramming - Cameron Laird's personal notes on Python GUIs
http://phaseit.net/claird/comp.lang.python/python_GUI.html - Python GUI development
http://pythoncentral.io/introduction-python-gui-development/ - Graphic User Interface FAQ
https://docs.python.org/2/faq/gui.html#graphic-user-interface-faq - TkInter
https://wiki.python.org/moin/TkInter - Tkinter 8.5 reference: a GUI for Python
http://infohost.nmt.edu/tcc/help/pubs/tkinter/web/index.html - TkInter (Wikipedia)
https://en.wikipedia.org/wiki/Tkinter - appJar
http://appjar.info/ - appJar (Wikipedia)
https://en.wikipedia.org/wiki/AppJar - appJar na Pythonhosted
http://pythonhosted.org/appJar/ - appJar widgets
http://appjar.info/pythonWidgets/ - Stránky projektu PyGTK
http://www.pygtk.org/ - PyGTK (Wikipedia)
https://cs.wikipedia.org/wiki/PyGTK - Stránky projektu PyGObject
https://wiki.gnome.org/Projects/PyGObject - Stránky projektu Kivy
https://kivy.org/#home - Stránky projektu PyQt
https://riverbankcomputing.com/software/pyqt/intro - PyQt (Wikipedia)
https://cs.wikipedia.org/wiki/PyGTK - Stránky projektu PySide
https://wiki.qt.io/PySide - PySide (Wikipedia)
https://en.wikipedia.org/wiki/PySide - Stránky projektu Kivy
https://kivy.org/#home - Kivy (framework, Wikipedia)
https://en.wikipedia.org/wiki/Kivy_(framework) - QML Applications
http://doc.qt.io/qt-5/qmlapplications.html - KDE
https://www.kde.org/ - Qt
https://www.qt.io/ - GNOME
https://en.wikipedia.org/wiki/GNOME - Category:Software that uses PyGTK
https://en.wikipedia.org/wiki/Category:Software_that_uses_PyGTK - Category:Software that uses PyGObject
https://en.wikipedia.org/wiki/Category:Software_that_uses_PyGObject - Category:Software that uses wxWidgets
https://en.wikipedia.org/wiki/Category:Software_that_uses_wxWidgets - GIO
https://developer.gnome.org/gio/stable/ - GStreamer
https://gstreamer.freedesktop.org/ - GStreamer (Wikipedia)
https://en.wikipedia.org/wiki/GStreamer - Wax Gui Toolkit
https://wiki.python.org/moin/Wax - Python Imaging Library (PIL)
http://infohost.nmt.edu/tcc/help/pubs/pil/ - Why Pyjamas Isn’t a Good Framework for Web Apps (blogpost z roku 2012)
http://blog.pyjeon.com/2012/07/29/why-pyjamas-isnt-a-good-framework-for-web-apps/





























