Obsah
1. Emergence: struktury vzniklé ze zdánlivého chaosu
2. Jednoduchý framework pro zobrazení částicového systému
3. Ukázka obrazovky s vizualizovaným statickým částicovým systémem
4. Realizace dynamického částicového systému
5. Výpočet nové pozice částic na základě jejich rychlosti a případných odrazů
6. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
7. Přidání pravidla pro vzájemné odpuzování částic
8. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
9. Větší množství částicových systémů
10. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
11. Pravidla pro interakci mezi částicemi z různých systémů
12. Změna funkce apply_rule na apply_rules
13. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
14. Další vylepšení interaktivity
15. Funkce se smyčkou pro obsluhu událostí
16. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
17. Realizace částicového systému v Pythonu
19. Repositář s demonstračními příklady
1. Emergence: struktury vzniklé ze zdánlivého chaosu
V některých dynamických systémech mohou i na základě aplikace mnohdy velmi jednoduchých pravidel vznikat složitější emergentní struktury. Tato vlastnost se týká mnoha typů komplexních systémů s mnohdy složitě popsanými entitami (nebo objekty, i když v kontextu IT je tento termín zavádějící), ovšem nás budou v dnešním (i v navazujícím) článku zajímat především takové komplexní systémy, v nichž je možné vlastnosti jejich jednotlivých entit, resp. elementů reprezentovat jako body v ploše či v prostoru. Stav takového dynamického systému je tedy popsán pozicemi těchto bodů, k nimž se většinou přidává i vektor rychlosti.
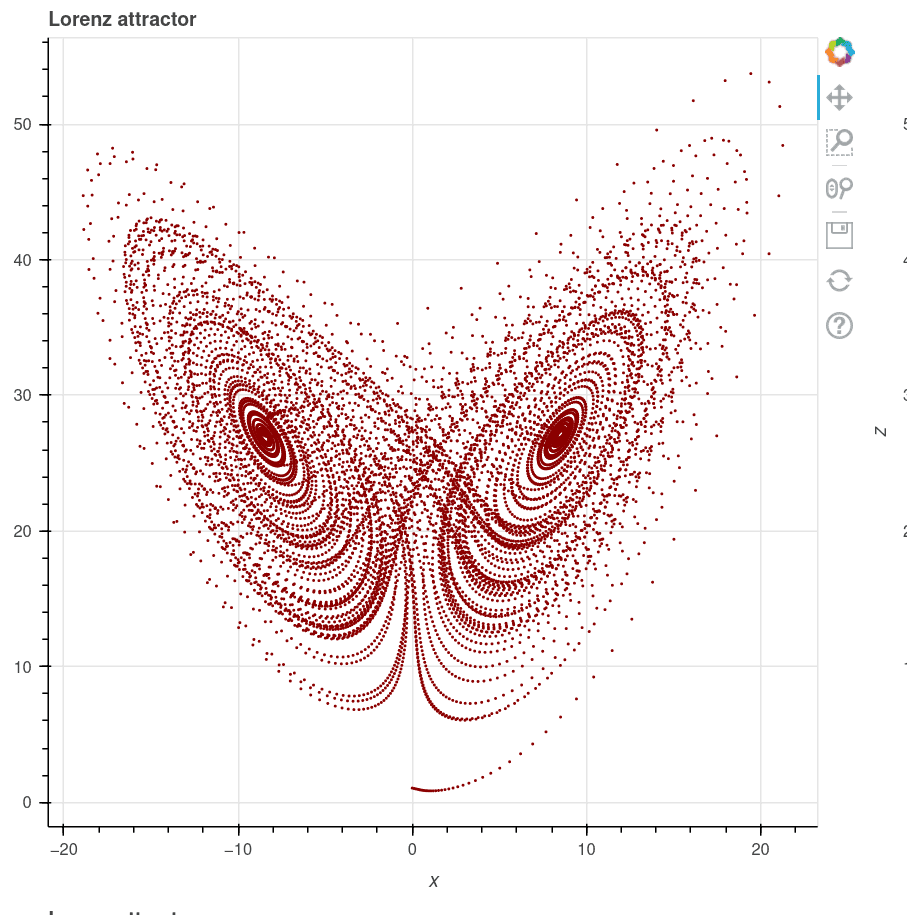
Obrázek 1: Lorenzův atraktor je známým dynamickým systémem s podivným atraktorem.
Poměrně známým příkladem mohou být různé systémy částic (particle systems), v nichž je možné při vhodné definici pravidel chování jednotlivých částic taktéž nalézt mnohdy velmi zajímavě vypadající emergentní struktury. Toto téma je sice poměrně rozsáhlé a vyžádá si nejméně jeden samostatný článek (navíc trošku mimo hlavní záběr Roota), ovšem již dnes si můžeme jeden takový jednoduše implementovatelný částicový systém ukázat. A vzhledem k tomu, že dále zmíněný částicový systém vede ke vzniku emergentní struktury (a nikoli pouze náhodného „oblaku“ bodů), budeme moci výsledek vizualizovat a to nikoli jako pouhý statický obrázek, ale jako animaci ukazující postupný rozvoj tohoto dynamického systému.
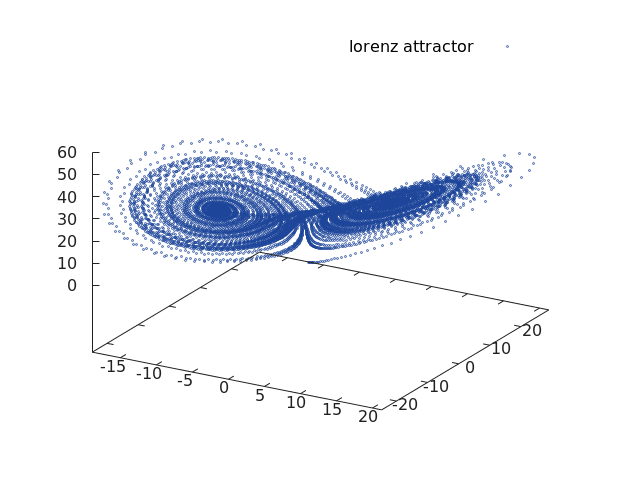
Obrázek 2: Lorenzův atraktor vykreslený ve formě 3D grafu.
2. Jednoduchý framework pro zobrazení částicového systému
Pro účely vizualizace postupné změny stavu dynamického systému (tedy pro tvorbu animací) si vytvoříme jednoduchý framework, který budeme v rámci dalších kapitol postupně vylepšovat. Nejprve nastavíme okraje okna, do kterých nebude zasahovat žádná částice. A taktéž specifikujeme maximální počet částic v systému:
/* model options */ #define BORDER 50 /* total number of particles */ #define MAX_PARTICLES 1000
Každá částice bude prozatím reprezentována strukturou s jejími souřadnicemi:
typedef struct {
float x;
float y;
} Particle;
Reprezentace barvy částic v systému je triviální:
typedef struct Color {
unsigned char r;
unsigned char g;
unsigned char b;
} Color;
Celý částicový systém bude prozatím reprezentován strukturou s částicemi (alokovaný blok – částice nevytváříme ani je neničíme), s počtem částic a taktéž s barvou všech částic v systému:
typedef struct {
Particle *particles;
int max;
Color color;
} ParticleSystem;
A modelovaný svět je prozatím reprezentován triviálním způsobem (opět se postupně tato struktura bude rozšiřovat):
typedef struct {
ParticleSystem particle_system;
} Model;
Pro prvotní náhodné rozmístění částic na obrazovce použijeme funkci nazvanou create_particles s pomocnými funkcemi random_x a random_y (používám zvláštní funkce, aby bylo možné generátor souřadnic částic později parametrizovat):
float random_x() {
return (WIDTH - BORDER * 2) * (float)rand() / RAND_MAX + BORDER;
}
float random_y() {
return (HEIGHT - BORDER * 2) * (float)rand() / RAND_MAX + BORDER;
}
void create_particles(int max, Particle *particles) {
int i;
for (i = 0; i < max; i++) {
particles[i].x = random_x();
particles[i].y = random_y();
}
}
Funkce init_model se stará o vytvoření celého modelovaného světa s částicemi:
Model init_model(void) {
Color color = {255, 255, 80};
Model model;
model.particle_system.color = color;
model.particle_system.particles =
(Particle *)malloc(MAX_PARTICLES * sizeof(Particle));
model.particle_system.max = MAX_PARTICLES;
createParticles(MAX_PARTICLES, model.particle_system.particles);
return model;
}
A konečně funkce redraw poslouží pro překreslení částicového systému na obrazovku. Povšimněte si, že každá částice je vykreslena jako malý symbol + (samotné vykreslování na úrovni pixelů je dosti pomalé! a lze ho optimalizovat):
void redraw(GraphicsState *graphicsState, SDL_Surface *pixmap, Model *model) {
int i;
ParticleSystem particle_system = model->particle_system;
SDL_FillRect(pixmap, NULL, 0x00);
for (i = 0; i < particle_system.max; i++) {
Particle particle = particle_system.particles[i];
Color color = particle_system.color;
putpixel(pixmap, particle.x, particle.y, color.r, color.g, color.b);
putpixel(pixmap, particle.x - 1, particle.y, color.r, color.g, color.b);
putpixel(pixmap, particle.x + 1, particle.y, color.r, color.g, color.b);
putpixel(pixmap, particle.x, particle.y - 1, color.r, color.g, color.b);
putpixel(pixmap, particle.x, particle.y + 1, color.r, color.g, color.b);
}
show_pixmap(graphicsState, pixmap);
}
3. Ukázka obrazovky s vizualizovaným statickým částicovým systémem
Pro překlad a slinkování programu určeného pro vykreslení statického částicového systému je nutný překladač céčka (GCC, TCC, Clang atd.) a knihovna SDL2 (její vývojářská varianta). Po spuštění příkladu by se měla zobrazit obrazovka s přibližně 1000 částicemi. Může jich být méně, pokud se některé částice překrývají:
Obrázek 3: Statický částicový systém vykreslený kódem popsaným v předchozí kapitole.
4. Realizace dynamického částicového systému
Ve druhém kroku začněme realizací velmi jednoduchého částicového systému, v němž se budou nacházet částice, které se pohybují v dvourozměrné ploše a po nárazu na okraje plochy (okna) se odrazí. Žádná další pravidla ovlivňující pohyb částic prozatím nebudou implementována. Každá částice je uložena jako dvojice údajů [poloha, rychlost], přičemž jak poloha, tak i rychlost jsou dvourozměrnými vektory. Částici tedy můžeme popsat běžnou strukturou (oproti předchozí variantě jsme přidali složky vektoru rychlosti):
typedef struct {
float x;
float y;
float vx;
float vy;
} Particle;
Celý částicový systém pak může být uložen taktéž ve formě struktury, která bude obsahovat alokovaný blok s částicemi (ty nebudou vznikat ani zanikat), počtem částic a taktéž barvou všech částic v systému. Později uvidíme, z jakého důvodu je barva uložena zrovna zde:
typedef struct Color {
unsigned char r;
unsigned char g;
unsigned char b;
} Color;
typedef struct {
Particle *particles;
int max;
Color color;
} ParticleSystem;
Částicový systém je navíc společně s takzvaným pravidlem (rule, prozatím jediná hodnota s plovoucí řádovou čárkou) uložen ve struktuře představující celý modelovaný svět, jenž je složený pouze z částic:
typedef struct {
float rule;
ParticleSystem particle_system;
} Model;
Inicializace hodnoty rule je prozatím triviální (později se funkce rozšíří):
void init_rule(Model *model) {
model->rule = 2.0 * (float)rand() / RAND_MAX - 1.0;
}
Následuje upravená varianta funkce create_particles, která kromě pozice částic nastaví i jejich počáteční rychlost:
void create_particles(int max, Particle *particles) {
int i;
for (i = 0; i < max; i++) {
particles[i].x = randomX();
particles[i].y = randomY();
particles[i].vx = (float)rand() / RAND_MAX - 0.5;
particles[i].vy = (float)rand() / RAND_MAX - 0.5;
}
}
Vykreslení částicového systému je realizováno naprosto stejnou funkcí, jako v prvním příkladu. Jen pro úplnost tedy:
void redraw(GraphicsState *graphicsState, SDL_Surface *pixmap, Model *model) {
int i;
ParticleSystem particle_system = model->particle_system;
SDL_FillRect(pixmap, NULL, 0x00);
for (i = 0; i < particle_system.max; i++) {
Particle particle = particle_system.particles[i];
Color color = particle_system.color;
putpixel(pixmap, particle.x, particle.y, color.r, color.g, color.b);
putpixel(pixmap, particle.x - 1, particle.y, color.r, color.g, color.b);
putpixel(pixmap, particle.x + 1, particle.y, color.r, color.g, color.b);
putpixel(pixmap, particle.x, particle.y - 1, color.r, color.g, color.b);
putpixel(pixmap, particle.x, particle.y + 1, color.r, color.g, color.b);
}
show_pixmap(graphicsState, pixmap);
}
5. Výpočet nové pozice částic na základě jejich rychlosti a případných odrazů
V každém snímku je nutné vypočítat nové pozice všech částic v částicovém systému. Každé částici je přiřazena rychlost, takže můžeme provést pseuodointegraci a vypočítat novou pozici částice a takto:
a->x += a->vx; a->y += a->vy;
Navíc do programového kódu přidáme i podmínku pro odraz částic od okrajů obrazovky (a posun částice do vyhrazené oblasti):
void apply_rule(Model *model) {
int i;
for (i = 0; i < model->particle_system.max; i++) {
Particle *a = &model->particle_system.particles[i];
/* move particle */
a->x += a->vx;
a->y += a->vy;
/* check if particle touches scene boundary */
if (a->x <= 0) {
a->vx = -a->vx;
a->x = 0;
}
if (a->x > WIDTH) {
a->vx = -a->vx;
a->x = WIDTH - 1;
}
if (a->y <= 0) {
a->vy = -a->vy;
a->y = 0;
}
if (a->y > HEIGHT) {
a->vy = -a->vy;
a->y = HEIGHT - 1;
}
}
}
Právě tuto funkci budeme postupně rozšiřovat a vylepšovat v rámci dalších kapitol.
6. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
Obrázek 4: Částicový systém s pohybujícími se částicemi.
Obrázek 5: Částicový systém s pohybujícími se částicemi.
Obrázek 6: Částicový systém s pohybujícími se částicemi.
7. Přidání pravidla pro vzájemné odpuzování částic
V následujícím kroku částicový systém poměrně razantně modifikujeme. Upravíme totiž funkci určenou pro aplikaci pravidel, jak se mají částice pohybovat. Nyní se budou částice odpuzovat ve chvíli, kdy se k sobě přiblíží na vzdálenost definovanou v konstantě:
#define MAX_DISTANCE 50
Na základě vzdálenosti dvou částic a a b se vypočítá vektor odpudivé síly:
float dx = a->x - b->x;
float dy = a->y - b->y;
if (dx != 0.0 || dy != 0.0) {
float d = dx * dx + dy * dy;
if (d < MAX_DISTANCE * MAX_DISTANCE) {
/* repel force */
float f = g / sqrt(d);
fx += f * dx;
fy += f * dy;
}
}
Navíc se pro dosažení větší stability (aby systém příliš „nekmital“ a nebyla v něm velká kladná zpětná vazba) rychlost částic v každém kroku zmenší o koeficient:
#define DAMPING_FACTOR 0.5
Tímto vztahem:
a->vx = (a->vx + fx * DT) * DAMPING_FACTOR; a->vy = (a->vy + fy * DT) * DAMPING_FACTOR;
Výsledkem je zcela nová podoba funkce apply_rule:
void apply_rule(Model *model) {
int i, j;
for (i = 0; i < model->particle_system.max; i++) {
float fx = 0.0;
float fy = 0.0;
Particle *a = &model->particle_system.particles[i];
/* compute force for selected particle */
for (j = 0; j < model->particle_system.max; j++) {
if (i != j) {
Particle *b = &model->particle_system.particles[j];
float g = model->rule;
float dx = a->x - b->x;
float dy = a->y - b->y;
if (dx != 0.0 || dy != 0.0) {
float d = dx * dx + dy * dy;
if (d < MAX_DISTANCE * MAX_DISTANCE) {
/* repel force */
float f = g / sqrt(d);
fx += f * dx;
fy += f * dy;
}
}
}
}
/* apply force to selected particle */
a->vx = (a->vx + fx * DT) * DAMPING_FACTOR;
a->vy = (a->vy + fy * DT) * DAMPING_FACTOR;
/* move particle */
a->x += a->vx;
a->y += a->vy;
/* check if particle touches scene boundary */
if (a->x <= 0) {
a->vx = -a->vx;
a->x = 0;
}
if (a->x > WIDTH) {
a->vx = -a->vx;
a->x = WIDTH - 1;
}
if (a->y <= 0) {
a->vy = -a->vy;
a->y = 0;
}
if (a->y > HEIGHT) {
a->vy = -a->vy;
a->y = HEIGHT - 1;
}
}
}
8. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
Pro malý počet částic bude výsledek vypadat přibližně následovně (povšimněte si, jak jsou částice od sebe odpuzeny na přibližně stejnou vzdálenost):
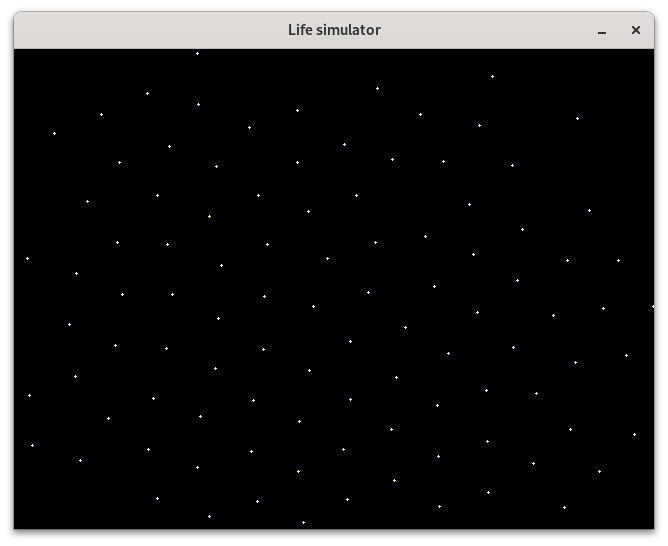
Obrázek 7: Částicový systém s pohybujícími se částicemi, které se odpuzují, po ustálení.
Postupná stabilizace systému s větším počtem částic:
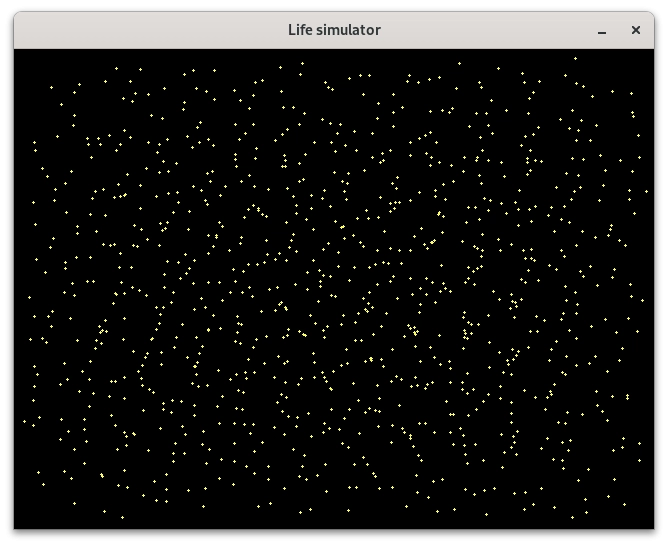
Obrázek 8: Částicový systém s pohybujícími se částicemi, které se odpuzují.
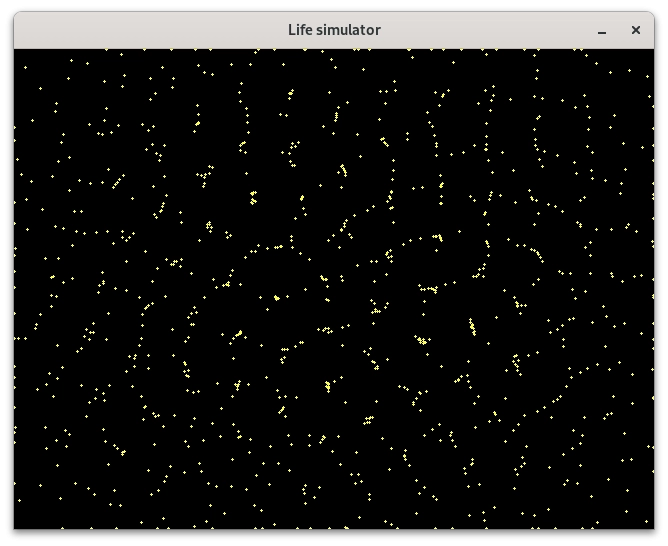
Obrázek 9: Částicový systém s pohybujícími se částicemi, které se odpuzují.
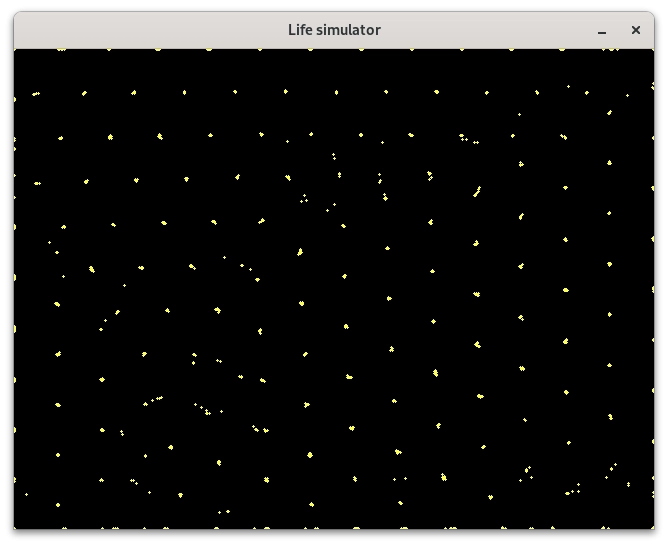
Obrázek 10: Částicový systém s pohybujícími se částicemi, které se odpuzují.
A pro systém s větším množstvím částic již dojde k seskupení některých částic do „atomů“ (i když se částice stále odpuzují). A v průběhu vývoje systému se stane, že některá částice doputuje od jednoho atomu k atomu dalšímu:

Obrázek 11: Částicový systém s pohybujícími se částicemi, které se odpuzují.
9. Větší množství částicových systémů
I přesto, že už v předchozím systému vznikla nějaká struktura, nejedná se o pravou emergenci. Abychom jí dosáhli, musíme provést ještě dvě úpravy systému. Nejdříve namísto jednoho částicového systému přidáme do modelového světa hned čtyři skupiny části. Prozatím se částice budou odlišovat jen svým typem a barvou vykreslení, takže by se modelovaný svět jako celek měl stále chovat stejně.
Nejprve si připravíme potřebné konstanty:
/* constants used by model */ #define RED 0 #define GREEN 1 #define YELLOW 2 #define BLUE 3 /* number of particles of different colors/attributes */ #define MAX_RED 3000 #define MAX_GREEN 200 #define MAX_BLUE 100 #define MAX_YELLOW 100 /* total number of particles */ #define MAX_PARTICLES (MAX_RED + MAX_GREEN + MAX_BLUE + MAX_YELLOW)
Samotná struktura s informacemi o částici bude navíc obsahovat i její typ, tj. ke které ze čtyř skupin částic náleží:
typedef struct {
float x;
float y;
float vx;
float vy;
int type;
} Particle;
Změní se i definice částicového systému, protože si musíme zapamatovat čtyři barvy částic:
typedef struct {
Particle *particles;
int max;
Color colors[4];
} ParticleSystem;
A konečně změníme i funkci pro inicializaci celého modelovaného světa tak, aby podporoval čtyři skupiny částic, každou skupinu s odlišnou barvou:
Model init_model(void) {
Color redColor = {255, 80, 80};
Color greenColor = {80, 255, 80};
Color blueColor = {80, 80, 255};
Color yellowColor = {255, 255, 80};
Model model;
init_rules(&model);
model.particle_system.colors[RED] = redColor;
model.particle_system.colors[GREEN] = greenColor;
model.particle_system.colors[BLUE] = blueColor;
model.particle_system.colors[YELLOW] = yellowColor;
model.particle_system.particles =
(Particle *)malloc(MAX_PARTICLES * sizeof(Particle));
model.particle_system.max = MAX_PARTICLES;
create_particles(MAX_RED, model.particle_system.particles, RED);
create_particles(MAX_GREEN, model.particle_system.particles + MAX_RED, GREEN);
create_particles(MAX_BLUE, model.particle_system.particles + MAX_RED + MAX_GREEN,
BLUE);
create_particles(MAX_YELLOW,
model.particle_system.particles + MAX_RED + MAX_GREEN + MAX_BLUE,
YELLOW);
return model;
}
10. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
Opět se podívejme na postupný vývoj dynamického systému, který reprezentuje náš modelovaný svět:
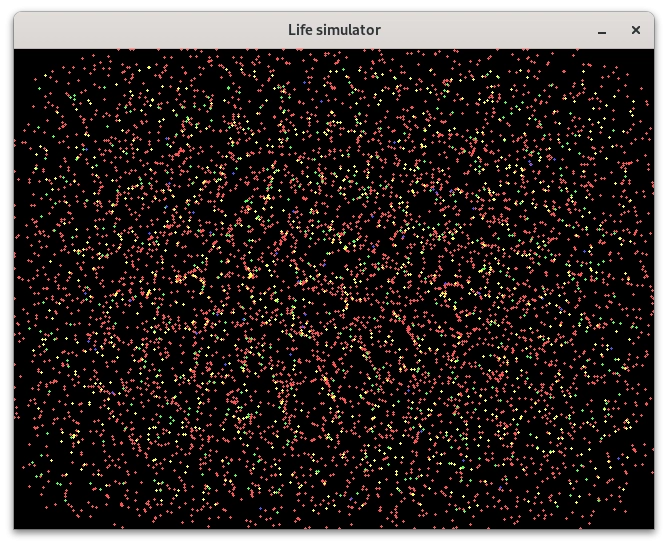
Obrázek 12: Postupný vývoj systému se čtyřmi typy částic.
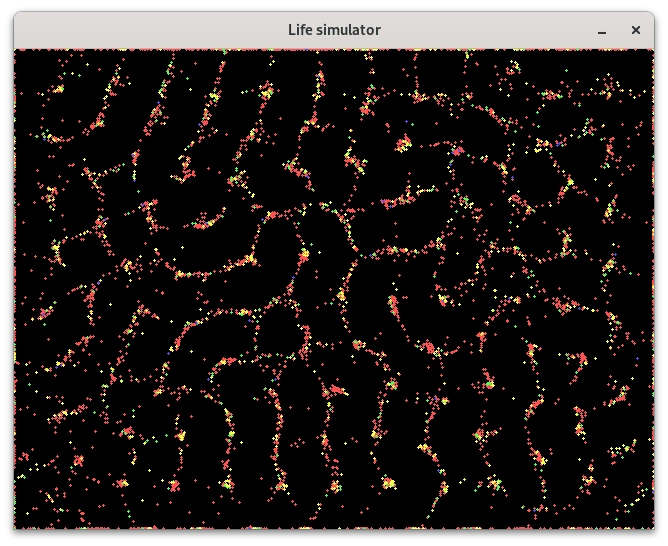
Obrázek 13: Postupný vývoj systému se čtyřmi typy částic.

Obrázek 14: Postupný vývoj systému se čtyřmi typy částic.
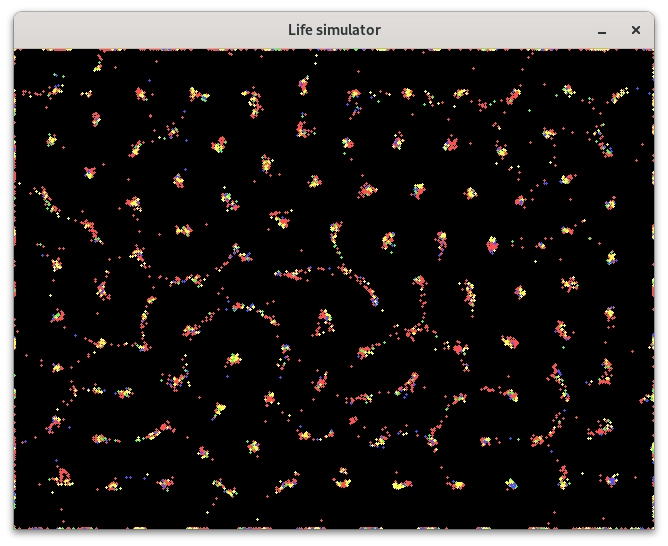
Obrázek 15: Postupný vývoj systému se čtyřmi typy částic.
11. Pravidla pro interakci mezi částicemi z různých systémů
Poslední a nejdůležitější modifikací částicového systému je specifikace pravidel aplikovaných na částice podle barev. V předchozím kódu jsme přiřadili každé částici jednu ze čtyř barev. Pokud se k sobě přiblíží dvě částice, budou od sebe stále odpuzovány, ale míra této odpudivé síly bude různá podle toho, jaké barvy částice jsou. Vzhledem k tomu, že obě interagující částice mohou nabývat jedné ze čtyř barev, máme k dispozici celkem 4×4=16 různých pravidel (hodnot typu float), takže si upravíme model našeho světa následovně:
typedef struct {
float rules[4][4];
ParticleSystem particle_system;
} Model;
Z funkce init_rule se tedy stane funkce nazvaná init_rules:
void init_rules(Model *model) {
int i, j;
for (j = 0; j < 4; j++) {
for (i = 0; i < 4; i++) {
model->rules[i][j] = 2.0 * (float)rand() / RAND_MAX - 1.0;
}
}
}
#define RED 0 #define GREEN 1 #define YELLOW 2 #define BLUE 3
12. Změna funkce apply_rule na apply_rules
Modifikovat pochopitelně musíme i funkci apply_rule, kterou přejmenujeme na apply_rules. To však není tak důležité jako změna logiky, která je na dalším výpisu zvýrazněná:
for (j = 0; j < model->particle_system.max; j++) {
if (i != j) {
Particle *b = &model->particle_system.particles[j];
float g = model->rules[a->type][b->type] * SCALE_FACTOR;
...
...
...
}
}
To znamená, že na základě typu první a druhé částice vybereme jedno ze šestnácti pravidel. A toto pravidlo (prozatím konstanta) je použita při výpočtu síly působící na částice.
Úplný kód funkce apply_rules, která tvoří jádro celého částicového systému, vypadá takto:
void apply_rules(Model *model) {
int i, j;
for (i = 0; i < model->particle_system.max; i++) {
float fx = 0.0;
float fy = 0.0;
Particle *a = &model->particle_system.particles[i];
/* compute force for selected particle */
for (j = 0; j < model->particle_system.max; j++) {
if (i != j) {
Particle *b = &model->particle_system.particles[j];
float g = model->rules[a->type][b->type] * SCALE_FACTOR;
float dx = a->x - b->x;
float dy = a->y - b->y;
if (dx != 0.0 || dy != 0.0) {
float d = dx * dx + dy * dy;
if (d < MAX_DISTANCE * MAX_DISTANCE) {
/* repel force */
float f = g / sqrt(d);
fx += f * dx;
fy += f * dy;
}
}
}
}
/* apply force to selected particle */
a->vx = (a->vx + fx * DT) * DAMPING_FACTOR;
a->vy = (a->vy + fy * DT) * DAMPING_FACTOR;
/* move particle */
a->x += a->vx;
a->y += a->vy;
/* check if particle touches scene boundary */
if (a->x <= 0) {
a->vx = -a->vx;
a->x = 0;
}
if (a->x > WIDTH) {
a->vx = -a->vx;
a->x = WIDTH - 1;
}
if (a->y <= 0) {
a->vy = -a->vy;
a->y = 0;
}
if (a->y > HEIGHT) {
a->vy = -a->vy;
a->y = HEIGHT - 1;
}
}
}
13. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
Opět se podívejme na výsledky, které sice nejsou na statických obrázcích příliš přesvědčivé, ale nic by nám nemělo bránit v překladu a pohledu na postupně se vyvíjející dynamický systém:
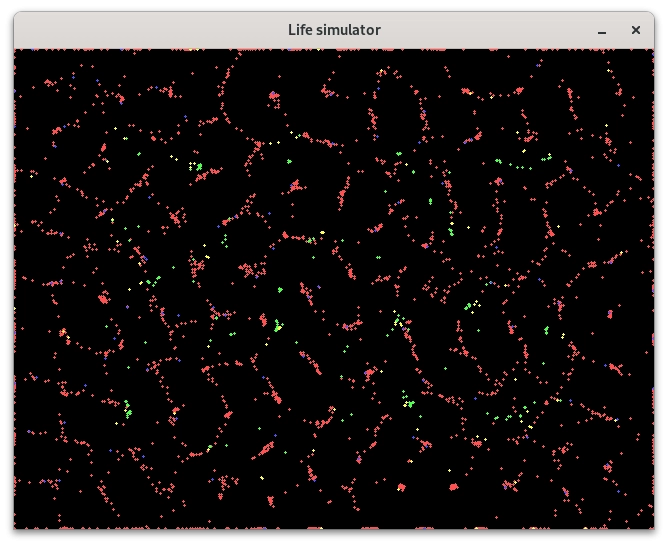
Obrázek 16: Pravidla jsou nastavena tak, že se červené částice snaží o vytvoření pravidelné mřížky, zatímco částice ostatních barev jsou „živější“.
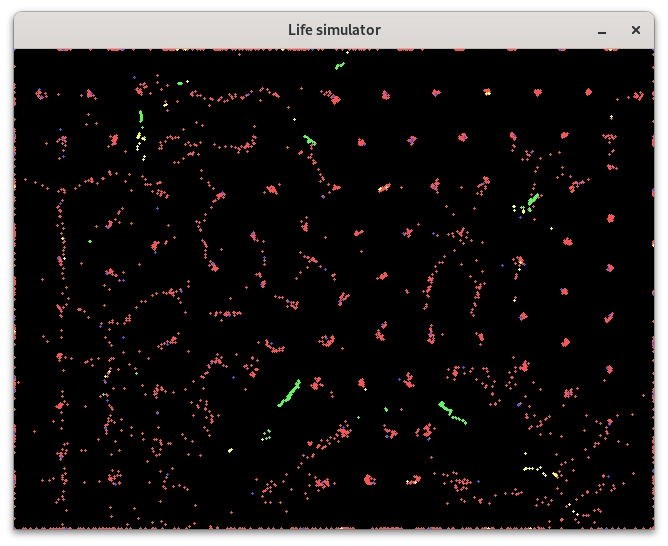
Obrázek 17: V systému začínají „oživovat“ zelené a žluté organismy.
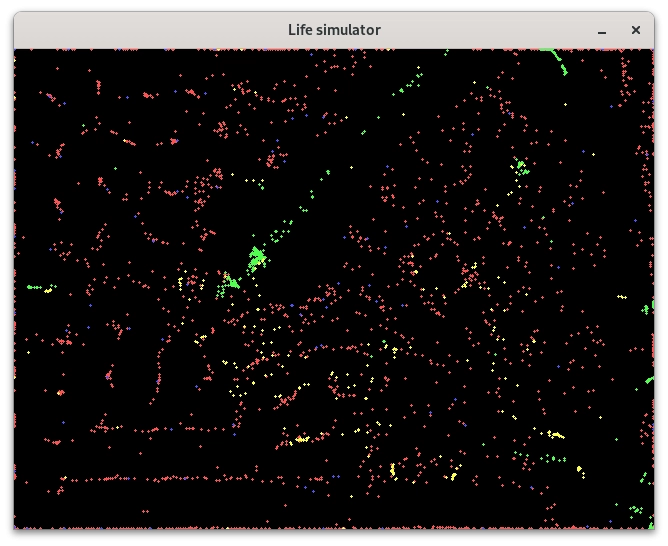
Obrázek 18: Žluté a zelené částice tvoří ucelenější struktury, které se v systému pohybují podobně jako hejno ryb.
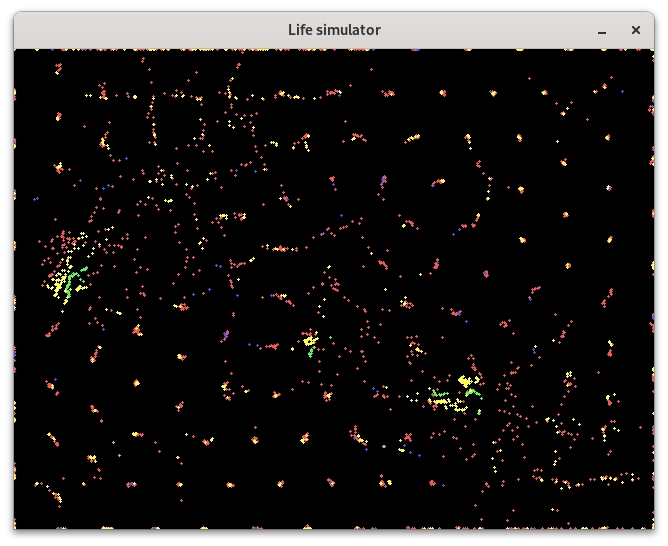
Obrázek 19: Podobné chování, jaké můžeme vidět na předchozím obrázku.
14. Další vylepšení interaktivity
Celý systém s modelem jednoduchého světa složeného z částic by mělo být možné interaktivně ovládat. Pro účely dnešního článku jsem ještě zdrojový kód upravil tak, aby reagoval na následující klávesové zkratky:
| Klávesa | Stručný popis | Funkce s implementací |
|---|---|---|
| d | pozastavení částic (delay, slow down) | slow_down(model) |
| i | nastavení nových pravidel (init rules) | init_rules(model) |
| c | vytvoření nového částicového systému (náhodné rozmístění částic) | create_particles(model) |
| s | povolení či zákaz rozmazání snímku (lze přidat i motion blur) | smooth_scene(pixma) |
15. Funkce se smyčkou pro obsluhu událostí
A takto vypadá programová smyčka pro obsluhu událostí. Reagujeme pouze na stisk kláves, popř. na uzavření okna s vizualizovaným částicovým systémem:
static void main_event_loop(GraphicsState *graphicsState, SDL_Surface *pixmap,
Model *model) {
SDL_Event event;
int done = 0;
do {
while (SDL_PollEvent(&event)) {
switch (event.type) {
case SDL_QUIT:
done = 1;
break;
case SDL_KEYDOWN:
switch (event.key.keysym.sym) {
case 'd':
slow_down(model);
break;
case 'i':
init_rules(model);
break;
case 'c':
create_particles_of_all_colors(model);
break;
case 's':
smooth_enabled = !smooth_enabled;
break;
case SDLK_ESCAPE:
case SDLK_q:
done = 1;
break;
default:
break;
}
break;
default:
break;
}
}
apply_rules(model);
redraw(graphicsState, pixmap, model);
SDL_Delay(10);
} while (!done);
}
16. Ukázky grafické plochy s vizualizovaným dynamickým částicovým systémem
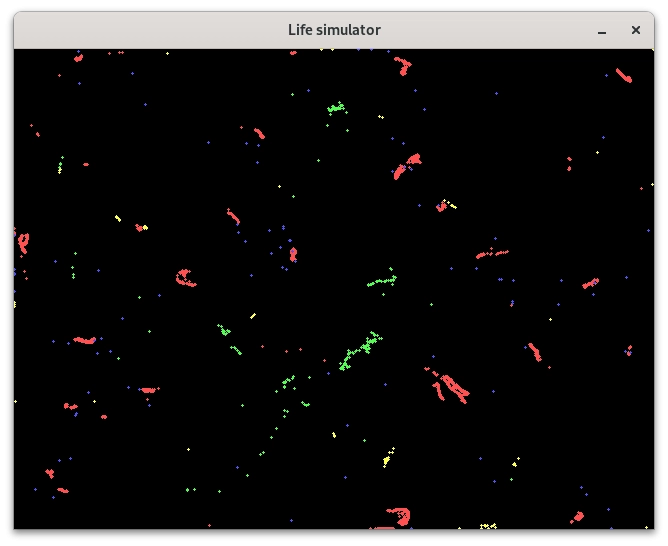
Obrázek 20: Vznik pohybujících se „živočichů“ na základě jednoduchých pravidel.
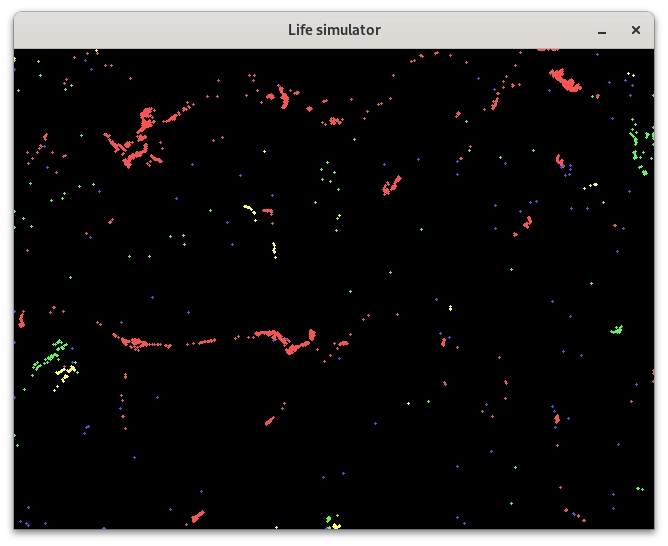
Obrázek 21: Vznik pohybujících se „živočichů“ na základě jednoduchých pravidel.
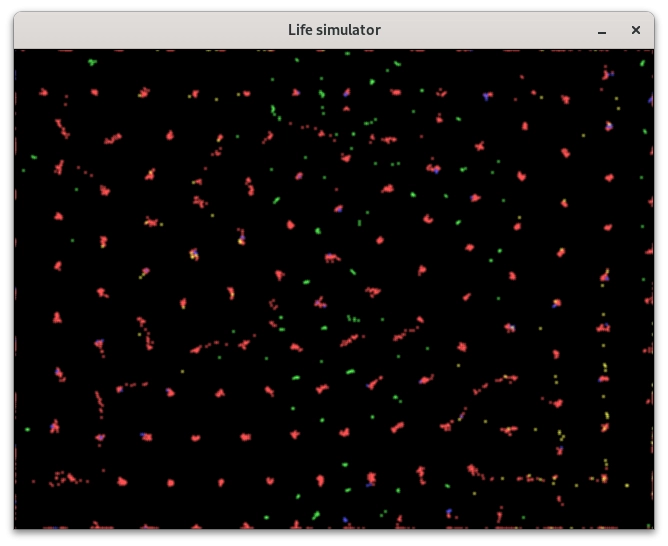
Obrázek 22: Červených částic je nejvíce, takže se odpuzují a mohou vytvořit pravidelné mřížky.
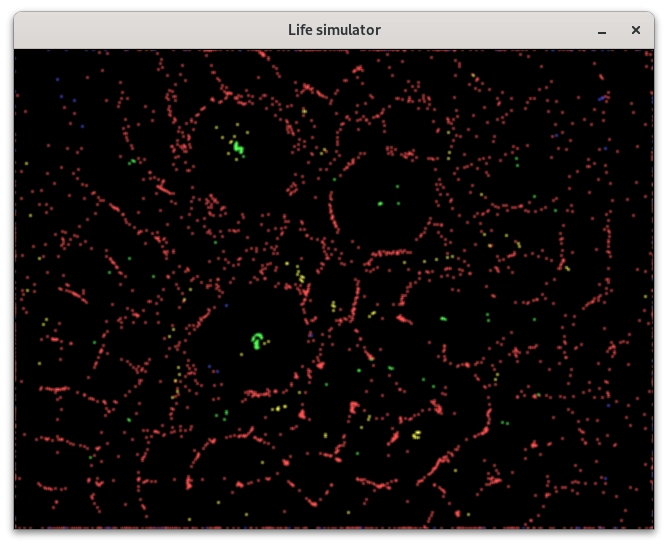
Obrázek 23: Odlišná pravidla vedou k vývoji jakýchsi sítí.
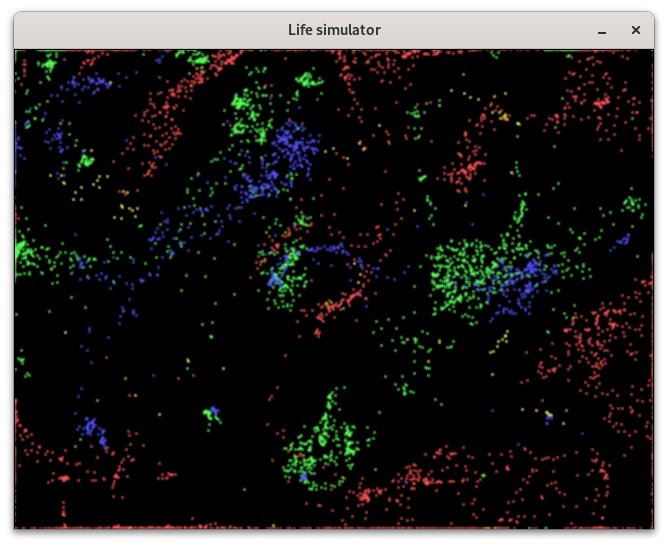
Obrázek 24: Odlišné nastavení pravidel.
17. Realizace částicového systému v Pythonu
Výše popsaný částicový systém lze pochopitelně realizovat v různých programovacích jazycích a s využitím různých knihoven pro vykreslování. Můžeme si tedy vyzkoušet variantu naprogramovanou v Pythonu. Struktura tohoto programu se nebude příliš lišit od céčkové varianty (použijeme zde knihovnu PyGame postavenou taktéž nad SDL), ovšem výpočty a vykreslování budou znatelně pomalejší – minimálně o jeden řád. Kdo má tedy dostatečně výkonný počítač, může si otestovat tuto variantu:
# vim: set fileencoding=utf-8
import sys
from enum import Enum
from random import random
from math import sqrt
import pygame
import pygame.locals
WINDOW_WIDTH = 800
WINDOW_HEIGHT = 600
WINDOW_TITLE = "Particle life simulator"
# Constants used by model
RED_GROUP = 0
GREEN_GROUP = 1
YELLOW_GROUP = 2
BLUE_GROUP = 3
# Model options
BORDER = 50
# Number of particles of different colors/attributes
MAX_RED = 1000
MAX_GREEN = 200
MAX_BLUE = 50
MAX_YELLOW = 10
# Total number of particles in the whole system
MAX_PARTICLES = MAX_RED+MAX_GREEN+MAX_BLUE+MAX_YELLOW
# Other model options
MAX_DISTANCE = 2000
DAMPING_FACTOR = 0.5
SLOW_DOWN_FACTOR = 0.1
SCALE_FACTOR = 1
class Colors(Enum):
"""Named colors used everywhere on demo screens."""
BLACK = (0, 0, 0)
BLUE = (0, 0, 255)
CYAN = (0, 255, 255)
GREEN = (0, 255, 0)
YELLOW = (255, 255, 0)
RED = (255, 0, 0)
MAGENTA = (255, 0, 255)
WHITE = (255, 255, 255)
class Particle:
def __init__(self, x : float, y : float, vx : float, vy : float, type : int):
self.x = x
self.y = y
self.vx = vx
self.vy = vy
self.type = type
class Atoms:
def __init__(self, max_particles : int):
self.colors = (0xffff0000, 0xff00ff00, 0xff2020ff, 0xffffff00)
self.particles = []
self.particles += (create_particles(MAX_RED, RED_GROUP))
self.particles += (create_particles(MAX_GREEN, GREEN_GROUP))
self.particles += (create_particles(MAX_BLUE, BLUE_GROUP))
self.particles += (create_particles(MAX_YELLOW, YELLOW_GROUP))
print("Particles in atoms:", len(self.particles))
class Model:
def __init__(self, max_particles : int):
self.rules = [[0,0,0,0], [0,0,0,0], [0,0,0,0], [0,0,0,0]]
self.init_rules()
self.atoms = Atoms(max_particles)
def init_rules(self):
for j in range(4):
for i in range(4):
self.rules[i][j] = 2.0*random() - 1.0
def random_x() -> float:
return (WINDOW_WIDTH - BORDER*2) * random() + BORDER
def random_y() -> float:
return (WINDOW_HEIGHT - BORDER*2) * random() + BORDER
def create_particles(max : int, type : int):
return [Particle(random_x(), random_y(), 0.0, 0.0, type) for i in range(max)]
def redraw(surface, model):
surface.fill(Colors.BLACK.value)
atoms = model.atoms
for particle in atoms.particles:
color = atoms.colors[particle.type]
surface.set_at((int(particle.x),int(particle.y)), color)
surface.set_at((int(particle.x-1),int(particle.y)), color)
surface.set_at((int(particle.x+1),int(particle.y)), color)
surface.set_at((int(particle.x),int(particle.y-1)), color)
surface.set_at((int(particle.x),int(particle.y+1)), color)
def apply_rules(model : Model):
for i in range(len(model.atoms.particles)):
fx : float = 0.0
fy : float = 0.0
a = model.atoms.particles[i]
# compute force for selected particle
for j in range(len(model.atoms.particles)):
if i != j:
b = model.atoms.particles[j]
g = model.rules[a.type][b.type] * SCALE_FACTOR
dx = a.x - b.x
dy = a.y - b.y
if dx != 0.0 or dy != 0.0:
d = dx*dx + dy*dy
if d < MAX_DISTANCE:
f = g / sqrt(d)
fx += f * dx
fy += f * dy
# apply force to selected particle
a.vx = (a.vx + fx) * DAMPING_FACTOR
a.vy = (a.vy + fy) * DAMPING_FACTOR
# move particle
a.x += a.vx
a.y += a.vy
# check if particle touches scene boundary
if a.x <= 0:
a.vx = -a.vx
a.x = 0
if a.x >= WINDOW_WIDTH:
a.vx = -a.vx
a.x = WINDOW_WIDTH - 1
if a.y <= 0:
a.vy = -a.vy
a.y = 0
if a.y >= WINDOW_HEIGHT:
a.vy = -a.vy
a.y = WINDOW_HEIGHT - 1
def write_particles(model, filename):
atoms = model.atoms
with open(filename, "w") as fout:
fout.write('"x","y"\n')
for particle in atoms.particles:
fout.write(f"{particle.x},{particle.y}\n")
# set window title
pygame.display.set_caption(WINDOW_TITLE)
display = pygame.display.set_mode([WINDOW_WIDTH, WINDOW_HEIGHT])
display.fill(Colors.BLACK.value)
surface = pygame.Surface([WINDOW_WIDTH, WINDOW_HEIGHT])
surface.set_at((101,100), 0xffff0000)
surface.set_at((100,101), 0xffff0000)
surface.set_at((101,101), 0xffff0000)
clock = pygame.time.Clock()
model = Model(MAX_PARTICLES)
while True:
for event in pygame.event.get():
if event.type == pygame.locals.QUIT:
pygame.quit()
sys.exit()
if event.type == pygame.locals.KEYDOWN:
if event.key == pygame.locals.K_ESCAPE:
pygame.quit()
sys.exit()
if event.key == pygame.locals.K_RETURN:
pygame.quit()
sys.exit()
if event.key == pygame.locals.K_w:
write_particles(model, "particles.csv")
# all events has been processed - update scene and redraw the screen
apply_rules(model)
redraw(surface, model)
display.blit(surface, (0, 0))
pygame.display.update()
# clock.tick(25)
18. Příloha: modul gfx
Pro inicializaci grafického subsystému, otevření okna i vykreslování se používá pomocný jednoduchý modul napsaný v jazyce C a operující nad knihovnou SDL2. Modul obsahuje pouze základní potřebné funkce a navíc i funkci pro práci s rastrovými obrázky, kterou lze využít například při tvorbě videa. Hlavičkový soubor modulu gfx:
#ifndef _GFX_H_
#define _GFX_H_
typedef struct GraphicsState {
SDL_Window *window;
SDL_Surface *screen_surface;
} GraphicsState;
void init_sdl(GraphicsState *graphicsState, const char *title, const int width,
const int height);
void finalize(GraphicsState *graphicsState, SDL_Surface *pixmap);
void show_pixmap(GraphicsState *graphicsState, SDL_Surface *surface);
SDL_Surface *create_pixmap(const int width, const int height);
void putpixel(SDL_Surface *surface, int x, int y, unsigned char r,
unsigned char g, unsigned char b);
#endif
Realizace všech funkcí v céčku:
#include <SDL2/SDL.h>
#include "gfx.h"
void init_sdl(GraphicsState *graphicsState, const char *title, const int width,
const int height) {
graphicsState->window = NULL;
graphicsState->screen_surface = NULL;
if (SDL_Init(SDL_INIT_VIDEO) < 0) {
fprintf(stderr, "Error initializing SDL: %s\n", SDL_GetError());
exit(1);
} else {
puts("SDL_Init ok");
}
graphicsState->window = SDL_CreateWindow(title, SDL_WINDOWPOS_UNDEFINED,
SDL_WINDOWPOS_UNDEFINED, width,
height, SDL_WINDOW_SHOWN);
if (!graphicsState->window) {
puts("Error creating window");
puts(SDL_GetError());
exit(1);
} else {
puts("SDL_CreateWindow ok");
}
graphicsState->screen_surface = SDL_GetWindowSurface(graphicsState->window);
if (!graphicsState->screen_surface) {
fprintf(stderr, "Error setting video mode: %s\n", SDL_GetError());
exit(1);
} else {
puts("SDL_GetWindowSurface ok");
}
}
void finalize(GraphicsState *graphicsState, SDL_Surface *pixmap) {
SDL_FreeSurface(pixmap);
SDL_FreeSurface(graphicsState->screen_surface);
SDL_DestroyWindow(graphicsState->window);
SDL_Quit();
}
void show_pixmap(GraphicsState *graphicsState, SDL_Surface *surface) {
SDL_BlitSurface(surface, NULL, graphicsState->screen_surface, NULL);
SDL_UpdateWindowSurface(graphicsState->window);
}
SDL_Surface *create_pixmap(const int width, const int height) {
SDL_Surface *pixmap;
pixmap = SDL_CreateRGBSurface(SDL_SWSURFACE, width, height, 32, 0x00ff0000,
0x0000ff00, 0x000000ff, 0x00000000);
if (!pixmap) {
puts("Can not create pixmap");
exit(1);
} else {
puts("Off screen pixmap created");
}
return pixmap;
}
void putpixel(SDL_Surface *surface, int x, int y, unsigned char r,
unsigned char g, unsigned char b) {
if (x >= 0 && x < surface->w && y >= 0 && y < surface->h) {
if (surface->format->BitsPerPixel == 24) {
Uint8 *pixel = (Uint8 *)surface->pixels;
pixel += x * 3;
pixel += y * surface->pitch;
*pixel++ = b;
*pixel++ = g;
*pixel = r;
return;
}
if (surface->format->BitsPerPixel == 32) {
Uint8 *pixel = (Uint8 *)surface->pixels;
pixel += x * 4;
pixel += y * surface->pitch;
*pixel++ = b;
*pixel++ = g;
*pixel = r;
return;
}
}
}
19. Repositář s demonstračními příklady
Jednotlivé postupně se vylepšující implementace částicového systému naprogramované v jazyku C i v Pythonu byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/presentations/. V případě, že nebudete chtít klonovat celý repositář, můžete namísto toho použít odkazy na jednotlivé projekty, které naleznete v následující tabulce:
| # | Projekt | Stručný popis projektu | Cesta k projektu |
|---|---|---|---|
| 1 | v0 | kostra jednoduchého frameworku pro zobrazení částicového systému | https://github.com/tisnik/presentations/tree/master/particle_life/v0/ |
| 2 | v1 | částicový systém s pohybujícími se částicemi | https://github.com/tisnik/presentations/tree/master/particle_life/v1/ |
| 3 | v2 | přidání pravidla pro vzájemné odpuzování částic | https://github.com/tisnik/presentations/tree/master/particle_life/v2/ |
| 4 | v3 | čtyři částicové systémy postavené nad stejnými pravidly | https://github.com/tisnik/presentations/tree/master/particle_life/v3/ |
| 5 | v4 | pravidla pro interakci částic z různých částicových systémů | https://github.com/tisnik/presentations/tree/master/particle_life/v4/ |
| 6 | v5 | interaktivní modifikace dynamického částicového systému uživatelem | https://github.com/tisnik/presentations/tree/master/particle_life/v5/ |
| 7 | particle_life.py | realizace částicového systému v Pythonu | https://github.com/tisnik/presentations/tree/master/particle_life/particle_life.py |
20. Odkazy na Internetu
- Emergence (Wikipedia CS)
https://cs.wikipedia.org/wiki/Emergence - Emergence (Wikipedia EN)
https://en.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Self-organization
https://en.wikipedia.org/wiki/Self-organization - Samoorganizace
https://cs.wikipedia.org/wiki/Samoorganizace - Spontaneous order
https://en.wikipedia.org/wiki/Spontaneous_order - Lorenzův atraktor
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-vi/#k02 - Lorenzův atraktor
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03 - Lorenz system
https://en.wikipedia.org/wiki/Lorenz_system - Dynamical system
https://en.wikipedia.org/wiki/Dynamical_system - What are Dynamical Systems?
https://math.libretexts.org/Bookshelves/Scientific_Computing_Simulations_and_Modeling/Introduction_to_the_Modeling_and_Analysis_of_Complex_Systems_(Sayama)/03%3A_Basics_of_Dynamical_Systems/3.01%3A_What_are_Dynamical_Systems%3F - TEACHING MATHEMATICS WITH A HISTORICAL PERSPECTIVE: Lecture 11: Dynamical systems
https://abel.math.harvard.edu/~knill/teaching/mathe320_2022/handouts/10-dynamics.pdf