Obsah
1. Nástroj Cython a typové anotace
3. Ukázky zápisu typových anotací
5. Překlad funkce s duck typingem do C Cythonem
6. Zajištění syntaxe kompatibilní s Pythonem
7. Přidání informace o typech parametrů funkce pro součet celých čísel
8. Přepis funkce s typy parametrů do podoby kompatibilní s Pythonem
9. Přidání informace o návratovém typu funkce pro součet celých čísel
10. Přepis funkce s plnými typovými informacemi do podoby kompatibilní s Pythonem
11. Zákaz použití GILu v překládané funkci
12. Volání funkcí ze standardní knihovny jazyka C
13. Základní varianta benchmarku naprogramovaná v čistém Pythonu
14. Přepis benchmarku do Cythonu
15. Varianta se syntaxí kompatibilní s Pythonem
16. Pole a předávání ukazatelů
17. Opětovná úprava se syntaxí kompatibilní s Pythonem
18. Výsledek transpilace Cythonem do céčka
19. Repositář s demonstračními příklady
1. Nástroj Cython a typové anotace
V článcích RPython vs Cython aneb dvojí přístup k překladu Pythonu do nativního kódu a Praktické použití nástroje Cython při překladu Pythonu do nativního kódu jsme se seznámili se základními vlastnostmi nástroje nazvaného Cython (pozor – nikoli CPython, což je označení standardního interpretru Pythonu naprogramovaného v céčku). Cython patří mezi takzvané AOT (Ahead Of Time) překladače Pythonu, což v tomto případě konkrétně znamená, že zdrojové kódy projektu napsaného v Pythonu jsou transformovány do céčkovského kódu a následně přeloženy standardním céčkovským překladačem (například GCC apod.) a poté slinkovány do výsledného spustitelného nativního souboru.

Obrázek 1: Logo Cythonu.
Na první pohled by se mohlo zdát, že výsledkem budou mnohem rychlejší aplikace, protože zcela odpadne fáze interpretace. Ve chvíli, kdy Cython nezná datový typ funkce/proměnné/argumentu, použije PyObject *, tedy ukazatel na datovou strukturu reprezentující v Pythonu libovolnou hodnotu. V dalším kódu je samozřejmě nutné z tohoto objektu získat skutečnou hodnotu. I takto vlastně velmi primitivně provedený překlad dokáže programový kód do určité míry zrychlit, což ostatně uvidíme i ve výsledku benchmarků. Cython jde ale ještě dále, protože rozšiřuje jazyk Python o další klíčová slova, především pak o slovo cdef. Toto klíčové slovo je možné použít pro přesnou specifikaci typu proměnné či argumentu, a to způsobem, který plně vychází z programovacího jazyka C. Tato typová informace samozřejmě umožňuje provedení dalších optimalizací ve výsledném kódu (opět uvidíme na výsledcích benchmarku).

Obrázek 2: Pro porovnání – logo standardního Pythonu.
Problém spočívá v tom, že původní zápis založený na cdef a „céčkovsky“ zapsaných datových typech je nekompatibilní se syntaxí standardního Pythonu. Tento problém je ovšem v současnosti do značné míry vyřešen, protože nyní Cython může používat typové anotace. Kombinaci těchto dvou technologií je věnován dnešní článek.
2. Typové anotace v Pythonu
Do syntaxe a sémantiky programovacího jazyka Python se postupně přidává a vylepšuje, resp. přesněji řečeno zjednodušuje a zpřesňuje podpora pro specifikaci takzvaných typových anotací, resp. typových nápověd (type annotations, type hints). V současné podobě se jedná o nová syntaktická pravidla, která v zápisu zdrojového kódu umožňují nepovinnou a do značné míry zcela dobrovolnou specifikaci typů parametrů funkcí a metod, typů návratových hodnot funkcí a metod, typů globálních i lokálních proměnných, typových parametrů u generických datových typů atd. Programovací jazyk Python sice umožňuje zápis typových anotací, ale (alespoň prozatím) neprovádí jejich kontrolu a vlastně je ani nijak nevyužívá pro běh aplikací. Tuto činnost ponechává na jiných nástrojích, které jsou typicky založeny na statické typové analýze nebo (jak uvidíme dále) pro podporu AOT (ahead of time) překladu s optimalizacemi.
Zavedení typových anotací do programovacího jazyka Python bylo, zejména zpočátku, provázeno určitým odporem částí vývojářů a někdy taktéž obavou o to, jestli se z původně poměrně jednoduchého a snadno naučitelného Pythonu nestává zcela odlišný programovací jazyk (z jazyka snadno naučitelného i lidmi, kteří nejsou profesionálními programátory na komplikovaný jazyk určený výhradně pro profesionály). Ovšem na tomto místě je nutné zdůraznit, že se jedná o zcela nepovinnou součást jazyka, která je vlastně do značné míry samotným Pythonem (přesněji řečeno standardním interpretrem Pythonu neboli CPythonem) ignorována.
Nástroje typu Mypy, Pyright, Cython či LSP servery, které typové informace zpracovávají a vyžadují pro svou činnost, pracují zcela nezávisle na standardním interpretru Pythonu (popř. je možná jejich integrace do vývojových prostředí). Na druhou stranu, i přes výše uvedené rozpaky, právě typové anotace a jejich kontrola (a nutno dodat: i zpracování integrovanými vývojovými prostředími) do značné míry usnadňují vývoj rozsáhlejších aplikací. Ostatně můžeme zde vidět souvislost s dvojicí JavaScript:TypeScript. A kvalita optimalizací prováděná nástrojem Cython do značné míry závisí právě na poskytnutých typových informacích.
3. Ukázky zápisu typových anotací
Typovými anotacemi v Pythonu jsme se již zabývali v článcích [1] [2] [3]. Proto si dnes pouze bez podrobnějších vysvětlení ukažme, jakým způsobem se typové informace zapisují. Stejný zápis, i když mnohdy s odlišnými typy, budeme realizovat i v Cythonu.
Definice funkce pro součet dvou celých čísel (s neomezeným rozsahem). Specifikovány jsou typy parametrů i typ návratové hodnoty:
def add(a:int, b:int) -> int:
return a+b
Definice funkce určené pro spojení dvou seznamů, přičemž prvky těchto seznamů jsou množiny celých čísel. Opět je specifikován jak typ parametrů funkce tak i typ návratové hodnoty:
def append(a:list[set[int]], b:list[set[int]]) -> list[set[int]]:
return a+b
Definice proměnné s typem n-tice. Každý prvek n-tice může mít specifikován vlastní typ (na rozdíl od seznamů):
p: tuple[int, float, bool, str] = (2.0, 3.14, 1, "Hello")
Definice proměnné typu slovník, se specifikací typu klíče i povolených hodnot:
d:dict[str, Union[int, float, str]] = {}
d["foo"] = 1
d["bar"] = 3.14
d[10] = 10
d[42] = "answer"
V novějších verzích Pythonu lze též psát:
d:dict[str, int | float | str] = {}
d["foo"] = 1
d["bar"] = 3.14
d[10] = 10
d[42] = "answer"
Definice generické funkce, u níž je zaručeno, že ve výsledné n-tici bude mít první prvek typ shodný s prvním parametrem a druhý prvek bude mít typ shodný s parametrem druhým:
def pair[T, U](first: T, second: U) -> tuple[T, U]:
x = (first, second)
return x
print(pair("A", "B"))
Poslední příklad ukazuje definici generické třídy, u níž je typově bezpečně určen typ ukládaných a načítaných prvků:
from typing import Generic, TypeVar
T = TypeVar('T')
class Collection(Generic[T]):
def __init__(self) -> None:
self.collection : list[T] = []
def append(self, item: T) -> None:
self.collection.append(item)
def get_all(self) -> list[T]:
return self.collection
c = Collection[int]()
c.append(1)
c.append(2)
print(c.get_all())
4. Duck typing v Pythonu
Jednou z typických a důležitých vlastností Pythonu je duck typing, který nám umožňuje zapsat například následující funkci:
def add_two_numbers(x, y):
return x + y
z = add_two_numbers(123, 456)
print(z)
Ve skutečnosti tato funkce, i přes své jméno, nesčítá pouze dvě celočíselné hodnoty, ale jakékoli Pythonovské objekty, pro které je definován operátor +. To si ostatně můžeme velmi snadno ověřit:
def add_two_numbers(x, y):
return x + y
class Foo:
def __init__(self, value):
self._value = value
def __add__(self, other):
return Foo(self._value + other._value)
def __str__(self):
return "*" * self._value
def test_adding():
f1 = Foo(1)
f2 = Foo(2)
print(add_two_numbers(123, 456))
print(add_two_numbers("foo", "bar"))
print(add_two_numbers([1,2,3], [4,5,6]))
print(add_two_numbers((1,2,3), (4,5,6)))
print(add_two_numbers(f1, f2))
test_adding()
Samotná funkce add_two_numbers je v bajtkódu reprezentována čtyřmi instrukcemi (zcela bez informace o typech):
4 0 LOAD_FAST 0 (x)
2 LOAD_FAST 1 (y)
4 BINARY_ADD
6 RETURN_VALUE
Tuto funkci lze volat s různými parametry:
; *****************************************
; předání dvou celých čísel
; *****************************************
22 16 LOAD_GLOBAL 1 (add_two_numbers)
18 LOAD_CONST 3 (123)
20 LOAD_CONST 4 (456)
22 CALL_FUNCTION 2
24 POP_TOP
; *****************************************
; předání dvou řetězců
; *****************************************
23 26 LOAD_GLOBAL 1 (add_two_numbers)
28 LOAD_CONST 5 ('foo')
30 LOAD_CONST 6 ('bar')
32 CALL_FUNCTION 2
34 POP_TOP
; *****************************************
; předání dvou seznamů
; *****************************************
24 36 LOAD_GLOBAL 1 (add_two_numbers)
38 LOAD_CONST 1 (1)
40 LOAD_CONST 2 (2)
42 LOAD_CONST 7 (3)
44 BUILD_LIST 3
46 LOAD_CONST 8 (4)
48 LOAD_CONST 9 (5)
50 LOAD_CONST 10 (6)
52 BUILD_LIST 3
54 CALL_FUNCTION 2
56 POP_TOP
; *****************************************
; předání dvou n-tic
; *****************************************
25 58 LOAD_GLOBAL 1 (add_two_numbers)
60 LOAD_CONST 11 ((1, 2, 3))
62 LOAD_CONST 12 ((4, 5, 6))
64 CALL_FUNCTION 2
66 POP_TOP
; *****************************************
; předání dvou instancí třídy Foo
; *****************************************
19 0 LOAD_GLOBAL 0 (Foo)
2 LOAD_CONST 1 (1)
4 CALL_FUNCTION 1
6 STORE_FAST 0 (f1)
20 8 LOAD_GLOBAL 0 (Foo)
10 LOAD_CONST 2 (2)
12 CALL_FUNCTION 1
14 STORE_FAST 1 (f2)
26 68 LOAD_GLOBAL 1 (add_two_numbers)
70 LOAD_FAST 0 (f1)
72 LOAD_FAST 1 (f2)
74 CALL_FUNCTION 2
76 POP_TOP
78 LOAD_CONST 0 (None)
80 RETURN_VALUE
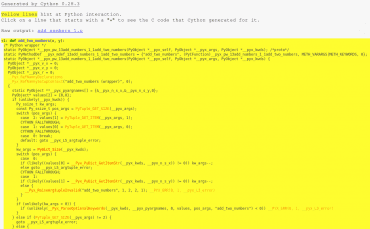
Obrázek 3: Část HTML souboru „add_numbers1.html“ vytvořeného Cythonem. Žlutě označené řádky označují ty bloky kódu, o nichž Cython nemá typové informace a které musel přeložit dosti neefektivním způsobem simulujícím chování interpretru Pythonu.
5. Překlad funkce s duck typingem do C Cythonem
Pokusme se nyní přeložit funkci pro součet dvou hodnot z Cythonu do C a posléze do nativního kódu. Použijeme původní syntaxi Cythonu (resp. Pyrexu) a definici funkce, která se má přeložit do nativního kódu, začneme klíčovým slovem cdef a nikoli pouze def:
cdef add_two_numbers(x, y):
return x + y
z = add_two_numbers(123, 456)
print(z)
Tato funkce bude Cythonem přeložena do poměrně komplikované céčkovské funkce:
static PyObject *__pyx_f_13add_numbers_2_add_two_numbers(PyObject *__pyx_v_x, PyObject *__pyx_v_y) {
PyObject *__pyx_r = NULL;
__Pyx_RefNannyDeclarations
PyObject *__pyx_t_1 = NULL;
int __pyx_lineno = 0;
const char *__pyx_filename = NULL;
int __pyx_clineno = 0;
__Pyx_RefNannySetupContext("add_two_numbers", 1);
__Pyx_XDECREF(__pyx_r);
__pyx_t_1 = PyNumber_Add(__pyx_v_x, __pyx_v_y); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 2, __pyx_L1_error)
__Pyx_GOTREF(__pyx_t_1);
__pyx_r = __pyx_t_1;
__pyx_t_1 = 0;
goto __pyx_L0;
/* function exit code */
__pyx_L1_error:;
__Pyx_XDECREF(__pyx_t_1);
__Pyx_AddTraceback("add_numbers_2.add_two_numbers", __pyx_clineno, __pyx_lineno, __pyx_filename);
__pyx_r = 0;
__pyx_L0:;
__Pyx_XGIVEREF(__pyx_r);
__Pyx_RefNannyFinishContext();
return __pyx_r;
}
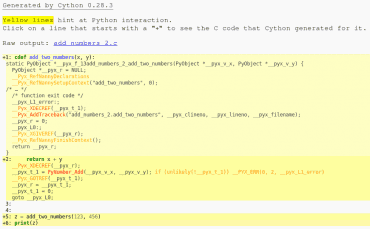
Obrázek 4: Část HTML souboru „add_numbers2.html“ vytvořeného Cythonem. Žlutě označené řádky opět označují ty bloky kódu, o nichž Cython nemá typové informace a které musel přeložit dosti neefektivním způsobem simulujícím chování interpretru Pythonu.
6. Zajištění syntaxe kompatibilní s Pythonem
Předchozí zdrojový kód nebyl kvůli cdef kompatibilní s Pythonem; proto má ostatně příponu „.pyx“ a nikoli pouze „.py“. Ovšem novější verze Cythonu již podporují zápis, který je čistě Pythonovským kódem. Namísto cdef se v tomto případě použije standardní definice funkce s def, ovšem funkce je označena dekorátorem cfunc:
import cython
@cython.cfunc
def add_two_numbers(x, y):
return x + y
z = add_two_numbers(123, 456)
print(z)
7. Přidání informace o typech parametrů funkce pro součet celých čísel
První důležitou úpravou a vlastně i optimalizací, kterou můžeme provést, je přidání informace o typech parametrů funkce. Zápis je v tomto případě naprosto stejný, jako v klasickém céčku, tj. používá se pořadí datový_typ jméno_parametru. V našem případě budeme vyžadovat, aby parametry byly typu celé číslo, tj. v céčku se jedná o základní typ pojmenovaný int. Změněná funkce bude vypadat následovně:
cdef add_two_numbers(int x, int y):
return x + y
z = add_two_numbers(123, 456)
print(z)
Překlad neboli transpilace do céčka dopadne následovně:
static PyObject *__pyx_f_13add_numbers_3_add_two_numbers(int __pyx_v_x, int __pyx_v_y) {
PyObject *__pyx_r = NULL;
__Pyx_RefNannyDeclarations
PyObject *__pyx_t_1 = NULL;
int __pyx_lineno = 0;
const char *__pyx_filename = NULL;
int __pyx_clineno = 0;
__Pyx_RefNannySetupContext("add_two_numbers", 1);
__Pyx_XDECREF(__pyx_r);
__pyx_t_1 = __Pyx_PyInt_From_int((__pyx_v_x + __pyx_v_y)); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 2, __pyx_L1_error)
__Pyx_GOTREF(__pyx_t_1);
__pyx_r = __pyx_t_1;
__pyx_t_1 = 0;
goto __pyx_L0;
/* function exit code */
__pyx_L1_error:;
__Pyx_XDECREF(__pyx_t_1);
__Pyx_AddTraceback("add_numbers_3.add_two_numbers", __pyx_clineno, __pyx_lineno, __pyx_filename);
__pyx_r = 0;
__pyx_L0:;
__Pyx_XGIVEREF(__pyx_r);
__Pyx_RefNannyFinishContext();
return __pyx_r;
}
Zvýrazněme si rozdíly mezi způsobem překladu původní funkce bez typových informací a funkce s informacemi o typech parametrů. Rozdíl spočívá v jediném řádku (a pochopitelně v odlišné hlavičce funkce – akceptuje odlišné typy parametrů):
__pyx_t_1 = PyNumber_Add(__pyx_v_x, __pyx_v_y); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 2, __pyx_L1_error) __pyx_t_1 = __Pyx_PyInt_From_int((__pyx_v_x + __pyx_v_y)); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 2, __pyx_L1_error)
Ve druhém případě se tedy sice provádí běžný součet nativním operátorem + (a tedy strojovou instrukcí add), ovšem výsledek se transformuje zpět na hodnotu typu PyObject *, tedy na obecnou hodnotu Pythonu podléhající duck typingu.
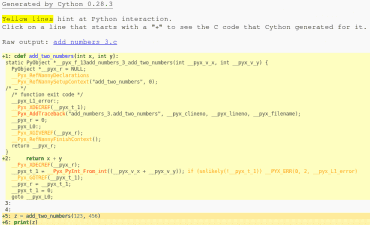
Obrázek 5: Část HTML souboru „add_numbers3.html“ vytvořeného Cythonem.
8. Přepis funkce s typy parametrů do podoby kompatibilní s Pythonem
Opět se podívejme na to, jakým způsobem je možné funkci z předchozí kapitoly upravit do takové podoby, aby byla její syntaxe kompatibilní s Pythonem. Opět tedy využijeme dekorátor @cfunc a navíc uvedeme typové informace o parametrech funkce. Tentokrát je ovšem zapíšeme nikoli „céčkovským“ stylem, ale tak, aby se jednalo o standardní type hinty:
import cython
@cython.cfunc
def add_two_numbers(x: cython.int, y: cython.int):
return x + y
z = add_two_numbers(123, 456)
print(z)
Povšimněte si, že nepoužíváme typ int (ten má totiž v Pythonu odlišný význam – celočíselná hodnota bez omezení rozsahu), ale typy importované přímo z Cythonu a plně odpovídající céčkovským protějškům:
| Cython/Pyrex | Zápis v Pythonu |
|---|---|
| bint | cython.bint |
| char | cython.char |
| signed char | cython.schar |
| unsigned char | cython.uchar |
| short | cython.short |
| unsigned short | cython.ushort |
| int | cython.int |
| unsigned int | cython.uint |
| long | cython.long |
| unsigned long | cython.ulong |
| long long | cython.longlong |
| unsigned long | longcython.ulonglong |
| float | cython.float |
| double | cython.double |
| long double | cython.longdouble |
| float complex | cython.floatcomplex |
| double complex | cython.doublecomplex |
| long double complex | cython.longdoublecomplex |
| size_t | cython.size_t |
| Py_ssize_t | cython.Py_ssize_t |
| Py_hash_t | cython.Py_hash_t |
| Py_UCS4 | cython.Py_UCS4 |
9. Přidání informace o návratovém typu funkce pro součet celých čísel
Další úprava naší funkce se již přímo nabízí – musíme totiž navíc specifikovat i typ návratové hodnoty. Pokud totiž tento typ není zadán, považuje Cython za nutné vracet PyObject *, aby byly výsledky kompatibilní s běžnými pythonovskými funkcemi a metodami. Specifikace návratové hodnoty se opět provádí stejným způsobem, jako v programovacím jazyku C, tj. zápisem příslušného typu před jméno funkce:
cdef int add_two_numbers(int x, int y):
return x + y
z = add_two_numbers(123, 456)
print(z)
Z podoby výsledné céčkovské funkce je patrné, že jsme se přiblížili deklaraci, kterou by mohl zapsat programátor v céčku, přičemž přebytečné závorky, nadbytečný příkaz goto atd. odstraní každý moderní céčkovský překladač:
static int __pyx_f_13add_numbers_4_add_two_numbers(int __pyx_v_x, int __pyx_v_y) {
int __pyx_r;
__pyx_r = (__pyx_v_x + __pyx_v_y);
goto __pyx_L0;
/* function exit code */
__pyx_L0:;
return __pyx_r;
}
10. Přepis funkce s plnými typovými informacemi do podoby kompatibilní s Pythonem
Opět si ukažme, jakým způsobem by bylo možné přepsat funkci s uvedením plných typových informací ze syntaxe Cythonu (Pyrexu) do syntaxe plně kompatibilní s moderním Pythonem, který podporuje zápis typových informací (hintů). Jak se zapisují typy parametrů funkce již víme, takže pouze doplníme informaci o návratovém typu funkce, která se zapisuje mezi šipku → a dvojtečku označující začátek bloku příkazů uvnitř funkce:
import cython
@cython.cfunc
def add_two_numbers(x: cython.int, y: cython.int) -> cython.int:
return x + y
z = add_two_numbers(123, 456)
print(z)
11. Zákaz použití GILu v překládané funkci
Zbývá nám udělat ještě poslední krok, a to odstranit přípravu takzvaného kontextu na začátku těla funkce a naopak odstranění kontextu na jejím konci. Jedná se o tuto trojici řádků:
__Pyx_RefNannyDeclarations
__Pyx_RefNannySetupContext("add_two_numbers", 0);
...
...
...
__Pyx_RefNannyFinishContext();
Zjednodušeně řečeno – kontext úzce souvisí s GIL (Global Interpreter Lock), který prozatím tvoří neoddělitelnou část klasického interpretru CPythonu (ovšem například v Jythonu ho nenajdeme, i když tento interpret má zase jiné problémy). GIL je zapotřebí nastavit tehdy, pokud naše (nyní vlastně céčková) funkce bude interně volat funkce naprogramované v Pythonu, popř. funkce z jeho interní knihovny. To my ovšem nepotřebujeme – pouze sčítáme dvě celá čísla a vracíme výsledek součtu – takže můžeme práci s GILem zcela zakázat, a to použitím specifikace nogil. Finální podoba naší funkce bude vypadat následovně:
cdef int add_two_numbers(int x, int y) nogil:
return x + y
z = add_two_numbers(123, 456)
print(z)
Ovšem zápis nogil za hlavičkou funkce pochopitelně není kompatibilní s Pythonem, který na tomto místě maximálně očekává typovou informaci. Musíme tedy specifikaci nogil umístit tam, kde bude syntakticky korektní. A tímto místem je opět dekorátor, který se nyní jmenuje @nogil, resp. @cython.nogil (podle způsobu jeho importu):
import cython
@cython.cfunc
@cython.nogil
def add_two_numbers(x: cython.int, y: cython.int) -> cython.int:
return x + y
z = add_two_numbers(123, 456)
print(z)
12. Volání funkcí ze standardní knihovny jazyka C
Odstranění GILu z nějaké funkce sice může vést ke zvýšení rychlosti, ale pojí se s tím jeden problém – naše funkce se sice bez GILu zdánlivě obejde, ovšem běžné Pythonovské funkce a operace z ní volané s ním počítají. Proto pokud použijeme nogil, budeme se muset v tomto bloku obejít bez podpory pythonních funkcí, takže tento kód již nebude korektní (nepůjde přeložit), protože se zde snažíme o volání pythonní funkce print:
cdef int add_two_numbers(int x, int y) nogil:
print(x)
return x + y
z = add_two_numbers(123, 456)
print(z)
resp. v pythoní syntaxi:
import cython
@cython.cfunc
@cython.nogil
def add_two_numbers(x: cython.int, y: cython.int) -> cython.int:
print(x)
return x + y
z = add_two_numbers(123, 456)
print(z)
V našem případě to nebude nic složitého – prostě použijeme funkci printf ze standardní céčkové knihovny (ta se stejně bude do výsledného binárního souboru linkovat z jiných důvodů). Řešení může vypadat následovně (pozor na slovo cimport a ne import):
from libc.stdio cimport printf
cdef int add_two_numbers(int x, int y) nogil:
printf("%i\n", x)
return x + y
z = add_two_numbers(123, 456)
print(z)
Při přepisu do syntaxe kompatibilní s Pythonem budeme muset nepatrně změnit i příkaz import, resp. přesněji řečeno jméno balíčku, který importujeme:
import cython
from cython.cimports.libc.stdio import printf
@cython.cfunc
@cython.nogil
def add_two_numbers(x: cython.int, y: cython.int) -> cython.int:
printf("%d\n", x)
return x + y
z = add_two_numbers(123, 456)
print(z)
13. Základní varianta benchmarku naprogramovaná v čistém Pythonu
Nyní již máme k dispozici všechny potřebné informace nutné pro úpravu našeho v několika článcích opakovaného benchmarku provádějícího výpočet Mandelbrotovy množiny. Naším cílem bude dosažení rychlosti srovnatelné s variantou naprogramovanou v čistém ANSI C:
#include <stdlib.h>
#include <stdio.h>
#include "palette_mandmap.h"
void calc_mandelbrot(unsigned int width, unsigned int height, unsigned int maxiter, unsigned char palette[][3])
{
puts("P3");
printf("%d %d\n", width, height);
puts("255");
double cy = -1.5;
int y;
for (y=0; y<height; y++) {
double cx = -2.0;
int x;
for (x=0; x<width; x++) {
double zx = 0.0;
double zy = 0.0;
unsigned int i = 0;
while (i < maxiter) {
double zx2 = zx * zx;
double zy2 = zy * zy;
if (zx2 + zy2 > 4.0) {
break;
}
zy = 2.0 * zx * zy + cy;
zx = zx2 - zy2 + cx;
i++;
}
unsigned char *color = palette[i % 256];
unsigned char r = *color++;
unsigned char g = *color++;
unsigned char b = *color;
printf("%d %d %d\n", r, g, b);
cx += 3.0/width;
}
cy += 3.0/height;
}
}
int main(int argc, char **argv)
{
if (argc < 4) {
puts("usage: ./mandelbrot width height maxiter");
return 1;
}
int width = atoi(argv[1]);
int height = atoi(argv[2]);
int maxiter = atoi(argv[3]);
calc_mandelbrot(width, height, maxiter, palette);
return 0;
}
Jen pro připomenutí – předchozí varianta, s níž jsme končili článek o RPythonu a Cythonu, vypadala následovně. Nejedná se o špatné řešení, ovšem již nyní je nutné říct, že ho můžeme vylepšit a cca dvojnásobně urychlit:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
# taken from Fractint
palette = (
(255, 255, 255), (224, 224, 224), (216, 216, 216), (208, 208, 208),
(200, 200, 200), (192, 192, 192), (184, 184, 184), (176, 176, 176),
...
...
...
(240, 240, 140), (244, 244, 152), (244, 244, 168), (244, 244, 180),
(244, 244, 196), (248, 248, 208), (248, 248, 224), (248, 248, 236),
(252, 252, 252), (248, 248, 248), (240, 240, 240), (232, 232, 232))
from sys import argv
def calc_mandelbrot(width, height, maxiter, palette):
print("P3")
print("{w} {h}".format(w=width, h=height))
print("255")
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
r = palette[i][0]
g = palette[i][1]
b = palette[i][2]
print("{r} {g} {b}".format(r=r, g=g, b=b))
cx += 3.0/width
cy += 3.0/height
if __name__ == "__main__":
if len(argv) < 4:
width = 512
height = 512
maxiter = 255
else:
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
calc_mandelbrot(width, height, maxiter, palette)

Obrázek 6: Mandelbrotova množina o rozlišení 512×512 pixelů vykreslená předchozím příkladem.
14. Přepis benchmarku do Cythonu
Nyní si postupně zdrojový kód z předchozí kapitoly přepíšeme do podoby zpracovatelné Cythonem. Použijeme přitom původní syntaxi Pyrexu. Přepisovat budeme pouze funkci calc_mandelbrot, ve které se stráví prakticky 100% času.
Nejprve je vhodné změnit hlavičku funkce – určíme, že se má funkce přeložit do céčka (a posléze do nativního kódu) a nastavíme typy parametrů funkce:
cdef calc_mandelbrot(int width, int height, int maxiter, palette):
Explicitně určíme typy všech lokálních proměnných ve funkci:
cdef double zx
cdef double zy
cdef double zx2
cdef double zy2
cdef double cx
cdef double cy
cdef int r
cdef int g
cdef int b
cdef int i
To je prozatím vše, takže se podívejme na výsledný skript:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
from sys import argv
# taken from Fractint
palette = (
(255, 255, 255), (224, 224, 224), (216, 216, 216), (208, 208, 208),
(200, 200, 200), (192, 192, 192), (184, 184, 184), (176, 176, 176),
...
...
...
(240, 240, 140), (244, 244, 152), (244, 244, 168), (244, 244, 180),
(244, 244, 196), (248, 248, 208), (248, 248, 224), (248, 248, 236),
(252, 252, 252), (248, 248, 248), (240, 240, 240), (232, 232, 232))
cdef calc_mandelbrot(int width, int height, int maxiter, palette):
cdef double zx
cdef double zy
cdef double zx2
cdef double zy2
cdef double cx
cdef double cy
cdef int r
cdef int g
cdef int b
cdef int i
print("P3")
print("{w} {h}".format(w=width, h=height))
print("255")
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
r = palette[i][0]
g = palette[i][1]
b = palette[i][2]
print("{r} {g} {b}".format(r=r, g=g, b=b))
cx += 3.0/width
cy += 3.0/height
if __name__ == "__main__":
if len(argv) < 4:
width = 512
height = 512
maxiter = 255
else:
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
calc_mandelbrot(width, height, maxiter, palette)
15. Varianta se syntaxí kompatibilní s Pythonem
Přepis ze syntaxe Cythonu/Pyrexu do formy plně kompatibilní se standardním Pythonem je již poměrně triviální a navíc veskrze mechanickou záležitostí. Hlavičku funkce uvodíme dekorátorem @cfunc a typy parametrů zapíšeme s využitím syntaxe totožné s typovými informacemi (type hints):
@cython.cfunc def calc_mandelbrot(width: cython.int, height: cython.int, maxiter: cython.int, palette):
Podobně explicitně specifikujeme typy všech lokálních proměnných, které se zúčastní výpočtů:
zx: cython.double
zy: cython.double
zx2: cython.double
zy2: cython.double
cx: cython.double
cy: cython.double
r: cython.int
g: cython.int
b: cython.int
i: cython.int
A takto bude vypadat výsledný skript, který lze přeložit Cythonem do nativního a poměrně rychlého kódu:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
from sys import argv
import cython
# taken from Fractint
palette = (
(255, 255, 255), (224, 224, 224), (216, 216, 216), (208, 208, 208),
(200, 200, 200), (192, 192, 192), (184, 184, 184), (176, 176, 176),
...
...
...
(244, 244, 196), (248, 248, 208), (248, 248, 224), (248, 248, 236),
(252, 252, 252), (248, 248, 248), (240, 240, 240), (232, 232, 232))
@cython.cfunc
def calc_mandelbrot(width: cython.int, height: cython.int, maxiter: cython.int, palette):
zx: cython.double
zy: cython.double
zx2: cython.double
zy2: cython.double
cx: cython.double
cy: cython.double
r: cython.int
g: cython.int
b: cython.int
i: cython.int
print("P3")
print("{w} {h}".format(w=width, h=height))
print("255")
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
r = palette[i][0]
g = palette[i][1]
b = palette[i][2]
print("{r} {g} {b}".format(r=r, g=g, b=b))
cx += 3.0/width
cy += 3.0/height
if __name__ == "__main__":
if len(argv) < 4:
width = 512
height = 512
maxiter = 255
else:
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
calc_mandelbrot(width, height, maxiter, palette)
16. Pole a předávání ukazatelů
Barvová paleta je prozatím realizována Pythonovskou n-ticí. Tento datový typ patří společně se seznamy k základním typům Pythonu, ovšem kvůli tomu, že jsou tyto datové struktury (kontejnery) nehomogenní, se s nimi musí zacházet poměrně neefektivně. Navíc je neefektivní i samotné uložení těchto datových typů v operační paměti. Řešením je použití klasických céčkových polí s případným převodem seznamů na pole. To lze provést například vytvořením klasického céčkového pole s prvky zadaného typu. Nejprve vytvoříme pole dle sémantiky samotného Pythonu:
from cpython cimport array
cdef array.array apalette = array.array('B')
Kdykoli později můžeme získat ukazatel na prvky pole:
apalette.data.as_uchars
Získáme tedy hodnotu typu unsigned char *, kterou předáme do funkce calc_mandelbrot, kde se s ní bude pracovat velmi efektivně. Navíc využijeme céčkovskou funkci printf a tudíž se můžeme zbavit GILu:
@cython.cdivision(True) cdef void calc_mandelbrot(int width, int height, int maxiter, unsigned char *palette) nogil:
A takto bude vypadat výsledný skript pro výpočet, který je opět založen na syntaxi Cythonu/Pyrexu:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
from sys import argv, exit
import cython
from cpython cimport array
from libc.stdio cimport printf
# taken from Fractint
palette = [
[255, 255, 255], [224, 224, 224], [216, 216, 216], [208, 208, 208],
[200, 200, 200], [192, 192, 192], [184, 184, 184], [176, 176, 176],
...
...
...
[244, 244, 196], [248, 248, 208], [248, 248, 224], [248, 248, 236],
[252, 252, 252], [248, 248, 248], [240, 240, 240], [232, 232, 232]]
@cython.cdivision(True)
cdef void calc_mandelbrot(int width, int height, int maxiter, unsigned char *palette) nogil:
cdef double zx
cdef double zy
cdef double zx2
cdef double zy2
cdef double cx
cdef double cy
cdef unsigned char r
cdef unsigned char g
cdef unsigned char b
cdef int i
cdef int index
printf("P3\n%d %d\n255\n", width, height)
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
index = i * 3
r = palette[index]
g = palette[index+1]
b = palette[index+2]
printf("%d %d %d\n", r, g, b)
cx += 3.0/width
cy += 3.0/height
cdef array.array apalette = array.array('B')
if __name__ == "__main__":
if len(argv) < 4:
width = 512
height = 512
maxiter = 255
else:
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
for color in palette:
for component in color:
apalette.append(component)
calc_mandelbrot(width, height, maxiter, apalette.data.as_uchars)
17. Opětovná úprava se syntaxí kompatibilní s Pythonem
Pro úplnost si ukažme, jakým způsobem je možné skript z předchozí kapitoly přepsat do podoby plně kompatibilní s Cythonem.
Alokace pole s prvky typu bajt (bude prázdné):
from cython.cimports.cpython import array
import array
apalette = cython.declare(array.array, array.array('B', []))
Přidání prvků (barev) do barvové palety:
for color in palette:
for component in color:
apalette.append(component)
Získání ukazatele na první barvu:
apalette.data.as_uchars
Začátek funkce calc_mandelbrot bude vypadat následovně:
@cython.cdivision(True)
@cython.nogil
@cython.cfunc
def calc_mandelbrot(width: cython.int, height: cython.int, maxiter: cython.int, palette: cython.p_uchar) -> cython.int:
zx: cython.double
zy: cython.double
zx2: cython.double
zy2: cython.double
cx: cython.double
cy: cython.double
r: cython.uchar
g: cython.uchar
b: cython.uchar
i: cython.int
index: cython.int
A takto vypadá celý skript:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
from sys import argv
import cython
from cython.cimports.cpython import array
import array
from cython.cimports.libc.stdio import printf
# taken from Fractint
palette = [
[255, 255, 255], [224, 224, 224], [216, 216, 216], [208, 208, 208],
[200, 200, 200], [192, 192, 192], [184, 184, 184], [176, 176, 176],
...
...
...
[244, 244, 196], [248, 248, 208], [248, 248, 224], [248, 248, 236],
[252, 252, 252], [248, 248, 248], [240, 240, 240], [232, 232, 232]]
@cython.cdivision(True)
@cython.nogil
@cython.cfunc
def calc_mandelbrot(width: cython.int, height: cython.int, maxiter: cython.int, palette: cython.p_uchar) -> cython.int:
zx: cython.double
zy: cython.double
zx2: cython.double
zy2: cython.double
cx: cython.double
cy: cython.double
r: cython.uchar
g: cython.uchar
b: cython.uchar
i: cython.int
index: cython.int
printf("P3\n%d %d\n255\n", width, height)
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
index = i * 3
r = palette[index]
g = palette[index+1]
b = palette[index+2]
printf("%d %d %d\n", r, g, b)
cx += 3.0/width
cy += 3.0/height
apalette = cython.declare(array.array, array.array('B', []))
if __name__ == "__main__":
if len(argv) < 4:
width = 512
height = 512
maxiter = 255
else:
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
for color in palette:
for component in color:
apalette.append(component)
calc_mandelbrot(width, height, maxiter, apalette.data.as_uchars)
18. Výsledek transpilace Cythonem do céčka
A na úplný závěr si ukažme, jak byla funkce pro výpočet Mandelbrotovy množiny transpilována do jazyka C:
static int __pyx_f_17mandelbrot_cython_calc_mandelbrot(int __pyx_v_width, int __pyx_v_height, int __pyx_v_maxiter, unsigned char *__pyx_v_palette) {
double __pyx_v_zx;
double __pyx_v_zy;
double __pyx_v_zx2;
double __pyx_v_zy2;
double __pyx_v_cx;
double __pyx_v_cy;
unsigned char __pyx_v_r;
unsigned char __pyx_v_g;
unsigned char __pyx_v_b;
int __pyx_v_i;
int __pyx_v_index;
CYTHON_UNUSED long __pyx_v_y;
CYTHON_UNUSED long __pyx_v_x;
int __pyx_r;
int __pyx_t_1;
int __pyx_t_2;
long __pyx_t_3;
int __pyx_t_4;
int __pyx_t_5;
long __pyx_t_6;
int __pyx_t_7;
(void)(printf(((char const *)"P3\n%d %d\n255\n"), __pyx_v_width, __pyx_v_height));
__pyx_v_cy = -1.5;
__pyx_t_1 = __pyx_v_height;
__pyx_t_2 = __pyx_t_1;
for (__pyx_t_3 = 0; __pyx_t_3 < __pyx_t_2; __pyx_t_3+=1) {
__pyx_v_y = __pyx_t_3;
__pyx_v_cx = -2.0;
__pyx_t_4 = __pyx_v_width;
__pyx_t_5 = __pyx_t_4;
for (__pyx_t_6 = 0; __pyx_t_6 < __pyx_t_5; __pyx_t_6+=1) {
__pyx_v_x = __pyx_t_6;
__pyx_v_zx = 0.0;
__pyx_v_zy = 0.0;
__pyx_v_i = 0;
while (1) {
__pyx_t_7 = (__pyx_v_i < __pyx_v_maxiter);
if (!__pyx_t_7) break;
__pyx_v_zx2 = (__pyx_v_zx * __pyx_v_zx);
__pyx_v_zy2 = (__pyx_v_zy * __pyx_v_zy);
__pyx_t_7 = ((__pyx_v_zx2 + __pyx_v_zy2) > 4.0);
if (__pyx_t_7) {
goto __pyx_L8_break;
}
__pyx_v_zy = (((2.0 * __pyx_v_zx) * __pyx_v_zy) + __pyx_v_cy);
__pyx_v_zx = ((__pyx_v_zx2 - __pyx_v_zy2) + __pyx_v_cx);
__pyx_v_i = (__pyx_v_i + 1);
}
__pyx_L8_break:;
__pyx_v_index = (__pyx_v_i * 3);
__pyx_v_r = (__pyx_v_palette[__pyx_v_index]);
__pyx_v_g = (__pyx_v_palette[(__pyx_v_index + 1)]);
__pyx_v_b = (__pyx_v_palette[(__pyx_v_index + 2)]);
(void)(printf(((char const *)"%d %d %d\n"), __pyx_v_r, __pyx_v_g, __pyx_v_b));
__pyx_v_cx = (__pyx_v_cx + (3.0 / ((double)__pyx_v_width)));
}
__pyx_v_cy = (__pyx_v_cy + (3.0 / ((double)__pyx_v_height)));
}
__pyx_r = 0;
return __pyx_r;
}
19. Repositář s demonstračními příklady
Všechny demonstrační příklady (resp. jednoduché benchmarky) ukazující vlastnosti Cythonu naleznete v repositáři https://github.com/tisnik/most-popular-python-libs:
| # | Příklad | Stručný popis | Adresa |
|---|---|---|---|
| 1 | add_numbers/add_numbers1.py | běžná funkce v Pythonu podporující duck typing | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers1.py |
| 2 | add_numbers/add_numbers2.pyx | funkce určená pro překlad do céčka, původní syntaxe Cythonu/Pyrexu | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers2.pyx |
| 3 | add_numbers/add_numbers2.py | funkce určená pro překlad do céčka, syntaxe kompatibilní s Pythonem | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers2.py |
| 4 | add_numbers/add_numbers3.pyx | přidání informace o typech parametrů funkce pro součet celých čísel, původní syntaxe Cythonu/Pyrexu | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers3.pyx |
| 5 | add_numbers/add_numbers3.py | přidání informace o typech parametrů funkce pro součet celých čísel, syntaxe kompatibilní s Pythonem | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers3.py |
| 6 | add_numbers/add_numbers4.pyx | přidání informace o návratovém typu funkce pro součet celých čísel, původní syntaxe Cythonu/Pyrexu | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers4.pyx |
| 7 | add_numbers/add_numbers4.py | přidání informace o návratovém typu funkce pro součet celých čísel, syntaxe kompatibilní s Pythonem | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers4.py |
| 8 | add_numbers/add_numbers5.pyx | zákaz použití GILu v překládané funkci, původní syntaxe Cythonu/Pyrexu | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers5.pyx |
| 9 | add_numbers/add_numbers5.py | zákaz použití GILu v překládané funkci, syntaxe kompatibilní s Pythonem | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers5.py |
| 10 | add_numbers/add_numbers6.pyx | zákaz použití GILu v překládané funkci, původní syntaxe Cythonu/Pyrexu | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers6.pyx |
| 11 | add_numbers/add_numbers6.py | zákaz použití GILu v překládané funkci, syntaxe kompatibilní s Pythonem | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers6.py |
| 12 | add_numbers/add_numbers7.pyx | volání funkcí ze standardní knihovny jazyka C, původní syntaxe Cythonu/Pyrexu | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers7.pyx |
| 13 | add_numbers/add_numbers7.py | volání funkcí ze standardní knihovny jazyka C, syntaxe kompatibilní s Pythonem | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers7.py |
| 14 | add_numbers/add_numbers_dis.py | zobrazení bajtkódu Pythonu po překladu funkce add_two_numbers | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/add_numbers/add_numbers_dis.py |
| 15 | mandelbrot/v1_python | benchmark s výpočtem Mandelbrotovy množiny, původní varianta naprogramovaná v čistém Pythonu | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/mandelbrot/v1_python |
| 16 | mandelbrot/v2_cython | přidání typových informací do funkce calc_mandelbrot, původní syntaxe Cythonu/Pyrexu | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/mandelbrot/v2_cython |
| 17 | mandelbrot/v2_python | přidání typových informací do funkce calc_mandelbrot, syntaxe kompatibilní s Pythonem | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/mandelbrot/v2_python |
| 18 | mandelbrot/v3_cython | alokace a použití céčkového pole, původní syntaxe Cythonu/Pyrexu | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/mandelbrot/v3_cython |
| 19 | mandelbrot/v3-python | alokace a použití céčkového pole, syntaxe kompatibilní s Pythonem | https://github.com/tisnik/most-popular-python-libs/blob/master/cython/mandelbrot/v3-python |
20. Odkazy na Internetu
- Cython (home page)
http://cython.org/ - Cython (wiki)
https://github.com/cython/cython/wiki - Cython (Wikipedia)
https://en.wikipedia.org/wiki/Cython - Cython (GitHub)
https://github.com/cython/cython - Statické typové kontroly zdrojových kódů Pythonu prováděné nástrojem Mypy
https://www.root.cz/clanky/staticke-typove-kontroly-zdrojovych-kodu-pythonu-provadene-nastrojem-mypy/ - Statické typové kontroly zdrojových kódů Pythonu prováděné nástrojem Mypy (2.část)
https://www.root.cz/clanky/staticke-typove-kontroly-zdrojovych-kodu-pythonu-provadene-nastrojem-mypy-2-cast/ - Statické typové kontroly zdrojových kódů Pythonu prováděné nástrojem Mypy (3)
https://www.root.cz/clanky/staticke-typove-kontroly-zdrojovych-kodu-pythonu-provadene-nastrojem-mypy-3/ - Praktické použití nástroje Cython při překladu Pythonu do nativního kódu
https://www.root.cz/clanky/prakticke-pouziti-nastroje-cython-pri-prekladu-pythonu-do-nativniho-kodu-1/ - Pyrex
https://wiki.python.org/moin/Pyrex - RPython vs Cython aneb dvojí přístup k překladu Pythonu do nativního kódu
https://www.root.cz/clanky/rpython-vs-cython-aneb-dvoji-pristup-k-prekladu-pythonu-do-nativniho-kodu/ - Python Implementations: Compilers
https://wiki.python.org/moin/PythonImplementations#Compilers - EmbeddingCython
https://github.com/cython/cython/wiki/EmbeddingCython - The Basics of Cython
http://docs.cython.org/en/latest/src/tutorial/cython_tutorial.html - Overcoming Python's GIL with Cython
https://lbolla.info/python-threads-cython-gil - GlobalInterpreterLock
https://wiki.python.org/moin/GlobalInterpreterLock - The Magic of RPython
https://refi64.com/posts/the-magic-of-rpython.html - RPython: Frequently Asked Questions
http://rpython.readthedocs.io/en/latest/faq.html - RPython’s documentation
http://rpython.readthedocs.io/en/latest/index.html - RPython (Wikipedia)
https://en.wikipedia.org/wiki/PyPy#RPython - Getting Started with RPython
http://rpython.readthedocs.io/en/latest/getting-started.html - Duck typing
https://en.wikipedia.org/wiki/Duck_typing - PyPy (home page)
https://pypy.org/ - PyPy (dokumentace)
http://doc.pypy.org/en/latest/ - Localized Type Inference of Atomic Types in Python (2005)
http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.90.3231 - Numba
http://numba.pydata.org/ - Tutorial: Writing an Interpreter with PyPy, Part 1
https://morepypy.blogspot.com/2011/04/tutorial-writing-interpreter-with-pypy.html - List of numerical analysis software
https://en.wikipedia.org/wiki/List_of_numerical_analysis_software - Pixie: lehký skriptovací jazyk s „kouzelnými“ schopnostmi
https://www.root.cz/clanky/pixie-lehky-skriptovaci-jazyk-s-kouzelnymi-schopnostmi/ - Programovací jazyk Pixie: funkce ze základní knihovny a použití FFI
https://www.root.cz/clanky/programovaci-jazyk-pixie-funkce-ze-zakladni-knihovny-a-pouziti-ffi/ - The future can be written in RPython now (článek z roku 2010)
http://blog.christianperone.com/2010/05/the-future-can-be-written-in-rpython-now/ - PyPy is the Future of Python (článek z roku 2010)
https://alexgaynor.net/2010/may/15/pypy-future-python/ - Portal:Python programming
https://en.wikipedia.org/wiki/Portal:Python_programming - RPython Frontend and C Wrapper Generator
http://www.codeforge.com/article/383293 - PyPy’s Approach to Virtual Machine Construction
https://bitbucket.org/pypy/extradoc/raw/tip/talk/dls2006/pypy-vm-construction.pdf - Tutorial: Writing an Interpreter with PyPy, Part 1
https://morepypy.blogspot.com/2011/04/tutorial-writing-interpreter-with-pypy.html - A simple interpreter from scratch in Python (part 1)
http://www.jayconrod.com/posts/37/a-simple-interpreter-from-scratch-in-python-part-1 - Brainfuck Interpreter in Python
https://helloacm.com/brainfuck-interpreter-in-python/