Obsah
1. Parametrické křivky používané v designu i při tvorbě animací (dokončení)
2. Lokalita změn tvaru spline křivek při posunu jednoho řídicího bodu
3. Ukázka lokality změn B-spline
5. Ukázka lokality změn Catmul-Romovy spline
7. Násobné řídicí body na začátku a konci spline křivek
8. Ukázka násobných bodů na začátku/konci B-spline
9. Ukázka násobných bodů na začátku/konci Catmul-Romovy spline
10. Násobné řídicí body uprostřed spline křivek
11. Ukázka násobných bodů v B-spline
12. Ukázka násobných bodů v Catmul-Romově spline
14. Hermitovské bázové polynomy Fergusonovy kubiky
15. Vykreslení Fergusonovy kubiky
16. Od klasických B-spline k NURBS
19. Repositář s demonstračními příklady
1. Parametrické křivky používané v designu i při tvorbě animací
Dnes se již naposledy budeme věnovat parametrickým křivkám používaným v počítačové grafice, a to například při návrhu fontů, v nástrojích pro kreslení, v CAD systémech, ale i při tvorbě animací na základě takzvaných klíčových snímků (keyframes). V předchozích dvou částech tohoto seriálu [1, 2] jsme si popsali parametrické křivky, které jsou po částech reprezentovány polynomem nízkého řádu, typicky polynomem třetího či čtvrtého stupně. Mezi tyto křivky patří jak křivky ryze aproximační (typickým příkladem jsou B-spline), tak i křivky interpolační (zástupcem tohoto typu křivek jsou Catmul-Romovy spline), popř. se jedná o křivky, které prochází jen některými svými řídicími body (sem spadají Bézierovy křivky, tedy většinou Bézierovy kvadriky a Bézierovy kubiky).
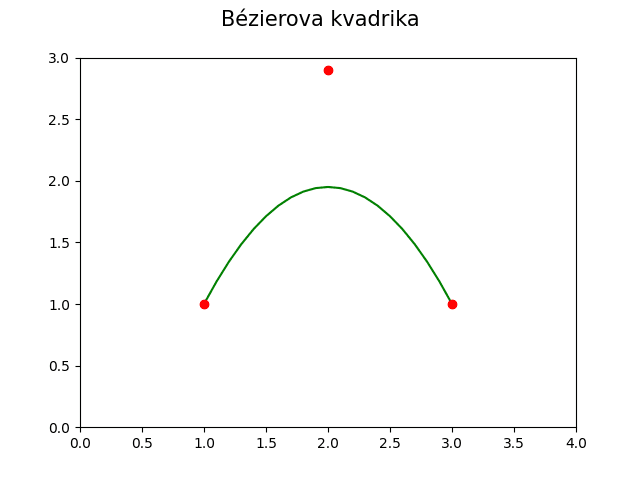
Obrázek 1: Bézierova kvadrika – nejpoužívanější parametrická křivka vůbec (použita je například v TrueType fontech apod.).
Tento článek je rozdělen do tří částí. V části první si ukážeme některé vlastnosti B-spline a Catmul-Romovy spline, zejména lokalitu změn a vliv násobných řídicích bodů na výsledný tvar křivky. Následně se (z pohledu historie) vrátíme na samotný začátek výzkumu polynomiálních křivek, protože se seznámíme s Fergusonovou kubikou. Ta je velmi důležitá pro konstrukci dalších typů spline křivek, ovšem se samotnou Fergusonovou kubikou se v interaktivních programech (grafických editorech atd.) prakticky nikdy nesetkáme (důvody budou uvedeny v dalším textu). Na základě Fergusonovy kubiky byly navrženy spline křivky, které známe pod jmény jejích tvůrců – Kochanek-Bartels. A pochopitelně není možné zapomenout na NURBS neboli Neuniformní racionální B-spline křivky (plochy). Tyto spline vznikly dvojím zobecněním B-spline křivek, s jejichž základními vlastnostmi i způsobem konstrukce jsme se již v tomto seriálu seznámili.

Obrázek 2: Bézierova kubika.
2. Lokalita změn tvaru spline křivek při posunu jednoho řídicího bodu
Důležitou vlastností všech spline křivek používaných v počítačové grafice a současně i jedním z důvodů, proč se v této oblasti nepoužívají klasické Lagrangeovy polynomy, je fakt, že u spline křivek má změna polohy jednoho řídicího bodu jen lokální vliv na segment (či segmenty) křivky, které jsou tímto bodem určeny – všechny ostatní segmenty zůstanou nezměněny. To má pochopitelně velký praktický význam, protože jiné chování, tedy změna tvaru celé křivky, by například neumožňovalo smysluplné editace tvaru znaků apod.

Obrázek 3: Interpolační křivka získaná Lagrangeovou metodou.
Prozatím jsme si popsali dva typy spline křivek, konkrétně B-spline a Catmul-Romovy spline. V navazujících kapitolách si na praktických příkladech ukážeme, jak se projeví změna polohy jediného řídicího bodu na výsledném tvaru těchto spline křivek, popř. na tvaru jednotlivých segmentů (které od sebe budou barevně odlišeny).

Obrázek 4: Zákmity na obou koncích křivky získané Lagrangeovou metodou.
3. Ukázka lokality změn B-spline
Nejprve se podívejme na to, jakým způsobem se změní tvar B-spline při posunu řídicího bodu umístěného uprostřed celé spline. Následující demonstrační příklad je nepatrně složitější, než prozatím ukázané příklady, ale princip zůstává stále jednoduchý – do funkce draw_b_spline se mj. předává i y-ová pozice čtvrtého řídicího bodu, který tak může měnit svoji horizontální polohu. Navíc je zajištěno, že sousední segmenty křivky jsou zobrazeny odlišnou barvou:
"""Parametrická křivka: B-spline složená z Coonsových oblouků, posun vybraného řídicího bodu."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 20)
# řídicí body B-spline
xc = [1, 2, 3, 4, 5, 6, 7]
yc = [1, 2, 1, 2, 1, 2, 1]
# Coonsovy polynomy
C = [(1-t)**3,
3*t**3 - 6*t**2 + 4,
-3*t**3 + 3*t**2 + 3*t + 1,
t**3]
def draw_coons_arc(xc, yc, ax, style):
# výpočet bodů ležících na Coonsově kubice
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*C[i]
y += yc[i]*C[i]
# konečná úprava sumy
x /= 6
y /= 6
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
def draw_b_spline(filename, xc, yc, y):
# změnit polohu prostředního řídicího bodu
yc[3] = y
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('B-spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0.5, 7.5)
ax.set_ylim(0.5, 2.5)
# řídicí body B-spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
last = len(xc)
# další oblouky
for start in range(0, last-3):
style = "r-" if start % 2 == 0 else "b-"
draw_coons_arc(xc[start:start+4], yc[start:start+4], ax, style)
# uložení grafu do rastrového obrázku
plt.savefig(filename)
draw_b_spline("B-spline_3A.png", xc, yc, 0.5)
draw_b_spline("B-spline_3B.png", xc, yc, 1.5)
draw_b_spline("B-spline_3C.png", xc, yc, 2.5)
Podívejme se nyní na výsledky získané pro tři různé polohy prostředního řídicího bodu:

Obrázek 5: B-spline; prostřední řídicí bod má souřadnice [4, 0.5].

Obrázek 6: B-spline; prostřední řídicí bod má souřadnice [4, 1.5].

Obrázek 7: B-spline; prostřední řídicí bod má souřadnice [4, 2.5].
Lokalita změn je v tomto konkrétním případě zřejmá – mění se prostřední dva segmenty přímo ovlivněné řídicím bodem. U obou dalších (vnějších) segmentů dojde pouze k menší změně, která se ale netýká jejich vnějších okrajů. Případné další segmenty by se nezměnily vůbec.
4. Animovaný příklad
Z předchozího demonstračního příkladu můžeme pro větší názornost odvodit jeho upravenou verzi, která vytvoří podklad pro animaci. Postup pro vytvoření animace vhodné pro vložení do HTML stránky jsme si již popsali ve třetím článku, takže nyní jen v krátkosti:
- Necháme skriptem (Python+Matplotlib+Numpy) vygenerovat několik PNG obrázků křivky, pokaždé pro odlišný koeficient.
- Vytvoříme z těchto obrázků animovaný GIF.
- Tento GIF zoptimalizujeme na velikost.
Druhý příkaz, tedy vytvoření animovaného GIFu, vypadá takto:
$ convert -delay 10 -loop 0 *.png animated.gif
Třetí příkaz, tj. optimalizace souboru na velikost, je založen na použití užitečného nástroje gifsicle:
$ gifsicle -O animated.gif > animated2.gif
Výsledná animace s postupnou změnou polohy jednoho řídicího bodu B-spline křivky vypadá takto:

Podklady pro tuto animaci byly získány následujícím skriptem:
"""Parametrická křivka: B-spline složená z Coonsových oblouků, násobné body."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 20)
# řídicí body B-spline
xc = [1, 2, 3, 4, 5, 6, 7]
yc = [1, 2, 1, 2, 1, 2, 1]
# Coonsovy polynomy
C = [(1-t)**3,
3*t**3 - 6*t**2 + 4,
-3*t**3 + 3*t**2 + 3*t + 1,
t**3]
def draw_coons_arc(xc, yc, ax, style):
# výpočet bodů ležících na Coonsově kubice
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*C[i]
y += yc[i]*C[i]
# konečná úprava sumy
x /= 6
y /= 6
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
def draw_b_spline(filename, xc, yc, draw_first_arcs, draw_second_arcs, y):
# změnit polohu prostředního řídicího bodu
yc[3] = y
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('B-spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0.5, 7.5)
ax.set_ylim(0.5, 2.5)
# řídicí body B-spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
# první dva oblouky s násobnými body
if draw_first_arcs:
draw_coons_arc((xc[0], xc[0], xc[0], xc[1]),
(yc[0], yc[0], yc[0], yc[1]), ax, "g-")
if draw_second_arcs:
draw_coons_arc((xc[0], xc[0], xc[1], xc[2]),
(yc[0], yc[0], yc[1], yc[2]), ax, "y-")
last = len(xc)
# další oblouky
for start in range(0, last-3):
style = "r-" if start % 2 == 0 else "b-"
draw_coons_arc(xc[start:start+4], yc[start:start+4], ax, style)
# poslední dva oblouky s násobnými body
if draw_second_arcs:
draw_coons_arc((xc[last-3], xc[last-2], xc[last-1], xc[last-1]),
(yc[last-3], yc[last-2], yc[last-1], yc[last-1]), ax, "y-")
if draw_first_arcs:
draw_coons_arc((xc[last-2], xc[last-1], xc[last-1], xc[last-1]),
(yc[last-2], yc[last-1], yc[last-1], yc[last-1]), ax, "g-")
# uložení grafu do rastrového obrázku
plt.savefig(filename)
frame = 0
for y in np.linspace(0.5, 2.5, 20):
draw_b_spline("b-spline_anim_{:02}.png".format(frame), xc, yc, True, True, y)
# další snímek
frame += 1
5. Ukázka lokality změn Catmul-Romovy spline
Nyní se podívejme, jakým způsobem se projeví změna jediného řídicího bodu v případě, že vykreslujeme Catmul-Romovu spline. Následující demonstrační příklad je do značné míry podobný příkladu ze třetí kapitoly (liší se prakticky jen výpočtem bázových polynomů), takže si ukažme jeho zdrojový kód bez dalších komentářů:
"""Parametrická křivka: Catmul-Romova spline složená z oblouků, posun vybraného řídicího bodu."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 20)
# řídicí body Catmul-Romovy spline
xc = [1, 2, 3, 4, 5, 6, 7]
yc = [1, 2, 1, 2, 1, 2, 1]
# koeficient Catmul-Romovy spline
tau = 0.5
# bázové polynomy
Q = [-tau*t + 2*tau*t**2 - tau*t**3,
1+(tau-3)*t**2+(2-tau)*t**3,
tau*t + (3-2*tau)*t**2 + (tau-2)*t**3,
-tau*t**2+tau*t**3]
def draw_catmul_rom_arc(xc, yc, ax, style):
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*Q[i]
y += yc[i]*Q[i]
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
def draw_catmul_rom_spline(filename, xc, yc, y):
# změnit polohu prostředního řídicího bodu
yc[3] = y
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Catmul-Rom spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0.5, 7.5)
ax.set_ylim(0.5, 2.5)
# řídicí body B-spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
last = len(xc)
# další oblouky
for start in range(0, last-3):
style = "r-" if start % 2 == 0 else "b-"
draw_catmul_rom_arc(xc[start:start+4], yc[start:start+4], ax, style)
# uložení grafu do rastrového obrázku
plt.savefig(filename)
draw_catmul_rom_spline("Catmul-Rom-spline_3A.png", xc, yc, 0.5)
draw_catmul_rom_spline("Catmul-Rom-spline_3B.png", xc, yc, 1.5)
draw_catmul_rom_spline("Catmul-Rom-spline_3C.png", xc, yc, 2.5)
Podívejme se nyní na výsledky získané pro tři různé polohy prostředního řídicího bodu:

Obrázek 8: Catmul-Romova spline; prostřední řídicí bod má souřadnice [4, 0.5].

Obrázek 9: Catmul-Romova spline; prostřední řídicí bod má souřadnice [4, 1.5].

Obrázek 10: Catmul-Romova spline; prostřední řídicí bod má souřadnice [4, 2.5].
6. Animovaný příklad
Předchozí skript je možné poměrně triviálním způsobem přepsat do stavu, kdy vytváří animaci postupné změny tvaru křivky změnou pozice jednoho řídicího bodu. Na animaci je ještě lépe patrné, jak se mění vnější segmenty křivky (spline):

Podklady pro tuto animaci byly získány následujícím skriptem:
"""Parametrická křivka: Catmul-Romova spline, násobné body."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 20)
# řídicí body Catmul-Romovy spline
xc = [1, 2, 3, 4, 5, 6, 7]
yc = [1, 2, 1, 2, 1, 2, 1]
# koeficient Catmul-Romovy spline
tau = 0.5
# bázové polynomy
Q = [-tau*t + 2*tau*t**2 - tau*t**3,
1+(tau-3)*t**2+(2-tau)*t**3,
tau*t + (3-2*tau)*t**2 + (tau-2)*t**3,
-tau*t**2+tau*t**3]
def draw_catmul_rom_arc(xc, yc, ax, style):
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*Q[i]
y += yc[i]*Q[i]
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
def draw_catmul_rom_spline(filename, xc, yc, draw_first_arcs, draw_second_arcs, y):
# změnit polohu prostředního řídicího bodu
yc[3] = y
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Catmul-Rom spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0.5, 7.5)
ax.set_ylim(0.5, 2.5)
# řídicí body Catmul-Romovy spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
# první dva oblouky s násobnými body
if draw_first_arcs:
draw_catmul_rom_arc((xc[0], xc[0], xc[0], xc[1]),
(yc[0], yc[0], yc[0], yc[1]), ax, "g-")
if draw_second_arcs:
draw_catmul_rom_arc((xc[0], xc[0], xc[1], xc[2]),
(yc[0], yc[0], yc[1], yc[2]), ax, "y-")
last = len(xc)
# další oblouky
for start in range(0, last-3):
style = "r-" if start % 2 == 0 else "b-"
draw_catmul_rom_arc(xc[start:start+4], yc[start:start+4], ax, style)
# poslední dva oblouky s násobnými body
if draw_second_arcs:
draw_catmul_rom_arc((xc[last-3], xc[last-2], xc[last-1], xc[last-1]),
(yc[last-3], yc[last-2], yc[last-1], yc[last-1]), ax, "y-")
if draw_first_arcs:
draw_catmul_rom_arc((xc[last-2], xc[last-1], xc[last-1], xc[last-1]),
(yc[last-2], yc[last-1], yc[last-1], yc[last-1]), ax, "g-")
# uložení grafu do rastrového obrázku
plt.savefig(filename)
frame = 0
for y in np.linspace(0.5, 2.5, 20):
draw_catmul_rom_spline("catmul-rom-spline_anim_{:02}.png".format(frame), xc, yc, False, True, y)
# další snímek
frame += 1
7. Násobné řídicí body na začátku a konci spline křivek
Spline křivky, v kontextu tohoto článku tedy B-spline i Catmul-Romovy spline, obecně nepochází svými koncovými body. V případě, že je nutné, aby spline začínaly a/nebo končily v koncových bodech (a to je mnohdy požadovaná vlastnost), je nutné použít triku – na začátku a konci křivek přidat násobné řídicí body, což je dvojice či trojice řídicích bodů s naprosto stejnými souřadnicemi. Chování B-spline a Catmul-Rom spline je v těchto případech nepatrně odlišné, takže si ho pro úplnost ukážeme na dvojici demonstračních příkladů uvedených v navazující dvojici kapitol.
8. Ukázka násobných bodů na začátku/konci B-spline
Příklad uvedený v této kapitole dokáže zobrazit B-spline křivku specifikovanou sedmi řídicími body. Přitom je možné při volání funkce draw_b_spline specifikovat, zda se má první a poslední řídicí bod použít dvakrát nebo dokonce třikrát a tím ke křivce přidat další dva resp. čtyři segmenty:
"""Parametrická křivka: B-spline složená z Coonsových oblouků, násobné body na začátku a na konci."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 20)
# řídicí body B-spline
xc = (1, 2, 3, 4, 5, 6, 7)
yc = (1, 2, 1, 2, 1, 2, 1)
# Coonsovy polynomy
C = [(1-t)**3,
3*t**3 - 6*t**2 + 4,
-3*t**3 + 3*t**2 + 3*t + 1,
t**3]
def draw_coons_arc(xc, yc, ax, style):
# výpočet bodů ležících na Coonsově kubice
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*C[i]
y += yc[i]*C[i]
# konečná úprava sumy
x /= 6
y /= 6
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
def draw_b_spline(filename, xc, yc, draw_first_arcs, draw_second_arcs):
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('B-spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0.5, 7.5)
ax.set_ylim(0.5, 2.5)
# řídicí body B-spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
# první dva oblouky s násobnými body
if draw_first_arcs:
draw_coons_arc((xc[0], xc[0], xc[0], xc[1]),
(yc[0], yc[0], yc[0], yc[1]), ax, "g-")
if draw_second_arcs:
draw_coons_arc((xc[0], xc[0], xc[1], xc[2]),
(yc[0], yc[0], yc[1], yc[2]), ax, "y-")
last = len(xc)
# další oblouky
for start in range(0, last-3):
style = "r-" if start % 2 == 0 else "b-"
draw_coons_arc(xc[start:start+4], yc[start:start+4], ax, style)
# poslední dva oblouky s násobnými body
if draw_second_arcs:
draw_coons_arc((xc[last-3], xc[last-2], xc[last-1], xc[last-1]),
(yc[last-3], yc[last-2], yc[last-1], yc[last-1]), ax, "y-")
if draw_first_arcs:
draw_coons_arc((xc[last-2], xc[last-1], xc[last-1], xc[last-1]),
(yc[last-2], yc[last-1], yc[last-1], yc[last-1]), ax, "g-")
# uložení grafu do rastrového obrázku
plt.savefig(filename)
# zobrazení grafu
plt.show()
# čtyři varianty B-spline křivky
draw_b_spline("B-spline_4A.png", xc, yc, False, False)
draw_b_spline("B-spline_4B.png", xc, yc, False, True)
draw_b_spline("B-spline_4C.png", xc, yc, True, False)
draw_b_spline("B-spline_4D.png", xc, yc, True, True)
Příklad po svém spuštění vygeneruje čtyři varianty téže křivky:

Obrázek 11: B-spline křivka bez násobných řídicích bodů.

Obrázek 12: B-spline křivka s dvojicí přidaných segmentů (dva násobné body).

Obrázek 13: B-spline křivka s dvojicí přidaných segmentů (dva násobné body).

Obrázek 14: B-spline křivka se čtveřicí přidaných segmentů (dva dvakrát násobné body).
9. Ukázka násobných bodů na začátku/konci Catmul-Romovy spline
Prakticky stejným způsobem se můžeme pokusit o vykreslení čtyř variant Catmul-Romovy spline křivky:
"""Parametrická křivka: Catmul-Romova spline, násobné body."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 20)
# řídicí body Catmul-Romovy spline
xc = [1, 2, 3, 4, 5, 6, 7]
yc = [1, 2, 1, 2, 1, 2, 1]
# koeficient Catmul-Romovy spline
tau = 0.5
# bázové polynomy
Q = [-tau*t + 2*tau*t**2 - tau*t**3,
1+(tau-3)*t**2+(2-tau)*t**3,
tau*t + (3-2*tau)*t**2 + (tau-2)*t**3,
-tau*t**2+tau*t**3]
def draw_catmul_rom_arc(xc, yc, ax, style):
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*Q[i]
y += yc[i]*Q[i]
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
def draw_catmul_rom_spline(filename, xc, yc, draw_first_arcs, draw_second_arcs):
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Catmul-Rom spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0.5, 7.5)
ax.set_ylim(0.5, 2.5)
# řídicí body Catmul-Romovy spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
# první dva oblouky s násobnými body
if draw_first_arcs:
draw_catmul_rom_arc((xc[0], xc[0], xc[0], xc[1]),
(yc[0], yc[0], yc[0], yc[1]), ax, "g-")
if draw_second_arcs:
draw_catmul_rom_arc((xc[0], xc[0], xc[1], xc[2]),
(yc[0], yc[0], yc[1], yc[2]), ax, "y-")
last = len(xc)
# další oblouky
for start in range(0, last-3):
style = "r-" if start % 2 == 0 else "b-"
draw_catmul_rom_arc(xc[start:start+4], yc[start:start+4], ax, style)
# poslední dva oblouky s násobnými body
if draw_second_arcs:
draw_catmul_rom_arc((xc[last-3], xc[last-2], xc[last-1], xc[last-1]),
(yc[last-3], yc[last-2], yc[last-1], yc[last-1]), ax, "y-")
if draw_first_arcs:
draw_catmul_rom_arc((xc[last-2], xc[last-1], xc[last-1], xc[last-1]),
(yc[last-2], yc[last-1], yc[last-1], yc[last-1]), ax, "g-")
# uložení grafu do rastrového obrázku
plt.savefig(filename)
# zobrazení grafu
plt.show()
# čtyři varianty B-spline křivky
draw_catmul_rom_spline("Catmul-Rom-spline_4A.png", xc, yc, False, False)
draw_catmul_rom_spline("Catmul-Rom-spline_4B.png", xc, yc, False, True)
draw_catmul_rom_spline("Catmul-Rom-spline_4C.png", xc, yc, True, False)
draw_catmul_rom_spline("Catmul-Rom-spline_4D.png", xc, yc, True, True)
I tento příklad po svém spuštění vygeneruje čtyři varianty téže křivky:

Obrázek 15: Catmul-Romova spline křivka bez násobných řídicích bodů.

Obrázek 16: Catmul-Romova spline křivka s dvojicí přidaných segmentů (dva násobné body).
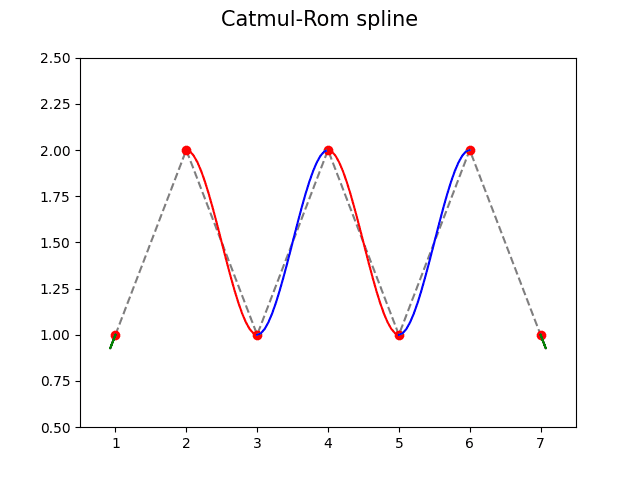
Obrázek 17: Catmul-Romova spline křivka s dvojicí přidaných segmentů (dva násobné body).

Obrázek 18: Catmul-Romova spline křivka se čtveřicí přidaných segmentů (dva dvakrát násobné body).
10. Násobné řídicí body uprostřed spline křivek
Násobné řídicí body se pochopitelně mohou použít i uprostřed spline křivek. V tomto případě dojde k tomu, že namísto C1 či C2 spojitosti získáme křivku pouze se spojitostí C0, což ovšem může být cílem některých operací – například budeme chtít vytvořit ostrý roh apod. Vliv násobných řídicích bodů uprostřed spline křivek si (opět) ukážeme na příkladu B-spline a posléze i na Catmul-Romově spline.
11. Ukázka násobných bodů v B-spline
Tento demonstrační příklad vykreslí B-spline bez násobných bodů, s jedním násobným bodem a taktéž s jedním „dvojitě“ násobným bodem – viz též zvýrazněná část kódu:
"""Parametrická křivka: B-spline složená z Coonsových oblouků, násobné body uprostřed křivky."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 20)
# řídicí body B-spline
xc1 = (1, 2, 3, 4, 5, 6, 7)
yc1 = (1, 2, 1, 2, 1, 2, 1)
# násobné řídicí body B-spline
xc2 = (1, 2, 3, 4, 4, 5, 6, 7)
yc2 = (1, 2, 1, 2, 2, 1, 2, 1)
# řídicí body B-spline
xc3 = (1, 2, 3, 4, 4, 4, 5, 6, 7)
yc3 = (1, 2, 1, 2, 2, 2, 1, 2, 1)
# Coonsovy polynomy
C = [(1-t)**3,
3*t**3 - 6*t**2 + 4,
-3*t**3 + 3*t**2 + 3*t + 1,
t**3]
def draw_coons_arc(xc, yc, ax, style):
# výpočet bodů ležících na Coonsově kubice
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*C[i]
y += yc[i]*C[i]
# konečná úprava sumy
x /= 6
y /= 6
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
def draw_b_spline(filename, xc, yc, draw_first_arcs, draw_second_arcs):
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('B-spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0.5, 7.5)
ax.set_ylim(0.5, 2.5)
# řídicí body B-spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
# první dva oblouky s násobnými body
if draw_first_arcs:
draw_coons_arc((xc[0], xc[0], xc[0], xc[1]),
(yc[0], yc[0], yc[0], yc[1]), ax, "g-")
if draw_second_arcs:
draw_coons_arc((xc[0], xc[0], xc[1], xc[2]),
(yc[0], yc[0], yc[1], yc[2]), ax, "y-")
last = len(xc)
# další oblouky
for start in range(0, last-3):
style = "r-" if start % 2 == 0 else "b-"
draw_coons_arc(xc[start:start+4], yc[start:start+4], ax, style)
# poslední dva oblouky s násobnými body
if draw_second_arcs:
draw_coons_arc((xc[last-3], xc[last-2], xc[last-1], xc[last-1]),
(yc[last-3], yc[last-2], yc[last-1], yc[last-1]), ax, "y-")
if draw_first_arcs:
draw_coons_arc((xc[last-2], xc[last-1], xc[last-1], xc[last-1]),
(yc[last-2], yc[last-1], yc[last-1], yc[last-1]), ax, "g-")
# uložení grafu do rastrového obrázku
plt.savefig(filename)
# zobrazení grafu
plt.show()
# vykreslení B-spline křivky
draw_b_spline("B-spline_5A.png", xc1, yc1, False, False)
draw_b_spline("B-spline_5B.png", xc2, yc2, False, False)
draw_b_spline("B-spline_5C.png", xc3, yc3, False, False)
Ze zobrazených výsledků je patrné, že skutečného ostrého bodu dosáhneme až při použití dvojitě-násobného řídicího bodu:

Obrázek 19: B-spline křivka bez násobných řídicích bodů.

Obrázek 20: B-spline křivka s jedním násobným bodem uprostřed křivky.

Obrázek 21: B-spline křivka s jedním „dvojitě“ násobným bodem uprostřed křivky.
12. Ukázka násobných bodů v Catmul-Romově spline
Podobným způsobem můžeme vykreslit Catmul-Romovu spline křivku s násobnými body uprostřed:
"""Parametrická křivka: Catmul-Romova spline, násobné body uprostřed křivky."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 20)
# řídicí body Catmul-Romovy spline
xc1 = [1, 2, 3, 4, 5, 6, 7]
yc1 = [1, 2, 1, 2, 1, 2, 1]
# násobné řídicí body Catmul-Romovy spline
xc2 = [1, 2, 3, 4, 4, 5, 6, 7]
yc2 = [1, 2, 1, 2, 2, 1, 2, 1]
# násobné řídicí body Catmul-Romovy spline
xc3 = [1, 2, 3, 4, 4, 4, 5, 6, 7]
yc3 = [1, 2, 1, 2, 2, 2, 1, 2, 1]
# koeficient Catmul-Romovy spline
tau = 0.5
# bázové polynomy
Q = [-tau*t + 2*tau*t**2 - tau*t**3,
1+(tau-3)*t**2+(2-tau)*t**3,
tau*t + (3-2*tau)*t**2 + (tau-2)*t**3,
-tau*t**2+tau*t**3]
def draw_catmul_rom_arc(xc, yc, ax, style):
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*Q[i]
y += yc[i]*Q[i]
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
def draw_catmul_rom_spline(filename, xc, yc, draw_first_arcs, draw_second_arcs):
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Catmul-Rom spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0.5, 7.5)
ax.set_ylim(0.5, 2.5)
# řídicí body Catmul-Romovy spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
# první dva oblouky s násobnými body
if draw_first_arcs:
draw_catmul_rom_arc((xc[0], xc[0], xc[0], xc[1]),
(yc[0], yc[0], yc[0], yc[1]), ax, "g-")
if draw_second_arcs:
draw_catmul_rom_arc((xc[0], xc[0], xc[1], xc[2]),
(yc[0], yc[0], yc[1], yc[2]), ax, "y-")
last = len(xc)
# další oblouky
for start in range(0, last-3):
style = "r-" if start % 2 == 0 else "b-"
draw_catmul_rom_arc(xc[start:start+4], yc[start:start+4], ax, style)
# poslední dva oblouky s násobnými body
if draw_second_arcs:
draw_catmul_rom_arc((xc[last-3], xc[last-2], xc[last-1], xc[last-1]),
(yc[last-3], yc[last-2], yc[last-1], yc[last-1]), ax, "y-")
if draw_first_arcs:
draw_catmul_rom_arc((xc[last-2], xc[last-1], xc[last-1], xc[last-1]),
(yc[last-2], yc[last-1], yc[last-1], yc[last-1]), ax, "g-")
# uložení grafu do rastrového obrázku
plt.savefig(filename)
# zobrazení grafu
plt.show()
# čtyři varianty B-spline křivky
draw_catmul_rom_spline("Catmul-Rom-spline_4A.png", xc1, yc1, False, False)
draw_catmul_rom_spline("Catmul-Rom-spline_4B.png", xc2, yc2, False, False)
draw_catmul_rom_spline("Catmul-Rom-spline_4C.png", xc3, yc3, False, False)
I zde můžeme vidět podstatný rozdíl oproti B-spline křivkám – k vytvoření skutečného „rohu“ nedojde, ale naproti tomu se vytvoří smyčka. To je dáno mj. tím, jak se Catmul-Romova křivka snaží interpolovat řídicí body (a to i ty nenásobné):

Obrázek 22: Catmul-Romova spline křivka bez násobných řídicích bodů.

Obrázek 23: Catmul-Romova spline křivka s jedním násobným bodem uprostřed křivky.

Obrázek 24: Catmul-Romova spline křivka s jedním „dvojitě“ násobným bodem uprostřed křivky.
13. Fergusonovy kubiky
Článek o parametrických křivkách založených na vyhodnocování polynomů nízkých stupňů by nebyl úplný, pokud bychom se nezmínili o Fergusonových kubikách. Jedná se o křivky zadané dvojicí koncových bodů, kterými křivka prochází. To však není vše, protože je ještě nutné zadat tečné vektory v těchto bodech, které pochopitelně mění tvar křivky. V případě „konkurenčních“ Bézierových kubik je situace nepatrně odlišná, protože tečné vektory (resp. směr křivky u koncových bodů) je ovlivněn ostatními dvěma řídicími body. U obou kubik je však celá křivka popsána čtveřicí parametrů – buď dvěma body a dvěma vektory nebo čtyřmi body (takže ve výsledku nemáme žádný stupeň volnosti při výpočtech, protože čtveřice parametrů odpovídá čtveřici koeficientů polynomu stupně tři).
Nevýhodou Fergusonových kubik je fakt, že práce s tečnými vektory je obtížnější a pro uživatele ne tak intuitivní (zejména u druhého koncového bodu). Nicméně v některých aplikacích to nevadí, protože Fergusojovy kubiky tvoří základ křivek Kochanek-Bartels.
14. Hermitovské bázové polynomy Fergusonovy kubiky
Fergusonovy se počítají a vykreslují naprosto stejným způsobem, jako je tomu u všech dalších parametrických křivek – máme tedy k dispozici bázové polynomy (zde konkrétně Hermitovské polynomy) a sadu 2D vektorů tvořících vstup do výpočtů. Tyto vektory představují dvojici koncových bodů a dvojici tečných vektorů v koncových bodech – což je ona změna oproti dalším dříve popsaným křivkám (u těch jsme měli jen sadu řídicích bodů). Podívejme se ovšem nejdříve na to, jak vypadají bázové polynomy těchto křivek:
"""Hermitovské bázové polynomy."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 50)
# bázové polynomy
H = [2*t**3 - 3*t**2+1,
t**3 - 2*t**2 + t,
-2*t**3 + 3*t**2,
t**3 - t**2]
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Bázové polynomy', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 1)
ax.set_ylim(-0.25, 1)
# bázové polynomy
ax.plot(t, H[0], 'r-')
ax.plot(t, H[1], 'g-')
ax.plot(t, H[2], 'b-')
ax.plot(t, H[3], 'k-')
# uložení grafu do rastrového obrázku
plt.savefig("hermite_basis.png")
# zobrazení grafu
plt.show()
Z výsledků je patrné, že bázové polynomu mají v některých místech i zápornou hodnotu, což je pro nás novinka (ovšem zde nevadí, protože výpočet probíhá i nad tečnými vektory):

Obrázek 25: Hermitovské bázové polynomy.
15. Vykreslení Fergusonovy kubiky
Již v předchozí kapitole jsem se zmínil o tom, že Fergusonovy kubiky se počítají a vykreslují prakticky stejným způsobem, jako ostatní polynomiální parametrické křivky (s tím rozdílem, že vstupy jsou odlišné). O tom, že postup výpočtu a vykreslení není žádným podstatným způsobem změněn, se můžeme přesvědčit v následujícím demonstračním příkladu, který Fergusonovu kubiku vykreslí a vykreslí i její koncové body a tečné vektory:
"""Fergusonova kubika."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.linspace(0, 1, 50)
# řídicí body spline
xc = (1, 3)
yc = (1, 1)
# tangenty
mx = (0, 0)
my = (1, -1)
# bázové polynomy
H = [2*t**3 - 3*t**2+1,
t**3 - 2*t**2 + t,
-2*t**3 + 3*t**2,
t**3 - t**2]
# výpočet bodů ležících na spline
x = xc[0]*H[0] + mx[0]*H[1] + xc[1]*H[2] + mx[1]*H[3]
y = yc[0]*H[0] + my[0]*H[1] + yc[1]*H[2] + my[1]*H[3]
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Hermitova spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 4)
ax.set_ylim(-0.5, 2.5)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# řídicí body
ax.plot(xc, yc, 'ro')
# tangenty
ax.plot([xc[0]+mx[0], xc[0]], [yc[0]+my[0], yc[0]], 'b-')
ax.plot([xc[1]+mx[1], xc[1]], [yc[1]+my[1], yc[1]], 'y-')
# uložení grafu do rastrového obrázku
plt.savefig("hermite_spline.png")
# zobrazení grafu
plt.show()
Výsledná Fergusonova kubika (spline) bude vypadat následovně:

Obrázek 26: Fergusonova kubika.
16. Od klasických B-spline k NURBS
V oblasti CAD a CAM se poměrně často setkáme s NURBS křivkami a plochami. Jedná se o dvojí zobecnění klasických B-spline křivek. Jedno zobecnění spočívá v zavedení „vah“ jednotlivých řídicích bodů (racionální B-spline křivky), druhé pak v zavedení takzvaného knot vectoru (uzlového vektoru), kterým se nahradí původní sekvence segmentů, z nichž každý začíná v t=0 a končí v t=1.
NURB křivky a plochy se v počítačové grafice, resp. nani navazujících oborech, staly velmi populární zejména díky některým svým výhodným vlastnostem, které krátce zmíníme v následujících odstavcích:
- Pomocí NURB křivek lze jednoduše a přesně vytvářet kuželosečky, tj. kružnici, elipsu, parabolu nebo jejich části (oblouky). Zejména možnost přesného vytváření kružnic a elips (a samozřejmě i jejich částí – oblouků) je v CAD/CAM aplikacích velmi důležitá a právě z tohoto důvodu se v CAD/CAM nepoužívají jinak oblíbené Bézierovy křivky.
- NURB plochy mohou přesně vytvářet povrch (nebo část povrchu) kvadrik, jež jsou obdobou kuželoseček v prostoru. Je tedy možné naprosto přesně vymodelovat kouli, válec, kužel apod.
- Vhodnou volbou uzlového vektoru a vah řídicích bodů je možné vytvářet povrchy se zlomy a hranami, například kvádry. Tato vlastnost se opět použije při práci v CAD/CAM systémech, ve kterých se běžně vytváří tělesa, jež mají střídavě spojité a nespojité povrchy. Lehce se tak může stát, že celá scéna je tvořena pouze NURB plochami, i když se v ní budou vyskytovat kvadriky, kostky atd.
- NURB křivky a plochy si přitom zachovávají veškeré vlastnosti parametrických křivek a ploch, například invarianci k transformacím, existenci komplexní obálky (pro nezáporné váhy řídicích bodů) atd. To je důležité zejména pro rychlé vykreslování – transformace je možné aplikovat pouze na řídicí body a ne na výsledné trojúhelníky. Existence konvexní obálky zajišťuje zrychlený výpočet kolizí a také – což je mnohdy důležitější – viditelnosti.
- Editace NURB je z uživatelského hlediska poměrně jednoduchá – mění se polohy řídicích bodů, jejich váhy a případně i uzlový vektor. Při interaktivním modelování se však téměř vždy mění pouze polohy řídicích bodů, jejichž cílenou změnou lze dosáhnout téměř jakéhokoli tvaru. Změna vah řídicích bodů a uzlového vektoru je aplikována automaticky při vytváření kvadrik a offsetových ploch – viz předchozí odstavce.
17. Racionální B-spline
Zvýšení modelovacích schopností klasických B-spline je možné dosáhnout použitím takzvaných racionálních B-spline, v nichž je každému řídicímu bodu navíc přiřazena jeho váha, což je reálné číslo určující „přitažlivost“ daného řídicího bodu ke křivce. Čím vyšší je váha řídicího bodu, tím více se křivka či plocha k tomuto bodu přimyká. Jestliže je naopak váha záporná, křivka je od bodu odpuzována. Uživatel má tedy k dispozici další nástroj, kterým může poměrně jednoduchou cestou ovlivnit tvar výsledné křivky. Další výhodou těchto typů spline je to, že díky racionalitě jsou tyto typy křivek invariantní kromě lineárních transformací i k perspektivní projekci (což nás však začne zajímat až v 3D grafice). Pokud označíme váhu řídicího bodu Pij symbolem Wij, můžeme racionální B-spline plochu vyjádřit vztahem:

Z vlastností bázových funkcí je možné relativně snadno zjistit, že pokud W{i,j}=1 pro všechny i, j (popř. jen i pro křivku), potom je jmenovatel zlomku vždy roven jedné a racionální B-spline křivka/plocha je rovnocenná neracionální B-spline, s nimiž jsme se již dobře seznámili v rámci předchozího textu.
18. NURBS
Dalším zobecněním racionálních B-spline je zavedení takzvaných normalizovaných B-spline bázových funkcí, které jsou na rozdíl od předchozích bázových funkcí (popsaných polynomem) určeny rekurentním vztahem ve kterém se vyskytuje interval hodnot, pro které je bázová funkce definována (naproti tomu u běžných B-spline i u racionálních B-spline byly bázové funkce definovány pro parametry t, resp. u a v, které vždy nabývaly hodnot z rozsahu <0, 1>:

Vznikají tak křivky popř. plochy NURBS neboli neuniformní racionální B-spline (Non-Uniform Rational B-spline nebo Non-Uniform Rational B-spline Surfaces). Ty v dnešní době představují průmyslový standard v geometrickém modelování ploch. NURBS plochy lze vyjádřit vztahem:

Tyto křivky resp. po zobecnění plochy mají mnoho výhodných vlastností, například umožňují přesně modelovat kvadriky nebo jejich části (povrch koule, elipsoidu, válce a kužele), které se používají například pro navrhování součástek v CAD systémech. Lze také jednoduše vytvářet rotační plochy (SOR – surfaces of revolution) a provádět volné modelování (free-form modelling). Především z těchto důvodů se dnes NURBS plochy stávají pro mnoho aplikací základním (elementárním) prvkem, ze kterého se vytváří složitější tělesa. Některé aplikace dokonce jiné reprezentace těles neumožňují, což mimo jiné značně zjednodušuje většinu algoritmů, které jsou nad modelem tělesa prováděny, protože tyto algoritmy jsou vždy prováděny pouze s NURBS plochami.
19. Repositář s demonstračními příklady
Všechny dříve i dnes popisované demonstrační příklady určené pro Python 3 a knihovnu Matplotlib byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/presentations. Příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý (dnes již poměrně rozsáhlý) repositář:
20. Odkazy na Internetu
- Famous Curves Index
https://mathshistory.st-andrews.ac.uk/Curves/ - Curve (Wikipedia)
https://en.wikipedia.org/wiki/Curve - Mathematical curves
https://www.2dcurves.com/index.html - Curves (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Curves.html - Smooth Curve (Wolfram MathWorld)
https://mathworld.wolfram.com/SmoothCurve.html - Spirals (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Spirals.html - An Interactive Introduction to Splines
https://ibiblio.org/e-notes/Splines/Intro.htm - Parabola
https://www.2dcurves.com/conicsection/conicsectionp.html - Hyperbola
https://www.2dcurves.com/conicsection/conicsectionh.html - Dioklova kisoida
https://cs.wikipedia.org/wiki/Dioklova_kisoida - Archimédova spirála
https://cs.wikipedia.org/wiki/Archim%C3%A9dova_spir%C3%A1la - Conchoid (mathematics)
https://en.wikipedia.org/wiki/Conchoid_(mathematics) - Algebraic curve
https://en.wikipedia.org/wiki/Algebraic_curve - Transcendental curve
https://en.wikipedia.org/wiki/Transcendental_curve - Spiral
https://en.wikipedia.org/wiki/Spiral - List of spirals
https://en.wikipedia.org/wiki/List_of_spirals - Hyperbolická spirála
https://cs.wikipedia.org/wiki/Hyperbolick%C3%A1_spir%C3%A1la - Hyperbolic Spiral
https://mathworld.wolfram.com/HyperbolicSpiral.html - Lituus (mathematics)
https://en.wikipedia.org/wiki/Lituus_(mathematics) - Spiral of Spirals Fractals 2 with Python Turtle (Source Code)
https://pythonturtle.academy/spiral-of-spirals-fractals-2-with-python-turtle-source-code/ - Cornu Spiral
http://hyperphysics.gsu.edu/hbase/phyopt/cornu.html - Spiral
https://www.2dcurves.com/spiral/spiral.html - Algebraic Curves
https://mathworld.wolfram.com/topics/AlgebraicCurves.html - Elliptic Curves
https://mathworld.wolfram.com/topics/EllipticCurves.html - Eukleidovská konstrukce
https://cs.wikipedia.org/wiki/Eukleidovsk%C3%A1_konstrukce - Euclidean Constructions
http://www.cs.cas.cz/portal/AlgoMath/Geometry/PlaneGeometry/GeometricConstructions/EuclideanConstructions.htm - Kvadratura kruhu
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Trisekce úhlu
https://cs.wikipedia.org/wiki/Trisekce_%C3%BAhlu - Straightedge and compass construction
https://en.wikipedia.org/wiki/Straightedge_and_compass_construction - C.a.R.
http://car.rene-grothmann.de/doc_en/index.html - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/C.a.R. - CaRMetal (Španělsky a Francouzsky)
http://carmetal.org/index.php/fr/ - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/CaRMetal - Regular Polygon
http://mathforum.org/dr.math/faq/formulas/faq.regpoly.html - Geometric Construction with the Compass Alone
http://www.cut-the-knot.org/do_you_know/compass.shtml - Kvadratura kruhu (Wikipedie)
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Compass equivalence theorem
https://en.wikipedia.org/wiki/Compass_equivalence_theorem - Curves we (mostly) don't learn in high school (and applications)
https://www.youtube.com/watch?v=3izFMB91K_Q - Can You Really Derive Conic Formulae from a Cone? – Menaechmus' Constructions
https://www.maa.org/press/periodicals/convergence/can-you-really-derive-conic-formulae-from-a-cone-menaechmus-constructions - Apollonius of Perga
https://en.wikipedia.org/wiki/Apollonius_of_Perga - Catenary arch
https://en.wikipedia.org/wiki/Catenary_arch - Parabolic arch
https://en.wikipedia.org/wiki/Parabolic_arch - Wattova křivka
https://www.geogebra.org/m/gNh4bW9r - Model stegosaura byl získán na stránce
http://www.turbosquid.com/HTMLClient/FullPreview/Index.cfm/ID/171071/Action/FullPreview - Obrázek nohy dinosaura byl získán na adrese
http://perso.wanadoo.fr/rimasson/3d/leg.htm - Spirograph
https://en.wikipedia.org/wiki/Spirograph - Epicykloida
https://cs.wikipedia.org/wiki/Epicykloida - Hypocykloida
https://cs.wikipedia.org/wiki/Hypocykloida - Hypotrochoida
https://cs.wikipedia.org/wiki/Hypotrochoida - Superelipsoidy a kvadriky v POV-Rayi
https://www.root.cz/clanky/superelipsoidy-a-kvadriky-v-pov-rayi/ - Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers
https://elepa.files.wordpress.com/2013/11/fifty-famous-curves.pdf - Barr, A.H.: Superquadrics and Angle Preserving Transformations,
IEEE Computer Graphics and Applications, January 1981 - Bourke Paul: Quadrics,
July 1996 - Bourke Paul: Superellipse and Superellipsoid,
January 1990 - Faux, I.D. a Pratt, M.J.: Computational Geometry for Design and Manufacture,
Ellis Horwood Ltd., Wiley & Sons, 1979 - Wallace A.: Differential Topology,
Benjamin/Cummings Co., Reading, Massachussetts, USA, 1968 - Glossary of Bridge Terminology
http://sdrc.lib.uiowa.edu/eng/bridges/WaddellGlossary/GlossC.htm - Brachistochrona
https://cs.wikipedia.org/wiki/Brachistochrona - Missions: Cassini
https://solarsystem.nasa.gov/missions/cassini/overview/ - Giovanni Domenico Cassini
https://en.wikipedia.org/wiki/Giovanni_Domenico_Cassini - Cassini Ovals
https://mathworld.wolfram.com/CassiniOvals.html - Geocentrismus
https://cs.wikipedia.org/wiki/Geocentrismus - Who was Giovanni Cassini?
https://www.universetoday.com/130823/who-was-giovanni-cassini/ - Special plane curves
http://xahlee.info/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html - Why Does Slicing a Cone Give an Ellipse?
https://infinityisreallybig.com/2019/02/08/why-does-slicing-a-cone-give-an-ellipse/ - Interpolace
https://mathonline.fme.vutbr.cz/pg/Algoritmy/05_APROX_KRIVKY.htm - Lagrange Polynomial Interpolation
https://pythonnumericalmethods.berkeley.edu/notebooks/chapter17.04-Lagrange-Polynomial-Interpolation.html - Python Program for Lagrange Interpolation Method (with Output)
https://www.codesansar.com/numerical-methods/python-program-lagrange-interpolation-method.htm - Smooth Paths Using Catmull-Rom Splines
https://qroph.github.io/2018/07/30/smooth-paths-using-catmull-rom-splines.html - Lecture 11: Linear Interpolation Again – Bézier Curves
http://www.math.kent.edu/~reichel/courses/intr.num.comp.1/fall09/lecture12/bez.pdf - Geometrie/Úvod do křivek
https://cs.wikibooks.org/wiki/Geometrie/%C3%9Avod_do_k%C5%99ivek - B-Spline Curves and Surfaces (1)
http://www.cad.zju.edu.cn/home/zhx/GM/006/00-bscs1.pdf - Praktické ukázky možností aplikace Mandelbulber při tvorbě animací
https://www.root.cz/clanky/prakticke-ukazky-moznosti-aplikace-mandelbulber-pri-tvorbe-animaci/ - Kochanek–Bartels spline
https://en.wikipedia.org/wiki/Kochanek%E2%80%93Bartels_spline - class KochanekBartels
https://splines.readthedocs.io/en/latest/_modules/splines.html#KochanekBartels


























