Obsah
1. Knihovna ipycanvas aneb kreslicí plátno pro Jupyter Notebook
2. Instalace knihovny ipycanvas do klasického Jupyter Notebooku popř. do Jupyter Labu
3. Import knihovny ipycanvas do prostředí JupyterLite
4. Vytvoření a zobrazení prázdného plátna na plochu diáře
5. Základní 2D entity nakreslené na plátno
6. Další dostupné 2D entity, které je možné nakreslit
7. Změna stylu vykreslovaných entit
8. Nastavení průhlednosti při vykreslování
9. Gradientní barevné přechody využitelné při kreslení vyplněných obrazců
10. Změna směru gradientního přechodu
11. Paprskovitý (radial) gradientní přechod
13. Vycentrování textu v obou směrech okolo zadaného bodu
14. Cesty (paths) v knihovně ipycanvas
15. Křivkové segmenty v cestách – oblouky a Bézierovy křivky
16. Vykreslení cesty, jejíž hrany se protínají
17. Repositář s demonstračními příklady
18. Odkazy na články o Jupyter Notebooku
19. Odkazy na články o formátu SVG
1. Knihovna ipycanvas aneb kreslicí plátno pro Jupyter Notebook
V prozatím posledním článku o nástroji Jupyter Notebook si popíšeme knihovnu, kterou je možné využít pro programové vykreslení různých diagramů, schémat, výsledků simulací či analýzy dat atd., a to přímo do plochy diáře zobrazeného v Jupyter Notebooku, Jupyter Labu či v nástroji JupyterLite. Tato knihovna se jmenuje příznačně ipycanvas; svým jménem tak navazuje na další technologie a knihovny založené na canvasu neboli na „kreslicím plátnu“ (canvas je mj. i součástí standardu HTML5, stejně jako SVG, na které taktéž navazuje). Kromě běžných 2D entit typu úsečka, oblouk, kružnice atd. umožňuje ipycanvas vykreslení textů, cest (path) a dokonce je možné použít režim, v němž vytvořená kresba napodobuje kreslení rukou (RoughCanvas). Dnes si popíšeme základní možnosti poskytované touto v mnoha ohledech užitečnou knihovnou.
2. Instalace knihovny ipycanvas do klasického Jupyter Notebooku popř. do Jupyter Labu
Instalace knihovny ipycanvas ve chvíli, kdy ji budeme chtít využít v klasickém Jupyter Notebooku či v novějším Jupyter Labu, je přímočará, protože postačuje použít nástroj pip popř. pip3 (podle konfigurace operačního systému):
# pip install ipycanvas
Využít lze v případě potřeby i instalaci pro aktuálně přihlášeného uživatele, popř. instalaci do virtuálního prostředí:
$ pip3 install --user ipycanvas Collecting ipycanvas Using cached https://files.pythonhosted.org/packages/b6/8b/ec60ae3d0596214c45c70788a7ecbc2ab303ab26decffd318a0e791f48e0/ipycanvas-0.9.0-py2.py3-none-any.whl Requirement already satisfied: numpy in ./.local/lib/python3.6/site-packages (from ipycanvas) Requirement already satisfied: pillow>=6.0 in ./.local/lib/python3.6/site-packages (from ipycanvas) Collecting ipywidgets>=7.6.0 (from ipycanvas) Using cached https://files.pythonhosted.org/packages/11/53/084940a83a8158364e630a664a30b03068c25ab75243224d6b488800d43a/ipywidgets-7.6.3-py2.py3-none-any.whl Requirement already satisfied: nbformat>=4.2.0 in /usr/lib/python3.6/site-packages (from ipywidgets>=7.6.0->ipycanvas) Requirement already satisfied: ipykernel>=4.5.1 in /usr/lib/python3.6/site-packages (from ipywidgets>=7.6.0->ipycanvas) ... ... ... Requirement already satisfied: ptyprocess>=0.5 in ./.local/lib/python3.6/site-packages (from pexpect; sys_platform != "win32"->ipython>=4.0.0; python_version >= "3.3"->ipywidgets>=7.6.0->ipycanvas) Requirement already satisfied: wcwidth in /usr/lib/python3.6/site-packages (from prompt-toolkit<2.1.0,>=2.0.0->ipython>=4.0.0; python_version >= "3.3"->ipywidgets>=7.6.0->ipycanvas) Installing collected packages: ipywidgets, ipycanvas Successfully installed ipycanvas-0.9.0 ipywidgets-7.6.3
Kontrolu, zda instalace proběhla v pořádku, provedeme přímo v diáři (nikoli tedy v běžném interpretru jazyka Python):
from ipycanvas import Canvas canvas = Canvas(width=320, height=240) canvas
V případě, že se kreslicí plátno po posledním předchozím příkazu nevykreslí, je možné jeho vykreslení vynutit funkcí display (importována ze základních knihoven Jupyter Notebooku):
display(canvas)
3. Import knihovny ipycanvas do prostředí JupyterLite
V případě, že si chcete možnosti kreslicího plátna vyzkoušet v nástroji JupyterLite, s nímž jsme se seznámili předminule, bude instalace probíhat poněkud odlišným způsobem. Je to ostatně logické, protože si musíme uvědomit, že jak instalace modulů, tak i jejich překlad probíhá v rámci webového prohlížeče, tedy v relativně izolovaném prostředí (což je ostatně jen dobře). Z tohoto důvodu byl do projektu Pyodide přidán i balíček nazvaný micropip, který zajišťuje právě instalaci, překlad atd. modulů v rámci prohlížeče. Ostatně i k této knihovně existuje nápověda, kterou si můžeme přímo v prostředí diáře zobrazit. Při práci s knihovnou micropip je nutné pouze vyřešit čekání na dokončení instalace zadaného balíčku, protože tato instalace probíhá na pozadí. Použijeme tedy klíčové slovo await:
# příprava knihovny určené pro instalaci dalších knihoven do prostředí prohlížeče
import micropip
# instalace knihovny ipycanvas do prostředí prohlížeče
await micropip.install("ipycanvas")
# nyní je již možné provést import nově nainstalované knihovny
import ipycanvas
# nyní je již možné zobrazit nápovědu
help(ipycanvas)
Po posledním zadaném příkazu by se měla zobrazit nápověda k nově nainstalované a naimportované knihovně:
Obrázek 1: Instalace a import knihovny v rámci webového prohlížeče (projekt JupyterLite).
4. Vytvoření a zobrazení prázdného plátna na plochu diáře
Nyní si již můžeme ukázat, jakým způsobem lze na plochu diáře vložit prázdné plátno. Při konstrukci plátna (resp. přesněji řečeno objektu typu „kreslicí plátno“) je nutné specifikovat jeho rozměry, v našem případě nastavené na 320×240 pixelů (používáme totiž mapování 1:1 z logických jednotek na fyzické pixely):
# příprava knihovny určené pro instalaci dalších knihoven do prostředí prohlížeče
import micropip
# instalace knihovny ipycanvas do prostředí prohlížeče
await micropip.install("ipycanvas")
# nyní je již možné provést import nově nainstalované knihovny
import ipycanvas
# vytvoření kreslicího plátna
canvas = ipycanvas.Canvas(width=320, height=240)
# vložení kreslicího plátna na plochu diáře
canvas
S výsledkem:
Obrázek 2: Prázdné kreslicí plátno vložené do diáře.
5. Základní 2D entity nakreslené na plátno
Základní 2D entitou, kterou je možné na plátno nakreslit, není pixel (s pixely se totiž pracuje poněkud složitějších způsobem), ale úsečka. Tato entita se na plátno vykreslí metodou Canvas.stroke_line, které se předávají souřadnice [x,y] obou vrcholů, celkem tedy čtyři hodnoty. Souřadný systém plátna je nastaven takovým způsobem, že levý horní roh má souřadnice [0,0] a pravý dolní roh souřadnice [šířka-1,výška-1], což je v počítačové grafice běžné. Ukázka vykreslení úsečky je ukázána v dalším příkladu:
# příprava knihovny určené pro instalaci dalších knihoven do prostředí prohlížeče
import micropip
# instalace knihovny ipycanvas do prostředí prohlížeče
await micropip.install("ipycanvas")
# nyní je již možné provést import nově nainstalované knihovny
import ipycanvas
# vytvoření kreslicího plátna
canvas = ipycanvas.Canvas(width=320, height=240)
# vložení kreslicího plátna na plochu diáře
canvas
# vykreslení základních entit – úseček
canvas.stroke_line(0, 0, 319, 239)
Výsledný diář by měl po provedení předchozích kroků vypadat následovně:
Obrázek 3: Úsečka s tloušťkou jednoho pixelu vykreslená na plochu plátna.
6. Další dostupné 2D entity, které je možné nakreslit
Na kreslicí plátno je možné vykreslit i další typy entit, především kružnice, kruhy (tedy vyplněné kružnice), kruhové oblouky (vyplněné i nevyplněné), obdélníky, polyčáry a polygony. Entity, které jsou „uzavřené“ (tedy mají plochu) existují ve dvou variantách, protože lze vykreslit buď jen obrys takové entity či vyplnit i její vnitřek. Varianta s obrysem začíná slovem stroke_, vyplněná varianta pak slovem fill_:
# příprava knihovny určené pro instalaci dalších knihoven do prostředí prohlížeče
import micropip
# instalace knihovny ipycanvas do prostředí prohlížeče
await micropip.install("ipycanvas")
# nyní je již možné provést import nově nainstalované knihovny
import ipycanvas
# vytvoření kreslicího plátna
canvas = ipycanvas.Canvas(width=320, height=240)
# vložení kreslicího plátna na plochu diáře
canvas
# vykreslení základních entit – úseček
canvas.stroke_line(0, 0, 319, 239)
Přidání vyplněného oblouku a kruhu:
# oblouk a kružnice canvas.fill_arc(160, 120, 50, 0, 3.14) canvas.stroke_circle(160, 120, 40)
Přidání obdélníku, z něhož se vykreslí pouze obrys:
# obdélník canvas.stroke_rect(0, 0, 320, 240)
Přidány polyčáry a polygonu:
# polygon canvas.fill_polygon([(20, 20), (180, 20), (100, 150)]) canvas.stroke_polygon([(0, 0), (160, 0), (160, 240)])
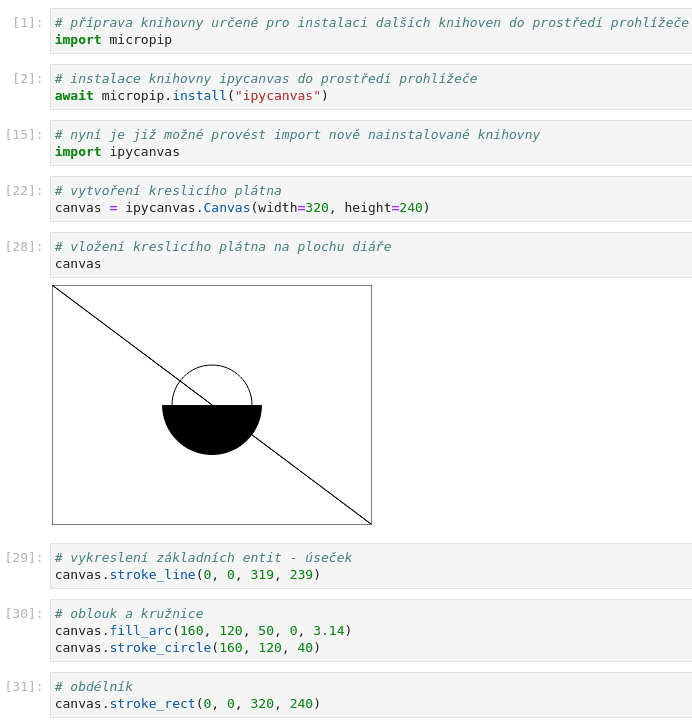
Obrázek 4: Další 2D entity vykreslené na plochu plátna.
7. Změna stylu vykreslovaných entit
U všech vykreslovaných entit lze pochopitelně modifikovat i styl vykreslení. U obrysů lze (kromě pokročilejších vlastností) změnit zejména šířku vykreslování atributem line_width a taktéž barvu atributem stroke_style (ve skutečnosti již název naznačuje, že možné je měnit i další vlastnosti obrysu, například styl napojení úseček apod.):
# změna stylu vykreslování 2D entit canvas.line_width = 5 canvas.stroke_style = 'green' # vykreslení základních entit - úseček canvas.stroke_line(0, 0, 319, 239)
U vyplněných entit se specifikuje barva výplně či styl výplně atributem fill_style:
# oblouk a kružnice canvas.fill_style = 'lightblue' canvas.fill_arc(160, 120, 50, 0, 3.14) canvas.stroke_style = '#4e6393' canvas.stroke_circle(160, 120, 40)
Barvu lze zadat jak názvem, tak i hexa kódem, podobně jako je tomu v HTML a CSS:
# obdélník canvas.stroke_style = 'red' canvas.stroke_style = '#4e6393' canvas.stroke_rect(0, 0, 320, 240)
Výsledek může vypadat následovně:
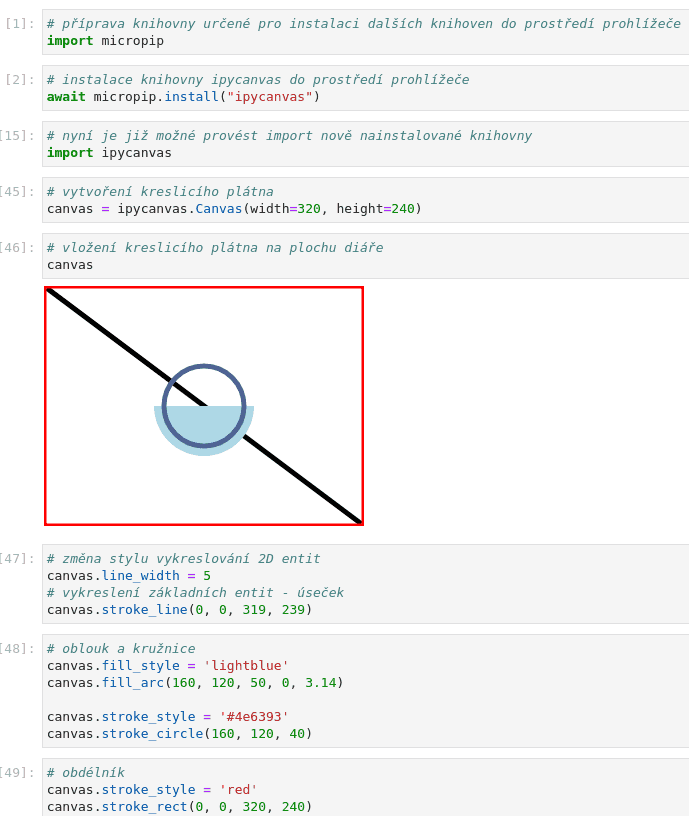
Obrázek 5: Změna stylu vykreslovaných entit.
8. Nastavení průhlednosti při vykreslování
Další důležitou vlastností je průhlednost entit, které jsou vykresleny na plátno. Tato vlastnost se nastavuje atributem global_alpha, přičemž nulová hodnota znamená úplnou průhlednost a jednička znamená neprůhlednost (tedy stav, kdy pod entitou neprosvítá její pozadí). Opět se podívejme na příklad použití tohoto atributu:
# oblouk a kružnice canvas.global_alpha = 0.8 canvas.fill_style = 'lightblue' canvas.fill_arc(160, 120, 50, 0, 3.14) canvas.global_alpha = 0.5 canvas.stroke_style = '#4e6393' canvas.stroke_circle(160, 120, 40)
Další změna v původním diáři tentokrát ovlivní vykreslení obdélníka, který bude mít průhlednost nastavenou na 90%:
# obdélník canvas.global_alpha = 0.1 canvas.fill_style = 'red' canvas.fill_rect(0, 0, 320, 240)
Výsledek zobrazený v diáři by měl vypadat takto:
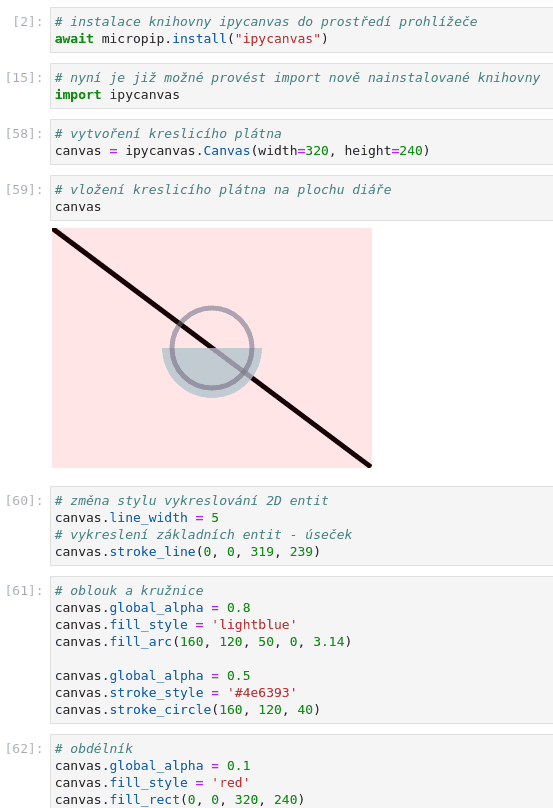
Obrázek 6: Poloprůhledné entity na kreslicím plátnu.
9. Gradientní barevné přechody využitelné při kreslení vyplněných obrazců
Další možnost vyplňování uzavřených tvarů 2D entit spočívá v použití gradientích (barevných) přechodů. Existuje několik variant těchto přechodů, přičemž nejpoužívanější je lineární přechod (v libovolném směru) nebo radiální přechod. U lineárních přechodů je nutné specifikovat dva body a taktéž libovolné množství barev. Přechod je vypočten na úsečce ležící mezi těmito dvěma body – tím je určen jak směr přechodu, tak i nepřímo jeho šířka (čím jsou body blíže u sebe, tím je šířka přechodu menší). Barvy je možné specifikovat jak přímo v zadaných bodech (relativní souřadnice na úsečce budou v tomto případě rovny 0,0 a 1,0, nebo v libovolném místě zmíněné úsečky). Celkový počet zadaných barev není omezen na dvě, můžeme například vytvořit přechod mezi třemi barvami nebo všechny barvy duhy:
gradient = canvas.create_linear_gradient(0, 0, 320, 0,
[
(0, 'red'),
(1 / 6, 'orange'),
(2 / 6, 'yellow'),
(3 / 6, 'green'),
(4 / 6, 'blue'),
(5 / 6, '#4B0082'),
(1, 'violet')
]
)
Tento gradientní přechod se použije následovně:
# obdélník canvas.fill_style = gradient canvas.fill_rect(0, 0, 320, 240)
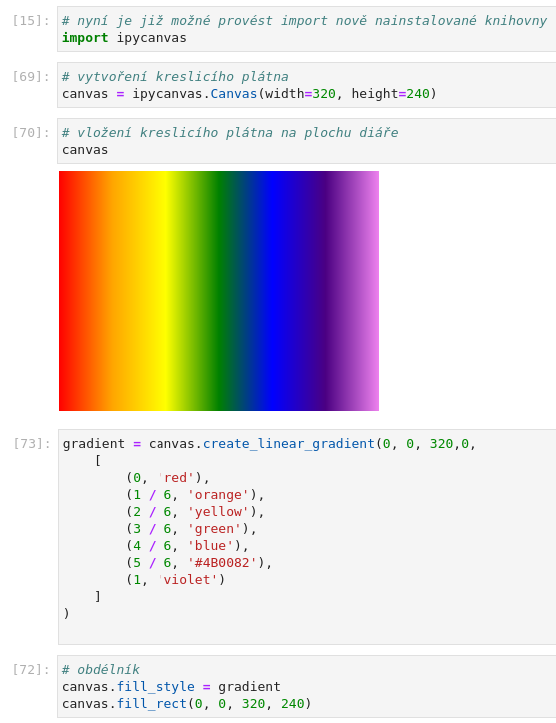
Obrázek 7: Duhový lineární barvový přechod.
10. Změna směru gradientního přechodu
Velmi snadno můžeme přechod otočit o 90° (povšimněte si odlišně zadaných koncových bodů úsečky – zvýrazněno):
gradient = canvas.create_linear_gradient(0, 0, 0, 240,
[
(0, 'red'),
(1 / 6, 'orange'),
(2 / 6, 'yellow'),
(3 / 6, 'green'),
(4 / 6, 'blue'),
(5 / 6, '#4B0082'),
(1, 'violet')
]
)
Tento přechod použijeme na stejný obdélník, jako tomu bylo v předchozím příkladu:
# obdélník canvas.fill_style = gradient canvas.fill_rect(0, 0, 320, 240)
S odlišným výsledkem:
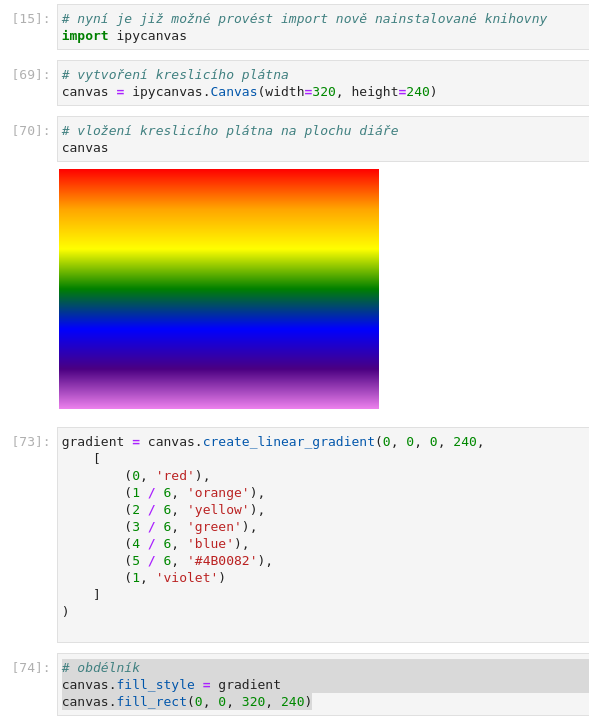
Obrázek 8: Duhový lineární barvový přechod, ovšem otočený o 90°.
11. Paprskovitý (radial) gradientní přechod
U specifikace radiálního přechodu se zadává střed a poloměr dvou kružnic, v níž k výpočtu změny barev dochází. Barvy se zadávají na úsečce vedoucí z obvodu první kružnice ke druhé kružnici. Ani zde není počet barev omezen, ovšem ukažme si nyní pro jednoduchost pouze dvojici barev. Menší kružnice má nenulový poloměr, což znamená, že celá její plocha bude vyplněna konstantní barvou, konkrétně první zvolenou barvou:
radial_gradient = canvas.create_radial_gradient(
160, 120, 10,
160, 120, 100,
[
(0, 'yellow'),
(1, 'white'),
]
)
Použití, resp. přesněji řečeno výběr takto definovaného přechodu při kreslení:
# kruh canvas.fill_style = radial_gradient canvas.fill_circle(160, 120, 200)
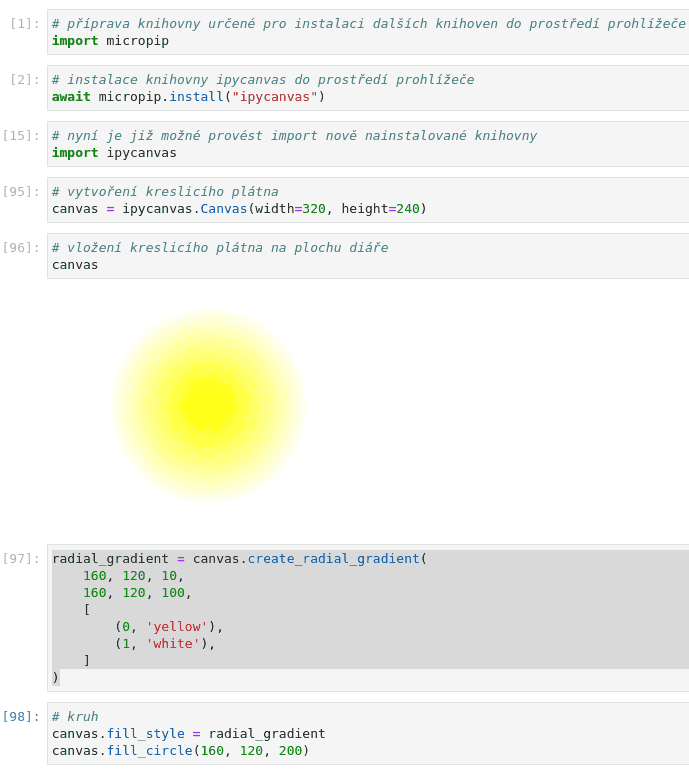
Obrázek 9: Radiální barevný přechod.
12. Text vykreslený na plátno
Plnohodnotné využití kreslicího plátna by nebylo možné v případě, kdyby na něj nebylo možné nakreslit text. Ovšem knihovna ipycanvas pochopitelně i tuto (nutno podotknout, že dosti složitou) 2D entitu podporuje. U textu lze specifikovat font, což je kombinace velikosti a stylu, ovšem s tím, že jsme omezeni pouze na ty fonty, které jsou k dispozici prohlížeči. Typicky se z důvodu lepší přenositelnosti používají pouze obecné názvy fontu (serif, sans-serif, cursive, fantasy a monospace). Příklad použití:
# parametry vykreslovaného textu
canvas.font = '32px serif'
# výpis textu
canvas.fill_text('www.root.cz', 10, 120)
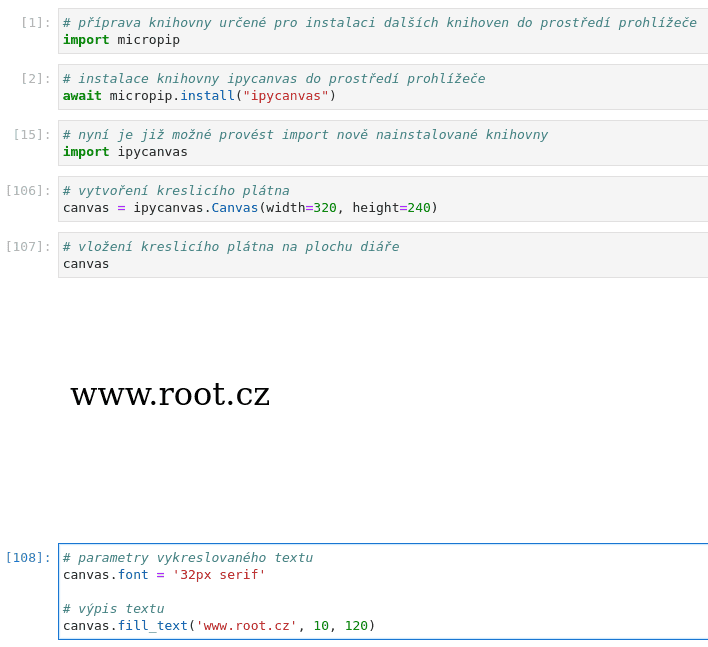
Obrázek 10: Text vykreslený na plochu kreslicího plátna.
13. Vycentrování textu v obou směrech okolo zadaného bodu
Poměrně často, například při kreslení schémat, je nutné vykreslit text vycentrovaný okolo zadaného bodu. V případě knihovny ipywidgets je v tomto případě nutné explicitně specifikovat horizontální vycentrování (atribut text_align) a taktéž relativní posun textu proti základní dotažnici (atribut text_baseline). Ukažme si příklad:
# parametry vykreslovaného textu
canvas.font = '32px serif'
# vycentrování textu okolo zadaného bodu
canvas.text_align = 'center'
# vertikální umístění textu na základní čáru
canvas.text_baseline = 'middle'
# výpis textu
canvas.fill_text('www.root.cz', 160, 120)
Nyní by měl být text na kreslicím plátnu vycentrován:
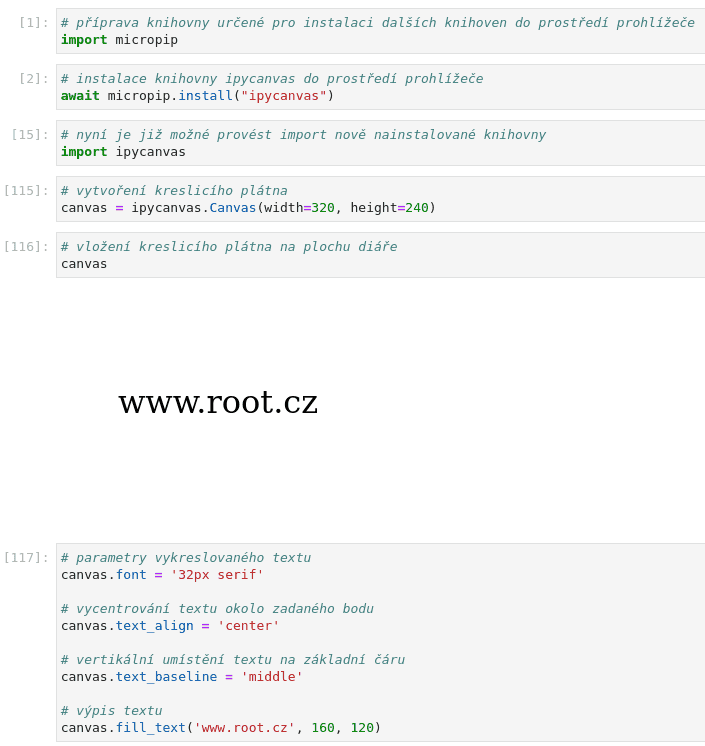
Obrázek 11: Vycentrovaný text vykreslený na plochu kreslicího plátna.
14. Cesty (paths) v knihovně ipycanvas
Pro kreslení složitějších tvarů se velmi často používají takzvané cesty neboli paths (což je mimochodem v počítačové grafice ustálený termín, s nímž se setkáme například v PostScriptu či SVG). Cesta může být složena z několika segmentů, přičemž každý segment je představován úsečkou, Bézierovou křivkou nebo eliptickým obloukem (kruhový oblouk je podmnožinou obecnějšího oblouku eliptického). Úsečkové segmenty jsou popsány třemi příkazy: move_to (posun grafického kurzoru bez kreslení), line_to (posun grafického kurzoru s kreslením) a close_path (posun grafického kurzoru zpět na začátek cesty).
Příkazy pro posun grafického kurzoru mohou používat absolutní nebo relativní souřadnice, existují i varianty pro posun pouze v horizontálním či vertikálním směru (to je výhodné z hlediska celkové velikosti výsledného řetězce – ovšem u jednodušších obrazců není rozdíl patrný). Relativní souřadnice pracují s předchozími souřadnicemi grafického kurzoru, ke kterým jsou přičteny zapsané číselné údaje, tj. je proveden výpočet:
xnew=xold+Δx
ynew=yold+Δy
Samotný zápis všech příkazů je zkrácen na pouhý jeden znak, přičemž při jejich zápisu záleží na velikosti písmen. Příkazy move_to a line_to obsahují parametry reprezentující souřadnice vrcholů úseček, tyto parametry jsou odděleny buď bílým znakem (nebo i několika bílými znaky), nebo dokonce nemusí být použity žádné oddělovače, pokud je konec číselné hodnoty možné zjistit z nečíselného znaku, který za ní následuje (například se může jednat o znaménko dalšího čísla či jméno následujícího příkazu) – řetězec s popisem cesty tedy může být dokonce kratší než odpovídající binární zápis! V tabulce níže jsou vypsány všechny příkazy pro tvorbu úsečkových segmentů cesty:
| Příkaz | Parametry | Popis |
|---|---|---|
| M | (x y)+ | absolutní pohyb na souřadnice [x, y] bez kreslení. Pokud je uvedeno více párů [x, y], všechny následující páry jsou považovány za parametry příkazu line_to |
| m | (x y)+ | relativní pohyb o souřadnice [x, y] bez kreslení. Pokud je uvedeno více párů [x, y], všechny následující páry jsou považovány za parametry příkazu line_to |
| L | (x y)+ | absolutní pohyb na souřadnice [x, y] s kreslením úsečkového segmentu. Je možné zapsat libovolné množství párů [x, y], výsledkem jejich vykreslení je lomená čára. |
| l | (x y)+ | relativní pohyb o souřadnice [x, y] s kreslením úsečkového segmentu. Je možné zapsat libovolné množství párů [x, y], výsledkem jejich vykreslení je lomená čára. |
| H | x+ | horizontální posun na absolutní souřadnici x s kreslením (vykreslení vodorovné úsečky). Je možné zapsat i více souřadnic, většinou to však nemá smysl (záleží však na nastaveném stylu cesty). |
| h | x+ | relativní posun o hodnotu x v horizontálním směru (vykreslení vodorovné úsečky) |
| V | y+ | vertikální posun na absolutní souřadnici y s kreslením (vykreslení svislé úsečky) |
| v | y+ | relativní posun o hodnotu y ve vertikálním směru (vykreslení svislé úsečky) |
| Z | (nejsou) | uzavření cesty úsečkovým segmentem |
| z | (nejsou) | má stejný význam jako příkaz Z |
15. Křivkové segmenty v cestách – oblouky a Bézierovy křivky
Cesta může obsahovat i segmenty složené z Bézierových křivek. V knihovně ipycanvas jsou podporovány jak Bézierovy kvadratické křivky, tak i Bézierovy křivky kubické. Kvadratické křivky jsou specifikovány trojicí řídicích bodů, zatímco křivky kubické potřebují pro zadání svého tvaru čtyři řídicí body. Bézierova křivka obecně prochází pouze svým prvním a posledním bodem (kotvicí body), ostatní body „pouze“ ovlivňují výsledný tvar křivky – jde tedy o aproximační křivky, i když je lze po programových výpočtech použít i pro interpolaci. Ve speciálních případech však křivka může procházet i dalšími (řídicími) body, například tehdy, když všechny body leží na jedné přímce.
Pomocí prvního bodu (kotvicího) a druhého bodu (řídicího) se určuje tečný vektor na začátku křivky. Předposlední bod (řídicí) a poslední bod (kotvicí) zase určují tečný vektor na konci křivky. Této vlastnosti se velmi často využívá při hladkém navazování Bézierových křivek. Samozřejmě je také možné hladce navázat Bézierovu křivku na úsečku či kruhový oblouk.
V ipycanvas se Bézierovy křivky zadávají pomocí čtyř variant příkazů, přičemž každá varianta existuje ve své absolutní a relativní podobě podle toho, jakým způsobem jsou zadávány souřadnice řídicích bodů. Celkem je tedy vyhrazeno osm znaků umožňujících různé způsoby zápisu křivek. Tyto znaky jsou spolu se svým významem popsány v následující tabulce:
| Příkaz | Parametry | Popis |
|---|---|---|
| Q | (x1 y1 x y)+ | kvadratická Bézierova křivka zadaná trojicí řídicích bodů s absolutními souřadnicemi. Konec aktuálně vytvářené cesty je chápán jako první řídicí bod, druhý řídicí bod má souřadnice [x1, y1] a třetí řídicí bod má souřadnice [x, y]. Po vytvoření křivky se konec cesty přesune do bodu [x, y]. Čtveřici souřadnice je možné opakovat, potom je vytvořeno více Bézierových křivek. |
| q | (x1 y1 x y)+ | má stejný význam jako příkaz Q s tím rozdílem, že souřadnice řídicích bodů jsou zadány relativně (vůči předchozím souřadnicím). |
| T | (x y)+ | kvadratická Bézierova křivka vedoucí od konce vytvářené cesty do zadaného bodu se souřadnicemi [x, y]. Řídicí bod této křivky není zadán, protože je dopočítán z pozice řídicího bodu předchozí kvadratické Bézierovy křivky tak, aby na sebe křivky hladce navazovaly (to znamená, že před příkazem T by měl být příkaz Q, q, T či t). |
| t | (x y)+ | má stejný význam jako příkaz T s tím rozdílem, že souřadnice koncového bodu Bézierovy kvadratické křivky jsou zadány relativně vůči koncovému bodu cesty. |
| C | (x1 y1 x2 y2 x y)+ | kubická Bézierova křivka zadaná čtyřmi řídicími body, přičemž konec aktuálně vytvářené cesty je počátečním bodem této křivky a jejím koncovým bodem je [x, y]. Souřadnice řídicích bodů jsou zadány absolutně. |
| c | (x1 y1 x2 y2 x y)+ | má stejný význam jako příkaz C s tím rozdílem, že souřadnice řídicích bodů jsou zadány relativně (vůči předchozím souřadnicím). |
| S | (x2 y2 x y)+ | tento příkaz je podobný příkazu T, ovšem s tím rozdílem, že se vytvoří kubická Bézierova křivka. První řídicí bod křivky je automaticky vypočítán ze druhého řídicího bodu předchozí kubické Bézierovy křivky, tak, aby na sebe křivky hladce navazovaly. To znamená, že před tímto příkazem by měl předcházet příkaz C či S. Norma neurčuje, že by se měly dopočítat návaznosti kvadratických a kubických křivek, proto kombinace příkazů Q a S nemusí dát očekávané výsledky (podobně není možné automaticky navázat kruhový oblouk na křivku). |
| s | (x2 y2 x y)+ | podobné příkazu S, ale všechny souřadnice řídicích bodů jsou zadány relativně. |
Příkazy T, t, S a s sice na první pohled vypadají složitě a možná i nadbytečně, ale mohou být velmi užitečné, protože není nutné zajišťovat hladkou návaznost Bézierových křivek na sebe. Podobným způsobem jsou ostatně dopočítávány řídicí body i v popisu fontů ve formátu True Type (TTF), ve kterých jsou kvůli rychlému vykreslování použity kvadratické Bézierovy křivky.
Podívejme se nyní na příklad použití cest s Bézierovými křivkami ve funkci segmentů:
# definice čtveřice cest
path1 = ipycanvas.Path2D('M80 80 A 45 45, 0, 0, 0, 125 125 L 125 80 Z')
path2 = ipycanvas.Path2D('M230 80 A 45 45, 0, 1, 0, 275 125 L 275 80 Z')
path3 = ipycanvas.Path2D('M80 230 A 45 45, 0, 0, 1, 125 275 L 125 230 Z')
path4 = ipycanvas.Path2D('M230 230 A 45 45, 0, 1, 1, 275 275 L 275 230 Z')
# vykreslení čtveřice cest canvas.fill_style = 'green' canvas.fill(path1) canvas.fill_style = 'purple' canvas.fill(path2) canvas.fill_style = 'red' canvas.fill(path3) canvas.fill_style = 'blue' canvas.fill(path4)
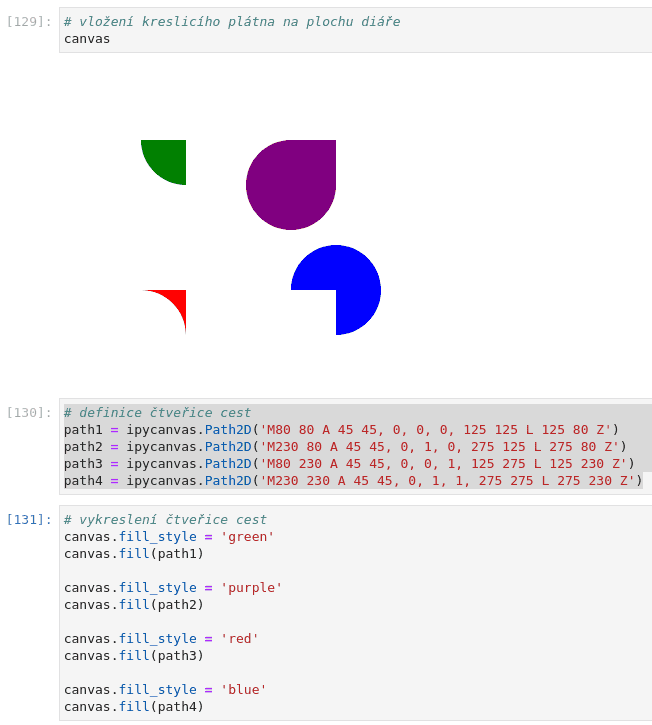
16. Vykreslení cesty, jejíž hrany se protínají
Ukažme si použití výše uvedených příkazů na jednoduchém demonstračním příkladu. Bude se jednat o vektorový obrázek známého domečku kresleného jedním tahem. Celý domek je vykreslen jednou cestou, jejíž barva je nastavena na černou barvu a výplň na konstantní oranžovou barvu (vzhledem k tomu, že se hrany domku protínají, není vykreslen celý jeho vnitřek. Cesta popisující domek má velikost jen několik desítek bajtů.
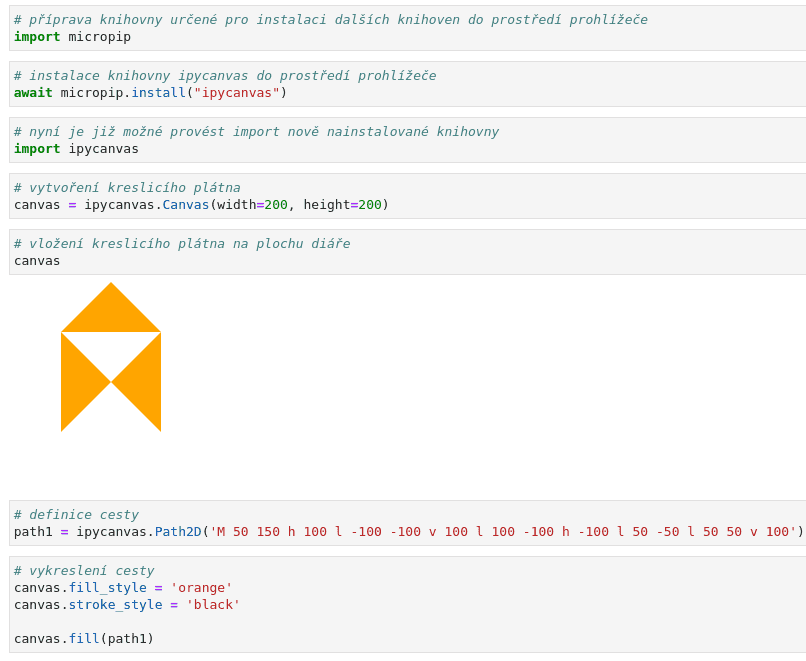
Obrázek 13: Domek vykreslený jedním tahem.
17. Repositář s demonstračními příklady
Všechny demonstrační příklady (resp. přesněji řečeno diáře), s nimiž jsme se seznámili v předchozích kapitolách, byly uloženy do Git repositáře umístěného na GitHubu (https://github.com/tisnik/jupyter-notebook-examples/). Poslední verze souborů s diáři naleznete pod odkazy uvedenými v tabulce pod tímto odstavcem. Diář by se měl otevřít přímo v rámci stránky GitHubu:
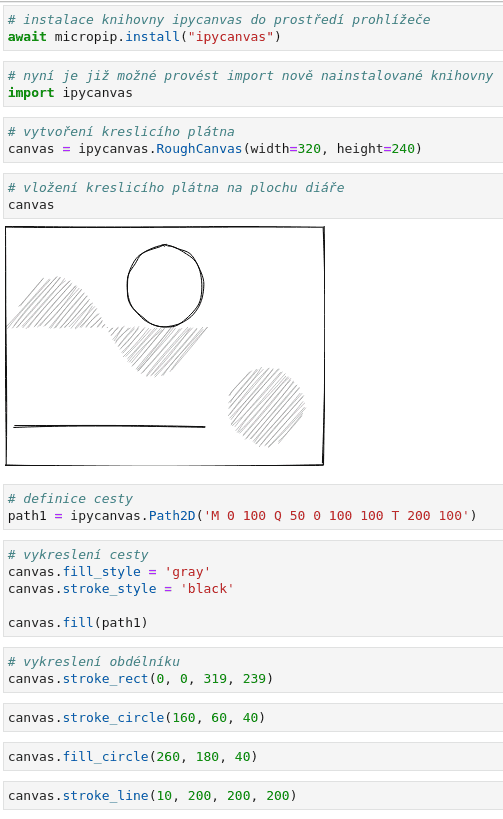
Obrázek 14: Simulaci kreslení rukou si popíšeme a ukážeme příště.
18. Odkazy na články o Jupyter Notebooku
Se samotným nástrojem Jupyter Notebook jsme se již na stránkách Rootu setkali několikrát, a to konkrétně v následujících článcích (přidán je i prozatím předposlední článek o projektu JupyterLite):
- Jupyter Notebook – nástroj pro programátory, výzkumníky i lektory
https://www.root.cz/clanky/jupyter-notebook-nastroj-pro-programatory-vyzkumniky-i-lektory/ - Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib
https://www.root.cz/clanky/tvorba-grafu-v-jupyter-notebooku-s-vyuzitim-knihovny-matplotlib/ - Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib (dokončení)
https://www.root.cz/clanky/tvorba-grafu-v-jupyter-notebooku-s-vyuzitim-knihovny-matplotlib-dokonceni/ - Jupyter Notebook – operace s rastrovými obrázky a UML diagramy, literate programming
https://www.root.cz/clanky/jupyter-notebook-operace-s-rastrovymi-obrazky-a-uml-diagramy-literate-programming/ - Interpret programovacího jazyka Clojure integrovaný do Jupyter Notebooku
https://www.root.cz/clanky/interpret-programovaciho-jazyka-clojure-integrovany-do-jupyter-notebooku/ - Calysto Hy: integrace programovacího jazyka Hy s Jupyter Notebookem
https://www.root.cz/clanky/calysto-hy-integrace-programovaciho-jazyka-hy-s-jupyter-notebookem/ - JupyterLite: nová alternativní architektura Jupyter Notebooku
https://www.root.cz/clanky/jupyterlite-nova-alternativni-architektura-jupyter-notebooku/ - Interaktivní ovládací prvky v Jupyter Notebooku
https://www.root.cz/clanky/interaktivni-ovladaci-prvky-v-jupyter-notebooku/
19. Odkazy na články o formátu SVG
Některé vlastnosti knihovny ipycanvas jsou odvozeny od vlastností vektorového formátu SVG. Týká se to například způsobu deklarace cest, řešení vyplnění cest, jejichž hrany se protínají atd. Z tohoto důvodu jsou pro úplnost v této příloze doplněny odkazy na již vydané články o tomto velmi užitečném formátu:
- Vektorový grafický formát SVG
https://www.root.cz/clanky/vektorovy-graficky-format-svg/ - Cesty v souborech typu Scalable Vector Graphics
https://www.root.cz/clanky/cesty-v-souborech-typu-scalable-vector-graphics/ - Scalable Vector Graphics a základní geometrické tvary
https://www.root.cz/clanky/scalable-vector-graphics-a-zakladni-geometricke-tvary/ - Vlastnosti cest a základních geometrických tvarů v SVG
https://www.root.cz/clanky/vlastnosti-cest-a-zakladnich-geometrickych-tvaru-v-svg/ - SVG – styly výplní a značky připojované ke křivkám
https://www.root.cz/clanky/svg-styly-vyplni-a-znacky-pripojovane-ke-krivkam/ - Gradientní výplně a textové objekty v SVG
https://www.root.cz/clanky/gradientni-vyplne-a-textove-objekty-v-svg/ - Grafický formát SVG a animace
https://www.root.cz/clanky/graficky-format-svg-a-animace/ - Pokročilejší animace ve formátu SVG
https://www.root.cz/clanky/pokrocilejsi-animace-ve-formatu-svg/ - Podpora skriptování v grafickém formátu SVG
https://www.root.cz/clanky/podpora-skriptovani-v-grafickem-formatu-svg/ - Zpracování událostí při skriptování výkresů SVG
https://www.root.cz/clanky/zpracovani-udalosti-pri-skriptovani-vykresu-svg/
20. Odkazy na Internetu
- ipycanvas: Interactive Canvas in Jupyter
https://ipycanvas.readthedocs.io/en/latest/index.html - ipycanvas na PyPi
https://pypi.org/project/ipycanvas/ - Canvas API
https://developer.mozilla.org/en-US/docs/Web/API/Canvas_API - ipycanvas usage
https://ipycanvas.readthedocs.io/en/latest/usage.html - ipywidgets (dokumentace)
https://ipywidgets.readthedocs.io/en/latest/ - Interactive Widgets
https://github.com/jupyter-widgets/ipywidgets/blob/master/docs/source/examples/Index.ipynb - Notebook interface
https://en.wikipedia.org/wiki/Notebook_interface - Jypyter: open source, interactive data science and scientific computing across over 40 programming languages
https://jupyter.org/ - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - showcase example code: xkcd.py
https://matplotlib.org/xkcd/examples/showcase/xkcd.html - Customising contour plots in matplotlib
https://philbull.wordpress.com/2012/12/27/customising-contour-plots-in-matplotlib/ - Graphics with Matplotlib
http://kestrel.nmt.edu/~raymond/software/python_notes/paper004.html - The IPython Notebook
http://ipython.org/notebook.html - nbviewer: a simple way to share Jupyter Notebooks
https://nbviewer.jupyter.org/ - Back to the Future: Lisp as a Base for a Statistical Computing System
https://www.stat.auckland.ac.nz/~ihaka/downloads/Compstat-2008.pdf - gg4clj: a simple wrapper for using R's ggplot2 in Clojure and Gorilla REPL
https://github.com/JonyEpsilon/gg4clj - Analemma: a Clojure-based SVG DSL and charting library
http://liebke.github.io/analemma/ - Clojupyter: a Jupyter kernel for Clojure
https://github.com/roryk/clojupyter - Incanter is a Clojure-based, R-like platform for statistical computing and graphics.
http://incanter.org/ - Evolution of incanter (Gource Visualization)
https://www.youtube.com/watch?v=TVfL5nPELr4 - Questions tagged [incanter] (na Stack Overflow)
https://stackoverflow.com/questions/tagged/incanter?sort=active - Data Sorcery with Clojure
https://data-sorcery.org/contents/ - What is REPL?
https://pythonprogramminglanguage.com/repl/ - What is a REPL?
https://codewith.mu/en/tutorials/1.0/repl - Programming at the REPL: Introduction
https://clojure.org/guides/repl/introduction - What is REPL? (Quora)
https://www.quora.com/What-is-REPL - Gorilla REPL: interaktivní prostředí pro programovací jazyk Clojure
https://www.root.cz/clanky/gorilla-repl-interaktivni-prostredi-pro-programovaci-jazyk-clojure/ - R Markdown: The Definitive Guide
https://bookdown.org/yihui/rmarkdown/ - Single-page application
https://en.wikipedia.org/wiki/Single-page_application - Video streaming in the Jupyter Notebook
https://towardsdatascience.com/video-streaming-in-the-jupyter-notebook-635bc5809e85 - How IPython and Jupyter Notebook work
https://jupyter.readthedocs.io/en/latest/architecture/how_jupyter_ipython_work.html - Jupyter kernels
https://github.com/jupyter/jupyter/wiki/Jupyter-kernels - Keras: The Python Deep Learning library
https://keras.io/ - TensorFlow
https://www.tensorflow.org/ - PyTorch
https://pytorch.org/ - Seriál Torch: framework pro strojové učení
https://www.root.cz/serialy/torch-framework-pro-strojove-uceni/ - Scikit-learn
https://scikit-learn.org/stable/ - Java Interop (Clojure)
https://clojure.org/reference/java_interop - Obrazy s balíčky Jupyter Notebooku pro Docker
https://hub.docker.com/u/jupyter/#! - Správce balíčků Conda (dokumentace)
https://docs.conda.io/en/latest/ - Lorenzův atraktor
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-vi/#k02 - Lorenzův atraktor
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03 - Graphics with Matplotlib
http://kestrel.nmt.edu/~raymond/software/python_notes/paper004.html - Embedding Matplotlib Animations in Jupyter Notebooks
http://louistiao.me/posts/notebooks/embedding-matplotlib-animations-in-jupyter-notebooks/ - Literate programing, Kolokviální práce Pavla Starého
https://www.fi.muni.cz/usr/jkucera/pv109/starylp.htm - PlantUML (home page)
http://plantuml.sourceforge.net/ - PlantUML (download page)
http://sourceforge.net/projects/plantuml/files/plantuml.jar/download - PlantUML (Language Reference Guide)
http://plantuml.sourceforge.net/PlantUML_Language_Reference_Guide.pdf - Plain-text diagrams take shape in Asciidoctor!
http://asciidoctor.org/news/2014/02/18/plain-text-diagrams-in-asciidoctor/ - Graphviz – Graph Visualization Software
http://www.graphviz.org/ - graphviz (Manual Page)
http://www.root.cz/man/7/graphviz/ - PIL: The friendly PIL fork (home page)
https://python-pillow.org/ - Python Imaging Library (PIL), (home page)
http://www.pythonware.com/products/pil/ - PIL 1.1.6 na PyPi
https://pypi.org/project/PIL/ - Pillow 5.2.0 na PyPi
https://pypi.org/project/Pillow/ - Python Imaging Library na Wikipedii
https://en.wikipedia.org/wiki/Python_Imaging_Library - Pillow na GitHubu
https://github.com/python-pillow/Pillow - Pillow – dokumentace na readthedocs.io
http://pillow.readthedocs.io/en/5.2.x/ - How to use Pillow, a fork of PIL
https://www.pythonforbeginners.com/gui/how-to-use-pillow - await in Python
https://docs.python.org/3/reference/expressions.html#await


























