Obsah
1. Křivky v přírodě i v počítačové grafice – svět spirál (dokončení)
3. Konvergence či divergence posloupnosti zn
4. Algoritmus vykreslení Mandelbrotovy množiny
5. Vykreslení Mandelbrotovy množiny knihovnou Matplotlib
6. Použití knihovny PIL/Pillow pro zobrazení Mandelbrotovy množiny
7. Vykreslení spirál v Mandelbrotově množině
8. Spirály v Mandelbrotově množině
11. Vzájemná souvislost mezi funkcemi S(x) a C(x)
12. Vykreslení klotoidy s využitím funkcí S(x) a C(x)
13. Obrazec s opakujícími se spirálami odvozený od Fresnelových integrálů
15. Evolventa vzniklá odvalováním polopřímky po kružnici
16. Zakomponování kružnice, okolo níž se polopřímka odvaluje
17. Přidání koeficientu a do rovnice evolventy
18. Evolventa vznikající odvalováním polopřímky po cykloidě
19. Repositář s demonstračními příklady
1. Křivky v přírodě i v počítačové grafice – svět spirál (dokončení)
V dnešní části seriálu o křivkách, které nalezneme v přírodě, architektuře, technice i v počítačové grafice dokončíme popis různých typů spirál, což je téma, kterému jsme se začali věnovat minule. Článek je rozdělen na dvě části. V první části si ukážeme, jak se vykresluje Mandelbrotova množina zmíněná minule a taktéž si na demonstračním příkladu ukážeme, kde v ní lze nalézt spirály (přitom s určitou dávkou zobecnění budeme Mandelbrotovu množinu považovat za implicitní popis křivky – zde konkrétně nekonečné křivky s topologickou dimenzí jedna a s fraktální dimenzí rovnou dvěma).
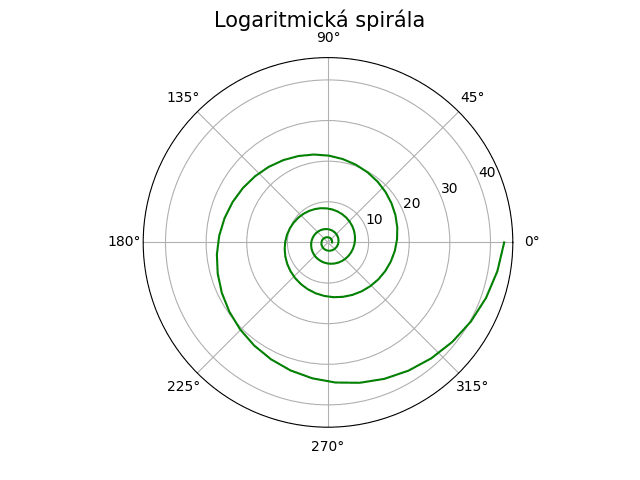
Obrázek 1: Logaritmická spirála je jednou z nejdůležitějších spirál vůbec.
Ve druhé části dnešního článku si popíšeme dvojici spirál, které v současnosti nacházejí velké praktické uplatnění. Jedná se v první řadě o klotoidu využívanou při návrzích tvarů silničních zatáček a železničních oblouků (přesněji řečeno při návrhu přechodnic mezi rovným úsekem a kruhovým obloukem, popř. přechodnic mezi dvojicí oblouků s různým poloměrem (popř. směrem ohybu). A druhou důležitou křivkou (která má v některých specifických případech tvar spirály) je evolventa, podle jejíhož tvaru se konstruují zuby ozubených kol.
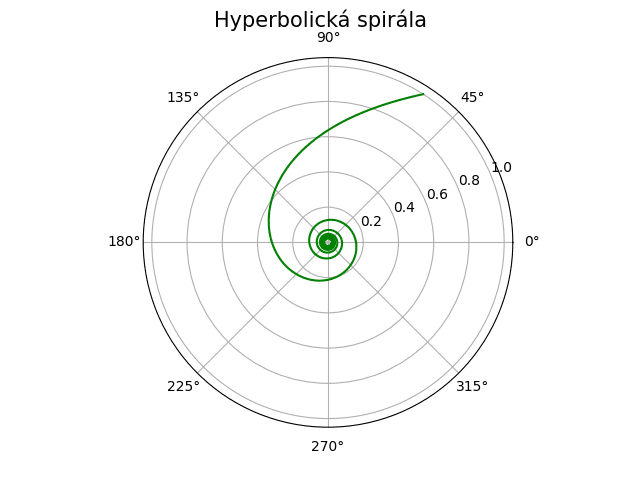
Obrázek 2: Hyperbolická spirála s jedním ramenem.
2. Mandelbrotova množina
„[I have] had the privilege to enrich Fatou-Julia's theory by adding a new part, by suggesting what Douady and Hubbard (1982) have called "Mandelbrot set or M-set“ … I have proceeded in a way loathed by theoreticians… I have wandered, contemplated, dissected, with the astonishing equivalent of a microscope that the computer is… Unforgettable images, even with the primitive tools of 1980… I did this work in 1979–1980…"
Benoit B. Mandelbrot
Mandelbrotova množina byla, podobně jako Juliovy množiny, objevena při analýze některých zdánlivě jednoduchých dynamických systémů se zpětnou vazbou. Analýza dynamických systémů se zabývá otázkou budoucího stavu systému, pokud iterativně provádíme výpočet s tou samou funkcí (resp. se skupinou funkcí). Některé výsledky z analytického i numerického výzkumu těchto systémů byly publikovány již počátkem minulého století (samozřejmě, že se bez pomoci počítačů jednalo o poměrně nezáživné matematické stati). Těmito dynamickými systémy se zabývali především matematici Gaston Julia (1893–1978) a Pierre Fatou (1878–1929). Na jejich práci, které souvisely především s Juliovými množinami (tak však byly nazvány až o více než půlstoletí později) navázal v sedmdesátých letech minulého století matematik Benoit B. Mandelbrot.
Jako součást své výzkumné práce využil Benoit Mandelbrot možností tehdy dostupné počítačové grafiky – to ovšem bylo na matematika dosti nezvyklé. V tomto období byly v pracovní skupině Mandelbrota a prakticky ve stejném čase i dvojicí Brookse a Matelskiho vytvořeny první obrazy fraktálu dnes nazývaného Mandelbrotova množina. První rastrové obrázky byly, vzhledem k dané době a omezeným možnostem použité výpočetní techniky, pouze černobílé, vzbudily však velký zájem jak mezi odbornou, tak i laickou veřejností. Z matematického pohledu jsou samozřejmě korektní pouze černobílé (resp. monochromatické) obrázky, protože se rozlišují pouze dvě možnosti: divergence či konvergence posloupnosti hodnot zn. V počítačové grafice se posléze došlo k barevnému „vylepšování “ obrázků, při kterém jsou barvy pixelům přiřazovány například podle počtu iterací, vzdálenosti čísla zn od počátku atd.
Mandelbrotova množina je vytvořena pomocí jednoduchého dynamického systému, který je založený na iteraci funkce komplexní paraboly:
zn+1=zn2+c
kde proměnné z a c leží v komplexní rovině.
V průběhu výpočtu se hodnota z postupně mění, zatímco hodnota c zůstává konstantní – tato se mění pouze při přesunu výpočtu na nový bod. Celý iterační proces začíná s určitou startovní hodnotou z0, takže systém postupně generuje sekvenci hodnot zk, které nazýváme orbit. Postup si ukážeme na prvních čtyřech iteracích:
z1=(z0)2+c
z2=((z0)2+c)2+c
z3=(((z0)2+c)2+c)2+c
z4=((((z0)2+c)2+c)2+c)2+c
3. Konvergence či divergence posloupnosti zn
Při práci se systémem popsaným v předchozím textu nás zajímá, zda pro danou startovní hodnotu z0 a konstantu c posloupnost zn konverguje či diverguje. Ukazuje se, že pro některé počáteční hodnoty nastává také oscilace – hodnoty zn se opakují s určitou periodou, to znamená, že platí rovnost zn=zn+i, kde i je perioda oscilace. Bližším studiem vlivu počátečních podmínek na budoucí stav systému se zabýval právě Benoit B. Mandelbrot a před ním i Fatou.
Mandelbrot se omezit na případ, kdy počáteční hodnota z0 je nulová a pro každý počítaný bod se mění pouze konstanta c. Iterativním výpočtem vzniknou pouze takzvané orbity nuly. Orbity nuly lze podle jejich vlastností rozdělit do dvou kategorií:
- Pro některé hodnoty c je orbit konečný, tzn. všechny hodnoty zn jsou konečné. Do této kategorie spadají také hodnoty, které oscilují.
- Pro další hodnoty c je orbit nekonečný, tzn. po určité době rostou hodnoty zn nade všechny meze.
Mandelbrotova množina je v tomto případě definována jako množina všech komplexních čísel c, které produkují konečný orbit nuly.
Abychom mohli úspěšně vykreslit hrubý obrázek Mandelbrotovy množiny, musíme zjistit, které body do této množiny zcela jistě nepatří. Jak již víme z předchozího textu, jedná se o ty body, jejichž orbit míří na Riemanově sféře (což je, zjednodušeně řečeno, komplexní rovina pouze s jedním nekonečnem) k nekonečnu. Je však možné jednoduše zjistit, že nějaký orbit míří k nekonečnu v konečném čase, resp. v konečném počtu kroků? Ukazuje se, že pro některé body je možné vytvořit jednoduchý test, jehož princip je ukázán na následujících řádcích.
Při testu na nekonečnost orbitu použijeme důkazu, že pro |c|<=|z| a |z|>2 posloupnost diverguje. Využije se přitom trojúhelníkové nerovnosti pro komplexní čísla:
|a+b| >= |a|-|b|,
kde za obecnou hodnotu a dosadíme z×z a za obecnou hodnotu b komplexní konstantu c:
|z×z+c| >= |z×z|-|c| = (|z|)2-|c|
Je nutné najít minimální hodnotu |z|, při jejímž překročení je |z×z+c|>|z|. Nazvěme tuto hodnotu r. Potom r×r-|c|=r resp. r×r-r-|c|=0 a dále z řešení kvadratické rovnice vyplývá:
r=(1+(1+4|c|)1/2)/2.
Známe tedy hodnotu r. Jestliže je velikost |z| větší než r, systém diverguje. Pokud iterace začíná s hodnotou z=0, je po první iteraci z=c. V předchozích vzorcích můžeme r nahradit |c| a dostaneme vztah:
|c|×|c|-2|c| = 0 tedy |c|=2 resp. |z|=2 protože z=c
Posloupnost tedy pro |z|>2 skutečně diverguje. V průběhu iteračního výpočtu tedy stačí testovat, zda je velikost |zk|>2. Podmínka pro divergenci posloupnosti mimo jiné také znamená, že všechny body Mandelbrotovy množiny leží v komplexní rovině uvnitř kružnice o poloměru 2. Je to dáno tím, že pro |c|>2 je po první iteraci také |z|>2 a z podmínek uvedených výše vyplývá, že posloupnost diverguje.
Z předchozího textu vyplývá, že všechny body Mandelbrotovy množiny mají absolutní hodnotu menší než 2. Také víme, že jestliže v průběhu iteračního procesu absolutní hodnota z překročí 2, posloupnost diverguje a počítaný bod tudíž neleží v Mandelbrotově množině. Opačný test, tj. test na konvergenci posloupnosti nelze přímo provést. Používá se proto metoda, při které se zvolí dostatečně velký počet iterací, přičemž v každém kroku je testováno, zda absolutní hodnota z nepřekročí 2. Pokud tato možnost nastane, bod uvnitř Mandelbrotovy množiny zcela jistě neleží. Pokud proběhne výpočet všech iterací aniž by absolutní hodnota z překročila 2, je počítaný bod prohlášen za prvek Mandelbrotovy množiny. Tato metoda je sice nepřesná, ale lze ji v podstatě libovolně zpřesňovat zvyšováním maximálního počtu iterací. Hodnota 2 použitá v testu se v literatuře nazývá bailout.
4. Algoritmus vykreslení Mandelbrotovy množiny
Postup při výpočtu bodů ležících v Mandelbrotově množině lze zapsat pomocí jednoduchého algoritmu. Vstupem algoritmu je komplexní číslo c a konstanta určující maximální počet iterací MaxIter:
- nastav iter:=0
- nastav z:=0
- pokud iter<MaxIter prováděj smyčku:
- nastav z:=z2+c
- jestliže |z|>2 bod neleží v Mandelbrotově množině; konec
- nastav iter:=iter+1
- konec smyčky
- bod leží uvnitř Mandelbrotovy množiny; konec
Tento algoritmus lze velmi jednoduše implementovat s tím, že proměnné z a c jsou komplexní čísla, tj. nabývají komplexních hodnot. Protože ve většině programovacích jazyků nejsou komplexní čísla zavedena jako základní datové typy, pomůžeme si tím, že každé komplexní číslo reprezentujeme jeho reálnou a imaginární složkou (v Pythonu to ovšem není nutné). Proto například původní komplexní proměnná z bude reprezentována dvojicí reálných proměnných zx a zy a komplexní proměnná c bude reprezentována dvojicí cx a cy.
Absolutní hodnotu |z| lze rozepsat jako sqrt(zx*zx+zy*zy), kde sqrt() je matematická funkce provádějící druhou odmocninu. V reálných programech není použit přímo výpočet absolutní hodnoty, protože vyčíslení odmocniny je časově velmi náročné. Poměrně složitou podmínku ve tvaru sqrt(zx*zx+zy*zy)>2 lze na obou stranách umocnit (obě strany jsou vždy kladné) a použít novou podmínku, kde není zapotřebí provádět časově náročný výpočet odmocnin. Výsledný tvar podmínky má tvar: zx*zx+zy*zy>4. Výraz z:=z2+c, jež je zapsán pomocí dvou komplexních proměnných z a c, lze rozepsat na jeho reálnou a imaginární část:
zx'=zx*zx-zy*zy+cx
zy'=2*zx*zy+cy
Kde zx, zy, cx, cy, zx' a zy' jsou proměnné nabývající reálných hodnot. Aby nebylo nutné používat dvou nových proměnných zx' a zy', použijí se již předpočítané mocniny reálné a imaginární složky z. Také je vhodné prohodit oba výrazy, aby nebylo nutné zavádět nové pomocné proměnné:
zx2=zx*zx
zy2=zy*zy
zy=2*zx*zy+cy
zx=zx2-zy2+cx
Hodnoty v proměnných zx2 a zy2 budou použity při testu zx2+zy2>4. Nyní již můžeme celý algoritmus pro výpočet bodů Mandelbrotovy množiny přepsat do konkrétního programovacího jazyka. Jako příklad je uveden zápis v programovacím jazyce C (praktické příklady ovšem budou používat Python, v němž je zápis jednodušší):
/*
* Parametrem této funkce je komplexní číslo C, pro které
* probíhá test.
*/
int MandelbrotTest(double cx, double cy)
{
double zx,zy,zx2,zy2,cx,cy; // komplexní proměnná Z
int iter; // počet iterací
zx=0; // vynulovat komplexní proměnnou C
zy=0;
iter=0; // nastavit počitadlo iterací
do { // iterační smyčka
zx2=zx*zx; // zx^2
zy2=zy*zy; // zy^2
zy=2.0*zx*zy+cy;
zx=zx2-zy2+cx; // z:=z^2+c
iter++; // zvýšit hodnotu počitadla iterací
} while (iter<maxiter && (zx2+zy2)<4.0);// test na počet iterací a bailout
if (iter==maxiter) // bod leží uvnitř Mandelbrotovy množiny
return LEZI_UVNITR;
else // bod leží vně Mandelbrotovy množiny
return LEZI_VNE;
}
Výše uvedený algoritmus lze přímo použít pro vykreslení Mandelbrotovy množiny. Bílé pixely reprezentují body v komplexní rovině, jež neleží v Mandelbrotově množině, černé pixely naopak reprezentují body v Mandelbrotově množině ležící. Symetrie Mandelbrotovy množiny okolo reálné osy je způsobena tím, že změna znaménka cy způsobí pouze změnu znaménka proměnné zy nikoliv zx. Na výpočet absolutní hodnoty |z| nemají znaménka reálné a imaginární složky žádný vliv. Funkce MandelbrotTest() je volaná pro každý počítaný (resp. zobrazovaný) pixel. Při větších velikostech pixelů může dojít ke znatelnému prodloužení výpočtu z důvodu častého volání této funkce. Proto je výhodnější vložit tělo funkce MandelbrotTest() přímo do hlavní výpočetní smyčky programu, kde se provádí nastavení jednotlivých pixelů.
5. Vykreslení Mandelbrotovy množiny knihovnou Matplotlib
Mandelbrotovu množinu je možné výše popsaným algoritmem vykreslit různými způsoby, a to v prakticky jakémkoli programovacím jazyce (ostatně se jedná o pravděpodobně jeden z nejvíce reimplementovaných algoritmů). Nejprve si ukažme způsob založený na použití knihovny Matplotlib. Nejedná se sice o ideální řešení, protože je výsledný rastrový obrázek přeškálován, ovšem zdrojový kód by měl být dobře pochopitelný:
"""Vykreslení klasické Mandelbrotovy množiny."""
import numpy as np
import matplotlib.pyplot as plt
import palette_greens
# velikost bitmapy s nakresleným fraktálem
WIDTH = 256
HEIGHT = 256
def mandelbrot(cx, cy, maxiter):
"""Výpočet, kolik iterací je nutné pro opuštění jednotkového kruhu."""
c = complex(cx, cy)
z = 0
for i in range(0, maxiter):
if abs(z) > 2:
return i
z = z * z + c
return 0
def recalc_fractal(image, palette, xmin, ymin, xmax, ymax, maxiter=1000):
"""Přepočet celého fraktálu."""
stepx = (xmax - xmin)/WIDTH
stepy = (ymax - ymin)/HEIGHT
y1 = ymin
for y in range(0, HEIGHT):
x1 = xmin
for x in range(0, WIDTH):
i = mandelbrot(x1, y1, maxiter)
i = 3*i % 256
for index in range(0, 3):
image[y][x][index] = palette[i][index]
image[y][x][index] = palette[i][index]
image[y][x][index] = palette[i][index]
x1 += stepx
y1 += stepy
# vytvoření prázdné bitmapy
image = np.zeros(shape=(HEIGHT, WIDTH, 3), dtype=np.uint8)
recalc_fractal(image, palette_greens.palette, -2.0, -1.5, 1.0, 1.5, 1000)
# vykreslení bitmapy do grafu
plt.figure(1, figsize=(8, 6), dpi=100)
plt.imshow(image)
# uložení grafu do rastrového obrázku
plt.savefig("test.png")
# zobrazení grafu s bitmapou
plt.show()
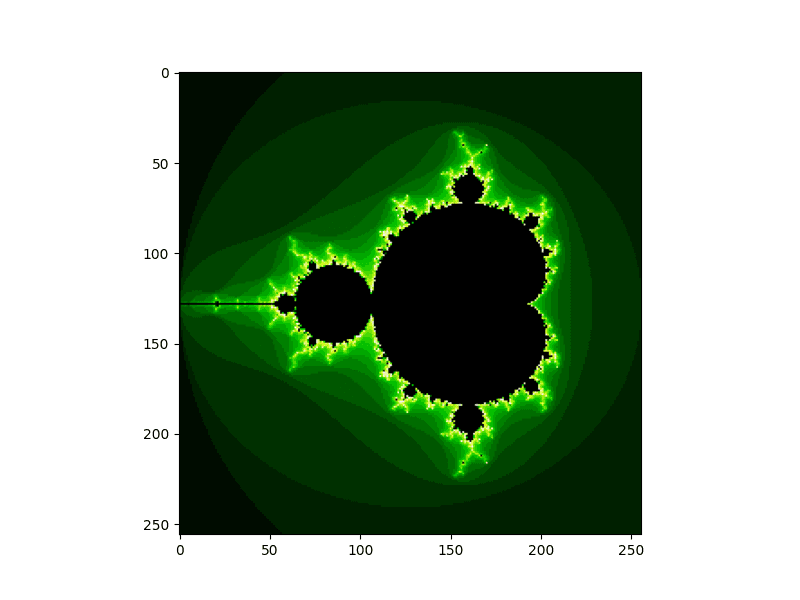
Obrázek 3: Mandelbrotova množina vykreslená předchozím demonstračním příkladem založeným na použití knihovny Matplotlib.
6. Použití knihovny PIL/Pillow pro zobrazení Mandelbrotovy množiny
V tomto konkrétním případě, v němž obarvujeme jednotlivé pixely rastrového obrázku, je vhodnější namísto knihovny Matplotlib použít knihovnu PIL, resp. Pillow, která je určena přímo pro manipulaci s rastrovými obrázky a umožňuje i jejich ukládání do souborů. Upravený tvar demonstračního příkladu, ovšem založený na stejném algoritmu výpočtu bodů v Mandelbrotově množině, bude vypadat takto:
#!/usr/bin/env python
"""Vykreslení klasické Mandelbrotovy množiny."""
from PIL import Image
import palette_greens
# textura by měla být čtvercová a její šířka i výška by měla být
# mocninou čísla 2
IMAGE_WIDTH = 256
IMAGE_HEIGHT = 256
def mandelbrot(cx, cy, maxiter):
"""Výpočet, kolik iterací je nutné pro opuštění jednotkového kruhu."""
c = complex(cx, cy)
z = 0
for i in range(0, maxiter):
if abs(z) > 2:
return i
z = z * z + c
return 0
def recalc_fractal(image, palette, xmin, ymin, xmax, ymax, maxiter=1000):
"""Přepočet celého fraktálu."""
width, height = image.size # rozměry obrázku
stepx = (xmax - xmin)/width
stepy = (ymax - ymin)/height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
i = mandelbrot(x1, y1, maxiter)
i = 3*i % 256
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
x1 += stepx
y1 += stepy
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
recalc_fractal(image, palette_greens.palette, -2.0, -1.5, 1.0, 1.5, 1000)
image.save("mandelbrot.png")
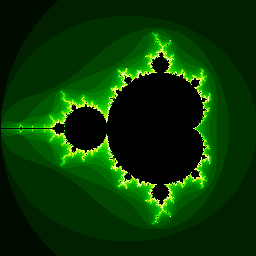
Obrázek 4: Mandelbrotova množina vykreslená předchozím demonstračním příkladem založeným na knihovně PIL, popř. Pillow.
7. Vykreslení spirál v Mandelbrotově množině
Nyní již zbývá udělat poslední krok – nepatrně upravit předchozí skript do takové podoby, aby vykreslil ty části Mandelbrotovy množiny, v nichž nalezneme spirály. Tento skript obsahuje souřadnice známých oblastí Mandelbrotovy množiny, o nichž jsme se ostatně zmínili minule:
#!/usr/bin/env python
"""Vykreslení spirál v Mandelbrotově množině."""
from PIL import Image
import palette_mandmap
IMAGE_WIDTH = 800
IMAGE_HEIGHT = 600
def mandelbrot(cx, cy, maxiter):
"""Výpočet, kolik iterací je nutné pro opuštění jednotkového kruhu."""
c = complex(cx, cy)
z = 0
for i in range(0, maxiter):
if abs(z) > 2:
return i
z = z * z + c
return 0
def recalc_fractal(image, palette, xmin, ymin, xmax, ymax, maxiter=1000):
"""Přepočet celého fraktálu."""
width, height = image.size # rozměry obrázku
stepx = (xmax - xmin)/width
stepy = (ymax - ymin)/height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
i = mandelbrot(x1, y1, maxiter)
i = 3*i % 256
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
x1 += stepx
y1 += stepy
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
recalc_fractal(image, palette_mandmap.palette,
-0.769824999999999998320, -0.109270000000000000000,
-0.766247499999999998426, -0.106570000000000000000, 1000)
image.save("spiral_1.png")
recalc_fractal(image, palette_mandmap.palette,
-0.171119200000000013445, 0.657309400000000000000,
-0.169318975000000013445, 0.658660750000000000000, 1000)
image.save("spiral_2.png")
recalc_fractal(image, palette_mandmap.palette,
-0.207190825000000012496, 0.676656624999999999983,
-0.206107925000000012496, 0.677468799999999999983, 1000)
image.save("spiral_3.png")
recalc_fractal(image, palette_mandmap.palette,
-0.540623850000000003876, 0.523798050000000000019,
-0.532306600000000003876, 0.530031950000000000019, 1000)
image.save("spiral_4.png")
8. Spirály v Mandelbrotově množině
Předchozí demonstrační příklad vykreslil tyto spirály:

Obrázek 5: Spirála se dvěma rameny.

Obrázek 6: Spirála se třemi rameny.

Obrázek 7: Opět spirála se třemi rameny.

Obrázek 8: Spirála se čtyřmi rameny.
9. Klotoidy
Ve druhé části dnešního článku si popíšeme dvojici spirál, které mají velké uplatnění v praxi. První z těchto spirál se nazývá klotoida, ovšem existují i její alternativní pojmenování – Cornuova spirála, popř. Eulerova spirála. Klotoida má jednu velmi důležitou vlastnost – její křivost se spojitě (tedy bez skoků) mění s proběhnutou dráhou; její zakřivení tedy plynule roste, přičemž v počátku (což ovšem v tomto případě není pól spirály) je zakřivení nulové (křivka je zde přímá). Klotoida ze svého počátku pokračuje oběma směry, přičemž zakřivení v jednom směru je shodné, jako zakřivení ve směru opačném – pouze se mění znaménko zakřivení (křivost je převrácená hodnota poloměru oskulační kružnice v daném místě křivky).
Právě výše zmíněná vlastnost klotoidy, tedy změna křivosti s proběhnutou dráhou, se ukázala jako velmi důležitá při návrhu přechodnic, což jsou úseky silnic, popř. železničních kolejí mezi rovným úsekem a kruhovým obloukem, popř. úseky mezi dvěma kruhovými oblouky. Pokud by totiž byl (na silnici) rovný úsek přímo navázán na kruhový oblouk, vyžadovalo by to skokovou změnu natočení volantu. Naproti tomu pokud bude mezi přímým úsekem a kruhovým obloukem přechodnice, bude změna natočení volantu plynulá, od nulové polohy až do polohy, která odpovídá poloměru oblouku.
10. Fresnelovy integrály
Před ukázáním příkladu, který nakreslí skutečnou klotoidu, se ještě musíme seznámit s jedním termínem – Fresnelův integrál. Ten popisuje dvojici funkcí, přičemž každá má jediný nezávislý parametr x:
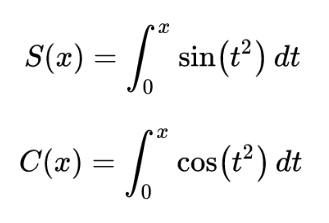
Při snaze o vykreslení průběhu těchto funkcí nahradíme výpočet integrálu za výpočet sumy s dostatečně malým krokem dt. Následující demonstrační příklad vykreslí průběh funkce S(x):
import numpy as np
import matplotlib.pyplot as plt
import math
# počet hodnot na x-ové ose
points = 300
# integrační krok
step = 0.001
# hodnoty na x-ové ose
x = np.linspace(0, 5, points)
# výpočet Fresnelova integrálu S(x)
def fresnel_s(x):
result = 0
for t in np.arange(0, x, step):
result += math.sin(t**2)
return result*step
# vektorizace předchozí funkce
fresnel_s_v = np.vectorize(fresnel_s)
# aplikace vektorizované funkce na všechny x-ové hodnoty
y = fresnel_s_v(x)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Fresnelův integrál S(x)', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("fresnel_s.png")
# zobrazení grafu
plt.show()
S tímto výsledkem:
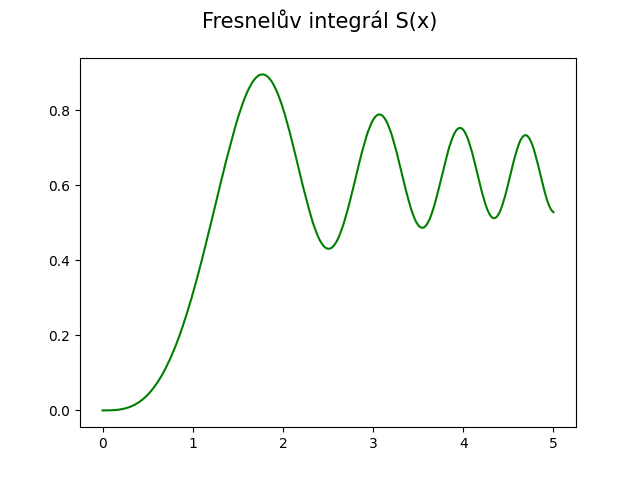
Obrázek 10: Výsledek postupného výpočtu Fresnelova integrálu S(x).
Prakticky totožným programovým kódem, jen s nepatrnou změnou ve výpočtu, můžeme vykreslit průběh funkce C(x), což je ukázáno na dalším demonstračním příkladu:
import numpy as np
import matplotlib.pyplot as plt
import math
# počet hodnot na x-ové ose
points = 300
# integrační krok
step = 0.001
# hodnoty na x-ové ose
x = np.linspace(0, 5, points)
# výpočet Fresnelova integrálu C(x)
def fresnel_c(x):
result = 0
for t in np.arange(0, x, step):
result += math.cos(t**2)
return result*step
# vektorizace předchozí funkce
fresnel_c_v = np.vectorize(fresnel_c)
# aplikace vektorizované funkce na všechny x-ové hodnoty
y = fresnel_c_v(x)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Fresnelův integrál C(x)', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("fresnel_c.png")
# zobrazení grafu
plt.show()
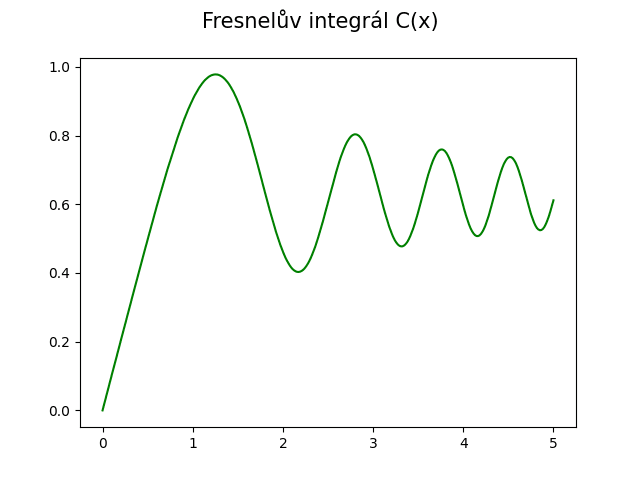
Obrázek 11: Výsledek postupného výpočtu Fresnelova integrálu C(x).
11. Vzájemná souvislost mezi funkcemi S(x) a C(x)
Označení funkcí S(x) a C(x) nám naznačuje, že se jedná o (zobecněné) obdoby funkcí sinus a kosinus. Jen pro úplnost se podívejme, jak vlastně vypadá průběh těchto dvou základních goniometrických funkcí při jejich vykreslení s postupnou změnou parametru x:
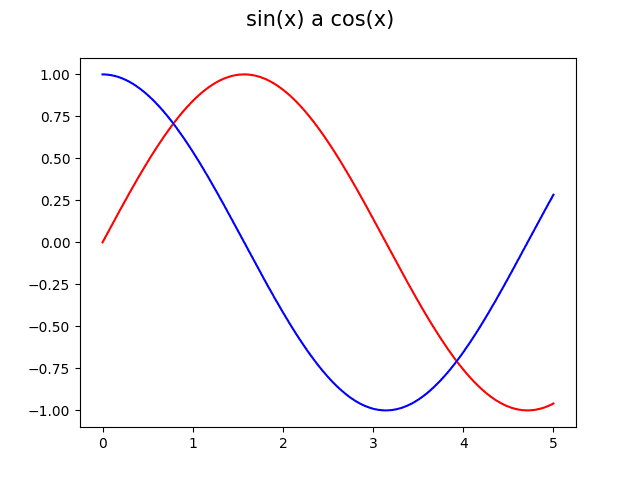
Obrázek 11: Průběh funkcí sin a cos.
Prakticky stejným způsobem můžeme vykreslit průběh funkcí S(x) a C(x) do stejného grafu, a to s následujícím výsledkem:
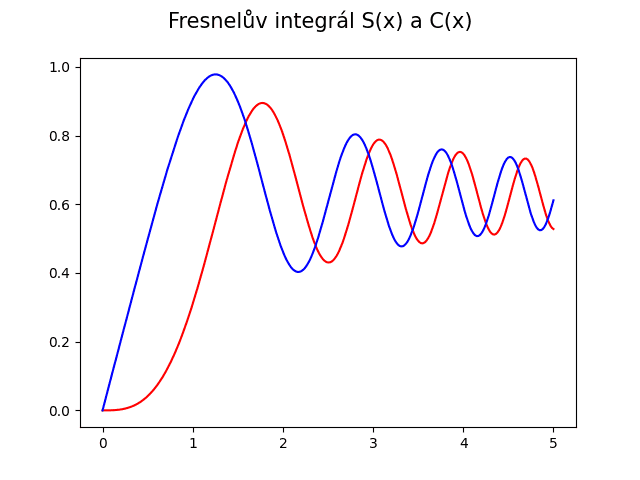
Obrázek 12: Porovnání průběhů funkcí S(x) a C(x).
Předchozí dva obrázky byly vykresleny touto dvojicí skriptů:
import numpy as np
import matplotlib.pyplot as plt
import math
# počet hodnot na x-ové ose
points = 300
# hodnoty na x-ové ose
x = np.linspace(0, 5, points)
# vektorizace předchozích funkcí
y_s = np.sin(x)
y_c = np.cos(x)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('sin(x) a cos(x)', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y_s, 'r-')
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y_c, 'b-')
# uložení grafu do rastrového obrázku
plt.savefig("sin_cos.png")
# zobrazení grafu
plt.show()
a:
import numpy as np
import matplotlib.pyplot as plt
import math
# počet hodnot na x-ové ose
points = 300
# integrační krok
step = 0.001
# hodnoty na x-ové ose
x = np.linspace(0, 5, points)
# výpočet Fresnelova integrálu S(x)
def fresnel_s(x):
result = 0
for t in np.arange(0, x, step):
result += math.sin(t**2)
return result*step
# výpočet Fresnelova integrálu C(x)
def fresnel_c(x):
result = 0
for t in np.arange(0, x, step):
result += math.cos(t**2)
return result*step
# vektorizace předchozích funkcí
fresnel_s_v = np.vectorize(fresnel_s)
fresnel_c_v = np.vectorize(fresnel_c)
# aplikace vektorizovaných funkcí na všechny x-ové hodnoty
y_s = fresnel_s_v(x)
y_c = fresnel_c_v(x)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Fresnelův integrál S(x) a C(x)', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y_s, 'r-')
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y_c, 'b-')
# uložení grafu do rastrového obrázku
plt.savefig("fresnel_c_s.png")
# zobrazení grafu
plt.show()
12. Vykreslení klotoidy s využitím funkcí S(x) a C(x)
Připomeňme si, že klasickou kružnici lze popsat parametrickou křivkou ve tvaru:
x=cos(t)
y=sin(t)
Vykreslení takto definované křivky je s využitím kombinace Python+Numpy+Matplotlib triviální.
Jaká křivka se ovšem nakreslí, pokud namísto cos a sin použijeme funkce C a S, tedy Fresnelovy integrály?:
x=C(t)
y=S(t)
Odpověď již zajisté znáte – vznikne právě klotoida:
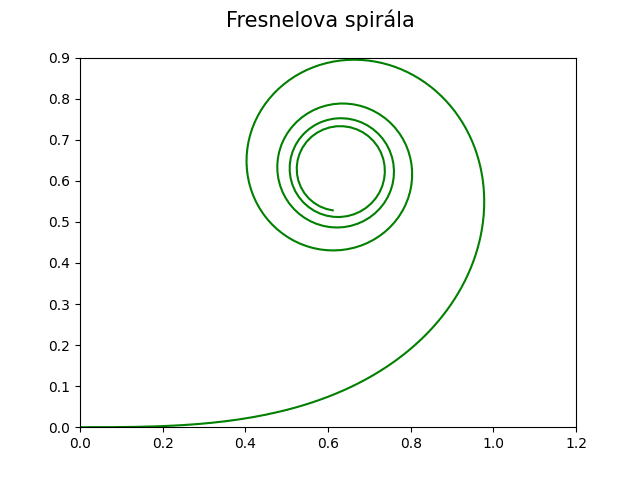
Obrázek 13: Klotoida.
Předchozí křivka byla vykreslena tímto demonstračním příkladem:
import numpy as np
import matplotlib.pyplot as plt
import math
# počet hodnot na x-ové ose
points = 300
# integrační krok
step = 0.001
# hodnoty na x-ové ose
x = np.linspace(0, 5, points)
# výpočet Fresnelova integrálu S(x)
def fresnel_s(x):
result = 0
for t in np.arange(0, x, step):
result += math.sin(t**2)
return result*step
# výpočet Fresnelova integrálu C(x)
def fresnel_c(x):
result = 0
for t in np.arange(0, x, step):
result += math.cos(t**2)
return result*step
# vektorizace předchozích funkcí
fresnel_s_v = np.vectorize(fresnel_s)
fresnel_c_v = np.vectorize(fresnel_c)
# aplikace vektorizovaných funkcí na všechny x-ové hodnoty
y_s = fresnel_s_v(x)
y_c = fresnel_c_v(x)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Fresnelův integrál S(x) a C(x)', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 1.2)
ax.set_ylim(0, 0.9)
# vrcholy na spirále
ax.plot(y_c, y_s, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("fresnel_spiral.png")
# zobrazení grafu
plt.show()
13. Obrazec s opakujícími se spirálami odvozený od Fresnelových integrálů
Na tomto místě uděláme malou odbočku od klasických spirál. Ukážeme si totiž skript, který vykreslí křivku (a to jedinou po částech spojitou křivku), která je obecně nekonečná a obsahuje opakující se spirály odvozené od Fresnelových integrálů. Výpočet je založen na následující iterační smyčce, v níž můžeme vidět, že se skutečně postupně numericky počítají hodnoty Fresnelových integrálů, ovšem přitom si zapamatujeme (a vykreslíme) i všechny mezivýsledky:
x = 0.0
y = 0.0
t = 0.0
for i in range(n):
t += 0.05
x += cos(t * t)
y += sin(t * t)
V případě, že pro dostatečně velké n do grafu vykreslíme sekvenci bodů [xi, yi] (popř. tyto body spojíme úsečkou), získáme tento zvláštní obrazec:
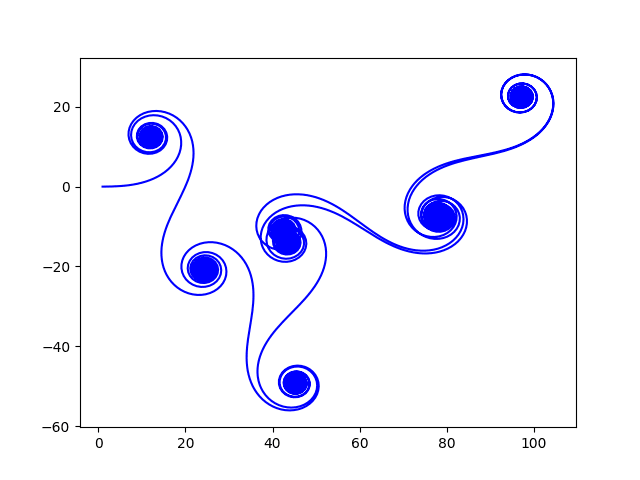
Obrázek 14: Obrazec s opakujícími se spirálami odvozený od Fresnelových integrálů.
Úplný zdrojový kód tohoto demonstračního příkladu vypadá následovně:
"""Fresnel fractal generator."""
import matplotlib.pyplot as plt
import numpy as np
from math import sin, cos
# Celkový počet vypočtených bodů
n = 10000
# Prozatím prázdná pole připravená pro uložení výsledků výpočtu.
xa = np.zeros((n,))
ya = np.zeros((n,))
x = 0.0
y = 0.0
t = 0.0
for i in range(n):
t += 0.05
x += cos(t * t)
y += sin(t * t)
xa[i] = x
ya[i] = y
# vrcholy na křivce pospojované úsečkami
plt.plot(xa, ya, 'b')
# uložení grafu do rastrového obrázku
plt.savefig("fresnel.png")
# zobrazení grafu
plt.show()
14. Evolventy
Další skupinou křivek, s níž se v tomto seriálu setkáme, jsou evolventy (v angličtině se setkáme i s pojmenováním involute). Tyto křivky vznikají odvalováním polopřímky okolo nějakého tvaru, což je (pro kružnici jako základní tvar) naznačeno na této animaci. Koncový bod polopřímky při jejím postupném odvalování kreslí příslušnou evolventu. Typů evolvent pochopitelně existuje značné množství, protože jejich tvar je určen základním tvarem, okolo něhož se polopřímka odvaluje.
Mezi různými tvary evolvent je z praktického hlediska nejdůležitější evolventa, která vznikne odvalováním polopřímky po kružnici. Tvar této evolventy je určen pouze poloměrem kružnice. Evolventa začíná přímo na kružnici a odvalováním vzniká spirála (pól spirály je určen středem kružnice). Část této spirály je použita v evolventním ozubení, což je v současnosti naprosto nejpoužívanější typ ozubení v praxi. Díky takto upravenému tvaru zubů je přenášený točivý moment konstantní, čímž se zabraňuje vibracím a velkému hluku. Přenos síly v případě, že mají zuby (resp. jejich činná část) tvar evolventy, je ukázán na této animaci.
15. Evolventa vzniklá odvalováním polopřímky po kružnici
Vraťme se však k evolventám z pohledu jejich vykreslování. Začneme tou nejpoužívanější evolventou vzniklou odvalováním polopřímky po kružnici. Trajektorii bodu tvořícího evolventu je možné v kartézské souřadné soustavě (nikoli tedy v soustavě polární, kterou jsme doposud používali) popsat těmito dvěma rovnicemi:
x = r*(cos(t) + t*sin(t))
y = r*(sin(t) – t*cos(t))
Evolventa pro kružnici je vypočtena a vykreslena následujícím skriptem:
"""Evolventa."""
import numpy as np
import matplotlib.pyplot as plt
# nezávislý parametr t
t = np.linspace(0.00, 3*np.pi, 100)
# koeficient evolventy
r = 10
# funkce evolventy
x = r*(np.cos(t) + t*np.sin(t))
y = r*(np.sin(t) - t*np.cos(t))
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Evolventa', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-100, 140)
ax.set_ylim(-80, 100)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("involute1.png")
# zobrazení grafu
plt.show()
Výsledný obrázek s evolventou vykreslený tímto demonstračním příkladem vypadá následovně:
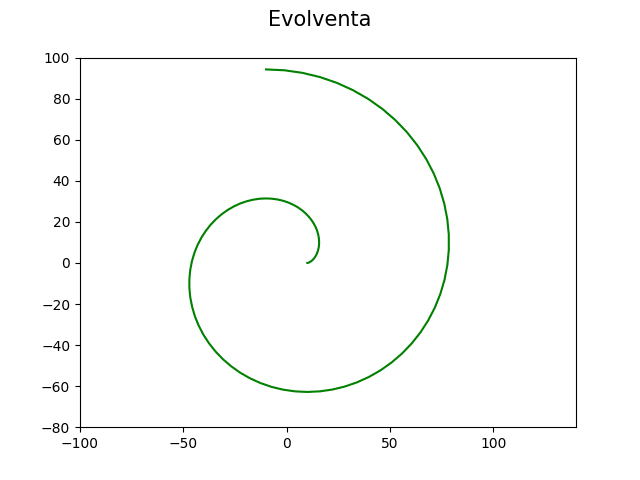
Obrázek 15: Evolventa vzniklá odvalováním polopřímky po kružnici.
16. Zakomponování kružnice, okolo níž se polopřímka odvaluje
Do obrázku je ovšem vhodné zakomponovat i kružnici, z níž je odvozen tvar evolventy. Předchozí zdrojový kód tedy nepatrně upravíme, a to tak, že do grafu vykreslíme dva průběhy souřadnic [x,y], přičemž jeden z průběhů představuje kružnici:
"""Evolventa."""
import numpy as np
import matplotlib.pyplot as plt
# nezávislý parametr t
t = np.linspace(0.00, 3*np.pi, 100)
# koeficient evolventy
r = 10
# funkce kružnice
xc = r*np.cos(t)
yc = r*np.sin(t)
# funkce evolventy
xe = r*(np.cos(t) + t*np.sin(t))
ye = r*(np.sin(t) - t*np.cos(t))
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Evolventa', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-100, 140)
ax.set_ylim(-80, 100)
# vrcholy na kružnici
ax.plot(xc, yc, 'r-')
# vrcholy na křivce pospojované úsečkami
ax.plot(xe, ye, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("involute2.png")
# zobrazení grafu
plt.show()
Výsledek nyní bude vypadat takto:
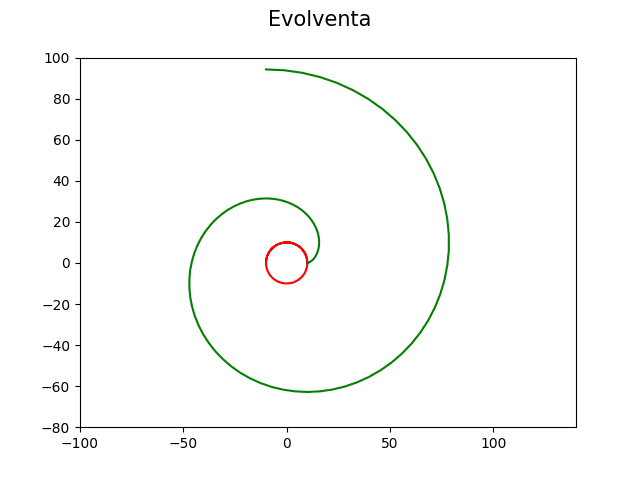
Obrázek 16: Evolventa i s kružnicí, která určuje její počátek i tvar.
17. Přidání koeficientu a do rovnice evolventy
Jak jsme se již řekli v předchozím textu, je tvar evolventy určen jediným koeficientem, a tím je poloměr kružnice r, po níž se odvaluje polopřímka. Ovšem začátek evolventy je taktéž modifikovatelný, a to po nepatrném zobecnění předchozích rovnic do podoby:
x = r*(cos(t) + (t-a)*sin(t))
y = r*(sin(t) – (t-a)*cos(t))
Následující skript vznikl zobecněním skriptu předchozího. Umožňuje volbu koeficientu a, jímž je specifikován počátek evolventy (na kružnici) a tím pádem i její natočení:
"""Evolventa."""
import numpy as np
import matplotlib.pyplot as plt
# nezávislý parametr t
t = np.linspace(0.00, 3*np.pi, 100)
# koeficient evolventy
r = 10
# funkce kružnice
xc = r*np.cos(t)
yc = r*np.sin(t)
def draw_evolvent(ax, a, style):
# funkce evolventy
xe = r*(np.cos(t) + (t-a)*np.sin(t))
ye = r*(np.sin(t) - (t-a)*np.cos(t))
# vrcholy na křivce pospojované úsečkami
ax.plot(xe, ye, style)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Evolventa', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-100, 140)
ax.set_ylim(-80, 100)
# vrcholy na kružnici
ax.plot(xc, yc, 'r-')
# vykreslení několika evolvent, pokaždé s jiným koeficientem a
draw_evolvent(ax, -0.5, 'g-')
draw_evolvent(ax, 0, 'm-')
draw_evolvent(ax, 0.5, 'c-')
# uložení grafu do rastrového obrázku
plt.savefig("involute3.png")
# zobrazení grafu
plt.show()
Výsledný obrázek s několika evolventami vykreslený tímto demonstračním příkladem bude vypadat následovně:
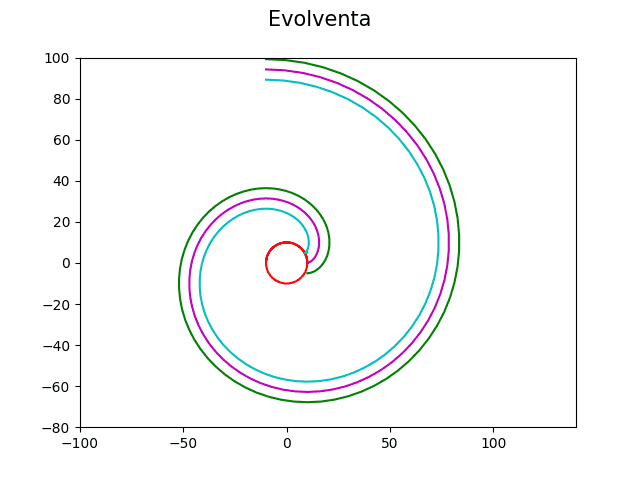
Obrázek 17: Vliv koeficientu a na tvar a otočení evolventy.
18. Evolventa vznikající odvalováním polopřímky po cykloidě
Víme již, že evolventa může vzniknout odvalováním po (prakticky) libovolném tvaru. Nemusí se tedy v žádném případě jednat pouze o kružnici. Podívejme se tedy nyní, jak budou vypadat rovnice popisující evolventu vzniknou odvalováním polopřímky po cykloidě (přičemž samotná cykloida vzniká odvalováním kružnice po přímce):
x = t + sin(t)
y = 3 + cos(t)
Pochopitelně si můžeme tuto evolventu nechat nakreslit, a to včetně cykloidy, která určuje její tvar:
"""Evolventa cykloidy."""
import numpy as np
import matplotlib.pyplot as plt
# nezávislý parametr t
t = np.linspace(0.00, 2*np.pi, 100)
# funkce cykloidy
xc = t-np.sin(t)
yc = 1-np.cos(t)
# funkce evolventy
xe = t + np.sin(t)
ye = 3 + np.cos(t)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Evolventa cykloidy', fontsize=15)
# vrcholy na cykloidě
ax.plot(xc, yc, 'r-')
# vrcholy na křivce pospojované úsečkami
ax.plot(xe, ye, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("involute4.png")
# zobrazení grafu
plt.show()
Z obrázku, který je vykreslen tímto demonstračním příkladem, je patrný jak výchozí bod evolventy, tak i to, že odvalování může probíhat v obou směrech:
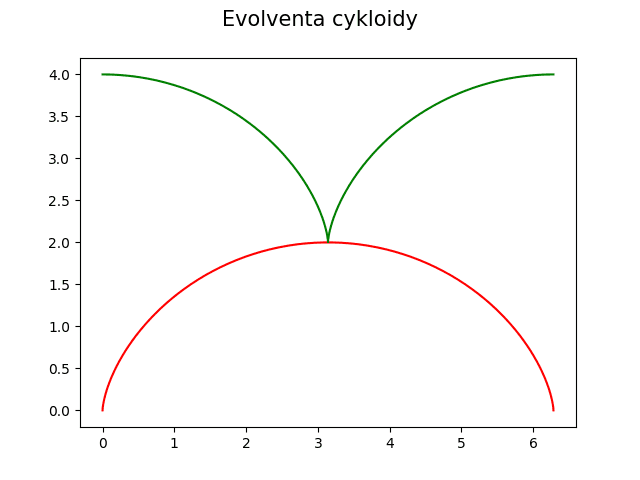
Obrázek 18: Evolventa, která vznikla odvalováním polopřímky po cykloidě.
19. Repositář s demonstračními příklady
Všechny dříve i dnes popisované demonstrační příklady určené pro Python 3 a knihovnu Matplotlib byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/presentations. Příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý (dnes již poměrně rozsáhlý) repositář:
20. Odkazy na Internetu
- The spiral: the eternal sign of the creative and organising principle at work in the universe
https://geoffjward.medium.com/the-spiral-the-eternal-sign-of-the-creative-and-organising-principle-at-work-in-the-universe-8889ba092300 - Speira(Spiral): one of the oldest and most powerful symbols in the world
https://www.greecehighdefinition.com/blog/speira-spiral-oldest-greek-symbols-in-the-world-ancient-greece - Spirals
https://web.stanford.edu/~siegelr/photography/spirals.html - Why Do Spirals Exist Everywhere in Nature?
https://www.samwoolfe.com/2014/05/spirals-everywhere.html - Patterns In Nature: Where to Spot Spirals
https://www.scienceworld.ca/stories/patterns-nature-where-spot-spirals/ - Spirals in Nature
https://extension.illinois.edu/blogs/naturalist-news/2021–06–23-spirals-nature - The Curves of Life (Dover Books Explaining Science)
https://www.amazon.com/Curves-Dover-Books-Explaining-Science/dp/048623701X - Famous Curves Index
https://mathshistory.st-andrews.ac.uk/Curves/ - Curve (Wikipedia)
https://en.wikipedia.org/wiki/Curve - Mathematical curves
https://www.2dcurves.com/index.html - Curves (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Curves.html - Smooth Curve (Wolfram MathWorld)
https://mathworld.wolfram.com/SmoothCurve.html - Spirals (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Spirals.html - An Interactive Introduction to Splines
https://ibiblio.org/e-notes/Splines/Intro.htm - Parabola
https://www.2dcurves.com/conicsection/conicsectionp.html - Hyperbola
https://www.2dcurves.com/conicsection/conicsectionh.html - Dioklova kisoida
https://cs.wikipedia.org/wiki/Dioklova_kisoida - Archimédova spirála
https://cs.wikipedia.org/wiki/Archim%C3%A9dova_spir%C3%A1la - Conchoid (mathematics)
https://en.wikipedia.org/wiki/Conchoid_(mathematics) - Algebraic curve
https://en.wikipedia.org/wiki/Algebraic_curve - Transcendental curve
https://en.wikipedia.org/wiki/Transcendental_curve - Spiral
https://en.wikipedia.org/wiki/Spiral - List of spirals
https://en.wikipedia.org/wiki/List_of_spirals - Hyperbolická spirála
https://cs.wikipedia.org/wiki/Hyperbolick%C3%A1_spir%C3%A1la - Hyperbolic Spiral
https://mathworld.wolfram.com/HyperbolicSpiral.html - Lituus (mathematics)
https://en.wikipedia.org/wiki/Lituus_(mathematics) - Spiral of Spirals Fractals 2 with Python Turtle (Source Code)
https://pythonturtle.academy/spiral-of-spirals-fractals-2-with-python-turtle-source-code/ - Cornu Spiral
http://hyperphysics.gsu.edu/hbase/phyopt/cornu.html - Spiral
https://www.2dcurves.com/spiral/spiral.html - Cornu’s spiral
https://www.johndcook.com/blog/2016/03/23/cornus-spiral/ - Cornu Spiral
https://mathworld.wolfram.com/CornuSpiral.html - Fresnel Integrals
https://mathworld.wolfram.com/FresnelIntegrals.html - Fresnel integral
https://en.wikipedia.org/wiki/Fresnel_integral - Algebraic Curves
https://mathworld.wolfram.com/topics/AlgebraicCurves.html - Elliptic Curves
https://mathworld.wolfram.com/topics/EllipticCurves.html - Eukleidovská konstrukce
https://cs.wikipedia.org/wiki/Eukleidovsk%C3%A1_konstrukce - Euclidean Constructions
http://www.cs.cas.cz/portal/AlgoMath/Geometry/PlaneGeometry/GeometricConstructions/EuclideanConstructions.htm - Kvadratura kruhu
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Trisekce úhlu
https://cs.wikipedia.org/wiki/Trisekce_%C3%BAhlu - Straightedge and compass construction
https://en.wikipedia.org/wiki/Straightedge_and_compass_construction - C.a.R.
http://car.rene-grothmann.de/doc_en/index.html - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/C.a.R. - CaRMetal (Španělsky a Francouzsky)
http://carmetal.org/index.php/fr/ - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/CaRMetal - Regular Polygon
http://mathforum.org/dr.math/faq/formulas/faq.regpoly.html - Geometric Construction with the Compass Alone
http://www.cut-the-knot.org/do_you_know/compass.shtml - Kvadratura kruhu (Wikipedie)
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Compass equivalence theorem
https://en.wikipedia.org/wiki/Compass_equivalence_theorem - Curves we (mostly) don't learn in high school (and applications)
https://www.youtube.com/watch?v=3izFMB91K_Q - Can You Really Derive Conic Formulae from a Cone? – Menaechmus' Constructions
https://www.maa.org/press/periodicals/convergence/can-you-really-derive-conic-formulae-from-a-cone-menaechmus-constructions - Apollonius of Perga
https://en.wikipedia.org/wiki/Apollonius_of_Perga - Catenary arch
https://en.wikipedia.org/wiki/Catenary_arch - Parabolic arch
https://en.wikipedia.org/wiki/Parabolic_arch - Wattova křivka
https://www.geogebra.org/m/gNh4bW9r - Model stegosaura byl získán na stránce
http://www.turbosquid.com/HTMLClient/FullPreview/Index.cfm/ID/171071/Action/FullPreview - Obrázek nohy dinosaura byl získán na adrese
http://perso.wanadoo.fr/rimasson/3d/leg.htm - Spirograph
https://en.wikipedia.org/wiki/Spirograph - Epicykloida
https://cs.wikipedia.org/wiki/Epicykloida - Hypocykloida
https://cs.wikipedia.org/wiki/Hypocykloida - Hypotrochoida
https://cs.wikipedia.org/wiki/Hypotrochoida - Superelipsoidy a kvadriky v POV-Rayi
https://www.root.cz/clanky/superelipsoidy-a-kvadriky-v-pov-rayi/ - Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers
https://elepa.files.wordpress.com/2013/11/fifty-famous-curves.pdf - Barr, A.H.: Superquadrics and Angle Preserving Transformations,
IEEE Computer Graphics and Applications, January 1981 - Bourke Paul: Quadrics,
July 1996 - Bourke Paul: Superellipse and Superellipsoid,
January 1990 - Faux, I.D. a Pratt, M.J.: Computational Geometry for Design and Manufacture,
Ellis Horwood Ltd., Wiley & Sons, 1979 - Wallace A.: Differential Topology,
Benjamin/Cummings Co., Reading, Massachussetts, USA, 1968 - Glossary of Bridge Terminology
http://sdrc.lib.uiowa.edu/eng/bridges/WaddellGlossary/GlossC.htm - Brachistochrona
https://cs.wikipedia.org/wiki/Brachistochrona - Missions: Cassini
https://solarsystem.nasa.gov/missions/cassini/overview/ - Giovanni Domenico Cassini
https://en.wikipedia.org/wiki/Giovanni_Domenico_Cassini - Cassini Ovals
https://mathworld.wolfram.com/CassiniOvals.html - Geocentrismus
https://cs.wikipedia.org/wiki/Geocentrismus - Who was Giovanni Cassini?
https://www.universetoday.com/130823/who-was-giovanni-cassini/ - Special plane curves
http://xahlee.info/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html - Why Does Slicing a Cone Give an Ellipse?
https://infinityisreallybig.com/2019/02/08/why-does-slicing-a-cone-give-an-ellipse/ - Interpolace
https://mathonline.fme.vutbr.cz/pg/Algoritmy/05_APROX_KRIVKY.htm - Lagrange Polynomial Interpolation
https://pythonnumericalmethods.berkeley.edu/notebooks/chapter17.04-Lagrange-Polynomial-Interpolation.html - Python Program for Lagrange Interpolation Method (with Output)
https://www.codesansar.com/numerical-methods/python-program-lagrange-interpolation-method.htm - Smooth Paths Using Catmull-Rom Splines
https://qroph.github.io/2018/07/30/smooth-paths-using-catmull-rom-splines.html - Lecture 11: Linear Interpolation Again – Bézier Curves
http://www.math.kent.edu/~reichel/courses/intr.num.comp.1/fall09/lecture12/bez.pdf - Geometrie/Úvod do křivek
https://cs.wikibooks.org/wiki/Geometrie/%C3%9Avod_do_k%C5%99ivek - B-Spline Curves and Surfaces (1)
http://www.cad.zju.edu.cn/home/zhx/GM/006/00-bscs1.pdf - Praktické ukázky možností aplikace Mandelbulber při tvorbě animací
https://www.root.cz/clanky/prakticke-ukazky-moznosti-aplikace-mandelbulber-pri-tvorbe-animaci/ - Kochanek–Bartels spline
https://en.wikipedia.org/wiki/Kochanek%E2%80%93Bartels_spline - class KochanekBartels
https://splines.readthedocs.io/en/latest/_modules/splines.html#KochanekBartels - Fraktály v počítačové grafice XVIII
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-xviii/ - Fraktály v počítačové grafice XVI
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-xvi/ - Fraktály v počítačové grafice IV
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iv/ - Systémy iterovaných funkcí a algoritmus náhodné procházky
https://www.root.cz/clanky/systemy-iterovanych-funkci-a-algoritmus-nahodne-prochazky/ - Pravděpodobnosti transformací v systémech iterovaných funkcí
https://www.root.cz/clanky/pravdepodobnosti-transformaci-v-systemech-iterovanych-funkci/ - Marie Alfred Cornu
https://en.wikipedia.org/wiki/Marie_Alfred_Cornu - Přechodnice
https://cs.wikipedia.org/wiki/P%C5%99echodnice - Evolventa
https://cs.wikipedia.org/wiki/Evolventa - Polopřímka
https://cs.wikipedia.org/wiki/Polop%C5%99%C3%ADmka - Involute (anglické označení pro evolventu)
https://en.wikipedia.org/wiki/Involute - Evolventní ozubení
https://cs.wikipedia.org/wiki/Evolventn%C3%AD_ozuben%C3%AD


























