Křivky popsané implicitní funkcí, animace křivek

Obsah

1. Křivky popsané implicitní funkcí

2. Hodnoty implicitní funkce v 3D grafu, průmět do z-ové roviny

3. Zobrazení křivek popsaných implicitní funkcí

4. Nejjednodušší, ovšem také jedna z nejdůležitějších křivek – přímka

5. Kuželosečky popsané implicitní funkcí

6. Elipsa v základní poloze a obecná elipsa

7. Parabola

8. Hyperbola s asymptotami otočenými o 45° i s asymptotami rovnoběžnými s osami souřadného systému

9. Od kuželoseček ke složitějším křivkám

10. Úloha z antického Řecka: průsečíky roviny s toroidem

11. Omyl vzniklý na základě geocentrismu – Cassiniho ovály (elipsy)

12. Tajemné eliptické křivky

13. Vytvoření katalogu eliptických křivek

14. Katalog eliptických křivek

15. Moderní pomůcka pro lepší studium křivek – animace

16. Animace průsečíku roviny s toroidem

17. Animace Cassiniho oválů s postupnou změnou vybraného koeficientu

18. Obsah čtvrté části seriálu

19. Repositář s demonstračními příklady

20. Odkazy na Internetu

1. Křivky popsané implicitní funkcí

Ve třetí části seriálu o křivkách, které můžeme nalézt v architektuře, přírodě, ale i v moderní počítačové grafice, se primárně budeme zabývat těmi křivkami, které je možné popsat implicitní funkcí (vyjádření v implicitním tvaru):

F(x,y)=0

Jedná se přitom o jeden ze tří nejčastěji používaných způsobů matematického popisu křivky ležící v rovině. Alternativní popisy jsou založeny na explicitní funkci:

y=f(x)

která má ovšem některá omezení, například nedokáže popsat ani tak jednoduchou křivku, jako je přímka rovnoběžná se souřadnou osou y.

Třetí matematický popis křivek používá bodovou funkci. V tomto případě jsou souřadnice na křivce vypočteny na základě parametru t ze vztahu:

x=f1(t)
y=f2(t)

kde f1 a f2 jsou na sobě nezávislé funkce.

Použití implicitní funkce pro popis křivek je nejobecnější a umožňuje nám popsat i útvary, které zpočátku za křivky nebyly považovány. Příkladem mohou být křivky vzniklé průsečíkem roviny a toroidu (anuloidu, oblounu). V některých případech totiž tento řez vede ke vzniku dvou zdánlivě samostatných uzavřených křivek (dnes samozřejmě známe nepřeberné množství podobných křivek).

2. Hodnoty implicitní funkce v 3D grafu, průmět do z-ové roviny

Vraťme se ještě jednou ke vztahu s implicitní funkcí, která popisuje křivku ležící v rovině:

F(x,y)=0

Pokud si z této rovnice vezmeme pouze levou část F(x,y), můžeme tuto funkci použít pro zobrazení 3D grafu:

z=F(x,y)

Trojrozměrné grafy je možné relativně bez problémů zobrazit i s využitím knihovny Matplotlib (viz zvýrazněný kód s udáním typu grafu). Příkladem může být zobrazení plochy odvozené od implicitní funkce paraboly:

"""Parabola zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(0, 8, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# implicitní funkce paraboly
f = 0.5
p = 2*f
z = x**2 - p*p*y
 
fig = plt.figure()
ax = fig.gca(projection='3d')
 
# titulek grafu
fig.suptitle('Parabola', fontsize=15)
 
# rozměry grafu ve směru osy x
ax.set_xlabel('X')
ax.set_xlim(-4, 4)
 
# rozměry grafu ve směru osy y
ax.set_ylabel('Y')
ax.set_ylim(0, 8)
 
# rozměry grafu ve směru osy z
ax.set_zlabel('Z')
ax.set_zlim(0, 10)
 
# uložení grafu do rastrového obrázku
plt.savefig("parabola1.png")
 
# zobrazení grafu
plt.show()

Výsledný graf by měl vypadat následovně:

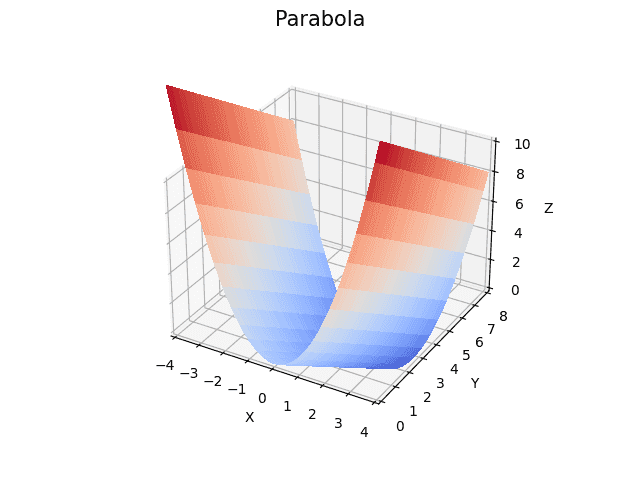
Obrázek 1: Funkce popisující parabolu v 3D zobrazení.

Knihovna Matplotlib dokáže do 3D grafu zobrazit i průmět zobrazované funkce (resp. jejích vybraných hodnot) do jednotlivých rovin. Přidáme tedy příkaz pro zobrazení tohoto průmětu (kontury) do z-ové roviny:

# zobrazení 3D grafu formou kontur
ax.contour3D(x, y, z, 50, cmap='binary')

Upravený skript tedy bude vypadat takto:

"""Parabola zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(0, 8, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# implicitní funkce paraboly
f = 0.5
p = 2*f
z = x**2 - p*p*y
 
fig = plt.figure()
ax = fig.gca(projection='3d')
 
# zobrazení 3D grafu formou kontur
ax.contour3D(x, y, z, 50, cmap='binary')
 
# titulek grafu
fig.suptitle('Parabola', fontsize=15)
 
# kontura: průmět na rovinu x-y
cset = ax.contour(x, y, z, zdir='z', offset=10)
 
# rozměry grafu ve směru osy x
ax.set_xlabel('X')
ax.set_xlim(-4, 4)
 
# rozměry grafu ve směru osy y
ax.set_ylabel('Y')
ax.set_ylim(0, 8)
 
# rozměry grafu ve směru osy z
ax.set_zlabel('Z')
ax.set_zlim(0, 10)
 
# uložení grafu do rastrového obrázku
plt.savefig("parabola2.png")
 
# zobrazení grafu
plt.show()

Nyní se do grafu zobrazí i průměty, resp. přesněji řečeno ty body na ploše, které mají shodnou z-ovou souřadnici:

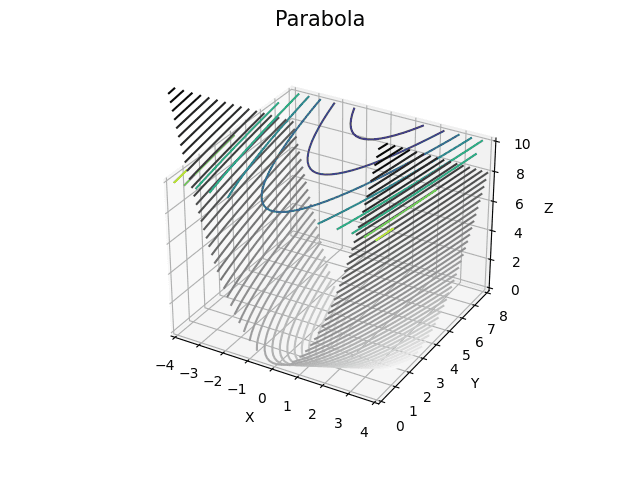
Obrázek 2: Parabola a její průměty do z-ové roviny.

Ještě lépe je výše uvedený postup patrný na zobrazení 3D grafu funkce, která je získána z implicitní funkce hyperboly. Nejprve si opět zobrazíme pouze 3D graf této funkce:

"""Hyperbola zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(-4, 4, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# implicitní funkce hyperboly
a = 1
z = (x**2 - y**2)/a**2 - 1
 
fig = plt.figure()
ax = fig.gca(projection='3d')
 
# zobrazení 3D grafu formou plochy
surface = ax.plot_surface(x, y, z, rstride=2, cstride=2, cmap=cm.coolwarm,
                          linewidth=0, antialiased=False)
 
# titulek grafu
fig.suptitle('Hyperbola', fontsize=15)
 
# rozměry grafu ve směru osy x
ax.set_xlabel('X')
ax.set_xlim(-4, 4)
 
# rozměry grafu ve směru osy y
ax.set_ylabel('Y')
ax.set_ylim(-4, 4)
 
# rozměry grafu ve směru osy z
ax.set_zlabel('Z')
ax.set_zlim(-10, 10)
 
# uložení grafu do rastrového obrázku
plt.savefig("hyperbola.png")
 
# zobrazení grafu
plt.show()

S výsledkem:

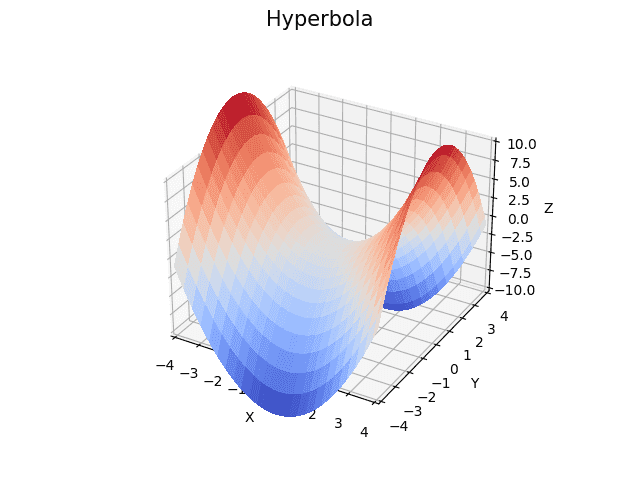
Obrázek 3: Funkce popisující hyperbolu v 3D zobrazení.

Nyní do tohoto grafu přidáme kontury promítnuté na z-ovou plochu:

"""Hyperbola zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(-4, 4, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# implicitní funkce hyperboly
a = 1
z = (x**2 - y**2)/a**2 - 1
 
fig = plt.figure()
ax = fig.gca(projection='3d')
 
# zobrazení 3D grafu formou plochy
surface = ax.plot_surface(x, y, z, rstride=2, cstride=2, cmap=cm.coolwarm,
                          linewidth=0, antialiased=False)
 
# titulek grafu
fig.suptitle('Hyperbola', fontsize=15)
 
# kontura: průmět na rovinu x-y
cset = ax.contour(x, y, z, zdir='z', offset=10)
 
# rozměry grafu ve směru osy x
ax.set_xlabel('X')
ax.set_xlim(-4, 4)
 
# rozměry grafu ve směru osy y
ax.set_ylabel('Y')
ax.set_ylim(-4, 4)
 
# rozměry grafu ve směru osy z
ax.set_zlabel('Z')
ax.set_zlim(-10, 10)
 
# uložení grafu do rastrového obrázku
plt.savefig("hyperbola.png")
 
# zobrazení grafu
plt.show()

S tímto výsledkem:

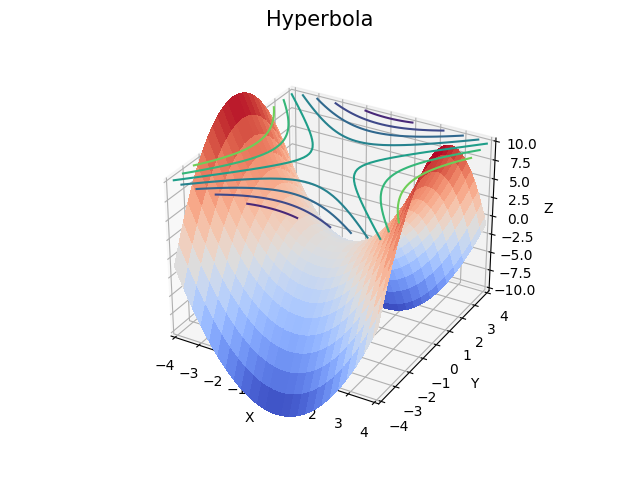
Obrázek 4: Hyperbola a její průměty do z-ové roviny.

3. Zobrazení křivek popsaných implicitní funkcí

Knihovna Matplotlib sice zdánlivě nepodporuje přímé zobrazení křivek popsaných implicitní funkcí, ovšem můžeme namísto toho použít malého triku – nechat si zobrazit kontury zvolené funkce typu z=F(x,y). A pokud pro konturu zvolíme hodnotu z=0, dostaneme kýžený výsledek: F(x,y)=0. Ukažme si tedy celý postup.

Nejprve si zvolíme rozsah hodnot na x-ové i y-ové ose a taktéž počet těchto hodnot. Získáme tak například vektor s hodnotami od –3 do 3, přičemž krok mezi nimi je zvolen tak, aby hodnot bylo celkem padesát (čím více, tím přesnější bude výsledná křivka):

# příprava vektorů pro konstrukci mřížky
x = np.linspace(-3, 3, 50)
y = np.linspace(-3, 3, 50)

V dalším kroku vytvoříme matici (nebo chcete-li mřížku) dvojic x,y. Každá hodnota této matice (mřížky) bude obsahovat souřadnici [x,y] ve výše zadaném rozsahu. V našem konkrétním případě získáme mřížku 50×50 dvojic:

# konstrukce mřížky
x, y = np.meshgrid(x, y)

Knihovna Numpy podporuje operace s celými vektory nebo maticemi, takže můžeme nadefinovat implicitní funkci:

# implicitní funkce
z = x**2-2*x*y+y**2-2*x

Tato funkce je aplikována na matici (trošku zjednodušuji), takže výsledkem bude matice z-ových hodnot. Nyní si zvolíme, které z těchto z-ových hodnot chceme zobrazit (a spojit shodné hodnoty):

# hodnoty, které se mají zvýraznit na isoploše
levels = np.arange(1, 5, 0.5)

Vlastní vykreslení kontur je již jednoduché:

# vykreslení implicitní funkce
ax.contour(x, y, z, levels)

Výsledný graf bude obsahovat trojici křivek, protože jsme zvolili trojici hodnot v proměnné levels:

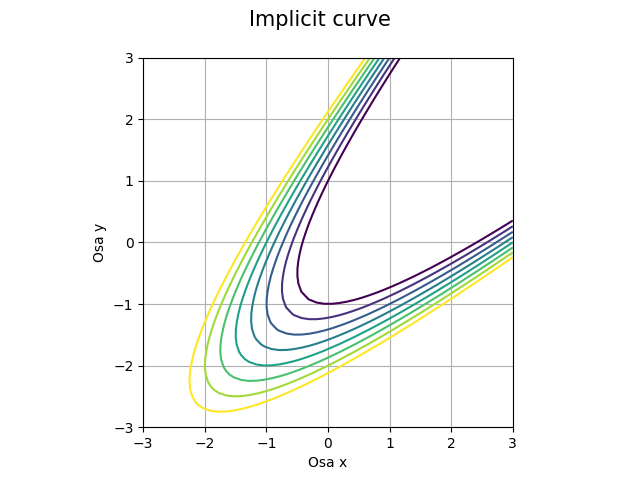
Obrázek 5: Křivky popsané implicitní funkcí.

Úplný skript pro vykreslení vypadá následovně:

"""Implicitně zadaná křivka."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-3, 3, 50)
y = np.linspace(-3, 3, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# implicitní funkce
z = x**2-2*x*y+y**2-2*x
 
# hodnoty, které se mají zvýraznit na isoploše
levels = np.arange(1, 5, 0.5)
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Implicit curve', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("implicit.png")
 
# zobrazení grafu
plt.show()

Samozřejmě nám nic nebrání použít i složitější funkci, tentokrát založenou na goniometrických funkcích:

# implicitní funkce
z = np.sin(x**2) - np.cos(y**2)

S výsledkem:

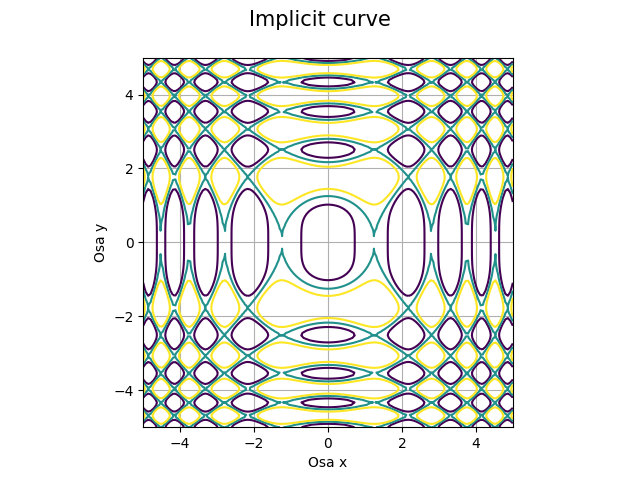
Obrázek 6: Křivka popsaná implicitní funkcí.

Opět si ukažme celý skript:

"""Implicitně zadaná křivka."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-5, 5, 150)
y = np.linspace(-5, 5, 150)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# implicitní funkce
z = np.sin(x**2) - np.cos(y**2)
 
# hodnoty, které se mají zvýraznit na isoploše
levels = [-0.5, 0, 0.5]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Implicit curve', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("implicit3.png")
 
# zobrazení grafu
plt.show()

4. Nejjednodušší, ovšem také jedna z nejdůležitějších křivek – přímka

Nejjednodušší křivkou (přesněji řečeno nesingulární křivkou), kterou nalezneme jak v architektuře, tak i v přírodě, je přímka popř. její část nazvaná úsečka. Přímku lze popsat implicitní funkcí, kterou si pravděpodobně pamatujete ze školy pod jménem obecná rovnice přímky:

ax + by + c = 0

Tato rovnice je sice skutečně velmi jednoduchá, ovšem má několik důležitých vlastností. Zejména nám umožňuje zcela bez problémů definovat přímky rovnoběžné se souřadnými osami – postačuje nastavit jeden z koeficientů a nebo b na nulu. To například není při použití explicitní funkce možné v případě přímky rovnoběžné s y-ovou osou. Dále dvojice [a,b] definuje normálový vektor přímky, který je na ni kolmý. Dokážeme tudíž přesně popsat jakkoli natočenou přímku vhodnou volbou těchto hodnot. Poslední parametr c přímku v rovině posouvá tak, aby procházela kýženým bodem.

Současně se jedná o rovnici se dvěma neznámými x a y. V případě, že budeme řešit protnutí dvou přímek, budeme vlastně řešit dvě rovnice o dvou neznámých. A jejich vyřešením získáme souřadnice [x,y] hledaného bodu (řešení nemusí existovat, což nám říká, že jsou přímky rovnoběžné). Podobně lze řešit protnutí přímky a kuželosečky, vzdálenost bodu od přímky atd. – to vše s využitím jednoduché lineární funkce.

Skript pro vykreslení přímky zadané implicitní funkcí:

"""Úsečka zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-2, 2, 10)
y = np.linspace(-2, 2, 10)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficienty úsečky
A = 1
B = 1
C = 0
 
# implicitní funkce úsečky
z = A*x + B*y + C
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Úsečka', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("line1.png")
 
# zobrazení grafu
plt.show()

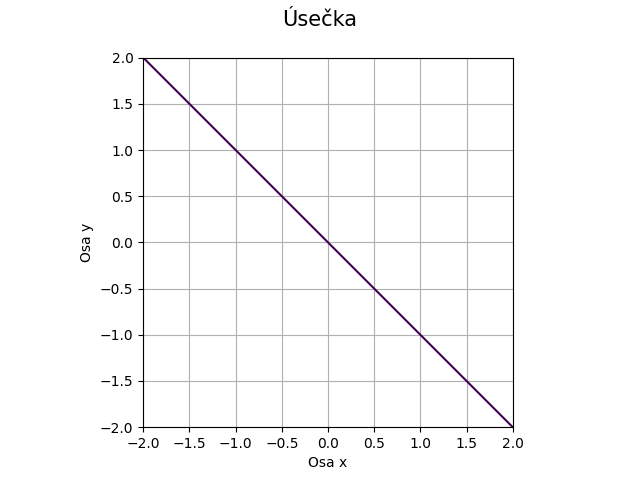
Obrázek 7: Přímka s koefeicienty a=1, b=1, c=0.

Změnou koeficientů a a b dosáhneme natočení přímky:

"""Úsečka zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-2, 2, 10)
y = np.linspace(-2, 2, 10)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficienty úsečky
A = -2
B = 1
C = 0
 
# implicitní funkce úsečky
z = A*x + B*y + C
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Úsečka', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("line2.png")
 
# zobrazení grafu
plt.show()

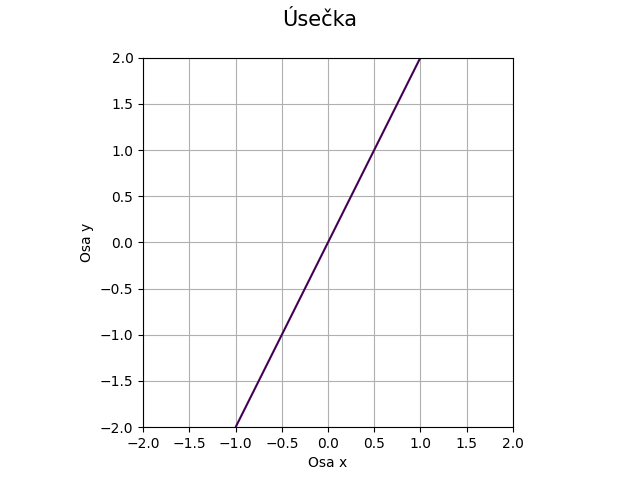
Obrázek 8: Přímka s koefeicienty a=-2, b=1, c=0.

5. Kuželosečky popsané implicitní funkcí

Po přímce jsou nejjednoduššími křivkami, které byly mimochodem zkoumány a popsány již ve starověku, kuželosečky, tj. křivky, které vzniknou průnikem roviny a kužele (přesněji řečeno dvou kuželů se společnou osou, které se dotýkají svými vrcholy – nesmíme totiž zapomenout na obě větve hyperboly). Podle vzájemného postavení roviny a kužele/kuželů může vzniknout skutečná kuželosečka (kružnice, elipsa, parabola či hyperbola) nebo takzvaná degenerovaná kuželosečka (přímka, dvě přímky popř. bod). Ovšem v dalším textu nás budou zajímat jen skutečné kuželosečky.

Všechny kuželosečky je možné popsat implicitní funkcí:

Ax² + Bxy + Cy² + Dx + Ey + F = 0

Ve skutečnosti jsou některé členy pro běžné kuželosečky nulové či mají hodnotu jedna a navíc mají speciální pojmenování či označení, což si ihned ukážeme na té nejjednodušší kuželosečce – kružnici – která je popsána všem známou funkcí (která mimochodem do značné míry souvisí s Pythagorovou větou):

x² + y² – r² = 0

kde r je poloměr kružnice.

Kružnici lze s využitím tohoto vzorce a se znalostmi možností knihovny Matplotlib popsanými ve třetí kapitole zobrazit velmi snadno:

"""Kružnice zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-2, 2, 10)
y = np.linspace(-2, 2, 10)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficienty kružnice
r = 1
 
# implicitní funkce kružnice
z = x**2 + y ** 2 - r ** 2
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Kružnice', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("circle1.png")
 
# zobrazení grafu
plt.show()

S tímto výsledkem:

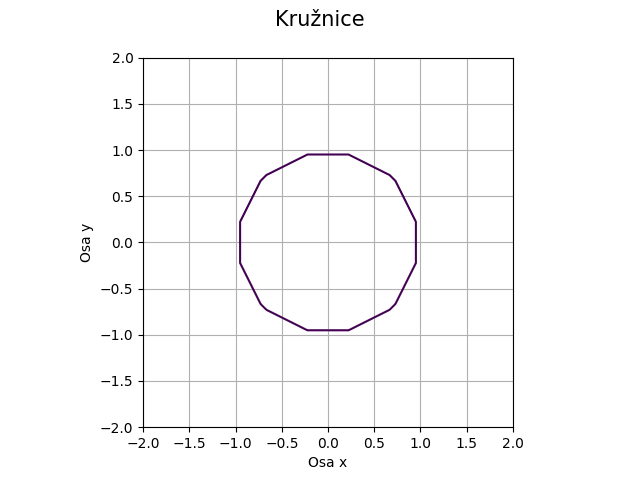
Obrázek 9: Kružnice při volbě malé hustoty mřížky).

Z předchozího obrázku je patrné, že musíme zvětšit hustotu mřížky, aby bylo zobrazení kvalitní:

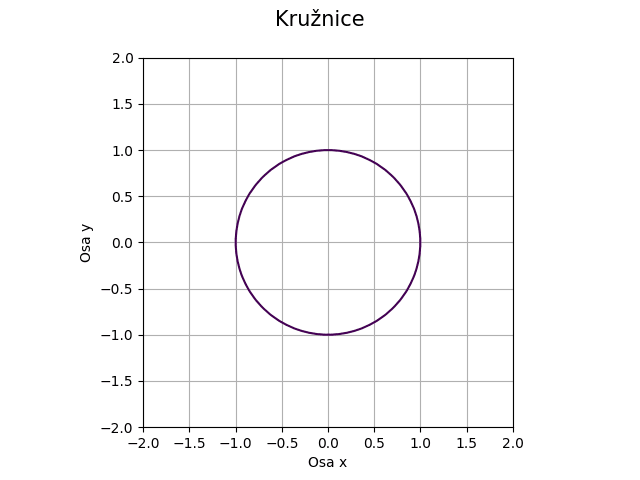
Obrázek 10: Kružnice při volbě větší hustoty mřížky).

6. Elipsa v základní poloze a obecná elipsa

Další kuželosečkou je elipsa. Mimochodem – důkaz toho, že řezem roviny a kužele vznikne skutečně elipsa (kužel přece nemá tak pravidelný plášť jako válec, takže by na první pohled mělo vzniknou nějaké „vajíčko“), je poměrně elegantní a můžete ho nalézt na stránce Why Does Slicing a Cone Give an Ellipse?, i s odkazy na videa s popisem doplněným animacemi.

Elipsa je popsána implicitní funkcí:

x²/a² + y²/b² – 1 = 0

kde a a b jsou poměry obou poloos.

Podívejme se nyní na způsob vykreslení elipsy popsané implicitní funkcí. V tomto příkladu jsou délky poloos nastaveny na hodnoty 3 a 2 délkové jednotky:

"""Elipsa zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(-4, 4, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficienty elipsy
a = 3
b = 2
 
# implicitní funkce elipsy
z = x**2/a**2 + y ** 2/b**2 - 1
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Elipsa', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("ellipse1.png")
 
# zobrazení grafu
plt.show()

Tento skript zobrazí graf s osově symetrickou elipsou:

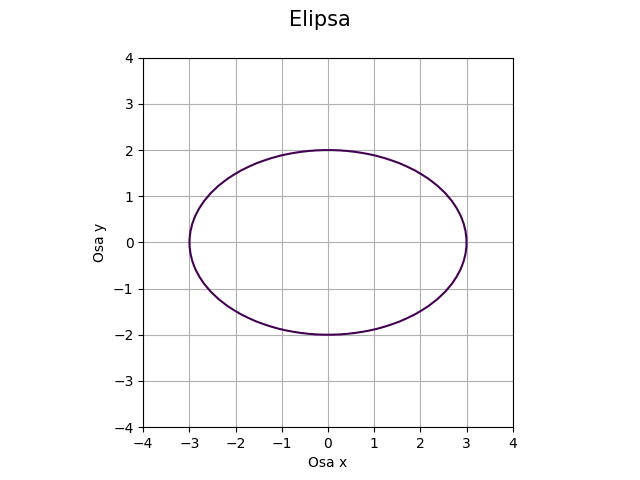
Obrázek 11: Osově symetrická elipsa.

V případě, že se má vykreslit obecná elipsa (tedy elipsa libovolně natočená a popř. i posunutá), je implicitní funkce složitější, což je ostatně velmi dobře patrné z následujícího skriptu. V něm nejdříve na základě parametrů obecné elipsy spočítáme pomocné koeficienty a z nich koeficienty A až E použité při popisu obecné elipsy:

"""Obecná elipsa zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(-4, 4, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# parametry obecné elipsy
x0 = 0
y0 = 0
a = 2
b = 3
phi = -np.pi/4
 
# pomocné členy
a2 = a**2
b2 = b**2
sin2 = np.sin(phi)**2
cos2 = np.cos(phi)**2
 
A = a2 * sin2 + b2 * cos2
B = 2*(b2-a2)*np.sin(phi)*np.cos(phi)
C = a2*cos2 + b2*sin2
D = -2*A*x0 - B*y0
E = -B*x0 - 2*C*y0
F = A*x0**2 + B*x0*y0 + C*y0**2 - a2*b2
 
# implicitní funkce obecné elipsy
z = A* x**2 + B * x * y + C * y**2 + D * x + E * y + F
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Elipsa', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("ellipse3.png")
 
# zobrazení grafu
plt.show()

Takto vykreslená obecná elipsa bude vypadat následovně:

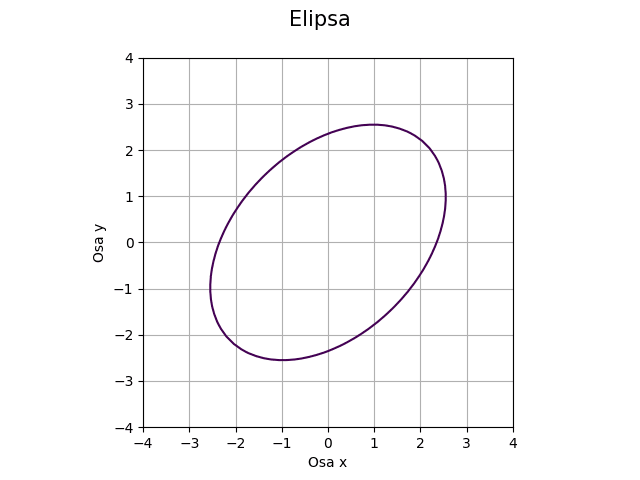
Obrázek 12: Obecná elipsa.

7. Parabola

Další kuželosečkou známou již v antickém Řecku je parabola, kterou lze implicitní funkcí popsat následovně:

x² – 2py = 0

kde p=2f

Následuje příklad skriptu pro vykreslení paraboly:

"""Parabola zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(0, 8, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficienty paraboly
f = 0.5
p = 2*f
 
# implicitní funkce paraboly
z = x**2 - p*p*y
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Parabola', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("parabola1.png")
 
# zobrazení grafu
plt.show()

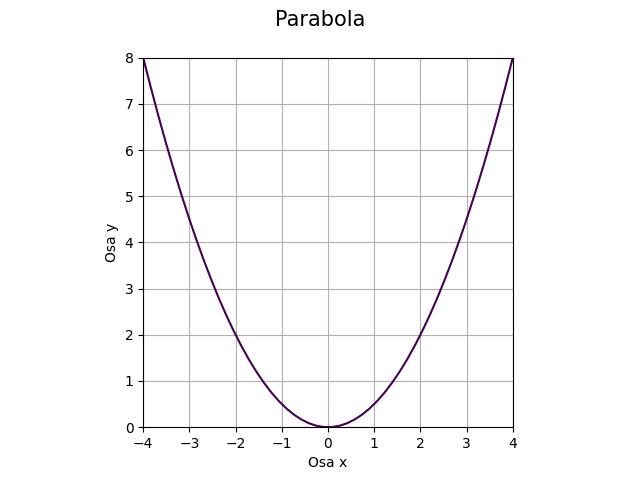
Obrázek 13: Parabola.

8. Hyperbola s asymptotami otočenými o 45° i s asymptotami rovnoběžnými s osami souřadného systému

Poslední běžnou (nesingulární) kuželosečkou je hyperbola. Můžeme ji vykreslit otočenou o 45° (její asymptoty tedy svírají s osami souřadného systému tento úhel) s využitím jednoduchého vzorečku:

(x² – y²)/a² – 1 = 0

Viz též následující skript pro vykreslení hyperboly:

"""Hyperbola zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(-4, 4, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficient hyperboly
a = 1
 
# implicitní funkce hyperboly
z = (x**2 - y**2)/a**2 - 1
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Hyperbola', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("hyperbola1.png")
 
# zobrazení grafu
plt.show()

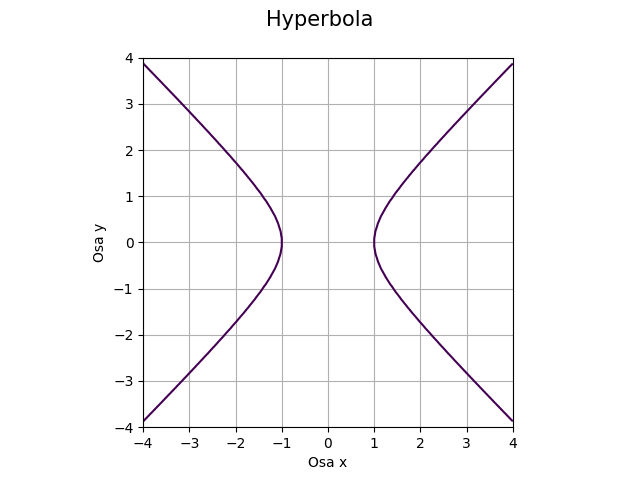
Obrázek 14: Hyperbola otočená o 45°.

Pro neotočenou hyperbolu ovšem použijeme odlišný vzorec:

a/x – y = 0

Opět viz následující skript, který hyperbolu vykreslí:

"""Hyperbola zadaná implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-10, 10, 50)
y = np.linspace(-10, 10, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficient hyperboly
a = 4
 
# implicitní funkce hyperboly
z = a/x - y
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Hyperbola', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("hyperbola2.png")
 
# zobrazení grafu
plt.show()

Výsledek:

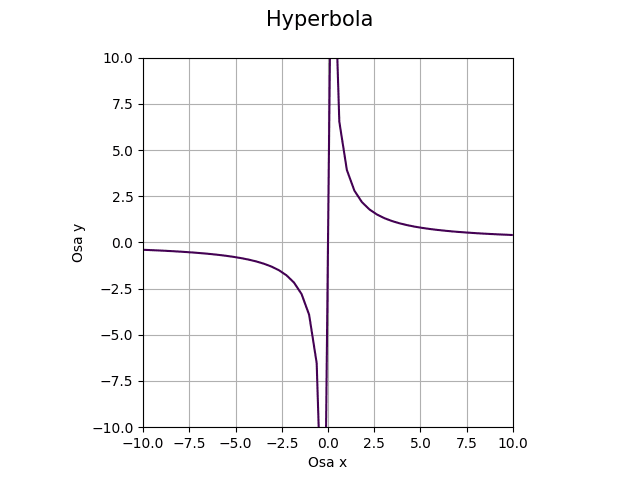
Obrázek 15: Hyperbola tak, jak je zobrazena ve škole.

9. Od kuželoseček ke složitějším křivkám

V úvodní části tohoto seriálu jsme si mj. řekli, že kuželosečky, tedy křivky získané průnikem roviny a kužele, byly zkoumány již v antickém Řecku. Tyto křivky objevil Menaechmus okolo roku 350 př.n.l. a na jeho spisy navázal Eukleidés a později i Apollónios z Pergy (přibližně 200 př.n.l.). Právě na studiu kuželoseček se ukázalo, že křivky nejsou pouze „křivé čáry“ vytvořené jediným tahem pera, protože hyperbola má dvě oddělené větve (ty objevil právě Apollónios, zatímco Eukleidés pracoval pouze s jednou větví). Z doby antického Řecka však pochází studie o dalších zajímavých křivkách – viz navazující kapitoly.

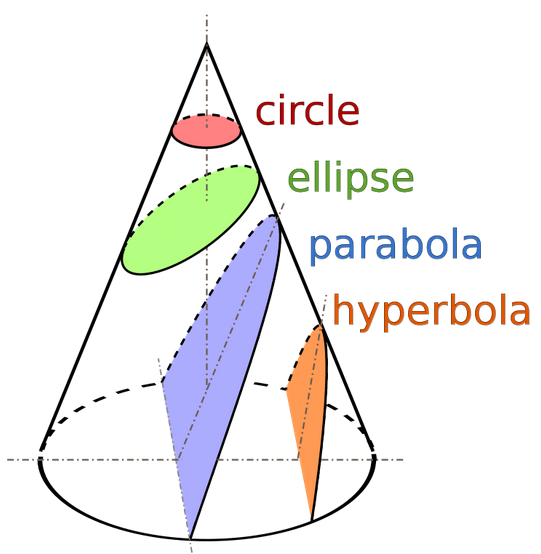
Obrázek 16: Nesingulární kuželosečky, zde pro zjednodušení nakresleny na jediné „větvi“ kužele, takže i hyperbola zde má jedinou větev.

10. Úloha z antického Řecka: průsečíky roviny s toroidem

V antickém Řecku se učenci nejdříve zabývali geometrickými konstrukcemi s kružítkem a pravítkem, posléze zkoumali i vlastnosti všech čtyř kuželoseček. Ovšem již okolo roku 150 př.n.l. zkoumal učenec Perseus (nikoli ovšem bájný hrdina) průsečíky roviny s toroidem (anuloidem), tedy s tvarem, který mají i „donuty“ milované Homerem Simpsonem. Perseus tak navázal na práci Apollónia z Perga, jenž zkoumal kuželosečky. Průsečíky roviny a toroidu mají složitější tvar, než běžné kuželosečky, protože v některých případech se toroid rozřízne tak, že vznikne křivka s dvojicí oddělených smyček, což vedlo k obecnějšímu pohledu na křivky:

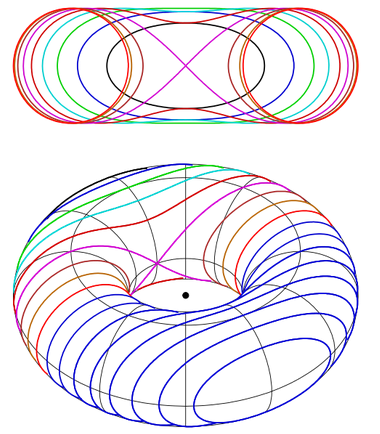
Obrázek 17: Řezy toroidem/anuloidem.

Implicitní funkce řezu je relativně jednoduchá:

(x² + y²)² – dx² – ey² – f = 0

Základní koeficienty jsou a, b a c, které se však ve výše uvedené funkci nevyskytují, protože jsou od nich odvozeny pomocné koeficienty d, e a f, které již v implicitní funkci nalezneme:

d = 2(a²+b²-c²)
e = 2(a²-b²-c²)
f = -(a+b+c)(a+b-c)(a-b+c)(a-b-c)

Příklad první křivky:

"""Křivka získaná řezem toru."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(-4, 4, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# parametry toru
a = 1
b = 2
c = 0
 
# pomocné členy
d = 2*(a**2+b**2-c**2)
e = 2*(a**2-b**2-c**2)
f = -(a+b+c)*(a+b-c)*(a-b+c)*(a-b-c)
 
# implicitní funkce křivky
z = (x**2+y**2)**2 - d*x**2 - e*y**2 - f
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Spiric', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("spiric1.png")
 
# zobrazení grafu
plt.show()

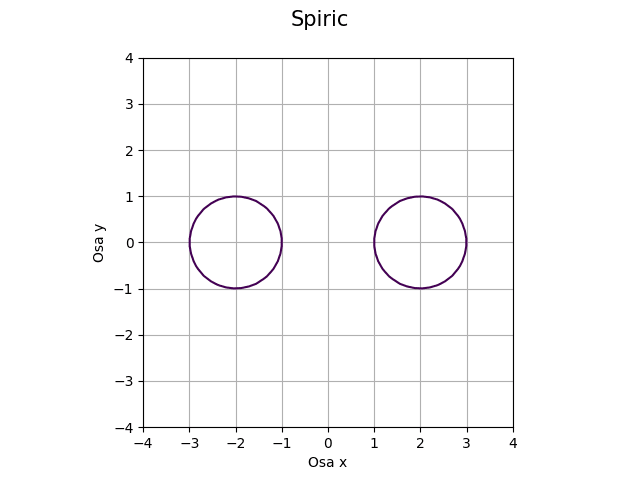
Obrázek 18: Řez toroidu s koeficienty a=1, b=2, c=0.

"""Křivka získaná řezem toru."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 150)
y = np.linspace(-4, 4, 150)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# parametry toru
a = 1
b = 2
c = 0.99
 
# pomocné členy
d = 2*(a**2+b**2-c**2)
e = 2*(a**2-b**2-c**2)
f = -(a+b+c)*(a+b-c)*(a-b+c)*(a-b-c)
 
# implicitní funkce křivky
z = (x**2+y**2)**2 - d*x**2 - e*y**2 - f
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Spiric', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("spiric2.png")
 
# zobrazení grafu
plt.show()

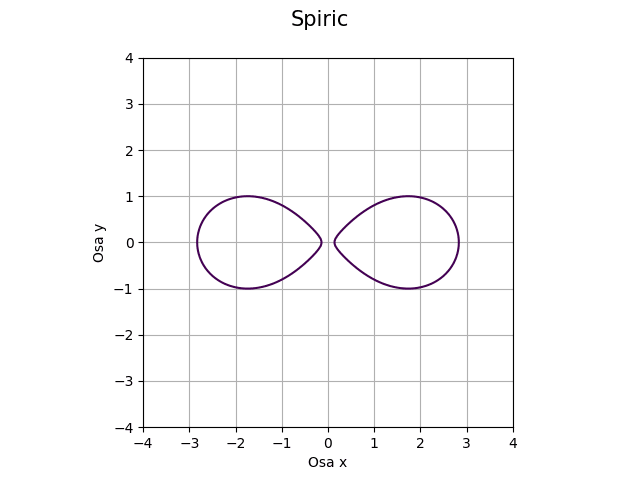
Obrázek 19: Řez toroidu s koeficienty a=1, b=2, c=0.99.

"""Křivka získaná řezem toru."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 150)
y = np.linspace(-4, 4, 150)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# parametry toru
a = 1
b = 2
c = 1.00
 
# pomocné členy
d = 2*(a**2+b**2-c**2)
e = 2*(a**2-b**2-c**2)
f = -(a+b+c)*(a+b-c)*(a-b+c)*(a-b-c)
 
# implicitní funkce křivky
z = (x**2+y**2)**2 - d*x**2 - e*y**2 - f
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Spiric', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("spiric3.png")
 
# zobrazení grafu
plt.show()

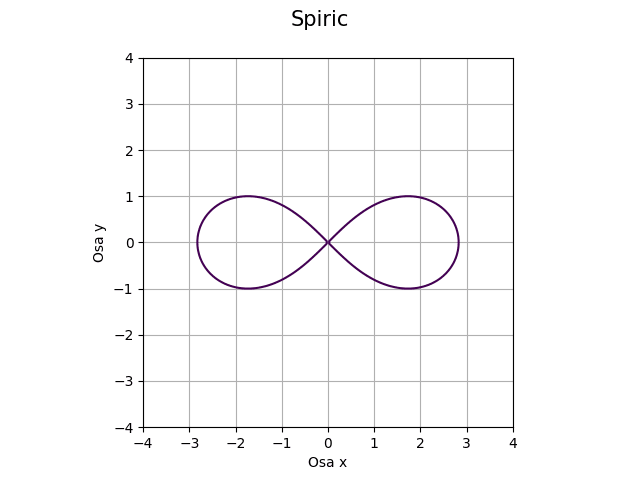
Obrázek 20: Řez toroidu s koeficienty a=1, b=2, c=1.

11. Omyl vzniklý na základě geocentrismu – Cassiniho ovály (elipsy)

Od antického Řecka se v čase přesuneme na konec sedmnáctého století. V té době slavný matematik a astronom Giovanni Domenico Cassini od řezu toroidu popsaného výše odvodil křivku, které se dnes říká Cassiniho ovál nebo taktéž Cassiniho elipsa. Cassini, který mj. objevil měsíce Saturnu či zjistil, že jeho prstenec je ve skutečnosti složen z několika prstenců (ostatně právě proto je po něm pojmenována sonda, která mířila k Saturnu), okolo roku 1680 ještě předpokládal, že Keplerův heliocentrický model je neplatný a navrhl namísto něj upravit geocentrický model, nyní již na základě přesnějších naměřených dat. Ovšem v takovém případě se Slunce nemůže okolo Země pohybovat po obyčejné kružnici – to neodpovídá měření. Proto Cassini navrhl svoji křivku – Cassiniho ovál, který sice odpovídal měření, ale jednalo se o umělý konstrukt. Nicméně i přesto má jeho křivka nezastupitelné místo v historii.

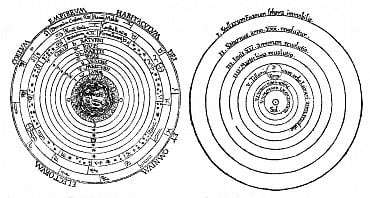
Obrázek 21: Geocentrický versus heliocentrický model vesmíru z dobové literatury.

Tvar Cassiniho oválu je určen dvojicí koeficientů a a c, které vystupují v implicitní funkci:

(x² + y²)² – 2c(x² – y²) – (a⁴ – c⁴)

Skript pro vykreslení Cassiniho oválů:

"""Cassiniho ovál zadaný implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-2, 2, 50)
y = np.linspace(-2, 2, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficienty Cassiniho oválu
a = 1.1
c = 1.0
 
# implicitní funkce Cassiniho oválu
z = (x**2 + y ** 2) ** 2 - 2*c*(x**2 - y**2) - (a**4 - c**4)
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Cassiniho ovál', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("cassini1.png")
 
# zobrazení grafu
plt.show()

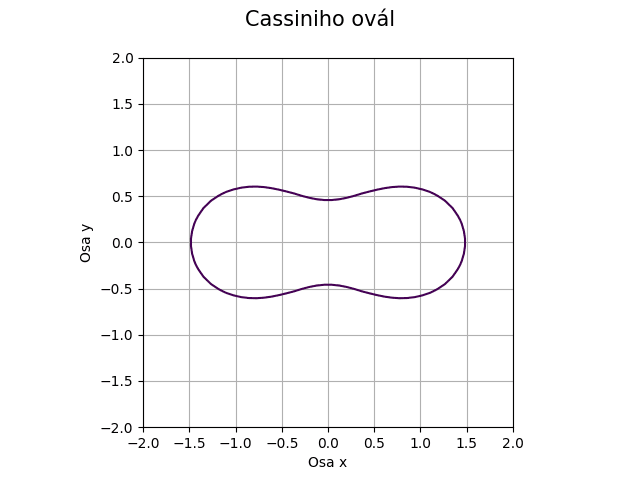
Obrázek 22: Cassiniho ovál – jediná uzavřená smyčka.

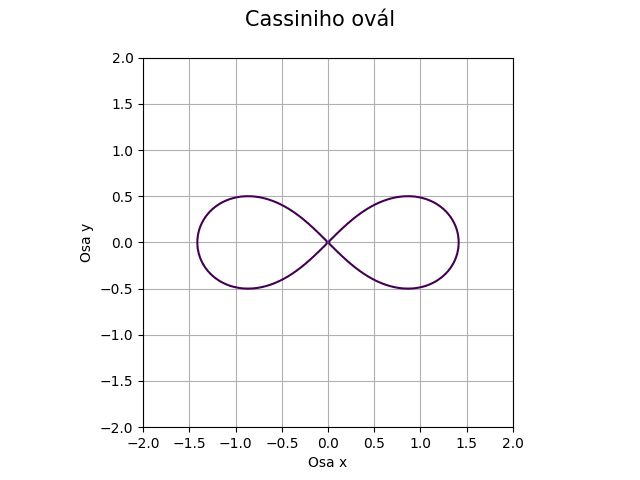
Obrázek 23: Cassiniho ovál – limitní případ.

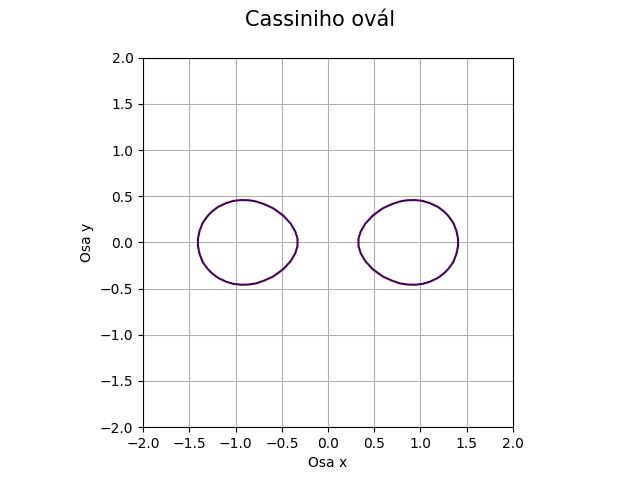
Obrázek 24: Cassiniho ovál – dvě uzavřené smyčky.

12. Tajemné eliptické křivky

Prozatím jen ve stručnosti se dnes musíme zmínit i o eliptických křivkách, které mají své místo v kryptografii (budeme se jim věnovat v samostatném článku). Jedná se o křivky popsané implicitní funkcí:

x³ + a*x + b – y² = 0

Eliptickou křivku určenou parametry a a b můžeme vykreslit tímto skriptem:

"""Eliptická křivka."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-2, 2, 50)
y = np.linspace(-2, 2, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficienty eliptické křivky
a = -2.0
b = 0.0
 
# implicitní funkce eliptické křivky
z = x**3 + a*x + b - y**2
 
# hodnota, která se má zvýraznit na isoploše
levels = [0]
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Eliptická křivka', fontsize=15)
 
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
 
# zobrazit mřížku
ax.grid(True)
 
# zachovat poměr stran
ax.axis('scaled')
 
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
 
# uložení grafu do rastrového obrázku
plt.savefig("elliptic1.png")
 
# zobrazení grafu
plt.show()

S tímto výsledkem:

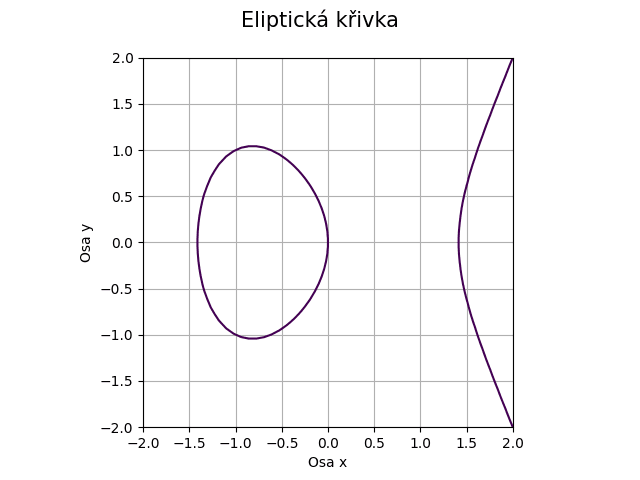
Obrázek 26: Eliptická křivka.

13. Vytvoření katalogu eliptických křivek

Eliptické křivky pro parametr a v rozsahu –2 až 1 a parametr b v rozsahu –1 až 2 lze vykreslit následujícím skriptem:

"""Katalog eliptických křivek."""
 
import numpy as np
import matplotlib.pyplot as plt
 
def plot_elliptic_curve(a, b):
        # příprava vektorů pro konstrukci mřížky
    x = np.linspace(-2, 2, 150)
    y = np.linspace(-2, 2, 150)
 
        # konstrukce mřížky
    x, y = np.meshgrid(x, y)
 
        # implicitní funkce eliptické křivky
    z = x**3 + a*x + b - y**2
 
        # hodnota, která se má zvýraznit na isoploše
    levels = [0]
 
        # rozměry grafu při uložení: 640x480 pixelů
    fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
        # titulek grafu
    fig.suptitle('Eliptická křivka', fontsize=15)
 
        # vykreslení implicitní funkce
    ax.contour(x, y, z, levels)
 
        # zobrazit mřížku
    ax.grid(True)
 
        # zachovat poměr stran
    ax.axis('scaled')
 
        # popisek os
    plt.xlabel('Osa x')
    plt.ylabel('Osa y')
 
        # uložení grafu do rastrového obrázku
    plt.savefig("elliptic_{}_{}.png".format(a, b))
 
 
for b in range(-1, 3):
    for a in range(-2, 2):
        plot_elliptic_curve(a, b)

14. Katalog eliptických křivek

Následuje slíbený minikatalog, z něhož je patrné, jak se mění jak tvar, tak i topologie křivek:

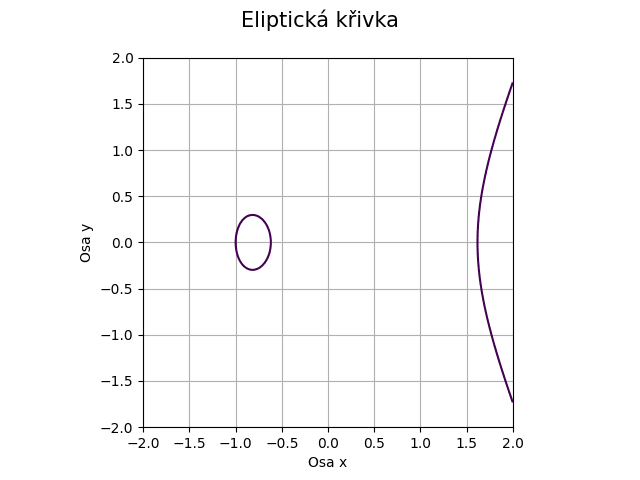
Obrázek 26: Eliptická křivka pro koeficienty a=-2, b=-1.

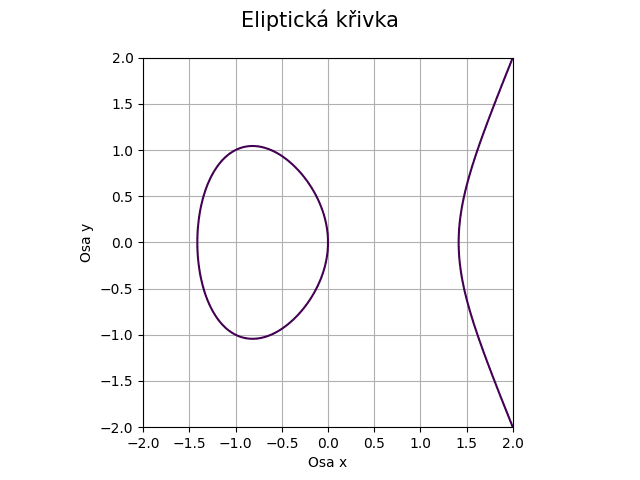
Obrázek 27: Eliptická křivka pro koeficienty a=-2, b=0.

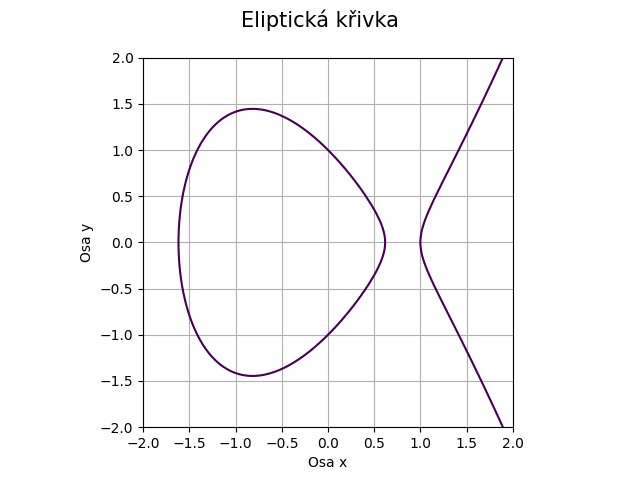
Obrázek 28: Eliptická křivka pro koeficienty a=-2, b=1.

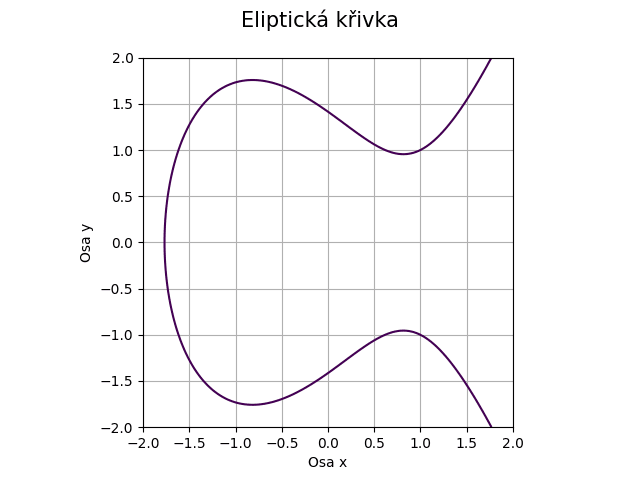
Obrázek 29: Eliptická křivka pro koeficienty a=-2, b=2.

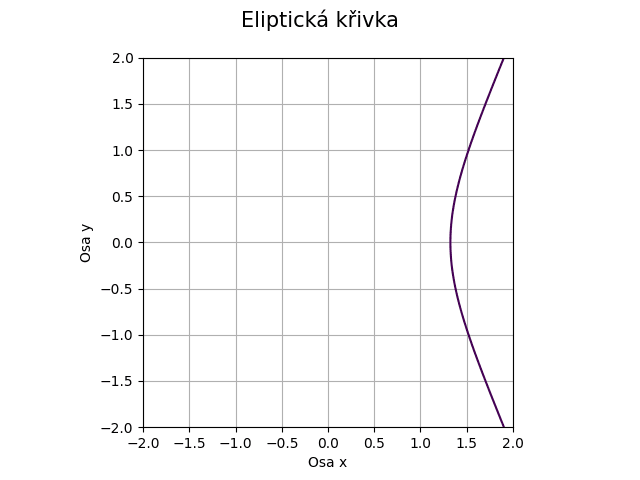
Obrázek 30: Eliptická křivka pro koeficienty a=-1, b=-1.

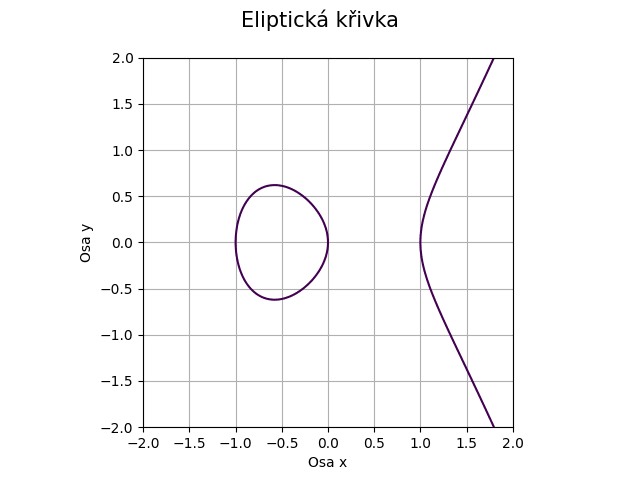
Obrázek 31: Eliptická křivka pro koeficienty a=-1, b=0.

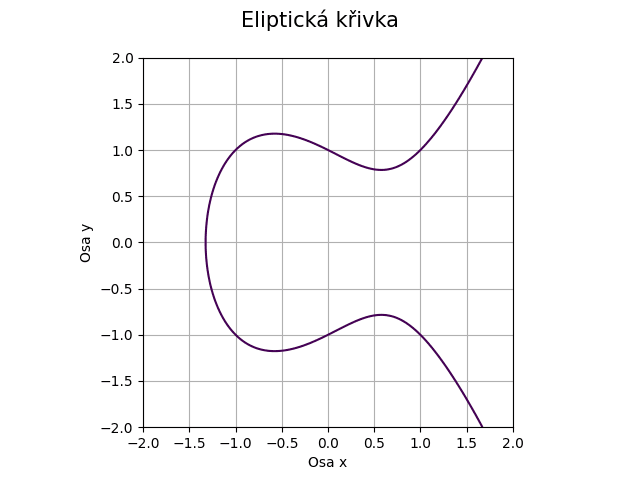
Obrázek 32: Eliptická křivka pro koeficienty a=-1, b=1.

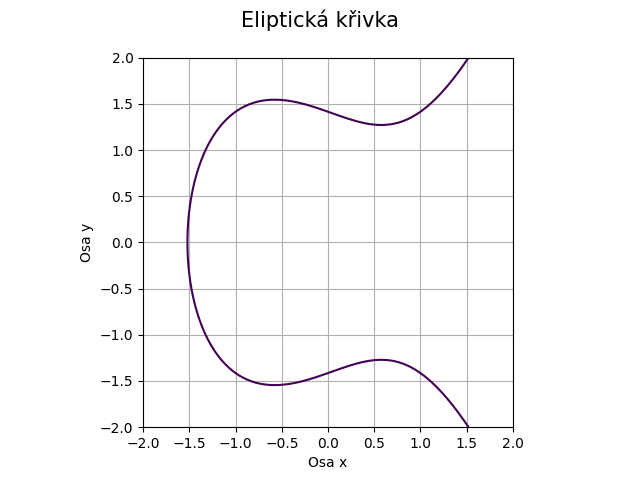
Obrázek 33: Eliptická křivka pro koeficienty a=-1, b=2.

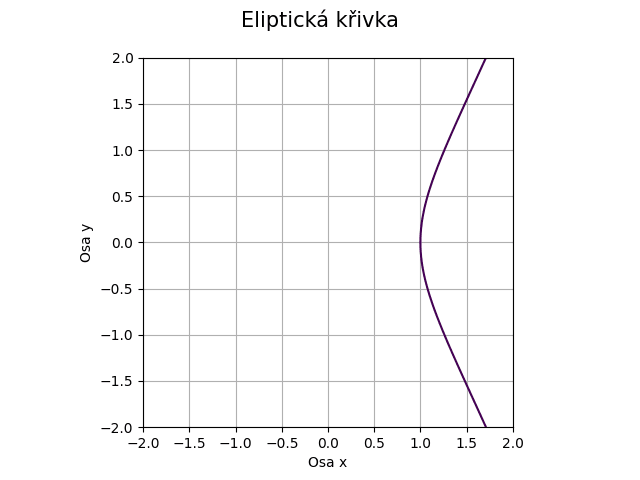
Obrázek 34: Eliptická křivka pro koeficienty a=0, b=-1.

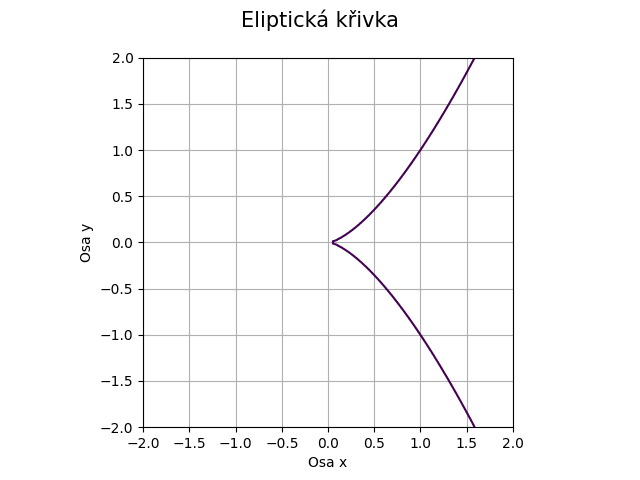
Obrázek 35: Eliptická křivka pro koeficienty a=0, b=0.

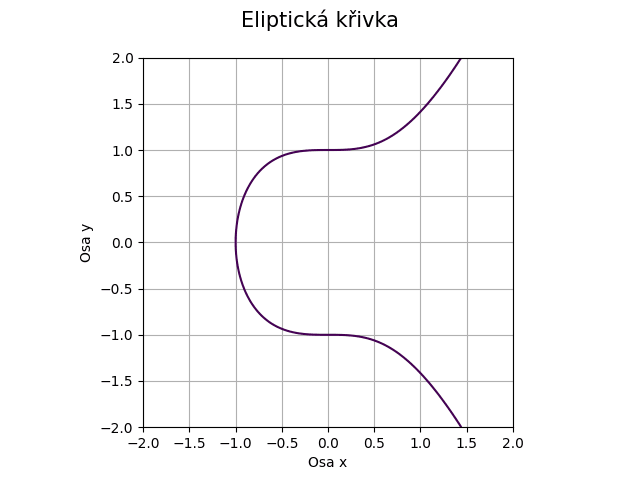
Obrázek 36: Eliptická křivka pro koeficienty a=0, b=1.

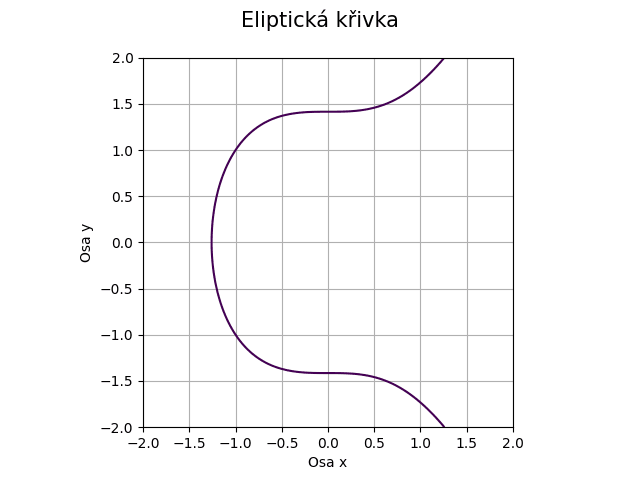
Obrázek 37: Eliptická křivka pro koeficienty a=0, b=2.

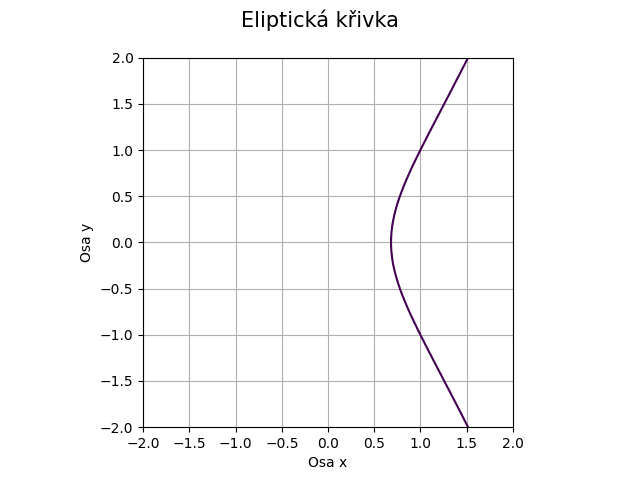
Obrázek 38: Eliptická křivka pro koeficienty a=1, b=-1.

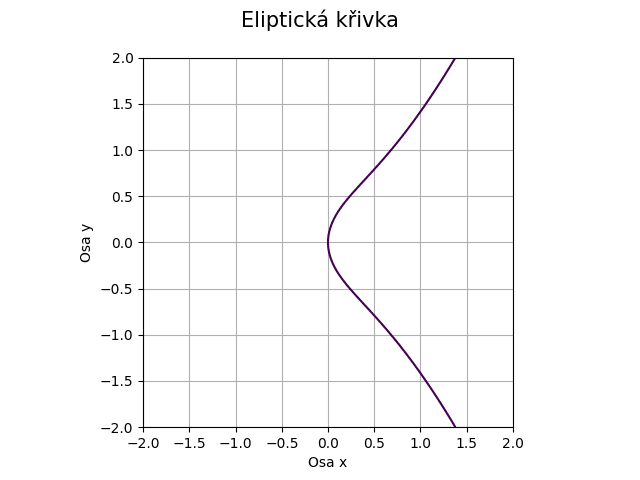
Obrázek 39: Eliptická křivka pro koeficienty a=1, b=0.

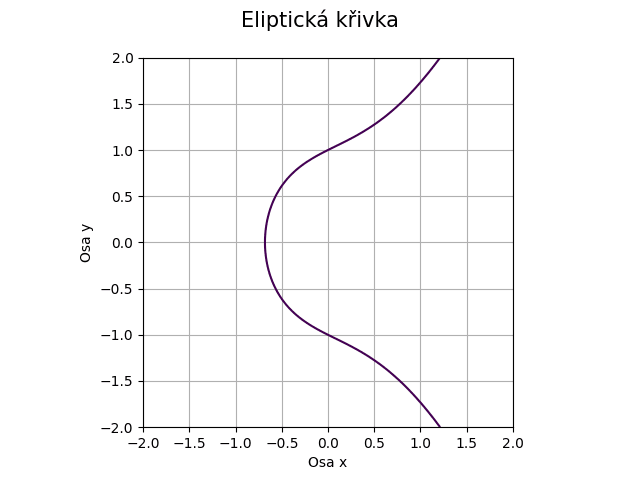
Obrázek 40: Eliptická křivka pro koeficienty a=1, b=1.

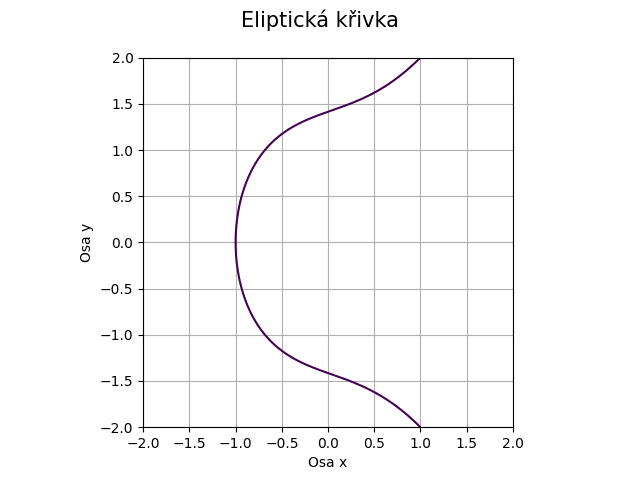
Obrázek 41: Eliptická křivka pro koeficienty a=1, b=2.

15. Moderní pomůcka pro lepší studium křivek – animace

Pro studium křivek se používaly různé pomůcky umožňující například zjištění inflexních bodů atd. Moderní pomůckou použitelnou u křivek s jedním či více koeficienty jsou animace. Ty vytvoříme následujícím postupem:

1. Necháme skriptem (Python+Matplotlib+Numpy) vygenerovat několik PNG obrázků křivky, pokaždé pro odlišný koeficient.
2. Vytvoříme z těchto obrázků animovaný GIF.
3. Tento GIF zoptimalizujeme na velikost.

Druhý příkaz, tedy vytvoření animovaného GIFu:

$ convert -delay 10 -loop 0 *.png animated.gif

Třetí příkaz, tj. optimalizace souboru na velikost:

$ gifsicle -O animated.gif > animated2.gif

16. Animace průsečíku roviny s toroidem

Výše uvedeným postupem můžeme vytvořit animaci průsečíku roviny toroidem pro proměnný koeficient c a stálé koeficienty a a b:

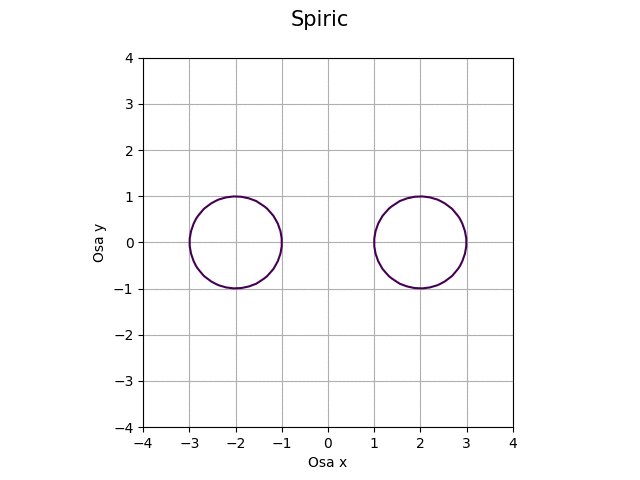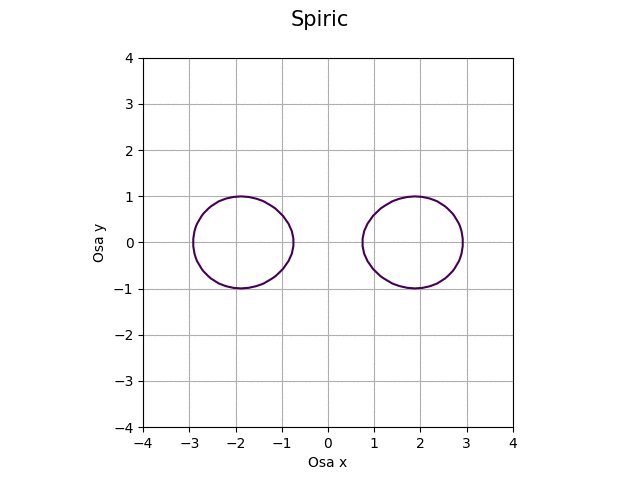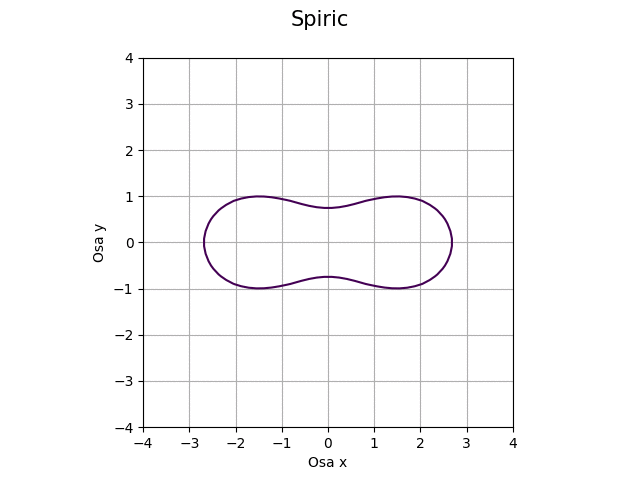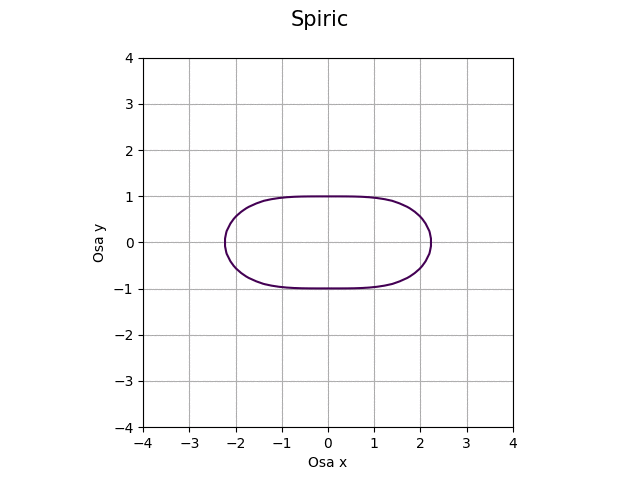
Obrázek 42: Průsečík roviny s toroidem pro proměnný koeficient c.

Skript, kterým byly snímky pro výše uvedenou animaci vytvořeny, vypadá následovně:

"""Křivka získaná řezem toru."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-4, 4, 50)
y = np.linspace(-4, 4, 50)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# parametry toru
a = 1
b = 2
c1 = 0.0
c2 = 2.0
 
frame = 1
for c in np.linspace(c1, c2, 25):
 
        # pomocné členy
    d = 2*(a**2+b**2-c**2)
    e = 2*(a**2-b**2-c**2)
    f = -(a+b+c)*(a+b-c)*(a-b+c)*(a-b-c)
 
        # implicitní funkce křivky
    z = (x**2+y**2)**2 - d*x**2 - e*y**2 - f
 
        # hodnota, která se má zvýraznit na isoploše
    levels = [0]
 
        # rozměry grafu při uložení: 640x480 pixelů
    fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
        # titulek grafu
    fig.suptitle('Spiric', fontsize=15)
 
        # vykreslení implicitní funkce
    ax.contour(x, y, z, levels)
 
        # zobrazit mřížku
    ax.grid(True)
 
        # zachovat poměr stran
    ax.axis('scaled')
 
        # popisek os
    plt.xlabel('Osa x')
    plt.ylabel('Osa y')
 
        # uložení grafu do rastrového obrázku
    plt.savefig("spiric_anim_{:02}.png".format(frame))
 
        # další snímek
    frame += 1

17. Animace Cassiniho oválů s postupnou změnou vybraného koeficientu

S křivkou nazvanou Cassiniho ovál či taktéž Cassiniho elipsa jsme se již setkali v jedenácté kapitole. Připomeňme si, že se jedná o křivku, jejíž tvar je určen dvěma koeficienty nazvanými a a c. Můžeme se například pokusit měnit průběžně parametr c, a to s tímto výsledkem:

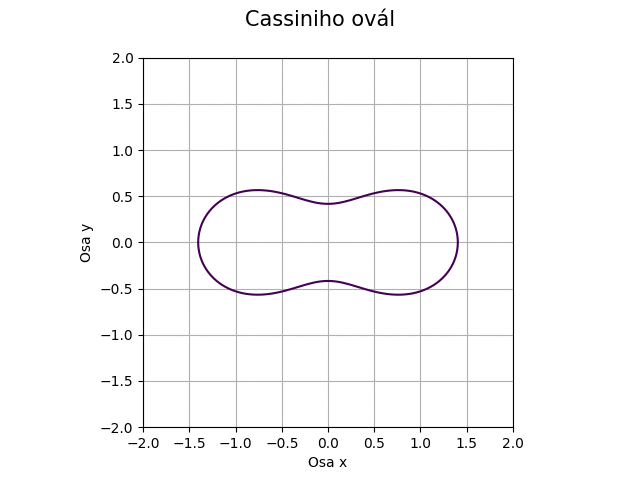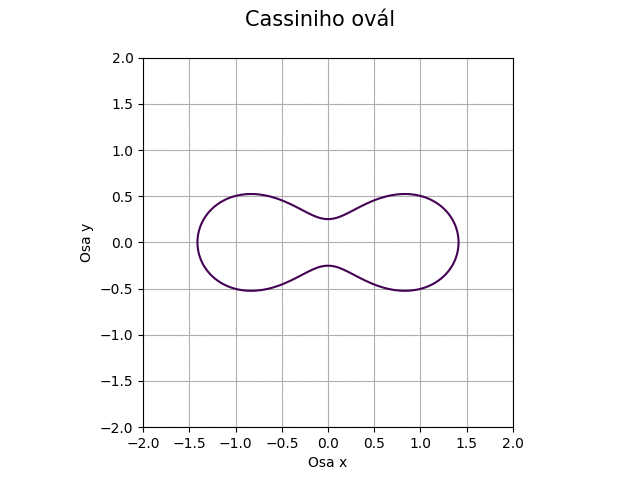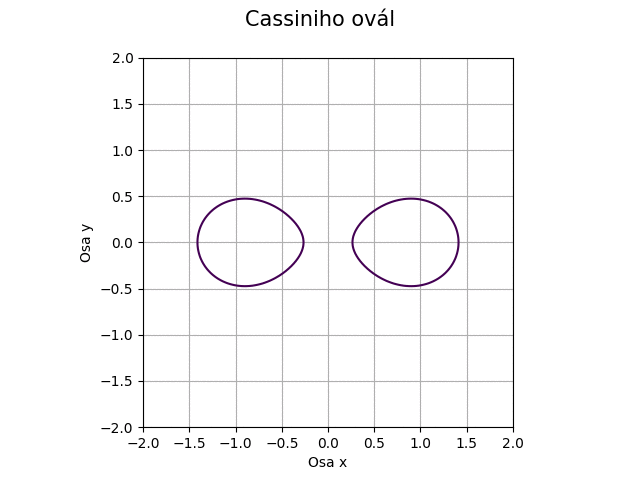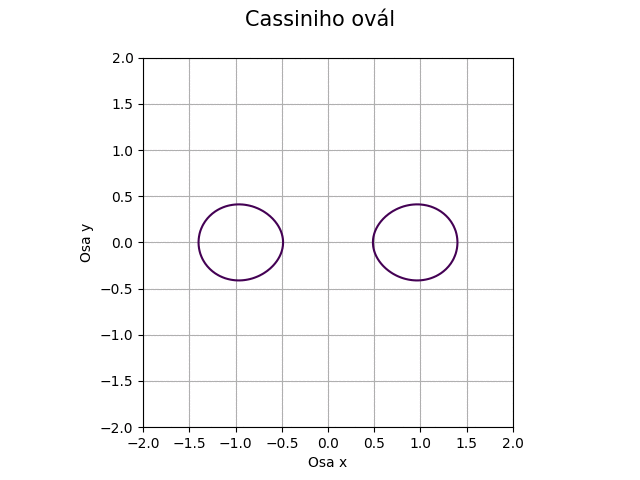
Obrázek 43: Cassiniho ovál pro proměnný koeficient c.

Skript, kterým byly snímky pro výše uvedenou animaci vytvořeny, vypadá následovně:

"""Cassiniho ovál zadaný implicitní funkcí."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-2, 2, 150)
y = np.linspace(-2, 2, 150)
 
# konstrukce mřížky
x, y = np.meshgrid(x, y)
 
# koeficienty Cassiniho oválu
a = 1.0
c1 = 0.90
c2 = 1.10
 
frame = 1
for c in np.linspace(c1, c2, 25):
 
        # implicitní funkce Cassiniho oválu
    z = (x**2 + y ** 2) ** 2 - 2*c*(x**2 - y**2) - (a**4 - c**4)
 
        # hodnota, která se má zvýraznit na isoploše
    levels = [0]
 
        # rozměry grafu při uložení: 640x480 pixelů
    fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
        # titulek grafu
    fig.suptitle('Cassiniho ovál', fontsize=15)
 
        # vykreslení implicitní funkce
    ax.contour(x, y, z, levels)
 
        # zobrazit mřížku
    ax.grid(True)
 
        # zachovat poměr stran
    ax.axis('scaled')
 
        # popisek os
    plt.xlabel('Osa x')
    plt.ylabel('Osa y')
 
        # uložení grafu do rastrového obrázku
    plt.savefig("cassini_anim_{:02}.png".format(frame))
 
        # další snímek
    frame += 1

18. Obsah čtvrté části seriálu

Ve čtvrté části seriálu o křivkách, které můžeme nalézt v architektuře, přírodě i v počítačové grafice, se (konečně) zaměříme právě na oblast počítačové grafiky a designu. Budeme se totiž zabývat parametrickými křivkami, které mají v moderní počítačové grafice nezastupitelné místo. Jedná se jak o křivky interpolační, tak i o křivky aproximační. Mezi parametrické křivky využívané v grafice patří například Coonsovy kubiky, dále slavné Bézierovy křivky, dále B-spline, jejich zobecnění známé pod zkratkou NURBS atd. Ovšem nesmíme zapomenout ani na křivky používané při animacích. Tyto křivky umožňují, aby se automaticky dopočítaly parametry animace mezi klíčovými snímky. Na tyto křivky jsou kladeny odlišné nároky, než na křivky využívané v designu (resp. přesněji ve 2D designu popř. při návrhu takzvaných plátů).

19. Repositář s demonstračními příklady

Všechny předminule, minule i dnes popisované demonstrační příklady určené pro Python 3 a knihovnu Matplotlib byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/pre­sentations. Příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý (dnes již poměrně rozsáhlý) repositář:

20. Odkazy na Internetu

1. Famous Curves Index
   https://mathshistory.st-andrews.ac.uk/Curves/
2. Curve (Wikipedia)
   https://en.wikipedia.org/wiki/Curve
3. Mathematical curves
   https://www.2dcurves.com/index.html
4. Curves (Wolfram MathWorld)
   https://mathworld.wolfram­.com/topics/Curves.html
5. Smooth Curve (Wolfram MathWorld)
   https://mathworld.wolfram­.com/SmoothCurve.html
6. Spirals (Wolfram MathWorld)
   https://mathworld.wolfram­.com/topics/Spirals.html
7. An Interactive Introduction to Splines
   https://ibiblio.org/e-notes/Splines/Intro.htm
8. Parabola
   https://www.2dcurves.com/co­nicsection/conicsectionp.html
9. Hyperbola
   https://www.2dcurves.com/co­nicsection/conicsectionh.html
10. Dioklova kisoida
    https://cs.wikipedia.org/wi­ki/Dioklova_kisoida
11. Archimédova spirála
    https://cs.wikipedia.org/wi­ki/Archim%C3%A9dova_spir%C3%A1la
12. Conchoid (mathematics)
    https://en.wikipedia.org/wi­ki/Conchoid_(mathematics)
13. Algebraic curve
    https://en.wikipedia.org/wi­ki/Algebraic_curve
14. Transcendental curve
    https://en.wikipedia.org/wi­ki/Transcendental_curve
15. Spiral
    https://en.wikipedia.org/wiki/Spiral
16. List of spirals
    https://en.wikipedia.org/wi­ki/List_of_spirals
17. Hyperbolická spirála
    https://cs.wikipedia.org/wi­ki/Hyperbolick%C3%A1_spir%C3%A1la
18. Hyperbolic Spiral
    https://mathworld.wolfram­.com/HyperbolicSpiral.html
19. Lituus (mathematics)
    https://en.wikipedia.org/wi­ki/Lituus_(mathematics)
20. Spiral of Spirals Fractals 2 with Python Turtle (Source Code)
    https://pythonturtle.academy/spiral-of-spirals-fractals-2-with-python-turtle-source-code/
21. Cornu Spiral
    http://hyperphysics.gsu.e­du/hbase/phyopt/cornu.html
22. Spiral
    https://www.2dcurves.com/spi­ral/spiral.html
23. Algebraic Curves
    https://mathworld.wolfram­.com/topics/AlgebraicCurves­.html
24. Elliptic Curves
    https://mathworld.wolfram­.com/topics/EllipticCurves­.html
25. Eukleidovská konstrukce
    https://cs.wikipedia.org/wi­ki/Eukleidovsk%C3%A1_konstruk­ce
26. Euclidean Constructions
    http://www.cs.cas.cz/portal/Al­goMath/Geometry/PlaneGeome­try/GeometricConstruction­s/EuclideanConstructions.htm
27. Kvadratura kruhu
    https://cs.wikipedia.org/wi­ki/Kvadratura_kruhu
28. Trisekce úhlu
    https://cs.wikipedia.org/wi­ki/Trisekce_%C3%BAhlu
29. Straightedge and compass construction
    https://en.wikipedia.org/wi­ki/Straightedge_and_compas­s_construction
30. C.a.R.
    http://car.rene-grothmann.de/doc_en/index.html
31. CaRMetal (Wikipedia)
    https://en.wikipedia.org/wiki/C.a.R.
32. CaRMetal (Španělsky a Francouzsky)
    http://carmetal.org/index.php/fr/
33. CaRMetal (Wikipedia)
    https://en.wikipedia.org/wi­ki/CaRMetal
34. Regular Polygon
    http://mathforum.org/dr.mat­h/faq/formulas/faq.regpoly­.html
35. Geometric Construction with the Compass Alone
    http://www.cut-the-knot.org/do_you_know/compass.shtml
36. Kvadratura kruhu (Wikipedie)
    https://cs.wikipedia.org/wi­ki/Kvadratura_kruhu
37. Compass equivalence theorem
    https://en.wikipedia.org/wi­ki/Compass_equivalence_the­orem
38. Curves we (mostly) don't learn in high school (and applications)
    https://www.youtube.com/wat­ch?v=3izFMB91K_Q
39. Can You Really Derive Conic Formulae from a Cone? – Menaechmus' Constructions
    https://www.maa.org/press/pe­riodicals/convergence/can-you-really-derive-conic-formulae-from-a-cone-menaechmus-constructions
40. Apollonius of Perga
    https://en.wikipedia.org/wi­ki/Apollonius_of_Perga
41. Catenary arch
    https://en.wikipedia.org/wi­ki/Catenary_arch
42. Parabolic arch
    https://en.wikipedia.org/wi­ki/Parabolic_arch
43. Wattova křivka
    https://www.geogebra.org/m/gNh4bW9r
44. Model stegosaura byl získán na stránce
    http://www.turbosquid.com/HTMLCli­ent/FullPreview/Index.cfm/ID/171071/Ac­tion/FullPreview
45. Obrázek nohy dinosaura byl získán na adrese
    http://perso.wanadoo.fr/ri­masson/3d/leg.htm
46. Spirograph
    https://en.wikipedia.org/wi­ki/Spirograph
47. Epicykloida
    https://cs.wikipedia.org/wi­ki/Epicykloida
48. Hypocykloida
    https://cs.wikipedia.org/wi­ki/Hypocykloida
49. Hypotrochoida
    https://cs.wikipedia.org/wi­ki/Hypotrochoida
50. Superelipsoidy a kvadriky v POV-Rayi
    https://www.root.cz/clanky/su­perelipsoidy-a-kvadriky-v-pov-rayi/
51. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers
    https://elepa.files.wordpres­s.com/2013/11/fifty-famous-curves.pdf
52. Barr, A.H.: Superquadrics and Angle Preserving Transformations,
    IEEE Computer Graphics and Applications, January 1981
53. Bourke Paul: Quadrics,
    July 1996
54. Bourke Paul: Superellipse and Superellipsoid,
    January 1990
55. Faux, I.D. a Pratt, M.J.: Computational Geometry for Design and Manufacture,
    Ellis Horwood Ltd., Wiley & Sons, 1979
56. Wallace A.: Differential Topology,
    Benjamin/Cummings Co., Reading, Massachussetts, USA, 1968
57. Glossary of Bridge Terminology
    http://sdrc.lib.uiowa.edu/en­g/bridges/WaddellGlossary/Glos­sC.htm
58. Brachistochrona
    https://cs.wikipedia.org/wi­ki/Brachistochrona
59. Missions: Cassini
    https://solarsystem.nasa.gov/mis­sions/cassini/overview/
60. Giovanni Domenico Cassini
    https://en.wikipedia.org/wi­ki/Giovanni_Domenico_Cassi­ni
61. Cassini Ovals
    https://mathworld.wolfram­.com/CassiniOvals.html
62. Geocentrismus
    https://cs.wikipedia.org/wi­ki/Geocentrismus
63. Who was Giovanni Cassini?
    https://www.universetoday­.com/130823/who-was-giovanni-cassini/
64. Special plane curves
    http://xahlee.info/Special­PlaneCurves_dir/ConicSecti­ons_dir/conicSections.html
65. Why Does Slicing a Cone Give an Ellipse?
    https://infinityisreallybig­.com/2019/02/08/why-does-slicing-a-cone-give-an-ellipse/