Obsah
1. Rychlost CPythonu 3.11 a 3.12 v porovnání s JIT a AOT překladači Pythonu (2)
2. Měříme skutečně rychlost výpočtů nebo rychlost zápisu výsledného rastrového obrázku?
3. Oddělení výpočtu od kódu pro uložení výsledku benchmarku
4. Vliv pomalosti I/O operací na rychlost běhu benchmarku
5. Grafy s časy výpočtů a I/O operací
7. Paralelizace výsledného kódu JIT překladačem Numba
8. Paralelizace kódu nemusí být zcela triviálním úkolem
9. Výsledek běhu příkladu upraveného do paralelní podoby
10. Úprava výpočtu pro paralelní běh
11. Přidání typových informací pro Numbu a refaktoring
12. Benchmarky zaměřené na FP operace, optimalizace smyček, podmínek a na paralelizaci
14. Výsledky omezené pouze na standardní interpretry Pythonu (CPython)
15. Vliv paralelizace na výsledky: Numba může překonat nativní céčkový kód
16. Krátké zamyšlení namísto závěru
17. Zdrojové kódy benchmarků použitých v dnešním článku
18. Repositář s demonstračními příklady pro nástroj Numba
1. Rychlost CPythonu 3.11 a 3.12 v porovnání s JIT a AOT překladači Pythonu (2)
Mikrobenchmarky, kterými jsme se zabývali v úvodním článku sice měřily rychlost interpretrů Pythonu v porovnání s just in time i ahead of time překladači, ovšem neukazují další vlastnosti nástrojů mypyc a především pak Numby – možnost paralelizace kódu. Jedná se o „detail“ s velkým praktickým dopadem, kterému se budeme věnovat dnes. A navíc musíme detailněji zjistit, jak vlastně interpretovat naměřená data – zda skutečně měříme rychlost výsledného kódu a/nebo rychlost I/O operací.
Obrázek 1: Rastrový obrázek generovaný benchmarky při nastavení rozlišení 400×400 pixelů a maximálního počtu iterací 255. Později budeme počet iterací zásadně zvětšovat, abychom omezili vliv pomalosti I/O operací na celkovou dobu trvání benchmarku.
2. Měříme skutečně rychlost výpočtů nebo rychlost zápisu výsledného rastrového obrázku?
V předchozím článku jsme měřili rychlost vykreslení Mandelbrotovy množiny Pythonním skriptem, který byl buď přímo spuštěn ve standardním interpretru CPythonu (verze 3.8 až 3.12), popř. byl přeložen JIT překladačem Numba nebo AOT překladačem mypyc. Výsledkem měření byl (mj.) i následující graf, v němž jsou porovnány rychlosti vykreslení Mandelbrotovy množiny do rastrových obrázků s rozlišením, které se pohybuje od 16×16 pixelů až po poměrně velké obrázky s rozlišením 4096×4096 pixelů:
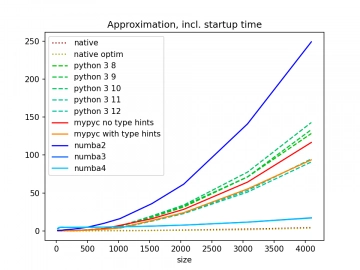
Obrázek 2: Časy běhu všech benchmarků v závislosti na požadovaném rozlišení výsledné bitmapy.
Ještě předtím, než vyneseme konečný verdikt, za jakých okolností je vhodné použít nějakou technologii, je vhodné se zamyslet nad tím, co jsme vlastně změřili (to platí pro všechny benchmarky). Jedná se o tři operace:
- JIT překlad, popř. překlad bajtkódu (pro mypyc nulový čas)
- Čas výpočtu (programové smyčky, podmínky a FP operace)
- I/O operace (volání funkce print pro vykreslení bitmapy)
Na první pohled by se mohlo zdát, že doba I/O operací nebude hrát při dlouhotrvajících výpočtech žádnou zásadní roli, ovšem je lepší si vše ověřit (mohli bychom například předpokládat, že doba výpočtu barvy pixelu bude mnohem delší, než zápis samotné barvy, což je trojice celých čísel). Ideální by samozřejmě bylo využití profileru, to je však v případě mypyc a Numby relativně složitá operace (více příště). Proto se pokusíme o oddělení obou částí programu přímo ve zdrojovém kódu benchmarku.
P3 16 16 255 224 224 224 224 224 224 224 224 224 224 224 224 216 216 216 216 216 216 216 216 216 216 216 216 232 232 232 232 232 232 216 216 216 ... ... ... 208 208 208 208 208 208 208 208 208 216 216 216 216 216 216 216 216 216 216 216 216 216 216 216
3. Oddělení výpočtu od kódu pro uložení výsledku benchmarku
Připomeňme si, že původní tvar benchmarku vypadá následovně. Uvádíme zde variantu určenou pro JITování nástrojem Numba, takže ve zdrojovém kódu příkladu nalezneme dekorátor @jit s parametrem nopython=True, kterým se určuje, že se nemají volat Pythonní funkce, ale pouze funkce nativní. Z toho důvodu jsme nuceni použít zjednodušenou nativní variantu funkcí print a range (podtrženo):
#!/usr/bin/env python
# vim: set fileencoding=utf-8
import palette_mandmap
from sys import argv, exit
from numba import jit
@jit(nopython=True)
def calc_mandelbrot(width, height, maxiter, palette):
print("P3")
print(width)
print(height)
print("255")
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
r = palette[i % 256][0]
g = palette[i % 256][1]
b = palette[i % 256][2]
print(r)
print(g)
print(b)
cx += 3.0/width
cy += 3.0/height
if __name__ == "__main__":
if len(argv) < 4:
width = 512
height = 512
maxiter = 255
else:
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
calc_mandelbrot(width, height, maxiter, palette_mandmap.palette)
Pokud se budeme snažit o zachování původního zdrojového kódu v co největší míře, můžeme provést rozdělení na výpočetní a exportní část například následujícím způsobem. Povšimněte si použití Numpy, což je ovšem zcela v pořádku, protože nástroj Numba je optimalizován právě pro dobrou a rychlou kooperaci s Numpy:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
import palette_mandmap
from sys import argv, exit
import numpy as np
from numba import jit
@jit(nopython=True)
def calc_mandelbrot(width, height, maxiter, palette):
iters = np.empty((height, width), dtype=np.uint8)
# calc part
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
iters[y][x] = i
cx += 3.0/width
cy += 3.0/height
# image export part
print("P3")
print(width)
print(height)
print("255")
for y in range(0, height):
for x in range(0, width):
i = iters[y][x]
r = palette[i % 256][0]
g = palette[i % 256][1]
b = palette[i % 256][2]
print(r)
print(g)
print(b)
if __name__ == "__main__":
if len(argv) < 4:
width = 512
height = 512
maxiter = 255
else:
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
calc_mandelbrot(width, height, maxiter, palette_mandmap.palette)
4. Vliv pomalosti I/O operací na rychlost běhu benchmarku
Nyní benchmark uvedený v předchozí kapitole budeme postupně modifikovat. Nejprve ho na testovacím počítači spustíme tak, jak byl napsán, samozřejmě s využitím JIT překladače nástroje Numba. Pro rastrové obrázky o rozlišení od 16×16 pixelů do 4096×4096 pixelů (a pro maximální počet iterací roven 255) dostaneme následující výsledky (první sloupec obsahuje velikost obrázku, druhý čas výpočtu v sekundách a třetí kapacitu alokované paměti z pohledu operačního systému – RSS):
16 3.45 271180 24 3.44 271444 32 4.27 271384 48 5.16 271136 64 5.13 271148 96 5.12 271184 128 5.07 271312 192 5.13 271304 256 5.13 271308 384 5.19 271268 512 5.25 271124 768 5.48 271316 1024 5.75 271316 1536 6.59 271184 2048 7.83 271008 3072 11.18 271296 4096 15.98 271316
Vidíme, že rastrový obrázek s rozlišením 4096×4096 byl spočten a uložen za cca šestnáct sekund.
Dále si zkusme zakomentovat poslední tři příkazy ve smyčce, v níž se rastrový obrázek ukládá:
# image export part
print("P3")
print(width)
print(height)
print("255")
for y in range(0, height):
for x in range(0, width):
i = iters[y][x]
r = palette[i % 256][0]
g = palette[i % 256][1]
b = palette[i % 256][2]
# print(r)
# print(g)
# print(b)
Nyní tedy budeme provádět celý výpočet, ovšem nebudeme vykreslovat jednotlivé pixely výsledného rastrového obrázku. Pokud nyní předpokládáte (stejně jako původně autor tohoto článku), že výsledné časy budou prakticky totožné, možná budete překvapeni:
16 2.93 266752 24 2.93 266812 32 2.93 266952 48 2.91 267072 64 3.66 266796 96 4.40 267060 128 4.37 266928 192 4.32 266944 256 4.34 266820 384 4.35 266948 512 4.35 266776 768 4.38 266816 1024 4.39 266688 1536 4.42 266820 2048 4.47 266500 3072 4.65 266932 4096 4.97 266804
Z výsledků je patrné, že samotný FP výpočet není zdaleka tou nejkritičtější operací. To má dalekosáhlé důsledky, ke kterým se ještě vrátíme.
Při třetím běhu naopak vynecháme výpočet a budeme ukládat prázdnou bitmapu (s černými pixely):
# calc part
cy = -1.5
for y in range(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
# while i < maxiter:
# zx2 = zx * zx
# zy2 = zy * zy
# if zx2 + zy2 > 4.0:
# break
# zy = 2.0 * zx * zy + cy
# zx = zx2 - zy2 + cx
# i += 1
iters[y][x] = i
cx += 3.0/width
cy += 3.0/height
Nyní již dokážeme výsledek do určité míry predikovat – samotné uložení rastrového obrázku je tak náročná I/O operace, že bude nejenom měřitelná, ale překročí dobu výpočtů:
16 3.48 271076 24 3.48 270880 32 3.45 270948 48 4.49 271016 64 5.23 270892 96 5.18 271068 128 5.15 271076 192 5.17 271020 256 5.18 271032 384 5.25 270952 512 5.29 270880 768 5.47 271040 1024 5.77 271212 1536 6.53 270952 2048 7.79 270928 3072 10.92 270868 4096 15.37 270856
Jen pro zajímavost vynechme výpočet, ovšem uložme každý pixel dvakrát, čímž se počet I/O operací prakticky zdvojnásobí (výsledná bitmapa ovšem nebude korektní):
# image export part
print("P3")
print(width)
print(height)
print("255")
for y in range(0, height):
for x in range(0, width):
i = iters[y][x]
r = palette[i % 256][0]
g = palette[i % 256][1]
b = palette[i % 256][2]
print(r)
print(g)
print(b)
print(r)
print(g)
print(b)
Časy nebudou dvojnásobné, ale to je již možné predikovat, protože víme, že samotné JITování kódu trvá cca 3–4 sekundy:
16 3.46 271212 24 3.44 271292 32 3.47 271320 48 3.45 271348 64 5.06 271456 96 5.13 271332 128 5.11 271336 192 5.12 271336 256 5.16 271208 384 5.25 271172 512 5.41 271308 768 5.81 271472 1024 6.37 271308 1536 8.35 271588 2048 10.43 271304 3072 16.79 271304 4096 25.89 271304
5. Grafy s časy výpočtů a I/O operací
Porovnání běhu benchmarků je pochopitelně výhodnější provést ve vizuální podobě, takže se vrátíme ke grafům. Na následujících grafech jsou zobrazeny časy všech čtyř variant téhož benchmarku popsaných v předchozí kapitole:
| Označení | Význam |
|---|---|
| normal | celý benchmark s výpočtem i exportem |
| no output | pouze výpočet |
| no calc | pouze export (černého) rastrového obrázku |
| double output | výpočet i export, ovšem každý pixel je zapsán dvakrát |
Pro velmi malé rozměry obrázků bude největší roli hrát samotný JIT překladač:
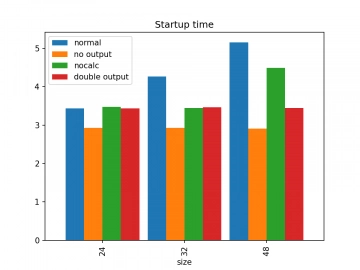
Obrázek 3: Vliv JIT překladu na dobu běhu benchmarků.
Naopak pro velké rastrové obrázky vychází, že největší vliv mají I/O operace (tedy konkrétně funkce print) a nikoli vlastní výpočet, což je překvapující:
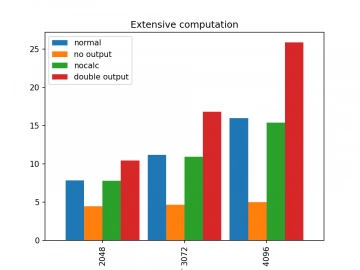
Obrázek 4: Vliv opakovaného volání funkce print na dobu běhu benchmarku.
A takto vypadá situace, kdy na horizontální osu vyneseme velikost výsledného obrázku a na osu vertikální dobu běhu benchmarku v sekundách. Jednotlivé naměřené hodnoty jsou proloženy lineárními úseky:
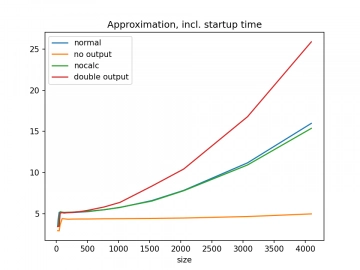
Obrázek 5: Rychlosti různých benchmarků pro rozdílné velikosti výsledných rastrových obrázků.
6. Eliminace I/O operací
V dnešním článku nás v prvé řadě zajímá rychlost provádění výpočtů a nikoli to, jak rychlá či naopak pomalá je implementace funkce print. Z tohoto důvodu se budeme snažit omezit vliv I/O operací na rozumné minimum. Využijeme přitom faktu, že u výpočtu Mandelbrotovy množiny lze ponechat relativně malou velikost výsledného rastrového obrázku a naopak zvýšit maximální počet iterací, což povede k razantnímu zvýšení počtu FP operací.
Konkrétně to bude v našem konkrétním případě bude znamenat, že rozlišení obrázku nastavíme na 256×256 pixelů, což je dostatečně velké rozlišení pro odhalení chyby („fast math“) ve výpočtu, ale počet I/O operací se oproti největšímu obrázku z předchozích benchmarků sníží na 1/256, což je méně než 1% (a proto bude jejich vliv malý). A počet iterací naopak vzroste až na 1000000, takže doby výpočtu budou v některých případech přesahovat půl hodiny.

Obrázek 6: Výsledek výpočtu Mandelbrotovy množiny při nastavení maximálního množství iterací na 100 000.

Obrázek 7: Výsledek výpočtu Mandelbrotovy množiny při nastavení maximálního množství iterací na 1 000 000.
7. Paralelizace výsledného kódu JIT překladačem Numba
Další optimalizace, kterou Numba dokáže zajistit, je paralelizace části kódu, typicky programové smyčky nebo častého volání nějaké funkce. Pro tento účel se používá parametr parallel=True předaný dekorátoru @jit a navíc je vhodné při generování indexů atd. použít namísto vestavěného generátoru range jeho paralelní variantu prange. Jak ale takový paralelní výpočet probíhá? Kód, resp. jednotlivé iterace nebo celé volání funkce, je spouštěn ve vláknech. Počet vláken lze nastavit; výchozí hodnota odpovídá počtu procesorových jader. Co to znamená v praxi? Testování probíhá na počítači se šestnácti jádry a tudíž prange rozdělí výpočet do šestnácti vláken, která běží samostatně (protože v nativní části nemáme žádný GIL!).
8. Paralelizace kódu nemusí být zcela triviálním úkolem
Mohlo by se zdát, že díky tomu, že nástroj Numba nabízí volbu parallel=True a navíc i „paralelní“ generátor prange bude paralelizace kódu zcela triviální. V některých případech je to samozřejmě pravda, ovšem platí to i pro náš benchmark? Můžeme se o tom snadno přesvědčit jeho úpravou:
- Před hlavičku funkce uvedeme @jit(nopython=True, parallel=True)
- Vnější výpočetní smyčka bude používat prange a nikoli range
- Smyčka pro uložení bitmapy nepoběží paralelně (je snad zřejmé proč)
- Přístup do pole iters lze provést z více vláken, pokud se nebude jednat o stejnou buňku
Vnější smyčka se tedy změní takto:
# calc part
cy = -1.5
for y in prange(0, height):
...
...
...
cy += 3.0/height
Upravený kód demonstračního příkladu bude vypadat následovně:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
import palette_mandmap
from sys import argv, exit
import numpy as np
from numba import jit, prange
@jit(nopython=True, parallel=True)
def calc_mandelbrot(width, height, maxiter, palette):
iters = np.empty((height, width), dtype=np.uint8)
# calc part
cy = -1.5
for y in prange(0, height):
cx = -2.0
for x in range(0, width):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
iters[y][x] = i
cx += 3.0/width
cy += 3.0/height
# image export part
print("P3")
print(width)
print(height)
print("255")
for y in range(0, height):
for x in range(0, width):
i = iters[y][x]
r = palette[i % 256][0]
g = palette[i % 256][1]
b = palette[i % 256][2]
print(r)
print(g)
print(b)
if __name__ == "__main__":
if len(argv) < 4:
width = 512
height = 512
maxiter = 255
else:
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
calc_mandelbrot(width, height, maxiter, palette_mandmap.palette)
9. Výsledek běhu příkladu upraveného do paralelní podoby
Podívejme se nyní na výsledný obrázek, který získáme po spuštění benchmarku z předchozí kapitoly:

Obrázek 8: Výsledek „paralelizovaného“ benchmarku.
Z výsledků je jasně patrné, že se v žádném případě nejedná o očekávaný obrázek Mandelbrotovy množiny. Namísto toho vidíme šestnáct kopií části množiny začínající na nulové imaginární souřadnici (cy=0). Tento obrázek nám současně poměrně přesně napovídá, co se stalo:
- Numba skutečně výpočet rozdělila do šestnácti vláken (na mém počítači se šestnácti jádry – jinde to může být odlišné)
- Ovšem s lokální proměnnou cy se nepracuje korektně – je v každém vláknu nastavena na nulu a poté „lokálně“ zvyšována, takže každé vlákno vlastně počítá stejnou část množiny
K lokální skalární proměnné není možné tímto způsobem přistupovat z většího množství vláken. Proto je nutné výpočet vhodným způsobem upravit, což si ukážeme v navazující kapitole.
10. Úprava výpočtu pro paralelní běh
Ve skutečnosti je úprava výpočetní části benchmarku do takové podoby, která umožní paralelní výpočet, poměrně triviální (benchmark založený na Mandelbrotově množině je skutečně v tomto ohledu dosti univerzální). Postačuje nám, aby se imaginární hodnota komplexního čísla c (tedy lokální proměnná cy) explicitně vypočítala uvnitř paralelizované vnější smyčky. To znamená, že namísto:
# calc part
cy = -1.5
for y in prange(0, height):
cx = -2.0
for x in range(0, width):
...
...
...
cx += 3.0/width
cy += 3.0/height
…přesuneme proměnnou cy dovnitř smyčky, což znamená, že každé vlákno bude vlastnit „svoji“ proměnnou cy nezávislou na ostatních vláknech:
# calc part
for y in prange(0, height):
cy = -1.5 + 3.0*y/height
cx = -2.0
for x in range(0, width):
...
...
...
cx += 3.0/width
11. Přidání typových informací pro Numba a refaktoring
I JIT překladač implementovaný v Numbě dokáže zpracovat informace o typech parametrů překládané funkce. Ovšem tyto typové informace nejsou zapisovány dnes standardním způsobem (type hints), ale přímo v dekorátoru @jit nebo @njit. V našem konkrétním případě, tj. pro funkci určenou pro vykreslení Mandelbrotovy množiny, se předává několik parametrů:
- šířka obrázku – celé číslo
- výška obrázku – celé číslo
- maximální počet iterací – celé číslo
- barvová paleta – 256 trojic celých čísel (což je UniTuple s 256 vnořenými UniTuple)
V tomto konkrétním případě bude informace o typech vypadat takto:
@jit((int64, int64, int64, UniTuple(UniTuple(int64, 3), 256)), nopython=True, parallel=True)
def calc_mandelbrot(width, height, maxiter, palette):
...
...
...
Další úprava spočívá v refaktoringu – ze zdrojového kódu „vytáhneme“ funkci pro výpočet počtu iterací pro jediný bod v komplexní rovině. Tato funkce bude plně přeložena do nativního kódu a dokonce bude vložena přímo do kódu (bez jejího volání). Tato úprava opět (kupodivu) pomůže JIT překladači, zde konkrétně při rozbalování smyčky:
@jit(nopython=True)
def calc_pixel(maxiter, cx, cy):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
return i
Výsledný zdrojový kód bude po všech úpravách vypadat následovně:
#!/usr/bin/env python
# vim: set fileencoding=utf-8
import palette_mandmap
from sys import argv, exit
import numpy as np
from numba import jit, prange
from numba.types import UniTuple, int64
@jit(nopython=True)
def calc_pixel(maxiter, cx, cy):
zx = 0.0
zy = 0.0
i = 0
while i < maxiter:
zx2 = zx * zx
zy2 = zy * zy
if zx2 + zy2 > 4.0:
break
zy = 2.0 * zx * zy + cy
zx = zx2 - zy2 + cx
i += 1
return i
@jit((int64, int64, int64, UniTuple(UniTuple(int64, 3), 256)), nopython=True, parallel=True)
def calc_mandelbrot(width, height, maxiter, palette):
iters = np.empty((height, width), dtype=np.uint8)
# calc part
for y in prange(0, height):
cy = -1.5 + 3.0*y/height
cx = -2.0
for x in range(0, width):
i = calc_pixel(maxiter, cx, cy)
iters[y][x] = i
cx += 3.0/width
# image export part
print("P3")
print(width)
print(height)
print("255")
for y in range(0, height):
for x in range(0, width):
i = iters[y][x]
r = palette[i % 256][0]
g = palette[i % 256][1]
b = palette[i % 256][2]
print(r)
print(g)
print(b)
if __name__ == "__main__":
if len(argv) < 4:
width = 512
height = 512
maxiter = 255
else:
width = int(argv[1])
height = int(argv[2])
maxiter = int(argv[3])
calc_mandelbrot(width, height, maxiter, palette_mandmap.palette)
# calc_mandelbrot.parallel_diagnostics(level=4)
iterations="1 10 100 1000 10000 100000 1000000"
OUTFILE="numba7.times"
PREFIX="numba7"
rm $OUTFILE
for iter in $iterations
do
echo $iter
echo -n "$iter " >> $OUTFILE
/usr/bin/time --output $OUTFILE --append --format "%e %M" python3 mandelbrot_python.py 256 256 $iter 255 > "${PREFIX}_${iter}.ppm"
done
12. Benchmarky zaměřené na FP operace, optimalizace smyček, podmínek a na paralelizaci
Podobně jako minule máme i dnes několik variant zdrojových kódů benchmarků:
- Původní zdrojový kód pro klasický interpret Pythonu
- Kód přepsaný do ANSI C
- Kód určený pro AOT překlad nástrojem mypyc bez typových informací (liší se způsobem spuštění)
- Kód určený pro AOT překlad nástrojem mypyc s přidanými typovými informacemi
- Numba: kód, do něhož byla pouze přidána anotace @jit
- Numba: varianta s jednodušší (nativní) funkcí print
- Numba: varianta s jednodušší (nativní) funkcí print a anotací @jit(nopython=True)
- Numba: varianta používající n-rozměrné pole (ndarray)
- Numba: nekorektní „paralelní“ varianta
- Numba: korektní „paralelní“ varianta
Tyto zdrojové kódy použijeme pro spuštění celkem dvanácti benchmarků, jejichž označení a význam je zapsán v tabulce:
| Označení | Stručný popis benchmarku |
|---|---|
| native | benchmark přepsaný do ANSI C, překlad bez optimalizací |
| native optim | benchmark přepsaný do ANSI C, překlad s optimalizacemi |
| python 3.8 | benchmark spuštěný standardním CPythonem verze 3.8 |
| python 3.9 | benchmark spuštěný standardním CPythonem verze 3.9 |
| python 3.10 | benchmark spuštěný standardním CPythonem verze 3.10 |
| python 3.11 | benchmark spuštěný standardním CPythonem verze 3.11 |
| python 3.12 | benchmark spuštěný standardním CPythonem verze 3.12 |
| mypyc no type hints | kód určený pro AOT překlad nástrojem mypyc bez typových informací |
| mypyc with type hints | kód určený pro AOT překlad nástrojem mypyc s přidanými typovými informacemi |
| numba 2 | Numba: kód, do něhož byla pouze přidána anotace @jit |
| numba 3 | Numba: varianta s jednodušší (nativní) funkcí print |
| numba 4 | Numba: varianta s jednodušší (nativní) funkcí print a anotací @jit(nopython=True) |
| numba 5 | Numba: varianta používající n-rozměrné pole (ndarray) |
| numba 6 | Numba: nekorektní „paralelní“ varianta |
| numba 7 | Numba: korektní „paralelní“ varianta |
13. Výsledky benchmarků
Na druhém grafu jsou zobrazeny časy běhu benchmarků pro malý počet iterací, což znamená i relativně malý počet FP operací, které se musí provést. Právě zde nehrají výpočty prakticky žádnou významnou roli, mnohem více se zde projeví inicializace procesu. To v případě nástroje Numba znamená JIT překlad. Jak je patrné, ten trvá přibližně 4 sekundy:
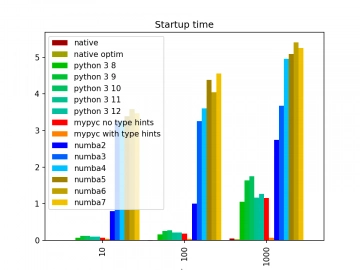
Obrázek 9: Časy běhu benchmarků pro malý počet iterací. Zde se nejvíce projeví čas inicializace procesu a popř. JITování kódu.
Pro větší počet iterací dostaneme zcela odlišné výsledky, protože JITovaný kód zde překonává jak klasické interpretry (což se dalo čekat), tak i Mypy! A navíc (což zde příliš dobře nevidíme) bude „paralelní“ výpočet realizovaný Numbou rychlejší, než nativní kód (viz další text):
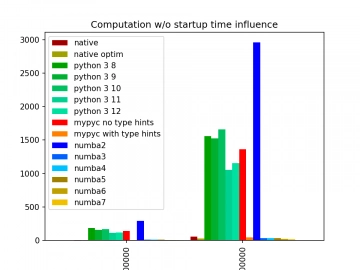
Obrázek 10: Časy běhu benchmarků pro velký počet iterací. Zde se nejvíce projeví čas inicializace procesu a popř. JITování kódu
Třetí graf ukazuje časy běhu všech benchmarků. Zvolil jsem liniový graf, který naznačuje, jak dobré či špatné jsou jednotlivé implementace nejenom pro dlouhé výpočty, ale i při započítání času inicializace procesu. Na horizontální osu jsou vyneseny maximální počty iterací, na vertikální osu pak doby běhu benchmarku v sekundách:
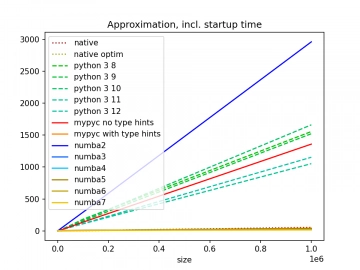
Obrázek 11: Časy běhu všech benchmarků v závislosti na požadovaném maximálním počtu iterací.
14. Výsledky omezené pouze na standardní interpretry Pythonu (CPython)
V úvodním článku jsme se taktéž zmínili o tom, že Python 3.11 (a 3.12) je obecně rychlejší, než předchozí interpretry Pythonu – tedy alespoň podle tvrzení tvůrců. Podívejme se, zda je tomu skutečně tak:
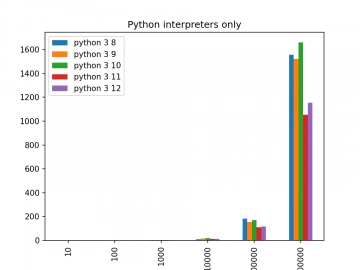
Obrázek 12: Porovnání rychlostí interpretrů Pythonu (CPython 3.x).
15. Vliv paralelizace na výsledky: Numba může překonat nativní céčkový kód
Hlavním důvodem, proč vlastně vznikl tento doplňkový článek, je zjištění, zda a jak vůbec se projeví (polo)automatická paralelizace kódu prováděná nástrojem Numba v případě, že se použije dekorátor @jit(parallel=True) a taktéž v případě použití funkce prange namísto standardní funkce range. Podívejme se tedy na výsledky, které porovnávají časy výpočtů pro JITovaný neparalelizovaný kód (numba5) a pro kód plně paralelizovaný (numba7). Z grafu je patrné více než dvojnásobné zrychlení pro velký počet iterací. Povšimněte si, že zrychlení není šestnáctinásobné, ovšem musíme si uvědomit, že cca 4–5 sekund trvá JITování kódu. To znamená, že poměr není 32:14, ale spíše 28:10, takže reálné zrychlení výpočtů je přibližně trojnásobné:
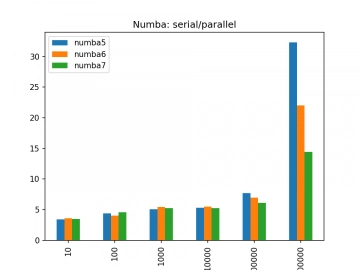
Obrázek 13: Neparalelizovaný (numba5) vs paralelizovaný (numba7) kód.
Nejzajímavější výsledek si necháváme na konec. Jedná se o porovnání rychlosti výpočtů prováděné nativním kódem (který pracuje v jediném vláknu) s paralelizovaným kódem, jenž je výsledkem JITování nástrojem Numba. Ukazuje se, že v tomto případě dostaneme lepší výsledek v případě použití Pythonu oproti nativnímu kódu (a to i když překladač C použije všechny nejmodernější optimalizace)!
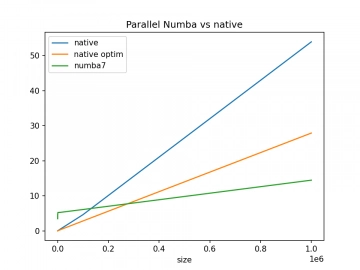
Obrázek 13: Nativní kód vs. kód psaný v Pythonu, jenž je JITován a paralelizován nástrojem Numba.
16. Krátké zamyšlení namísto závěru
Je zajímavé, do jaké míry dokážou nástroje mypyc a ještě více nástroj Numba poměrně kvalitně překládat zdrojové kódy Pythonu v případě, že jim jsou poskytnuty typové informace (a jak špatný je výsledek bez nich). V tom spočívá jedna část úspěchu těchto nástrojů. Druhá část spočívá v tom, že nám umožňuje označit ty funkce, které lze přeložit do nativního kódu bez toho, aby se v nich interně používal (ne)slavný GIL. Pravděpodobně není jen náhoda, že se jedná o stejné strategie, jaké jsou použity v nástroji CPython, kterým jsme se zabývali v článku Praktické použití nástroje Cython při překladu Pythonu do nativního kódu – i zde se v první řadě jednalo o zápis typových informací, odstranění volání Pythonovských funkcí (původní print) a tím pádem i možnost ignorování GILu. Pravděpodobně zde tedy vede cesta (nezávisle na tom, zda se jedná o JIT nebo AOT) k rychlejšímu Pythonu (pokud tedy vynecháme nekonečné diskuse o odstranění GILu přímo z CPythonu).
17. Zdrojové kódy benchmarků použitých v dnešním článku
Pro změření výkonnosti různých variant spuštění projektů naprogramovaných v Pythonu bylo použito celkem deset verzí zdrojových kódů benchmarku. První verze je určena pro klasický CPython (my jsme využili verze 3.8 až 3.12), dalších šest verzí jsou určeny pro použití společně s JIT překladačem Numba (přičemž dvě verze umožní paralelní běh ve více vláknech). Následují dvě verze určené pro AOT překladač Mypy a konečně poslední verze byla přepsána do ANSI C, abychom mohli porovnat, jak může být sémanticky totožný kód rychlejší při použití odlišného ekosystému:
| # | Příklad | Stručný popis | Adresa |
|---|---|---|---|
| 1 | mandelbrot-v1 | benchmark, v němž se nepoužívají anotace projektu Numba | https://github.com/tisnik/most-popular-python-libs/blob/master/numba/mandelbrot-v1/ |
| 2 | mandelbrot-v2 | použití anotace @jit ve funkci, v níž se provádí mnoho výpočtů | https://github.com/tisnik/most-popular-python-libs/blob/master/numba/mandelbrot-v2/ |
| 3 | mandelbrot-v3 | volání zjednodušených variant funkce print | https://github.com/tisnik/most-popular-python-libs/blob/master/numba/mandelbrot-v3/ |
| 4 | mandelbrot-v4 | použití anotace @jit s parametrem nopython | https://github.com/tisnik/most-popular-python-libs/blob/master/numba/mandelbrot-v4/ |
| 5 | mandelbrot-v5 | úprava předchozího příkladu: rozdělení části provádějící výpočet od části provádějící export obrázku | https://github.com/tisnik/most-popular-python-libs/blob/master/numba/mandelbrot-v5/ |
| 6 | mandelbrot-v6 | úprava příkladu tak, aby byl umožněn jeho běh ve více vláknech (s nekorektním výsledkem) | https://github.com/tisnik/most-popular-python-libs/blob/master/numba/mandelbrot-v6/ |
| 7 | mandelbrot-v7 | přidání typových informací pro zlepšení rychlosti paralelního běhu benchmarku | https://github.com/tisnik/most-popular-python-libs/blob/master/numba/mandelbrot-v7/ |
| 8 | mypyc/mandelbrot5 | varianta benchmarku určená pro překlad s využitím mypyc | https://github.com/tisnik/most-popular-python-libs/blob/master/mypyc/mandelbrot5.py |
| 9 | mypyc/mandelbrot6 | přidání typových informací využitelných AOT překladačem mypyc | https://github.com/tisnik/most-popular-python-libs/blob/master/mypyc/mandelbrot6.py |
| 10 | mandelbrot.c | varianta benchmarku naprogramovaná v ANSI C | https://github.com/tisnik/most-popular-python-libs/blob/master/mypyc/mandelbrot.c |
18. Repositář s demonstračními příklady pro nástroj Numba
Všechny demonstrační příklady ukazující vlastnosti nástroje Numba naleznete v repositáři https://github.com/tisnik/most-popular-python-libs:
19. Odkazy na Internetu
- Python 3.12: More Faster and More Efficient Python
https://medium.com/@HeCanThink/python-3–12-more-faster-and-more-efficient-python-b636f00b047 - Statické typové kontroly zdrojových kódů Pythonu prováděné nástrojem Mypy
https://www.root.cz/clanky/staticke-typove-kontroly-zdrojovych-kodu-pythonu-provadene-nastrojem-mypy/ - Statické typové kontroly zdrojových kódů Pythonu prováděné nástrojem Mypy (2.část)
https://www.root.cz/clanky/staticke-typove-kontroly-zdrojovych-kodu-pythonu-provadene-nastrojem-mypy-2-cast/ - Statické typové kontroly zdrojových kódů Pythonu prováděné nástrojem Mypy (3)
https://www.root.cz/clanky/staticke-typove-kontroly-zdrojovych-kodu-pythonu-provadene-nastrojem-mypy-3/ - mypy homepage
https://www.mypy-lang.org/ - mypy documentation
https://mypy.readthedocs.io/en/stable/ - Mypy na PyPi Optional static typing for Python
https://pypi.org/project/mypy/ - 5 Reasons Why You Should Use Type Hints In Python
https://www.youtube.com/watch?v=dgBCEB2jVU0 - Python Typing – Type Hints & Annotations
https://www.youtube.com/watch?v=QORvB-_mbZ0 - What Problems Can TypeScript Solve?
https://www.typescriptlang.org/why-create-typescript - How to find code that is missing type annotations?
https://stackoverflow.com/questions/59898490/how-to-find-code-that-is-missing-type-annotations - Do type annotations in Python enforce static type checking?
https://stackoverflow.com/questions/54734029/do-type-annotations-in-python-enforce-static-type-checking - Understanding type annotation in Python
https://blog.logrocket.com/understanding-type-annotation-python/ - Static type checking with Mypy — Perfect Python
https://www.youtube.com/watch?v=9gNnhNxra3E - Static Type Checker for Python
https://github.com/microsoft/pyright - Differences Between Pyright and Mypy
https://github.com/microsoft/pyright/blob/main/docs/mypy-comparison.md - 4 Python type checkers to keep your code clean
https://www.infoworld.com/article/3575079/4-python-type-checkers-to-keep-your-code-clean.html - Pyre: A performant type-checker for Python 3
https://pyre-check.org/ - „Typing the Untyped: Soundness in Gradual Type Systems“ by Ben Weissmann
https://www.youtube.com/watch?v=uJHD2×yv7×o - Covariance and contravariance (computer science)
https://en.wikipedia.org/wiki/Covariance_and_contravariance_(computer_science) - Functional Programming: Type Systems
https://www.youtube.com/watch?v=hy1wjkcIBCU - A Type System From Scratch – Robert Widmann
https://www.youtube.com/watch?v=IbjoA5×VUq0 - „Type Systems – The Good, Bad and Ugly“ by Paul Snively and Amanda Laucher
https://www.youtube.com/watch?v=SWTWkYbcWU0 - Type Systems: Covariance, Contravariance, Bivariance, and Invariance explained
https://medium.com/@thejameskyle/type-systems-covariance-contravariance-bivariance-and-invariance-explained-35f43d1110f8 - Statická vs. dynamická typová kontrola
https://www.root.cz/clanky/staticka-dynamicka-typova-kontrola/ - Typový systém
https://cs.wikipedia.org/wiki/Typov%C3%BD_syst%C3%A9m - Comparison of programming languages by type system
https://en.wikipedia.org/wiki/Comparison_of_programming_languages_by_type_system - Flow
https://flow.org/ - TypeScript
https://www.typescriptlang.org/ - Sorbet
https://sorbet.org/ - Pyright
https://github.com/microsoft/pyright - Mypy: Type hints cheat sheet
https://mypy.readthedocs.io/en/stable/cheat_sheet_py3.html - PEP 484 – Type Hints
https://peps.python.org/pep-0484/ - Numba
http://numba.pydata.org/ - numba 0.57.0
https://pypi.org/project/numba/ - Pushing Python toward C speeds with SIMD
https://laurenar.net/posts/python-simd/ - Retrieve generated LLVM from Numba
https://stackoverflow.com/questions/25213137/retrieve-generated-llvm-from-numba - Numba documentation
http://numba.pydata.org/numba-doc/latest/index.html - Numba na GitHubu
https://github.com/numba/numba - First Steps with numba
https://numba.pydata.org/numba-doc/0.12.2/tutorial_firststeps.html - Numba and types
https://numba.pydata.org/numba-doc/0.12.2/tutorial_types.html - Just-in-time compilation
https://en.wikipedia.org/wiki/Just-in-time_compilation - Cython (home page)
http://cython.org/ - Cython (wiki)
https://github.com/cython/cython/wiki - Cython (Wikipedia)
https://en.wikipedia.org/wiki/Cython - Cython (GitHub)
https://github.com/cython/cython - Python Implementations: Compilers
https://wiki.python.org/moin/PythonImplementations#Compilers - EmbeddingCython
https://github.com/cython/cython/wiki/EmbeddingCython - The Basics of Cython
http://docs.cython.org/en/latest/src/tutorial/cython_tutorial.html - Overcoming Python's GIL with Cython
https://lbolla.info/python-threads-cython-gil - GlobalInterpreterLock
https://wiki.python.org/moin/GlobalInterpreterLock - The Magic of RPython
https://refi64.com/posts/the-magic-of-rpython.html - RPython: Frequently Asked Questions
http://rpython.readthedocs.io/en/latest/faq.html - RPython’s documentation
http://rpython.readthedocs.io/en/latest/index.html - RPython (Wikipedia)
https://en.wikipedia.org/wiki/PyPy#RPython - Getting Started with RPython
http://rpython.readthedocs.io/en/latest/getting-started.html - PyPy (home page)
https://pypy.org/ - PyPy (dokumentace)
http://doc.pypy.org/en/latest/ - Localized Type Inference of Atomic Types in Python (2005)
http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.90.3231 - Tutorial: Writing an Interpreter with PyPy, Part 1
https://morepypy.blogspot.com/2011/04/tutorial-writing-interpreter-with-pypy.html - List of numerical analysis software
https://en.wikipedia.org/wiki/List_of_numerical_analysis_software - Pixie: lehký skriptovací jazyk s „kouzelnými“ schopnostmi
https://www.root.cz/clanky/pixie-lehky-skriptovaci-jazyk-s-kouzelnymi-schopnostmi/ - Programovací jazyk Pixie: funkce ze základní knihovny a použití FFI
https://www.root.cz/clanky/programovaci-jazyk-pixie-funkce-ze-zakladni-knihovny-a-pouziti-ffi/ - The future can be written in RPython now (článek z roku 2010)
http://blog.christianperone.com/2010/05/the-future-can-be-written-in-rpython-now/ - PyPy is the Future of Python (článek z roku 2010)
https://alexgaynor.net/2010/may/15/pypy-future-python/ - Portal:Python programming
https://en.wikipedia.org/wiki/Portal:Python_programming - RPython Frontend and C Wrapper Generator
http://www.codeforge.com/article/383293 - PyPy’s Approach to Virtual Machine Construction
https://bitbucket.org/pypy/extradoc/raw/tip/talk/dls2006/pypy-vm-construction.pdf - Tutorial: Writing an Interpreter with PyPy, Part 1
https://morepypy.blogspot.com/2011/04/tutorial-writing-interpreter-with-pypy.html - A simple interpreter from scratch in Python (part 1)
http://www.jayconrod.com/posts/37/a-simple-interpreter-from-scratch-in-python-part-1 - Brainfuck Interpreter in Python
https://helloacm.com/brainfuck-interpreter-in-python/ - Interpretry, překladače, JIT překladače a transpřekladače programovacího jazyka Lua
https://www.root.cz/clanky/interpretry-prekladace-jit-prekladace-a-transprekladace-programovaciho-jazyka-lua/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (2)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-2/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (3)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-3/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (4)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-4/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (5 – tabulky a pole)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-5-tabulky-a-pole/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (6 – překlad programových smyček do mezijazyka LuaJITu)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-6-preklad-programovych-smycek-do-mezijazyka-luajitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (7 – dokončení popisu mezijazyka LuaJITu)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-7-dokonceni-popisu-mezijazyka-luajitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (8 – základní vlastnosti trasovacího JITu)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-8-zakladni-vlastnosti-trasovaciho-jitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (9 – další vlastnosti trasovacího JITu)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-9-dalsi-vlastnosti-trasovaciho-jitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (10 – JIT překlad do nativního kódu)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-10-jit-preklad-do-nativniho-kodu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (11 – JIT překlad do nativního kódu procesorů s architekturami x86 a ARM)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-11-jit-preklad-do-nativniho-kodu-procesoru-s-architekturami-x86-a-arm/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (12 – překlad operací s reálnými čísly)
https://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-12-preklad-operaci-s-realnymi-cisly/ - Podpora SIMD (vektorových) instrukcí na RISCových procesorech
https://www.root.cz/clanky/podpora-simd-vektorovych-instrukci-na-riscovych-procesorech/ - Užitečné rozšíření GCC – podpora SIMD (vektorových) instrukcí: nedostatky technologie
https://www.root.cz/clanky/uzitecne-rozsireni-gcc-podpora-simd-vektorovych-instrukci-nedostatky-technologie/ - Podpora SIMD operací v GCC s využitím intrinsic pro nízkoúrovňové optimalizace
https://www.root.cz/clanky/podpora-simd-operaci-v-gcc-s-vyuzitim-intrinsic-pro-nizkourovnove-optimalizace/ - Podpora SIMD operací v GCC s využitím intrinsic: technologie SSE
https://www.root.cz/clanky/podpora-simd-operaci-v-gcc-s-vyuzitim-intrinsic-technologie-sse/ - Rozšíření instrukční sady „Advanced Vector Extensions“ na platformě x86–64
https://www.root.cz/clanky/rozsireni-instrukcni-sady-advanced-vector-extensions-na-platforme-x86–64/ - Rozšíření instrukční sady F16C, FMA a AVX-512 na platformě x86–64
https://www.root.cz/clanky/rozsireni-instrukcni-sady-f16c-fma-a-avx-512-na-platforme-x86–64/ - Použití instrukcí SSE a AVX pro zrychlení bitových operací
https://www.root.cz/clanky/pouziti-instrukci-sse-a-avx-pro-zrychleni-bitovych-operaci/ - Rozšíření instrukční sady AVX-512 na platformě x86–64 (dokončení)
https://www.root.cz/clanky/rozsireni-instrukcni-sady-avx-512-na-platforme-x86–64-dokonceni/ - Nuitka
https://github.com/Nuitka/Nuitka - SIMD Autovectorization in Numba
https://tbetcke.github.io/hpc_lecture_notes/simd.html




























