Obsah
1. Tvorba grafů a diagramů s využitím doménově specifického jazyka nástroje Graphviz (dokončení)
5. Odlišné názvy atributů v uzlech typu „záznam“
6. Napojení uzlů na konkrétní atribut záznamu
8. Odstranění původních tvarů uzlů pro tabulky
9. Porty – napojení na konkrétní řádek tabulky
10. „Vstupní“ „výstupní“ porty
11. Okraje tabulek a jejich buněk
12. Barevné zvýraznění buněk tabulky
13. Gradientní barevné přechody
14. Úhel gradientních barevných přechodů
15. Odstranění podgrafů příkazem prune
16. Podpora jazyka DOT v dalších nástrojích
17. Ukázka některých možnosti xfigu
18. Repositář s demonstračními příklady
19. Odkazy na články s tématem programové tvorby grafů a diagramů
1. Tvorba grafů a diagramů s využitím doménově specifického jazyka nástroje Graphviz (dokončení)
Ve třetím a současně i závěrečném článku o nástroji Graphviz si ukážeme některé další triky, které tento zdánlivě jednoduchý nástroj nabízí. Popíšeme si například způsob vykreslení tabulek, vykreslení uzlů typu záznam, hledání cest v grafu, zvýraznění automaticky nalezeného podgrafu atd. Taktéž si, ovšem pouze ve stručnosti, popíšeme některé užitečné aplikace, které jsou nad Graphviz postaveny, a to včetně pradávného vektorového editoru xfig. Ten je sice skutečně vyvíjen už velmi dlouho, ale v některých ohledech je praktičtější, než například on-line editor draw.io, jenž je dnes velmi populární.
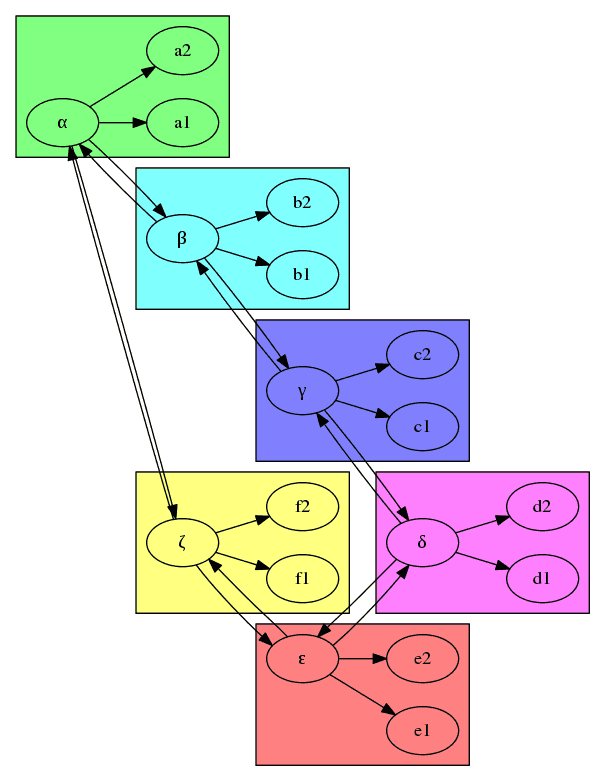
Obrázek 1: Graf se šesti podgrafy (clustery).
2. Tvary uzlů
Vraťme se nyní krátce k předchozímu článku, v němž jsme si kromě jiného řekli, že s využitím atributu shape je možné měnit tvar uzlů v grafech. Tuto důležitou funkcionalitu si ukážeme na několika demonstračních příkladech. Začneme grafem se standardními tvary uzlů (které navíc nejsou nijak propojeny):
graph {
rankdir=LR
a[label="a"]
b[label="b"]
c[label="c"]
d[label="d"]
e[label="e"]
f[label="f"]
g[label="g"]
h[label="h"]
i[label="i"]
j[label="j"]
k[label="k"]
l[label="l"]
m[label="m"]
n[label="n"]
}
Výsledný graf by po vykreslení měl vypadat takto:
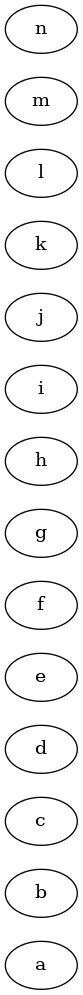
Obrázek 2: Příklad, z něhož budeme dále vycházet.
Nyní diagram upravíme – změníme tvary jednotlivých uzlů:
graph {
rankdir=LR
a[label="a", shape="box"]
b[label="b", shape="polygon"]
c[label="c", shape="ellipse"]
d[label="d", shape="oval"]
e[label="e", shape="circle"]
f[label="f", shape="point"]
g[label="g", shape="egg"]
h[label="h", shape="triangle"]
i[label="i", shape="plaintext"]
j[label="j", shape="plain"]
k[label="k", shape="diamond"]
l[label="l", shape="trapezium"]
m[label="m", shape="parallelogram"]
n[label="n", shape="house"]
}
Modifikovaný diagram:
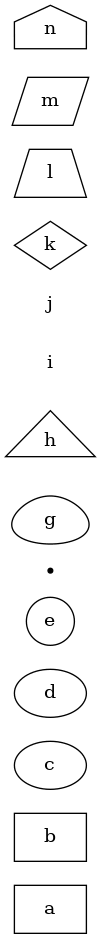
Obrázek 3: Diagram s modifikovanými tvary uzlů.
Podporovaných tvarů uzlů je ve skutečnosti ještě mnohem více:
graph {
rankdir=LR
a[label="a", shape="pentagon"]
b[label="b", shape="hexagon"]
c[label="c", shape="septagon"]
d[label="d", shape="octagon"]
e[label="e", shape="doublecircle"]
f[label="f", shape="doubleoctagon"]
g[label="g", shape="tripleoctagon"]
h[label="h", shape="invtriangle"]
i[label="i", shape="invtrapezium"]
j[label="j", shape="invhouse"]
k[label="k", shape="Mdiamond"]
l[label="l", shape="Msquare"]
m[label="m", shape="Mcircle"]
n[label="n", shape="rect"]
}

Obrázek 4: Další diagram s modifikovanými tvary uzlů.
A konečně následuje diagram s dalšími čtrnácti tvary uzlů:
graph {
rankdir=LR
a[label="a", shape="rectangle"]
b[label="b", shape="square"]
c[label="c", shape="star"]
d[label="d", shape="none"]
e[label="e", shape="underline"]
f[label="f", shape="cylinder"]
g[label="g", shape="note"]
h[label="h", shape="tab"]
i[label="i", shape="folder"]
j[label="j", shape="box3d"]
k[label="k", shape="component"]
l[label="l", shape="promoter"]
m[label="m", shape="cds"]
n[label="n", shape="terminator"]
}

Obrázek 5: Další diagram s modifikovanými tvary uzlů.
3. Tvary hran
I tvary šipek (tedy ukončení hran) je možné v případě potřeby modifikovat. Styl šipky lze pojmenovat, stejně jako styl uzlu, nebo (což je častější) je možné styl určit přímo u definice hrany. A právě tuto druhou možnost si ukážeme v dalším demonstračním příkladu s orientovaným grafem, v němž je definováno osm hran, každá s odlišným stylem šipky:
digraph {
splines="line"
a[label="start"]
b[color="red"]
c[color="blue"]
a -> b [arrowhead=box];
b -> c [arrowhead=crow];
c -> d [arrowhead=curve];
d -> a [arrowhead=icurve];
b -> a [arrowhead=diamond];
c -> b [arrowhead=dot];
d -> c [arrowhead=tee];
d -> a [arrowhead=vee];
}
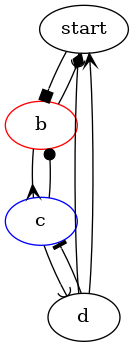
Obrázek 6: Orientovaný graf s různými styly konců hran.
Některé typy šipek mohou být vykresleny s výplní nebo bez výplně. Varianta bez výplně se volí tak, že se před jméno tvaru přidá znak „o“:
d -> e [arrowhead=obox]; d -> f [arrowhead=odiamond]; d -> g [arrowhead=odot]; d -> h [arrowhead=oinv]; d -> i [arrowhead=onormal];
na:
d -> e [arrowhead=obox]; d -> f [arrowhead=odiamond]; d -> g [arrowhead=odot]; d -> h [arrowhead=oinv]; d -> i [arrowhead=onormal];
Příklad takového diagramu:
digraph {
splines="line"
a[label="start"]
b[color="red"]
c[color="blue"]
a -> b [arrowhead=box];
b -> c [arrowhead=crow];
c -> d [arrowhead=curve];
d -> e [arrowhead=icurve];
b -> a [arrowhead=diamond];
c -> b [arrowhead=dot];
d -> c [arrowhead=tee];
d -> e [arrowhead=vee];
d -> e [arrowhead=obox];
d -> f [arrowhead=odiamond];
d -> g [arrowhead=odot];
d -> h [arrowhead=oinv];
d -> i [arrowhead=onormal];
}
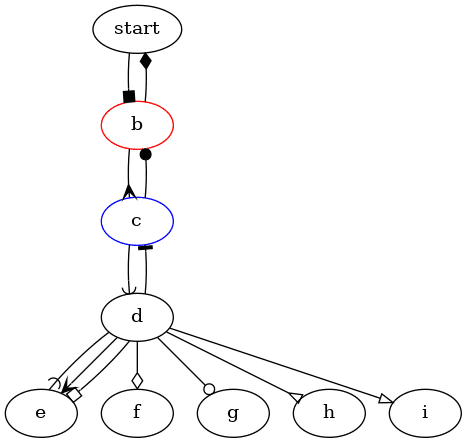
Obrázek 7: Orientovaný graf s různými styly konců hran; některé konce hran (šipky) nejsou vyplněny.
4. Uzly typu „záznam“
Potenciálně velmi užitečné jsou uzly typu „záznam“, což jsou uzly, jejichž tvar je nastaven na hodnotu record. Takové uzly totiž mohou ve svém popisu obsahovat několik řádků s atributy (fields), takže výsledkem je uzel, který svým tvarem a obsahem připomíná jednoduchou tabulku:
shape="record"
Samotné atributy se specifikují, jak je ostatně zvykem, s využitím vlastnosti label. Každý atribut začíná svým jménem, které je umístěno do úhlových závorek, podobně jako v HTML. Pro oddělení jednotlivých atributů se používá znak „pipe“. Všechny atributy jsou zapsány do jediného řetězce, který může vypadat následovně:
label="<f0>x| <f1>y| <f3>z"
Následuje úplný demonstrační příklad s trojicí uzlů, z nichž dva jsou typu record a poslední je běžný kulatý uzel:
digraph {
rankdir=LR
a[label="<f0>x| <f1>y| <f3>z"
shape="record"]
b[label="<f0>α| <f1>β| <f3>γ"
shape="record"]
c[label="result"]
a -> b;
b -> c;
}
S výsledkem:
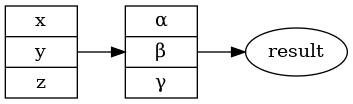
Obrázek 8: Graf s trojicí uzlů, z nichž dva jsou typu record.
5. Odlišné názvy atributů v uzlech typu „záznam“
Názvy atributů jsou sice v dokumentaci vždy psány stylem „f0“, „f1“ atd., ovšem ve skutečnosti může být atribut pojmenován jako jakýkoli jiný identifikátor, což je ostatně ukázáno i na dalším demonstračním příkladu, jehož zdrojový kód vypadá následovně:
digraph {
rankdir=LR
a[label="<atribut0>x| <atribut1>y| <atribut2>z"
shape="record"]
b[label="<atributA>α| <atributB>β| <atributC>γ"
shape="record"]
c[label="result"]
a -> b;
b -> c;
}
I přes odlišné názvy atributů bude výsledek vypadat stejně, jako v příkladu uvedeném ve čtvrté kapitole:
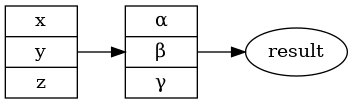
Obrázek 9: Opět graf s trojicí uzlů, z nichž dva jsou typu record.
6. Napojení uzlů na konkrétní atribut záznamu
Názvy jednotlivých atributů v záznamu mají svůj význam, protože umožňují, aby hrany (ať již orientované či neorientované) nepropojovaly pouze celé uzly, ale aby naopak bylo možné propojit jednotlivé řádky s atributy. Specifikace hran v takovém případě musí vypadat následovně:
a:atribut0 -> b:atributC; b:atributA -> c; e -> b:atributA;
Podívejme se nyní na poněkud upravený demonstrační příklad, do něhož byl přidán jeden nový uzel a hrany nyní propojují jednotlivé atributy uzlů typu record:
digraph {
rankdir=LR
a[label="<atribut0>x| <atribut1>y| <atribut2>z"
shape="record"]
b[label="<atributA>α| <atributB>β| <atributC>γ| <atributD>δ"
shape="record"]
c[label="result"]
d[label="error"]
a:atribut0 -> b:atributC;
b:atributA -> c;
b:atributD -> d;
}
Výsledek bude v tomto případě vypadat následovně:
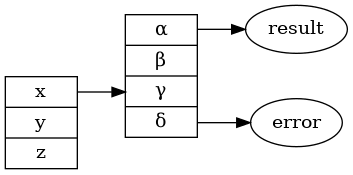
Obrázek 10: Graf, v němž jednotlivé hrany propojují přímo vybrané atributy, ne pouze celé uzly.
7. Tabulky v diagramech
Struktura uzlů může být ve skutečnosti ještě složitější. Relativně nedávno (viz poznámku) totiž byla do Graphvizu přidána možnost zapisovat strukturu uzlů ve formátu, který do značné míry připomíná HTML. To pochopitelně není náhoda, protože nám to umožňuje využít znalostí, které již vývojář má.
Tabulka se opět zapisuje do vlastnosti label a její zápis začíná znakem < a končí znakem >. Mezi touto dvojicí znaků je umístěna celá tabulka – jak již bylo řečeno výše definovaná HTML značkami table, tr, td apod.:
a[label=< <table> <tr><td>x=</td><td>10</td></tr> <tr><td>y=</td><td>20</td></tr> <tr><td>z=</td><td>30</td></tr> </table>>]
Následuje zdrojový kód popisující diagram se třemi uzly, přičemž každý z těchto uzlů obsahuje definici tabulky se dvěma sloupci:
digraph {
rankdir=LR
a[label=<
<table>
<tr><td>x=</td><td>10</td></tr>
<tr><td>y=</td><td>20</td></tr>
<tr><td>z=</td><td>30</td></tr>
</table>>]
b[label=<
<table>
<tr><td>α=</td><td>1</td></tr>
<tr><td>β=</td><td>2</td></tr>
<tr><td>γ=</td><td>3</td></tr>
<tr><td>δ=</td><td>4</td></tr>
<tr><td>ε=</td><td>5</td></tr>
<tr><td>ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table>
<tr><td>result=</td><td>42</td></tr>
</table>>]
a -> b;
b -> c;
}
Výsledek by měl vypadat následovně:
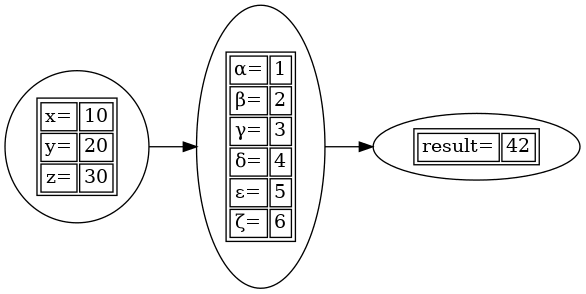
Obrázek 11: Diagram se třemi uzly, přičemž každý z těchto uzlů obsahuje definici tabulky se dvěma sloupci. Uzly mají zachován původní tvar.
8. Odstranění původních tvarů uzlů pro tabulky
Již při letmém pohledu na obrázek číslo 11 je zřejmé, že uzly sice obsahují tabulku, ovšem stále je vykreslen i jejich původní tvar. Ten je vhodné odstranit a ponechat pouze vnitřek uzlu. Tvar všech uzlů v grafu lze změnit globálně, a to konkrétně následujícím způsobem:
node [shape=plain]
Upravený zdrojový kód s definicí grafu tedy může vypadat takto:
digraph {
node [shape=plain]
rankdir=LR
a[label=<
<table>
<tr><td>x=</td><td>10</td></tr>
<tr><td>y=</td><td>20</td></tr>
<tr><td>z=</td><td>30</td></tr>
</table>>]
b[label=<
<table>
<tr><td>α=</td><td>1</td></tr>
<tr><td>β=</td><td>2</td></tr>
<tr><td>γ=</td><td>3</td></tr>
<tr><td>δ=</td><td>4</td></tr>
<tr><td>ε=</td><td>5</td></tr>
<tr><td>ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table>
<tr><td>result=</td><td>42</td></tr>
</table>>]
a -> b;
b -> c;
}
Výsledek vykreslený příkazem dot je již akceptovatelný:
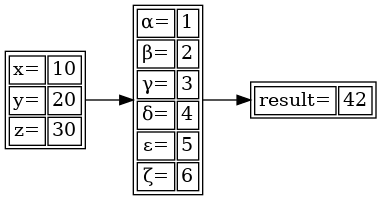
Obrázek 12: Diagram se třemi uzly, přičemž každý z těchto uzlů obsahuje definici tabulky se dvěma sloupci. Původní tvar uzlů je odstraněn.
9. Porty – napojení na konkrétní řádek tabulky
Tabulky se v určitém smyslu podobají uzlům typu record. Platí to i v případě, kdy budeme potřebovat, aby hrany mířily nikoli na celý uzel, ale na konkrétní řádek tabulky (přesněji řečeno na jednotlivou buňku, což je rozdíl). Tento požadavek je řešen s využitím takzvaných portů, které můžeme pro jednoduchost považovat za nový atribut HTML značky td. Příklad specifikace portu u buňky:
<table> <tr><td port="1">x=</td>;<td>10</td></tr> </table>
Hrana, která má začínat u portu či na něj mířit, se definuje takto:
a:1 -> b:3
Opět si pochopitelně ukažme úplný příklad s uzly, které obsahují tabulky s buňkami, u nichž jsou definovány porty:
digraph {
node [shape=plain]
rankdir=LR
a[label=<
<table>
<tr><td port="1">x=</td><td>10</td></tr>
<tr><td port="2">y=</td><td>20</td></tr>
<tr><td port="3">z=</td><td>30</td></tr>
</table>>]
b[label=<
<table>
<tr><td port="1">α=</td><td>1</td></tr>
<tr><td port="2">β=</td><td>2</td></tr>
<tr><td port="3">γ=</td><td>3</td></tr>
<tr><td port="4">δ=</td><td>4</td></tr>
<tr><td port="5">ε=</td><td>5</td></tr>
<tr><td port="6">ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table>
<tr><td>result=</td><td>42</td></tr>
</table>>]
a:1 -> b:3
a:2 -> b:6
a:3 -> b:2
b -> c
}
Graf vykreslený příkazem dot bude nyní vypadat takto:
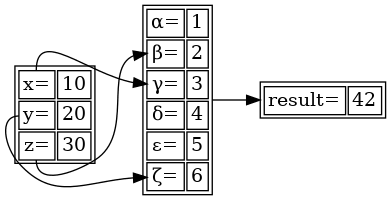
Obrázek 13: Uzel s hranami, které začínají, resp. končí v určitém portu.
10. „Vstupní“ „výstupní“ porty
Ze třináctého obrázku je patrné, že hrany skutečně míří na buňky s definovaným portem, nikoli na celé řádky tabulky. To je ostatně jeden z rozdílů mezi tabulkou a uzlem typu record. Nic nám ovšem nezabraňuje v tom, aby byly porty definovány pro pravé sloupce tabulek a byly tak ze sémantického pohledu nikoli „vstupní“, ale „výstupní“. Provedená změna je naznačena tučným písmem:
digraph {
node [shape=plain]
rankdir=LR
a[label=<
<table>
<tr><td>x=</td><td port="1">10</td></tr>
<tr><td>y=</td><td port="2">20</td></tr>
<tr><td>z=</td><td port="3">30</td></tr>
</table>>]
b[label=<
<table>
<tr><td port="1">α=</td><td>1</td></tr>
<tr><td port="2">β=</td><td>2</td></tr>
<tr><td port="3">γ=</td><td>3</td></tr>
<tr><td port="4">δ=</td><td>4</td></tr>
<tr><td port="5">ε=</td><td>5</td></tr>
<tr><td port="6">ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table>
<tr><td>result=</td><td>42</td></tr>
</table>>]
a:1 -> b:3
a:2 -> b:6
a:3 -> b:2
b -> c
}
Výsledný obrázek by již měl vypadat kultivovaněji:
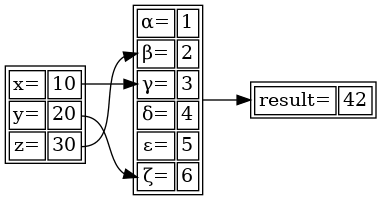
Obrázek 14: Hrany, které míří z „výstupních“ portů na port „vstupní“.
11. Okraje tabulek a jejich buněk
U tabulek, které se zobrazí ve formě obsahu uzlů, je možné specifikovat šířku okrajů okolo tabulky, šířku okrajů okolo jednotlivých buněk i mezery mezi buňkami. Používají se přitom stejné atributy uzlu table, jako je tomu v běžném HTML. Základním atributem je border, kterým se současně určuje šířka okraje tabulky i buněk (pokud není specifikována explicitně). Všechny okraje tedy můžeme zakázat takto:
<table border="0">
Použití v demonstračním příkladu:
digraph {
node [shape=plain]
rankdir=LR
a[label=<
<table border="0">
<tr><td>x=</td><td port="1">10</td></tr>
<tr><td>y=</td><td port="2">20</td></tr>
<tr><td>z=</td><td port="3">30</td></tr>
</table>>]
b[label=<
<table border="0">
<tr><td port="1">α=</td><td>1</td></tr>
<tr><td port="2">β=</td><td>2</td></tr>
<tr><td port="3">γ=</td><td>3</td></tr>
<tr><td port="4">δ=</td><td>4</td></tr>
<tr><td port="5">ε=</td><td>5</td></tr>
<tr><td port="6">ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table border="0">
<tr><td>result=</td><td>42</td></tr>
</table>>]
a:1 -> b:3
a:2 -> b:6
a:3 -> b:2
b -> c
}
Výsledek bude vypadat následovně:
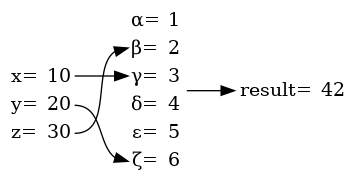
Obrázek 15: Uzly, v nichž jsou zobrazeny tabulky bez okrajů.
Okraje tabulky lze zakázat, ovšem současně je možné specifikovat okraje okolo jednotlivých buněk, což je ukázáno na dalším příkladu:
digraph {
node [shape=plain]
rankdir=LR
a[label=<
<table border="0" cellborder="1">
<tr><td>x=</td><td port="1">10</td></tr>
<tr><td>y=</td><td port="2">20</td></tr>
<tr><td>z=</td><td port="3">30</td></tr>
</table>>]
b[label=<
<table border="0" cellborder="1">
<tr><td port="1">α=</td><td>1</td></tr>
<tr><td port="2">β=</td><td>2</td></tr>
<tr><td port="3">γ=</td><td>3</td></tr>
<tr><td port="4">δ=</td><td>4</td></tr>
<tr><td port="5">ε=</td><td>5</td></tr>
<tr><td port="6">ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table border="0" cellborder="1">
<tr><td>result=</td><td>42</td></tr>
</table>>]
a:1 -> b:3
a:2 -> b:6
a:3 -> b:2
b -> c
}
Výsledný graf bude v tomto případě vypadat odlišně:
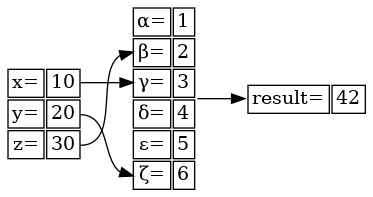
Obrázek 16: Okraje jsou zobrazeny pouze okolo jednotlivých buněk, nikoli okolo celé tabulky.
A konečně můžeme specifikovat (i zakázat) mezery mezi jednotlivými buňkami, a to konkrétně atributem nazvaným cellspacing:
digraph {
node [shape=plain]
rankdir=LR
a[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td>x=</td><td port="1">10</td></tr>
<tr><td>y=</td><td port="2">20</td></tr>
<tr><td>z=</td><td port="3">30</td></tr>
</table>>]
b[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td port="1">α=</td><td>1</td></tr>
<tr><td port="2">β=</td><td>2</td></tr>
<tr><td port="3">γ=</td><td>3</td></tr>
<tr><td port="4">δ=</td><td>4</td></tr>
<tr><td port="5">ε=</td><td>5</td></tr>
<tr><td port="6">ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td>result=</td><td>42</td></tr>
</table>>]
a:1 -> b:3
a:2 -> b:6
a:3 -> b:2
b -> c
}
Opět se podívejme na dosažený výsledek:
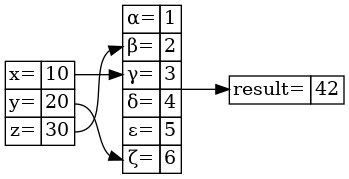
Obrázek 17: Zákaz mezer mezi jednotlivými buňkami.
12. Barevné zvýraznění buněk tabulky
Možnosti, které nám nabízí subrutiny určené pro vykreslení tabulek, jsou ve skutečnosti ještě větší. Například je možné specifikovat barvu výplně jednotlivých buněk tabulky, konkrétně uvedením atributu bgcolor, kterému se předá buď jméno barvy nebo klasický hexa triplet, opět zpopularizovaný právě v HTML a CSS (posléze byl tento koncept použit i v dalších technologiích):
<td port="1" bgcolor="#ff8080">10</td>
Náš předchozí demonstrační příklad nyní upravíme takovým způsobem, že některé buňky tabulky obarvíme, například pro zvýraznění důležitých hodnot:
digraph {
node [shape=plain]
rankdir=LR
a[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td>x=</td><td port="1" bgcolor="#ff8080">10</td></tr>
<tr><td>y=</td><td port="2">20</td></tr>
<tr><td>z=</td><td port="3" bgcolor="#80ff00">-1</td></tr>
</table>>]
b[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td port="1">α=</td><td>1</td></tr>
<tr><td port="2">β=</td><td>2</td></tr>
<tr><td port="3">γ=</td><td>3</td></tr>
<tr><td port="4">δ=</td><td>4</td></tr>
<tr><td port="5">ε=</td><td>5</td></tr>
<tr><td port="6">ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td>result=</td><td bgcolor="#8080ff">42</td></tr>
</table>>]
a:1 -> b:3
a:2 -> b:6
a:3 -> b:2
b -> c
}
Výsledný obrázek s grafem získaný příkazem dot:
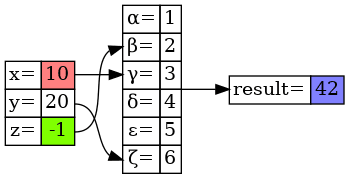
Obrázek 18: Vybrané buňky v tabulkách dvou uzlů jsou zvýrazněny barevným pozadím.
13. Gradientní barevné přechody
V doménově specifickém jazyce nástroje Graphviz dokonce můžeme specifikovat barevné přechody u pozadí okrajů jednotlivých buněk tabulky nebo dokonce i celé tabulky. V tomto případě (který již přesahuje možnosti klasického HTML) je nutné uvést dvě barvy pozadí oddělené dvojtečkou, tedy například:
<td port="3" bgcolor="#80ff00:#ffffff">-1</td>
popř:
<table border="0" cellborder="1" cellspacing="0" bgcolor="yellow:lightblue">
Opět si ukažme způsob použití. Upravíme předchozí demonstrační příklad takovým způsobem, aby se použily lineární (gradientní) barevné přechody:
digraph {
node [shape=plain]
rankdir=LR
a[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td>x=</td><td port="1" bgcolor="#ff8080:#ffffff">10</td></tr>
<tr><td>y=</td><td port="2">20</td></tr>
<tr><td>z=</td><td port="3" bgcolor="#80ff00:#ffffff">-1</td></tr>
</table>>]
b[label=<
<table border="0" cellborder="1" cellspacing="0" bgcolor="yellow:lightblue">
<tr><td port="1">α=</td><td>1</td></tr>
<tr><td port="2">β=</td><td>2</td></tr>
<tr><td port="3">γ=</td><td>3</td></tr>
<tr><td port="4">δ=</td><td>4</td></tr>
<tr><td port="5">ε=</td><td>5</td></tr>
<tr><td port="6">ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td>result=</td><td bgcolor="#8080ff:#ffffff">42</td></tr>
</table>>]
a:1 -> b:3
a:2 -> b:6
a:3 -> b:2
b -> c
}
Výsledek:
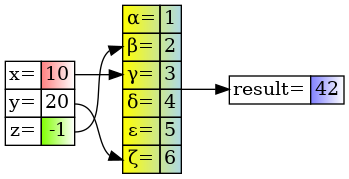
Obrázek 19: Tabulky s gradientními barevnými přechody.
14. Úhel gradientních barevných přechodů
Ve stručnosti ještě doplňme, že úhel gradientních barevných přechodů se specifikuje dalším nestandardním (v HTML neexistujícím) atributem gradientangle. Tento úhel se přitom udává ve stupních tak, jak je to ukázáno v dalším příkladu:
digraph {
node [shape=plain]
rankdir=LR
a[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td>x=</td><td port="1" bgcolor="#ff8080:#ffffff">10</td></tr>
<tr><td>y=</td><td port="2">20</td></tr>
<tr><td>z=</td><td port="3" bgcolor="#80ff00:#ffffff">-1</td></tr>
</table>>]
b[label=<
<table border="0" cellborder="1" cellspacing="0" bgcolor="yellow:lightblue" gradientangle="90">
<tr><td port="1">α=</td><td>1</td></tr>
<tr><td port="2">β=</td><td>2</td></tr>
<tr><td port="3">γ=</td><td>3</td></tr>
<tr><td port="4">δ=</td><td>4</td></tr>
<tr><td port="5">ε=</td><td>5</td></tr>
<tr><td port="6">ζ=</td><td>6</td></tr>
</table>>]
c[label=<
<table border="0" cellborder="1" cellspacing="0">
<tr><td>result=</td><td bgcolor="#8080ff:#ffffff">42</td></tr>
</table>>]
a:1 -> b:3
a:2 -> b:6
a:3 -> b:2
b -> c
}
Výsledkem je nyní tento graf:
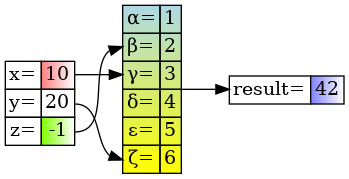
Obrázek 20: Změna úhlu barevných gradientních přechodů.
15. Odstranění podgrafů příkazem prune
Graphviz neobsahuje pouze nástroje určené pro vykreslení grafů. Uživatelům jsou totiž k dispozici i nástroje, jež je možné použít pro dotazy provedené nad grafem (počet uzlů atd.) i nástroje, které grafy určitým způsobem (tedy s použitím specifikovaného algoritmu) modifikují. Příkladem takového nástroje je prune, kterým lze z grafu odstranit vybraný podgraf nebo podgrafy. Podívejme se nyní na způsob volání tohoto příkazu. Začneme s následujícím grafem, jenž obsahuje poměrně velké množství uzlů sdružených do clusterů:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph cluster1 {
rank = same;
style = "filled";
fillcolor = "#80ff80";
a;
a1;
a2;
}
subgraph cluster2 {
rank = same;
style = "filled";
fillcolor = "#80ffff";
b;
b1;
b2;
}
subgraph cluster3 {
rank = same;
style = "filled";
fillcolor = "#8080ff";
c;
c1;
c2;
}
subgraph cluster4 {
rank = same;
style = "filled";
fillcolor = "#ff80ff";
d;
d1;
d2;
}
subgraph cluster5 {
rank = same;
style = "filled";
fillcolor = "#ff8080";
e;
e1;
e2;
}
subgraph cluster6 {
rank = same;
style = "filled";
fillcolor = "#ffff80";
f;
f1;
f2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Tento graf vypadá následovně:
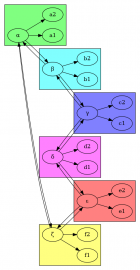
Obrázek 21: Původní graf před úpravou.
Dále příkazem prune odstraníme uzel nazvaný „b“, přičemž další dotčené uzly nebo clustery budou mít červený okraj (nepovinný parametr N). Výsledkem je nový soubor popisující graf v jazyku dot:
$ prune -n b -N color=red path1.dot >path2_.dot
Tento nový graf bude upravenou podobou grafu předchozího:
digraph {
graph [rankdir=LR];
subgraph cluster1 {
graph [fillcolor="#80ff80",
rank=same,
style=filled
];
a [label="α"];
a1;
a2;
}
subgraph cluster2 {
graph [fillcolor="#80ffff",
rank=same,
style=filled
];
b [color=red,
label="β"];
}
subgraph cluster3 {
graph [fillcolor="#8080ff",
rank=same,
style=filled
];
c [label="γ"];
c1;
c2;
}
subgraph cluster4 {
graph [fillcolor="#ff80ff",
rank=same,
style=filled
];
d [label="δ"];
d1;
d2;
}
subgraph cluster5 {
graph [fillcolor="#ff8080",
rank=same,
style=filled
];
e [label="ε"];
e1;
e2;
}
subgraph cluster6 {
graph [fillcolor="#ffff80",
rank=same,
style=filled
];
f [label="ζ"];
f1;
f2;
}
a -> b;
a -> f;
a -> a1;
a -> a2;
c -> b;
c -> d;
c -> c1;
c -> c2;
d -> c;
d -> e;
d -> d1;
d -> d2;
e -> d;
e -> f;
e -> e1;
e -> e2;
f -> a;
f -> e;
f -> f1;
f -> f2;
}
Po vykreslení příkazem dot bude upravený graf vypadat následovně:
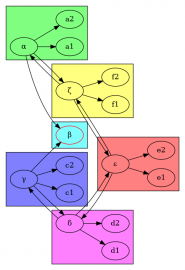
Obrázek 22: Nový graf po odstranění uzlu b.
16. Podpora jazyka DOT v dalších nástrojích
Jazyk DOT (graph description language) je podporován nikoli pouze sadou nástrojů Graphviz, ale i některými dalšími aplikacemi. Především se jedná o jednoúčelové (a z pohledu uživatelského rozhraní i poněkud zastaralé) grafické editory lefty a dotty, které se již staly součástí instalace Graphvizu. Tento jazyk je však využíván i složitějšími nástroji, například aplikací Gephi (the open graph viz platform), knihovnou Canviz pro JavaScript atd. Mezi vektorové editory, které jazyk DOT podporují, patří i nástroj xfig, jenž patří mezi „pravěké“ unixové aplikace – jeho první verze totiž vyšla již v roce 1985! I přesto může pro některé účely dobře sloužit dodnes – například právě pro úpravu souborů DOT, které nebývají v dalších vektorových editorech přímo podporovány.
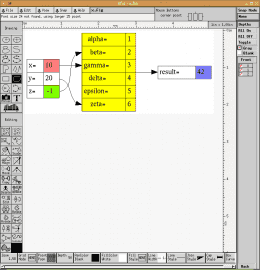
Obrázek 23:
xfig je většinou dostupný ve formě balíčku pro běžné Linuxové distribuce, takže ho lze nainstalovat i dnes na moderní desktop:
$ sudo dnf install xfig Last metadata expiration check: 3:00:37 ago on Fri 11 Jun 2021 02:25:12 PM CEST. Dependencies resolved. ================================================================================ Package Arch Version Repository Size ================================================================================ Installing: xfig x86_64 3.2.6a-7.fc30 updates 5.4 M Installing dependencies: Xaw3d x86_64 1.6.2-12.fc30 fedora 177 k xorg-x11-fonts-100dpi noarch 7.5-18.fc30 fedora 3.1 M Transaction Summary ================================================================================ Install 3 Packages Total download size: 8.7 M Installed size: 18 M Is this ok [y/N]:
Součástí instalace xfigu jsou i manuálové stránky vytvořené v HTML:
Obrázek 24: Manuálové stránky, které jsou součástí instalace xfigu.
Specifikace diagramů vytvořené v jazyku DOT jsou přímo importovatelné a editovatelné, což je patrné i z následujícího screenshotu:
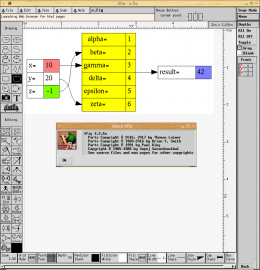
Obrázek 25: Importovaná specifikace diagramu vytvořená v jazyku DOT. Současně je zobrazen dialog s informacemi o autorech xfigu, a to včetně jeho historické verze.
17. Ukázka některých možnosti xfigu
Vektorový editor xfig patří do kategorie aplikací ze „staré školy“, podobně jako například Autodesk Animator – oba nástroje nabízí poměrně velké množství funkcí dostupných přes grafické uživatelské rozhraní, které je však v porovnání s dnešními aplikacemi velmi úsporné a tím pádem i poněkud nepřehledné. K tomu připočtěme nestandardní použití tlačítek myši, které došlo tak daleko, že xfig stále nabízí nápovědu k jednotlivým tlačítkům (pravý horní roh). Některé vlastnosti xfigu jsou ukázány na následujících screenshotech.
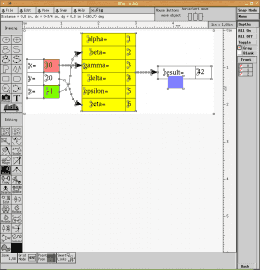
Obrázek 26: Jednotlivé části diagramu jsou dostupné jako plnohodnotné editovatelné vektorové objekty. Zajímavé je, že pozadí buněk tabulky je reprezentováno odděleně od okraje tabulky.
Obrázek 27: Možnosti exportu vektorové kresby jsou velmi široké. Kromě doposud používaných formátů zde nalezneme i vyloženě historické formáty typu „slide“ z AutoCADu, rastrový formát PCX atd.
Obrázek 28: Nastavení vlastností kreslicího „pera“, včetně podpory pro vlastní barvovou paletu.
Obrázek 29: Další typický dialog ze staré školy – editace polyčáry (lomené čáry, popř. polygonu).
18. Repositář s demonstračními příklady
Zdrojové kódy všech dnes i minule použitých demonstračních příkladů byly uloženy do nového Git repositáře, který je dostupný na adrese https://github.com/tisnik/diagrams (stále na GitHubu :-). V případě, že nebudete chtít klonovat celý repositář (ten je ovšem – alespoň prozatím – velmi malý, dnes má přibližně jednotky kilobajtů), můžete namísto toho použít odkazy na jednotlivé demonstrační příklady, které naleznete v následující tabulce:
19. Odkazy na články s tématem programové tvorby grafů a diagramů
V této kapitole jsou uvedeny odkazy na předchozí články, v nichž jsme se zabývali tvorbou různých typů grafů a diagramů – a to v naprosté většině případů s využitím nějakého doménově specifického jazyka neboli DSL (Domain Specific Language), popř. nějakého univerzálního programovacího jazyka (zejména Python, Go, Clojure):
- Nástroje pro tvorbu UML diagramů
https://www.root.cz/clanky/nastroje-pro-tvorbu-uml-diagramu/ - Nástroje pro tvorbu UML diagramů z příkazové řádky
https://www.root.cz/clanky/nastroje-pro-tvorbu-uml-diagramu-z-prikazove-radky/ - Nástroje pro tvorbu UML diagramů z příkazové řádky (II)
https://www.root.cz/clanky/nastroje-pro-tvorbu-uml-diagramu-z-prikazove-radky-ii/ - Nástroje pro tvorbu grafů a diagramů z příkazové řádky
https://www.root.cz/clanky/nastroje-pro-tvorbu-grafu-a-diagramu-z-prikazove-radky/ - Sledování správy paměti v Pythonu s využitím nástroje objgraph
https://www.root.cz/clanky/sledovani-spravy-pameti-v-pythonu-s-vyuzitim-nastroje-objgraph/ - Programová tvorba diagramů v jazyku Clojure s využitím knihovny Rhizome
https://www.root.cz/clanky/programova-tvorba-diagramu-v-jazyku-clojure-s-vyuzitim-knihovny-rhizome/ - Tvorba sekvenčních diagramů v Pythonu s využitím knihovny Napkin
https://www.root.cz/clanky/tvorba-sekvencnich-diagramu-v-pythonu-s-vyuzitim-knihovny-napkin/ - Tvorba vývojových diagramů přímo ze zdrojových kódů Pythonu
https://www.root.cz/clanky/tvorba-vyvojovych-diagramu-primo-ze-zdrojovych-kodu-pythonu/ - Tvorba diagramů s architekturou systémů s využitím knihovny Diagrams
https://www.root.cz/clanky/tvorba-diagramu-s-architekturou-systemu-s-vyuzitim-knihovny-diagrams/ - Knihovny Diagrams a go-diagrams určené pro tvorbu diagramů s architekturou systémů
https://www.root.cz/clanky/knihovny-diagrams-a-go-diagrams-urcene-pro-tvorbu-diagramu-s-architekturou-systemu/ - Tvorba grafů a diagramů s využitím doménově specifického jazyka nástroje Graphviz
https://www.root.cz/clanky/tvorba-grafu-a-diagramu-s-vyuzitim-domenove-specifickeho-jazyka-nastroje-graphviz/ - Tvorba grafů a diagramů s využitím doménově specifického jazyka nástroje Graphviz (2.část)
https://www.root.cz/clanky/tvorba-grafu-a-diagramu-s-vyuzitim-domenove-specifickeho-jazyka-nastroje-graphviz-2-cast/
20. Odkazy na Internetu
- GraphViz Pocket Reference
https://graphs.grevian.org/example - Xfig home page
http://mcj.sourceforge.net/ - Xfig (Wikipedia)
https://en.wikipedia.org/wiki/Xfig - Xfig user manual
http://mcj.sourceforge.net/ - HTML Entity List
https://www.freeformatter.com/html-entities.html - Flowchart (Wikipedia)
https://en.wikipedia.org/wiki/Flowchart - DRAKON
https://en.wikipedia.org/wiki/DRAKON - Modeling language
https://en.wikipedia.org/wiki/Modeling_language - Napkin na GitHubu
https://github.com/pinetr2e/napkin - Napkin 0.6.8 na PyPi
https://pypi.org/project/napkin/ - PlantUML (home page)
http://plantuml.sourceforge.net/ - PlantUML (download page)
http://sourceforge.net/projects/plantuml/files/plantuml.jar/download - PlantUML (Language Reference Guide)
http://plantuml.sourceforge.net/PlantUML_Language_Reference_Guide.pdf - Rhizome
https://github.com/ztellman/rhizome - Swagger to UML
https://github.com/nlohmann/swagger_to_uml - pydiagrams
https://github.com/billingtonm/pydiagrams - graphviz(3) – Linux man page
https://linux.die.net/man/3/graphviz - dot(1) – Linux man page
https://linux.die.net/man/1/dot - neato(1) – Linux man page
https://linux.die.net/man/1/neato - twopi(1) – Linux man page
https://linux.die.net/man/1/twopi - circo(1) – Linux man page
https://linux.die.net/man/1/circo - fdp(1) – Linux man page
https://linux.die.net/man/1/fdp - sfdp(1) – Linux man page
https://linux.die.net/man/1/sfdp - Plain-text diagrams take shape in Asciidoctor!
http://asciidoctor.org/news/2014/02/18/plain-text-diagrams-in-asciidoctor/ - Graphviz – Graph Visualization Software
http://www.graphviz.org/ - graphviz (Manual Page)
http://www.root.cz/man/7/graphviz/ - dot (Manual page)
http://www.root.cz/man/1/dot/ - dot (Manual v PDF)
https://graphviz.org/pdf/dot.1.pdf - Ditaa home page
http://ditaa.sourceforge.net/ - Ditaa introduction
http://ditaa.sourceforge.net/#intro - Ditaa usage
http://ditaa.sourceforge.net/#usage - Node, Edge and Graph Attributes
http://www.graphviz.org/doc/info/attrs.html - Graphviz (Wikipedia)
http://en.wikipedia.org/wiki/Graphviz - Unified Modeling Language
https://en.wikipedia.org/wiki/Unified_Modeling_Language - UML basics: The sequence diagram
http://www.ibm.com/developerworks/rational/library/3101.html - UML 2 State Machine Diagrams: An Agile Introduction
http://www.agilemodeling.com/artifacts/stateMachineDiagram.htm - Sequence diagram (Wikipedia)
https://en.wikipedia.org/wiki/Sequence_diagram - UML 2 Sequence Diagrams: An Agile Introduction
http://www.agilemodeling.com/artifacts/sequenceDiagram.htm - A Quick Introduction to UML Sequence Diagrams
http://www.tracemodeler.com/articles/a_quick_introduction_to_uml_sequence_diagrams/ - UML Sequence Diagrams
https://www.uml-diagrams.org/sequence-diagrams.html - Web Sequence Diagrams
https://www.websequencediagrams.com/ - Drawing sequence diagrams “napkin style”
https://modeling-languages.com/drawing-sequence-diagrams-napkin-style/ - Curated list of UML tools – 2020 edition
https://modeling-languages.com/uml-tools/#textual - Flowchart diagrams vs. UML activity diagrams
https://stackoverflow.com/questions/7081215/flowchart-diagrams-vs-uml-activity-diagrams - Kopenograms – Graphical Language for Structured Algorithms
https://kopenogram.org/Assets/Kopenograms_Graphical_Language_for_Structured_Algorithms.pdf - Kopenograms and Their Implementation in BlueJ
https://link.springer.com/chapter/10.1007%2F978–3–319–46535–7_8 - The simplest way to describe your flows
https://code2flow.com/ - Allan Mogensen and his Legacy
http://www.worksimp.com/articles/allan-mogensen.htm - Diagrams: Diagram as Code
https://diagrams.mingrammer.com/ - Diagrams: Guides
https://diagrams.mingrammer.com/docs/guides/diagram - Diagrams: Nodes
https://diagrams.mingrammer.com/docs/nodes/onprem - go-diagrams
https://github.com/blushft/go-diagrams - GoJS
https://gojs.net/latest/index.html - Code visualization: How to turn complex code into diagrams
https://www.lucidchart.com/blog/visualize-code-documentation - Create dependency diagrams from your code
https://docs.microsoft.com/en-us/visualstudio/modeling/create-layer-diagrams-from-your-code?view=vs-2019 - Software Architecture Diagrams as Code
https://shekhargulati.com/2020/04/21/software-architecture-diagrams-as-code/ - Processing spreadsheet data in Go
https://appliedgo.net/spreadsheet/ - Stránka projektu plotly
https://plot.ly/ - Plotly JavaScript Open Source Graphing Library
https://plot.ly/javascript/ - Domain coloring
https://en.wikipedia.org/wiki/Domain_coloring - The Gonum Numerical Computing Package
https://www.gonum.org/post/introtogonum/ - Gomacro na GitHubu
https://github.com/cosmos72/gomacro - gophernotes – Use Go in Jupyter notebooks and nteract
https://github.com/gopherdata/gophernotes - gonum
https://github.com/gonum - go-gota/gota – DataFrames and data wrangling in Go (Golang)
https://porter.io/github.com/go-gota/gota - A repository for plotting and visualizing data
https://github.com/gonum/plot - Gonum Numerical Packages
https://www.gonum.org/ - Getting started with Go modules
https://medium.com/@fonseka.live/getting-started-with-go-modules-b3dac652066d - Create projects independent of $GOPATH using Go Modules
https://medium.com/mindorks/create-projects-independent-of-gopath-using-go-modules-802260cdfb51o - Anatomy of Modules in Go
https://medium.com/rungo/anatomy-of-modules-in-go-c8274d215c16 - Modules
https://github.com/golang/go/wiki/Modules - Go Modules Tutorial
https://tutorialedge.net/golang/go-modules-tutorial/ - Module support
https://golang.org/cmd/go/#hdr-Module_support - Go vs. Python
https://www.peterbe.com/plog/govspy - PackageManagementTools
https://github.com/golang/go/wiki/PackageManagementTools - Sketchviz
https://sketchviz.com/ - SchemaSpy (verze pro starší JVM)
http://schemaspy.sourceforge.net/ - SchemaSpy na GitHubu
https://github.com/schemaspy/schemaspy - Table Relationship Diagrams with Graphviz
https://spin.atomicobject.com/2017/11/15/table-rel-diagrams-graphviz/ - HTML-Like Labels
https://www.graphviz.org/doc/info/shapes.html#html - Grafický formát PCX – výlet do historie PC
https://www.root.cz/clanky/graficky-format-pcx-vylet-do-historie-pc/


























